531平行线的性质同步练习题

合集下载

2022-2023学年人教版七年级数学下册《5-3平行线的性质》同步练习题(附答案)

2022-2023学年人教版七年级数学下册《5.3平行线的性质》同步练习题（附答案）一．选择题1．如图，AB∥EC，则下列结论正确的是（）A．∠A＝∠ECD B．∠A＝∠ACE C．∠B＝∠ACE D．∠B＝∠ACB 2．如图，已知AB∥EF，DE∥BC，则与∠1相等的角有（）A．1个B．2个C．3个D．4个3．已知直线m∥n，将一块含30°角的直角三角板ABC按如图方式放置（∠ABC＝30°），其中A，B两点分别落在直线m，n上，若∠1＝20°，则∠2的度数为（）A．20°B．30°C．45°D．50°4．如图，在△ABC中，∠ACB＝90°，CD∥AB，∠ACD＝40°，则∠B的度数为（）A．40°B．50°C．60°D．70°5．如图，直线a∥b，直线c与a、b相交，∠1＝55°，则∠2＝（）6．如图，将矩形ABCD沿GH折叠，点C落在点Q处，点D落在AB边上的点E处，若∠AGE＝32°，则∠GHC等于（）A．112°B．110°C．108°D．106°7．如图，直线a，b，a∥b，点C在直线b上，∠DCB＝90°，若∠1＝70°，则∠2的度数为（）A．20°B．25°C．30°D．40°8．如图，一条公路修到湖边时，需拐弯绕湖而过，如果第一次拐弯处的∠A是66°，第二次拐弯处的角是∠B，第三次拐弯处的∠C是153°，这时道路恰好和第一次拐弯之前的道路平行，则∠B是（）A．87°B．93°C．39°D．109°9．一艘轮船从A港出发，沿着北偏东63°的方向航行，行驶至B处时发现前方有暗礁，所以转向北偏西27°方向航行，到达C后需要把航向恢复到出发时的航向，此时轮船航行的航向向顺时针方向转过的度数为（）10．一把直尺与一块直角三角板按如图方式摆放，若∠1＝47°，则∠2＝（）A．40°B．43°C．45°D．47°二．填空题（共6小题）11．如图，已知AB∥CD，CE平分∠ACD，交AB于点B，∠ABE＝150°，则∠A为．12．如图，AB∥DE，FC⊥CD于点C，∠ABC＝107°，∠CDE＝130°，点G在BC的延长线上，则∠FCG的度数是．13．如图，直线a∥b，直线c与直线a，b分别交于点A，B．若∠1＝45°，则∠2＝．14．如图，直线a∥b，一块含60°角的直角三角板ABC（∠A＝60°），按如图所示放置，若∠1＝55°，则∠2的度数为．15．如图，已知l1∥l2，直线l与l1、l2相交于C、D两点，把一块含30°角的三角尺按如图位置摆放．若∠1＝130°，则∠2＝．16．如图1是我们常用的折叠式小刀，图2中刀柄外形是一个矩形挖去一个小半圆，其中刀片的两条边缘线可看成两条平行的线段，转动刀片时会形成如图2所示的∠1与∠2，则∠1与∠2的度数和是度．三．解答题（共6小题）17．如图：已知AB∥DE∥CF，若∠ABC＝70°，∠CDE＝130°，求∠BCD的度数．18．如图，MN∥BC，BD⊥DC，∠1＝∠2＝60°．（1）AB与DE平行吗？请说明理由；（2）若DC是∠NDE的平分线．①试说明∠ABC＝∠C；②试说明BD是∠ABC的平分线．19．如图所示，已知AB∥CD，分别探讨下面四个图形中，∠APC，∠P AB与∠PCD的关系．20．如图所示，直线a∥b，AC丄AB，AC交直线b于点C，∠1＝60°，求∠2的度数．21．如图，∠BAP+∠APD＝180°，∠1＝∠2，求证：∠E＝∠F．22．如图，已知AB∥ED，∠C＝90°，∠ABC＝∠DEF，∠D＝130°，∠F＝100°，求∠E的大小．参考答案一．选择题1．解：∵AB∥EC，∴∠A＝∠ACE，∠B＝∠ECD．故选：B．2．解：如图所示，与∠1相等的角有∠B、∠DEF、∠EFC共3个，故选：C．3．解：∵直线m∥n，∴∠2＝∠ABC+∠1＝30°+20°＝50°，故选：D．4．解：∵CD∥AB，∠ACD＝40°，∴∠A＝∠ACD＝40°，∵在△ABC中，∠ACB＝90°，∴∠B＝90°﹣∠A＝50°．故选：B．5．解：∵a∥b，∴∠1＝∠3，∵∠1＝55°，∴∠3＝55°，又∵∠2＝∠3，∴∠2＝55°，故选：A．6．解：∵∠AGE＝32°，∴∠DGE＝148°，由折叠可得，∠DGH＝∠DGE＝74°，∵AD∥BC，∴∠GHC＝180°﹣∠DGH＝106°，故选：D．7．解：∵∠1＝70°，∠1与∠3是对顶角，∴∠3＝∠1＝70°．∵a∥b，点C在直线b上，∠DCB＝90°，∴∠2+∠DCB+∠3＝180°，∴∠2＝180°﹣∠3﹣∠DCB＝180°﹣70°﹣90°＝20°．故选：A．8．解：如图：过B作直线b平行于拐弯之前的道路a，由平行线的传递性得a∥b∥c，∵a∥b，∴∠A＝∠1＝66°，∵b∥c，∴∠2＝180°﹣∠C＝180°﹣153°＝27°，∴∠ABC＝∠1+∠2＝66°+27°＝93°．故选：B．9．解：根据题意，得AE∥BF，AM∥CN；∠A＝63°，∠FBC＝27°．∵AE∥BF，∴∠1＝∠A＝63°．∵AM∥CN，∴∠DCN＝∠DBM＝∠1+∠FBC＝63°+27°＝90°．故选：C．10．解：方法1：如图，∵∠1＝47°，∠4＝45°，∴∠3＝∠1+∠4＝92°，∵矩形对边平行，∴∠5＝∠3＝92°，∵∠6＝45°，∴∠2＝180°﹣45°﹣92°＝43°．方法2：如图，作矩形两边的平行线，∵矩形对边平行，∴∠3＝∠1＝47°，∵∠3+∠4＝90°，∴∠4＝90°﹣47°＝43°∴∠2＝∠4＝43°．故选：B．二．填空题11．解：∠ABC＝180°﹣∠ABE＝180°﹣150°＝30．∵AB∥CD，∴∠BCD＝∠ABC＝30°．∵CE平分∠ACD，∴∠ACD＝2∠BCD＝60°．∴∠A＝180°﹣∠ACD＝180°﹣60°＝120°．故答案为：120°．12．解：过点C作CH∥AB∴∠GCH＝∠ABC＝107°∴∠HCD+∠CDE＝180°∴∠HCD＝180°﹣130°＝50°∴∠GCD＝∠GCH﹣∠HCD＝107°﹣50°＝57°∴∠FCG＝90°﹣57°＝33°．故答案为33°．13．解：∵直线a∥b，∠1＝45°，∴∠3＝45°，∴∠2＝180°﹣45°＝135°．故答案为：135°．14．解：∵∠1＝55°，∠A＝60°，∴∠3＝∠4＝65°，∵a∥b，∴∠4+∠2＝180°，∴∠2＝115°．故答案为：115°．15．解：∵∠1＝130°，∴∠3＝50°，又∵l1∥l2，∴∠BDC＝50°，又∵∠ADB＝30°，∴∠2＝20°，故答案为：20°．16．解：如图2，AB∥CD，∠AEC＝90°，作EF∥AB，则EF∥CD，所以∠1＝∠AEF，∠2＝∠CEF，所以∠1+∠2＝∠AEF+∠CEF＝∠AEC＝90°．故答案为90．三．解答题17．解：∵AB∥CF，∠ABC＝70°，∴∠BCF＝∠ABC＝70°，又∵DE∥CF，∠CDE＝130°，∴∠DCF+∠CDE＝180°，∴∠DCF＝50°，∴∠BCD＝∠BCF﹣∠DCF＝70°﹣50°＝20°．18．解：（1）AB∥DE，理由如下：∵MN∥BC，（已知）∴∠ABC＝∠1＝60°．（两直线平行，内错角相等）又∵∠1＝∠2，（已知）∴∠ABC＝∠2．（等量代换）∴AB∥DE．（同位角相等，两直线平行）；（2）①∵MN∥BC，∴∠NDE+∠2＝180°，∴∠NDE＝180°﹣∠2＝180°﹣60°＝120°．∵DC是∠NDE的平分线，∴∠EDC＝∠NDC＝∠NDE＝60°．∵MN∥BC，∴∠C＝∠NDC＝60°．∴∠ABC＝∠C．②∠ADC＝180°﹣∠NDC＝180°﹣60°＝120°，∵BD⊥DC，∴∠BDC＝90°．∴∠ADB＝∠ADC﹣∠BDC＝120°﹣90°＝30°．∵MN∥BC，∴∠DBC＝∠ADB＝30°．∴∠ABD＝∠DBC＝∠ABC．∴BD是∠ABC的平分线．19．解：图1：∠APC＝∠P AB+∠PCD．理由：过点P作PE∥AB，∵AB∥CD，∴AB∥PE∥CD（平行线的传递性），∴∠1＝∠A，∠2＝∠C，∴∠APC＝∠1+∠2＝∠P AB+∠PCD，即∠APC＝∠P AB+∠PCD；图2：∠APC+∠P AB+∠PCD＝360°．理由：过点P作PE∥AB．∵AB∥CD，∴AB∥PE∥CD（平行线的传递性），∴∠A+∠1＝180°，∠2+∠C＝180°，∴∠A+∠1+∠2+∠C＝360°，∴∠APC+∠P AB+∠PCD＝360°；图3：∠APC＝∠PCD﹣∠P AB．理由：延长DC交AP于点E．∵AB∥CD，∴∠1＝∠P AB（两直线平行，同位角相等）；又∵∠PCD＝∠1+∠APC，∴∠APC＝∠PCD﹣∠P AB；图4：∴∠P AB＝∠APC+∠PCD．理由：∵AB∥CD，∴∠1＝∠P AB（两直线平行，内错角相等）；又∵∠1＝∠APC+∠PCD，∴∠P AB＝∠APC+∠PCD．20．解：∵AC丄AB，∴∠BAC＝90°，∵∠1＝60°，∴∠B＝180°﹣∠1﹣∠BAC＝30°，∵a∥b，∴∠2＝∠B＝30°．21．证明：∵∠BAP+∠APD＝180°（已知），∴AB∥CD（同旁内角互补，两直线平行）．∴∠BAP＝∠APC（两直线平行，内错角相等）．又∵∠1＝∠2（已知），∴∠FP A＝∠EAP，∴AE∥PF（内错角相等，两直线平行）．∴∠E＝∠F（两直线平行，内错角相等）．22．解：延长DC、AB交于G，∵ED∥AB，∠D＝130°，∴∠G＝50°，又∵∠BCD＝90°，∠BCD＝∠G+∠CBG，∴∠CBG＝40°，∴∠ABC＝140°，∴∠E＝∠ABC＝140°．。

人教版七年级数学下册 5.3 平行线的性质同步测试题(有答案)

5.3 平行线的性质同步测试题班级：_____________姓名：_____________一、选择题（本题共计8 小题，每题3 分，共计24分）1. 如图，AB // CD // EF，AF // CG，则图中与∠A（不包括∠A）相等的角有（）A.1个B.2个C.3个D.4个2. 如图所示，过点P画直线a的平行线b的作法的依据是（）A.两直线平行，同位角相等B.同位角相等，两直线平行C.两直线平行，内错角相等D.内错角相等，两直线平行3. 下列命题中错误的是()A.任何一个命题都有逆命题B.一个真命题的逆命题可能是真命题C.一个定理不一定有逆定理D.任何一个定理都没有逆定理4. 师范大学学生张丽、王云、李玲三人一起去银行柜员机取钱，张丽取款一次，王云取款两次，李玲取款三次，假设每取款一次所用时间相同，请问她们三人按什么样的顺序取款，才能使三人所花总时间最少（包括等待时间）（）A.张丽，王云，李玲B.李玲，张丽，王云C.张丽，李玲，王云D.王云，李玲，张丽5. 甲、乙、丙三人用擂台赛形式进行训练．每局两人单打比赛，另一人当裁判．每一局输者当下一局的裁判，而原来的裁判与赢者比赛．一天训练结束时，统计甲共打12局，乙共打21局，而丙共当裁判8局．那么整个比赛中第10局的输者（）A.必是甲B.必是乙C.必是丙D.不能确定6. 如图，直线l // m，将含有45∘角的三角形板ABC的直角顶点C放在直线m上，若∠1=20∘，则∠2的度数为()A.20∘B.25∘C.30∘D.35∘7. 下列语句是命题的是()A.对角线相等吗？B.作线段AB=10cmC.若a=b，则−a=−bD.连接A，B两点8. 下列句子是命题的是()A.求1+2+3+4+5+6的值B.过点P作PC//OAC. 能根据等式的性质解方程吗D. 房屋顶棚是彩钢做的二、填空题（本题共计9 小题，每题3 分，共计27分）9. 如图，a // b，∠1+∠2=70∘，则∠3+∠4=________∘．10. 如图，若l1 // l2，∠1=50∘，则∠2=________∘．11. 如图，直线a // b，将三角尺的直角顶点放在直线b上，∠1=35∘，则∠2=________．12. 如图，直线a // b，三角板的直角顶点A落在直线a上，两条直角边分别交直线b于B，C两点．若∠1=50∘，则∠2的度数是________∘．13. 写出命题“角平分线上的点到这个角两边的距离相等”的逆命题是________．14. 把“对顶角相等”改写成“如果…，那么…”的形式是________，________，是________命题．15. 将“等角的余角相等”改写成“如果……，那么……”的形式________16. 命题“两个锐角的和是钝角”是________命题(填“真”或“假”).17. 如图，直线AB // CD，BC平分∠ABD，∠1＝65∘，求∠2的度数________．三、解答题（本题共计7 小题，共计69分）18. 如图，AB // CD，点P在AB，CD内部，则∠B，∠D，∠BPD之间有何数量关系？证明你的结论19. 已知如图：AD // BC，E、F分别在DC、AB延长线上.∠DCB=∠DAB，AE⊥EF，∠DEA=30∘.（1）求证：DC//AB.（2）求∠AFE的大小20. 如图，已知：AB // CD，不添加辅助线，试再添加一个条件，使∠1=∠2成立．(1)写出两个合适的条件；(2)选择其中一个加以证明．21. 已知：如图，△ABC中，AD⊥BC于点D，点E在AB上，EF⊥BC于点F，∠1=∠2，求证：DE // AC．22. 已知AB // DE，∠B=60∘，且CM平分∠DCB，CM⊥CN，垂足为C，求∠NCE的度数．23. 如图所示，△ADF和△BCE中，∠A=∠B，点D，E，F，C在同一条直线上，有如下三个关系式：①AD=BC；①DE=CF；①BE // AF.(1)请你用其中两个关系式作为条件，另一个作为结论，写出一个你认为正确的命题；（用序号写出命题的书写形式，如：如果⊗⊗，那么⊗）(2)说明你写的一个命题的正确性．24. 如图，已知AM // BN，∠A＝60∘．点P是射线AM上一动点（与点A不重合），BC、BD分别平分∠ABP 和∠PBN，分别交射线AM于点C，D．（1）①∠________的度数是________；①① ________ // ________，① ∠________＝∠________；（2）求∠CBD的度数；（3）当点P运动时，∠APB与∠ADB之间的数量关系是否随之发生变化？若不变化，请写出它们之间的关系，并说明理由；若变化，请写出变化规律．参考答案一、选择题（本题共计8 小题，每题 3 分，共计24分）1.【答案】D【解答】解：ABICD，∠A=∠ADCABIIEF，∴ A=∠AFEAFCGEE=∠AFE=E=：CDIEF，加EGC=∠DCG=∠A所以与2A相等的角有∠ADC.∠AFE,∠EGC.2GCD四个，故选：D2.【答案】D【解答】解：如图所示，根据图中直线a、b被c所截形成的内错角相等，可得依据为内错角相等，两直线平行．故选D3.【答案】D【解答】解：A、任何一个命题都有逆命题，所以A选项的说法正确；B、一个真命题的逆命题可能是真命题，也可能为假命题，所以B选项的说法正确；C、一个定理不一定有逆定理，所以C选项的说法正确；D、有的定理有逆定理，有的定理不一定有逆定理，所以D选项的说法错误．故选D．4.【答案】A【解答】解：设取款一次时间为t，根据题意可得出ABCD四种取款相对取款时间及等待时间之和，则：A、张丽，王云，李玲，张丽取款时间为t，王云等待时间为t、取款时间为2t，李玲等待时间为2t、取款时间为3t，即总时间为：t+t+2t+2t+3t=9t；B、李玲，张丽，王云，李玲取款时间为3t，张丽等待时间为3t、取款时间为t，王云等待时间为t、取款时间为2t，即总时间为：3t+3t+t+t+2t=10t；C、张丽，李玲，王云，张丽取款时间为t，李玲等待时间为t、取款时间为3t，王云等待时间为3t、取款时间为2t，即总时间为：t+t+3t+3t+2t=10t；D、王云，李玲，张丽，王云取款时间为2t，李玲等待时间为2t、取款时间为3t，张丽等待时间为3t、取款时间为t，即总时间为：2t+2t3t+3t+t=11t；所以按A、张丽，王云，李玲顺序取款才能使三人所花总时间最少（包括等待时间）；故选：A．5.【答案】A【解答】解：根据题意，知丙共当裁判8局，所以甲乙之间共有8局比赛，又甲共打了12局，乙共打了21局，所以甲和丙打了4局，乙和丙打了13局，三个人之间总共打了(8+4+13)=25局，考查甲，总共打了12局，当了13次裁判，所以他输了12次．所以当n是偶数时，第n局比赛的输方为甲，从而整个比赛的第10局的输方必是甲．故选：A．6.【答案】B【解答】解：如图，过点B作BD // l，① 直线l // m，① BD // l // m，① ∠3=∠1=20∘，① △ABC是有一个角是45∘的直角三角板，① ∠4=45∘−∠3=45∘−24∘=25∘，① ∠2=∠4=25∘．故选B．7.【答案】C【解答】解：A，对角线相等吗？是疑问句，不符合命题的定义，不是命题；B，作线段AB=10cm，这是作图语言，不符合命题的定义，不是命题；C，若a=b，则−a=−b符合命题的定义，是命题；D，连接A，B两点，这是作图语言，不符合命题的定义，不是命题.故选C.8.【答案】D【解答】解：A，求1+2+3+4+5+6的值，不是命题，故A错误；B，过点P作PC//OA，不是命题，故B错误；C，能根据等式的性质解方程吗，不是命题，故C错误；D，房屋顶棚是彩钢做的，是命题，故D正确.故选D.二、填空题（本题共计9 小题，每题 3 分，共计27分）9.【答案】110【解答】解：如图，① a // b，① ∠3=∠5．① ∠1+∠2=70∘，① ∠6=110∘，① ∠3+∠4=∠4+∠5=∠6=110∘.故答案为：110．10.【答案】130【解答】解：① l1 // l2，∠1=50∘，① ∠2=180∘−∠1=180∘−50∘=130∘，故答案为：130．11.【答案】55∘【解答】解：如图，① ∠1=35∘，① ∠3=180∘−35∘−90∘=55∘，① a // b，① ∠2=∠3=55∘．故答案为：55∘．12.【答案】40【解答】解：如图：① ∠BAC=90∘，∠1=50∘，① ∠3=90∘−∠1=90∘−50∘=40∘．① 直线a // b，① ∠2=∠3=40∘．故答案为：40．13.【答案】到角的两边距离相等的点在角平分线上【解答】解：命题“角平分线上的点到这个角两边的距离相等”的逆命题是“到角的两边距离相等的点在角平分线上”．14.【答案】如果这两个角是对顶角，那么这两个角相等；,如果这两个角是对顶角，那么这两个角相等；,真.【解答】解：“对顶角相等”改写成“如果...，那么...”的形式是“如果这两个角是对顶角，那么这两个角相等”；这种命题是成立的，故这是真命题.故答案为：如果这两个角是对顶角，那么这两个角相等；如果这两个角是对顶角，那么这两个角相等；真.15.【答案】如果两个角相等，那么它们的余角也相等；【解答】根据命题的特点，可以改写为：“如果两个角相等，那么它们的余角也相等”，故答案为如果两个角相等，那么它们的余角也相等．16.【答案】假【解答】解：两个锐角的和可能是锐角，直角或钝角，即两个锐角的和是钝角是假命题.故答案为：假.17.【答案】50∘【解答】① AB // CD，① ∠ABC＝∠1＝65∘（两直线平行，同位角相等），∠ABD+∠BDC＝180∘（两直线平行，同旁内角互补），① BC平分∠ABD，① ∠ABD＝2∠ABC＝130∘（角平分线定义）① ∠BDC＝180∘−∠ABD＝50∘，① ∠2＝∠BDC＝50∘（对顶角相等）．三、解答题（本题共计7 小题，每题10 分，共计70分）18.【答案】∠B+∠D＝∠BPD．理由如下：作PQ // AB，如图，① AB // CD，① AB // PQ，① ∠B＝∠BPQ，∠D＝∠DPQ，① ∠B+∠D＝∠BPQ+∠DPQ＝∠BPD．【解答】∠B+∠D＝∠BPD．理由如下：作PQ // AB，如图，① AB // CD，① AB // PQ，① ∠B＝∠BPQ，∠D＝∠DPQ，① ∠B+∠D＝∠BPQ+∠DPQ＝∠BPD．19.【答案】（1）证明见解析，（2）&nbsp60∘【解答】（1）∵ AD/BCC&（2）:AEE,&nbsp△AEF=90∘,∠DEA=30∘&nbsp∴ DEF=30∘+90∘=120∘⋅DC/AB ∠DEF+∠F=180∘&nbsp△AFE=60∘20.【答案】解：(1)AE // FH；∠EAH=∠FHA；∠E=∠F（写出两个即可）.(2)选择：AE // FH．证明：因为AB // CD，所以∠BAH=∠CHA，又因为AE // FH，所以∠EAH=∠FHA，所以∠BAH−∠EAH=∠CHA−∠FHA，即∠1=∠2．【解答】解：(1)AE // FH；∠EAH=∠FHA；∠E=∠F（写出两个即可）.(2)选择：AE // FH．证明：因为AB // CD，所以∠BAH=∠CHA，又因为AE // FH，所以∠EAH=∠FHA，所以∠BAH−∠EAH=∠CHA−∠FHA，即∠1=∠2．21.【答案】证明：① AD⊥BC于点D，EF⊥BC于点F，① AD // EF．① ∠1=∠3．① ∠1=∠2，① ∠2=∠3．① DE // AC．【解答】证明：① AD⊥BC于点D，EF⊥BC于点F，① AD // EF．① ∠1=∠3．① ∠1=∠2，① ∠2=∠3．① DE // AC．22.【答案】解：① AB // DE，∠B=60∘，① ∠BCD=120∘．① CM平分∠DCB，∠DCB=60∘．① ∠DCM=12① CM⊥CN，① ∠MCN=90∘，① ∠DCM+∠NCE=90∘，① ∠NCE=90∘−60∘=30∘．【解答】解：① AB // DE，∠B=60∘，① ∠BCD=120∘．① CM平分∠DCB，∠DCB=60∘．① ∠DCM=12① CM⊥CN，① ∠MCN=90∘，① ∠DCM+∠NCE=90∘，① ∠NCE=90∘−60∘=30∘．23.【答案】解：(1)如果①，①，那么①；如果①，①，那么①；(2)对于命题“如果①，①，那么①”证明如下：① BE // AF，① ∠AFD=∠BEC．① AD=BC，∠A=∠B，① △ADF≅△BCE，① DF=CE．① DF−EF=CE−EF，即DE=CF；对于命题“如果①，①，那么①”证明如下：① BE // AF，① ∠AFD=∠BEC．① DE=CF，① DE+EF=CF+EF，即DF=CE．① ∠A=∠B，① △ADF≅△BCE，① AD=BC．【解答】解：(1)如果①，①，那么①；如果①，①，那么①；(2)对于命题“如果①，①，那么①”证明如下：① BE // AF，① ∠AFD=∠BEC．① AD=BC，∠A=∠B，① △ADF≅△BCE，① DF=CE．① DF−EF=CE−EF，即DE=CF；对于命题“如果①，①，那么①”证明如下：① BE // AF，① ∠AFD=∠BEC．① DE=CF，① DE+EF=CF+EF，即DF=CE．① ∠A=∠B，① △ADF≅△BCE，① AD=BC．24.【答案】ABN,120∘,AM,BN,ACB,CBN① AM // BN，① ∠ABN+∠A＝180∘，① ∠ABN＝180∘−60∘＝120∘，① ∠ABP+∠PBN＝120∘，① BC平分∠ABP，BD平分∠PBN，① ∠ABP＝2∠CBP，∠PBN＝2∠DBP，① 2∠CBP+2∠DBP＝120∘，① ∠CBD＝∠CBP+∠DBP＝60∘；不变，∠APB:∠ADB＝2:1．① AM // BN，① ∠APB＝∠PBN，∠ADB＝∠DBN，① BD平分∠PBN，① ∠PBN＝2∠DBN，① ∠APB:∠ADB＝2:1．【解答】①① AM // BN，∠A＝60∘，① ∠A+∠ABN＝180∘，① ∠ABN＝120∘；①① AM // BN，① ∠ACB＝∠CBN，故答案为：120∘，CBN；① AM // BN，① ∠ABN+∠A＝180∘，① ∠ABN＝180∘−60∘＝120∘，① ∠ABP+∠PBN＝120∘，① BC平分∠ABP，BD平分∠PBN，① ∠ABP＝2∠CBP，∠PBN＝2∠DBP，① 2∠CBP+2∠DBP＝120∘，① ∠CBD＝∠CBP+∠DBP＝60∘；不变，∠APB:∠ADB＝2:1．① AM // BN，① ∠APB＝∠PBN，∠ADB＝∠DBN，① BD平分∠PBN，① ∠PBN＝2∠DBN，① ∠APB:∠ADB＝2:1．。

人教版七年级数学下册《5.3 平行线的性质》同步练习-附答案

人教版七年级数学下册《5.3 平行线的性质》同步练习-附答案学校:___________班级：___________姓名：___________考号：___________一、选择题1．下列角的平分线中，互相垂直的是（）A．平行线的同旁内角的平分线B．平行线的同位角的平分线C．平行线的内错角的平分线D．对顶角的平分线2．如图，已知∠1=70°，CD∥BE，则∠B的度数为（）A．70°B．100°C．110°D．120°3．下列命题中，是真命题的是（）A．在同一平面内，垂直于同一条直线的两条直线平行B．三角形一个外角大于它的任何一个内角C．两条直线被第三条直线所截，同旁内角互补D．过一点有且只有一条直线与已知直线平行4．将一直角三角板与两边平行的纸条如图所示放置，若∠1=55°，则∠2的度数为（）A．135°B．130°C．45°D．35°5．如图∠1=30°，∠B=60°，AB⊥AC则下列说法正确的是（）A．AB//CD B．AC⊥CD C．∠D=60°D．AD//BC 6．如图，直线l1//l2，则∠α为（）A．150°B．140°C．130°D．120°7．如图，下列结论中不正确的是（）A．若AD∥BC，则∠1=∠B B．若∠1=∠2，则AD∥BCC．若∠2=∠C，则AE∥CD D．若AE∥CD，则∠1+∠3=180°8．如图AB//EF，∠ABD=13∠ABC，∠EFD=13∠EFC若∠BCF=120°，则∠D的度数为（）A．60°B．80°C．90°D．100°二、填空题9．命题“如果x2=9，那么x=3”是命题(填“真”或“假”).10．如图，AB∥CD，∠C=55°，则∠1的度数是.11．把命题“对顶角相等”改写成“如果……，那么……”的形式为．12．如图AB∥CD，∠A=24°，∠C=55°则∠E=°．13．如图，将直角三角板ABC与直尺贴在一起，使三角板ABC的直角顶点C（∠ACB=90°）在直尺的一边上，若∠1=65°，则∠2的度数等于.14．如图，点E在DF上，点B在AC上∠1=∠2，∠C=∠D若∠A=45°，试求∠F的度数．15．如图，△ABC中，点D，E分别在AB，AC上，F，G在BC上，EF与DG交于点O，∠B=∠3若∠1+∠2= 180°，∠C=60°．（1）判断线段DE和BC的位置关系，并说明理由；（2）求∠DEC的度数．16．如图∠BCD=∠BFE，∠1+∠2=180°．（1）求证：AD∥CE；（2）若DA⊥AB，∠1−∠2=80°求∠BEF的度数．1．A2．C3．A4．D5．D6．D7．A8．B9．假10．125°11．如果两个角是对顶角，那么这两个角相等12．3113．25°14．解：∵∠1=∠2，∠2=∠ANC∴∠1=∠ANC∴DB//EC∴∠ABD=∠C∵∠C=∠D∴∠D=∠ABD∴DF//AC∴∠A=∠F=45°∴∠F的度数为45°．15．（1）解：DE与BC平行，理由如下：∵∠1+∠2=180°∴BD∥EF∴∠B=∠OFC∵∠3=∠B∴∠OFC=∠3∴DE∥BC；（2）解：∵DE∥BC∴∠DEC+∠C=180°又∵∠C=60°∴∠DEC=180°−∠C=180°−60°=120°．16．（1）证明：∵∠BCD=∠BFE∴CD∥EF∴∠2=∠DCE∵∠1+∠2=180°∴∠1+∠DCE=180°∴AD∥CE；（2）解：∵∠1+∠2=180°，∠1−∠2=80°∴∠2=50°∵AD∥CE，DA⊥AB∴∠CEB=∠DAB=90°∴∠BEF=90°−∠2=40°。

初中数学人教版七年级下册 5.3 平行线的性质同步练习

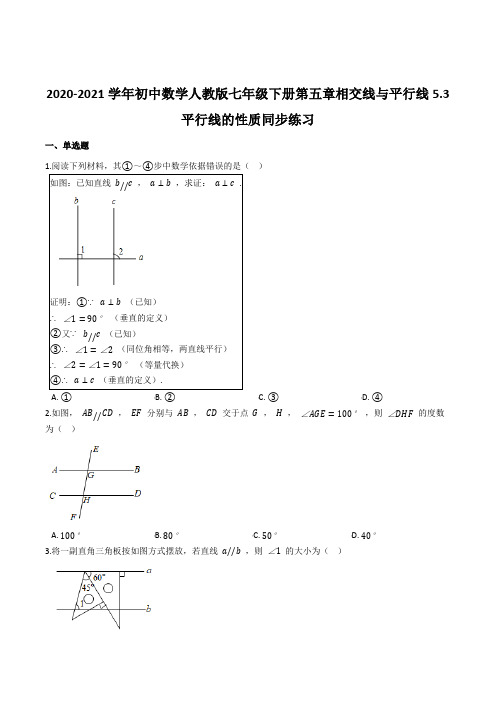
2020-2021学年初中数学人教版七年级下册第五章相交线与平行线5.3平行线的性质同步练习一、单选题1.阅读下列材料，其①～④步中数学依据错误的是（）如图：已知直线b//c，a⊥b，求证：a⊥c.证明：①∵a⊥b（已知）∴∠1=90°（垂直的定义）②又∵b//c（已知）③∴∠1=∠2（同位角相等，两直线平行）∴∠2=∠1=90°（等量代换）④∴a⊥c（垂直的定义）.A. ①B. ②C. ③D. ④2.如图，AB//CD，EF分别与AB，CD交于点G，H，∠AGE=100°，则∠DHF的度数为（）A. 100°B. 80°C. 50°D. 40°3.将一副直角三角板按如图方式摆放，若直线a//b，则∠1的大小为（）A. 45°B. 60°C. 75°D. 105°4.某同学的作业如下框，其中※处填的依据是（）.A. 两直线平行，内错角相等B. 内错角相等，两直线平行C. 两直线平行，同位角相等D. 两直线平行，同旁内角互补5.一副三角板按如图方式放置，含45°角的三角板的斜边与含30°角的三角板的长直角边平行，则∠α的度数是（）A. 10°B. 15°C. 20°D. 25°6.如图，已知AB//CD，∠A=140°，∠E=120°，则∠C的度数是（）A. 80°B. 120°C. 100°D. 140°7.如图，AB//CD，点E在BC上，DE=EC，若∠B=35°，则∠BED=（）A. 70°B. 145°C. 110°D. 140°8.如图，将一副三角板和一张对边平行的纸条按下列方式摆放，两个三角板的一直角边重合，含30°角的直角三角板的斜边与纸条一边重合，含45°角的三角板的一个顶点在纸条的另一边上，则∠1的度数是（）A. 14°B. 15°C. 20°D. 30°9.如图，∠1=80°，∠2=80°，∠5=70°，则∠3的大小是( )A. 70°B. 80°C. 100°D. 110°10.如图，l1∥l2，点O在直线l1上，将三角板的直角顶点放在点O处，三角板的两条直角边与l2交于A，B两点，若∠1＝35°，则∠2的度数为（）A. 35°B. 45°C. 55°D. 65°11.已知AB//CD，CE平分∠ACD，交AB于点E，∠A=124°，则∠1的度数为（）A. 56°B. 38°C. 36°D. 28°12.如图，已知直线AB∥CD，∠GEB的平分线EF交CD于点F，∠1＝40°，则∠2等于（）A. 130°B. 140°C. 150°D. 160°二、填空题13.下图是可调躺椅示意图（数据如图）， AE 与 BD 的交点为 C ，且 ∠A ， ∠B ， ∠E 保持不变．为了舒适，需调整 ∠D 的大小，使 ∠EFD =110° ，则图中 ∠D 应________（填“增加”或“减少”）________度．14.如图，已知等腰梯形 ABCD 中， AD//BC,BC =3AD ，如果 BC ⃗⃗⃗⃗⃗ =a ,BD⃗⃗⃗⃗⃗⃗ =b ⃗ ，那么 AB ⃗⃗⃗⃗⃗ = ________．15.如图， AC//BD,∠C =72°,∠ABC =70° ，那么 ∠ABD 的度数为________．16.如图，直线l 1∥l 2 ， ∠BAE ＝125°，∠ABF ＝85°，则∠1＋∠2=________．17.实验证明，平面镜反射光线的规律是：射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等，如图，一束光线m 射到平面镜a 上，被a 反射到平面镜b 上，又被b 反射，如果被b 反射出的光线n 与光线m 平行，且 ∠1=37° ，那么 ∠2 的度数为________．18.完成下面的证明：已知：如图，∠AEC=∠A+∠C．求证：AB∥CD．证明：过点E作EF∥AB．∴∠A=▲（）．∵∠AEC=∠1+∠2,∠AEC=∠A+∠C，∴∠C=∠2．∴▲∥▲（）．∴AB∥CD（）．三、综合题19. 如图所示,AD∥BC,∠1=78°,∠2=40°,求∠ADC的度数。

人教版七年级下册数学 5.3.1平行线的性质同步测试 (含答案)

5.3.1平行线的性质同步测试一．选择题1．下列四个图形中，不能推出∠2与∠1相等的是（）A．B．C．D．2．如图，已知AC∥DE，∠B＝50°，∠C＝20°，则∠E的度数是（）A．40°B．50°C．60°D．70°3．如图所示，已知AB∥CD，则（）A．∠1＝∠2+∠3B．∠1＞∠2+∠3C．∠2＝∠1+∠3D．∠1＜∠2+∠3 4．如图，AB∥CD，BF平分∠ABE，且BF⊥DE垂足为F，则∠ABE与∠EDC的数量关系是（）A．∠ABE＝∠EDC B．∠ABE+∠EDC＝180°C．∠EDC﹣∠ABE＝90°D．∠ABE+∠EDC＝90°5．如图所示，已知AD∥BC，BE平分∠ABC，∠A＝128°，∠ADB的度数是（）A．40°B．52°C．26°D．34°6．如图，AB∥CD，∠1＝∠2，∠3＝130°，则∠2等于（）A．30°B．25°C．35°D．40°7．如图，已知AB∥CD，∠A＝60°，∠ECD＝120°，∠ECA的度数是（）A．90°B．120°C．135°D．150°8．如图，已知AB∥CD，HI∥FG，EF⊥CD于F，∠1＝40°，那么∠EHI＝（）A．60°B．50°C．45°D．40°9．如图，若AB∥DE，∠B＝130°，∠D＝35°，则∠C的度数为（）A．80°B．85°C．90°D．95°10．如图，下列命题：①若∠1＝∠2，则∠D＝∠4；②若∠C＝∠D，则∠4＝∠C；③若∠A＝∠F，则∠1＝∠2；④若∠1＝∠2，∠C＝∠D，则∠A＝∠F；⑤若∠C＝∠D，∠A＝∠F，则∠1＝∠2．其中正确的个数有（）个．A．1B．2C．3D．4二．填空题11．如图，AB∥CD，∠A＝75°，∠C＝30°，∠E的度数为．12．如图，一束光线从点C出发，经过平面镜AB反射后，沿与AF平行的线段DE射出（此时∠1＝∠2），若测得∠DCF＝100°，则∠A＝．13．如图，直线a∥b，点B在直线b上，且AB⊥BC，∠1＝57°，则∠2的度数是．14．如图，已知AB∥CD，BE平分∠ABD，∠BED＝25°，则∠D＝°．15．如图，AB∥CD，CE交AB于F，∠C＝55°，∠AEC＝18°，则∠A＝°．三．解答题16．已知：如图，在△ABC中，CD⊥AB于点D，G是BC上一点，过点G作GF⊥AB于点F，且满足∠B＝∠ADE．求证：∠CDE＝∠BGF．17．补全证明过程：（括号内填写理由）一条直线分别与直线BE、直线CE、直线BF、直线CF相交于A、G、H、D，如果∠1＝∠2，∠A＝∠D，求证：∠B＝∠C．证明：∵∠1＝∠2（已知），∠1＝∠3，（）∴∠2＝∠3，（）∴CE∥BF，（）∴∠C＝∠4，（）又∵∠A＝∠D，（）∴AB∥，（）∴∠B＝∠4，（）∴∠B＝∠C．（等量代换）18．如图（1），直线AB、CD被直线EF所截，AB∥CD，EG平分∠AEF，FG平分∠CFE．（1）试判断EG与GF的位置关系；（2）过点G作直线m∥AB（如图（2）），点P为直线m上一点，当∠EPF＝80°时，求∠AEP+∠CFP的度数．参考答案1．D2．D3．A4．C5．C6．B7．B8．B9．B10．C11．45°12．50°13．33．14．13015．3716．证明：∵CD⊥AB，GF⊥AB，∴FG∥CD，∴∠FGB＝∠DCB，∵∠B＝∠ADE，∴DE∥BC，∴∠EDC＝∠DCG，∴∠CDE＝∠BGF．17．证明：∵∠1＝∠2（已知），∠1＝∠3（对顶角相等），∴∠2＝∠3（等量代换），∴CE∥BF（同位角相等，两直线平行），∴∠C＝∠4（两直线平行，同位角相等），又∵∠A＝∠D（已知），∴AB∥CD（内错角相等，两直线平行），∴∠B＝∠4（两直线平行，内错角相等），∴∠B＝∠C（等量代换）．答案：对顶角相等；等量代换；同位角相等，两直线平行；两直线平行，同位角相等；已知；CD；内错角相等，两直线平行；两直线平行，内错角相等．18．（1）EG⊥GF，∵AB∥CD，∴∠AEF+∠CFE＝180°，∵EG平分∠AEF，FG平分∠CFE，∴∠AEF＝2∠GEF，∠CFE＝2∠GFE，∴∠EGF+∠GFE＝90°，∴EG⊥GF；（2）分为两种情况：①如图（1），∵PG∥AB，AB∥CD，∴PG∥AB∥CD，∴∠AEP＝∠EPG，∠CFP＝∠FPG，∵∠EPF＝∠EPG+∠FPG＝80°，∴∠AEP+∠CFF＝80°；②如图（2），∵PG∥AB，AB∥CD，∴PG∥AB∥CD，∴∠AEP+∠EPG＝180°，∠CFP+∠FPG＝180°，∵∠EPF＝∠EPG+∠FPG＝80°，∴∠AEP+∠CFP＝180°+180°﹣80°＝280°．。

人教版数学七年级下册-《5.3平行线的性质》同步测试卷含答案解析

2017年春季学期七年级数学下册5.3平行线的性质同步测试卷解析版一、选择题1. 下列命题正确的是 ( )A．两直线与第三条直线相交，同位角相等 B．两直线与第三条直线相交，内错角相等 C．两直线平行，内错角相等 D．两直线平行，同旁内角相等答案：C 本题考查了平行线的性质根据平行线的性质依次判断即可。

A、缺少两直线平行的前提，故本选项错误；B、缺少两直线平行的前提，故本选项错误；C、两直线平行，内错角相等，正确；D、两直线平行，同旁内角应该互补，故本选项错误；故选C.2.如图，小聪把一块含有60°角的直角三角板的两个顶点放在直尺的对边上，并测得∠1=23°，则∠2的度数是（）A．23° B．22° C．37° D．67°答案：C解析：∵直尺的两边互相平行，∠1=23°，∴∠3=∠1=23°，∴∠2=60°-∠3=60°-23°=37°．故选 C．考点：平行线的性质．3.如图所示，AB∥CD，点E在CB的延长线上．若∠ABE＝70°，则∠ECD的度数为（）A．20° B．70° C．100° D．110°答案：D．解析根据邻补角的性质可得∠ABC的度数，再根据两直线平行内错角相等可得答案：∵∠ABE=70°，∴∠ABC=180°-70°=110°.∵AB∥CD，∴∠ECD=∠ABC=110°.故选 D．考点：1.邻补角的性质；2.平行线的性质．4.如图，AB=AC， AD∥BC，∠BAC=100°，则∠CAD的度数是（）A．30° B．35° C．40° D．50°答案： C．解析：根据等腰三角形性质，三角形内角和定理求出∠C，根据平行线的性质得出∠CAD=∠C，即可求出答案:∵AB=AC，∠BAC=100°，∴∠B=∠C=40°.∵AD∥BC，∴∠CAD=∠C=40°.故选 C．考点：1.平行线的性质；2.等腰三角形的性质．5.如图，已知AB∥CD，EA是∠CEB的平分线，若∠BED=40°，则∠A的度数是（）A．40° B．50° C．70° D．80°答案：C．解析：根据邻补角性质可得∠BEC=180°-40°=140°，然后算出∠AEC的度数，再根据两直线平行，内错角相等可得答案：∵∠BED=40°，∴∠BEC=180°-40°=140°.∵EA是∠CEB的平分线，∴∠AEC=70°.∵AB∥CD，∴∠A=∠AEC=70°.故选 C．考点：平行线的性质．6.如图，把一块等腰直角三角板的直角顶点放在直尺的一边上，如果∠1=40°，那么∠2=（）A．40° B．45° C．50° D．60°答案： C.解析：∵∠∠1+∠3=90°，∠1=40°，∴∠3=50°，∵AB∥CD，∴∠2=∠3=50°．故选： C．考点：平行线的性质．7.如图，已知AC∥BD，∠CAE=30°，∠DBE=45°，则∠AEB等于（）A．30° B．45° C．60° D．75°答案： D．解析：过E作EF∥AC，如图：∵AC∥BD，∴EF∥BD，∴∠B=∠2=45°，∵AC∥EF，∴∠1=∠A=30°，∴∠AEB=30°+45°=75°，故选 D．考点：平行线的性质．.8. 如图，已知a∥b，∠1=130°，∠2=90°，则∠3=（）A．70° B．100° C．140° D．170°答案：C．解析：如图，延长∠1的边与直线b相交，∵a∥b，∴∠4=180°∠1=180°130°=50°，由三角形的外角性质，∠3=∠2+∠4=90°+50°=140°．故选： C．考点：平行线的性质．9.如图，AB∥CD，则根据图中标注的角，下列关系中成立的是（）A．∠1=∠3 B．∠2+∠3=180° C．∠2+∠4＜180° D．∠3+∠5=180°答案： D．解析：根据平行线的性质对各选项分析判断利用排除法求解：A、∵OC与OD不平行，∴∠1=∠3不成立，故本选项错误；B、∵OC与OD不平行，∴∠2+∠3=180°不成立，故本选项错误；C、∵AB∥CD，∴∠2+∠4=180°，故本选项错误；D、∵AB∥CD，∴∠3+∠5=180°，故本选项正确．故选 D．考点：平行线的性质．10.如图所示，已知AB∥CD，CE平分∠ACD，当∠A=120°时，∠ECD的度数是（）A．45° B．40° C．35° D．30°答案：D．解析：∵AB∥CD，∠A=120°，∴∠DCA=180°-∠A=60°，∵CE平分∠ACD，∴∠ECD=∠DCA=30°，故选 D．考点：平行线的性质．11. 如图，点D是△ABC的边AB的延长线上一点，BE∥AC，若∠C=50°，∠DBE=60°，则∠CBD的度数等于A．120° B．110° C．100° D．70°答案： B.解析：∵BE∥AC，∴∠CBE=∠C而∠C=50°∴∠CBE=50°又∠DBE=60°∴∠CBD=∠CBE+∠DBE=50°+60°=110°.故选B.考点：平行线的性质.12.如图，AB∥ED，则∠A＋∠C＋∠D＝( )A．180° B．270° C．360° D．540°答案： C．解析：过点C作CF∥AB，∵AB∥ED，∴CF∥AB∥DE，∴∠1+∠A=180°，∠2+∠D=180°，∴∠A+∠ACD+∠D=∠A+∠1+∠2+∠D=360°．故选 C．考点：平行线的性质．二、填空题13. 如图，已知AB//DE，∠ABC=75°，∠CDE=150°，则∠BCD的度数为．答案： 45°．解析：根据两直线平行，内错角相等以及三角形外角和定理即可解答．试题解析：反向延长DE交BC于M，∵AB∥DE，∴∠BMD=∠ABC=75°，∴∠CMD=180°-∠BMD=105°；又∵∠CDE=∠CMD+∠BCD，∴∠BCD=∠CDE-∠CMD=150°-105°=45°．考点：平行线的性质．14.如图，已知AD∥BE，∠DAC=29°，∠EBC=45°，则∠ACB= °．答案： 74.解析：根据平行线的性质得出∠DAC+∠CAB+∠ABC+∠EBC=180°，求出∠CAB+∠ABC=106°，根据三角形内角和定理得出∠ACB=180°-（∠CAB+∠ABC），代入求出即可：∵AD∥BE，∴∠DAC+∠CAB+∠ABC+∠EBC=180°.∵∠DAC=29°，∠EBC=45°，∴∠CAB+∠ABC=106°.∴∠ACB=180°-（∠CAB+∠ABC）=180°-106°=74°.考点：平行线的性质．15.如图，已知AB∥CD，∠1=130°，则∠2= ．答案： 50°.解析：如图：∵∠1=130°，∴∠3=180°∠1=180°130°=50°，∵AB∥CD，∴∠2=∠3=50°．考点：平行线的性质．16.如图，AB∥CD，∠1=64°，FG平分∠EFD，则∠EGF= °．答案： 32°．解析：根据两直线平行，同位角相等求出∠EFD，再根据角平分线的定义求出∠GFD，然后根据两直线平行，内错角相等解答．试题解析：∵AB∥CD，∠1=64°，∴∠EFD=∠1=64°，∵FG平分∠EFD，∴∠GFD= ∠EFD= ×64°=32°，∵AB∥CD，∴∠EGF=∠GFD=32°．考点：平行线的性质．三、解答题17. 如图：BD平分∠ABC,F在AB上，G在AC上，FC与BD相交于点H.，求证：.答案：证明见解析.解析：先证明FG∥BD，再利用角平分线的性质知∠2=∠ABD利用平行线的性质即得∠1=∠2.∵∠BHC=∠DHF，且∴∴FG∥BD∴∠1=∠ABD∵BD平分∠ABC∴∠ABD=∠2∴∠1=∠2.考点：1.平行线的性质2.角平分线的性质．18.如图，已知∠B=∠C，AD∥BC,求证：AD平分∠CAE．答案：证明见解析．解析：利用两直线平行，同位角相等和角平分线的定义进行即可．∵AD∥BC（已知）∴∠B=∠EAD（两直线平行，同位角相等）∠DAC=∠C（两直线平行，内错角相等）又∵∠B=∠C（已知）∴∠EAD=∠DAC（等量代换）∴AD平分∠CAE（角平分线的定义）．考点：1，平行线的性质2.角平分线的定义．19. 如图，已知AB//CD，分别写出下列四个图形中，∠P与∠A、∠C的关系，请你从所得的四个关系中任选一个加以证明．答案：（1）∠A+∠C+∠P=360；（2）∠A+∠C=∠P；（3）∠A+∠P=∠C；（4）∠C+∠P=∠A．理由见解析.解析：本题考查的是平行线的性质以及平行线的判定定理．（1），（2）都需要用到辅助线利用两直线平行，内错角相等的定理加以证明；（3），（4）是利用两直线平行，同位角相等的定理和三角形外角的性质加以证明．（1）∠A+∠C+∠P=360；（2）∠A+∠C=∠P；（3）∠A+∠P=∠C；（4）∠C+∠P=∠A．说明理由（以第三个为例）：已知AB∥CD，根据两直线平行，同位角相等及三角形的一个外角等于两不相邻内角之和，可得∠C=∠A+∠P．考点：1.平行线的性质；2.三角形的外角性质．20.如图，点E在直线DF上，点B在直线AC上，若∠1＝∠2，∠3＝∠4，则∠A＝∠F，请说明理由．解：∵∠1＝∠2（已知），∠2＝∠DGF（）∴∠1＝∠DGF∴BD∥CE（）∴∠3＋∠C＝180º（）又∵∠3＝∠4（已知）∴∠4＋∠C＝180º∴∥（同旁内角互补，两直线平行）∴∠A＝∠F（）答案：（对顶角相等）、（同位角相等，两直线平行）、（两直线平行，同旁内角互补）、DF、AC、（两直线平行，内错角相等）解析：根据平行线的判定是由角的数量关系判断两直线的位置关系，平行线的性质是由平行关系来寻找角的数量关系，分别分析得出即可．试题解析：∵∠1=∠2（已知）∠2=∠DGF（对顶角相等），∴∠1=∠DGF，∴BD∥CE，（同位角相等，两直线平行），∴∠3+∠C=180°，（两直线平行，同旁内角互补），又∵∠3=∠4（已知）∴∠4+∠C=180°∴DF∥AC（同旁内角互补，两直线平行）∴∠A=∠F（两直线平行，内错角相等）．考点：平行线的判定与性质．。

人教版七年级下册数学 5.3.1平行线的性质同步练习(含解析)

5.3.1平行线的性质同步练习一．选择题1．如图，若直线l1∥l2，则下列各式成立的是（）A．∠1＝∠2B．∠4＝∠5C．∠2+∠5＝180°D．∠1+∠3＝180°2．如图，下列推理错误的是（）A．∵∠1＝∠2，∴a∥b B．∵b∥c，∴∠2＝∠4C．∵a∥b，b∥c，∴a∥c D．∵∠2+∠3＝180°，∴a∥c3．将一块直角三角尺ABC按如图所示的方式放置，其中点A、C分别落在直线a、b上，若a∥b，∠1＝62°，则∠2的度数为（）A．28°B．30°C．38°D．62°4．如图，a∥b，c∥d，则图中与∠1互补的角有（）A．1个B．2个C．3个D．4个5．如图，已知AB∥CD，∠1＝113°，∠2＝63°，则∠C的度数是（）A．40°B．45°C．50°D．60°6．如图，直线AB∥DE，AB与DF相交于点C，CE⊥DF，∠FCB＝33°，则∠E的度数是（）A．33°B．47°C．53°D．57°7．下列四个图形中，不能推出∠2与∠1相等的是（）A．B．C．D．8．如图，AB∥DE，那么∠BCD＝（）A．180°+∠1﹣∠2B．∠1+∠2C．∠2﹣∠1D．180°+∠2﹣2∠19．如图，AB∥CD，∠1＝∠2，∠3＝130°，则∠2等于（）A．30°B．25°C．35°D．40°10．如图，将长方形纸片ABCD进行折叠，如果∠BHG＝82°，那么∠BHE的度数为（）A．49°B．50°C．51°D．59°二．填空题（共5小题）11．如图，a∥b，∠2＝95°，∠3＝150°，则∠1的度数是．12．如图，AB∥MN，点C在直线MN上，CB平分∠ACN，∠A＝40°，则∠B的度数为．13．将一把直尺和一块含30°角的三角板ABC按如图所示的位置放置，如果∠CDE＝42°，那么∠BAF的度数为．14．如图，若AB∥CD，BF平分∠ABE，DF平分∠CDE，∠BED＝90°，则∠BFD＝．15．如图，AB∥CD，CB平分∠ABD，若∠ABC＝40°，则∠D的度数为．三．解答题（共3小题）16．阅读理解填空，并在括号内填注理由．如图，已知AB∥CD，M，N分别交AB，CD于点E，F，∠1＝∠2，求证：EP∥FQ．证明：∵AB∥CD（）∴∠MEB＝∠MFD（）．又∵∠1＝∠2（）∠MEB﹣∠1＝∠MFD﹣∠2（）即：∠MEP＝∠EP∥．（）17．如图，已知AD∥BC，AE平分∠BAD交BC延长线于点E，CD与AE相交于点F，∠CFE＝∠E，求证：AB∥DC．18．如图：已知：∠ADE+∠BCF＝180°，BE平分∠ABC交CD的延长线于点E，AF平分∠BAD交DC的延长线于点F，若∠ABC＝2∠E，则∠E+∠F＝90°，完成下列推理过程．证明：∵∠ADE+∠BCF＝180°，∠ADE+∠ADF＝180°∴∠ADF＝∠BCF（）∴AD∥BC（）∵BE平分∠ABC∴∠ABC＝2∠ABE（）又∵∠ABC＝2∠E∴∠ABE＝∠E∴AB∥EF（）∵AD∥BC∴∠BAD+∠ABC＝180°（）∵BE平分∠ABC，AF平分∠BAD∴∠ABE＝∠ABC，∠BAF＝∠BAD∴∠ABE+∠BAF＝∠ABC+∠BAD＝×180°＝90°∵AB∥EF（）∴∠BAF＝∠F（）∵∠ABE＝∠E∴∠E+∠F＝90°（）参考答案一．选择题1．解：∵直线l1∥l2，∴∠1+∠3＝180°，∠2+∠4＝180°，故选：D．2．解：∵∠1＝∠2，∴a∥b，选项A正确；∵b∥c，∴∠2＝∠4，选项B正确；∵a∥b，b∥c，∴a∥c，选项C正确；∵∠2+∠3＝180°，∴b∥c，选项D错误；故选：D．3．解：如图，∵a∥b，∴∠1＝∠3＝62°，∵∠2+∠3＝90°，∴∠2＝90°﹣∠3＝90°﹣62°＝28°，故选：A．4．解：∵a∥b，c∥d，∴∠2＝∠3，∠1+∠2＝180°，∴∠1+∠3＝180°，∵∠3＝∠4，∠2＝∠5，∴∠1+∠4＝180°，∠1+∠5＝180°，故选：D．5．解：∵AB∥CD，∴∠1＝∠FGD＝113°，∴∠C＝∠FGD﹣∠2＝113°﹣63°＝50°，故选：C．6．解：∵AB∥DE，∠FCB＝33°，∴∠D＝∠FCB＝33°，又∵CE⊥DF，∴∠DCE＝90°，∴∠D+∠E＝90°，则∠E＝90°﹣∠D＝57°，故选：D．7．解：A、∵∠1和∠2互为对顶角，∴∠1＝∠2，故本选项不合题意；B、如图，∵a∥b，∴∠1＝∠3（两直线平行，同位角相等），∵∠2＝∠3（对顶角相等），∴∠1＝∠2，故本选项不合题意；C、∵a∥b，∴∠1＝∠2（两直线平行，内错角相等），故本选项不合题意；D、∵a∥b，∴∠1+∠2＝180°（两直线平行，同旁内角互补），不能判断∠1＝∠2，故本选项符合题意；故选：D．8．解：过点C作CF∥AB，如图：∵AB∥DE，∴AB∥DE∥CF，∴∠BCF＝∠1①，∠2+∠DCF＝180°②，∴①+②得，∠BCF+∠DCF+∠2＝∠1+180°，即∠BCD＝180°+∠1﹣∠2．故选：A．9．解：∵AB∥CD，∠3＝130°，∴∠GAB＝∠3＝130°，∵∠BAE+∠GAB＝180°，∴∠BAE＝180°﹣∠GAB＝180°﹣130°＝50°，∵∠1＝∠2，∴∠2＝∠BAE＝×50°＝25°．故选：B．10．解：∵四边形ABCD是长方形，∴AD∥BC，∴∠DEH＝∠BHE，∠DEH+∠EHC＝180°，根据折叠可知：∠CHE＝∠EHG，∵∠EHC＝∠BHE+∠BHG，∴∠BHE+∠BHE+∠BHG＝180°，∴2∠BHE＝180°﹣82°＝98°，∴∠BHE＝49°．故选：A．二．填空题（共5小题）11．解：过点C作CD∥a，∵a∥b，∴CD∥a∥b，∴∠1+∠ECD＝180°，∠3+∠DCF＝180°，∵∠2＝95°，∠3＝150°，∴∠1+∠2+∠3＝360°，∴∠1＝360°﹣∠2﹣∠3＝360°﹣150°﹣95°＝115°，故答案为：115°．12．解：∵AB∥MN，∴∠A+∠ACN＝180°，又∵∠A＝40°，∴∠ACN＝180°﹣∠A＝140°，∵CB平分∠ACN，∴∠ACB＝∠ACN＝70°，∴∠B＝180°﹣∠A﹣∠ACB＝70°，故答案为：70°．13．解：由题意知DE∥AF，∠CDE＝42°，∴∠AFD＝∠CDE＝42°，∵∠B＝30°，∴∠BAF＝∠AFD﹣∠B＝42°﹣30°＝12°，故答案为：12°．14．解：∵AB∥CD，∴∠ABE＝∠4，∠1＝∠2，∵∠BED＝90°，∠BED＝∠4+∠EDC，∴∠ABE+∠EDC＝90°，∵BF平分∠ABE，DF平分∠CDE，∴∠1+∠3＝45°，∵∠5＝∠2+∠3，∴∠5＝∠1+∠3＝45°，即∠BFD＝45°，故答案为：45°．15．解：∵CB平分∠ABD，∴∠ABD＝2∠ABC＝80°，∵AB∥CD，∴∠ABD+∠D＝180°，∴∠D＝180°﹣80°＝100°，则∠D的度数为100°．故答案为：100°．三．解答题（共3小题）16．证明：∵AB∥CD（已知）∴∠MEB＝∠MFD（两直线平行同位角相等）．又∵∠1＝∠2（已知）∠MEB﹣∠1＝∠MFD﹣∠2（角的和差定义）即：∠MEP＝∠MFQEP∥FQ．（同位角相等两直线平行）故答案为：已知，两直线平行同位角相等，已知，角的和差定义，MFQ，FQ，同位角相等两直线平行．17．证明：∵AD∥BC，∴∠2＝∠E，∵AE平分∠BAD，∴∠1＝∠2，∴∠1＝∠E，∵∠CFE＝∠E，百度文库精品文档∴∠1＝∠CFE，∴AB∥DC．18．证明：∵∠ADE+∠BCF＝180°，∠ADE+∠ADF＝180°∴∠ADF＝∠BCF（同角的补角相等）∴AD∥BC（同位角相等，两直线平行）∵BE平分∠ABC∴∠ABC＝2∠ABE（角平分线定义）又∵∠ABC＝2∠E∴∠ABE＝∠E∴AB∥EF（内错角相等，两直线平行）∵AD∥BC∴∠BAD+∠ABC＝180°（两直线平行，同旁内角互补）BE平分∠ABC，AE平分∠BAD∴∠ABE＝∠ABC，∠BAF＝∠BAD∴∠ABE+∠BAF＝∠ABC+∠BAD＝×180°＝90°∵AB∥EF（己证）∴∠BAF＝∠F（两直线平行，内错角相等）∠ABE＝∠E∴∠E+∠F＝90°（等量代换）。

人教版数学七年级下册 5.3-平行线的性质同步练习

七年级下册 5.3-平行线的性质同步练习一、选择题1.下列命题中，是真命题的是()A. 同位角相等B. 相等的角是直角C. 若|y|=2，则y=±2D. 若ab=0，则a=2.下列语句中，是命题的是() ①若∠1=60∘，∠2=60∘，则∠1=∠2; ②同位角相等吗? ③画线段AB=CD; ④如果a> b，b>c，那么a>c; ⑤直角都相等．A. ① ④ ⑤B. ① ② ④C. ① ② ⑤D. ② ③ ④ ⑤3.有下列四个命题：①相等的角是对顶角；②同位角相等；③若一个角的两边与另一个角的两边互相平行，则这两个角一定相等；④从直线外一点到这条直线的垂线段，叫做点到直线的距离．其中是真命题的个数有()A. 0个B. 1个C. 2个D. 3个4.如图，直线l1//l2，它们之间的距离是()A. 线段PA的长度B. 线段PB的长度C. 线段PC的长D. 线段PD的长度5.如图，a//b，AB//CD，CE⊥b，FG⊥b，E，G为垂足，则下列说法不正确的是()A. AB=CDB. EC=FGC. A，B两点的距离就是线段AB的长度D. a与b的距离就是线段CD的长度6.对于命题“如果∠1+∠2=90°，那么∠1≠∠2”，说明它是假命题的反例可以是()A. ∠1=50°，∠2=40°B. ∠1=50°，∠2=50°C. ∠1=40°，∠2=40° D. ∠1=∠2=45°7.下列说法中：①过直线外一点有且只有一条直线与已知直线平行；②过一点有且只有一条直线与已知直线垂直；③垂直于同一直线的两条直线互相平行；④平行于同一直线的两条直线互相平行；⑤两条直线被第三条直线所截，如果同旁内角相等，那么这两条直线互相平行；⑥连结A、B两点的线段的长度就是A、B两点之间的距离，其中正确的有()A. 1个B. 2个C. 3个D. 4 个8.如图，直线a，b被直线c，d所截，若∠1=80°，∠2=100°，∠3=85°，则∠4度数是()A. 80°B. 85°C. 95°D. 100°9.如图，AF平分∠BAC，D在AB上，DE平分∠BDF且∠1=∠2，则下面四个结论：①DF//AC；②DE//AF；③∠EDF=∠DFA；④∠C+∠DEC=180°，其中成立的有()A. ①②③B. ①②④C. ①③④D. ②③④10.如图，AB//CD，点P为CD上一点，PF是∠EPC的平分线．若∠1=55°，则∠EPD的大小为()A. 60°B. 70°C. 80°D. 100°11.如图，AB//CD，EG、EM、FM分别平分∠AEF，∠BEF，∠EFD，则图中与∠DFM相等的角(不含它本身)的个数为()A. 5B. 6C. 7D. 8二、填空题12.如图，在四边形ABCD中，AB//CD，∠B=60°，当∠D=°时，AD//BC．13.如图，直线a，b，c，d，已知c⊥a，c⊥b，直线b，c，d交于一点，若∠1=50°，则∠2的度数是______．14.已知：如图，AB//EF，∠ABC=75°，∠CDF=135°，则∠BCD=．15.命题“两直线平行，同旁内角互补”的题设__________，结论是__________.它是一个___命题(真或假)16.如图，一只船从点A出发沿北偏东60°方向航行到点B，再以南偏西25°方向返回，则∠ABC=_________．三、计算题17.已知：如图，EF//CD,∠1+∠2=180°．(1)求证：GD//CA．(2)若CD平分∠ACB，DG平分∠CDB，且∠A=36°，求∠ACB的度数．18.已知DB//FG//EC，A是FG上一点，∠ABD=60°，∠ACE=36°，AP平分∠BAC，求∠BAC，∠PAG的大小．19.如图，∠1+∠2=180°，∠B=∠3．(1)判断DE与BC的位置关系，并说明理由；(2)若∠C=63°，求∠DEC的度数．20.如图，已知直线l1//l2，l3和l1，l2分别交于C，D两点，点A，B分别在直线l1，l2上，且位于l3的左侧，点P在直线l3上，且不和点C，D重合．(1)如图①，当动点P在线段CD上运动时，试确定∠1、∠2、∠3之间的关系，并给出证明；(2)如图②，当动点P在线段DC的延长线上运动时，(1)中的结论是否成立？若不成立，试写出新的结论，并给出证明．答案1.【答案】C2.【答案】A3.【答案】A4.【答案】B5.【答案】D6.【答案】D7.【答案】C8.【答案】B9.【答案】A10.【答案】B11.【答案】C12.【答案】6013.【答案】40°14.【答案】30°15.【答案】两直线平行；同旁内角互补；真16.【答案】35°17.【答案】(1)证明：∵EF//CD，∴∠1+∠ECD=180°(两直线平行，同旁内角互补)，又∵∠1+∠2=180°，∴∠2=∠ECD，∴GD//CA；(2)解：由(1)得：GD//CA，∴∠BDG=∠A=36°，∠ACD=∠2，∵DG平分∠CDB，∴∠2=∠BDG=36°，∴∠ACD=∠2=36°，∵CD平分∠ACB，∴∠ACB=2∠ACD=72°．18.【答案】解：∵DB//FG//EC，∴∠BAG=∠ABD=60°，∠CAG=∠ACE=36°，∴∠BAC=∠BAG+∠CAG=96°；∵AP为∠BAC的平分线，∴∠BAP=∠CAP=1∠BAC=48°，2∴∠PAG=∠CAP−∠CAG=12°．19.【答案】解：(1)DE//BC，理由是：∵∠1+∠2=180°，∴AB//EF，∴∠ADE=∠3，∵∠B=∠3，∴∠ADE=∠B，∴DE//BC．(2)解：∵DE//BC，∴∠C+∠DEC=180°，∵∠C=63°，∴∠DEC=117°．20.【答案】解：(1)∠3+∠1=∠2成立．理由如下：过点P作PE//l1，∴∠1=∠APE；∵l1//l2，∴PE//l2，∴∠3=∠BPE，又∵∠BPE+∠APE=∠2，∴∠3+∠1=∠2．(2)∠3+∠1=∠2不成立，新的结论为∠3−∠1=∠2．理由如下：过点P作PE//l1，∴∠1=∠APE；∵l1//l2，∴PE//l2，∴∠3=∠BPE；又∵∠BPE−∠APE=∠2，∴∠3−∠1=∠2．。

531平行线的性质(1)同步练习(含答案).docx

5.3.1平行线的性质(1)班级 _______ 姓名____________ 座号_____主要内容:平行线的性质一、课堂练习：1.如图，完成下列各题的说理过程，括号内填写说理根据：①若DE//BC,则可得出Z1二___ ,根据 _____________________________ ;②若AB//EF.则可得出,1二 _______ ,根据 ___________________________ :③若____ // _____ ,则可得1BZ5+Z4+ZO180°,根据 __________________________________ •2.如图，直线a//b, Zl = 54e,那么Z2、Z3、Z4各是多少度?3.如图，在四边形ABCD中，如果AD//BC, ZA二60°,求ZB的度数，不用度量的方法，能否求得ZD的度数？门c二、课后作业：4•如图所示,(1) 若DE//BC,则可得到：① Zl= ______ ,根据 __________________________________ ；② Z2二 _____ ,根据；③ Z4+ ______ =180°,根据 _______________________________(2) 若EF//AB,则可得到：① _________ Zl= ____________ ；②ZB 二 ________ ； ③Z2+____________ =180°.5. 如图，平行线AB 、CD 被直线AE 所截.⑴从Zl = 110\则可知道Z2二 ______ 度，根据 _________________________________________(2)从Z1 = 110°，则可知道Z3二 ___ 度，根据 _________________________________⑶从Zl = 110\则可知道Z4二 _______ 度,根据 ____________________________ .6. 如下图所示,一条公路两次转弯后，和原来的方向相同，如果第一次拐的角是36',第二次拐的角是 _____ 度,根据 ____________________________7. 如图，要在公路的两侧铺设平行管道，如果公路一侧铺设的角度为120：那么力了使管道对接，另一侧应以 ____ 角度铺设，根据8. 如图,用式子表示下列句子(阅读⑴，完成⑵(3))C第6题第7题第8题⑴因为Z1和ZB相等，根据“同位角相等，两直线平行”，所以DE和BC平行;9.如图，已知d〃"c・、d是截线，若Z1二80°, Z5二70°.求Z2、Z3、Z4各是多少度?为什么？三、新课预习：10.如图，"60°, Z2=60°, Z3=85°求Z4 的度数.b参考答案一、课堂练习：1.如图，完成下列各题的说理过程，括号内填写说理根据：①若DE//BC,则可得出Z1=Z B ,根据两直线平行，同位角相等；②若AB//EF.则可得出,1二Z_5_,根据两直线平行，内错角相等；③若DE〃BC ,则可得出Z5+Z4+ZO180°,根据两直线平行，同旁内角耳补•2.如图，直线a//b t Zl = 54e,那么Z2、Z3、Z4各是多少度?解:I Z1 = 54°・・・Z2 = Z1 = 54°'：a// b・•・ Z2 + Z3 = 180°・•・ Z3 = 180°-Z2 = 180°一54° = 126°9： a// b・•・ Z4 = Z2 = 54°3.如图，在四边形ABCD屮，如果AD//BC. ZA=60\求ZB的度数，不用度量的方法，能否求得ZD的度数？解:*：AD//BC:.ZA+Z3二180°又・・・ZA= 60°・・・ZB二120°不用度量的方法,仅根据平行线的性质，不能求得ZD的度数二、课后作业：4.如图所示，(1)若DE//BC,则可得到：①Z1 ,根据两直线平行，同位角相等②Z2二Z5 、根据两直线平行，内错角相等；③Z4+ ZB 二180",根据两直线平行，同旁内角互补⑵若EF//AB,则可得到：①Zl= Z2 ；②ZB= Z5 ；③ Z2+ Z4 二180°.5.如图，平行线AB、CD被直线AE所截.⑴从Zl=110\则可知道Z2二110 度, 根据两右线平行，内错角相等；(2)从Zl = 110\则可知道Z3二110度, 根据两直线平行，同位角相等；(3)从Z1二110°,则可知道Z4二70 度,根据两直线平行,同旁内角互补•6.如下图所示,一条公路两次转弯后，和原来的方向相同，如果第一次拐的角是36。

人教七年级下数学_53全练《平行线的性质》知识能力练

《5.3.1平行线的性质》知识能力练知识点一平行线的性质1.（2020四川自贡中考）如下图，直线a∥b，∠1=150°，则∠2的度数为（）A.40°B.50°C.55°D.60°2.如下图，直线a∥b，直线c分别交a、b于点A、C，∠BAC的平分线交直线b于点D，若∠2=50°，则∠1的度数是（）A.50°B.60°C.80°D.100°3.（2020独家原创试题）如下图，将一块含有30°角的直角三角板的两个顶点放在作业本两行线上如果∠1=26°，那么∠2的度数是（）A.26°B.30°C.34°D.60°4.（2017江苏宿迁中考）如下图，直线a，b被直线c，d所截，若∠1=80°，∠2=100°，∠3=85°，则∠4的度数是（）A.80°B.85°C.95°D.100°5.（2018浙江衢州中考）如下图，将长方形ABCD沿GH所在直线折叠，点C落在点Q处，点D落在AB边上的点E处，若∠AGE=32°，则∠GHC等于（）A.112°B.110°C.108°D.106°6.（2016山东滨州中考）如下图，AB ∥CD ，直线EF 与AB ，CD 分别交于点M ，N ，过点N 的直线GH 与AB 交于点P ，则下列结论错误的是（）A.∠EMB=∠ENDB.∠BMN=∠MNCC.∠CNH=∠BPGD.∠DNG=∠AME7. （2019湖南张家界中考）已知直线a ∥b ，将一块含30°角的直角三角板ABC 按如下图所示的方式放置（∠BAC=30°），并且顶点A ，C 分别落在直线a ，b 上，若∠1=18°，则∠2的度数是_________.8.（2019山东菏泽中考）如下图，AD ∥CE ，∠ABC=100°，则∠2-∠1的度数是______.9.如下图，已知直线12//l l ，3l 和1l ，2l 分别交于C ，D 两点，点A ，B 分别在直线1l ，2l 上，且能会位于3l 的左侧，点P 在直线3l 上，且不和点C ，D 重合.（1）如图①，当动点P 在线段CD 上运动时，试确定∠1、∠2、∠3之间的关系，并给出证明；（2）如图②，当动点P在线段DC的延长线上运动时，（1）中的结论是否成立？若不成立，试写出新的结论，并给出证明.10.（2020江西丰城期末）图①是一张长方形的纸带，将这张纸带沿EF折叠成图②，再沿BF 折叠成图③.（1）若∠DEF=20°，请你求出图③中∠CFE度数；（2）若∠DEF=α，请你直接用含α的式子表示图③中∠CFE的度数.参考答案1.答案：B解析：如图所示，a b，∴∠3=∠1=50°，∵//∴∠2=∠3=50°.故选B.2.答案：C解析：∵AB∥CD，∴∠BAD=∠2=50°，∵AD平分∠BAC，∴∠DAC=∠BAD=50°，∴∠1=180°-∠BAD-∠DAC=80°，故选C.3.答案：C解析：如图，∵BE∥CD，∴∠EBC=∠1=26°，∵∠ABC=60°，∴∠2=∠ABC-∠EBC=60°-26°=34°.故选C.4.答案：Ba b，根据两直线平行，内错角相等得解析：因为∠1+∠2=80°+100°=180°，所以//∠4=∠3=85°.5.答案：D解析：由折叠可得∠DGH=12∠DGE=12×（180°-32°）=74°，再根据AD ∥BC 可得 ∠GHC=180°-∠DGH=106°.故选D. 6.答案：D解析：∵AB ∥CD ，∴∠EMB=∠END （两直线平行，同位角相等），故A 中结论正确； ∵AB ∥CD ，∴∠BMN=∠MNC （两直线平行，内错角相等），故B 中结论正确；∵AB ∥CD ，∴∠CNH=∠MPN （两直线平行，同位角相等），∵∠MPN=∠BPG （对顶角相等）， ∴∠CNH=∠BPG （等量代换），故C 中结论正确；无法判定∠DMG 与∠AME 相等.故选D. 7.答案：48°解析：∵//a b ，∴∠2=∠1+∠CAB=18°+30°=48°. 8.答案：80°解析：如图，过B 作BF ∥AD ，∵AD ∥CE ，∴AD ∥BF ∥EC ， ∴∠1=∠3，∠4+∠2=180°， ∵∠ABC=100°， ∴∠3+∠4=100°，∴∠1+∠4=100°，∴∠2-∠1=80°.9.解析：（1）∠2=∠1+∠3. 证明：如图①，过点P 作PE ∥1l ， ∴∠1=∠APE ，∵12//l l ， ∴PE ∥2l ，∴∠3=∠BPE. 又∵∠2=∠APE+∠BPE ， ∴∠2=∠1+∠3.（2）（1）中结论不成立，新的结论：∠3=∠1+∠2. 证明：如图②，过点P 作PE ∥1l ，∴∠1=∠APE.∵12//l l ，∴PE ∥2l ，∴∠3=∠BPE ，又∵∠BPE=∠APE+∠2，∴∠3=∠1+∠2.10.解析（1）∵长方形对边AD∥BC，∴题图①中，CF∥DE，∴题图①中，∠CFE=180°-∠DEF=180°-20°=160°，∠BFE=∠DEF=20°，∴题图②中，∠BFC=160°-20°=140°∵题图③中，∠CFE+∠BFE=∠BFC，∴题图③中，∠CFE+20°=140°，∴题图③中，∠CFE=120°.（2）∵长方形对边AD∥BC，∴题图①中，CF∥DE，∴题图①中，∠CFE=180°-∠DEF=180°-α，∠BFE=∠DEF=α，∴题图②中，∠BFC=180°-2α，∵题图③中，∠CFE+∠BFE=∠BFC，∴题图③中，∠CFE+ α=180°-2α，∴题图③中，∠CFE=180°-3α.。

人教版数学七年级下册《531平行线的性质》习题3

1．两条平行直线被第三条直线所截，同位角_______，内错角____，同旁内角______．2．同时垂直于两条平行线，并且夹在这两条平行线间的______叫做这两条平行线的距离．3．（阅读理解题）如图，若∠3=∠4，你能说明AD∥BC，AB∥DC吗？
小亮回答：都行，∵∠3=∠4，∴AD∥BC，AB∥DC
小亮错在哪里，请指出错因，并改正．
4．如图，已知∠AED=60°，∠2=30°，EF平分∠AED，可以判断EF∥BD吗？为什么？
5．如图所示，若∠1+∠2=180°，∠3=110°，求∠4．
1．相等，相等，互补
2．线段的长度
3．错误，不能识别AD∥BC．
因为∠3=∠4，所以AB∥CD．
思路点拨：∠3与∠4是直线AB，CD被BD所截得到的内错角．
4．可以，∵∠AED=60°，EF平分∠AED
∴∠FED=30°
又∵∠EDB=∠2=30°
∴EF∥BD
解题规律：证两直线平行，找内错角相等．
5．设∠2对顶角为∠5，则∠2=∠5
∵∠1+∠2=180°
∴∠1+∠5=180°
∴AB∥CD，∴∠3=∠4
又∵∠3=110°
∴∠4=110°
解题规律：先判断AB∥CD，再运用平行线的性质定理．。

人教版七年级数学下册5.3.1平行线的性质同步测试(含答案)

绝密★启用前平行线的性质班级：姓名：一、单项选择题1．如图，a∥b，点B在直线b上，且AB BC ， 1 40 ，那么 2 的度数是（）A．40B．50C．60D．702．如图，一副直角三角板按如下图的方式摆放，此中点C在FD的延伸线上，且AB∥ FC，则CBD 的度数为（）A． 15°B． 30°C．45°D．60°3．如图，∠ BCD＝ 95°， AB∥DE，则∠ α与∠β知足（）A．∠α+∠ β＝ 95°B．∠ β﹣∠ α＝ 95°C．∠ α+∠ β＝ 85°D．∠ β﹣∠ α＝ 85°4．如图，能判断EB∥ AC 的条件是（）A．∠C＝∠ABE B．∠ A＝∠ EBD C．∠ C＝∠ ABC D．∠ A＝∠ ABE5．向来尺与一缺了一角的等腰直角三角板如图摆放，若∠ 1=115°，则∠ 2的度数为（）A． 65°B． 70°C．75°D．80°6．如图， AB∥ CD , ∠ BED=110°， BF 均分∠ ABE,DF均分∠ CDE,则∠ BFD=（）A． 110 °B． 115 °C．125 °D．130 °7．如图，点E、 F 分别是 AB、 CD上的点，点 G 是 BC的延伸线上一点，且∠ B=∠ DCG=∠ D则以下判断错误的选项是（）A．∠BEF=∠ EFD B．∠ A=∠BCF C．∠ AEF=∠ EBC D．∠ BEF+∠ EFC=180°8．如图，已知BE∥ CF，若要 AB∥ CD，则需使（）A．∠1=∠ 3 B．∠2=∠ 3 C．∠ 1=∠4D．∠2=∠ 4二、填空题9．如图，直线 a / / b ，直线l与直线a订交于点P，与直线b订交于点Q，且PM l于点P，若1 58 ，则2___________．10．如图，已知a∥ b， a∥ c， AB⊥ BC，∠ 1＝ 117 °，则∠ 2＝ _____．11．如下图，是我们生活中常常接触的小刀，刀柄外形是一个直角梯形（挖去一小半圆），刀片上下是平行的，转动刀片刻会形成∠ 1、∠2，则12__________ ．12．如图，直线a//b ，将向来角三角形的直角极点置于直线 b 上，若∠1＝ 28°，则∠ 2 的度数是_______________________________三、解答题13．如图， EF∥ AD，∠ 1=∠2，∠ BAC=70°．将求∠ AGD的过程填写完好．∵EF∥ AD，（ ________）∴ ∠2=______．（两直线平行，同位角相等；）又∵∠ 1=∠ 2，（ ________）∴ ∠1=∠ 3．（ ________）∴ AB∥ DG．（ ________）∴ ∠BAC+______=180 （°）又∵∠ BAC=70°，（ ________）∴ ∠AGD=______．一、单项选择题1．如图，AB/ /CD ，且A25 ， C 45，则E的度数是（）A． 60°B． 70°C．110 °D．80°2．如图，已知 a / / b ，点B在直线 b 上，且AB BC , 1 46，则 2 的度数是（）A．46B．44C．56D．543．如图，在三角形中，，点是上的点，于点，则以下结论中，不正确的是（）A．B．C．D．4．如图，直线l1∥ l2l交于C D两点，把一块含30°，且分别与直线，角的三角尺按如下图的地点摆放，若∠ 1＝ 50°，则∠ 2 的度数为（）A． 90°B． 110 °C．108 °D．100 °5．如图， AD∥EF∥ BC，且 EG∥ AC．那么图中与∠1相等的角（不包含∠ 1）的个数是（）A． 2B． 4C．5D．66．如图 ,在 ?ABCD中 ,BC=7,CD=5,∠ D=50°,BE 均分∠ ABC,则以下结论中不正确的选项是（）A．∠C=130°B． AE=5C．∠ BED=130°D． ED=27．如图，将含角的直角三角板的直角极点放在直尺的一边上，已知，则的度数是（）A．B．C．D．8．把长方形与按如图的方式搁置在直线上，若，则的度数为（）A．B．C．D．二、填空题9．如图，直线a∥ b， C 为直线 a、b 之间一个点，∠ 1＝ 45°，∠2＝ 30°，则∠ C＝ _____．10．如图，a c ， b c ， 1 70 ，则2_________.11．如图，点D、 E 分别在 AB、 BC 上， DE∥ AC， AF∥ BC，∠1＝ 70°，则∠ 2＝ _____ °．12．如图 ,AB∥ CD,直线 EF分别交 AB、 CD 于点 E. F,HF均分∠ EFD,若∠ 1=110 °,则∠ 2 的度数为 _____三、解答题13．已知：如图，DE⊥ AC，垂足为点E，∠ AGF＝∠ABC，∠ BFG+∠ BDE＝ 180 °，求证： BF⊥ AC．请达成下边的证明的过程，并在括号内注明原因．证明：∵ ∠ AGF＝∠ABC（已知）∴FG∥（）∵ ∠BFG+∠ BDE＝ 180 （°已知）∴ ∠FBC+∠ BDE＝ 180 （°）∴ BF∥ DE（）∴ ∠BFA＝（两直线平行，同位角相等）∵ DE⊥ AC（已知）∴ ∠DEA＝ 90 °（）∴ ∠BFA＝ 90 °（等量代换）∴ BF⊥ AC（垂直的定义）参照答案1-5．BADDB6-8．CCC9．3210．27°11．9012． 118 °13．已知∠3已知等量代换内错角相等，两直线平行∠ AGD 两直线平行，同旁内角互补已知 110°1-5．BBBDC6-8．CCA9．75°10．7011．7012． 35°13． BC，同位角相等，两直线平行，两直线平行，内错角相等，等量代换，同旁内角互补，两直线平行，∠ DEA，垂直的定义．。

人教版七年级数学下学期《5.3 平行线的性质》同步练习

5.3 平行线的性质一．选择题1．下列语句是命题的是（）A．画直线AB B．直线a∥bC．如果a∥b，b∥c，则a∥c D．点M与点N都在直线AB上2．下列命题中，真命题的个数是（）①过一点有且只有一条直线与已知直线平行；②过一点有且只有一条直线与已知直线垂直；③图形平移的方向一定是水平的；④内错角相等；⑤相等的角是对顶角；⑥垂线段最短A．3B．2C．1D．03．下列五个命题：①如果两个数的绝对值相等，那么这两个数的平方相等；②内错角相等；③在同一平面内，垂直于同一条直线的两条直线互相平行；④两个无理数的和一定是无理数；⑤坐标平面内的点与有序数对是一一对应的．其中真命题的个数是（）A．2个B．3个C．4个D．5个4．下列选项中a，b的取值，可以说明“若a＞b，则|a|＞|b|”是假命题的反例为（）A．a＝﹣5 b＝﹣6B．a＝6 b＝5C．a＝﹣6 b＝5D．a＝6 b＝﹣5 5．下列命题中，逆命题为真命题的是（）A．对顶角相等B．邻补角互补C．两直线平行，同位角相等D．互余的两个角都小于90°6．如图是婴儿车的平面示意图，其中AB∥CD，∠1＝120°，∠3＝40°，那么∠2的度数为（）A．80°B．90°C．100°D．102°7．如图，直线a，b被直线m所截，若a∥b，∠2＝62°，则∠1＝（）A．62°B．108°C．118°D．128°8．能说明“锐角α，锐角β的和是锐角”是假命题的例证图是（）A．B．C．D．9．如图，将直尺与含30°角的三角尺摆放在一起，若∠1＝20°，则∠2的度数是（）A．30°B．40°C．50°D．60°10．若直线a∥b，点M到直线a的距离是5cm，到直线b的距离是3cm，那么直线a，b间的距离是（）cm．A．2B．8C．2或8D．4二．填空题11．若a2＝b2，那么a＝b；请举出一个反例，说明该命题是假命题；12．把命题“两直线平行，同位角相等”改写成“如果…那么…”的形式是：．13．“同角的余角相等”，这个命题改写成如果…那么…形式应该为．三．解答题14．已知：如图，AD∥BE，∠1＝∠2，求证：∠A＝∠E．15．如图，已知∠ABC+∠ECB＝180°，∠P＝∠Q．求证：∠1＝∠2．参考答案一．选择题1．解：C是用数学式子表达的可以判断真假的陈述句，是命题；A、B、D均不是可以判断真假的陈述句，没有题设和结论之分，都不是命题．故选：C．2．解：过直线外一点有且只有一条直线与已知直线平行，①是假命题；在同一平面内，过一点有且只有一条直线与已知直线垂直，②是假命题；图形平移的方向不一定是水平的，③是假命题；两直线平行，内错角相等，④是假命题；相等的角不一定是对顶角，⑤是假命题；垂线段最短，⑥是真命题，故选：C．3．解：①如果两个数的绝对值相等，那么这两个数的平方相等，是真命题；②两直线平行，内错角相等，原命题是假命题；③在同一平面内，垂直于同一条直线的两条直线互相平行，是真命题；④两个无理数的和不一定是无理数，原命题是假命题；⑤坐标平面内的点与有序数对是一一对应的，是真命题；故选：B．4．解：当a＝﹣5，b＝﹣6时，a＞b，但|a|＜|b|，∴“若a＞b，则|a|＞|b|”是假命题，故选：A．5．解：A、对顶角相等的逆命题是相等的角是对顶角，逆命题是假命题；B、邻补角互补的逆命题是互补的角是邻补角，逆命题是假命题；C、两直线平行，同位角相等逆命题是同位角相等，两直线平行，逆命题是真命题；D、互余的两个角都小于90°的逆命题是都小于90°的角互余，逆命题是假命题；故选：C．6．解：∵AB∥CD，∴∠A＝∠3＝40°，∵∠1＝120°，∴∠2＝∠1﹣∠A＝80°，故选：A．7．解：如图，∵a∥b，∴∠3＝∠2＝62°，∵∠3+∠1＝180°，∴∠1＝180°﹣62°＝118°．故选：C．8．解：例如C选项图中：三角形三个内角都是锐角，则∠α+∠β＞90°．故选：C．9．解：如图，∵∠BEF是△AEF的外角，∠1＝20°，∠F＝30°，∴∠BEF＝∠1+∠F＝50°，∵AB∥CD，∴∠2＝∠BEF＝50°，故选：C．10．解：分为两种情况：如图1，直线a，b间的距离是5cm﹣3cm＝2cm，如图2，直线a，b间的距离是5cm+3cm＝8cm，故选：C．二．填空题11．解：若a2＝b2，那么a＝b，是假命题．例如：22＝（﹣2）2＝4但是2≠﹣2．所以答案可以是：若22＝（﹣2）2＝4，但是2≠﹣2．12．解：“两直线平行，同位角相等”的条件是：“两直线平行”，结论为：“同位角相等”，∴写成“如果…，那么…”的形式为：“如果两直线平行，那么同位角相等”，故答案为：如果两直线平行，那么同位角相等．13．解：根据命题的特点，可以改写为：“如果两个角是同一个角的余角，那么这两个角相等”，故答案为：如果两个角是同一个角的余角，那么这两个角相等．三．解答题14．证明：∵AD∥BE，∴∠A＝∠3，∵∠1＝∠2，∴DE∥AC，∴∠E＝∠3，∴∠A＝∠EBC＝∠E．15．证明：∵∠ABC+∠ECB＝180°，∴AB∥DE，∴∠ABC＝∠BCD，∵∠P＝∠Q，∴PB∥CQ，∴∠PBC＝∠BCQ，∵∠1＝∠ABC﹣∠PBC，∠2＝∠BCD﹣∠BCQ，∴∠1＝∠2．。

5.3.1《平行线的性质》同步训练(含答案)

5.3平行线的性质课时1平行线的性质基础训练知识点1 两直线平行，同位角相等1.如图，直线a∥b,∠1=60°，则∠2=( )A.30°B.60°C.45°D.120°2.(2018新疆乌鲁木齐中考)如图，把一个直角三角尺的直角顶点放在直尺的一边上，若∠1=50°,则∠2=( )A.20°B.30°C.40°D.50°3.如图AC∥DF,AB∥EF，点D，E分别在AB，AC上，若∠2=50°，则∠1的度数为 .知识点2 两直线平行，内错角相等4.(2018四川泸州中考)如图，直线a∥b，直线c分别交a,b于点A,C,∠BAC的平分线交直线b于点D，若∠1=50°，则∠2的度数是( )A.50°B.70°C.80°D.110°5.如图，点A在直线BG上,AD∥BC，AE平分∠GAD，若∠CBA=80°,则( )A.60°B.50°C.40°D.30°6.如图，点D,E分别在AB，BC上，DE∥AC，AF∥BC，∠1=70°，则∠2= °.知识点3两直线平行，同旁内角互补7.(2018湖北仙桃中考)如图，AD∥BC，∠C =30°，∠ADB:∠BDC= 1:2，则∠DBC的度数是( )A.30°B.36°C.45°D.50°8.如图，AB∥CD∥EF，AC∥DF，若∠BAC=120°，则∠CDF=( )A.60°B.65°C.50°D.45°知识点4 平行线的判定与性质的综合运用9.如图，已知c⊥a,c⊥b，直线b，c，d交于一点，若∠1=50°，则∠2等于( )A.60°B.50°C.40°D.30°10.如图，∠1=∠2，∠3=40°，则∠4等于( )A.120°B.130°C.140°D.40°11.(2017河北唐山路北区期中)如图，已知直线AB∥DF,∠D+∠B=180°.(1)试说明DE∥BC；(2)若∠AMD=75°，求∠AGC的度数.参考答案1.B解析：∵a∥b,∴∠2=∠1,又∠1=60°，∴∠2=60°.故选B2.C解析：如图，∵直尺的对边互相平行，∴∠3=∠1=50°,又∠3+90°+∠2=180°,∴∠2= 180°-50°-90°=40°.故选 C.名师点睛：本题考查平行线的性质和平角的定义，熟记性质并准确识图是解题的关键.3.50°解析：因为AB∥EF，所以∠A=∠2=50°.因为AC∥DF,所以∠1=∠A =50°.4.C解析：∵a∥b,∠1=50°,∴∠BAD=∠1=50°，∵AD平分∠BAC,∴∠BAC=2∠BAD = 100°,∴∠2=180°-∠BAC =180°-100°=80°.故选 C.5. B解析：∵AD∥BC,∠CBA=80°,∠DAB=∠CBA= 80°,∴∠DAG=180°-80°=100°.∵AE平分∠GAD,∴∠GAE=12∠DAG=50°.故选 B.6.10解析：DE∥AC,∴∠C=∠1 =70°. ∵AF∥BC,∴∠2=∠C=10°.7.D解析：∵AD∥BC,∴∠ADC+∠C=180°.又∠C=30°，∠ADC=180°-∠C=180°-30°=150°. ∵∠ADB：∠BDC=1：2,∴∠ADB+∠BDC=∠ADC=150°,∴∠ADB =13∠ADC =13×150°=50°.∵AD∥BC，∴∠DBC=∠ADB=50°.故选D8.A解析：∵AB∥CD,∴∠BAC+∠C=180°，又∠BAC=120°，∴∠C=180°-∠BAC=60°.∵AC∥DF,∠CDF =∠C=60°.故选A.9.B解析：a⊥c,b⊥c. ∴a∥b,∴∠2=∠1 =50°.故选 B.10.C解析：∵∠1=∠2,∴a∥b, ∴∠3 =∠5.∵∠3=40°,∴∠5=40°,∴∠4=180°-40°=140°.故选 C.11.解析：(1)∵AB∥DF,∴∠D+∠BHD= 180°,∵∠D+∠B=∠DHB,∴DE∥B C.(2)由（1)知DE∥BC,∴∠AGB=∠AMD=75°,∴AGC=180°-∠AGB =180°-75°= 105°.课时1平行线的性质提升训练1.(2018广东深圳中考)如图，直线a,b被c,d所截，且a∥b，则下列结论中正确的是( )A.∠1=∠2 C.∠3+∠4=180°B.∠3=∠4 D.∠1+∠4=180°2.(2018河南安阳五中课时作业)如图，小岛C在小岛A的北偏东60°方向，在小岛B的北偏西45°方向，那么从C岛看A，B两岛的视角∠ACB的度数为.3.(2018四川广安中考)一大门栏杆的平面示意图如图所示，BA垂直地面AE于点A，CD平行于地面AE，若∠BCD=150°，则∠ABC=度.4.(2018安徽芜湖二十七中课时作业)如图，AB∥DC，AC和BD相交于点O, E是CD上一点，F是OD上一点，且∠1=∠A.(1)试说明FE∥OC;(2)若∠BFE=70°，求∠DOC的度数.5.(2018天津市实验中学课时作业)如图,CD∥AB,CD∥GF,FA与AB交于点A，与CD交于点E.试说明∠4=∠1+∠C.6.(2018河北张家口五中课时作业)如图，已知∠1+∠2=180°，∠3=∠B，试判断∠AED与∠C的大小关系，并对结论进行说明.7.(2018山西朔州一中课时作业)课上老师呈现一个问题：如图，AB∥CD，EF⊥AB于点O，FG交CD于点P,当∠1=30°时，求∠EFG的度数.甲、乙、丙三位同学用不同的方法添加辅助线解决问题，如下图：甲同学辅助线的作法和分析思路如下：辅助线:过点F作MN∥CD分析思路：(1)欲求∠EFG的度数，由图可知只需求∠2和∠3的度数；(2)由MN∥CD可知，∠2=∠1，已知∠1的度数，可得∠2的度数；(3)由AB∥CD，MN∥CD推出AB∥MN，由此可推出∠3=∠4；(4)已知EF⊥AB，可得∠4=90°，所以可得∠3的度数；(5)从而可求∠EFG的度数.请你选择乙同学或丙同学所画的图形,描述辅助线的作法，并写出相应的分析思路.参考答案1.B解析：根据两直线平行，同位角相等,可得∠3=∠4故选B.2.105°解析：如图，过点C作CE∥AF,交AB于点E，则CE∥AF∥BD, ∴∠FAC=∠ACE,∠CBD=∠BCE,∴∠ACB=∠ACE+∠BCE=∠FAC+∠CBD=60°+45°=105°.3.120解析：如图，过点B作BG∥AE.∵CD∥AE,∴BG∥CD,∴∠GBC+∠BCD =180°.又∠BCD= 150°，∴∠GBC=180°-∠BCD=180o -150°=30°.∵BA⊥AE,∴∠BAE = 90°.∵BG∥AE,∴∠GBA+∠BAE =180°，∴∠GBA=180°-∠BAE =90°.∴∠ABC=∠GBA+∠GBC=90°+30°=120°.4.解析：(1)∵AB∥CD,∴∠A=∠C .又∠1=∠A,∴∠C=∠1.∴FE∥O C.(2)由(1)知FE∥OC,∴∠BFE+∠DOC =180°又∠BFE=70°,∴∠DOC =110°.5.解析：∵CD∥GF,∴∠C= ∠GF C.∵∠GFA=∠1+∠GFC,∴∠GFA=∠1+∠C.∵CD∥AB,CD∥GF,∴AB∥GF.∴∠A=∠GFA,∴∠A=∠1+∠C.6.解析：∠AED=∠C.理由如下：∵∠1+∠4=180°,∠1+∠2=180°,∴∠2=∠4.∴EF∥AB，∴∠3=∠ADE.又∠B=∠3，∴∠ADE=∠B，∴DE∥BC，∴∠AED=∠C.7.解析：选择乙同学所画的图形.辅助线:过点P作PH∥EF，交于点H.分析思路：(1)欲求∠EFG的度数，由PH∥EF可知，∠EFG=∠HPG,因此，只需求出∠HPG的度数；(2)欲求∠HPG的度数，由图可知只需求出∠1和∠2的度数；(3)已知∠1的度数,所以只需求出∠2的度数；(4)已知EF⊥AB可得∠4=90°；(5)由PH∥EF可推出∠3=∠4,由AB∥CD可推出∠2=∠3,由此可推出∠2=∠4，所以可得∠2的度数；(6)从而可求出∠EFG的度数.选择丙同学所画的图形.辅助线:过点O作交CD于点Q.分析思路：(1)欲求的度数，由OQ∥FG可知，∠EFG=∠EOQ，因此，只需求出∠EOQ的度数；(2)欲求∠EOQ的度数，由图可知只需求出∠2和∠3的度数；(3)已知EF⊥AB,可得∠3=90°；(4)由AB∥CD可推出∠2=∠4，由OQ∥FG可推出∠4 =∠1，由此可推出∠2=∠1,所以可得∠2的度数；(5)从而可求出∠EFG的度数.(选择任一种即可）。

人教版七年级数学下册《5.3.1平行线的性质》同步练习(含答案)

5.3 平行线的性质5.3.1平行线的性质关键问答①“三线八角”图形中，有些角不是同位角、内错角、同旁内角，那么可以通过什么方法把它们转化成同位角、内错角或同旁内角？②由平行线可以得到哪些角的数量关系？1．①如图5－3－1，直线a∥b，直线c与直线a，b相交，若∠1＝56°，则∠2等于()图5－3－1A．24°B．34°C．56°D．124°2．2018·黔南州如图5－3－2，已知AD∥BC，∠B＝30°，DB平分∠ADE，则∠DEC的度数为()图5－3－2A．30°B．60°C．90°D．120°3．②如图5－3－3，BD平分∠ABC，点E在BC上且EF∥AB，若∠FEB＝80°，则∠ABD的度数为()图5－3－3A．50°B．65°C．30°D．80°命题点1两直线平行，同位角相等[热度：92%]4．2018·襄阳如图5－3－4，把一个三角尺的直角顶点放在一直尺的一边上，若∠1＝50°，则∠2的度数为()A．55°B．50°C．45°D．40°图5－3－4 图5－3－55.③如图5－3－5，直线AB∥CD，BC平分∠ABD.若∠1＝54°，则∠2＝________°.解题突破③在能用图中字母表示的角中，∠1的同位角是哪个角？∠2的同位角是哪个角？它们之间有什么关系？命题点2两直线平行，内错角相等[热度：92%]6．2018·自贡在平面内，将一个直角三角尺按如图5－3－6所示方式摆放在一组平行线上．若∠1＝55°，则∠2的度数是()A．50°B．45°C．40°D．35°图5－3－6 图5－3－77．如图5－3－7，AB∥CD∥EF，若∠A＝30°，∠AFC＝15°，则∠C＝________°.命题点3两直线平行，同旁内角互补[热度：92%]8．2018·临沂如图5－3－8，AB∥CD，∠D＝42°，∠CBA＝64°，则∠CBD的度数是()A．42°B．64°C．74°D．106°图5－3－8 图5－3－99.④将一副三角尺和一张对边平行的纸条按如图5－3－9所示的方式摆放，两个三角尺的一直角边重合，含30°角的三角尺的斜边与纸条一边重合，含45°角的三角尺的一个顶点在纸条的另一边上，则∠1的度数是________．解题突破④∠ABD，∠CDB分别是多少度？∠1，∠ABD和∠CDB是“三线八角”中的角吗？如果不是，如何添加辅助线可以使这些角成为“三线八角”中的角？10．⑤如图5－3－10，AB∥DE∥GF，∠1∶∠D∶∠B＝2∶3∶4.求∠1的度数．图5－3－10方法点拨⑤有关角的比例问题，先设每一份为x，然后根据题意，转化为方程求解.命题点4平行线的性质与判定的综合应用[热度：96%]11．已知：如图5－3－11，∠B＝∠C，∠1＝∠2.BE与CF平行吗？请说明理由．图5－3－1112.⑥已知：如图5－3－12，∠1＝∠2，∠3＝∠4，∠5＝∠C.DE与BF平行吗？请说明理由．图5－3－12解题突破⑥(1)已知条件给出多对相等的角，可先判断这些角中是否存在同位角或内错角，若存在，则可得两直线平行；(2)利用平行线的性质时，尽可能得到与已知条件相关的角的数量关系.13．平面镜反射光线的规律：射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等．如图5－3－13①，一束光线m射到平面镜a上，被a反射后的光线为n，则入射光线m、反射光线n与平面镜a所夹的锐角相等，即∠1＝∠2.如图②所示，AB，CD为两面平面镜，经过两次反射后，入射光线m与反射光线n之间的位置关系会随之改变，请你计算：图②中，当两平面镜AB，CD的夹角∠ABC是多少度时，可以使入射光线m与反射光线n 平行但方向相反．图5－3－13典题讲评与答案详析1．C 2.B 3.A 4.D5．72[解析] 如图，∵AB∥CD，∴∠ABC＝∠1＝54°，∠2＝∠3.∵BC平分∠ABD，∴∠ABC＝∠CBD.∵∠ABC＋∠CBD＋∠3＝180°，∴∠3＝72°，∴∠2＝∠3＝72°.6．D[解析] 由题意可得：∠3＝∠1＝55°，∠2＝∠4＝90°－55°＝35°.7．15[解析]∵AB∥EF，∴∠AFE＝∠A＝30°.∵∠AFC＝15°，∴∠EFC＝15°.∵CD∥EF，∴∠C＝∠EFC＝15°.8．C[解析]∵AB∥CD，∴∠ABD＝180°－∠D＝138.∵∠CBA＝64°，∴∠CBD＝∠ABD－∠CBA＝74°. 9．15°[解析] 过点B作BE∥AF，点E在点B的左侧，∴∠ABE＝∠1.∵AF∥CD，∴BE∥CD，∴∠EBC＝∠BCD＝30°.∵∠ABC＝45°，∴∠ABE＝45°－30°＝15°，∴∠1＝∠ABE＝15°.10．解：∵∠1∶∠D∶∠B＝2∶3∶4，∴设∠1＝(2x)°，∠D＝(3x)°，∠B＝(4x)°.∵AB∥GF，∴∠GCB＝(180－4x)°.∵DE∥GF，∴∠FCD＝(180－3x)°.∵∠1＋∠GCB＋∠FCD＝180°，∴2x＋180－4x＋180－3x＝180，解得x＝36，∴∠1＝72°.11．解：BE∥CF.理由如下：∵∠1＝∠2，∠2＝∠EHB，∴∠1＝∠EHB，∴AC∥BD，∴∠B＋∠BAC＝180°(两直线平行，同旁内角互补)．∵∠B＝∠C，∴∠C＋∠BAC＝180°(等量代换)，∴BE∥CF(同旁内角互补，两直线平行)．12．解：DE∥BF.理由如下：∵∠3＝∠4，∴BD∥CF，∴∠C＋∠CDB＝180°.又∵∠5＝∠C，∴∠CDB＋∠5＝180°，∴AB∥CD，∴∠2＝∠BGD.又∵∠1＝∠2，∴∠1＝∠BGD，∴DE∥BF.13．解：由题意可知∠1＝∠2，∠3＝∠4.若使入射光线m与反射光线n平行，则∠5＋∠6＝180°.∵∠1＋∠2＋∠5＝180°，∠3＋∠6＋∠4＝180°，∴∠1＋∠2＋∠3＋∠4＝180°，∴∠2＋∠3＝90°，∴在三角形ABC中，∠ABC＝90°.【关键问答】①通过对顶角相等、邻补角互补等进行转化．②两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补．。

人教版七年级数学 5.3 平行线的性质同步训练(含答案)

人教版七年级数学 5.3 平行线的性质同步训练一、选择题（本大题共10道小题） 1. 如图，直线l 1∥l 2，则∠α为()A. 150°B. 140°C. 130°D. 120°2. （2020·河南）如图， 1l ∥2l ，3l ∥4l ，若∠1=70°，则∠2的度数为( ) A.100° B.110° C.120° D.130°3. 如图，直线m n ∥，155∠=°，245∠=°则3∠的度数为（） A ．80°B ．90°C ．100°D ．110°mn1234. （2020·随州）2.如图，直线1l ∥2l ，直线l 与1l ，2l 分别交于A ，B 两点，若∠1=60°，则∠2的度数是（） B.60° D.100°C.120°D.140°5. 如图，AB ∥CD ，DA ⊥AC ，垂足为A ，若∠ADC ＝35°，则∠1的度数为( )A . 65°B . 55°C . 45°D . 35°6. （2020·常州）如图，直线a、b被直线c所截，a∥b，∠1＝140°，则∠2的度数是() A．30°B．40°C．50°D．60°7. 将一幅直角三角板（∠A＝∠FDE＝90°，∠F＝45°，∠C＝60°，点D在边AB上）按图中所示位置摆放，两条斜边为EF，BC，且EF//BC，则∠ADF等于（）A．70°B．75°C．80°D．85°EFAC BD8. 一个等腰直角三角尺和一把直尺按如图所示的位置摆放，若∠1＝20°，则∠2的度数是（）A．15°B．20°C．25°D．40°9. 如图，∠AOB的一边OA为平面镜，∠AOB＝37°36′，在OB上有一点E，从E点射出一束光线经OA上一点D反射，反射光线DC恰好与OB平行，则∠DEB 的度数是()A．75°36′B．75°12′C．74°36′D．74°12′10. 如图所示，两直线AB CD、平行，则l23456∠+∠+∠+∠+∠+∠=( ) A．630︒B．720︒C．800︒D．900︒65HG 4321DCFEBA二、填空题（本大题共8道小题）11. 如图，直线l与直线a，b相交．若a b∥，170∠=°，则2∠的度数是．图221bal12. 如图，已知a b∥，170∠=︒，240∠=︒，则3∠=__________．ba321CBA13. 有一直的纸带，如图折叠时，α∠=_________．α30°E DCBA14. （2020·黄冈）已知：AB∥EF，∠ABC=75°，∠CDF=135°，则∠BCD=________度．135°75°A BE FD15. （2019·上海）如图，已知直线l1∥l2，含90°角的三角板的直角顶点C在l1上，30°角的顶点A在l2上，如果边AB与l1的交点D是AB的中点，那么∠1＝度．16. （2020·恩施）如图，直线12//l l，点A在直线1l上，点B在直线2l上，AB BC=，30C ∠=︒，180∠=︒，则2∠=______．17. （2020·永州）已知直线//a b ，用一块含30°角的直角三角板按图中所示的方式放置，若125∠=︒，则2∠=_________．18. （2020·新疆）如图，若AB ∥CD ，∠A ＝110°，则∠1＝________°．三、解答题（本大题共3道小题）19. 已知如图所示，AB DE ∥,116D ∠=︒，93DCB ∠=︒，求B ∠的度数.D CEBA20. 如下图所示，已知AB CD ∥，分别探讨下面四个图形中BPD ∠与B ∠，D ∠的关系.PPPDC BA(1) (2) (3) (4)DD CC BBAA A BCD P21. 请你分析下面的题目，从中总结规律，填写在空格上，并选择一道题目具体书写证明.（1）如图⑴，已知：AB CD ∥，直线EF 分别交AB ，CD 于M ，N ，MG ，NH 分别平分AME ∠，CNE ∠.求证：MG NH ∥.从本题我能得到的结论是： . （2）如图⑵，已知：AB CD ∥，直线EF 分别交AB ，CD 于M ，N ，MG ，NH 分别平分BMF ∠， CNE ∠.求证：MG NH ∥.从本题我能得到的结论是： . （3）如图⑶，已知：AB CD ∥，直线EF 分别交AB ，CD 于M ，N ，MG ，NH 分别平分AMF ∠， CNE ∠，相交与点O .求证：MG NH ⊥. 从本题我能得到的结论是： . （4）如图⑷，已知：AB ，CD 相交于O ，OF 平分AOC ∠，OE 平分BOD ∠.求证：F ，O ，E 三点共线.从本题我能得到的结论是： .(1)A B C DE FG H M N(2)NMFEDC B A GH (3)NM FEDC B A G H O (4)A BCD E F O人教版七年级数学 5.3 平行线的性质同步训练-答案一、选择题（本大题共10道小题） 1. 【答案】D 【解析】α＝70°＋(180°－130°)＝120°.2. 【答案】B【解析】如图，∵直线l1∥l2，∴∠3＝∠1＝70°，∵3l ∥4l，∴∠3＋∠2＝180°，∴ ∠2＝110°．3. 【答案】C ．4. 【答案】C【解析】本题考查了平行线的性质、邻补角的性质，解答过程如下：如图所示，∵1l ∥2l ，∴∠3=∠1=60°， ∵∠2+∠3=180°，∴∠2=180°-∠3=180°-60°=120°.因此本题选C ．5. 【答案】B【解析】∵DA ⊥AC ，∠ADC ＝35°，∴∠ACD ＝90°－∠ADC ＝90°－35°＝55°，∵AB ∥CD ，∴∠1＝∠ACD ＝55°，故选B.6. 【答案】B【解析】本题考查了平行线的性质，如图，由于a ∥b ，所以∠3＝∠2，又由于∠1＋∠3＝180°，∠1＝140°，所以∠2＝40°．7. 【答案】B，【解析】本题考查平行线的性质．解：∵EF //BC ，∴∠CGD ＝∠E ＝45°，3∵∠CGD 是△GDB 的外角，∴∠GDB ＝∠CGD －∠B ＝45°－30°＝15°． ∵∠EDF ＝90°，∴∠ADF ＝180°－15°－90°＝75°．故选B.GE F ACBD8. 【答案】C【解析】∵AB ∥CD ， ∴∠3＝∠1＝20°，∵三角形是等腰直角三角形，∴∠2＝45°﹣∠3＝25°．9. 【答案】B【解析】根据平面镜反射原理可知，∠ADC ＝∠ODE ，∵DC ∥OB ，∴∠ADC ＝∠AOE ，∴∠ODE ＝∠AOE ＝37°36′，∴∠DEB ＝∠ODE ＋∠AOE ＝37°36′＋37°36′＝75°12′，故选B.10. 【答案】D.【解析】分别过E F C H ，，，点做AB 的平行线，再求各个角度的和．选D二、填空题（本大题共8道小题） 11. 【答案】110°．12. 【答案】70︒13. 【答案】75︒【解析】∵AC BD ∥ ∴30CBE ∠=︒由折叠问题可知：ABC ABD ∠=∠∴()118030752ABD ∠=︒-︒=︒∵AC BD ∥∴75ABD α∠=∠=︒14. 【答案】30【解析】本题考查了平行线的性质，对顶角以及三角形外角等知识．如答题所示，由AB ∥EF 可得∠B+∠1=180°，而∠B=75°，则∠1=105°；有对顶角相等可得∠1=∠2=105°；由三角形的一个外角等于与它不相邻的两个内角之和，得∠2+∠C=135°，进而求出∠C=30°，因此本题答案为30．21135°75°A BEFCD15. 【答案】120【解析】∵D 是斜边AB 的中点，∴DA ＝DC ，∴∠DCA ＝∠DAC ＝30°，∴∠2＝∠DCA ＋∠DAC ＝60°，∵11∥l2，∴∠1＋∠2＝180°，∴∠1＝180°－60°＝120°．16. 【答案】40°【解析】∵AB =BC ，∠C =30︒， ∴∠CAB =30︒，∴∠CBA =120︒， ∵∠1=80︒， ∴∠EBA =40︒， ∵12//l l∴240EBA ∠∠==︒，故答案为：40︒．17. 【答案】35°【详解】如图，标注字母，延长ED 交a 于C ，由题意得：30,90,B DEB ∠=︒∠=︒ 60,BDE ∴∠=︒//,a b 2,DCA ∴∠=∠1,125,BDE DCA ∠=∠+∠∠=︒602535,DCA ∴∠=︒-︒=︒235.∴∠=︒故答案为：35.︒18. 【答案】70【解析】本题考查了平行线的性质以及对顶角的性质．如答图，因为AB ∥CD ，所以∠A ＋∠2＝180°，所以∠2＝180°－∠A ＝180°－110°＝70°．因为∠1＝∠2，所以∠1＝70°．三、解答题（本大题共3道小题）19. 【答案】29︒【解析】过点C 作直线CF AB ∥，因为AB DE ∥,所以AB DE CF ∥∥，DCFEBA因为116D ∠=︒，18011664DCF ∠=︒︒=︒-因为93C ∠=︒，所以936429BCF ∠=︒-︒=︒，因为B BCF ∠=∠，所以29B ∠=︒．20. 【答案】过P 做AB 、CD 的平行线，即可得如下结论： ⑴360BPD B D ∠+∠+∠= ； ⑵BPD D B ∠=∠-∠ ； ⑶BPD B D ∠=∠+∠ ； ⑷BPD B D ∠=∠-∠ .21. 【答案】（1）两直线平行，同位角的角平分线平行. （2）证明：∵AB ∥CD ，∴BMF CNE ∠=∠ 又∵MG ，NH 分别平分BMF ∠，CNE ∠∴1122GMF BMF CNE HNM ∠=∠=∠=∠，∴MG ∥NH从本题我能得到的结论是：两直线平行，内错角的角平分线平行. （3）证明：∵AB ∥CD ，∴180AMF CNE ∠+∠= 又∵MG ，NH 分别平分AMF ∠，CNE ∠∴119022GMF HNE AMF CNE ∠+∠=∠+∠=∴18090MON GMF HNE ∠=-∠-∠=，∴MG ⊥NH从本题我能得到的结论是：两直线平行，同旁内角的角平分线垂直. （4）证明：∵AB ，CD 相交于O ，∴AOC BOD ∠=∠ ∵OF 平分AOC ∠，OE 平分BOD ∠∴12AOF AOC ∠=∠，12DOE BOD ∠=∠∵180AOC AOD ∠+∠=，∴180AOF AOD DOE ∠+∠+∠=即F ，O ，E 三点共线从本题我能得到的结论是：对顶角的平分线，在一条直线上. 要证明三点共线，我们可以通过证明这三点所成的角为180.。

人教版七年级数学下册第五章 5.3.1 平行线的性质同步练习题(含答案)

第五章相交线与平行线5.3.1 平行线的性质一、选择题1、如图1，在甲，乙两地之间修一条笔直公路，从甲地测得公路的走向是北偏东50°，甲，乙两地同时开工，若干天后，公路准确接通，则乙地所修公路走向是（）A．北偏45° B．南北方向 C．南偏西50° D．以上都不对2、如图2所示，AD∥EF∥BC，AC平分∠BCD，图中和α相等的角有（）A．2个 B．3个 C．4个 D．5个3、如图3，直线AB∥CD，直线EF分别与直线AB，CD相交于点G，H.若∠1＝135°，则∠2的度数为( )A．65°B．55°C．45°D．35°4、如图，nm//，那么∠1.∠2.∠3的关系是（）A.∠1+∠2+∠3=360°B.∠1+∠2-∠3=180°C.∠1-∠2+∠3=180°D.∠1+∠2+∠3=180°5、如图，已知AB∥CD，EA是∠CEB的平分线，若∠BED=40°，则∠A的度数是（）A．40°B．50°C．70°D．80°二、填空题6、如图6所示，若AB∥CD，∠DEF=120°，则∠B=_______．7、在同一平面内，两条直线的位置关系只有两种．8、如图，AB∥CD，直线l分别与AB，CD相交，若∠1＝50°，则∠2的度数为．9、如图，AB∠CD，OE平分∠BOC，OF∠OE，OP∠CD，∠ABO＝40°，则下列结论：∠∠BOE＝70°；∠OF平分∠BOD；∠∠POE＝∠BOF；∠∠POB＝2∠DOF.其中正确结论有（只填序号）.10、如图，AB∥CD，∠1=64°，FG平分∠EFD，则∠EGF= °．三、解答题11、如图，直线AB∥CD，BC平分∠ABD，∠1＝65°，求∠2的度数．12、如图，C岛在A岛的北偏东45°方向，在B岛的北偏西25°方向，则从C岛看A，B两岛的视角∠ACB的度数是多少？13、如图，已知EAB 是直线，AD ∥BC ，AD 平分∠EAC，试判定∠B 与∠C 的大小关系，并说明理由．14、如图，点A 在直线MN 上，且MN//BC.求证：∠BAC+∠B+∠C=180°.NB C 15、如图，已知AB ∥DE ∥CF ，若∠ABC ＝70°，∠CDE ＝130°，求∠BCD 的度数．16、已知：如图，D ，F ，E 分别是BC ，AC ，AB 上的点，DF ∥AB ，DE ∥AC ，试说明∠EDF ＝∠A.17、如图，已知AD∥BE，∠A ＝∠E，求证：∠1＝∠2.18、如图，已知∠B=∠C ，AD ∥BC,求证：AD 平分∠CAE ．19、阅读下列解答过程：如图甲，AB ∥CD ，探索∠P 与∠A ，∠C 之间的关系．参考答案：一、1、C 2、C（点拨：∠FGC=∠FCA=∠BCA=∠DAC） 3、C 4、B 5、C二、6、60°7、相交，平行8、50°9、①②③10、32三、11、解：∵直线AB∥CD，∠1＝65°，∴∠ABC＝∠1＝65°.∵BC平分∠ABD，∴∠ABD＝2∠ABC＝130°.∵直线AB∥CD，∴∠ABD＋∠BDC＝180°.∴∠2＝∠BDC＝180°－∠ABD＝180°－130°＝50°.12、70°13、解：∠B＝∠C.理由：∵AD平分∠EAC，∴∠EAD＝∠DAC.∵AD∥BC，∴∠EAD＝∠B，∠DAC＝∠C.∴∠B＝∠C.14、证明：∵MN∥BC，∴∠B=∠MAB，∠C=∠NAC.∵∠BAC+∠MAB+∠NAC=180°，∴∠BAC+∠B+∠C=180°.15、解：∵AB∥CF，∠ABC＝70°，∴∠BCF＝∠ABC＝70°.又∵DE∥CF，∠CDE＝130°，∴∠DCF＋∠CDE＝180°.∴∠DCF＝50°.∴∠BCD＝∠BCF－∠DCF＝70°－50°＝20°.16、解：∵DF∥AB(已知)，∴∠A＋∠AFD＝180°(两直线平行，同旁内角互补)．∵DE∥AC(已知)，∴∠AFD＋∠EDF＝180°(两直线平行，同旁内角互补)．∴∠A＝∠EDF(同角的补角相等)．17、证明：∵AD∥BE，∴∠A＝∠EBC.∵∠A＝∠E，∴∠EBC＝∠E.∴DE∥AB.∴∠1＝∠2.18、证明：∵AD∥BC，∴∠2=∠B，∠1=∠C.∵∠B=∠C，∴∠1=∠2，∴AD平分∠CAE．解：过点P作PE∥AB.∵AB∥CD，∴PE∥AB∥CD(平行于同一条直线的两条直线互相平行)．∴∠1＋∠A＝180°(两直线平行，同旁内角互补)，∠2＋∠C＝180°(两直线平行，同旁内角互补)．∴∠1＋∠A＋∠2＋∠C＝360°.又∵∠APC＝∠1＋∠2，∴∠APC＋∠A＋∠C＝360°.如图乙和图丙，AB∥CD，请根据上述方法分别探索两图中∠P与∠A，∠C之间的关系．19、解：如图乙，过点P作PE∥AB.∵AB∥CD(已知)，∴PE∥AB∥CD(平行于同一直线的两条直线平行)．∴∠A＝∠EPA，∠EPC＝∠C(两直线平行，内错角相等)．∵∠APC＝∠EPA＋∠EPC，∴∠APC＝∠A＋∠C(等量代换)．如图丙，过点P作PF∥AB.∴∠FPA＝∠A(两直线平行，内错角相等)．∵AB∥CD(已知)，∴PF∥CD(平行于同一直线的两条直线平行)．∴∠FPC＝∠C(两直线平行，内错角相等)．∵∠FPC－∠FPA＝∠APC，∴∠C－∠A＝∠APC(等量代换)．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

-----好资料学习 5.3.1平行线的性质同步练习题:
一、基础过关）∠2的依据是（a、b被c所截，得到∠1=b1．如图1，a∥， B．两直线平行，内错角相等 A．两直线平行，同位角相等 D．内错角相等，两直线平行 C．同位角相等，两直线平行
(1) (2) (3)
的位置关系d，则直线c、⊥c，b⊥d、b、c、d，若a∥b，a2．同一平面内有四条直线a ）为（．无法确定．相交 D B A．互相垂直．互相平行 C ），那么（ 2，AB∥CD3．如图5 1=．∠∠．∠2=∠3 DA．∠1=∠4 B．∠1=∠3 C ）3，在平行四边形ABCD中，下列各式不一定正确的是（4．如图 3=180°．∠2+∠2=180 A．∠1+∠° B °2+∠
4=180．∠．∠3+∠4=180° DC ）的度数为（ DB°，平分∠ADE，则∠DEC45．如图，AD ∥BC，∠B=30 120°90° D．°A．30° B．60
C．
(4) (5)
________．，则∠E+∠B的度数为DEEF56．如图，AB∥，BC∥
的角平分线，CDABAD、∠DFCD．如图，AB∥，AE、分别是∠7 为什么？DF与平行吗？?AE
更多精品文档
学习-----好资料
二、综合创新:
8．（综合题）如图，已知∠AMB=∠EBF，∠BCN=∠BDE，求证：∠CAF=∠
AFD．
9．（应用题）如图，一条公路修到湖边时，需拐弯绕湖而过，如果第一次拐的角A是120°，第二次拐的角B是150°，第三次拐的角是∠C，这时的道路恰好和第一次拐弯之前的道路平行，
问∠C是多少度？说明你的理由．
10．（创新题）（1）如图，若AB∥DE，∠B=135°，∠D=145°，你能求出∠C的度数吗？
（2）在AB∥DE的条件下，你能得出∠B、∠C、∠D之间的数量关系吗？并说明理
由．
更多精品文档．
学习-----好资料
11．（1）（2005年，江苏常州）如图6，已知AB∥CD，直线L分别交AB、CD?于点E、F，EG平分∠BEF，若∠EFG=40°，则∠EGF的度数是（）
A．60° B．70° C．80° D．90°
(6) (7)
（2）（2005年，新疆乌鲁木齐）已知：如图7，AB∥DE，∠E=65°，则∠B+∠C?的度数是（） A．135° B．115° C．65° D．35°
三、名校培优:
12．（探究题）如图，在折线ABCDEFG中，已知∠1=∠2=∠3=∠4=?∠5，?延长AB、GF交于点M．试探索∠AMG与∠3的关系，并说明理
由．
13．（开放题）已知如图，四边形ABCD中，AB∥CD，BC∥AD，那么∠A与∠C，∠B与∠D的大小关系如何？请说明你的理
由．
更多精品文档．
学习-----好资料
橡皮膜上的几何学
有一种只研究图形各部分位置的相对次序，?而不考虑它们尺寸大小的新的几何学，叫做拓扑学，有时也称它是橡皮膜上的几何学．因为橡皮膜上的图形，随着橡皮膜的拉动，其长度、面积都将发生变化，但有些性质不变．
现用一个正方体做游戏：如图，假设正方体的八个顶点表示均匀分布在地球上的八个城市，而每个城市都有三条路线与毗邻城市相连．某学者从A城出发，要到C′城作考察，途中顺便到其他的六个城市旅游．?要求这六个城市都只经过一次而最后到达C′城．请画出他的旅行路
线．
更多精品文档．
学习-----好资料
答案:
1．A 2．B 3．D 4．D 5．B
6．180°点拨：∵AB∥EF，∴∠B=∠CFG．
∵BC∥DE，
∴∠E+∠BFE=180°．
∵∠GFC=∠BFE，
∴∠B+∠E=180°．
7．解：平行．
∵AB∥CD，
∴∠BAD=∠CDA（两直线平行，内错角相等）．
∵AE、DF分别是∠BAD、∠CDA的平分线，
11∠BAD，∠FDA=∴∠EAD=∠CDA．22∴∠EAD=∠FDA．∴AE∥DF（内错角相等，两直线平行）．
8．证明：∵∠AMB=∠DMN，又∠ENF=∠AMB，∴∠DMN=∠ENF，
∴BD∥CE．∴∠BDE+∠DEC=180°．
又∠BDE=∠BCN，∴∠BCN+∠CED=180°，
∴BC∥DE，∴∠CAF=∠AFD．
点拨：本题重点是考查两直线平行的判定与性质．
9．解：∠C=150°．
理由：如答图，过点B作BE∥AD，则∠ABE=∠A=120°（两直线平行，内错角相等）．∴∠CBE=∠ABC-∠ABE=150°-120°=30°．
∵BE∥AD，CF∥AD，
∴BE∥CF（平行于同一条直线的两直线平行）．
∴∠C+∠CBE=180°（两直线平行，同旁内角互补）．
∴∠C=180°-∠CBE=180°-30°
=150°．
10．解：（1）如答图5-3-2，过点C作CF∥AB，
则∠1=180°-∠B=180°-135°=45°（两直线平行，同旁内角互补）．更多精品文档．
学习-----好资料
AB，AB，DE∥∵CF∥（平行于同一条直线的两直线平行）．∴CF∥DE
°（两直线平行，同旁内角互补）．°-145°=352=∠180°-∠D=180 ∴∠°．+35°=80∴∠BCD=∠1+∠2=45°
°．C+∠D=360 （2）∠B+∠同旁内角互1=180°（两直线平行，?CF作∥AB，得∠B+∠理由：如答图5-3-2过点C ．补），∥AB，DE∥AB ∵CF ．∴CF∥DE（平行于同一条直线的两直线平行）
D+∴∠∠2=180°（两直线平行，同旁内角互补）．
∠2+∠D=360°．∴∠B+∠1+ BCD+∠D=360°．即∠B+∠ AB与的纽带．DE 点拨：辅助线CF是联系C ）（211．（1）B
3．∠12．解：∠AMG=
2，理由：∵∠1=∠
．∥∴ABCD（内错角相等，两直线平行），∵∠3=∠4
∥∴CDEF（内错角相等，两直线平行）．
∥EF（平行于同一条直线的两直线平行）．AB ∴．5（两直线平行，同位角相等）AMG= ∴∠∠ 3，5= 又∠∠
．AMG= ∴∠∠3
即可．∥EFAMAMG=3= 点拨：因为∠∠5，所以欲证∠∠3，只要证∠∠A=C，∠B=D．．解：∠13 ABBCAD 理由：∵∥，∥，CD更多精品文档．
学习-----好资料
∴∠A+∠B=180°（两直线平行，同旁内角互补）．
∠C+∠B=180°．
∴∠A=∠C．
同理∠B=∠D．
数学世界（答案）
要找出这条路线，最好是把它化为平面上的图形来考虑，为此，?我们不妨设想这个正方体是由有弹性的橡皮膜制成的，再用剪刀沿着棱剪掉它的一个面，然后扯着这个缺口把它拉开铺平，就成为一个平面图形．这个图形叫做正方体的拓扑平面图，如答图．图中带箭头的路线就表示它的一种解答．
更多精品文档．。