混沌映射(序列)matlab算法“小全”:Logistic、Henon、帐篷、kent(含混沌二值图像生成函数)
4种混沌映射的特点

4种混沌映射的特点
混沌映射是一种重要的非线性动力学系统,具有复杂的动力学特性,已经被广泛应用于许多领域。
本文介绍了四种常见的混沌映射及其特点。
1. Logistic映射
Logistic映射是一种广泛应用于混沌理论研究中的典型非线性动力学系统。
它的特点是简单易行,具有双稳态和混沌行为,是研究混沌现象的经典示例。
2. Henon映射
Henon映射是一种双参数混沌映射,它的特点是具有分形结构、非周期性、高度敏感依赖于初值和参数,并且在参数空间中形成了复杂的混沌吸引子。
3. Lorenz映射
Lorenz映射是一种具有吸引子的三维非线性动力学系统,它的特点是具有强的混沌行为和灵敏的初始条件依赖性,常被用于模拟大气和海洋中的流体运动。
4. Ikeda映射
Ikeda映射是一种典型的非线性动力学系统,它的特点是具有高度敏感的初值和参数、分形结构和复杂的混沌吸引子,常被用于研究光学系统中的非线性动力学现象。
以上是四种典型的混沌映射及其特点。
混沌映射在科学研究、信息加密、密码学、图像处理等领域有着广泛的应用价值,未来将会有
更多的研究和应用。
Matlab混沌仿真实现
些混沌系统进行研究及Matlab仿真是非常必要的,可以为进一步研究混沌系统及控制和利用混沌提供简便的程序方法。
1 Logistic映射Logistic映射,在19世纪中叶由荷兰生物学数学家Verhulst提出,表达式为:xn+1=μxn(1-xn) (xn∈[0,1],μ∈[0,4],n=0,1,…) (1)对于每个确定的m,可以得到相应的一系列x0,x1,…,xn。
通过对μ取值的讨论,我们不难看出:当0<μ≤1时,系统项目号:广西区教育厅立项项目(06年度),学校学科软环境项目“混沌系统的神经网络控制研究(Z20664)”典型混沌系统的Matlab仿真实现王改云 马姝靓 桂林电子科技大学计算机与控制学院 541004引言自20世纪60年代,洛伦兹发现混沌现象以来,混沌理论研究一直受到普遍的关注。
随着混沌研究的不断发展,人们开始把目光聚焦在控制混沌和利用混沌的研究上。
控制和利用混沌的研究都是基于一些典型的混沌系统来进行的。
因此,对这动力学形态非常简单,只有一个周期点x0=0;当1<μ<3时,系统动力学形态也比较简单,有两个周期点0,;当3≤μ≤4时,系统动力学形态十分复杂,系统由倍周期通向混沌。
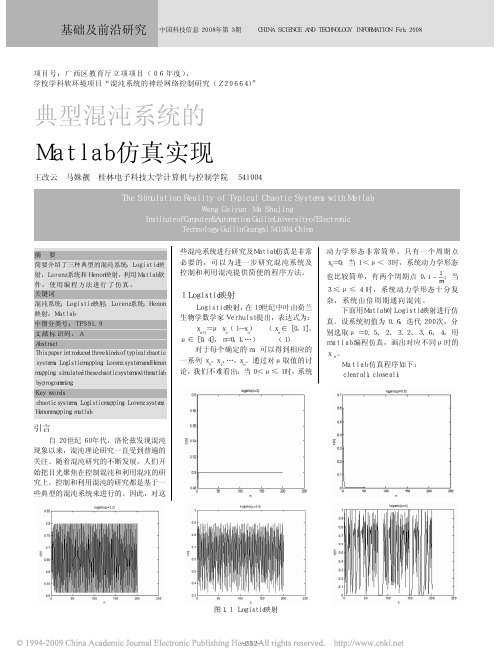
下面用Matlab对Logistic映射进行仿真。
设系统初值为0.6,迭代200次,分别选取μ=0.5、2、3.2、3.6、4,用matlab编程仿真,画出对应不同μ时的xn。
Matlab仿真程序如下:clear all;close all;图1.1 Logistic映射mu=0.5;x=0.6*ones(1,200);for n=1:200 x(n+1)=mu*x(n)*(1-x(n));endplot(x(1,:),'k','markersize',10);xlabel('n');ylabel('x(n)');title('logistic(\mu=0.5)');得到的仿真结果:(图1.1)进一步研究m的不断变化对系统的影响。
Logistic映射论文:Logistic映射与Henon映射的算法实现及其序列分析

Logistic映射论文:Logistic映射与Henon映射的算法实现及其序列分析摘要:混沌是一种复杂的非线性、非平衡的动力学过程。
该文实现了分别用logistic映射与henon映射实现了对txt 文本文件进行加密解密。
通过对混沌映射产生的序列进行matlab仿真实验分析,证明了混沌映射具有对初值极端敏感、便历性、非周期性和类随机性等特点。
混沌序列非常适合用于作为密码算法中的密钥流产生器,用以构成性能良好的密码系统。
关键词:logistic映射;henon映射;matlab仿真algorithm implementation and sequence analysis of logistic map and henon mapwu wei-gao(city college of dongguan university of technology, dongguan 523106, china)abstract: by chaos is a complex non-linear and non-equilibrium dynamics process. this paper realizes the implementation of encryption and decryption on tet text file through using logistic map and henon map respectively. it is proved that chaotic map has the characteristics of extreme sensitivity on initialvalue, convenience, and class aperiodic random and so on through carrying out matlab simulation sequence analysis on sequences generated by chaotic map. chaotic sequence is very suitable for being used as key stream generator in cryptographic algorithm, which constitutes a password system with good performance.key words: henon map; rc4 algorithm; client/server model随着计算机技术和网络通信技术的不断发展和迅速普及,通信保密问题日益突出。
2第二章 Logistic 映射和混沌

x0 = 0.4 µ = 4.0
图 2.8a
x0 = 0.4001 µ = 4.0
图 2.8b
xn
1
0.8
0.6
0.4
0.2
0 0
xn
1
0.8
0.6
0.4
0.2
0 0
10
20
10
20
Logistic 映射
n
30
40
50
n
30
40
50
Logistic 映射
4、迭代的几何表示
在 µ = 0.5 ,µ = 2.0 和 µ = 3.2 三种情况下迭代过程的
C. 周期4解 周期4出现时,初值轨迹构成的序列为: x 0 , x1, x 2 ," , x a , x b , x c , x d , x a , x b , x c , x d ,"
周期4解 x 满足: x = f ( f ( f ( f ( x )))) = f 4 ( x )
无论如何,上式可以简化为:
xn
1
0.8
0.6
0.4
0.2
0
n
0
100 200 300 400 500
图 2.7 µ = 4.0, x0 = 0.9系统演化
Logistic 映射
当 µ = 4.0 时,系统最终状态两个特点:
a、给定初值,即使迭代步数 n 足够大,系统最 终的演化状态不确定;
b、初始条件敏感:即初始条件有微小的差别, 迭代一定次数后,系统状态有很大的差别。(如下 图,两初值分别为 x 0 = 0.4000 , 0.4001)。
df (x) ⋅ df (x) < 1 dx X=XA dx X=XB
混沌映射(序列)matlab算法“小全”:Logistic、Henon、帐篷、kent(含混沌二值图像生成函数)

混沌映射(序列)matlab 算法“小全”:Logistic 、Henon 、帐篷、kent (含混沌二值图像生成函数)1.Logistic (罗切斯特)映射变换核:)1(1n n n x ax x −=+绘图程序:n=64;key=0.512;an=linspace(3.1,3.99,400);hold on;box on;axis([min(an),max(an),-1,2]);N=n^2;xn=zeros(1,N);for a=an;x=key;for k=1:20;x=a*x*(1-x);%产生公式end;for k=1:N;x=a*x*(1-x);xn(k)=x;b(k,1)=x;%一维矩阵记录迭代结果end;plot(a*ones(1,N),xn,'k.','markersize',1);end;%figure;%imhist(b)实用混沌加密函数:function ichao_ans=ichaos_logistic(varargin)%logistic 序列生成算法%函数名:%logistic 混沌序列生成函数%参数:%(n ,key ),n 为矩阵阶数,key 为迭代初始值。
%(n ),n 为矩阵阶数,key=0.600。
%()或(n ,key ,...),n=64,key=0.600。
switch nargin;case 1;n=varargin{1};key=0.600;case 2;n=varargin{1};key=varargin{2};otherwisekey=0.600;n=64;endN=n^2;xn=zeros(1,N);a=4;x=key;for k=1:20;x=a*x*(1-x);%产生公式end;for k=1:N;x=a*x*(1-x);xn(k)=x;%一维矩阵记录迭代结果end;c=reshape(xn,n,n);%一维矩阵转换二维矩阵d=zeros(n,n);%二维混沌矩阵调制for a1=1:n;for a2=1:n;if c(a1,a2)>=0.5;d(a1,a2)=1;else d(a1,a2)=0;end;end;end;%figure;title('logistic 映射');%imshow(d);ichao_ans=d;2.Henon (埃农)映射变换核:21n 11x {n n nn ax y bx y −+==++绘图程序:b=0.3;N=400;an=ones(1,N);xn=zeros(1,N);hold on;box on;x=0;y=0;for a=0:0.001:1.4for k=1:N;xm=x;ym=y;x=ym+1-a*xm.*xm;y=b*xm;endxn(1)=x;for n=2:N;xm=x;ym=y;x=ym+1-a*xm.*xm;y=b*xm;xn(n)=x;endplot(an*a,xn,'k.','markersize',1);endxlim([0,a]);实用混沌加密函数:function ichao_ans=ichaos_henon(varargin)%埃农(Henon )映射%0.2<key<0.314;理想范围(0.25—0.314)。
Logistic满映射混沌序列性能分析

Logistic满映射混沌序列性能分析作者:严三国陈永彬来源:《现代电子技术》2010年第03期摘要:通过建立Logistic满映射混沌模型,产生Logistic满映射混沌模拟序列,再进行二值量化后,利用Matlab 7.0对其性能进行仿真分析。
主要分析其初值敏感性、相关性、平衡性、遍历性、相空间及倍周期分岔特性。
分析结果表明,Logistic满映射混沌序列具有良好的自相关性、互相关性、平衡性,而且其序列数量众多,其性能优于传统的伪随机序列。
该序列可广泛用于数字加密、扩频通信等领域中。
关键词:混沌序列;相关性;平衡性;相空间;Matlab仿真中图分类号:TN914 文献标识码:A文章编号:1004-373X(2010)03-194-03Performance Analysis of Full Mapping Chaotic Sequence about LogisticYAN Sanguo,CHEN Yongbin(Chengdu Electromechanical College,Chengdu,610031,China)Abstract:To produce Logistic full mapping chaos analog sequence,a Logistic full mapping chaos model is built,and then it is guantified two level digital sequence. The performance analysis of this chaotic sequence is carried out by use of Matlab 7.0 simulation. Senstivity of initialvalue,correlation,balance,ergodic,phase dimensional and double-periods forks characteristic are mainly analyzed. The analysis results show that the performance of this chaotic sequence is better than that of traditional pseudo random sequences for more well correlative performance and balance performance,and their number is large. It can be widely used in digital encryption and spread spectrum communcation.Keywords:chaotic sequence;correlation;balance;phase dimensional;Matlab simulation混沌现象是在非线性动态系统中出现的确定性、类似随机的过程,这种过程非周期、不收敛但有界,并且对初始值具有及其敏感的依赖性[1]。
混沌信号的产生 matlab

混沌信号的产生及其在Matlab中的实现一、混沌信号的概念与特点混沌是一种在确定性系统中表现出的随机、不可预测的行为。
混沌系统具有以下几个显著特征:1. 灵敏依赖于初值:在混沌系统中,微小的初值变化会导致系统行为的巨大变化,这就是所谓的“蝴蝶效应”。
2. 随机性和周期性:混沌系统表现出随机性和周期性的叠加,使得系统的行为呈现出复杂的、看似无序的特征。
3. 分形结构:混沌系统的轨迹具有分形结构,表现出自相似性和自组织性。
二、混沌信号的产生原理混沌信号的产生通常基于非线性动力系统模型,其中最经典的混沌系统包括 Logistic 映射、Henon 映射等。
混沌信号的产生一般遵循以下步骤:1. 选择合适的混沌系统模型,比如 Logistic 映射:$x_{n+1} =rx_n(1-x_n)$。
2. 选择初值和模型参数,并设定迭代次数。
3. 进行迭代计算,得到混沌信号的时域序列。
三、Matlab 中的混沌信号生成Matlab 是一种强大的科学计算软件,提供了丰富的工具箱和函数,使得混沌信号的产生和分析变得非常简单。
在Matlab 中,可以通过以下几种方法产生混沌信号:1. 直接求解微分方程:利用ode45函数求解混沌系统的微分方程,得到混沌时域序列。
2. 迭代计算:利用for循环结构进行模型的迭代计算,得到混沌信号的时域序列。
3. 利用现成的工具箱:Matlab 提供了一些专门用于产生混沌信号的工具箱,比如 ChaosBox。
四、示例代码以下是一个利用 Logistic 映射产生混沌信号的示例代码:```matlabLogistic 映射参数r = 3.9;时域序列长度N = 1000;初值x0 = 0.1;初始化时域序列x = zeros(1, N);x(1) = x0;迭代计算for i = 1:N-1x(i+1) = r * x(i) * (1 - x(i));end绘制混沌信号时域图plot(x);xlabel('时域');ylabel('信号幅值');title('Logistic 映射产生的混沌信号');```五、混沌信号的应用混沌信号作为一种具有随机性和周期性的信号,具有广泛的应用价值,包括但不限于:1. 加密通信:混沌信号可用于加密通信系统中的信息传输,利用混沌的随机特性可以提高数据的安全性。
基于matlab的四种映射生成的混沌序列

相关性分析 Rx=xcorr(x,'biased'); Ry=xcorr(y,'biased'); Rz=xcorr(z,'biased'); Rp=xcorr(p,'biased'); %求互相关函数 Rxy=xcorr(x,y,'biased'); %chebyshev 与 logistic 的互相关 Rxp=xcorr(x,p,'biased'); %chebyshev 与 tent 的互相关 Rxz=xcorr(x,z,'biased'); %chebyshev 与改进型 logistic 序列的互相关 Ryz=xcorr(y,z,'biased'); %logistic 序列与改进型 logistic 序列的互相关
clear;clc; n=128; %序列长度 w=20; %chebyshev 的分形参数 u=4; %logistic 的分形参数 a=2; %改进型 logistic 的分形参数 b=0.3; %Tent 的分形参数 x(1)=0.32; %初值 y(1)=0.32; z(1)=0.32; p(1)=0.32; %以上所给的初值和分形参数满足各自的混沌条件 for i=1:n x(i+1)=cos(w*acos(x(i)));%chebyshev 的映射关系 end for i=1:n %对序列进行 2 值量化 if x(i)>=0 x(i)=1; else x(i)=-1; end end for i=1:n y(i+1)=u*y(i)*(1-y(i));%logistic 的映射关系 end for i=1:n if y(i)>=0.5 y(i)=1; else y(i)=-1; end end for i=1:n z(i+1)=1-a*z(i)^2;%改进型 logistic 的映射关系 end for i=1:n if z(i)>=0 z(i)=1; else z(i)=-1; end end for i=1:n if (p(i)>0 & p(i)<b) %不能写成 0<x(i)<b p(i+1)=p(i)/b; else p(i+1)=(1-p(i))/(1-b);
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
混沌映射(序列)matlab 算法“小全”:Logistic 、Henon 、帐篷、kent (含混沌二值图像生成函数)1.Logistic (罗切斯特)映射变换核:)1(1n n n x ax x −=+绘图程序:n=64;key=0.512;an=linspace(3.1,3.99,400);hold on;box on;axis([min(an),max(an),-1,2]);N=n^2;xn=zeros(1,N);for a=an;x=key;for k=1:20;x=a*x*(1-x);%产生公式end;for k=1:N;x=a*x*(1-x);xn(k)=x;b(k,1)=x;%一维矩阵记录迭代结果end;plot(a*ones(1,N),xn,'k.','markersize',1);end;%figure;%imhist(b)实用混沌加密函数:function ichao_ans=ichaos_logistic(varargin)%logistic 序列生成算法%函数名:%logistic 混沌序列生成函数%参数:%(n ,key ),n 为矩阵阶数,key 为迭代初始值。
%(n ),n 为矩阵阶数,key=0.600。
%()或(n ,key ,...),n=64,key=0.600。
switch nargin;case 1;n=varargin{1};key=0.600;case 2;n=varargin{1};key=varargin{2};otherwisekey=0.600;n=64;endN=n^2;xn=zeros(1,N);a=4;x=key;for k=1:20;x=a*x*(1-x);%产生公式end;for k=1:N;x=a*x*(1-x);xn(k)=x;%一维矩阵记录迭代结果end;c=reshape(xn,n,n);%一维矩阵转换二维矩阵d=zeros(n,n);%二维混沌矩阵调制for a1=1:n;for a2=1:n;if c(a1,a2)>=0.5;d(a1,a2)=1;else d(a1,a2)=0;end;end;end;%figure;title('logistic 映射');%imshow(d);ichao_ans=d;2.Henon (埃农)映射变换核:21n 11x {n n nn ax y bx y −+==++绘图程序:b=0.3;N=400;an=ones(1,N);xn=zeros(1,N);hold on;box on;x=0;y=0;for a=0:0.001:1.4for k=1:N;xm=x;ym=y;x=ym+1-a*xm.*xm;y=b*xm;endxn(1)=x;for n=2:N;xm=x;ym=y;x=ym+1-a*xm.*xm;y=b*xm;xn(n)=x;endplot(an*a,xn,'k.','markersize',1);endxlim([0,a]);实用混沌加密函数:function ichao_ans=ichaos_henon(varargin)%埃农(Henon )映射%0.2<key<0.314;理想范围(0.25—0.314)。
重量较大。
%参数:%(n ,key ),n 为矩阵阶数,key 为迭代初始值。
%(n ),n 为矩阵阶数,key=0.314。
%()或(n ,key ,...),n=64,key=0.314。
switch nargin;case 1;n=varargin{1};key=0.314;case 2;n=varargin{1};key=varargin{2};otherwisekey=0.314;n=64;endn=64;N=n^2;an=ones(1,N);xn=zeros(1,N);x=0;y=0;a=1.4;for cir1=1:N;xm=x;ym=y;x=ym+1-a*xm.*xm;y=key*xm;endxn(1)=x;for cir2=2:N;xm=x;ym=y;x=ym+1-a*xm.*xm;y=key*xm;xn(cir2)=x;endc=reshape(xn,n,n);%一维矩阵转换二维矩阵d=zeros(n,n);%二维混沌矩阵调制for a1=1:n;for a2=1:n;if c(a1,a2)>=0;d(a1,a2)=1;else d(a1,a2)=0;end;end;end;ichao_ans=d;314.02.0)4.1,0(a ≤<∈b3.帐篷映射变换核:||)1(1n n x a a x +−=+绘图程序:%帐篷映射%0<a<1%a 理想值0.99—1%0<x<1n=20;N=n^2;xp=zeros(1,N);Aa=ones(1,N);hold on;box on;x=0.01;%初值for a=0:0.001:1;for n=1:N;x=a-(1+a)*abs(x);endfor k=1:N;x=a-(1+a)*abs(x);xp(k)=x;endplot(Aa*a,xp,'k.','markersize',1);endxlim([0,a]);实用混沌加密函数:function ichao_ans=ichaos_tent(varargin)%帐篷映射%0<a<1%a 理想值0.99—1%x 初值作为密钥%0<x<1%参数:%(n ,key ),n 为矩阵阶数,key 为迭代初始值。
%(n ),n 为矩阵阶数,key=0.99。
%()或(n ,key ,...),n=64,key=0.99。
switch nargin;case 1;n=varargin{1};key=0.99;case 2;n=varargin{1};key=varargin{2};otherwisekey=0.99;n=64;endN=n^2;xp=zeros(1,N);x=key;a=0.998;for cir1=1:N;x=a-(1+a)*abs(x);endfor cir2=1:N;x=a-(1+a)*abs(x);xp(cir2)=x;endc=reshape(xp,n,n);%一维矩阵转换二维矩阵d=zeros(n,n);%二维混沌矩阵调制for a1=1:n;for a2=1:n;if c(a1,a2)>=0;d(a1,a2)=1;else d(a1,a2)=0;end;end;end;%sum(sum(d))ichao_ans=d;%imshow(ichao_ans);)1,0(∈a4.kent (肯特)映射a x a x x a ax n nx ≤<≤<−−=0,1,11{绘图程序:%肯特映射n=20;N=n^2;xp=zeros(1,N);Aa=ones(1,N);x=0.36;hold on;box on;for a=0.01:0.001:0.5;for cir1=1:N;if x<=a;x=x/a;elsex=(1-x)/(1-a);end endfor cir3=1:N;if x<=a;x=x/a;elsex=(1-x)/(1-a);endxp(cir3)=x;endplot(Aa*a,xp,'k.','markersize',1);endxlim([0,a]);实用混沌加密函数:function ichao_ans=ichaos_kent(varargin)%0.1<x<1,将初值作为密钥key %a<0.5,当大于0.4时比较理想%参数:%(n ,key ),n 为矩阵阶数,key 为迭代初始值。
%(n ),n 为矩阵阶数,key=0.8。
%()或(n ,key ,...),n=64,key=0.8。
switch nargin;case 1;n=varargin{1};key=0.8;case 2;n=varargin{1};key=varargin{2};otherwisekey=0.8;n=64;endN=n^2;xp=zeros(1,N);x=key;a=0.4;for cir1=1:N;if x<=a;x=x/a;elsex=(1-x)/(1-a);end endfor cir3=1:N;if x<=a;x=x/a;elsex=(1-x)/(1-a);endxp(cir3)=x;endc=reshape(xp,n,n);%一维矩阵转换二维矩阵%figure;%imhist(c);d=zeros(n,n);%二维混沌矩阵调制for a1=1:n;for a2=1:n;if c(a1,a2)>=0.5;d(a1,a2)=1;else d(a1,a2)=0;end;end;end;%sum(sum(d))ichao_ans=d;figure;imshow(ichao_ans);。
