基于Logistic混沌序列的灰度图像加密算法(1)
logistic混沌加密原理

logistic混沌加密原理Logistic混沌加密原理是一种基于混沌理论的加密算法,它利用混沌系统的不可预测性和复杂性来保护数据的安全性。
Logistic混沌加密原理的基本思想是通过对明文进行混沌变换,使其变得随机和不可预测,从而达到加密的目的。
Logistic混沌加密原理的核心是Logistic映射函数,它是一种非线性的动态系统,可以产生复杂的混沌序列。
Logistic映射函数的公式为:Xn+1 = r * Xn * (1 - Xn)其中,Xn表示第n次迭代的结果,r是一个常数,通常取值在3.57到4之间。
通过不断迭代,Logistic映射函数可以产生一个随机的、不可预测的序列,这个序列被称为Logistic混沌序列。
Logistic混沌加密原理的加密过程如下:1. 初始化:选择一个初始值X0和一个密钥K,将X0作为明文的一部分,K作为加密密钥。
2. 生成密钥流:使用Logistic映射函数生成一个随机的、不可预测的密钥流,将其与明文进行异或运算,得到密文。
3. 解密:使用相同的初始值X0和密钥K,使用Logistic映射函数生成相同的密钥流,将其与密文进行异或运算,得到明文。
Logistic混沌加密原理具有以下优点:1. 安全性高:Logistic混沌序列具有随机性和不可预测性,使得攻击者无法破解密文。
2. 速度快:Logistic混沌加密算法的加密和解密速度都很快,适用于实时加密和解密。
3. 灵活性强:Logistic混沌加密算法可以根据需要选择不同的参数,以适应不同的加密需求。
4. 实现简单:Logistic混沌加密算法的实现非常简单,只需要进行一些基本的数学运算即可。
总之,Logistic混沌加密原理是一种非常有效的加密算法,它利用混沌系统的不可预测性和复杂性来保护数据的安全性。
在实际应用中,Logistic混沌加密算法可以用于保护敏感数据的安全,例如网络通信、金融交易等领域。
logistic映射混沌加密算法

logistic映射混沌加密算法混沌理论是一种非线性动力学系统的研究方法,其核心思想是通过微小的初始条件差异引起系统的巨大变化,表现出复杂、随机且不可预测的行为。
混沌理论在信息安全领域具有重要的应用,其中logistic映射混沌加密算法是一种常用的加密方法。
logistic映射是一种简单而有效的动力学系统,其公式为Xn+1 = r*Xn*(1-Xn),其中Xn表示第n个时间点的状态值,r为控制参数,通常取值在0到4之间。
通过迭代计算,logistic映射可以产生一系列的状态值,这些值呈现出混沌的特性。
logistic映射混沌加密算法的基本思想是将待加密的数据与logistic映射的状态值进行异或运算,以增加数据的随机性和不可预测性。
具体加密过程如下:1. 初始化:设置初始状态X0和控制参数r的值,选择合适的初始状态和控制参数是保证加密效果的关键。
2. 生成密钥流:通过迭代计算logistic映射的状态值,得到一系列的随机数作为密钥流。
密钥流的长度取决于需要加密的数据长度。
3. 加密:将待加密的数据与密钥流进行异或运算,生成密文。
异或运算的特点是相同位上的数字相同则结果为0,不同则结果为1,这样可以实现简单而高效的加密过程。
4. 解密:使用相同的初始状态和控制参数,再次生成密钥流,将密文与密钥流进行异或运算,得到原始数据。
logistic映射混沌加密算法具有以下特点:1. 高度随机性:由于logistic映射本身的混沌性质,生成的密钥流具有高度随机性,使得加密后的数据无法被破解。
2. 非线性变换:logistic映射混沌加密算法采用非线性的异或运算,使得加密后的数据与原始数据之间的关系变得非常复杂,增加了破解的难度。
3. 实时性:logistic映射混沌加密算法具有较高的加密速度,适用于对大量数据进行实时加密和解密的场景。
4. 简单性:logistic映射混沌加密算法的实现较为简单,只需要进行简单的数学运算,不需要复杂的计算和存储。
基于混沌的图像加密算法研究

基于混沌的图像加密算法研究图像加密算法是信息安全领域中的重要研究方向之一,它通过对图像进行加密和解密操作,实现保护图像隐私和安全传输等目的。
本文将重点探讨基于混沌的图像加密算法的研究,分析其原理、优势和应用场景。
首先,我们来了解一下混沌理论。
混沌理论是一种非线性动力学系统的研究分支,其在计算机科学和密码学领域有着广泛的应用。
混沌系统具有随机性、不可预测性和灵敏性等特点,这使得混沌可作为图像加密算法的基础。
基于混沌的图像加密算法主要包括两个部分,即混沌映射和置乱操作。
混沌映射是将图像像素映射到一个混沌的迭代序列上,而置乱操作则通过对混沌序列进行重新排列实现对图像的置乱加密。
下面我们将详细介绍这两个部分。
首先是混沌映射。
混沌映射通常选取经典的混沌系统,如Logistic映射和Henon映射等作为基础。
这些映射具有高度的不可预测性和混沌性质,适用于图像加密。
在加密过程中,首先将图像像素值归一化到[0,1]的范围内,然后通过混沌映射将像素值映射到一个混沌序列上。
通过迭代映射操作,可以得到一个与原图像无关的混沌序列。
这个序列将作为后续置乱操作的密钥,确保了加密的随机性和安全性。
接下来是置乱操作。
在加密过程中,通过对混沌序列进行重新排列,实现对图像像素的混乱置乱。
最常用的方法是基于Arnold置乱算法和Baker映射置乱算法。
Arnold置乱算法是一种二维置乱算法,通过对图像像素的行列位置进行迭代映射操作,实现像素位置的混乱。
而Baker映射置乱算法则是通过对图像像素进行乘积操作,实现图像像素值的混乱。
这两种置乱算法具有较高的随机性和不可逆性,能够有效地保障图像的安全性。
基于混沌的图像加密算法具有以下优势:第一,混沌映射和置乱操作具有高度的随机性和不可线性特征,使得加密过程中产生的密钥和置乱后的图像难以被破解和恢复。
这大大增强了图像的安全性。
第二,基于混沌的图像加密算法具有较好的抗攻击性。
混沌系统的不可预测性和随机性能够防止统计分析和密码分析等攻击手段。
基于混沌算法的图像加密技术研究

基于混沌算法的图像加密技术研究图像加密技术是一种将数字图像转化为不可读的密文,以保护图像的安全性和隐私性的方法。
在信息传输和存储过程中,图像加密技术起到了至关重要的作用。
随着计算机技术的不断发展,混沌算法作为一种新型的加密技术,逐渐引起了研究者们的兴趣。
本文将以基于混沌算法的图像加密技术为研究主题,系统地介绍混沌算法在图像加密中的应用和研究成果。
首先,我们来了解一下混沌算法。
混沌是一种表现出无序、不可预测性和敏感性依赖于初始条件的动态行为的系统。
混沌算法通过利用这种系统的特性,将图像中的像素值进行随机重排或者替代,以实现对图像的加密。
在基于混沌算法的图像加密技术中,最常见的方法是混沌映射法。
混沌映射法通过选择适当的混沌映射函数,将图像中的像素值和密钥进行混淆,从而实现图像的加密。
常用的混沌映射函数有Logistic映射、Tent映射、Henon映射等。
这些映射函数具有迭代快速、初始值敏感等特点,能够有效地对图像进行加密。
在具体的图像加密过程中,混沌算法通常与其他加密算法结合使用。
最常见的是混合加密算法,即将混沌算法和传统的对称加密算法(如AES算法)结合使用。
首先,将图像进行分块处理,然后使用混沌算法生成随机数序列作为密钥,并将密钥和图像的像素值进行异或操作。
接下来,采用对称加密算法对密钥进行加密,进一步提高了图像的安全性。
在解密过程中,按照相反的步骤进行操作,即先使用对称加密算法解密密钥,再将密钥和密文进行异或操作,最后利用混沌算法恢复原始图像。
除了混淆像素值和密钥之外,基于混沌算法的图像加密技术还可以采用其他手段对图像进行加密。
例如,可以通过对图像进行像素位移、差分扩散、像素替代等操作,进一步增加图像的复杂性和随机性,提高加密强度。
此外,还可以引入模糊化技术和水印技术,使得加密后的图像满足一定的鲁棒性要求,以增强图像的安全性和可用性。
基于混沌算法的图像加密技术具有许多优点。
首先,混沌算法具有天然的随机性和不可预测性,能够充分满足图像加密的安全性要求。
基于Logistic混沌序列的灰度图像加密算法

Ab t a t On t e b ss o h o h o y a g a — c l ma e e cy t n ag r h i p e e td I g n r t s XOR ma r e n e sr c : h a i f c a s t e r , r y s ae i g n r p i lo i m s r s ne . e e a e o t t tx s a d r— i p a e n tie b sn t e o it Ma p n ,h n ii e h r y s ae ma e n o i c s n e c p s t e l c me t mar s y u i g h L g si x c p i g t e dv d s t e g a — c l i g it pe e a d n r t h m i t r . — y n u n Ex p rme tl smu a in s o s t a h n r p i n ag r h h s a g o f c f e c y t n e i n a i lt h w h t t e e c t lo i m a o d ef t o n r p i . o y o t e o Ke r s L gsi h o i e u n e XOR ma r ; e l c me t mar i g n r p i n y wo d : o i c c a t s q e c ; t c ti rp a e n ti ma e e c y t x x; o
) _
性变 得越 来越重 要 。 各种不 同的图像 加密技 术 中 , 在 基于 混 沌理 论的 加密技术 , 正成为 图像加 密研究 的热点 】 中以 。文 L g t 混沌系统为基础 , oii sc 提出了一种新的图像加密算法 , 通过 实验分析表明 , 该算法具有 良好的加 密性能 。
一种基于Logistic映射的图像加密算法

p = 、 (){霄 / 【
f— — — — 一
0
0 】 <<
其 它
() 2
p( ) 依 赖 于初 始 值 。所 以式 ( ) 达 的混 沌 系统 具 有 不 , 1表 遍 历性 , 根据 概 率论 的理论 定 义 , 我们 可 以从 概 率分 布 函数 得 到L gs c 成 的混沌 序列 具备 以下 性质 : oit 生 i
第 7 第 l 期 卷 2
2 0年 1 08 2月
软 件 导 刊
So t r fwa eGl d l e i
VO1 .2 . No 1 7 De . 0 C 2 o8
一
种基于L gsi映射 的图像加密算法 o it c
袁树 雄
( 长沙航 空职 业技 术 学院 , 南 长沙 4 0 1 ) 湖 1 0 4
(’ 列 的均值 : 1序 )
_ - ∑ f (a0 n k 5 - I ):
.
() 3
() 2 自相 关 函 数 :
a( = c m)
l i m1
一
统 的稳态 解 由周 期2 叉 为周 期4 当/ ̄335 4 9 时 , 分 ; a = .4 0 0 系统 的 , 稳 态解 由周 期4 叉为 周期 8 当 达 到极 限值 = .6 9 5 时 , 分 ; 35 9 4 6
高 ,数字 图像 加密技 术在 多媒 体通 信 中获得 了广 泛 的应 用 , 而 混沌 系统 因为 具有迭 代产 生 的时 间序列 对初 始条 件敏 感 , 结构
2 改 进 的L gsi映 射 oi c t
由于混沌 具 有伪 随机性 , 以利用 概率 统计 的方 法定 量地 可
研究 混 沌序列 的特 性 。 c utr G. 明式 ( ) 成 的混沌 序列 S h se H. 证 1生
一类基于logistic混沌系统的图像加密算法
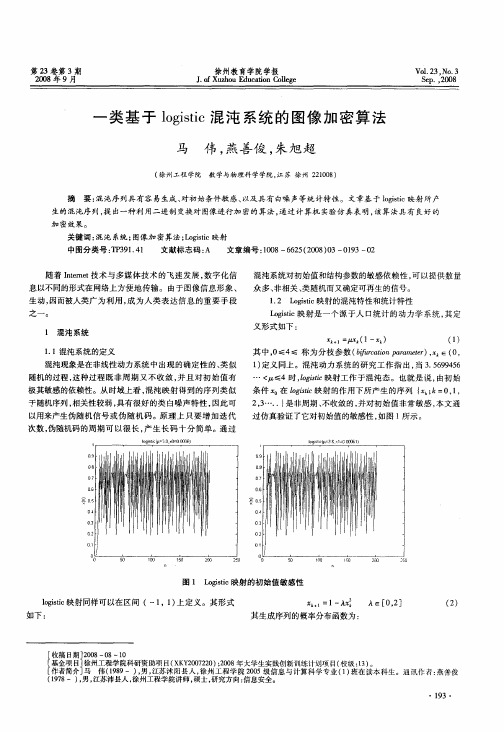
之一 。
混沌系统对初始值和结 构参数 的敏感依赖 性 , 以提供数量 可
众多、 非相关 、 类随机而 又确定可再生的信号。 12 L g t . o sc映射的混沌特性和统计特性 i i Lg t oii 射是一个 源于人 口统计 的动力 学系 统 , 定 sc映 其
・
1 3・ 9
p ) ( :—— = 7 / r、1一
一l <1 <
() 3
的 混 沌 序 列 的 一些 很有 意 义 的 统 计 特 性 。 例 如 , 时 间 平 x的 均 即混 沌 序 列 轨迹 点 的 均 值 是 :
1
=
于公式 1 式的 l ii 形 o sc映射 , gt 如果 = ,P F可 以改写 4 D
第 2 卷第 3 3 期
20 0 8年 9月
徐州教 育学院学报
J o z o u ainCo e e .fXu h uEd c t l g o l
V 12 N . o . 3, o 3 S p ,0 8 e .2 0
一
类 基 于 g t l ii o sc混沌 系统 的 图像 加 密 算 法
( 6 )
单, 对初始条件值敏感 , 具备 白噪音的统计特性等 , 因而可 应 用于包括数字 通讯 和多 媒体数 据安全等 领域 的噪声调
I 。
( )将序 列 I 4 x转换 成矩 阵 I, 到的 图像即 为加密后 得 的图像。
2 2 解密算法 的实现 .
z与 法 解 撙
条件 0 l ii映射 的作 用下所产生 的序列 { ; 在 o sc gt =0 1 ,, 2,…. } 3 . 是非周期 、 不收敛 的, 并对初始 值非常敏感 , 本文通 过仿真验证了它对初始值 的敏感性 , 如图 1 所示 。
基于混沌系统的图像加密算法研究[开题报告]
![基于混沌系统的图像加密算法研究[开题报告]](https://img.taocdn.com/s3/m/c6afd736524de518974b7d4c.png)
开题报告通信工程基于混沌系统的图像加密算法研究一、课题研究意义及现状意义:随着计算机技术和网络通信技术不断发展和迅速普及,通信保密问题日益突出。
信息安全问题已经成为阻碍经济持续稳定发展和威胁国家安全的一个重要问题,而密码学是用来保证信息安全的一种必要的手段,现代密码学便应运而生,如经典的私钥密码算法DES、IDEA、AES和公钥密码算法RSA、EIGamal等,新颖的量子密码、椭圆曲线密码算法等,在信息安全的保密方面都发挥了重要作用。
图像信息生动形象,它已经成为人类表达信息的重要手段之一,网络上的图像数据有很多是要求发送方和接收方要进行保密通信的,信息安全与保密显得越来越重要。
目前,国际上正在探讨使用一些非传统的方法进行信息加密与隐藏,其中混沌理论就是被采纳和得到广泛应用的方法之一。
混沌加密是近年来兴起的一个研究课题,基于混沌理论的保密通信、信息加密和信息隐藏技术的研究已成为国际非线性科学和信息科学两个领域交叉融合的热门前沿课题之一,也是国际上高科技研究的一个新领域,基于混沌理论的密码学近来成为很热门的科学。
对于数字图像来说,具有其特别的一面就是数字图像具有数据量大、数据相关度高等特点,用传统的加密方式对图像加密时存在效率低的缺点;而新型的混沌加密方式为图像加密提供了一种新的有效途径。
基于这种原因,本论文主要探讨基于混沌理论的数字图像加密算法。
混沌现象是在非线性动力系统中出现的确定性、类似随机的过程,这种过程既非周期又非收敛,并且对初值具有极其敏感的依赖性,混沌系统所具有的这些基本特性恰好能够满足保密通信及密码学的基本要求。
图像加密过程就是通过加密系统把原始的图像信息(明文),按照加密算法变换成与明文完全不同的数字信息(密文)的过程。
国内外现状:1963年,洛伦兹发表论文“决定论非周期流”,讨论了天气预报的困难和大气湍流现象,给出了著名的洛伦兹方程,这是在耗散系统中,一个确定的方程却能导出混沌解的第一个实例,从而揭歼了对混沌现象深入研究的序幕。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
乙
R (l ) =lim (x , y)
0 0
N→∞ 1
1 N
1 0
N-1
軃) (x -x (y Σ
i i=0
(i+l )
軃) -y =
軃) 軃) y ) (x-x (τ (y ) -y dxdy=0 乙 乙ρ(x,
l 0
而序列的自相关函数值趋向于 0, 类似于 δ函数, 接近白噪声的
基金项目: 现代通信国家重点实验室基金项目 (No.9140c1102060702 ) ; 徐州工程学院科研资助项目 (No.XKY2007220 ) 。 作者简介: 燕善俊 (1978) , 男, 讲师, 主要研究领域: 信息安全、 图像加密; 余昭平 (1962) , 男, 教授, 硕士生导师, 主要研究领域: 密码理论与应用数学。 收稿日期: 2008-08-25 修回日期: 2008-10-27
Computer Engineering and Applications 计算机工程与应用 ◎ 图形 、 图像 、 模式识别 ◎
2008 ,44 (36 )
179
基于 Logistic 混沌序列的灰度图像加密算法
燕善俊 1, 余昭平 2 YAN Shan-jun1, YU Zhao-ping2
1.徐州工程学院 数学与物理科学学院, 江苏 徐州 221008 郑州 450004 2.解放军信息工程大学 电子技术学院, Xuzhou Institute of Technology, Xuzhou, Jiangsu 221008, China 1.Department of Mathematics and Physical Sciences, 2.Electronic Technology Institute, PLA Information Engineering University, Zhengzhou 450004, China YAN Shan -jun , YU Zhao -ping.Gray image encryption algorithm based on chaotic sequences of Logistic .Computer 2008, 44 (36 ) : 179-180. Engineering and Applications, Abstract:On the basis of chaos theory, a gray-scale image encryption algorithm is presented.It generates XOR matrixes and re - placement matrixes by using the Logistic Mapping, then divides the gray-scale image into pieces and encrypts them in turn.Ex - perimental simulation shows that the encryption algorithm has a good effect of encryption. Key words:Logistic chaotic sequence; XOR matrix; replacement matrix; image encryption 以混沌理论为基础, 提出了一种灰度图像加密算法, 该算法利用 Logistic 映射分别产生异或矩阵和置换矩阵, 然后对灰度 摘 要: 图像进行分块加密。实验仿真表明, 该加密算法具有良好的加密效果。 异或矩阵; 置换矩阵; 图像加密 关键词: Logistic 混沌序列; DOI: 10.3778/j.issn.1002-8331.2008.36.050 文章编号: 1002-8331 (2008 ) 36-0179-02 文献标识码: A 中图分类号: TP391.41
k
m2; j=1, 2, …, n2。
4.2 置换方法
置换算法可简单地看作如下函数: Bm ×n =E (Am ×n , Zm ×n )
2 2 2 2 2 2
k
1
4 基于混沌序列的置换矩阵 4.1 置换矩阵的构造
对于给定置换矩阵的大小 m2×n( n2 为大于 1 的整数) 2 m2、 和给定的正整数 k ,在整数列 x ′ 1, x ′ 2, x ′ 3… 中依次选取 x ′ k+1, x′k+2, …, x′k+m ×n , 组成一个长度为 m2×n2 的序列, 对此序列按从
2 2
图 1 中, 图像 “jiamihou.jpg” 为图像 “lena.jpg” 的加密结果, 显然已看不出图像 “lena.jpg” 的任何信息, 加密取得了较好的 效果; 图像 “jiemihou.jpg” 为对图像 “jiamihou.jpg” 的解密结果, 通过比较得知, 两个图像的像素值完全相同, 说明文中提出的 加密算法没有任何信息丢失; 图像 “cuomiyao.jpg” 为 x0=0.783 55 时的解密结果, 显然, 对于 x0 仅仅相差 0.000 01 时, 由解密结 果得不到图像 “lena.jpg” 的任何信息, 说明该算法对 x0 具有高 度的敏感性。
当 μ=4, 则 Logistic 映射所生成的序列的概率分布函数为: 姨 1 姨 x∈ (0, 1 ) 姨 姨 ρ (x ) =姨 x ( ) π 姨 1-x 姨 姨 姨 0 else 姨 Logistic 映射所产生的混沌序列轨迹点的均值是:
1 1 軃 =lim 1 Σxi= xρ x (x ) dx= 0 N→∞ N 2 i=0 对于相关性, 独立选取两个初始值 x0 和 y0, 则相应序列的 互相关函数为: N-1
其中, 0≤μ≤4 称为分枝参数, xk∈ (0, 1 ) , 定义同上。混沌动力 系统的研究工作指出, 当 3.569 945 6…<μ≤4 时, Logistic 映射 工作于混沌态。也就是说, 由初始条件 x0 在 Logistic 映射的作 用下所产生的序列{xk}, k=0, 1, 2, …是非周期的、 不收敛的并对 初始值非常敏感。 对于一般的混沌映射 xk+1=( f xk ) , 概率密度 ρ (x ) 可由 Perron-Froenious 方程得到, 即 ρ (x ) =
1
引言
随着 Internet 技术与多媒体技术的飞速发展,多媒体通信 逐渐成为人们进行信息交流的重要手段。 而宽带网的发展使得 图像数据的应用更加广泛和方便, 与此同时, 图像数据的安全 在各种不同的图像加密技术中, 基于混 性变得越来越重要 。 沌理论的加密技术, 正成为图像加密研究的热点 [1-4]。文中以 Logistic 混沌系统为基础, 提出了一种新的图像加密算法, 通过 实验分析表明, 该算法具有良好的加密性能。
2 2
lena.jpg
jiamihou.jpg
jiemihou.jpg
cuomiyao.jpg
图1
加密/解密结果
小到大的顺序进行排序, 由各个元素位置的变化可以得到一个 “sort ( ) ” 排序置换, 此置换可以在 MATLAB7.0 中利用排序函数 直接得到, 其长度为 m2×n2, 将此置换序列按长度 n2 逐段截取, 并排成置换矩阵 Zm ×n , 其中 zi, 2, 3, …, m2×n2}, i =1, 2, …, j∈{1,
{xk-f -1 (x ) }
Σ
ρ (xk ) |f ( ′ xk ) |
2
Logistic 混沌系统
混沌是一种非线性动力学规律控制的行为, 表现为对初始 值和系统参数的敏感性、白噪声的统计特性和区间遍历特性, 具有很好的密码学特性。 一个一维离散时间非线性动力系统定义如下: xk+1=τ (xk ) 其中, xk∈V (k=0, 1, 2, …) , 称为状态; 而 τ: V→V 是一个映射, 将当前状态 xk 映射到下一个状态 xk+1。 如果从一个初始值 x0 开 始, 反复应用 τ 就得到一个序列 {xk}, k =0, 1, 2, …, 这一序列称 为该离散时间动力系统的一条轨迹。 一类非常简单却被广泛研究的动力系统是 Logistic 映射, 其定义如下: xk+1=μx( ) (1 ) k 1-xk
1 1
k
换矩阵 Zm ×n ;
2 2
k
(4 ) 将像素矩阵 F1 按 m1×n1 的大小进行分块, 并利用异或 矩阵 Pm ×n 进行逐块加密,将得到的加密分块再组合成像素图
1 1
k
像, 设其为 F2; (5 ) 将像素矩阵 F2 按 m2×n2 的大小进行分块, 并利用置换 矩阵 Zm ×n 进行逐块置换,将得到的加密分块再组合成加密图
180
2008 ,44 (36 )
Computer Engineering and Applications 计算机工程与应用 (0, 1 ) , 3.569 945 6… <μ0≤4; k1、 k2、 m1、 n1、 m2、 n2 均为正整数, 且 m1 与 m2 不能互相整除, n1 与 n2 不能互相整除, 令 k=k1; (2 ) 对于一个图像的像素矩阵 F , 令 M=mul (m1, m2 ) , N= mul (n1, n2 ) (其中 mul (x, y ) 表示 x 与 y 的最小公倍数) , 在图像 矩阵的边界填充像素值 255 (白色) , 增加 F 的行数和列数, 使 它们分别是 M 和 N 的整数倍, 设生成的图像像素矩阵为 F1; ) 利用密钥和 Logistic 映射分别产生异或矩阵 Pm ×n 和置 (3
1 1 1 1 1
6 仿真实验及算法分析 6.1 仿真实验
利用 MATLAB 7.0 软件, 结合上述算法, 对 “lena.jpg” 图像 进行了加/解密的仿真实验, 密钥选取为: K= (0.783 54, 4, 10 000, 20 000, 50, 50, 8, 8 ) , 结果如图 1 所示。
