(完整版)八年级数学角平分线的性质练习题
人教版_部编版八年级数学上册第十二章第三节角的平分线的性质考试复习题(含答案) (28)

人教版_部编版八年级数学上册第十二章第三节角的平分线的性质考试复习题(含答案)一、单选题1.如图,在Rt△ABC中,∠ACB=90°,AD平分∠CAB,若CD=4,则点D到AB的距离是( )A.4 B.3 C.2 D.5【答案】A【解析】【分析】根据角平分线的性质定理得出CD=DE,代入求出即可.【详解】如图,过D点作DE⊥AB于点E,则DE即为所求,∵∠C=90°,AD平分∠BAC交BC于点D,∴CD=DE(角的平分线上的点到角的两边的距离相等),∵CD=4,∴DE=4.故选A .【点睛】本题主要考查了角平分线的性质的应用,注意:角平分线上的点到角两边的距离相等.2.如图,在中,,是角平分线,垂直平分,,则的长为( )A .9B .5C .4D .【答案】A【解析】【分析】 根据垂直平分线的性质,得到BD=CD,进而得到,根据直角三角形可得 由角平分线的性质可以得到AD=DE=3,由的直角三角形中,直角边是斜边的一半,可求出CD 的长度,进而求出AC 的长度,【详解】DE 垂直平分BC,BD=CD,,BD 为的平分线,Rt ABC ∆90A ∠=BD DE BC 3AD =AC ABD CBD C ∠=∠=∠C ∠=30,︒30∴C CBD ∴∠=∠ABC ∠,,,BD 为的角平分线,, ,故AC 的长度为9,应选A.【点睛】熟练运用垂直平分线的性质和角平分线的性质是解决本题的关键.3.如图,小聪把一块含有30°角的直角三角尺ABC 的两个顶点A ,C 放在长方形纸片DEFG 的对边上,若AC 平分∠BAE ,则∠DAB 的度数是( )A .100°B .150°C .130°D .120°【答案】D【解析】【分析】 利用角平分线定义求得∠BAC=∠CAE=30°,再利用平角定义即可解答.【详解】ABD CBD ∴∠=∠ABD CBD C ∴∠=∠=∠90A ∠=︒19030,3C ∴∠=⨯︒=︒ABC ∠90A ∠=︒DE BC ⊥3,AD DE ∴==26,CD DE ∴==9.AC AD CD ∴=+=∵AC 平分∠BAE∴∠BAC=∠CAE=30°∵∠DAB+∠BAC+∠CAE=180°∴∠DAB=120°故选D【点睛】本题考查了角平分线的定义以及平角的定义,熟练掌握相关定理是解题关键.4.如图,在中,,BD 平分,交AC 于点D ,且,,则点D 到BC 的距离是( )A .3B .4C .5D .6【答案】A【解析】【分析】 首先根据勾股定理求得AD 的长,再根据角平分线的性质定理即可求得结果.【详解】解:∵,,,∴.∵BD 平分,Rt ABC △90A ∠=︒ABC ∠4AB =5BD=90A ∠=︒4AB =5BD=3AD =ABC ∠∴点D 到BC 距离.故选:A【点睛】本题考查了勾股定理和角平分线上的点到角两边距离相等的性质,读懂题意,明确所求,正确计算是解题的关键.5.如图,,,平分,则的度数为( )A .B .C .D .【答案】C【解析】【分析】 根据题意,由角度相加,得到∠ABD 的度数,由角平分线性质,得到∠ABE 的度数,然后求出∠CBE.【详解】解:∵,,∴∠ABD=82°,∵平分,∴∠ABE=41°,∴∠CBE=;故选择:C.3AD ==32ABC ︒∠=50CBD ︒∠=BE ABD ∠CBE∠8︒18︒9︒10︒32ABC ︒∠=50CBD ︒∠=BE ABD ∠41329︒-︒=︒本题考查了角平分线的性质,解题的关键是正确的进行角度的运算.6.下列是假命题的是()A.对顶角相等B.角的对称轴是这个角的平分线C.同角的余角相等D.角平分线上的点到角两边的距离相等【答案】B【解析】【分析】根据对顶角,对称轴,余角及角平分线的定义和性质依次判断各选项即可.【详解】A、对顶角相等,则A正确;B、角的对称轴是这个角的平分线所在的直线,则B错误;C、同角或等角的余角相等,则C正确;D、根据角平分线的性质,角平分线上的点到角两边的距离相等,则D正确;故选B.【点睛】熟练掌握对顶角,对称轴,余角及角平分线的定义和性质是解决本题的关键,难度不大.7.如图,△ABC的两个外角平分线交于点P,则下列结论正确的是()A.AB=AC B.BP平分∠APC C.BP平分∠ABC D.PA=PC【解析】【分析】过点P 作PD ⊥AB 于D ,作PE ⊥BC 于E ,作PF ⊥AC 于F ,根据角平分线上的点到角的两边距离相等可得到PD=PE=PF ,再根据到角的两边距离相等的点在角的平分线上判断出BP 平分∠ABC .【详解】如图,过点P 作PD ⊥AB 于D ,作PE ⊥BC 于E ,作PF ⊥AC 于F , ∵△ABC 的两个外角平分线相交于点P ,∴PD=PF ,PE=PF ,∴PD=PE ,又∵PD ⊥AB ,PE ⊥BC ,∴BP 平分∠ABC ,故选C .【点睛】本题考查了角平分线上的点到角的两边距离相等的性质,到角的两边距离相等的点在角的平分线上,熟记性质是解题的关键,作出图形更形象直观.8.如图,在中,,是的角平分线,若,,则的面积是( )ABC ∆90C ∠=︒AD BAC ∠1CD =4AB =ABD ∆A .1.5B .2.5C .2D .3【答案】C【解析】【分析】 过点D 作DE ⊥AB 于E ,根据角平分线上的点到角的两边的距离相等可得DE=CD=1,然后根据三角形的面积公式列式计算即可得解.【详解】过点D ,作DE ⊥AB ,垂足为E.∵AD 是∠BAC 的角平分线,,故选:.90︒∠=C 1CD =1DE CD ∴==4AB =12ABDS AB DE ∴=⋅1412=⨯⨯2=C【点睛】本题考查角平分线的性质,能正确作辅助线并通过角平分线上的点到角的两边的距离相等求出DE 是解决此题的关键.9.已知射线,,,能判定是的平分线的是( )A .B .C .D .A 、B 、C 都能 【答案】A【解析】【分析】根据角平分线的定义来解答即可.【详解】A 、当∠AOC =∠BOC 时,OC 一定在∠AOB 的内部且OC 是∠AOB 的平分线,故本选项正确;B 、当∠AOB =2∠AOC 时,OC 在∠AOB 的外部也成立,故本选项错误;C 、当时,OC 在∠AOB 的外部也成立,故本选项错误;D 、因为A 正确,故本选项错误;故答案为:A.【点睛】此题考查角平分线的定义,解题关键在于掌握其定义.10.如图,在△ABC 中,BD 为∠ABC 的平分线,DE ⊥AB 于点E ,且DE =3cm ,AB =8cm ,BC =6cm ,则△ABC 的面积( )cm 2.OA OB OC OC AOB ∠AOC BOC ∠=∠2AOB AOC ∠=∠1BOC AOB 2∠=∠1BOC AOB 2∠=∠A .17B .21C .42D .52【答案】B【解析】【分析】 过点D 作DF ⊥BC 于点F ,根据角平分线的性质可知DE=DF ,则根据S △ABC =S △ABD + S △BCD ,即可得出结论.【详解】解:过点D 作DF ⊥BC 于点F ,∵BD 为∠ABC 的平分线,DE ⊥AB 于点E ,且DE=3cm , ∴DE=DF=3cm ,∴S △ABC =S △ABD +S △BCD =AB •DE+BC •DF =×8×3+×6×3 =12+9=21.故选:B .12121212【点睛】本题考查的是角平分线的性质,熟知角的平分线上的点到角的两边的距离相等是解答此题的关键.11.如图,∠AOB=30°,OP 平分∠AOB,PC∥OB,PD⊥OB,如果PC=6,那么PD 等于()A.4 B.3 C.2 D.1【答案】B【解析】【分析】根据角平分线的性质,角平分线上的点到两角的距离相等,因而过P作PE⊥OA于点E,则PD=PE,因为PC∥OB,得角相等,而OP平分∠AOB,得∠ECP=∠COP+∠OPC=30°根据三角形的外角的性质得到答案.【详解】解:过P作PE⊥OA于点E,∵OP 平分∠AOB,则PD=PE,∵PC∥OB,∠AOB=30°∴∠ECP=∠AOB=30°在中, ∴PD=PE=3,故选:B .【点睛】 本题主要考查了角平分线的性质,角平分线上的点到角的两边距离相等.12.如图,点O 是△ABC 的内心,过点O 作EF ∥BC 交AB 于E ,交AC于F ,过点O 作OD ⊥AC 于D .下列四个结论:①∠BOC =90°+∠A ;②EF 不可能是△ABC 的中位线;③设OD =m ,AE+AF =n ,则S △AEF =mn ;④以E 为圆心、BE 为半径的圆与以F 为圆心、CF 为半径的圆外切.其中正确结论的个数是( )A .1个B .2个C .3个D .4个【答案】D【解析】【分析】 由在△ABC 中,∠ABC 和∠ACB 的平分线相交于点O ,根据角平分线的定义与三角形内角和定理,即可求得①∠BOC =90°+∠A 正确;假设EF 是△ABC 的中位线,由三角形中两边之和大于第三边可得假设不成立,故②正确;过点O 作OM ⊥AB 于M ,作ON ⊥BC 于N ,由角平分线定理与三角形面积的Rt ECP 132126PE PC ==⨯=121212求解方法,即可求得当OD =m ,AE+AF =n 时,则S △AEF =mn ,故③正确;又由在△ABC 中,∠ABC 和∠ACB 的平分线相交于点O ,过点O 作EF ∥BC 交AB 于E ,可判定△BEO 与△CFO 是等腰三角形,根据两圆位置关系与圆心距d ,两圆半径R ,r 的数量关系,即可求得④正确.【详解】解:∵在△ABC 中,∠ABC 和∠ACB 的平分线相交于点O ,∴∠OBC =∠ABC ,∠OCB =∠ACB ,∠A+∠ABC+∠ACB =180°, ∴∠OBC+∠OCB =90°﹣∠A , ∴∠BOC =180°﹣(∠OBC+∠OCB )=90°+∠A ;故①正确; 假设EF 是△ABC 的中位线,则EA =EB ,FA =FC ,∴EO =EA ,FO =FA ,∴EA+FA =EO+FO =EF ,推出在△AEF 中两边之和等于第三边,不成立,∴EF 不可能是△ABC 的中位线,故②结论正确;过点O 作OM ⊥AB 于M ,作ON ⊥BC 于N ,连接OA ,∵在△ABC 中,∠ABC 和∠ACB 的平分线相交于点O ,∴ON =OD =OM =m ,∴S △AEF =S △AOE +S △AOF =AE •OM+AF •OD =OD •(AE+AF )=mn ,故③正确;∵在△ABC 中,∠ABC 和∠ACB 的平分线相交于点O ,121212121212121212∴∠EBO =∠OBC ,∠FCO =∠OCB ,∵EF ∥BC ,∴∠EOB =∠OBC ,∠FOC =∠OCB ,∴∠EBO =∠EOB ,∠FOC =∠FCO ,∴EB =EO ,FO =FC ,∴EF =EO+FO =BE+CF ,∴以E 为圆心、BE 为半径的圆与以F 为圆心、CF 为半径的圆外切,故④正确.∴其中正确的结论是①②③④.故选:D .【点睛】此题考查了角平分线的定义与性质,等腰三角形的判定与性质,以及圆与圆的位置关系.此题难度适中,解题的关键是注意数形结合思想的应用.13.如图,在△ABC 中,△C=90°,以点B 为圆心,任意长为半径画弧,分别交AB 、BC 于点M 、N 分别以点M 、N 为圆心,以大于MN 的长度为半径画弧两弧相交于点P 过点P 作线段BD,交AC 于点D,过点D 作DE △AB 于点E,则下列结论△CD=ED ;△△ABD=△ABC ;△BC=BE ;△AE=BE 中,一定正确的是( )1212A .△②△B .△ △ △C .△△△D .△△△【答案】A【解析】【分析】 由作法可知BD 是∠ABC 的角平分线,故②正确,根据角平分线上的点到角两边的距离相等可得①正确,由HL 可得Rt △BDC ≌Rt △BDE,故BC=BE ,③正确,【详解】解:由作法可知BD 是∠ABC 的角平分线,故②正确,∵∠C=90°,∴DC ⊥BC ,又DE ∠AB ,BD 是∠ABC 的角平分线,∴CD=ED ,故①正确,在Rt △BCD 和 Rt △BED 中,, ∴△BCD ≌△BED ,∴BC=BE ,故③正确.故选:A.DE DC BD BD =⎧⎨=⎩【点睛】本题考查了角平分线的画法及角平分线的性质,熟练掌握相关知识是解题关键.14.如图,在Rt △ABC 中,∠C =90°,以原点A 为圆心,适当的长为半径画弧,分别交AC ,AB 于点M ,N ,再分别以点M 、N 为圆心,大于MN 的长为半径画弧,两弧交于点E ,作射线AE 交BC 于点D ,若BD =5,AB =15,△ABD 的面积30,则AC +CD 的值是( )A .16B .14C .12D .【答案】A【解析】【分析】 过D 点作DF ⊥AB ,垂足为F ,利用三角形ABD 的面积,求出CD=DF=4,得到BC=9,再利用勾股定理求出AC ,最后即可得答案【详解】过D 点作DF ⊥AB ,垂足为F∵S △ABD =30∴AB ·DF=30 ∴DF=4根据作图得到AD 是∠CAB 的角平分线1212∴CD=DF=4∵BD=5∴BC=5+4=9在Rt△ABC中,∴AC+CD=12+4=16故选A【点睛】本题主要考查角平分线性质与勾股定理,解题关键在于能够做出正确辅助线15.如图,在Rt△ABC 中,△C=90°,在AC和AB 上分别截取AE、AD,使AE=AD分别以点D、E 为圆心,大于立DE 长为半径作弧,两弧在△BAC 内交于点F,作射线AF交边BC 于点G,若CG=4,AB=10,则△ABG 的面积为()A.12 B.20 C.30 D.40【答案】B【解析】12=12【分析】根据角平分线性质得△ABG 的面积为:【详解】作GH ⊥AB,由已知可得AF 是∠BAC 的平分线,因为∠C=90°所以GH=CG=4,所以△ABG 的面积为:故选B【点睛】考核知识点:角平分线的性质.16.如图,AE 与BF 交于点O ,点O 在CG 上,根据尺规作图的痕迹,判断下列说法不正确的是( )A .AE 、BF 是△ABC 的内角平分线B .CG 也是△ABC 的一条内角平分线C .AO =BO =CO1110 4.22AB GH •=⨯⨯111042022AB GH •=⨯⨯=D .点O 到△ABC 三边的距离相等【答案】C【解析】【分析】根据三角形角平分线的性质:三角形三条角平分线交于一点,且到三边的距离相等可以作判断.【详解】解:A 、由尺规作图的痕迹可知:AE 、BF 是△ABC 的内角平分线,所以选项A 正确;B 、根据三角形三条角平分线交于一点,且点O 在CG 上,所以CG 也是△ABC 的一条内角平分线,所以选项B 正确;C 、三角形三边中垂线的交点到三个顶点的距离相等,所以选项C 不正确;D 、因为角平分线的点到角两边的距离相等得:点O 到△ABC 三边的距离相等,所以选项D 正确;故选C .【点睛】本题考查了基本作图−角的平分线、角平分线的性质,明确三角形的角平分线交于同一点,且交点到三边的距离相等.17.下列说法:①若点C 是AB 的中点,则AC =BC ;②若AC =BC ,则点C 是AB 的中点;③若OC 是∠AOB 的平分线,则∠AOC =∠AOB ;④若∠AOC =∠AOB ,则OC 是∠AOB 的平分线.其中正确的有( ) 1212A .1个B .2个C .3个D .4个【答案】B【解析】【分析】 根据线段的中点的定义及角平分线的定义对选项进行判断,即可得出正确答案.【详解】①若C 是AB 的中点,则AC=BC ,该说法正确;②若AC=BC ,则点C 不一定是AB 的中点,该说法错误;③若OC 是∠AOB 的平分线,则∠AOC=∠AOB ,该说法正确; ④若∠AOC=∠AOB ,则OC 不一定是∠AOB 的平分线,该说法错误; 综上所述正确个数为2个.故选:B.【点睛】此题考查线段中点及角平分线,解题关键在于掌握线段中点及角平分线的定义.18.如图,已知点O 在直线AB 上,,OD 平分,,则的度数为( )A .B .C .D . 121290COE ︒∠=AOE ∠25COD ︒∠=BOD∠65︒100︒115︒130︒【答案】C【解析】【分析】先根据∠COE=90°,∠COD=25°,求得∠DOE=90°-25°=65°,再根据OD 平分∠AOE ,得出∠AOD=∠DOE=65°,最后得出∠BOD=180°-∠AOD=115°.【详解】解:∵∠COE=90°,∠COD=25°,∴∠DOE=90°-25°=65°,∵OD 平分∠AOE ,∴∠AOD=∠DOE=65°,∴∠BOD=180°-∠AOD=115°,故选:C .【点睛】本题主要考查了角的计算以及角平分线的定义的综合应用,解决问题的关键是运用角平分线以及直角的定义,求得∠AOD 的度数,再根据邻补角进行计算.19.如图,, AD 、BD 、CD 分别平分外角、内角、外角.以下结论:①:②;③;④:⑤.其中正确的结论有( )A ABC CB =∠∠ABC △EAC ∠ABC ∠ACF ∠//AD BC 2ABC ADB ∠=∠90ADC ABD ︒∠=-∠BDC BAC ∠=∠12ADC ABC ∠=∠A.1个B.2个C.3个D.4个【答案】C【解析】【分析】根据角平分线定义得出∠ABC=2∠ABD=2∠DBC,∠EAC=2∠EAD,∠ACF=2∠DCF,根据三角形的内角和定理得出∠BAC+∠ABC+∠ACB=180°,根据三角形外角性质得出∠ACF=∠ABC+∠BAC,∠EAC=∠ABC+∠ACB,根据已知结论逐步推理,即可判断各项.【详解】解:∵AD平分∠EAC,∴∠EAC=2∠EAD,∵∠EAC=∠ABC+∠ACB,∠ABC=∠ACB,∴∠EAD=∠ABC,∴AD∥BC,∴①正确;∵AD∥BC,∴∠ADB=∠DBC,∵BD平分∠ABC,∠ABC=∠ACB,∴∠ABC=∠ACB=2∠DBC,∴∠ACB=2∠ADB ,∴②正确;∵AD 平分∠EAC ,CD 平分∠ACF ,∴∠DAC=∠EAC ,∠DCA=∠ACF , ∵∠EAC=∠ACB+∠ACB ,∠ACF=∠ABC+∠BAC ,∠ABC+∠ACB+∠BAC=180°,∴∠ADC=180°-(∠DAC+∠ACD )=180°-(∠EAC+∠ACF ) =180°-(∠ABC+∠ACB+∠ABC+∠BAC ) =180°-(180°-∠ABC ) =90°-∠ABC ,∴③正确; ∵BD 平分∠ABC ,∴∠ABD=∠DBC ,∵∠ADB=∠DBC ,∠ADC=90°-∠ABC , ∴∠ADB 不等于∠CDB ,∴④错误;∵AD ∥BC ,∴∠ADC=∠DCF ,∵BD 平分∠ABC ,∴∠ABC=∠DBC , ∵∠DCF=∠DBC +∠BDC ,1212121212121212∴∠DCF >∠DBC ,∴∠ADC >∠ABC ∴⑤错误; 即正确的有3个,故选:C .【点睛】本题考查了三角形外角性质,角平分线定义,平行线的判定,三角形内角和定理的应用,主要考查学生的推理能力,有一定的难度.20.如图,∠MON =90°,OB =4,点A 是直线OM 上的一个动点,连结AB ,作∠MAB 与∠ABN 的角平分线AF 与BF ,两条角平分线所在的直线相交于点F ,则点A 在运动过程中线段BF 的最小值为( )A .4BC .8 D.【答案】D【解析】【分析】 分情况讨论:当点A 在射线OM 上时,过F 作FE ⊥ON 于E ,FH ⊥OM 于H ,FG ⊥AB 于G ,由角平分线的性质得出FH =FG ,FG =FE ,得出FH =FE ,证出点F 在∠MON 的角平分线上;当点A 在射线OM 的反向延长线上时,同理得出点F 在∠MON 的角平分线上;当BF ⊥OF 时,BF 取最小值,证出△BOF 12是等腰直角三角形,即可得出答案.【详解】解:当点A在射线OM上时,过F作FE∠ON于E,FH∠OM于H,FG∠AB 于G,如图1所示:∠AF与BF分别是∠MAB与∠ABN的角平分线,∠FH=FG,FG=FE,∠FH=FE,∠点F在∠MON的角平分线上;当点A在射线OM的反向延长线上时,过F作FE∠ON于E,FH∠OM于H,FG∠AB交AB的延长线于G,如图2所示:∠AF与BF分别是∠MAB与∠ABN的角平分线,∠FH=FG,FG=FE,∠FH=FE,∠点F在∠MON的角平分线上;综上所述,点F在∠MON的角平分线上,∠当BF∠OF时,BF取最小值,∠∠MON =90°,OB =4,∠∠FON =∠MON =45°, ∠∠BOF 是等腰直角三角形,∠BF =OB =;故选:D .【点睛】本题考查了角平分线的判定与性质、等腰直角三角形的判定与性质、以及勾股定理等知识;熟练掌握角平分线的判定与性质是解题的关键. 122。
【初中数学】人教版八年级上册第1课时 角的平分线的性质(练习题)

人教版八年级上册第1课时角的平分线的性质(348) 1.如图,已知∠1=∠2,BA<BC,P为BN上的一点,PF⊥BC于点F,PA=PC.求证:∠PCB+∠BAP=180∘2.证明命题“角的平分线上的点到角的两边的距离相等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程,下面是小明同学根据题意画出的图形,并写出了不完整的已知和求证.已知:如图,∠AOC=∠BOC,点P在OC上,. 求证:.请你补全已知和求证,并写出证明过程.3.如图,已知AD//BC,∠D=90∘.(1)如图①,若∠DAB的平分线与∠CBA的平分线交于点P,CD经过点P.试问:P是线段CD的中点吗?为什么?(2)如图②,如果P是DC的中点,BP平分∠ABC,∠CPB=35∘,求∠PAD的度数4.如图OP是∠AOB的平分线,点P到OA的距离为3,N是OB上的任意一点,则线段PN的取值范围为()A.PN<3B.PN>3C.PN≥3D.PN≤35.如图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于点D,如果AC=3cm,那么AE+DE等于()A.2cmB.3cmC.4cmD.5cm6.如图,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC的长为()A.3B.4C.6D.57.如图,在△ABC中,∠C=90∘,AD平分∠BAC,过点D作DE⊥AB于点E,测得BC=9,BE=3,则△BDE的周长是.8.如图,在△ABC中,两条外角平分线交于点P,PM⊥AC交AC的延长线于点M.若PM=6cm,则点P到AB的距离为.9.如图,已知AB//CD,O是∠BAC与∠ACD的平分线的交点.OE⊥AC于点E,OE=2,则AB与CD之间的距离为.10.如图,已知点B,D分别在∠DAB的两边上,C为∠DAB的内部的一点,且AB=AD,DC=BC,CE⊥AD交AD的延长线于点E,CF⊥AB交AB的延长线于点F.试判断CE与CF是否相等,并说明理由.11.如图,利用尺规作∠AOB的平分线OC,其作法如下:①以O为圆心,任意长为半径画弧,分别交OA,OB于点D,E;DE的长为半径画弧,两弧在∠AOB的内部交于点②分别以D,E为圆心,以大于12C;③画射线OC,则OC就是∠AOB的平分线.这样作图的原理是一种三角形全等的判定方法,这种判定方法是()A.SSSB.SASC.ASAD.AAS12.如图,OP为∠AOB的平分线,PC⊥OA,PD⊥OB,垂足分别是C,D,则下列结论错误的是()A.PC=PDB.∠CPD=∠DOPC.∠CPO=∠DPOD.OC=OD13.求证:直角三角形的两锐角互余14.如图,在△ABC中,∠C=90∘,∠CAB=50∘,按以下步骤作图:①以点A为圆心,小于AC长为半径画弧,分别交AB,AC于点E,F;EF的长为半径画弧,两弧相交于点G;②分别以点E,F为圆心,大于12③作射线AG,交BC边于点D.则∠ADC的度数为()A.40∘B.55∘C.65∘D.75∘15.如图,AB∥CD,以点A为圆心,小于AC长为半径画圆弧,分别交AB,AC于E,EF的长为半径画圆弧,两条圆弧交于点G,F两点,再分别以E,F为圆心,大于12作射线AG交CD于点H.若∠C=140∘,则∠AHC的大小是()A.20∘B.25∘C.30∘D.40∘参考答案1.【答案】:证明:如图,过点P 作PE ⊥BA 交BA 的延长线于点E . ∵∠1=∠2,PF ⊥BC 于点F ,∴PE =PF ,∠PEA =∠PFC =90∘.在Rt △PEA 与Rt △PFC 中,PA =PC ,PE =PF ,∴Rt △PEA ≌Rt △PFC(HL ),∴∠PAE =∠PCB .∵∠PAE +∠BAP =180∘,∴∠PCB +∠BAP =180∘.2.【答案】:解:PD ⊥OA ,PE ⊥OB ,垂足分别为D,E 求证:PD =PE证明:∵PD ⊥OA ,PE ⊥OB ,∴∠PDO =∠PEO =90∘.在△PDO 和△PEO 中,{∠PDO =∠PEO ,∠AOC =∠BOC ,OP =OP.∴△PDO ≌△PEO(AAS ),∴PD =PE .3(1)【答案】解:P 是线段CD 的中点.理由如下: 如图,过点P 作PE ⊥AB 于点E .∵AD//BC ,∠D =90∘,∴∠C =180∘−∠D =90∘,即PC ⊥BC .∵∠DAB 的平分线与∠CBA 的平分线交于点P ,∴PD =PE ,PC =PE ,∴PC=PD,∴P是线段CD的中点.(2)【答案】解:如图,过点P作PE⊥AB于点E.∵AD//BC,∠D=90∘,∴∠C=180∘−∠D=90∘,即PC⊥BC.在△PBE与△PBC中,{∠PEB=∠C,∠PBE=∠PBC,PB=PB.∴△PBE≌△PBC(AAS),∴∠EPB=∠CPB=35∘,PE=PC.∵PC=PD,∴PD=PE.在Rt△PAD与Rt△PAE中,{PA=PA,PD=PE∴Rt△PAD≌Rt△PAE(HL),∴∠APD=∠APE.∵∠APD+∠APE=180∘−2×35∘=110∘,∴∠APD=55∘,∴∠PAD=90∘−∠APD=35∘.4.【答案】:C【解析】:作PM⊥OB于点M.∵OP是∠AOB的平分线,PE⊥OA,PM⊥OB,∴PM=PE=3,∴PN≥3. 故选 C5.【答案】:B【解析】:因为BE平分∠ABC,∠ACB=90°,DE⊥AB于点D,所以DE=EC,AE+DE=AE+EC=AC=3cm.故选 B.6.【答案】:A【解析】:如图,过点D作DF⊥AC于点F.∵AD是△ABC中∠BAC的平分线,DE⊥AB,∴DE=DF=2.由图可知S△ABC=S△ABD+S△ACD,即12×4×2+12AC×2=7,解得AC=3.故选A.7.【答案】:12【解析】:解:∵∠C=90∘,∴AC⊥CD.∵AD平分∠BAC,DE⊥AB,∴DE=CD.∵BC=9,BE=3,∴△BDE的周长=BE+BD+DE=BE+BD+CD=BE+BC=3+9=12.8.【答案】:6cm【解析】:如图,过点P作PN⊥BC于点N,PQ⊥AB,交AB的延长线于点Q.∵PB,PC分别是∠ABC与∠ACB的外角平分线,PM⊥AC,∴PN=PM,PQ=PN,∴PQ=PM.∵PM=6cm,∴PQ=6cm,即点P到AB的距离为6cm.9.【答案】:4【解析】:如图,过点O作MN,使MN⊥AB于M,交CD于N.∵AB//CD,∴MN⊥CD.∵AO是∠BAC的平分线,OM⊥AB,OE⊥AC,OE=2,∴OM=OE=2.∵CO是∠ACD的平分线,OE⊥AC,ON⊥CD,∴ON=OE=2,∴MN=OM+ON=4,即AB与CD之间的距离是4.10.【答案】:解:CE=CF.理由:∵AD=AB,DC=BC,AC=AC,∴△ACD≌△ACB,∴∠DAC=∠BAC,∴AC为∠EAF的平分线.∵CE⊥AE,CF⊥AF,∴CE=CF(角平分线上的点到角两边的距离相等).11.【答案】:A12.【答案】:B【解析】:∵OP为∠AOB的平分线,PC⊥OA,PD⊥OB,垂足分别是C,D,∴PC=PD,故A项正确.在Rt△OCP与Rt△ODP中,∵OP=OP,PC=PD,∴Rt△OCP≌Rt△ODP,∴∠CPO=∠DPO,OC=OD,故C,D两项正确.不能得出∠CPD=∠DOP,故B项错误.故选B13.【答案】:已知:在△ABC中,∠C=90∘.求证:∠A+∠B=90∘.证明:∵∠A+∠B+∠C=180∘,而∠C=90∘,∴∠A+∠B=90∘,即∠A与∠B互余.14.【答案】:C【解析】:根据作图方法可得AG是∠CAB的平分线,∵∠CAB=50∘,∠CAB=25∘,∴∠CAD=12∵∠C=90∘,∴∠CDA=90∘−25∘=65∘.故选C.15.【答案】:A【解析】:解:由题意可得AH平分∠CAB.∵AB∥CD,∴∠C+∠CAB=180∘,∠HAB=∠AHC.∵∠ACD=140∘,∴∠CAB=40∘.∵AH平分∠CAB,∴∠HAB=20∘,∴∠AHC=20∘.。
人教版八年级数学上册12.3角的平分线的性质同步练习解析版
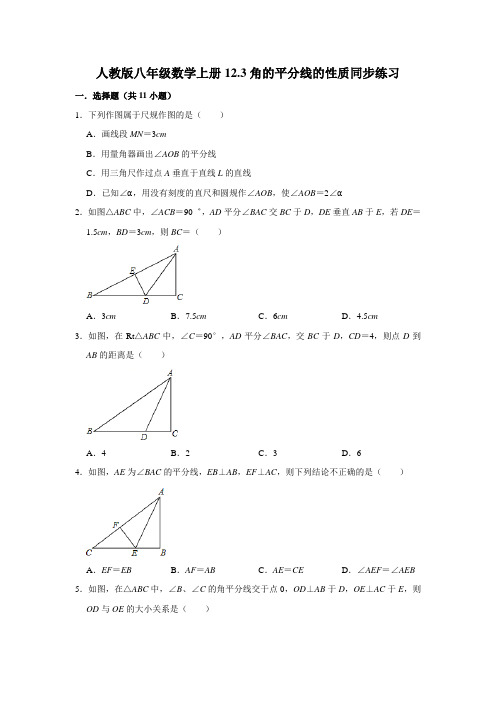
人教版八年级数学上册12.3角的平分线的性质同步练习一.选择题(共11小题)1.下列作图属于尺规作图的是()A.画线段MN=3cmB.用量角器画出∠AOB的平分线C.用三角尺作过点A垂直于直线L的直线D.已知∠α,用没有刻度的直尺和圆规作∠AOB,使∠AOB=2∠α2.如图△ABC中,∠ACB=90゜,AD平分∠BAC交BC于D,DE垂直AB于E,若DE=1.5cm,BD=3cm,则BC=()A.3cm B.7.5cm C.6cm D.4.5cm3.如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于D,CD=4,则点D到AB的距离是()A.4B.2C.3D.64.如图,AE为∠BAC的平分线,EB⊥AB,EF⊥AC,则下列结论不正确的是()A.EF=EB B.AF=AB C.AE=CE D.∠AEF=∠AEB 5.如图,在△ABC中,∠B、∠C的角平分线交于点0,OD⊥AB于D,OE⊥AC于E,则OD与OE的大小关系是()A.OD>OE B.OD<OE C.OD=OE D.不能确定6.如图,PC⊥OC于C,PD⊥OD于D,若PC=PD,则()A.∠1>∠2B.∠1=∠2C.∠1<∠2D.不能确定7.如图所示,点D在∠AOB的内部,DE⊥OA,DF⊥OB,垂足分别为E,F,DE=DF,则∠AOD与∠BOD的大小关系是()A.∠AOD>∠BOD B.∠AOD=∠BOD C.∠AOD<∠BOD D.无法确定8.下列关于三角形角平分线的说法错误的是()A.两角平分线交点在三角形内B.两角平分线交点在第三个角的平分线上C.两角平分线交点到三边距离相等D.两角平分线交点到三顶点距离相等9.给出下列结论,正确的有()①到角两边距离相等的点,在这个角的平分线上;②角的平分线与三角形平分线都是射线;③任何一个命题都有逆命题;④假命题的逆命题一定是假命题.A.1个B.2个C.3个D.4个10.如图,已知点P、D、E分别在OC、OA、OB上,下列推理:①∵OC平分∠AOB,∴PD=PE;②∵OC平分∠AOB,PD⊥OA,PE⊥OB,∴PD=PE;③∵PD⊥OA,PE⊥OB,∴PD=PE;其中正确的个数有()A.0个B.1个C.2个D.3个11.如图所示,PD=PE,PD⊥OA,PE⊥OB,垂足分别为D,E,则下列结论中错误的是()A.∠DOP=∠EOP B.OD=OE C.∠DPO=∠EPO D.PD=OD二.填空题(共8小题)12.如图,∠B=∠D=90°,根据角平分线性质,填空:(1)若∠1=∠2,则=;(2)若∠3=∠4,则=.13.点M在∠AOB的平分线上,点M到OA的距离为6,则点M到OB的距离为.14.射线OC平分∠AOB,点P在OC上,且PM⊥OA于点M,PN⊥OB予点N,且PM=2cm,则PN=cm.15.如图所示,在△ABC中,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F.则下列结论:①DA平分∠EDF;②AE=AF,DE=DF;③AD上的点到B,C两点的距离相等;④图中共有3对全等三角形,正确的有.16.如图,△ABC中,∠C=90°,AD为角平分线.若BC=5,BD=2,则点D到边AB 的距离为.17.如图,在△ABC中,∠C=90°,AD是∠CAB的平分线,DE⊥AB于点E,且DE=3cm,BD=5cm,则BC=cm.18.(1)如图,已知∠1=∠2,DE⊥AB,DF⊥AC,垂足分别为E、F,则DE DF.(2)已知DE⊥AB,DF⊥AC,垂足分别为E、F,且DE=DF,则∠1∠2.19.如图,△ABC中,∠C=90°,AB=13,AC=5,BC=12,点O为∠CAB和∠CBA的平分线的交点,则OP=.三.解答题(共9小题)20.如图,在直线MN上找一点P,使点P到直线AB和直线CD的距离相等.21.如图,△ABC中,∠C=90゜,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,且BE=CF,求证:(1)DE=DC;(2)BD=DF.22.如图所示,D是△ABC外角∠ACG的平分线上的一点.DE⊥AC,DF⊥CG,垂足分别为E,F.求证:CE=CF.23.如图,E是∠APB内的一点,CE⊥P A于点C,ED⊥PB于点D,CE=ED,点F在P A 上,∠APB=60°,∠PEF=15°.求∠CFE的度数.24.∠B=∠C=90°,EB=EC,DE平分∠ADC,求证:AE是∠DAB平分线.25.△ABC中,∠C=90°,AD为角平分线,BC=64,BD:DC=9:7,求D到AB的距离.26.如图,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=90,AB=18,BC=12,求DE 的长.27.如图,若S△ABD:S△ACD=AB:AC,求证:AD平分∠BAC.28.已知:如图所示,AQ,BM,CN是△ABC的三条角平分线.试说明AQ,BM,CN交于一点.参考答案一.选择题(共11小题)1.下列作图属于尺规作图的是()A.画线段MN=3cmB.用量角器画出∠AOB的平分线C.用三角尺作过点A垂直于直线L的直线D.已知∠α,用没有刻度的直尺和圆规作∠AOB,使∠AOB=2∠α【解答】解:A、画线段MN=3cm,需要知道长度,而尺规作图中的直尺是没有长度的,错误;B、用量角器画出∠AOB的平分线,量角器不在尺规作图的工具里,错误;C、用三角尺作过点A垂直于直线L的直线,三角尺也不在作图工具里,错误;D、正确.故选:D.2.如图△ABC中,∠ACB=90゜,AD平分∠BAC交BC于D,DE垂直AB于E,若DE=1.5cm,BD=3cm,则BC=()A.3cm B.7.5cm C.6cm D.4.5cm【解答】解:∵∠ACB=90°,∴AC⊥BC,∵DE⊥AB,AD平分∠BAC,∴DE=DC=1.5cm,∵BD=3cm,∴BC=BD+DC=3cm+1.5cm=4.5cm,故选:D.3.如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于D,CD=4,则点D到AB的距离是()A.4B.2C.3D.6【解答】解:如图,过D点作DE⊥AB于点E,则DE即为所求,∵∠C=90°,AD平分∠BAC交BC于点D,∴CD=DE(角的平分线上的点到角的两边的距离相等),∵CD=4,∴DE=4.故选:A.4.如图,AE为∠BAC的平分线,EB⊥AB,EF⊥AC,则下列结论不正确的是()A.EF=EB B.AF=AB C.AE=CE D.∠AEF=∠AEB 【解答】解:∵AE为∠BAC的平分线,EB⊥AB,EF⊥AC,∴EF=EB,在Rt△ABE和Rt△AFE中,,∴Rt△ABE≌Rt△AFE(HL),∴AF=AB,∠AEF=∠AEB,∴结论不正确的是AE=CE.故选:C.5.如图,在△ABC中,∠B、∠C的角平分线交于点0,OD⊥AB于D,OE⊥AC于E,则OD与OE的大小关系是()A.OD>OE B.OD<OE C.OD=OE D.不能确定【解答】解:如图,连接AO,∵∠B、∠C的角平分线交于点0,∴AO平分∠BAC,∵OD⊥AB,OE⊥AC,∴OD=OE.故选:C.6.如图,PC⊥OC于C,PD⊥OD于D,若PC=PD,则()A.∠1>∠2B.∠1=∠2C.∠1<∠2D.不能确定【解答】解:∵PC⊥OC,PD⊥OD,PC=PD,∴P在∠COD的角平分线上,即∠1=∠2,故选:B.7.如图所示,点D在∠AOB的内部,DE⊥OA,DF⊥OB,垂足分别为E,F,DE=DF,则∠AOD与∠BOD的大小关系是()A.∠AOD>∠BOD B.∠AOD=∠BOD C.∠AOD<∠BOD D.无法确定【解答】解:∵DE⊥OA,DF⊥OB,DE=DF,∴点D在∠AOB的平分线上,∴∠AOD=∠BOD.故选:B.8.下列关于三角形角平分线的说法错误的是()A.两角平分线交点在三角形内B.两角平分线交点在第三个角的平分线上C.两角平分线交点到三边距离相等D.两角平分线交点到三顶点距离相等【解答】解:A、两角平分线交点在三角形内,正确;B、两角平分线交点在第三个角的平分线上,正确;C、根据角平分线的性质,两角平分线交点到三边距离相等,正确;D、根据角平分线的性质,两角平分线交点到三边距离相等,不是到三顶点距离相等,故本选项错误.故选:D.9.给出下列结论,正确的有()①到角两边距离相等的点,在这个角的平分线上;②角的平分线与三角形平分线都是射线;③任何一个命题都有逆命题;④假命题的逆命题一定是假命题.A.1个B.2个C.3个D.4个【解答】解:①根据角平分线性质的逆定理,在角的内部到角两边距离相等的点,在这个角的平分线上,故本选项错误;②角平分线是射线,三角形的角平分线是线段,故本选项错误;③任何一个命题都有逆命题,正确;④假命题的逆命题不一定是假命题,如:假命题“相等的两个角是对顶角”的逆命题“对顶角相等”是真命题,故本选项错误.故选:A.10.如图,已知点P、D、E分别在OC、OA、OB上,下列推理:①∵OC平分∠AOB,∴PD=PE;②∵OC平分∠AOB,PD⊥OA,PE⊥OB,∴PD=PE;③∵PD⊥OA,PE⊥OB,∴PD=PE;其中正确的个数有()A.0个B.1个C.2个D.3个【解答】解:∵OC平分∠AOB,PD⊥OA,PE⊥OB,∴PD=PE.故选:B.11.如图所示,PD=PE,PD⊥OA,PE⊥OB,垂足分别为D,E,则下列结论中错误的是()A.∠DOP=∠EOP B.OD=OE C.∠DPO=∠EPO D.PD=OD【解答】解:A、根据HL可求得Rt△POE≌Rt△POD,∴∠DOP=∠EOP,故正确;B、OD=OE,正确;C、DPO=∠EPO,正确;D、错误.故选:D.二.填空题(共8小题)12.如图,∠B=∠D=90°,根据角平分线性质,填空:(1)若∠1=∠2,则BC=DC;(2)若∠3=∠4,则AB=AD.【解答】解:(1)若∠1=∠2,则BC=DC;(2)若∠3=∠4,则AB=AD.故答案为:BC,DC;AB,AD.13.点M在∠AOB的平分线上,点M到OA的距离为6,则点M到OB的距离为6.【解答】解:∵点M在∠AOB的平分线上,点M到OA的距离为6,∴点M到OB的距离=6.故答案为:6.14.射线OC平分∠AOB,点P在OC上,且PM⊥OA于点M,PN⊥OB予点N,且PM=2cm,则PN=2cm.【解答】解:∵OC平分∠AOB,点P在OC上,且PM⊥OA于M,PN⊥OB于N,PM =2cm,∴PN=PM=2cm.故答案为:2.15.如图所示,在△ABC中,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F.则下列结论:①DA平分∠EDF;②AE=AF,DE=DF;③AD上的点到B,C两点的距离相等;④图中共有3对全等三角形,正确的有①②.【解答】解:∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,∴DE=DF,在Rt△ADE与Rt△ADF中,,∴Rt△ADE≌Rt△ADF,∴∠ADF=∠ADE,AE=AF,∴DA平分∠EDF;故①②正确,∵无法判定AD⊥BC且平分BC,∴AD上的点到B,C两点的距离相等错误,∵图中只有1对全等三角形,故③④错误.故答案为:①②.16.如图,△ABC中,∠C=90°,AD为角平分线.若BC=5,BD=2,则点D到边AB 的距离为3.【解答】解:过D作DE⊥AB,∵BC=5,BD=2,∴CD=5﹣2=3,∵AD为角平分线,∴CD=DE=3,故答案为:3.17.如图,在△ABC中,∠C=90°,AD是∠CAB的平分线,DE⊥AB于点E,且DE=3cm,BD=5cm,则BC=8cm.【解答】解:∵∠C=90°,AD是∠CAB的平分线,DE⊥AB,∴CD=DE,∵DE=3cm,BD=5cm,∴BC=CD+BD=3+5=8cm.故答案为:8.18.(1)如图,已知∠1=∠2,DE⊥AB,DF⊥AC,垂足分别为E、F,则DE=DF.(2)已知DE⊥AB,DF⊥AC,垂足分别为E、F,且DE=DF,则∠1=∠2.【解答】解:(1)∵已知∠1=∠2∴AD为∠BAC的平分线又∵DE⊥AB,DF⊥AC,∴由角平分线性质得DE=DF.(2)∵已知DE⊥AB,DF⊥AC,∴DE,DF为点D到角两边的距离.又∵DE=DF,∴由角平分线性质知AD为角平分线.19.如图,△ABC中,∠C=90°,AB=13,AC=5,BC=12,点O为∠CAB和∠CBA的平分线的交点,则OP=2.【解答】解:作OE⊥BC,OF⊥AC,∴∠C=∠CFO=∠OEC=90°,∴四边形CFOE是矩形;∵∠CAB,∠CBA的平分线相交于点O,OE⊥BC,OF⊥AC,OP⊥AB,∴OE=OP=OF,∴四边形CFOE是正方形,设OE=OP=OF=x,则AP=AF=5﹣x,BP=BE=12﹣x,∴5﹣x+12﹣x=13,解得x=2,∴OP=OE=2.故答案为2.三.解答题(共9小题)20.如图,在直线MN上找一点P,使点P到直线AB和直线CD的距离相等.【解答】解:点P如图所示.21.如图,△ABC中,∠C=90゜,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,且BE=CF,求证:(1)DE=DC;(2)BD=DF.【解答】证明:(1)∵∠C=90°,AD是∠BAC的平分线,DE⊥AB,∴DE=DC;(2)在△BDE和△FDC中,,∴△BDE≌△FDC(SAS),∴BD=DF.22.如图所示,D是△ABC外角∠ACG的平分线上的一点.DE⊥AC,DF⊥CG,垂足分别为E,F.求证:CE=CF.【解答】证明:∵CD是∠ACG的平分线,DE⊥AC,DF⊥CG,∴DE=DF,在Rt△CDE和Rt△CDF中,,∴Rt△CDE≌Rt△CDF(HL),∴CE=CF.23.如图,E是∠APB内的一点,CE⊥P A于点C,ED⊥PB于点D,CE=ED,点F在P A 上,∠APB=60°,∠PEF=15°.求∠CFE的度数.【解答】解:∵CE⊥P A,ED⊥PB,CE=ED,∴∠APE=∠APB=×60°=30°,在△PEF中,∠CFE=∠APE+∠PEF=30°+15°=45°.24.∠B=∠C=90°,EB=EC,DE平分∠ADC,求证:AE是∠DAB平分线.【解答】证明:如图,过点E作EF⊥AD于F,∵DE平分∠ADC,∠C=90°,∴EC=EF,∵EB=EC,∴EF=BE,又∵∠B=90°,∴AE是∠DAB平分线.25.△ABC中,∠C=90°,AD为角平分线,BC=64,BD:DC=9:7,求D到AB的距离.【解答】解:∵BD:DC=9:7,BC=64,∴CD==28,∵AD为角平分线,∠C=90°,DE⊥AB,∴DE=DC=28.答:D到AB的距离为28.26.如图,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=90,AB=18,BC=12,求DE 的长.【解答】解:如图,过点D作DF⊥BC于F,∵BD是∠ABC的平分线,DE⊥AB,∴DE=DF,∴S△ABC=AB•DE+BC•DF=90,即×18•DE+×12•DE=90,解得DE=6.27.如图,若S△ABD:S△ACD=AB:AC,求证:AD平分∠BAC.【解答】证明:如图,过D作DM⊥AB于M,DN⊥AC于N,则S△ABD=AB•DM,S△ACD=AC•DN,∵S△ABD:S△ACD=AB:AC,∴DM=DN,∴AD平分∠BAC.28.已知:如图所示,AQ,BM,CN是△ABC的三条角平分线.试说明AQ,BM,CN交于一点.【解答】证明:设BM,CN交于点P,过点P作PD⊥AB,PE⊥BC,PF⊥AC,垂足分别为:D,E,F,∵BM平分∠ABC,CN平分∠ACB,∴PD=PE,PE=PF,∴PD=PF,∴AP平分∠BAC,即AQ,BM,CN交于一点P.。
人教版八年级数学上册《角的平分线的性质》练习题附答案

13.3 角的均分线的性质一、选择题 1.如图 1 所示 ,∠ 1=∠ 2,PD ⊥ OA ,PE ⊥ OB ,垂足分别为 D ,E ,则以下结论中错误的选项是 ( ).A . PD=PEB .OD=OE C.∠ DPO=∠ EPO D . PD=ODBEACPDEFOD ABDCA E B( 1) (2) (3)2.如图 2 所示,在△ ABC 中, AB=AC , AD 是△ ABC 的角均分线, DE ⊥AB , DF ⊥ AC ,垂足分别是 E ,F ,则以下四个结论:① AD 上随意一点到C ,B 的距离相等;② AD 上随意一点到 AB ,AC 的距离相等;③ BD=CD , AD ⊥ BC ;④∠ BDE=∠ CDF ,此中正确的个数是( ). A .1个 B.2个 C .3个 D. 4 个3.如图 3 所示,在 Rt △ ABC 中,∠ C=90°, AC=BC=1, AB=2 ,AD 在∠ BAC?的均分线上,DE ⊥ AB 于点 E ,则△ DBE 的周长为( ).A .2B .1+2C . 2D.没法计算AAAEDC EFPOEBOFB BDC(4)(5)(6)4.如图 4 所示,已知∠ AOB ,求作射线 OC ,使 OC 均分∠ AOB , ?作法的合理次序是().( 1)作射线 OC ;( 2)在 OA 和 OB 上,分别截取 OD , OE ,使 OD=OE ; ( 3)分别以 D , E 为圆心,大于1DE 的长为半径作弧,在∠ AOB 内,两弧交于点 C .2A .( 1)( 2)( 3)B .( 2)( 1)( 3)C .( 2)( 3)( 1)D .( 3)( 2)( 1) 二、填空题1.( 1)若 OC 为∠ AOB 的均分线,点 P 在 OC 上, PE ⊥OA , PF ⊥ OB ,垂足分别为 E ,F ,则PE=________,依据是 ________________ .( 2)如图 5 所示,若在∠ AOB 内有一点 P ,PE ⊥ OA ,PF ⊥ OB ,垂足分别为 E ,F ,且 PE=PF ,则点 P 在 _______,依据是 ____________ .2.△ ABC 中,∠ C=90°, AD均分∠ BAC,已知 BC=8cm,BD=5cm,则点 D?到 AB?的距离为 _______.3.如图 6 所示, DE⊥AB 于 E,DF⊥ AC 于点 F,若 DE=DF,只要O 增添一个条件, ?这个条件是 __________ .4.以下图,∠ AOB=40°, OM均分∠ AOB, MA⊥ OA于 A, MB?⊥OB?于 B, ?则∠ MAB的度数为 ________.三、解答题1.以下图,AD是∠ BAC的均分线, DE⊥ AB 于 E, DF⊥ AC于 F,且 BD=CD,那么相等吗?为何?AN M BBE与 CFEBDA F C2.以下图,∠ B=∠ C=90°, M是 BC中点, DM均分∠ ADC,判断 AM?能否均分∠ DAB,说明原因.M DCA B3.以下图,已知 PB⊥ AB,PC⊥ AC,且 PB=PC,D是 AP 上一点,由以上条件能够获得∠BDP= ∠ CDP吗?为何?ADCBP研究应用拓展性训练1.(与现实生活联系的应用题)以下图,在一次军事演习中,?红方侦探员发现蓝方指挥部设在 A 区,到公路、铁路的交错处 B 点 700m.假如你是红方指挥员,?请你以下图的作图地图上标出蓝方指挥部的地点.BA区比率尺 1:200002.(研究题)已知:在△ABC中, AB=AC.(1)依据以下要求画出图形:①作∠BAC的均分线交 BC于点 D;②过 D作 DE⊥ AB,垂足为点 E;③过点 D作 DF⊥ AC,垂足为点 F .(2)依据上边所画的图形,能够获得哪些相等的线段(AB=AC除外)?说明原因.3.以下图,在△ ABC中, P, Q?分别是 BC, AC上的点,作 PR⊥ AB, PS⊥ AC,垂足分别是R,S.若 AQ=PQ, PR=PS, ?下边三个结论① AS=AR,② QP∥ AR,③△ BRP≌△ CSP中,正确的是().A .①和③B.②和③C.①和② C .①,②和③BRPA Q S C、、答案 :一、1. D 分析:∵∠ 1=∠ 2, PD ⊥ OA 于 E , PE ⊥ OB 于 E ,∴ PD=PE .又∵ OP=OP ,∴△ OPE ≌△ OPD .∴ OD=OE ,∠ DPO=∠ EPO .故 A ,B , C 都正确.2. D 分析:如答图,设点 P 为 AD 上随意一点,连接PB ,PC .∵ AD 均分∠ BAC ,∴∠ BAD=∠ CAD .又∵ AB=AC , AP=AP ,∴△ ABP ≌△ ACP ,∴ PB=PC . A故①正确.由角的均分线的性质知②正确.∵ AB=AC ,∠ BAD=∠ CAD ,AD=AD ,P∴△ ABD ≌△ ACD .E F∴ BD=CD ,∠ ADB=∠ ADC .BDC又∵∠ ADB+∠ ADC=180°, ∴∠ ADB=∠ ADC=90°, ∴ AD ⊥BC ,故③正确.由△ ABD ≌△ ACD 知,∠ B=∠ C .又∵ DE ⊥ AB 于点 E , DF ⊥AC 于点 F ,∴∠ BED=∠ CFD=90°,∴∠ BDE=∠ CDF .故④正确.4. C 分析:∵ AD 均分∠ CAB , AC ⊥ BC 于点 C ,DE ⊥ AB 于 E ,∴ CD=DE .又∵ AD=AD ,∴ Rt △ACD ≌ Rt △ AED ,∴ AC=AE . 又∵ AC=BC ,∴ AE=BC ,∴△ DBE 的周长为 DE+BD+EB=CD+BD+EB=BC+EB=AC+EB=AE+EB=AB= 2 .提示:想法将 DE+BD+EB 转成线段 AB .5. C二、 1.( 1) PF 角均分线上的点到角的两边的距离同样( 2)∠ AOB 的均分线上 到角的两边距离相等的点在角的均分线上2.分析:以下图,AD 均分∠ CAB , DC ⊥ AC 于点 C , DM ⊥AB 于点 M .∴ CD=DM ,∴ DM=CD=BC-BD=8-5=3.答案: 3C提示:利用角的均分线的性质.D3. AD 均分∠ BAC .4.分析:∵ OM 均分∠ AOB ,∴∠ AOM=∠ BOM=AOB=20°.AMB2又∵ MA ⊥ OA 于 A , MB ⊥ OB 于 B ,∴MA=MB.∴Rt △OAM≌ Rt△ OBM,∴∠ AMO=∠ BMO=70°,∴△ AMN≌△ BMN,∴∠ ANM=∠ BNM=90°,∴∠ MAB=90° -70 ° =20°.答案: 20°三、 1.分析: BE=CF.∵AD均分∠ BAC, DE⊥ AB于点 E, DF⊥ AC于点 F,∴DE=DF.又∵ BD=DC,∴ Rt△ BDE≌Rt △ CDF,∴ BE=CF.提示:由角的均分线的性质可知DE=DF,进而为证△ BDE≌△ CDF供给了条件.2.分析: AM均分∠ DAB.原因:如答图13-9 所示,作 MN⊥ AD于点 N,∵ DM均分∠ CDA,MC ⊥ DC于点 C,MN⊥ AD于点 N,∴MC=MN.又∵ M是 BC的中点,∴ CM=MB,∴MN=BM,∴ AM均分∠ DAB.3.分析:能够.∵ PB⊥AB于点 B, PC⊥ AC于点 C,且 PB=PC,D CNM A B∴AP均分∠ BAC,∴∠ BAP=∠CAP.在 Rt△ ABP和 Rt△ ACP中,PB=PC , AP=AP,∴Rt △ABP≌ Rt△ ACP,∴ AB=AC.在△ ABD与△ ACD中,AB=AC ,∠ BAP=∠CAP, AD=AD,∴△ ABD≌△ ACD,∴∠ ADB=∠ ADC,∴∠ BDP=∠ CDP.研究应用拓展性训练1.如答图所示.分析:由题意可知,蓝方指挥部P 应在∠MBN的均分线上.又∵比率尺为1: 20000,∴ P 离 B 为 3. 5cm.提示:到角的两边距离相等的点在角的均分线上.2.( 1)分析:按题意绘图,如答图13-11 .(2)能够获得 ED=FD, AE=AF, BE=CF,BD=CD.原因以下:∵ AB=AC,∠ 1=∠ 2, AD=AD,∴△ ABD≌△ ACD,∴ BD=DC.∵∠ 1=∠2, DE⊥AB 于点 E, DF⊥ AC于点 F,∴DE=DF.A1 2E F BD C又∵ AD=AD,∴Rt △AED≌ Rt△ AFD,∴ AE=AF,∴AB-AE=AC-AF,即 BE=CF.提示:正确地画出图形是解决问题的重点,另三角形全等来找寻相等的线段.3. C分析:如答图所示,连接AP.∵PR⊥AB于点 R, PS⊥ AC于点 S, PR=PS,∴ AP均分∠ BAC,∴∠ 1=∠2.又∵ AQ=QP,∴∠ 2=∠ 3,∴∠ 1=∠ 3,∴ PQ∥ AR.在 Rt △APR和 Rt△ APS中,外此题主要应用角的均分线的性质及BRP312PR=PS , AP=AP,A Q S C ∴Rt △APR≌ Rt△ APS,∴ AR=AS.而△ BRP与△ CSP不具备三角形全等的条件,故①②正确.提示:此题的打破口是判断出点P 在∠ BAC的均分线上.。
八年级数学上册12.3角平分线的性质(讲+练)(8大题型)-【重要笔记】2022-2023学年八年级

12.3 角平分线的性质角的平分线的性质角的平分线的性质:角的平分线上的点到角两边的距离相等。
注意:用符号语言表示角的平分线的性质定理:若CD平分∠ADB,点P是CD上一点,且PE⊥AD于点E,PF⊥BD于点F,则PE=PF.角的平分线的尺规作图角平分线的尺规作图(1)以O为圆心,适当长为半径画弧,交OA于D,交OB于E.(2)分别以D、E为圆心,大于12DE的长为半径画弧,两弧在∠AOB内部交于点C.(3)画射线OC.射线OC即为所求.题型1:作已知角的平分线1.尺规作图:已知:∠CBA,求作∠CAB的平分线.【变式1-1】如图,在直线MN上求作一点P,使点P到射线OA和OB的距离相等。
(不写作法,保留作图痕迹)【变式1-2】如图,在Rt△ABC中,△C=90°.(1)作△BAC的平分线AD交边BC于点D.(尺规作图,保留作图痕迹,不写作法).(2)在(1)的条件下,若△BAC=28°,求△ADB的度数.题型2:角平分线的性质的应用-证明线段2.如图,已知OE平分△AOB,BC△OA于点C,AD△OB于点D,求证:EA=EB.【变式2-1】如图,点D、B分别在△A的两边上,C是△A内一点,AB = AD,BC = CD,CE△AD于E,CF△AF于F.求证:CE = CF.【变式2-2】已知:如图,OC是△AOB的平分线,P是OC上的一点,PD△OA,PE△OB,垂足分别为D、E,点F是OC上的另一点,连接DF,EF.求证:DF=EF.题型3:角平分线的性质的应用-和差关系3.如图,在△ABC中,△C=90°,△CAD=△BAD,DE△AB于E,点F在边AC 上,连接DF.(1)求证:AC=AE;(2)若AC=8,AB=10,求DE的长;(3)若CF=BE,直接写出线段AB,AF,EB的数量关系.【变式3-1】如图,△ABC的边BC的垂直平分线DE交△ABC的外角平分线AD于点D,DF△AB于点F,且AB>AC,试探究BF、AC、AF之间的数量关系,并说明理由.【变式3-2】题型4:角平分线的性质的应用-面积相关4.如图,BD是ΔABC的角平分线,DE⊥AB垂足为E,ΔABC的面积为70,AB= 16,BC=12,求DE的长.【变式4-1】如图,AD是△ABC的角平分线,DF△AB,垂足为F,如图DE=DG,△ADG和△AED的面积分别为50和38,求△EDF的面积【变式4-2】如图,在ΔABC中,AD为∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,若ΔABC的面积为21cm2,AB=8cm,AC=6cm,求DE的值.角的平分线的判定角平分线的判定:角的内部到角两边距离相等的点在角的平分线上.注意:用符号语言表示角的平分线的判定:若PE⊥AD于点E,PF⊥BD于点F,PE=PF,则PD平分∠ADB题型5:角平分线的判定5.如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,求证:AM平分∠DAB.【变式5-1】如图所示,PA=PB,△1+△2=180°.求证:OP平分△AOB.【变式5-2】如图所示,AP、CP分别是△ABC外角△MAC和△NCA的平分线,它们交于点P.求证:BP为△MBN的平分线.题型7:角平分线的性质与判定综合6.如图,已知点A、C分别在△GBE的边BG、BE上,且AB=AC,AD△BE,△GBE的平分线与AD交于点D,连接CD.求证:(1)AB=AD;(2)CD平分△ACE.【变式6-1】如图,已知△ABC中BC边的垂直平分线DE与∠BAC的平分线交于点E,EF⊥AB交AB的延长线于点F,BG⊥AC交AC于点G.求证.(1)BF=CG.(2)若AB=6,AC=8,求AF的长度.【变式6-2】如图,在△ABC外作两个大小不同的等腰直角三角形,其中∠DAB=∠CAE=90°,AB=AD,AC=AE.连接DC、BE交于F点.(1)求证:△DAC△△BAE.(2)直线DC、BE是否互相垂直,请说明理由.(3)求证:AF平分∠DFE.【变式6-3】如图1,射线BD交△ABC的外角平分线CE于点P,已知△A=78°,△BPC=39°,BC=7,AB=4.(1)求证:BD平分△ABC;(2)如图2,AC的垂直平分线交BD于点Q,交AC于点G,QM△BC于点M,求MC的长度.题型7:角平分线的实际应用7.某地有两条相交叉的公路,计划修建一个饭馆:希望饭馆点P既在MN这条公路上,又到直线OA、OB的距离相等.你能确定饭馆应该建在什么位置吗?(保留作图痕迹)【变式7-1】如图:某地要在三条公路围成的一块平地上修建一个公园,要使公园到三条公路的距离相等,应在何处修建?(使用尺规作图,保留作图痕迹)并证明你的观点.【变式7-2】太和中学校园内有一块直角三角形(Rt △ABC)空地,如图所示,园艺师傅以角平分线AD为界,在其两侧分别种上了不同的花草,在△ABD区域内种植了月季花,在△ACD区域内种植了牡丹花,并量得两直角边AB=10m,AC=6m,分别求月季花与牡丹花两种花草的种植面积.题型8:三角形中的角平分线8.已知△ABC的三条角平分线相交于点O,过点O作OD△BC,OE△AC,OF△AB.求证:OD=OE=OF.【变式8-1】如图,△ABC中,AB=6,AC=7,BD、CD分别平分△ABC、△ACB,过点D作直线平行于BC,交AB、AC于E、F. 求△AEF的周长.【变式8-2】如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分为三个三角形,则S△ABO:S△BCO:S△CAO等于?【变式8-3】如图①,在△ABC中,△ABC和△ACB的平分线交于点O,△A=α.(1)如图①,若△A=50°,求△BOC的度数.(2)如图②,连接OA,求证:OA平分△BAC.(3)如图③,若射线BO与△ACB的外角平分线交于点P,求证OC△PC.一、单选题1.如图,在△ABC中,△C=90°,BD平分△ABC,交AC于点D;若DC=3,AB=8则△ABD的面积是()A.8B.12C.16D.242.如图,OP平分△MON,PA△ON于点A,点Q是射线OM上的一个动点,若PA= 4,则PQ的长不可能是()A.3.5B.4C.4.5D.53.如图,已知点O是△ABC内一点,且点O到三边的距离相等,△A=40°,则△BOC=()A.110°B.120°C.130°D.140°4.如图,在四边形ABCD中,AB=CD,BA和CD的延长线交于点E,若点P使得S△PAB=S△PCD,则满足此条件的点P()A.有且只有1个B.有且只有2个C.组成△E的平分线D.组成△E的平分线所在的直线(E点除外)5.如图,在Rt△ACB中,∠ACB=90°,BC=12,BD=2CD,AD平分∠BAC,则点D到AB的距离等于()A.3B.4C.5D.9二、填空题6.如图,在△ABC中,BE平分△ABC交AC于点E,AF△BC于点F,BE、AF交于点P,若AB=9,PF=3,则△ABP的面积是.7.如图,已知△COB=2△AOC,OD平分△AOB,且△COD=18°,则△AOB的度数为.8.如图,在Rt△ABC中,∠ACB=90°, AC=6, BC=8, AB=10, AD是∠BAC的平分线.若P, Q分别是AD和AC上的动点,则PC+PQ的最小值是.9.如图,OP平分△AOB,PM△OA于M,点D在OB上,DH△OP于H.若OD=4,OP=7,PM=3,则DH的长为.三、作图题10.如图,电信部门要在S区修建一座电视信号发射塔.按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条高速公路m和n的距离也必须相等.发射塔应修建在什么位置?请用尺规作图标出它的位置.四、解答题11.如图,已知AD⊥BC于点D,E是延长线BA上一点,且EC⊥BC于点C,若∠ACE=∠E.求证:AD平分∠BAC.12.如图,在△ABC中,AD为△BAC的平分线,DE△AB于E,DF△AC于F,△ABC 面积是28cm2,AB=20cm,AC=8cm,求DE的长.13.如图,点P是△AOB的角平分线OC上一点,PE△OA,OE=12cm,点G是线段OP的中点,连接EG,点F是射线OB上的一个动点,若PF的最小值为4cm,求△PGE的面积.14.如图,直线AB△CD,点E在CD上,点O、点F在AB上,连接OE,过点F作FH△OE于点H.(1)尺规作图:作△EOF的角平分线OG交CD于点G;(不写作法,保留作图痕迹,并标明字母)(2)在(1)的条件下,已知△OFH=20°,求△OGD的度数.15.如图,△ABC和△EBD中,△ABC=△DBE=90°,AB=CB,BE=BD,连接AE,CD,AE与CD交于点M,AE与BC交于点N.(1)求证:AE=CD;(2)求证:AE△CD;(3)连接BM,有以下两个结论:①BM平分△CBE;②MB平分△AMD,其中正确的一个是(请写序号),并给出证明过程.。
人教版_部编版八年级数学上册第十二章第三节角的平分线的性质习题(含答案) (64)

人教版_部编版八年级数学上册第十二章第三节角的平分线的性质考试复习题(含答案)如图,OC平分∠AOB,点D,E分别在OA,OB上,点P在OC上且有PD=PE.求证:∠PDO =∠PEB.【答案】证明见解析;【解析】试题分析:过点P作AO、BO的垂线,利用直角三角形全等的判定可证出结论.试题解析:过P做PM垂直OA于M PN垂直OB于N因为OC平分∠AOB所以PM="PN" (角平分线上的点到2边的距离相等)因为PD=PE所以∠PDM全等于∠PEN(HL)所以∠PDO=∠PEB考点:1.角平分线的性质;2.直角三角形全等的判定与性质.32.已知:如图,CD∠AB于D,BE∠AC于E,∠1=∠2.求证:OB=OC.【答案】证明见解析【解析】试题分析:又CD∠AB,BE∠AC,∠1=∠2,可得OE=OD,∠BDO=∠CEO=90°,再由∠BOD=∠COE,可得∠BOD∠∠COE,从而OB=OC.试题解析:∠CD∠AB,BE∠AC,∠1=∠2,∠OE=OD,∠BDO=∠CEO=90°,又∠∠BOD=∠COE,∠∠BOD∠∠COE,∠OB=OC.考点:1.角平分线的性质;2.三角形全等的判定与性质.33.如图,BD是△ABC的角平分线,DE⊥AB,垂足为E,AB=16,BC=12.(1)△ABD与△CBD的面积之比为;(2)若△ABC的面积为70,求DE的长.【答案】4:3;5.【解析】AB求出BC两个三角形的面积之比等于底的比求出△ABD与△CBD的面积之比;根据(1)求出的△ABD与△CBD的面积之比,得到△ABD的面积,根据三角形的面积公式求出DE.试题解析:(1)、∵BD是△ABC的角平分线,ABBC =43,∴△ABD与△CBD的面积之比为4:3;(2)、∵△ABC的面积为70,△ABD与△CBD的面积之比为4:3,∴△ABD的面积为40,又AB=16,则DE=5.考点:角平分线的性质34.根据图中尺规作图的痕迹,先判断得出结论:.然后证明你的结论(不要求写出已知、求证).【答案】OM平分∠BOA.【解析】试题分析:根据角作图的画法得出三角形全等,从而说明角平分线.试题解析:OM是∠AOB的角平分线连接CM、DM∠OC=OD,CM=DM,OM=OM,∠∠OCM∠∠OCD,∠∠BOM=∠AOM,∠OM是∠AOB的角平分线.考点:(1)、尺规作图;(2)、三角形全等35.(8分)已知:如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC.(1)求证:AM平分∠BAD;(2)试说明线段DM与AM有怎样的位置关系?(3)线段CD、AB、AD间有怎样的关系?直接写出结果.【答案】(1)见解析(2)DM⊥AM,(3)CD+AB=AD【解析】试题分析:(1)首先要作辅助线,ME⊥AD则利用角的平分线上的点到角的两边的距离相等可知ME=MC,再利用中点的条件可知ME=MB,再利用到角两边距离相等的点在角的平分线上的逆定理证明AM平分∠DAB.(2)根据平行线性质得出∠CDA+∠BAD=180°,求出∠1+∠3=90°,根据三角形内角和定理求出即可.(3)证Rt△DCM≌Rt△DEM,推出CD=DE,同理得出AE=AB,即可得出答案.试题解析:(1)证明:作ME⊥AD于E,∵MC⊥DC,ME⊥DA,MD平分∠ADC,∴ME=MC,∵M为BC中点,∴MB=MC,又∵ME=MC,∴ME=MB,又∵ME⊥AD,MB⊥AB,∴AM平分∠DAB.(2)解:DM⊥AM,理由是:∵DM平分∠CDA,AM平分∠DAB,∴∠1=∠2,∠3=∠4,∵DC∥AB,∴∠CDA+∠BAD=180°,∴∠1+∠3=90°,∴∠DMA=180°﹣(∠1+∠3)=90°,即DM⊥AM.(3)解:CD+AB=AD,理由是:∵ME⊥AD,MC⊥CD,∴∠C=∠DEM=90°,在Rt△DCM和Rt△DEM中DM DM EM CM=⎧⎨=⎩ ∴Rt △DCM ≌Rt △DEM (HL ),∴CD=DE ,同理AE=AB ,∵AE+DE=AD ,∴CD+AB=AD .考点:角平分线的性质;全等三角形的判定与性质36.如图,在∠ABC 中,∠ACB=90°,AC=BC=AD(1)作∠A 的平分线交CD 于E ;(2)过B 作CD 的垂线,垂足为F ;(3)请写出图中两对全等三角形(不添加任何字母),并选择其中一对加以证明.【答案】(1)作图见试题解析;(2)作图见试题解析;(3)∠ACE ∠∠ADE ,∠ACE ∠∠CFB .【解析】试题分析:(1)利用角平分线的作法得出∠A的平分线;(2)利用钝角三角形高线的作法得出BF;(3)利用等腰三角形的性质及全等三角形的判定得出答案.试题解析:(1)如图所示:AE即为所求;(2)如图所示:BF即为所求;(3)如图所示:∠ACE∠∠ADE,∠ACE∠∠CFB,∠AC=AD,AE平分∠CAD,∠AE∠CD,EC=DE,在∠ACE和∠ADE中,∠AE=AE,∠AEC=∠AED,EC=ED,∠∠ACE∠∠ADE(SAS).考点:1.作图—复杂作图;2.全等三角形的判定.37.(8分)如图,在∠ABC中,∠B=90°,AB=BC=4,点E在BC上,将∠ABC沿AE折叠,使点B落在AC边上的点F处.(1)求BE的长;(2)判断∠CEF是什么特殊三角形.【答案】BE=4√2-4【解析】试题分析:(1)先由勾股定理求出AC的长,由折叠可得∠CEF为直角三角形,BE="EF," 设BE=,根据勾股定理可得;(2)由(1)可得EF=FC=,所以直角三角形CEF是等腰直角三角形.试题解析:在∠ABC中,∠B=90°,AB=BC=4,∠AC=42分将∠ABC沿AE折叠,使点B落在AC边上的点F处.所以BE=EF,∠∠CEF为直角三角形EC2=EF2+FC2 4分设BE=,(4-)2=2+(4-4)24分∠6分EF=FC=7分∠∠CEF是等腰直角三角形8分考点:1.勾股定理;2. 图形折叠的性质;3.等腰直角三角形的判定.38.如图,AD⊥BC于点D,EG⊥BC于点G,⊥E=⊥3.请问:AD平分⊥BAC吗?若平分,请说明理由.【答案】平分,理由见解析.【解析】【分析】先利用平面内垂直于同一条直线的两条直线互相平行,得到AD∥EG,再利用平行线的性质和已知条件求出∥1=∥2即可.【详解】解:平分.证明:∥AD∥BC于D,EG∥BC于G,(已知)∥∥ADC=∥EGC=90°,(垂直的定义)∥AD∥EG,(同位角相等,两直线平行)∥∥2=∥3,(两直线平行,内错角相等)∥E=∥1,(两直线平行,同位角相等)又∥∥E=∥3(已知)∥∥1=∥2(等量代换)∥AD平分∥BAC(角平分线的定义).【点睛】本题考查平行线的判定与性质;角平分线的定义.39.画图说明题,试用几何方法说明你所得结果的正确性.(1)作∠AOB=90°;(2)在∠AOB的内部任意画一条射线OP;(3)画∠AOP的平分线OM以及∠BOP的平分线ON;(4)用量角器量得∠MON= 度.【答案】45,理由见解析【解析】【分析】首先根据题意画出图形,再根据角平分线的性质可得∠POM=1∠POB,2∠PON=12∠POA,然后可得∠POM+∠PON=12(∠POB+∠POA),进而可得答案.【详解】如图所示:∥OM是∥AOP的平分线,ON是∥BOP的平分线,∥∥POM=12∥POA,∥PON=12∥POB,∥∥POB+∥POA=∥AOB=90°,∥∥POM+∥PON=12(∥POB+∥POA)=12∥AOB=12×90°=45°.【点睛】考查了基本作图,以及角平分线的作法,关键是掌握角平分线的画法.40.(本题满分10分)如图,把∠EFP按图所示的方式放置在菱形ABCD 中,使得顶点E、F、P分别在线段AB、AD、AC上.已知EP=FP=,EF=,∠BAD=60°,且AB.(1)求∠EPF的大小;(2)若AP=6,求AE+AF的值;(3)若∠EFP的三个顶点E、F、P分别在线段AB、AD、AC上运动,请直接写出AP长的最大值和最小值.【答案】(1)∠EPF=120°;(2)AE+AF=;(3)AP的最大值为8,AP 的最小值为4.【解析】试题分析:(1)过点P作PG∠EF,垂足为G,在RtFPG中,利用锐角三角函数求得∠FPG=60°,即可得∠EPF的度数.(2)作PM∠AB,PN∠ND,垂足分别为M、N,可证RtPME∠RtPNF,可得FN=EM;在RtPMA中,利用锐角三角函数求得AM的长,同样的方法求得AN的长,根据AE+AF=(AM-EM)+(AN+NF)=AM+AN即可求得AE+AF的值.(3)当PE∠AB,PF∠AD时,AP的值最大为8,当点A与点E(或点F)重合时,PA的值最小为4.试题解析:解:(1)过点P作PG∠EF,垂足为G,∠PE=PF,PG∠EF,∠FG=EG=,∠FPG=∠EPG=∠EPF.在RtFPG中,,∠∠FPG=60°∠∠EPF=2∠FPG=120°.作PM∠AB,PN∠ND,垂足分别为M、N,在菱形ABCD中,∠AD=AB,,DC=BC,AC=AC,∠∠ABC∠∠ADC,∠∠DAC=∠BAC∠点P到AB、CD两边的距离相等,即PM=PN.在RtPME和RtPNF中,∠PM=PN,PE=PF,∠RtPME∠RtPNF∠FN=EM在RtPMA中,∠PMA=90°,∠PAM=∠DAB=30°,∠AM=同理,AN=∠AE+AF=(AM-EM)+(AN+NF)=AM+AN=.(3)AP的最大值为8,AP的最小值为4.考点:菱形的性质;角平分线的性质;全等三角形的判定及性质.。
部编数学八年级上册专题06角的平分线性质问题(解析版)含答案

2023--2024学年度人教版数学八年级上册期末复习核心考点三种题型精炼专题06 角的平分线性质问题一、选择题1. (2023湖南张家界)如图,已知直线AB CD P ,EG 平分BEF Ð,140Ð=︒,则2Ð的度数是( )A. 70︒B. 50︒C. 40︒D. 140︒【答案】A 【解析】根据平行线的性质可得140EFG ︒Ð=Ð=, 180EFG BEF Ð+Ð=︒,EGF BEG Ð=Ð,推得140BEF Ð=︒,根据角平分线的性质可求出BEG Ð的度数,即可求得2Ð的度数.∵AB CD P ,∴140EFG ︒Ð=Ð=,180EFG BEF Ð+Ð=︒,EGF BEG Ð=Ð,∴18040140BEF Ð=︒-︒=︒,又∵EG 平分BEF Ð,∴1702BEG BEF Ð=Ð=︒,∴027BEG =Ð=︒Ð故选:A .【点睛】考查平行线的性质和角平分线的性质.掌握平行线的性质和角平分线的性质是解决本题的关键.2.如图,CE 是△ABC 的外角∠ACD 的平分线,若∠B=35°,∠ACE=60°,则∠A=( )A .35°B .95°C .85°D .75°【答案】C .【解析】本题考查了三角形外角性质,角平分线定义的应用,注意:三角形的一个外角等于和它不相邻的两个内角的和.根据三角形角平分线的性质求出∠ACD ,根据三角形外角性质求出∠A 即可.∵CE 是△ABC 的外角∠ACD 的平分线,∠ACE=60°∴∠ACD=2∠ACE=120°∵∠ACD=∠B+∠A∴∠A=∠ACD ﹣∠B=120°﹣35°=85°3.如图,△ABC 中,AD 为△ABC 的角平分线,BE 为△ABC 的高,∠C=70°,∠ABC=48°,那么∠3是( )A.59°B.60°C.56°D.22°【答案】A .【解析】本题考查了三角形的内角和定理,角平分线的定义,高线的定义,熟记概念与定理并准确识图是解题的关键.根据高线的定义可得∠AEC=90°,然后根据∠C=70°,∠ABC=48°求出∠CAB ,再根据角平分线的定义求出∠1,然后利用三角形的内角和等于180°列式计算即可得解。
八年级数学上册《第二章 角平分线的性质》同步练习题及答案(青岛版)

八年级数学上册《第二章角平分线的性质》同步练习题及答案(青岛版)学校:___________班级:___________姓名:___________考号:___________一、选择题1.如图,OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论错误的是( )A.PC=PDB.∠CPD=∠DOPC.∠CPO=∠DPOD.OC=OD2.如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,且∠ADC=110°,则∠MAB=( )A.30°B.35°C.45°D.60°3.下列命题中真命题是( )A.三角形按边可分为不等边三角形,等腰三角形和等边三角形B.等腰三角形任一个内角都有可能是钝角或直角C.三角形的一个外角大于任何一个内角D.三角形三条内角平分线相交于一点,这点到三角形三边的距离相等4.如图,在四边形ABCD中,AB=CD,BA和CD的延长线交于点E,若点P使得S△PAB =S△PCD,则满足此条件的点P( )A.有且只有1个B.有且只有2个C.组成∠E的角平分线D.组成∠E的角平分线所在的直线(E点除外)5.如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )A.10B.7C.5D.46.如图,两条笔直的公路l1、l2相交于点O,公路的旁边建三个加工厂A、B、D,已知AB=AD=5.2km,CB=CD=5km,村庄C到公路l1的距离为4km,则C村到公路l2的距离是( )A.3kmB.4kmC.5kmD.5.2km7.数学课上,小明进行了如下的尺规作图(如图所示):(1)在△AOB(OA<OB)边OA、OB上分别截取OD、OE,使得OD=OE;(2)分别以点D、E为圆心,以大于0.5DE为半径作弧,两弧交于△AOB内的一点C;(3)作射线OC交AB边于点P.那么小明所求作的线段OP是△AOB的( )A.一条中线B.一条高C.一条角平分线D.不确定8.如图,已知△ABC,∠ABC,∠ACB的角平分线交于点O,连接AO并延长交BC于D,OH⊥BC 于H,若∠BAC=60°,OH=3cm,OA长为( )cm.A.6B.5C.4D.3二、填空题9.如图所示,AO为∠A的平分线,OE⊥AC于E,且OE=2,则点O到AB的距离等于 .10.如图,在△ABC中,CD平分∠ACB交AB于点D,DE⊥AC交于点E,DF⊥BC于点F,且BC=4,DE=2,则△BCD的面积是.11.如图,△ABC中,∠C=90°,AD平分∠BAC,AB=5,CD=2,则△ABD的面积是 .12.如图,△ABC中,∠C=90°,BD是∠ABC的平分线,DE⊥AB于点E,AB=8cm,BC=6cm,=14cm2,则DE的长是 cm.S△ABC13.通过学习我们已经知道三角形的三条内角平分线是交于一点的.如图,P是△ABC的内角平分线的交点,已知P点到AB边的距离为1,△ABC的周长为10,则△ABC的面积为.14.如图,已知射线OC上的任意一点到∠AOB的两边的距离都相等,点D、E、F分别为边OC、OA、OB上,如果要想证得OE=OF,只需要添加以下四个条件中的某一个即可,请写出所有可能的条件的序号.①∠ODE=∠ODF;②∠OED=∠OFD;③ED=FD;④EF⊥OC.三、作图题15.如图,三条公路两两相交于点A,B,C,现在要在公路边建一所加油站,要求加油站的位置到三条公路的距离都相等,则符合要求的位置有几个?请你找出所有加油站的位置(要求:尺规作图,保留作图痕迹,写出结论).四、解答题16.如图,在△ABC中,点O是∠ABC、∠ACB平分线的交点,AB+BC+AC=20,过O作OD⊥BC 于D点,且OD=3,求△ABC的面积.17.如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF(1)求证:AD平分∠BAC;(2)已知AC=20, BE=4,求AB的长.18.如图,AC平分∠BCD,AB=AD,AE⊥BC于E,AF⊥CD于F.(1)若∠ABE=60°,求∠CDA的度数.(2)若AE=2,BE=1,CD=4.求四边形AECD的面积.19.如图,在△ABC中,M为BC的中点,DM⊥BC,DM与∠BAC的角平分线交于点D,DE⊥AB,DF⊥AC,E、F为垂足,求证:BE=CF.20.如图,在四边形ABCD中,BC>BA,AD=CD,BD平分∠ABC.求证:∠A+∠C=180°.答案1.B2.B.3.D.4.D.5.C6.B7.C.8.A.9.答案为:2.10.答案为:4.11.答案为:5.12.答案为:2.13.答案为:5.14.答案为:①②④.15.解:如图所示,P1,P2,P3,P4即为加油站的位置,共有4个符合要求的位置.16.解:如图,过点O作OE⊥AB于E,OF⊥AC于F,连接OA.∵点O是∠ABC,∠ACB平分线的交点∴OE=OD,OF=OD,即OE=OF=OD=3∴S△ABC =S△ABO+S△BCO+S△ACO=12AB•OE+12BC•OD+12AC•OF=12×2×(AB+BC+AC)=12×3×20=30.17.证明:(1)∵DE⊥AB,DF⊥AC∴∠E=∠DFC=90°∴在Rt△BED和Rt△CFD中BD=CD,BE=CF.∴Rt△BED≌Rt△CFD(HL)∴DE=DF∵DE⊥AB,DF⊥AC∴AD平分∠BAC;(2)解:∵Rt△BED≌Rt△CFD∴AE=AF,CF=BE=4∵AC=20∴AE=AF=20﹣4=16∴AB=AE﹣BE=16﹣4=12.18.解:(1)∵AC平分∠BCD,AE⊥BC AF⊥CD∴AE=AF在Rt△ABE和Rt△ADF中,AE=AF,AB=AD.∴Rt△ABE≌Rt△ADF∴∠ADF=∠ABE=60°∴∠CDA=180°﹣∠ADF=120°;(2)由(1)知:Rt△ABE≌Rt△ADF∴FD=BE=1,AF=AE=2,CE=CF=CD+FD=5∴BC=CE+BE=6∴四边形AECD的面积=△ABC的面积+△ACD的面积=10.19.证明:连接DB.∵点D在BC的垂直平分线上∴DB=DC;∵D在∠BAC的平分线上,DE⊥AB,DF⊥AC∴DE=DF;∵∠DFC=∠DEB=90°在Rt△DCF和Rt△DBE中DB=DC,DE=DF.∴Rt△DCF≌Rt△DBE(HL)∴CF=BE(全等三角形的对应边相等).20.证明:过点D作DE⊥BC于E,过点D作DF⊥AB交BA的延长线于F∵BD平分∠ABC∴DE=DF,∠DEC=∠F=90°在RtCDE和Rt△ADF中∴Rt△CDE≌Rt△ADF(HL)∴∠FAD=∠C∴∠BAD+∠C=∠BAD+∠FAD=180°.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
角平分线的性质练习题
1角平分线上的点到_________________距离相等;到一个角的两边距离相等的点都在
_____________.
2、∠AOB 的平分线上一点M ,M 到 OA 的距离为1.5 cm ,则M 到OB 的距离为_________.
3、如图,∠AOB =60°,CD ⊥OA 于D ,CE ⊥OB 于E ,且CD =CE ,则∠DOC =_________.
4、如图,在△ABC 中,∠C =90°,AD 是角平分线,DE ⊥AB 于E ,且DE =3 cm ,BD =5 cm ,则BC =_____cm .
5、三角形的三条角平分线相交于一点,并且这一点到________________相等。
6、点O 是△ABC 内一点,且点O 到三边的距离相等,∠A =60°,则∠BOC 的度数为_____________.
7、在△ABC 中,∠C =90°,AD 平分∠BAC 交BC 于D ,若BC =32,且BD ∶CD =9∶7,则D 到AB 的距离为 .
8、三角形中到三边距离相等的点是( )
A 、三条边的垂直平分线的交点
B 、三条高的交点
C 、三条中线的交点
D 、三条角平分线的交点
9、如图,∠1=∠2,PD ⊥OA ,PE ⊥OB ,垂足分别为D ,E ,下列结论错误的是( )
A 、PD =PE
B 、OD =OE
C 、∠DPO =∠EPO
D 、PD =OD
10、如图,直线l 1,l 2,l 3表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
A 、1处
B 、2处
C 、3处
D 、4处
11、如图,△ABC 中,∠C =90°,AC =BC ,AD 平分∠CAB 交BC 于D ,DE ⊥AB 于E ,且AB =6㎝,则△DEB 的周长为( )
A 、4㎝
B 、6㎝
C 、10㎝
D 、不能确定 2
1
D
A
P
O
E
B
l 2
l 1
l 3
第9题 第10题 第11题
第3题
第4题
D
C
A
E
B
12、如图,MP ⊥NP ,MQ 为△MNP 的角平分线,MT =MP ,连接TQ ,则下列结论中不正确的是( )
A 、TQ =PQ
B 、∠MQT =∠MQP
C 、∠QTN =90°
D 、∠NQT =∠MQT
N
T
Q
P
M
E
D
C
B A
E
D
C B
A
F
第12题 第13题 第14题
13、如图在△ABC 中,∠ACB =90°,BE 平分∠ABC ,DE ⊥AB 于D ,如果AC =3 cm ,那么AE +DE 等于( )
A .2 cm
B .3 cm
C .4 cm
D .5 cm
14、如图,已知AB =AC ,AE =AF ,BE 与CF 交于点D ,则对于下列结论:①△ABE ≌△ACF ;②△BDF ≌△CDE ;③D 在∠BAC 的平分线上.其中正确的是( )
A .①
B .②
C .①和②
D .①②③
15、△ABC 中,∠C =90°,点O 为△ABC 三条角平分线的交点,OD ⊥BC 于D ,OE ⊥AC 于E ,OF ⊥AB 于F ,且AB =10cm ,BC =8cm ,AC =6cm ,则点O 到三边AB 、AC 、BC 的距离为( )
A .2cm ,2cm ,2cm ;
B . 3cm ,3cm ,3cm ;
C . 4cm ,4cm ,4cm ;
D . 2cm ,3cm ,5cm
16、在Rt △ABC 中,∠C =90°,DE 是AB 的垂直平分线, 且∠BAD ∶∠BAC =1∶3,求∠B 的度数.
17、已知:如图△ABC 中,AB=AC ,∠C=30°, AB ⊥AD ,AD=4cm ,求BC 的长.
18、如图11.3—4,在△ABC中∠C=900,AC=BC,AD平分.交BC于点D,DE⊥BE
求证:(1)DE+BD=AC
(2)若AB=6cm,求△DBE的周长
19、如图11.3—6,已知:AB=AC,BD=CD,
求证:DE=DF
20、如图11.3—3,在,交BC于D,
若BC=10cm,BD=6cm,
求点D到AB的距离.
21、如图ll.3—7,BN是的平分线,P在BN上,D、E分别在AB、BC上,
都不是直角,
求证:PD=PE
22.如图11.3—10,已知0为的平分线的交点,
0E_kAC于E,若0E=2
求0到AB与0到CD的距离之和.
23.如图11.3一ll,已知于F,BE、CF相交于点D若BD=CD 求证:。
