第一节微分方程的概念
合集下载
微分方程的基本概念
3．具有初始条件的微分方程： 此类微分方程的特点是给定了某些函数值 ，如 都是给定的数（称为初值） 等，其中 y0 ， y0 y x x y0 ， y x x y0 。此时所求出
0 0
的微分方程的解称为微分方程的特解，不包含任意常数 C 。
注 1：微分方程的特解不包含任意常数 C ，因为此时可利用初始条件将常数 C 变 为确定的数。
例 1：解微分方程
现将初始条件 y x 0 1 代入通解 y x 2 C ，得： 1 02 C ，从而有 C 1 于是，该微分方程的特解为 y x 2 1
注：解具有初始条件的微分方程大致分为两步：求出微分方程的通解（此时无需
理会初始条件） ；代入初始条件求得特解。
第一节 微分方程的基本概念
1．微分方程：微分方程主要处理未知函数、未知函数的导数与自变量间的关系。
例 1：
dy 2 x 为一阶微分方程。 dx
例 2： x
d2y dy x2 4 x 3x 3 为二阶微分方程。 2 dx dx
注：微分方程的阶数等于方程中的导数的最高阶数。 2．微分方程的通解：微分方程中的通解包含任意常数，且任意常数的个数等于 微分方程的阶数。
再将初始条件 y x 1 2 代入 y
于是，该微分方程的特解为 y
先将初始条件 y x 1 3 代入 y x 2 C1 ，得： 3 12 C1 ，从而有 C1 2 于是有 y
x3 x3 C1 x C2 2 x C2 3 3
x3 13 1 2 x C2 ， 得：2 2 1 C2 ， 从而有 C2 3 3 3 x3 1 2x 3 3
d2y 例 2：解微分方程 2 2 x 。 dx
高等数学第七章第一节微分方程的基本概念课件.ppt
解: 如图所示, 点 P(x, y) 处的法线方程为
令 Y = 0 , 得 Q 点的横坐标
即 yy 2x 0
y P
Qo xx
引例1 通解:
dy dx
2x
y x1 2
引例2
y x2 C
d2y dx2
0.4
s t0 0 ,
ds dt
t0 20
s 0.2t 2 C1t C2
特解: y x2 1
s 0.2t 2 20t
例1. 验证函数 是微分方程
(C1 , C2为常数 )
的解, 并求满足初始条件
x
t0
A, dx
dt
t00
的特解 .
解:
k 2 (C1 sin kt C2 cos kt ) 这说明 x C1 cos kt C2 sin kt 是方程的解 .
是两个独立的任意常数, 故它是方程的通解.
利用初始条件易得:
故所求特解为
x Acos k t
例2. 已知曲线上点 P(x, y) 处的法线与 x 轴交点为 Q 且线段 PQ 被 y 轴平分, 求所满足的微分方程 .
微分方程的基本概念
含未内容)
分类 偏微分方程
方程中所含未知函数导数的最高阶数叫做微分方程 的阶.
一般地 , n 阶常微分方程的形式是
F (x, y, y,, y(n) ) 0
或 y(n) f (x, y, y,, y(n1) ) ( n 阶显式微分方程)
微分方程的解 — 使方程成为恒等式的函数.
通解 — 解中所含独立的任意常数的个数与方程 的阶数相同.
特解 — 不含任意常数的解, 其图形称为积分曲线.
定解条件 — 确定通解中任意常数的条件.
令 Y = 0 , 得 Q 点的横坐标
即 yy 2x 0
y P
Qo xx
引例1 通解:
dy dx
2x
y x1 2
引例2
y x2 C
d2y dx2
0.4
s t0 0 ,
ds dt
t0 20
s 0.2t 2 C1t C2
特解: y x2 1
s 0.2t 2 20t
例1. 验证函数 是微分方程
(C1 , C2为常数 )
的解, 并求满足初始条件
x
t0
A, dx
dt
t00
的特解 .
解:
k 2 (C1 sin kt C2 cos kt ) 这说明 x C1 cos kt C2 sin kt 是方程的解 .
是两个独立的任意常数, 故它是方程的通解.
利用初始条件易得:
故所求特解为
x Acos k t
例2. 已知曲线上点 P(x, y) 处的法线与 x 轴交点为 Q 且线段 PQ 被 y 轴平分, 求所满足的微分方程 .
微分方程的基本概念
含未内容)
分类 偏微分方程
方程中所含未知函数导数的最高阶数叫做微分方程 的阶.
一般地 , n 阶常微分方程的形式是
F (x, y, y,, y(n) ) 0
或 y(n) f (x, y, y,, y(n1) ) ( n 阶显式微分方程)
微分方程的解 — 使方程成为恒等式的函数.
通解 — 解中所含独立的任意常数的个数与方程 的阶数相同.
特解 — 不含任意常数的解, 其图形称为积分曲线.
定解条件 — 确定通解中任意常数的条件.
第四章 第一节微分方程的概念
2
2
dy dx
4x
0;
(4) cos(y) ln y x 1.
解 (1) 该方程是一阶线性微分方程, 因方程中含有的 dy 和 y 都是一次. dx
(2) 该方程是一阶非线性微分方程, 因方程中含有的 dy 的平方项. dx
(3) 该方程是二阶非线性微分方程, 因方程中含有的 dy 的三次方. dx
根据题意, x x(t) 还需满足条件 x(0) 0, dx 0. dt t0
O m x=x(t)
x 图4-2
21
第四章 微分方程
例 6 试指出下列方程是什么方程, 并指出微分方程的阶数.
(1) dy x2 y; dx
(3)x
d2 y dx2
2
dy dx
3
5xy
0;
(2)x
dy dx
d2s dt 20Fra bibliotek4(称为二阶微分方程)
(4)
此外, 未知函数 s s(t) 还应满足下列条件:
t 0 时, s 0 , v ds 20 dt
简记为 s |t0 0 , s ' |t0 20 . (两个初始条件)
(5)
7
第四章 微分方程
例 2 列车在平直线路上以 20m/ s (相当于 72km/h )的速度行驶, 当制动时列
F (x,(x),(x),(x) , (n) (x)) 0, 则称函数 y (x) 为微分方程(10)在区间 I 上的解.
16
第四章 微分方程
3､微分方程的解: 微分方程的解可能含有也可能不含有任意常数. 含有相互独立的任意常数, 且任意常数的个数与微分方程的阶数相等的解称为微分方程的通解(一般解). 一 般地, 微分方程的不含有任意常数的解称为微分方程的特解. 方程的通解是一类 解, 而不是指方程的“全部解”. 实际上, 我们在求解方程时得到一些解, 很难说 明这些解是否构成了方程的“全部解”, 这种工作有时会比求解方程本身还困难, 而实际工作中又告诉我们无须去做这样的工作, 因此我们将关注点放在求方程 的通解和特解上. 注 这里所说的相互独立的任意常数, 是指它们不能通过合并而使得通解 中的任意常数的个数减少.
第十章第一节微分方程的概念
y dx 2 xdx 得
y x 2 C1
2 y dx ( x C1 )dx
ห้องสมุดไป่ตู้
第一节 微分方程的基本概念
2、通解 若微分方程的解中含有独立的任意常数,且 任意常数的个数与微分方程的阶数相同， 则称这样的解 为微分方程的通解 （一般解）。
2 前例中， y 3 x ,
其中x0 , y0为已知常数. 二阶微分方程y f ( x, y, y)的初始条件为 , 其中x0 , y0 , y0 为已知常数. y x x y0 , y x x y0
0 0 0
y x x y0 ,
第一节 微分方程的基本概念
称为 4、初始条件 确定通解中的任意常数的条件， 初始条件， 也称为定值条件。
线斜率等于该点的横坐标平方的3倍,求此曲线的方程. 解： 设所求曲线方程为 y y( x ), dy 2 ① 微分方程 3 x 由导数的几何意义得
因曲线通过点 (1,2), 故 y | x 1 2
dx
② 初始条件 对(1)式求积分, 得 y 3 x 2dx x 3 C ③ 方程通解
n阶线性微分方程的一般形式为 ( n) ( n1) y a1 ( x) y ... an1 ( x) y an ( x) y g( x) （3） 其中a1 ( x),.a2 ( x)...,an ( x)和g( x)均为自变量x的
已知函数。 例： y P ( x ) y Q( x ), y 2 yy 3 y x 2 一阶线性常微分方程 二阶线性常微分方程
微分方程是一门独立的数学学科，有完整的理论体系。 是现代数学的一个重要分支。 本章我们主要介绍微分方程的一些基本概念，几种 常用的微分方程的求解方法，微分方程在经济中的应用。
高等数学第十一章课件.ppt
这类方程的特点是经过适当的变换，可以将方程
右边分解成只含 x 的函数与只含 y 的函数的乘积，而左 边是关于 y 的一阶导数.具体解法如下：
(1) 分离变量 将方程写成 1 dy f (x)dx 的形式
g( y)
(2) 两 端 积 分
1 g( y)
dy
f
(x)dx
设积分后得
G( y) F(x) C ； 则 G( y) F(x) C 称为隐式通解，隐式解有时可以
知 u 0, 取 u( x) x, 则 y2 xerx ,
得齐次方程的通解为 y (C1 C2x)erx;
3.有一对共轭复根 ( 0)
特征根为 r1 i , r2 i ,
y1 e( i ) x , y2 e( i )x ,
重新组合
1
y1
( 2
y1
y2 )
ex cos x,
y py qy f1(x) f2 (x)
的特解．
定理 4 若 Y 是线性齐次方程 y py qy 0 的
通解， y 是线性非齐次方程 y py qy f (x) 的一个
解，则Y y 是 y py qy f (x) 的通解．
设非齐方程特解为
代入原方程
综上讨论
注意 上述结论可推广到n阶常系数非齐次线性 微分方程（k是重根次数）.
第二节 一阶微分方程
一、可分离变量的微分方程 二、齐次方程 三、一阶线性微分方程 四、伯努利方程
一、可分离变量的微分方程
一阶微分方程的一般形式为
F(x, y, y) 0 或 dy f (x, y) dx
形如
dy f (x)g( y)(g( y) 0) dx
的一阶微分方程，称为可分离变量的微分方程．
第一节微分方程的基本概念
第十二章 微分方程一、 学时分配：讲课学时：14 习题学时：2 共 16 学时二、 基本内容：1．微分方程的基本概念 2．可分离变量的微分方程 3．齐次方程 4．一阶线性微分方程 5．全微分方程 6．可降阶的高阶微分方程 7．高阶线性微分方程 8．一阶常系数齐次线性微分方程 9． 一阶常系数非齐次线性微分方程三、 教学要求：1．理解并掌握微分方程的基本概念，主要包括微分方程的阶，微分方程 的通解、特解及微分方程的初始条件等．2．熟练掌握可分离变量的微分方程的解法．3．熟练掌握齐次微分方程的解法4．掌握一阶线性微分方程的形式，熟练掌握其解法；掌握利用变量代换解微分方程的方法；了解贝努利方程的形式及解法5．掌握全微分方程成立的充要条件，掌握全微分方程的解法，会用观察法找积分因子6．掌握)()(x f y n =、),(///y x f y =、),(///y y f y =三种高阶微分方程的解法，即降阶法，理解降阶法的思想7．掌握二阶线性方程解的结构，齐次线性方程的通解，非齐线性方程的特解及通解的形式8．掌握二阶常系数齐次线性微分方程的特征方程，特征根，及对应于特征根的三种情况，通解的三种不同形式９．掌握自由项为x m e x P x f λ)()(=和x m m e x x Q x x P x f λωω]sin )(cos )([)(+=的二阶常系数非齐次线性微分方程特解的方法四、重点难点：1．重点：2．难点：第一节 微分方程的基本概念教学目的：理解并掌握微分方程的基本概念，主要包括微分方程的阶，微分方程 的通解、特解及微分方程的初始条件等．教学重点：常微分方程的基本概念，常微分方程的通解、特解及初始条件教学难点：微分方程的通解概念的理解教学内容：一、 两个实例1．一条曲线通过点（1,2），且在该曲线上任一点),(y x M 处的切线的斜率为2x ，求这条曲线的方程。
解：设曲线方程为)(x y y =.由导数的几何意义可知函数)(x y y =满足x dxdy 2= （1） 同时还满足以下条件：1=x 时，2=y （2）把（1）式两端积分，得⎰=xdx y 2 即 C x y +=2 （3）其中C 是任意常数。
高等数学上册第七章课件.ppt
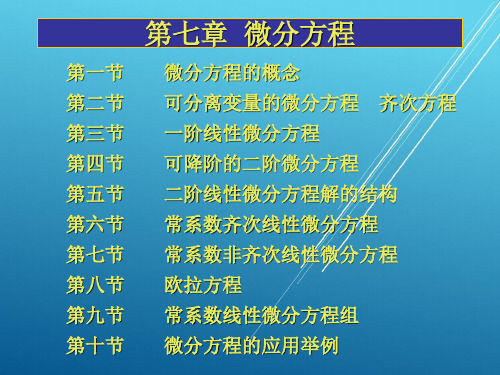
y C2 ex ,再利用 y (0) = 1 得 C2 1, 故所求曲线方程为
第四节 可降阶的二阶微分方程
小结 可降阶微分方程的解法 —— 降阶法
逐次积分
令 y p(x) ,
令 y p(y) ,
第五节 二阶线性微分方程解的结构
•n 阶线性微分方程的一般形式为
y(n) a1(x) y(n1) an1(x) y an (x) y f (x) f (x) 0 时, 称为非齐次方程 ; f (x) 0 时, 称为齐次方程.
第四节 可降阶的二阶微分方程
例 求解 解
代入方程得
则 y d p d p dy p d p dx dy dx dy
两端积分得 ln p ln y ln C1 , 即 p C1y,
(一阶线性齐次方程)
故所求通解为
第四节 可降阶的二阶微分方程
例
解初值问题
y e2y 0 y x 0 0 ,
y p(x) y q(x) y f (x), 为二阶线性微分方程.
复习: 一阶线性方程 y P(x) y Q(x)
通解:
y
C
e
P(x)d
x
eP(x)d x
Q(x) eP(x)d x dx
齐次方程通解Y 非齐次方程特解 y
第五节 二阶线性微分方程解的结构
•线性齐次方程解的结构
定理 若函数 y1(x), y2 (x) 是二阶线性齐次方程 y P(x) y Q(x) y 0
的两个解, 则 y C1y1(x) C2 y2 (x)
也是该方程的解. (叠加原理)
证 将 y C1y1(x) C2 y2 (x) 代入方程左边, 得 [C1y1 C2 y2 ] P(x)[C1y1 C2 y2 ]
高等数学基础第十一章
形如 y'' +py' qy f (x)
（11-2）
的方程(其中p，q为常数)，称为二阶常系数非齐次线性微分方
程。称 y'' +py' qy 0为方程（11-2）所对应的齐次方程。
定理11.2 (非齐次线性方程解的结构) 若 yp是线性非齐次方程(2)的 某个特解， yc 为对应的齐次线性方程的通解，则 y yp yc 为
以 s t
t0 0
，ds
dt
t0 0
。代入上式得
C1 C2=0
所以
s t 1 gt2
2
二、微分方程的基本概念
定义11.1 凡表示未知函数、未知函数的导数与自变量之间的关系 的方程称为微分方程。未知函数是一元函数的微分方程称为常微 分方程，未知函数是多元函数的微分方程称为偏微分方程。 微分方程中出现的未知函数的最高阶导数的阶数称为微分方程的阶
把初始条件y x0 2 代入上式,得C 2
所以方程的特解为
y (x2 2)ex2
第三节 可降阶的高阶微分方程
一、y(n) f (x) 型的微分方程
例1 求微分方程 y 2x sinx 的通解。
解
因为 y 2x sinx，所以
y' x2 cosx C1
y
1 3
x3
sinx
C1x
x3
1 5
x5 )
+
C2
例4 求微分方程(1 ex ) y'' y' 0 的通解。
解
设 y' p(x) ，代入方程，得
(1 ex ) p' p 0
分离变量得
dp p
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
dy P(x) y Q(x) (2)
dx
一阶线性非齐次方程
dy P(x) y 0 (3)
dx
一阶线性齐次方程
方程(3)是可分离变量方程, 其通解为:
y Ce P(x)dx 方程(2)的通解 常数变易法 设(2)的通解: y C(x)e P(x)dx
代入方程(2):
y C(x)eP(x)dx C(x)P(x)e P(x)dx
例5: y xy y2
y 1 y 1 y2
x 两端同除以 y2,
x y2
y
1
y 1
1
x
x
令 z y1, z 1 z 1 ,
xx
z
e
1 x
dx
[
1
e
1 x
dx
dx
C]
x
1 (x C)
x
代入 z y1, 通解为 y x .
xc
山东水利职业学院数理化教研室
《应用数学》精品课程——电子教案
《应用数学》精品课程——电子教案
第二节 一阶微分方程
本节介绍一阶微分方程的基本类型和常见类型.
一、可分离变量的方程
一阶微分方程一般形式: F(x, y, y) 0
我们研究其基本形式:
dy f (x, y) dx
(1)
如果可化成: f (x)dx g( y)dy 则(1)称为可分离变量的方程.
ln | y | x2 C1, y ex2 C1 eC1ex2
绝对值号可省略 y Cex2
任意常数,记为C
(2). y
x y
xy 2 x2 y
,
y |x0 1
y 1 y2
dy
x 1 x2
dx
y 1 y2
dy
x 1 x2
dx
ln(1 y2 ) ln(1 x2 ) C1 1 y2 C(1 x2 ), (C eC2 ) 定解条件代入: C=2 故特解为: 1 y2 2(1 x2 ).
C(x) Q(x)eP(x)dx
C(x) Q(x)e P(x)dxdx C
山东水利职业学院数理化教研室
《应用数学》精品课程——电子教案
则方程(2)的通解:
y e [ P(x)dx Q(x)e P(x)dxdx C] (4)
注:1. 一阶线性非齐次方程的通解可用常数变易法或公式(4) 计算皆可;.
定解条件的个数要和阶数相同,才能确定唯一特解; 定解条件中自变量取相同值时,叫做初始条件.
5. 几何意义: 通解 积分曲线族 特解 积分曲线
例:验证 x2 y2 c 是 y x 的通解
y
对
x2
y2
c用隐函数求导法得:
y
x y
故 x2 y2 c 是方程的解, 且含有一个任意常数.
通解
山东水利职业学院数理化教研室
2. 公式(4)中不定积分只求一个原函数即可;
3. y Ce P(x)dx e P(x)dx Q(x)e P(x)dxdx
非齐次方程 解的结构
齐次方程的通解 非齐次方程的特解
例3: dy 2xy ex2 cosx dx
y e2xdx[
ex2
cos
x
e
2
xdxdx
C]
ex2 [ cosxdx C] ex2 (sin x C)
两端同除以 yn , yn dy P(x) y1n Q(x),
dx
1 d ( y1n ) P(x) y1n Q(x), 1 n dx
令 z y1n , 则 dz (1 n)P(x)z (1 n)Q(x).
dx
关于 z 的线性方程
求出通解后再还原回 y
山东水利职业学院数理化教研室
《应用数学》精品课程——电子教案
山东水利职业学院数理化教研室
《应用数学》精品课程——电子教案
例4:
求方程( x
y2)
dy dx
y
满足初始条件y |x3 1
的特解.
将 y 视为自变量,可以变成关于 x 的线性方程:
dx 1 x y dy y
P(y) 1 ,Q(y) y y
x
e
1 y
dy
[
ye
1 y
dy
dy
C]
y(y C)
注意:其他类型的微分方程往往可以化成上述类型
例6:
y
1
x cos y sin 2 y
视 x 为 y 函数,可化成线性方程
《应用数学》精品课程——电子教案
二. 概念 1. 微分方程: 含有未知函数的导数或微分的方程.
未知函数为一元函数的微分方程称为常微分方程.(前例) 未知函数为多元函数的微分方程称为偏微分方程. 本章内容 2. 阶: 未知函数的最高阶导数的阶数.
例1是一阶微分方程,例2是二阶微分方程. 必须出现 n阶方程一般形式: F (x, y, y, y,, y(n) ) 0
山东水利职业学院数理化教研室
《应用数学》精品课程——电子教案
二.齐次方程的解法
如果方程(1)可化成:
dy ( y )
dx x
齐次方程解法:令来自uy x化成可分离变量方程.
y xu
dy u x du
dx
dx
u x du (u)
dx
例2:
dy dx
y2 xy x2
du 1 dx
(u) u x
解法: 1.分离变量: f (x)dx g( y)dy
2.两边积分: f (x)dx g(y)dy
3.得出通解: G( y) F(x) C 只写一个任意常数
山东水利职业学院数理化教研室
例1:
(1). dy dx
2xy
《应用数学》精品课程——电子教案
1 dy 2xdx y
1 y
dy
2xdx
3. 解: 如果将函数 y=y(x) 代入方程后恒等,则称其为方程的解. 如果解中含有任意常数,且个数与阶数相同 通解 必须独立 不含任意常数的解 特解
n阶方程通解一般形式:
山东水利职业学院数理化教研室
y y(x, c1, c2 ,, cn )
《应用数学》精品课程——电子教案
4. 定解条件: 确定通解中任意常数值的条件.
由 y |x3 1 得: C 2
故所求特解为: x y( y 2)
山东水利职业学院数理化教研室
四.伯努利方程
《应用数学》精品课程——电子教案
一般形式为: dy P(x) y Q(x) yn,(n 0,1) 的方程称为伯努利方程
dx
当 n= 0 或1时,这是线性方程.
当 n 0,1 时,可以化成线性方程:
dy
(
y )2 x
dx y 1
x
u y
x
u
u y
x
du dx
u2 u 1
y
(1
1 )du u
1 x
dx
u ln u C1 ln x
x y Ce x
山东水利职业学院数理化教研室
《应用数学》精品课程——电子教案
三.一阶线性方程微分方程 自由项
一般形式:
Q(x) 0 : Q(x) 0 :