材料力学-杆件强度计算
工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 第10章 组合受力与变形杆件的强度计算

解:危险截面在 A 处,其上之内力分量为: 弯矩: M y = FP1 a , M z = FP2 H 扭矩: M x = FP2 a 轴力: FNx = FP1 在截面上垂直与 M 方向的垂直线 ab 与圆环截 求得 M y 与 M z 的矢量和 M 过截面中心, 面边界交于 a、b 两点,这两点分别受最大拉应力和最大压应力。但由于轴向压力的作用,最 大压应力值大于最大拉应力值,故 b 点为危险点,其应力状态如图所示。 10-7 试求图 a 和 b 中所示之二杆横截面上最大正应力及其比值。 解: (a)为拉弯组合
7
y
y
A
O
0.795
B
14.526
+13.73MPa
z
(a)
O O
+14.43MPa
(b)
C
y
A
C
B B
y
A
O O
B
z
12.6mm
14.1mm
zC
−15.32MPa
16.55MPa
zC
z
(c)
(d)
习题 10-9 解图
∴
+ σ max
= 14.526 − 0.795 = 13.73 MPa
− σ max = −14.526 − 0.795 = −15.32 MPa
Ebh
由此得
2 FP 6e
e=
10-9
ε1 − ε 2 h × ε1 + ε 2 6
图中所示为承受纵向荷载的人骨受力简图。试:
1.假定骨骼为实心圆截面,确定横截面 B-B 上的应力分布; 2.假定骨骼中心部分(其直径为骨骼外直径的一半)由海绵状骨质所组成,忽略海绵状承受 应力的能力,确定横截面 B-B 上的应力分布;
杆件承载力计算公式

杆件承载力计算公式
在工程设计中,经常需要计算杆件的承载力。
杆件承载力的计算公式是根据材料力学理论和结构力学原理推导出来的。
以下是常见的杆件承载力计算公式:
1.压杆的计算公式:
如果杆件为压杆,那么其承载力的计算公式为:
Pc=Ac*Fc*σc
其中,Pc为杆件的承载力,Ac为杆件的截面面积,Fc为截面的调整系数,σc为相应材料的抗压强度。
2.拉杆的计算公式:
如果杆件为拉杆,那么其承载力的计算公式为:
Pt=At*Ft*σt
其中,Pt为杆件的承载力,At为杆件的截面面积,Ft为截面的调整系数,σt为相应材料的抗拉强度。
3.弯曲杆件的计算公式:
如果杆件受到弯曲作用,那么其承载力的计算公式为:
M=σb*W
其中,M为杆件的弯矩,σb为相应材料的弯曲强度,W为截面的抵抗弯曲矩的有效宽度。
4.扭转杆件的计算公式:
如果杆件受到扭转作用,那么其承载力的计算公式为:
T=τt*J
其中,T为杆件的扭矩,τt为相应材料的抗扭强度,J为截面的极
惯性矩。
以上是常见杆件承载力的计算公式,但需要根据具体情况选择适用的
公式。
此外,还应根据杆件的实际情况和要求,结合工程经验和相关规范,考虑到其他因素如安全系数、边界条件等进行修正,以确保杆件的安全可靠。
工程力学(静力学与材料力学)-10-组合受力与变形杆件的强度计算

TSINGHUA UNIVERSITY
My Mz
max M y
x
z
max M z
第10章 组合受力与变形杆件的强度计算
斜弯曲
TSINGHUA UNIVERSITY
对于圆截面,因为过形心的任 意轴均为截面的对称轴,所以当横 截面上同时作用有两个弯矩时,可 以将弯矩用矢量表示,然后求二者 的矢量和,这一合矢量仍然沿着横 截面的对称轴方向,合弯矩的作用 面仍然与对称面一致,所以平面弯 曲的公式依然适用。
max=
My Wy
+
Mz Wz
max
第10章 组合受力与变形杆件的强度计算
斜弯曲
最大正应力叠加公式应用限制
max
TSINGHUA UNIVERSITY
=
My Wy
+
Mz Wz
max=
My Wy
+
Mz Wz
本章将介绍杆件在斜弯曲、拉伸(压缩)与弯曲组 合、弯曲与扭转组合以及薄壁容器承受内压时的强度问题。
第10章 组合受力与变形杆件的强度计算
TSINGHUA UNIVERSITY
斜弯曲 拉伸(压缩)与弯曲的组合 弯曲与扭转组合 圆柱形薄壁容器应力状态与强度计算 结论与讨论
返回总目录
第10章 组合受力与变形杆件的强度计算
斜弯曲
TSINGHUA UNIVERSITY
以矩形截面为例,当梁的横截面上同时作用两个弯矩My 和 Mz(二者分别都作用在梁的两个对称面内)时,两个弯矩在同一 点引起的正应力叠加后,得到总的应力分布图。
Mz
第10章 组合受力与变形杆件的强度计算
杆件的轴向拉压变形及具体强度计算

根据强度条件,可以解决三类强度计算问题
1、强度校核:
max
FN A
2、设计截面:
A
FN
3、确定许可载荷: FN A
目录
拉压杆的强度条件
例题3-3
F
F=1000kN,b=25mm,h=90mm,α=200 。
〔σ〕=120MPa。试校核斜杆的强度。
解:1、研究节点A的平衡,计算轴力。
目录
——横截面上的应力
目录
FN
A
——横截面上的应力
该式为横截面上的正应力σ计 算公式。正应力σ和轴力FN同号。 即拉应力为正,压应力为负。
根据杆件变形的平面假设和材料均匀连续性假设 可推断:轴力在横截面上的分布是均匀的,且方向垂 直于横截面。所以,横截面的正应力σ计算公式为:
目录
• 拉(压)杆横截面上的应力
FN 2 45° B
F
FN1 28.3kN FN 2 20kN
2、计算各杆件的应力。
B
1
FN1 A1
28.3103 202 106
4
F
90106 Pa 90MPa
x
2
FN 2 A2
20103 152 106
89106 Pa 89MPa
目录
三、材料在拉伸和压缩时的力学性质
教学目标:1.拉伸、压缩试验简介; 2.应力-应变曲线分析; 3.低碳钢与铸铁的拉、压的力学性质; 4.试件的伸长率、断面收缩率计算。
教学重点:1.应力-应变曲线分析; 2.材料拉、压时的力学性质。
教学难点:应力-应变曲线分析。 小 结: 塑性材料与脆性材料拉伸时的应力-应变曲线分析。 作 业: 复习教材相关内容。
工程力学(材料力学)6拉压杆件的强度与变形问题

机械制造中的拉压杆件
机械制造中的拉压杆件主要用于 实现运动传递、力的传递和变形 等,如连杆、活塞杆、传动轴等。
这些杆件需要在高速、高温、重 载等极端条件下工作,因此需要 具备优异的力学性能和耐久性。
在机械制造中,拉压杆件的设计 和制造需要精确控制尺寸、形状 和材料,以确保其工作性能和可
靠பைடு நூலகம்。
其他工程领域中的拉压杆件
总结词
新型材料如碳纤维复合材料、钛合金等具有高强度、轻质等优点,在拉压杆件中得到广 泛应用。
详细描述
随着科技的不断发展,新型材料如碳纤维复合材料、钛合金等逐渐应用于拉压杆件的制 作。这些新型材料具有高强度、轻质、耐腐蚀等优点,能够提高杆件的力学性能和使用
寿命。
高性能的拉压杆件设计
总结词
通过优化设计,可以显著提高拉压杆件的性能。
刚度分析
对杆件的刚度进行分析, 可以确定其变形程度和承 载能力,为结构设计提供 依据。
拉压杆件的稳定性问题
稳定性定义
01
稳定性是指杆件在受到载荷作用时,保持其平衡状态的能力。
稳定性分析
02
通过稳定性分析,可以确定杆件在受到载荷作用时是否会发生
失稳现象,以及失稳的临界载荷。
稳定性要求
03
在工程应用中,杆件的稳定性需要满足一定的要求,以保证结
强度失效准则
当拉压杆件内部的应力达到或超过材料的屈服极限时,杆件会发生屈服失效, 丧失承载能力。
拉压杆件的强度计算
静力分析
根据外力的大小和方向,以及杆件的几何尺寸和材料属性,计算杆件内部的应力 分布。
动力分析
考虑动载荷的影响,分析杆件在振动、冲击等动态过程中的应力变化。
拉压杆件的强度校核
工程力学-第7章-轴向拉压杆件的强度与变形计算

7
Guang Zhou Auto College
工程力学
第7章 轴向拉压杆件的强度与变形计算
广 州 汽
斜拉桥承受拉力的钢缆 车 学 院
8
Guang Zhou Auto College
工程力学
第7章 轴向拉压杆件的强度与变形计算
广 州 汽 车 学 院9来自 7-1轴向拉压杆横截面上的应力
胡克定律
车
学
院
工程力学
17
轴向拉压的变形分析
P
P
A 细长杆受拉会变长变细,
P
B 受压会变短变粗
C 长短的变化,沿轴线方向, 称为纵向变形
l+Dl l
d-Dd d
D 粗细的变化,与轴线垂直,
称为横向变形
P
P
P
7-3轴向拉压杆的变形计算 胡克定律
工程力学
Guang Zhou Auto College
变形量的代数和:
汽
车
Δ
l
=
FNi li FNi ADlEADA+i
=Dl AD DlDE DlEB Dl
FNDElDE + FNEBlEB + FNBClBC
BC
学
Ec AAD
Ec ADE
Es AEB
Es ABC
=1.2106 m 0.6106 m 0.285106 m 0.428106 m
广
承受轴向载荷的拉(压)杆在工程中的
州
应用非常广泛。
汽
由汽缸、活塞、连
杆所组成的机构中,不
车
仅连接汽缸缸体和汽缸
盖的螺栓承受轴向拉力,
学
带动活塞运动的连杆由
杆件应力及强度计算

P
BC
FNAB 30 103 149Mpa 6 AAB 201 10
FNBC 26 103 2.6Mpa 4 ABC 100 10
拉伸、压缩与剪切
•斜截面上的应力
P
拉压的内力和应力
有些材料在破坏时并不总是沿横截面,有的是沿斜截面。因此要进 一步讨论斜截面上的应力。 k 设拉力为P,横截面积 为A, P
材料力学
长沙理工大学
蔡明兮
2018年8月8日星期三
第四章
杆件应力与强度计算
拉伸、压缩与剪切
•横截面上的应力
A、几何方面: 根据实验现象,作如下假设:
拉压的内力和应力
平截面假设:变形前的横截面,变形后仍然保持为横截面, 只是沿杆轴产生了相对的平移。 应变假设:变形时纵向线和横向线都没有角度的改变,说明 只有线应变而无角应变。
o
o
拉伸、压缩与剪切
•高温短期
When t 250o ~ 300o C When t 2时间的影响
以低碳钢为例,当温度升高,E、S降低。
b b
& &
在低温情况下。象低碳钢, p 、S增大,减小。即发生冷脆现象。
max
s
拉伸、压缩与剪切
剪切的实用计算:
剪切和挤压的实用计算
FS A
剪切的强度条件:
P
P
FS [ ] A
Q
) [1 ] (塑性材料) (0.6 ~ 0.8 [] 0.8 ~ 1.0) [1 ] (脆性材料) ( [1 ] 为材料的许用拉应力
拉伸、压缩与剪切
2、选择截面
(参考资料)材料力学72-必做题
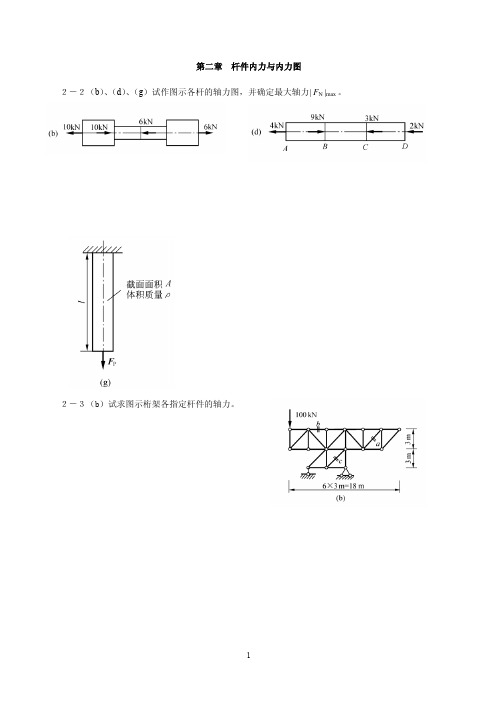
第二章杆件内力与内力图2-2(b)、(d)、(g)试作图示各杆的轴力图,并确定最大轴力| F N |max 。
2-3(b)试求图示桁架各指定杆件的轴力。
2-4(c)试作图示各杆的扭矩图,并确定最大扭矩| T |max 。
2-5图示一传动轴,转速n =200 r/min ,轮C为主动轮,输入功率P=60 kW ,轮A、B、D均为从动轮,输出功率为20 kW,15 kW,25 kW。
(1)试绘该轴的扭矩图。
(2)若将轮C与轮D对调,试分析对轴的受力是否有利。
2-8(a)、(c)、(e)、(g)、(h)试列出图示各梁的剪力方程和弯矩方程。
作剪力图和弯矩图,并确定|F s |max及|M |max值。
2-9(a)、(c)、(d)、(f)、(g)、(i)、(k)、(l)、(m)试用简易法作图示各梁的剪力图和弯矩图,并确定|F s |max及|M |max值,并用微分关系对图形进行校核。
2-10设梁的剪力图如图(a)(d)所示(见教材p39)。
试作弯矩图和荷载图。
已知梁上无集中力偶。
2-11(b)试用叠加法绘出图示梁的弯矩图。
2-6一钻探机的功率为10 kW,转速n =180 r/min。
钻杆钻入土层的深度l= 40m。
若土壤对钻杆的阻力可看作是均匀分布的力偶,试求分布力偶的集度m,并作钻杆的扭矩图。
2-14图示起重机横梁AB承受的最大吊重F P=12kN,试绘出横梁AB的内力图。
第三章轴向拉压杆件的强度与变形计算3-1图示圆截面阶梯杆,承受轴向荷载F1=50kN与F2的作用,AB与BC段的直径分别为d1=20mm与d2=30mm,如欲使AB与BC段横截面上的正应力相同,试求荷载F2之值。
3-5变截面直杆如图所示。
已知A1=8cm2,A2=4cm2,E=200GPa 。
求杆的总伸长量。
3-7图示结构中,AB为水平放置的刚性杆,1、2、3杆材料相同,其弹性模量E=210GPa ,已知l =1m,A1=A2=100mm2,A3=150mm2,F P=20kN 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x x
Iz Iy
tan
12 1
从式(12-1’)可看出,只要 Iz I y ,则 ,即荷载作
用平面与中性轴不垂直,这是斜弯曲与平面弯曲的区别之一。
对于圆截面,正方形截面及正多边形,形心主惯性矩Iz=Iy, 此时 ,说明是平面弯曲,荷载作用面与中性轴垂直。
b. 强度条件
max
材料力学
组合变形时杆件的强度计算
解组合变形的一般步骤(见框图)
一、斜弯曲
(一)平面弯曲与斜弯曲的区分
平面弯曲: ① 外力作用平面必须通过截面的弯曲中心(S)。 ② 外力作用平面必须通过或平行截面的任一主形心惯性平面。
斜弯曲: ① 外力作用平面必须通过截面的弯曲中心(S)。 ② 外力作用平面不通过也不平行截面的任一主形心惯性平面。 ③ 外力作用平面与中性轴不垂直。
max
min
N A
My Wy
Mz Wz
12 5
例2 构件受偏心压力如图示,已知P=100KN, a=0.2m, b=0.4m, ey=0.05m, ez=0.2m, 5MPa, 10MPa ,试确定中性 轴位置并校核构件的强度。
解(一)外力简化(见图)
P 100KN
ba
b2 12
0.0133m 2
ay
iz2 ey
0.0667m
az
i
2 y
ez
0.0665m
中性轴见图示位置
(四)校核危险点的强度
由于各横截面上的内
力相同,可取底截面来计 算。中性轴位置确定后, 离中性轴最远的点就是危 险点。图中A点为拉应力 最大,B点为压应力最大。
max
A
N A
My Wy
二、拉(压)与弯曲、偏心压缩(拉伸)
(一)拉伸(压缩)与弯曲的组合
最大正应力和最小正应力发生在弯矩最大的横截面上离中 性轴最远的点(由于是单向应力状态)建立的强度条件为:
max
min
N A
Mmax Wz
12 3
(二)偏心压缩(拉伸)
a. 中性轴的位置
ay
az
iz2 ey
点为最大拉应力和最大压应力点,即为危险点。
应力分布图
(四)计算中性轴位置及最大正应力
AB段中性轴与z轴的夹角为:(坐标原点可设在C截面处)
tan
Iz Iy
My x Mz x
Iz Iy
P2
x 0.5
P1 x
0.5m
x
1m
从上式可看出,中性轴位置在AB段内是随x的变化而变化 的。在A截面处(x=1m),中性轴位置为:
i
2 y
ez
12
4
式(12-4)中ay, az为中性轴在直角坐标轴上的截距(图12-3); ey, ez为偏心力P的作用点的位置(图中E点),iy, iz为惯性半径, 其计算式为:
i
y
Iy A
iz
Iz A
b. 正应力强度条件 最大正应力和最小正应力发生在离中性轴最远的点,危
险点的应力状态是单向应力状态,建立的强度条件为:
的弯形为两个平面弯曲 的组合——斜弯曲。受 力简图如图示。
受力简图
(二)内力分析
受力简图
分别绘出Mz(x) 和My(x)图如图示。 两个平面内的最大
弯矩都发生在固定 端A截面上,A截面 为危险截面。
Mz 1KN m
M
y
1KN
m
(三)应力分析和最大应力 绘出A截面的应力分布图,从应力分布图可看出a、b两
m y Pez 20KN m
mz
Pe y
5KN
m
例2图
(二)内力计算
任意横截面上的内力为:
N P 100KN 压
M y my 20KN m
M
z
mz
5KN
m
例2图
(三)中性轴位置
iz2
Iz A
1 ba3 12
ba
a2 12
0.00333m 2
i
2 y
Iy A
1 ab3 12
合成后总变矩为:
M
M
2 z
M
2 y
1.41KN
m
max
min
c
d
M W
115MPa
A截面应力分布图
a b
容易出现的一种计算错误:
max
Mz Wz
My Wy
163MPa
A截面应力分布图
的应力此时M式y 中WMMyyz引在起图的中应b点力,显M然z 不WM能zz 将在不图同中点a点处;的M应y引力起进 行相加,作为该截面上的最大正应力。
A截面中性轴确定后可绘出总应力分布图(见图)。
最大和最小正应力为:
max
min
a
b
Mz Wz
My Wy
70.2MPa
(五)改为圆截面时的计算
矩形截面改为圆截面后,受力图不变,内力图也不变。
此时对于圆截面来说,不存在斜弯曲问题,两个平面弯曲合 成后,还是一个平面弯曲的问题。危险截面A截面上弯矩的 合成由矢量来表示(见图)。总弯矩的矢量方向与中性轴重 合,说明总弯矩是绕中性轴弯曲(荷载作用平面与中性轴垂 直)离中性轴最远的两点(c,d)是正应力最大和最小的点。
M z max Wz
M y max Wy
12 2
例1 矩形截面的悬臂梁受荷载如图示。试确定危险截面、危 险点所在位置;计算梁内最大正应力及AB段的中性轴位 置;若将截面改为直径 D=50mm 的圆形,试确定危险点 的位置,并计算最大正应力。
例1图
解(一)外力分析 例1图
梁在P1作用下绕z轴 弯曲(平面弯曲),在 P2作用下绕y轴弯曲 (平面弯曲),故此梁
(二)斜弯曲时的强度条件 a. 中性轴与z轴的夹角
tan Iz M y 12 1
Iy Mz
以图12-2为例,此时中性轴位置的表达式为:
图12-2
tan
Iz Iy
P sin l P cos l
x x
Iz Iy
tan
12 1
tan
Iz Iy
P sin l P cos l
40 803
tan
Iz Iy
P2 0.5 P1 1
12 80 403
1 103 1103
4
12
应力分布图
40 803
tan
Iz Iy
P2 0.5 P1 1
12 80 403
1 1
103 103
4
12
解得: 76(o 见图)
应力分布图
如以合成后的总
弯矩以矢量表示,中 性轴与M的矢量不重 合,说明荷载作用平 面与中性轴不垂直, 这是斜弯a
min
B
N A
My Wy
Mz Wz
6.87 MPa
最后得出结论,构件强度满足
三、弯曲与扭转的组合
工程中有些杆件受弯曲和扭转的联合作用,对于一些圆截 面杆件,在弯和扭共同作用下危险点的应力状态都为图12-4所 示的单元体。
