清华大学结构力学习题集
结构力学习题集含答案
《结构力学》课程习题集一、单选题1、弯矩图肯定发生突变的截面就是( D )。
A、有集中力作用的截面;B、剪力为零的截面;C、荷载为零的截面;D、有集中力偶作用的截面。
2、图示梁中C截面的弯矩就是( D )。
4m2m4mA、12kN、m(下拉);B、3kN、m(上拉);C、8kN、m(下拉);D、11kN、m(下拉)。
3、静定结构有变温时,(C)。
A、无变形,无位移,无内力;B、有变形,有位移,有内力;C、有变形,有位移,无内力;D、无变形,有位移,无内力。
4、图示桁架a杆的内力就是(D)。
A、2P;B、-2P;C、3P;D、-3P。
5、图示桁架,各杆EA为常数,除支座链杆外,零杆数为(A)。
A、四根;B、二根;C、一根;D、零根。
l= a66、图示梁A点的竖向位移为(向下为正)(C)。
A、)24/(3EIPl; B、)16/(3EIPl; C、)96/(53EIPl; D、)48/(53EIPl。
PEI EI A l/l/2227、 静定结构的内力计算与( A )。
A 、EI 无关;B 、EI 相对值有关;C 、EI 绝对值有关;D 、E 无关,I 有关。
8、 图示桁架,零杆的数目为:( C )。
A 、5;B 、10;C 、15;D 、20。
9、 图示结构的零杆数目为( C )。
A 、5;B 、6;C 、7;D 、8。
10、 图示两结构及其受力状态,它们的内力符合( B )。
A 、弯矩相同,剪力不同;B 、弯矩相同,轴力不同;C 、弯矩不同,剪力相同;D 、弯矩不同,轴力不同。
PPEI EI EIEI 2EI EIllhl l11、 刚结点在结构发生变形时的主要特征就是( D )。
A 、各杆可以绕结点结心自由转动; B 、不变形; C 、各杆之间的夹角可任意改变; D 、各杆之间的夹角保持不变。
12、 若荷载作用在静定多跨梁的基本部分上,附属部分上无荷载作用,则( B )。
A 、基本部分与附属部分均有内力;B 、基本部分有内力,附属部分没有内力;C 、基本部分无内力,附属部分有内力;D 、不经过计算,无法判断。
清华大学版理论力学课后习题答案大全_____第3章静力学平衡问题习题解
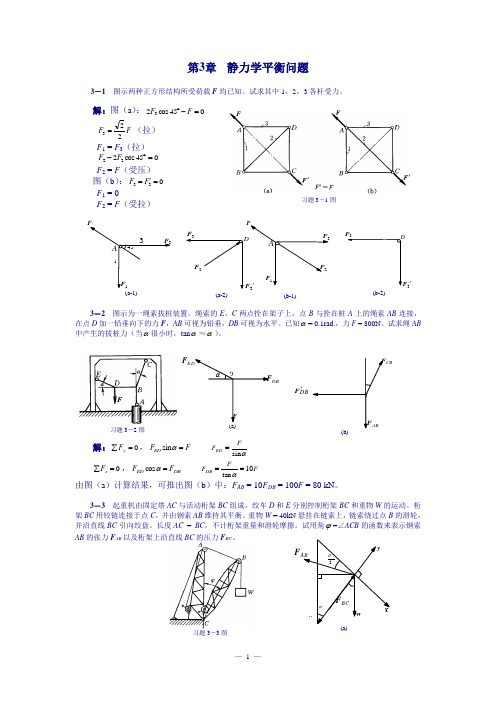
F DBCBDBF '习题3-3图第3章 静力学平衡问题3-1 图示两种正方形结构所受荷载F 均已知。
试求其中1,2,3各杆受力。
解:图(a ):045cos 23=-︒F FF F 223=(拉) F 1 = F 3(拉) 045cos 232=︒-F F F 2 = F (受压) 图(b ):033='=F F F 1 = 0F 2 = F (受拉)3-2 图示为一绳索拔桩装置。
绳索的E 、C 两点拴在架子上,点B 与拴在桩A 上的绳索AB 连接,在点D 加一铅垂向下的力F ,AB 可视为铅垂,DB 可视为水平。
已知α= 0.1rad.,力F = 800N 。
试求绳AB 中产生的拔桩力(当α很小时,tan α≈α)。
解:0=∑y F ,F F ED =αsin αs i nFF ED = 0=∑x F ,DB ED F F =αcos F FF DB 10tan ==α由图(a )计算结果,可推出图(b )中:F AB = 10F DB = 100F = 80 kN 。
3-3 起重机由固定塔AC 与活动桁架BC 组成,绞车D 和E 分别控制桁架BC 和重物W 的运动。
桁架BC 用铰链连接于点C ,并由钢索AB 维持其平衡。
重物W = 40kN 悬挂在链索上,链索绕过点B 的滑轮,并沿直线BC 引向绞盘。
长度AC = BC ,不计桁架重量和滑轮摩擦。
试用角ϕ=∠ACB 的函数来表示钢索AB 的张力F AB 以及桁架上沿直线BC 的压力F BC 。
(b-1)习题3-1图(a-1)(a-2)'3(b-2)习题3-2图F习题3-5图习题3-4图 解:图(a ):0=∑x F ,0sin 2cos=-ϕϕW F AB ,2sin2ϕW F AB =0=∑y F ,02sincos =---ϕϕAB BC F W W F即 2s i n 2c o s 2ϕϕW W W F BC ++=W W W W 2)c o s 1(c o s =-++=ϕϕ3-4 杆AB 及其两端滚子的整体重心在G 点,滚子搁置在倾斜的光滑刚性平面上,如图所示。
清华大学版理论力学课后习题答案大全 第7章质点动力学.

第3篇工程动力学基础第7章质点动力学习题7-1图7-1图示滑水运动员刚接触跳台斜面时,具有平行于斜面方向的速度 40.2km/h ,忽略摩擦,并假设他一经接触跳台后,牵引绳就不再对运动员有作用力。
试求滑水运动员从飞离斜面到再落水时的水平长度。
解:接触跳台时m/s设运动员在斜面上无机械能损失m/sm/s, m/sOmsssm习题7-2图7-2 图示消防人员为了扑灭高 21m 仓库屋顶平台上的火灾,把水龙头置于离仓库墙基 15m 、距地面高 1m 处,如图所示。
水柱的初速度m/s ,若欲使水柱正好能越过屋顶边缘到达屋顶平台,且不计空气阻力,试问水龙头的仰角应为多少?水柱射到屋顶平台上的水平距离为多少?解:(1 (1(2(1代入(2,得,(2 (到最高点所经过时间)m7-3 图示三角形物块置于光滑水平面上,并以水平等加速度向右运动。
另一物块置于其斜面上,斜面的倾角为θ。
设物块与斜面间的静摩擦因数为,且tanθ>,开始时物块在斜面上静止,如果保持物块在斜面上不滑动,加速度的最大值和最小值应为多少?(b习题7-3图(a 解:1、物块不上滑时受力图(a(1(2临界: (3(3代入(1、(2,消去,得(42、物块不下滑时受力图(b:(5(6临界: (7(7代入(5、(6,消去,得(87-4 图示物体的质量为m,悬挂在刚度系数为k的弹簧上,平衡时弹簧的静伸长为δst。
开始时物体离开平衡位置的距离为a,然后无初速度地释放。
试对图中各种不同坐标原点和坐标轴列出物体的运动微分方程,写出初始条件,求出运动规律,并比较所得到的结果。
习题7-4图解:(a受力图(e,且(1(2(3(1、(2代入(3,得(4记,则(5初始条件:时,, (6(f(6 代入 (5 ,得(e;(b受力图(e令,则初始条件:时,,(c受力图(f代入上式,即当时,,;(d受力图(f当时,,;习题7-5图7-5图示质量为m的平板置于两个反向转动的滑轮上,两轮间的距离为 2 d,半径为R。
清华大学版理论力学课后习题答案大全(免费下载)(第9章动量矩定理

清华大学版理论力学课后习题答案大全(免费下载)(第9章动量矩定理第9章动量矩定理及其应用9-1 计算下列情形下系统的动量矩。
1. 圆盘以ω的角速度绕O轴转动,质量为m的小球M 可沿圆盘的径向凹槽运动,图示瞬时小球以相对于圆盘的速度vr运动到OM = s 处;求小球对O点的动量矩。
2. 图示质量为m的偏心轮在水平面上作平面运动。
轮心为A,质心为C,且AC = e;轮子半径为R,对轮心A的转动惯量为JA;C、A、B三点在同一铅垂线上。
当轮子只滚不滑时,若vA已知,求轮子的动量和对B点的动量矩;当轮子又滚又滑时,若vA、ω已知,求轮子的动量和对B点的动量矩。
解:1、LO?m?s2 2、vr ω M O ω A B (a) C R vA ep?mvC?m(vA??e)?mvA(1?)Rv(R?e)2LB?mvC(R?e)?JC??mvA?(JA?me2)A RR(b) p?mvC?m(vA??e) 习题9-1图LB?mvC(R?e)?JC??m(vA??e)(R?e)?(JA? me2)??m(R?e)vA?(JA?meR)? 9-2 图示系统中,已知鼓轮以ω的角速度绕O轴转动,其大、小半径分别为R、r,对O轴的转动惯量为JO;物块A、B 的质量分别为mA和mB;试求系统对O 轴的动量矩。
ω O r 解:R LO?(JO?mAR2?mBr2)? A 习题9-2图 B θ 9-3 图示匀质细杆OA和EC的质量分别为50kg和100kg,并在点A焊成一体。
若此结构在图示位置静止状态释放,计算刚释放时,杆的角加速度及铰链O处的约束力。
不计铰链摩擦。
解:令m = mOA = 50 kg,则mEC = 2m 质心D位置:3612n?0,FOx?0 ??0,aDFOy?3mg?3m -1- 9-4 卷扬机机构如图所示。
可绕固定轴转动的轮B、C,其半径分别为R和r,对自身转轴的转动惯量分别为J1和J2。
被提升重物A的质量为m,作用于轮C的主动转矩为M,求重物A的加速度。
《结构力学习题集》(下)-结构的动力计算习题及答案

第九章 结构的动力计算一、判断题:1、结构计算中,大小、方向随时间变化的荷载必须按动荷载考虑。
2、仅在恢复力作用下的振动称为自由振动。
3、单自由度体系其它参数不变,只有刚度EI 增大到原来的2倍,则周期比原来的周期减小1/2。
4、结构在动力荷载作用下,其动内力与动位移仅与动力荷载的变化规律有关。
5、图示刚架不计分布质量和直杆轴向变形,图a 刚架的振动自由度为2,图b 刚架的振动自由度也为2。
6、图示组合结构,不计杆件的质量,其动力自由度为5个。
7、忽略直杆的轴向变形,图示结构的动力自由度为4个。
8、由于阻尼的存在,任何振动都不会长期继续下去。
9、设ωω,D 分别为同一体系在不考虑阻尼和考虑阻尼时的自振频率,ω与ωD 的关系为ωω=D 。
二、计算题:10、图示梁自重不计,求自振频率ω。
l l /411、图示梁自重不计,杆件无弯曲变形,弹性支座刚度为k ,求自振频率ω。
l /2l /212、求图示体系的自振频率ω。
l l0.5l 0.513、求图示体系的自振频率ω。
EI = 常数。
ll 0.514、求图示结构的自振频率ω。
l l15、求图示体系的自振频率ω。
EI =常数,杆长均为l 。
16、求图示体系的自振频率ω。
杆长均为l 。
17、求图示结构的自振频率和振型。
l /2l /2l /18、图示梁自重不计,W EI ==⨯⋅2002104kN kN m 2,,求自振圆频率ω。
B2m2m19、图示排架重量W 集中于横梁上,横梁EA =∞,求自振周期ω。
EIEIW20、图示刚架横梁∞=EI 且重量W 集中于横梁上。
求自振周期T 。
EIEIWEI 221、求图示体系的自振频率ω。
各杆EI = 常数。
a aa22、图示两种支承情况的梁,不计梁的自重。
求图a 与图b 的自振频率之比。
l /2l/2(a)l /2l /2(b)23、图示桁架在结点C 中有集中重量W ,各杆EA 相同,杆重不计。
求水平自振周期T 。
清华大学1995年结构力学试卷

清华大学 (硕)士生入学考试试题专用纸
准考证号 系 别 考试日期 95.1 专 业 考试科目
一、(10分)求图示半圆拱截面D 的内力。
二、(10分)画图示结构的弯矩图(每小题5分)
三、(10分)求图示桁架中杆1、2的轴力。
四、(15分)梁支座位移如图,l
a 2=θ,试用力法求M 图,并求C 点竖向位移。
五、(20分)试用位移法求刚架的M 、Q 、N 图。
六、(10分)求图示桁架杆1、2轴力的影响线,单位荷载在短梁上移动。
七、(10分)求图示结构的整体刚度方程,不计轴向变形的单元刚度矩阵为
八、(15分)梁端集中重量W=10kN ,分布质量不计,弹性支座刚度32l
EI k =,m l 3=, 241070.2m kN EI ⋅⨯=,阻尼比05.0=ξ,简谐荷载幅值P=2kN ,机器转速为500转/分钟,求质体的振幅及动力弯矩图。
清华大学结构力学上-2012年期末考题
结构力学期末考试题 2012年6月17日2013-06-15 19:40 |(分类:默认分类)本试题由3A学术资料部整理,感谢提供课堂照片资源的孝苇和乃冰姐姐!题目如果有误,希望大家提出,我们将立即改正,谢谢,祝一字班的筒子们考试顺利!一填空题(每道题5分,共40分,请将答案写到答题卡上面)1 图一.1所示结构,EI=10^6KN*M^2,结点C 的转角为:(顺时针为正,逆时针为负)2 图一.2所示桁架,各杆EA=常数,杆BE的轴力为:(压为负,拉为正)3 图一.3所示钢架,EI=常数,若已知C端的竖向线位移△cv=0,则M= P4 图一.4所示梁,EI=常数,支座C发生向下移动a,则支座反力Rc= (向上为正,向下为负)5 图一.5所示钢架,EI=常数,杆端弯矩MAB= (顺时针为正,逆时针为负)6 图一.6所示结构,梁AB的抗弯刚度为无穷大,其余杆件EI=常数,若用位移法,基本未知量有个,分别是(转角用Ө,线位移用△表示,并用箭头指出)7 图一.7所示结构,EI=4*10^6KN*M^2,EA=∞,q=16KN/m,杆端弯矩MAB= (顺时针为正,逆时针为负)8 利用力矩分配法分析图一.8所示结构,放松结点B后,分配到BC 杆的杆端弯矩MBC=二(20分)图二所示钢架,各杆EI=常数,结构尺寸与受力状态如图所示。
(1)画出结构的弯矩图、剪力图和轴力图(15分)(2)计算C点的竖向位移△c(5分)三(20分)图三所示钢架,杆CF的EI为无穷大,其余各杆EI=常数,结构尺寸与受力状态如图所示。
求M BH。
四(20分)图四所示桁架,各杆EA=常数,结构尺寸与受力状态如图所示。
计算杆CE的轴力和支座B 的反力。
清华大学 钢结构 4章例题
y
l0 y iy
300 47 .7 [ ] 150 6.29
因对x轴和y轴 值均属于b类,故长细比的较大值 x 55.6 查表得 0.83 。
设计原理
钢结构
第四章 轴心受力构件例题
N 1600 103 209N / mm 2 f 215N / mm 2 A 0.83 92.18 10 2
设计原理
钢结构
第四章 轴心受力构件例题
需要的截面几何量为:
A N
min
l0 x
1600 10 3 119 .8cm2 f 0.621 215 10 2
600 ix 6.67 cm 90 l0 y 300 iy 3.33cm 90
由附表7.1中不可能选出同时满足 A , ix 和 i y 的型号,
第四章 轴心受力构件例题
设计原理
钢结构
第四章 轴心受力构件例题
设计原理
钢结构
第四章 轴心受力构件例题
第4章 例题
【例4.1】图4.9示一有中级工作制吊车的厂房屋架的双
角钢拉杆,截面为2┗100×10,角钢上有交错排列的普
通螺栓孔,孔径 d=200mm。试计算此拉杆所能承受的 最大拉力及容许达到的最大计算长度。钢材为Q235钢。
设计原理
钢结构
第四章 轴心受力构件例题
图4.22
设计原理
例4.3图
钢结构
第四章 轴心受力构件例题
答案(A) 主要作答过程:
7000 70 查附表4.2得 y 0.751 100 N 2698 103 191.5 N mm 2 205 N mm 2 y A 0.75118760
清华大学混凝土结构设计原理试题库及其参考答案
清hua 大学混凝土结构设计原理试题库及其参考答案一、判断题(请在你认为正确陈述的各题干后的括号内打“√”,否则打“×”。
每小题1分。
)第1章 钢筋和混凝土的力学性能1.混凝土立方体试块的尺寸越大,强度越高。
( )2.混凝土在三向压力作用下的强度可以提高。
( )3.普通热轧钢筋受压时的屈服强度与受拉时基本相同。
( )4.钢筋经冷拉后,强度和塑性均可提高。
( )5.冷拉钢筋不宜用作受压钢筋。
( )6.C20表示f cu =20N/mm 。
( )7.混凝土受压破坏是由于内部微裂缝扩展的结果。
( )8.混凝土抗拉强度随着混凝土强度等级提高而增大。
( )9.混凝土在剪应力和法向应力双向作用下,抗剪强度随拉应力的增大而增大。
( )10.混凝土受拉时的弹性模量与受压时相同。
( )11.线性徐变是指压应力较小时,徐变与应力成正比,而非线性徐变是指混凝土应力较大时,徐变增长与应力不成正比。
( )12.混凝土强度等级愈高,胶结力也愈大( )13.混凝土收缩、徐变与时间有关,且互相影响。
( )第1章 钢筋和混凝土的力学性能判断题答案1. 错;对;对;错;对;2. 错;对;对;错;对;对;对;对;第3章 轴心受力构件承载力1.轴心受压构件纵向受压钢筋配置越多越好。
( )2.轴心受压构件中的箍筋应作成封闭式的。
( )3.实际工程中没有真正的轴心受压构件。
( )4.轴心受压构件的长细比越大,稳定系数值越高。
( )5.轴心受压构件计算中,考虑受压时纵筋容易压曲,所以钢筋的抗压强度设计值最大取为2/400mm N 。
( )6.螺旋箍筋柱既能提高轴心受压构件的承载力,又能提高柱的稳定性。
( )第3章 轴心受力构件承载力判断题答案1. 错;对;对;错;错;错;第4章 受弯构件正截面承载力1.混凝土保护层厚度越大越好。
( )2.对于'f h x 的T 形截面梁,因为其正截面受弯承载力相当于宽度为'f b 的矩形截面梁,所以其配筋率应按0'h b A f s =ρ来计算。
清华大学《结构力学习题集》
清华⼤学《结构⼒学习题集》第三章静定结构的位移计算⼀、判断题:1、虚位移原理等价于变形谐调条件,可⽤于求体系的位移。
2、按虚⼒原理所建⽴的虚功⽅程等价于⼏何⽅程。
3、在⾮荷载因素(⽀座移动、温度变化、材料收缩等)作⽤下,静定结构不产⽣内⼒,但会有位移且位移只与杆件相对刚度有关。
4、求图⽰梁铰C 左侧截⾯的转⾓时,其虚拟状态应取:5、功的互等、位移互等、反⼒互等和位移反⼒互等的四个定理仅适⽤于线性变形体系。
6、已知M p 、M k 图,⽤图乘法求位移的结果为:()/()ωω1122y y EI +。
7、图a 、b 两种状态中,粱的转⾓?与竖向位移δ间的关系为:δ=? 。
8、图⽰桁架各杆E A 相同,结点A 和结点B 的竖向位移均为零。
9、图⽰桁架各杆EA =常数,由于荷载P 是反对称性质的,故结点B 的竖向位移等于零。
⼆、计算题:10、求图⽰结构铰A 两侧截⾯的相对转⾓?A ,EI = 常数。
11、求图⽰静定梁D 端的竖向位移 ?DV 。
EI = 常数,a = 2m 。
12、求图⽰结构E 点的竖向位移。
EI = 常数。
13、图⽰结构,EI=常数,M =?90kN m , P = 30kN 。
求D 点的竖向位移。
14、求图⽰刚架B 端的竖向位移。
15、求图⽰刚架结点C 的转⾓和⽔平位移,EI = 常数。
16、求图⽰刚架中D点的竖向位移。
EI =常数。
17、求图⽰刚架横梁中D点的竖向位移。
EI =常数。
18、求图⽰刚架中D 点的竖向位移。
E I = 常数。
19、求图⽰结构A、B两截⾯的相对转⾓,EI =常数。
20、求图⽰结构A 、B 两点的相对⽔平位移,E I = 常数。
21、求图⽰结构B 点的竖向位移,EI = 常数。
22、图⽰结构充满⽔后,求A 、B 两点的相对⽔平位移。
E I = 常数,垂直纸⾯取1 m 宽,⽔⽐重近似值取10 kN / m 3。
23、求图⽰刚架C 点的⽔平位移 ?CH ,各杆EI = 常数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章 静定结构的位移计算一、判断题:1、虚位移原理等价于变形谐调条件,可用于求体系的位移。
2、按虚力原理所建立的虚功方程等价于几何方程。
3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下,静定结构不产生内力,但会有位移且位移只与杆件相对刚度有关。
4、求图示梁铰C 左侧截面的转角时,其虚拟状态应取:A.;; B.D.C.M =15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。
6、已知M p 、M k 图,用图乘法求位移的结果为:()/()ωω1122y y EI +。
M k M p 21y 1y 2**ωω( a )M 17、图a 、b 两种状态中,粱的转角ϕ与竖向位移δ间的关系为:δ=ϕ 。
8、图示桁架各杆E A 相同,结点A 和结点B 的竖向位移均为零。
a a9、图示桁架各杆EA =常数,由于荷载P 是反对称性质的,故结点B 的竖向位移等于零。
二、计算题:10、求图示结构铰A 两侧截面的相对转角ϕA ,EI = 常数。
q l l l /211、求图示静定梁D 端的竖向位移 ∆DV 。
EI = 常数 ,a = 2m 。
a a a 10kN/m12、求图示结构E 点的竖向位移。
EI = 常数 。
l l l l /3 2 /3/3q13、图示结构,EI=常数 ,M =⋅90kN m , P = 30kN 。
求D 点的竖向位移。
P 3m 3m 3m14、求图示刚架B 端的竖向位移。
q15、求图示刚架结点C 的转角和水平位移,EI = 常数 。
16、求图示刚架中D点的竖向位移。
EI =常数。
l ll/217、求图示刚架横梁中D点的竖向位移。
EI=常数。
18、求图示刚架中D点的竖向位移。
E I = 常数。
qll l/l/2219、求图示结构A、B两截面的相对转角,EI=常数。
l/23l/320、求图示结构A、B两点的相对水平位移,E I = 常数。
ll21、求图示结构B点的竖向位移,EI = 常数。
l l22、图示结构充满水后,求A、B两点的相对水平位移。
E I = 常数,垂直纸面取1 m 宽,水比重近似值取10 kN / m3。
23、求图示刚架C点的水平位移∆CH,各杆EI = 常数。
4m4m3m2kN/m24、求图示刚架B的水平位移∆BH,各杆EI = 常数。
3m4m 4mq7kN/m25、求图示结构C截面转角。
已知:q=10kN/m , P=10kN , EI = 常数。
P26、求图示刚架中铰C两侧截面的相对转角。
27、求图示桁架中D 点的水平位移,各杆EA 相同 。
a28、求图示桁架A 、B 两点间相对线位移 ∆AB ,EA=常数。
a 一a 一a 一29、已知b a b au u u u ]2/)([sin d cos sin 2⎰=,求圆弧曲梁B 点的水平位移,EI =常数。
A BR30、求图示结构D 点的竖向位移,杆AD 的截面抗弯刚度为EI ,杆BC 的截面抗拉(压)刚度为EA 。
a331、求图示结构D点的竖向位移,杆ACD的截面抗弯刚度为EI,杆BC抗拉刚度为EA 。
32、求图示结构S杆的转角ϕS。
( EI = 常数,EA EI a=/2)。
aaa a33、刚架支座移动与转动如图,求D点的竖向位移。
a a/a//4002234、刚架支座移动如图,c1= a / 2 0 0 ,c2= a /3 0 0 ,求D点的竖向位移。
c2a a35、图示结构B支座沉陷∆= 0.01m ,求C点的水平位移。
l/236、结构的支座A发生了转角θ和竖向位移∆如图所示,计算D点的竖向位移。
θA Dl/ll 237、图示刚架A 支座下沉 0.01l ,又顺时针转动 0.015 rad ,求D 截面的角位移。
D0.015radA0.01l l l38、图示桁架各杆温度均匀升高t o C ,材料线膨胀系数为α,求C 点的竖向位移。
a a a39、图示刚架杆件截面为矩形,截面厚度为h , h/l = 1/ 20 ,材料线膨胀系数为 α,求C点的竖向位移。
C A-3-3+t+ttt l40、求图示结构B 点的水平位移。
已知温变化t 110=℃,t 220=℃ ,矩形截面高h=0.5m ,线膨胀系数a = 1 / 105。
t 1t 2t 4m B141、图示桁架由于制造误差,AE 长了1cm ,BE 短了1 cm ,求点E 的竖向位移。
A C BE2cm2cm2cm42、求图示结构A点竖向位移(向上为正)∆AV。
aaA43、求图示结构C点水平位移∆CH,EI = 常数。
2EIl3 =644、求图示结构D点水平位移∆DH。
EI= 常数。
lEI l=33 lk45、BC为一弹簧,其抗压刚度为k,其它各杆EA = 常数,求A点的竖向位移。
第四章超静定结构计算——力法一、判断题:1、判断下列结构的超静定次数。
(1)、 (2)、(a)(b)(3)、 (4)、(5)、 (6)、(7)、(a)(b)2、力法典型方程的实质是超静定结构的平衡条件。
3、超静定结构在荷载作用下的反力和内力,只与各杆件刚度的相对数值有关。
4、在温度变化、支座移动因素作用下,静定与超静定结构都有内力。
5、图a 结构,取图b 为力法基本结构,则其力法方程为δ111X c =。
(a)(b)X 16、图a 结构,取图b 为力法基本结构,h 为截面高度,α为线膨胀系数,典型方程中∆12122t a t t l h =--()/()。
t 21t lA h (a)(b)X 17、图a 所示结构,取图b 为力法基本体系,其力法方程为。
(a)(b)1二、计算题:8、用力法作图示结构的M 图。
3m m9、用力法作图示排架的M 图。
已知 A = 0.2m 2,I = 0.05m 4,弹性模量为E 0。
q10、用力法计算并作图示结构M 图。
EI =常数。
a a11、用力法计算并作图示结构的M 图。
ql /212、用力法计算并作图示结构的M 图。
q3 m4 m13、用力法计算图示结构并作出M 图。
E I 常数。
(采用右图基本结构。
)l 2/3l /3/3l/314、用力法计算图示结构并作M 图。
EI =常数。
3m3m15、用力法计算图示结构并作M 图。
EI =常数。
2m2m 2m2m16、用力法计算图示结构并作M 图。
EI =常数。
l lql l17、用力法计算并作图示结构M 图。
E I =常数。
18、用力法计算图示结构并作弯矩图。
161kN m m m m19、已知EI = 常数,用力法计算并作图示对称结构的M 图。
l l20、用力法计算并作图示结构的M 图。
EI =常数。
a a21、用力法作图示结构的 M 图 。
EI = 常数。
2q l22、用力法作M 图。
各杆EI 相同,杆长均为 l 。
23、用力法计算图示结构并作M 图。
EI = 常数。
4m 2kN24m mm24、用力法计算并作出图示结构的M 图。
E = 常数。
25、用力法计算图示结构并作M 图。
EI =常数。
20kN3m 4m 3m26、用力法计算图示结构并作M 图。
EI =常数。
ll /2l /2l /2l /227、利用对称性简化图示结构,建立力法基本结构(画上基本未知量)。
E =常数。
l l28、用力法计算图示结构并作M 图。
E =常数。
l ll /2/2/229、已知EA 、EI 均为常数,用力法计算并作图示结构M 图。
l l30、求图示结构A 、D 两固定端的固端力矩,不考虑轴力、剪力的影响。
ll /231、选取图示结构的较简便的力法基本结构。
EI =常数。
6m 6m32、选择图示结构在图示荷载作用下,用力法计算时的最简便的基本结构。
PP33、用力法求图示桁架杆AC 的轴力。
各杆EA 相同。
a D34、用力法求图示桁架杆BC 的轴力,各杆EA 相同。
aD35、用力法计算图示桁架中杆件1、2、3、4的内力,各杆EA =常数。
d d d36、用力法求图示桁架DB 杆的内力。
各杆EA 相同。
4 m 4 m 4 m 4 m37、用力法作图示结构杆AB 的M 图。
各链杆抗拉刚度EA 1相同。
梁式杆抗弯刚度为EI EI a EA ,=21100,不计梁式杆轴向变形。
a38、用力法计算并作出图示结构的M 图。
已知EI =常数,EA =常数。
a a a a a39、用力法计算并作图示结构M 图,其中各受弯杆EI=常数,各链杆EA EI l =()42。
40、图示结构支座A 转动θ,EI =常数,用力法计算并作M 图。
l A θ41、图a 所示结构EI =常数,取图b 为力法基本结构列出典型方程并求∆1c 和∆2c 。
l(a)(b)42、用力法计算图示超静定梁并作M 图。
E =常数。
l /2=1I2ϕI l /243、用力法计算并作图示结构由支座移动引起的M 图。
EI =常数。
cl l l44、用力法计算并作图示结构由支座移动引起的M 图。
EI =常数。
l /245、用力法作图示结构的M 图。
EI =常数,截面高度h 均为1m ,t = 20℃,+t 为温度升高,-t为温度降低,线膨胀系数为α。
6m -t +t -t46、用力法计算图示结构由于温度改变引起的M 图。
杆件截面为矩形,高为h ,线膨胀系数为α。
l EI+10-10CC47、用力法计算并作图示结构的M 图,已知:α=0.00001及各杆矩形截面高h EI ==⨯⋅0321052.,m kN m 。
6m +10EI +30+10C CC EI48、图示连续梁,线膨胀系数为α,矩形截面高度为h ,在图示温度变化时,求M B 的值。
EI 为常数。
l CC l -10+20B C -1049、已知EI=常数,用力法计算,并求解图示结构由于AB 杆的制造误差(短∆)所产生的M 图。
a a /2/2ABEA=o o50、求图示单跨梁截面C 的竖向位移∆C V 。
l l /2/251、图示等截面梁AB ,当支座A 转动θA ,求梁的中点挠度f C 。
l θC EI BA f C/2l /2A52、用力法计算并作图示结构M 图。
E I =常数,K EI l ϕ=。
53、图b 为图a 所示结构的M 图,求B 点的竖向位移。
EI 为常数。
ql ql 23ql 26ql 28(a) (b) M 图54、求图示结构中支座E 的反力R E ,弹性支座A 的转动刚度为k 。
l l l55、用力法作图示梁的M 图。
EI =常数,已知B 支座的弹簧刚度为k 。
B Al 1k=EI/l 356、用力法计算图示结构并作M 图。
EI =常数,k EI a =353。
aa第五章超静定结构计算——位移法一、判断题:1、判断下列结构用位移法计算时基本未知量的数目。
(1)(2)(3)(4)(5)(6)EIEIEIEI 2EI EIEIEI EA EA ab EI=EI=EI=244422、位移法求解结构内力时如果P M 图为零,则自由项1P R 一定为零。
