活塞式压缩机惯性力平衡分析与计算
第五章-活塞式压缩机动力计算3
tg
F IIl F IIv
3 tg 2
F IIl
3 2
m s r sin 2
2
力的合力虽然是定值,但其变化频率是转速的 两倍,故不能简单加平衡重加以平衡
13
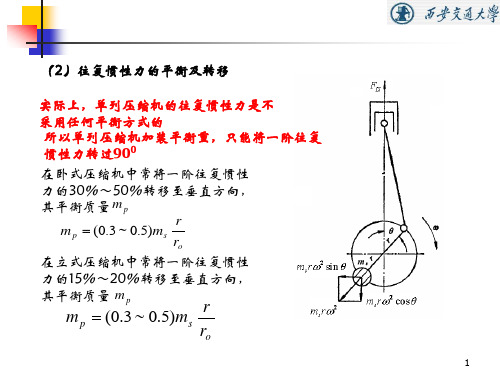
为计算方便起见,在分析计算惯性力 及惯性力矩的平衡中,采用平面直角 坐标系,并将坐标原点 O 设在压缩机 曲轴旋转平面中心,图是双重v形 压缩机在平面直角坐标系中的位置示 意图
3
立式或卧式压缩机
第一列各惯性力为
F IS m s r co s
' ' 2
F IIS m s r co s 2
' ' 2
Fr m s r
' '
2
第二列的惯性力,若以第一列 曲柄转角 为基准,则得
F IIS m s r cos(1 8 0 )
'' '' 2
'' 2
2
FI
F Iv F Il
2
2
2 m s r co s
2
2
2
co s(
2
)
F Il m s r co s sin
' 2
2
m s r co s( ) sin
'' 2
2
tg
F Il F Iv
2 m s r sin
2
2
2
ms ms
'
''
8
一阶往复惯性力它们各自作用在自己的气缸轴线方向上 把这两个周期相同,作用方向不同的力,分别投影到垂直方向和水 平方向,并各自相加,则沿一阶往复惯性力的两个分力:
活塞式压缩机惯性力的平衡有哪些措施

活塞式压缩机惯性力的平衡有哪些措施活塞式压缩机是一种常见的压缩机类型,广泛应用于工业生产中。
压缩机的运行中存在着惯性力的平衡问题,即活塞的往复运动会产生惯性力,对机器的稳定性和工作效率造成一定的影响。
因此,为了解决这一问题,人们采取了多种措施来平衡活塞式压缩机的惯性力。
1. 采用平衡重一种常见的平衡活塞惯性力的方法是采用平衡重。
平衡重通常位于活塞的接头处,在活塞的运动过程中,平衡重的质量会产生与活塞的运动方向相反的惯性力,从而实现惯性力的平衡。
平衡重的质量、形状和运动轨迹的设计对于平衡效果的影响较大,需要工程师进行精确计算和优化设计。
2. 使用双缸结构双缸结构是另一种常见的平衡活塞惯性力的方式。
在双缸结构中,主缸与副缸通过连杆相连,呈对称排列。
活塞在运动过程中,主缸和副缸的运动状态是反向的,从而相互抵消了惯性力的影响。
这种结构需要两个独立的气缸和连杆,增加了制造成本,但可以有效地平衡活塞的惯性力。
3. 使用平衡轴平衡轴是另一种常见的平衡活塞惯性力的解决方案。
平衡轴是一根平行于曲轴的轴,通过齿轮或链条与曲轴相连。
当活塞运动时,平衡轴会产生相反方向的惯性力,从而平衡活塞的惯性力。
平衡轴的设计需要考虑到与曲轴的同步性和平衡重量的配比等因素。
4. 优化活塞结构除了以上的平衡方法,优化活塞的结构也可以在一定程度上平衡活塞的惯性力。
例如,设计活塞的形状和重量分布,减小活塞的惯性力。
此外,采用轻质材料制造活塞,如铝合金等,也能减小活塞的质量,降低惯性力的影响。
综上所述,平衡活塞的惯性力是活塞式压缩机设计中需要解决的一个重要问题。
通过采用平衡重、双缸结构、平衡轴和优化活塞结构等措施能够有效地平衡活塞的惯性力,提高机器的稳定性和工作效率。
在实际应用中,需要根据具体的工况条件和要求选择合适的平衡方法,并进行精确的设计和优化。
这样才能满足生产过程中对活塞式压缩机性能的要求,确保其可靠、高效地工作。
活塞式压缩机旋转惯性力平衡方法有哪些

活塞式压缩机旋转惯性力平衡方法有哪些活塞式压缩机是一种常见的空气压缩设备,广泛应用于各个行业领域。
在活塞式压缩机的工作过程中,活塞的旋转惯性力会对整个设备的稳定性和性能产生一定的影响。
因此,为了提高活塞式压缩机的工作效率和使用寿命,我们需要采取合适的方法来平衡活塞的旋转惯性力。
一种常见的活塞式压缩机旋转惯性力平衡方法是采用配重块。
通过在活塞上安装适当的配重块,可以在活塞的轨迹上引入一个合适的离心力,来平衡活塞的旋转惯性力。
这种方法可以有效地减少活塞的振动和噪声,并提高设备的工作效率和稳定性。
同时,在设计配重块时需要考虑到活塞运动的频率和振幅,以确保配重块的安装位置和质量能够达到平衡效果。
另一种常用的平衡方法是采用对称布置。
通过在活塞上对称布置一定数量的配重块,可以使活塞在旋转过程中受到的惯性力相互抵消,从而达到平衡的效果。
这种方法相对于单一配重块的方法更加灵活,可以根据活塞的旋转情况和需求进行调整。
同时,对称布置的方法还能够提高活塞的稳定性和运行平衡度,降低因旋转惯性力带来的额外负荷和磨损。
此外,还可以采用其他辅助装置来平衡活塞的旋转惯性力。
例如,可以在活塞的轴承上安装一个阻尼器,通过阻尼器的摩擦力来平衡活塞的旋转惯性力。
这种方法结构简单,成本较低,可以在一定程度上减少活塞的振动和噪声。
另外,还可以通过改变活塞的几何形状,如增加活塞的长度或改变活塞的重心位置等,来改善活塞的旋转平衡性。
综上所述,为了平衡活塞式压缩机的旋转惯性力,我们可以采用配重块、对称布置和辅助装置等方法。
这些方法都可以有效地减少活塞的振动和噪声,提高设备的工作效率和稳定性。
在实际应用中,我们可以根据具体情况选择合适的方法,进行设计和调整,以达到最佳的平衡效果。
通过合理的旋转惯性力平衡方法,可以有效地提高活塞式压缩机的性能,延长其使用寿命。
活塞式压缩机受力分析小结

4
D2
内止点
外止点
三、摩擦力
270
0
90
180
360
F f
0
180
360
2、旋转惯性力:
Fmr mr r 2
m0 r0 2 mr r 2
1
四川理工学院过控系周(欢迎批评指正)
受力分析
1、活塞组件
F Fq Fm F f
Fq
0
Fm
F பைடு நூலகம்
180 360
Fm
F
F f
Fq
F Fq Fm F f
2、十字头
有三个力:活塞杆作用力 F 、 连杆力 Ft、十字头侧向力 Fn
Ft
F
Fn
F F = cos 1-2 sin 2 F sin Fn Ftg = 1 2 sin 2 Ft
2
四川理工学院过控系周(欢迎批评指正)
基础
1、侧向力及侧覆力矩:
sin( ) Fn A F r Ft r M cos
Mh
2、总阻力矩: M h M M f Ft F fR r F0 r 3、基础受到的净力矩
Fmr G Fm
W M e M h J
Me
4
小结
惯性力
0
四川理工学院过控系周(欢迎批评指正)
Ft=Ft sin M Ft r
Fq F f Fn Ft Fmr
W M e M h J
5
3、连杆
F F Ft = cos 1-2 sin 2
4、曲轴
cos Ft=Ft cos =F cos
活塞式压缩机旋转惯性力平衡方法是什么原理

活塞式压缩机旋转惯性力平衡方法是什么原理活塞式压缩机是一种常见的压缩机类型,广泛应用于空气压缩、制冷和空调等领域。
在活塞式压缩机的运转过程中,由于活塞的旋转惯性力,会产生不平衡力,给设备的稳定性和运行效率带来一定影响。
为了解决这个问题,人们提出了活塞式压缩机旋转惯性力平衡方法。
活塞式压缩机旋转惯性力平衡方法的原理就是通过设计和安装平衡重量来抵消旋转惯性力。
具体而言,可以采取以下几种方法:1.对称平衡:活塞式压缩机的活塞通常设置在转子的中心,且有两个对称的活塞,在相对位置上呈对称排列。
这样,在活塞旋转的过程中,两个活塞上的旋转惯性力相互抵消,从而实现平衡。
2.平衡重量:通过在活塞和连杆上安装平衡重量,使得整个系统的旋转惯性力实现平衡。
平衡重量根据旋转惯性力需要产生的力矩大小来确定,并且需要与活塞和连杆的质量、长度等参数相协调。
3.旋转平衡器:使用旋转平衡器可以在转子的旋转轴上移动平衡质量,从而改变旋转惯性力的分布。
旋转平衡器的设计需要考虑旋转惯性力的大小、旋转速度等参数,以确保平衡效果。
4.惯性力矩补偿:通过在转子上设置惯性力矩的补偿结构来平衡旋转惯性力。
这种方法的关键是设计出合适的补偿结构,以产生与旋转惯性力大小相反的力矩,从而实现平衡。
综上所述,活塞式压缩机旋转惯性力平衡方法可以通过对称平衡、平衡重量、旋转平衡器和惯性力矩补偿等方式来实现。
这些方法的目的都是通过合理的设计和安装,抵消旋转惯性力,从而提高活塞式压缩机的稳定性和运行效率。
通过采用这些技术手段,可以使得活塞式压缩机在工作过程中更加平稳、可靠,并且更加节能高效。
在实际的工程应用中,需要根据具体的情况选择合适的平衡方法。
同时,还需要进行前期的设计计算和试验验证,以确保平衡方法的可行性和有效性。
通过不断的优化和改进,活塞式压缩机的旋转惯性力平衡技术将进一步发展,使得活塞式压缩机在各个领域的应用更加广泛和可靠。
(完整版)活塞式压缩机的受力分析

I I I II
因动力计算中规定使连杆产生拉伸应力的 力为正,反之为负故式中将负号去掉。
2
一阶往复惯性力
II msr 2 cos 为一阶往复惯
性力。其变化的周期等于曲轴转一周的时 间。
当 00 时,为最大值:
旋转的作用,故称为阻力矩。
自由力
至于PL 又可( P / PL cos )再分解
为一个侧向力 N 和活塞力 P 。 N
和十字头销上的 N 构成一个力矩 Nh'
(图2);
活塞力 P Pg I 。
自由力
气体力和从固定件传来的气体力相互
抵后,主轴O点处只作用着惯性力 I 。
它和曲柄销中心B点处作用着的旋转惯 性力(离心力),这两个力无法在内部 平衡,都会传到机器外,故称自由力或 外力。
卧式机器设计支承的问提
卧式机器由于气缸轴线方向串联有机身、 中体、接筒以及级差式气缸等零件而使机器 过长,为支承其重量应设计成为不要限制其 轴向位移的支承。否则会使中体与机身连接 法兰处受力不均,甚至造成中体连接螺栓在 下半周者断裂事故。
惯性力、活塞力
2)、惯性力 I ,也是交变力。其 和气体力构成活塞力。即:P Pg I
旋转惯性力
旋转惯性力的作用方向始终沿着曲柄
半径指向外,而且规定使曲柄承受拉伸为
正值,受压缩为负值,故式中负号可不顾
及。
mr —旋转质量=曲轴的旋转质量+
(0.6-0.7)连杆质量。
第二节、压缩机中的作用力
一、压缩机运行时的作用力
①空负载运行中:曲柄连杆机构只产生惯 性力和摩擦力。
②满负载运行而突然在止点停车时,压缩 机中只有最大气体力作用在有关零件上。
高压直联压缩机惯性力平衡及活塞优化

~ 一 使一 ~用
文章 编号 :062 7 (0 )20 2 -6 10 -9 1 2 1 0 -0 40 1
~ 直联 压缩机惯性 力平衡及 活塞优 化 高压
钟 美 鹏
( 嘉兴学院机电分院 , 浙江 嘉兴 34 0 ) 10 1
b ss t e e p rme tlc mp r o sc  ̄id o t eo e a d atro t z t n frd r c ih p e s r o r s a i ,h x e i n a o a s n i a e u f r n f p i ai i t g ・ r s u e c mp e — i b e mi o o e h
综观近 代压缩机 技术 的发 展可知 , 的前 进与发 它 展是 与其它 相关 行业 的发展 进 步分 不 开 的 。直 联 便 携式 空气压 缩 机 的生 产发 展 同样 也不 例 外 。 目前
压直 联 压缩 机 中 , 子 的平 衡 就 是解 决 偏 心 轮 和连 转
杆 等效 到偏 心轮 的不 平衡 旋转 质量 所 产生 的离 心惯 性力 的问题 ; 构 的平 衡 就 是 解 决 活塞 做 往 复运 动 机
摘
要: 高压直联压缩机 因为体 积小 、 力大 , 易产 生振动 。为 了减小高压直联压 缩机 的转速 波动 , 压 容 研
究 了高 压 直联 压 缩 机 旋 转 、 复 惯 性 力 平 衡 , 出 了 L式 高压 直联 压 缩 机 配 重 的 位 置 布 置 方 法 ; 了 平 往 提 为 衡 L式 高压 直联 压 缩机 的 一 阶 往 复 惯 性 力 , 析 了要 减 小低 压 端 活 塞 质 量 的 必 要 性 , 分 对低 压 端 活 塞 进 行
活塞式压缩机曲轴的质量在进行惯性力计算的转化时

活塞式压缩机曲轴的质量在进行惯性力计算的转化时活塞式压缩机是一种常见的工业设备,广泛应用于空调、制冷、石油化工等领域。
其中,活塞式压缩机曲轴是其重要的动力传输部件之一,其质量对于整个压缩机的运行稳定性和效率起着重要作用。
在进行活塞式压缩机的设计和计算时,需要对曲轴的质量进行惯性力计算与转化,以确保设备的正常运行。
活塞式压缩机曲轴的质量可以简单理解为曲轴本身的质量和各构件的附加质量之和。
在设计和制造过程中,曲轴的质量需要经过严格的控制,以确保其材料的优异性能和合理的几何形状。
质量较大或不均匀的曲轴可能会引发不同程度的振动和惯性力,并且可能导致设备的性能下降、噪音增加甚至设备的损坏。
在进行活塞式压缩机的惯性力计算时,需要将曲轴的质量转化为对应的惯性力。
惯性力是由于物体在运动或静止状态下由于惯性所产生的力,常常会对设备的稳定性和运行造成影响。
对于活塞式压缩机的曲轴,其在旋转过程中,由于转动的惯性会产生一定的惯性力,这会对轴承和设备的其他部件产生一定的负荷,因此需要进行合理的计算和转化。
在进行惯性力计算的过程中,常常采用矩阵方法进行分析。
通过设定曲轴的转动速度、转动方向等参数,并结合曲轴的几何形状和质量分布情况,可以得到曲轴在运动中所产生的惯性力。
这些惯性力可以通过传递或转化到其他部件上,如轴承、机架等,以实现整个系统的平衡和稳定。
惯性力计算的结果可以为活塞式压缩机的设计和优化提供重要的依据。
通过合理控制曲轴的质量分布和几何形状,可以降低曲轴自身的振动和惯性力,提高设备的运行效率和稳定性。
同时,惯性力计算也可以为活塞式压缩机系统的其他部件的设计和优化提供参考依据,以实现整体性能的提升。
在实际应用中,除了对活塞式压缩机曲轴质量进行惯性力计算和转化外,还需要考虑其他因素的影响。
例如,曲轴的材料选择、加工工艺和装配精度等,都将对曲轴的质量和惯性力产生重要影响。
因此,在设计和制造过程中,需要综合考虑多个因素,以确保活塞式压缩机曲轴质量的合理控制和惯性力的有效转化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
钱新春,屈宗长
Copyright © 2017 by authors and Hans Publishers Inc. This work is licensed under the Creative Commons Attribution International License (CC BY). /licenses/by/4.0/
′2= ′′rω 2 FIIs λ ms
2 s
( ) cos 2 (θ + 90 ) = −λ m′′rω
(5) (6)
cos 2θ
130
钱新春,屈宗长
′′rω 2 Fr′2 = mr
(7)
′ m ′′ ms ; 将二列往复惯性力分别转化到质心平面 s − s ,取二列的往复和旋转质量相同,即 m = = s s 1 ′ m ′′ mr ,其列间距 b= c= a ,得到一、二阶往复惯性力的合力和合力矩: m = = r r 2
(9) (10) (11)
M IIs = λ ms rω 2 a cos 2θ
而两列的旋转惯性力的相位角相差 90˚,按照矢量合成的法则,旋转惯性力合力为
= Fr
(∑ F ) + (∑ F )
2 ry rx
2
(12)
= Fry mr rω 2 ∑ cos θ + cos θ + 90 式中: ∑ Fry —各列沿气缸中心线方向(垂直方向)的分力,其值为 = mr rω 2 [ cos θ − sin θ ]
Analysis and Calculation of Inertia Force and Torque Equilibrium for Piston Compressor
Xinchun Qian1, Zongchang Qu2
1 2
Jiangsu Fengtai Fluid Machinery Technology co., LTD., Yancheng Jiangsu Compressor Engineering, Xi’an Jiaotong University, Xi’an Shaanxi
Keywords
Piston Compressor, Inertia Force Equilibrium, Phase Angle
活塞式压缩机惯性力平衡分析与计算
钱新春1,屈宗长2
1 2
江苏丰泰流体机械科技有限公司,江苏 盐城 西安交通大学压缩机工程系,陕西 西安
收稿日期:2017年5月25日;录用日期:2017年6月7日;发布日期:2017年6月14日
129
钱新春,屈宗长
Figure 1. Two columns vertical compressor organization graph of crankshaft angle δ = 900 图 1. 两列立式曲柄错角为 δ = 900 运动机构简图
3. 惯性力的计算
根据牛顿定理,往复和旋转惯性力的一般表达式为:
由式(2)和式(5),两列一阶往复惯性力的合力为
= FIs ms rω 2 ( cos θ − sin θ )
由式(3)和式(6),两列二阶往复惯性力的合力为
(8)
= FIIs λ ms rω 2 ( cos 2θ − cos = 2θ ) 0
= M Is 1 ms rω 2 a ( cos θ + sin θ ) 2
−ms a = −ms rω 2 ( cos θ + λ cos 2θ ) = − ( FIs + FIIs ) FIs = Fr = −mr rω 2
(1)
式中: a -活塞运动加速度(m/s2);
FIs 、 FIIs -分别为一阶和二阶往复惯性力(N);
Fr -旋转惯性力(N); ms -往复运动质量(kg);
旋转惯性力的合力矩为
(
)
(16)
Mr =
(M ) + (M )
2 ry rx
2
=
2 mr rω 2 a 2
(17)
合力矩 M r 与垂直轴(气缸中心线平面内)的夹角为
∑ M rx arctg sin θ − cos θ = α arctg = sin θ + cos θ ∑ M ry
二列与第一列转角之间的函数关系为 θ = θ1 + 90 ,则各列的一、二阶惯性力分别为 2 第一列
′1 = ms ′ rω 2 cos θ FIs
(2) (3) (4)
′ 1 = λ ms ′ rω 2 cos 2θ FIIs
′ rω 2 Fr′1 = mr
第二列
′2 = ′′rω 2 cos θ + 90 = ′′rω 2 sin θ −ms FIs ms
r -曲轴的回转半径(m);
λ -曲柄半径连杆比(即回转半径 r 与连杆长度 l 的比值); θ -曲轴的转角(˚); ω -曲轴的旋转角速度(1/s);
在压缩机作用的分析计算中,一般规定使连杆受拉的力为正,受压为负。曲柄承受拉力为正,否则为 负,这样式(1)中符号不再考虑。
′ 和 ms ′′ ,而旋转质量为 mr ′和 根据式(1),当两列的曲柄夹角 δ = 90 时,二列的往复运动质量分别为 ms ′′ ,由相位角确定准则,取第一列为基准列,其曲柄的转角为 θ1 ,则同一瞬时第二列曲柄转角为 θ 2 ,第 mr
θ1 ,θ 2 , ,θi 。由于各列处于同一瞬时合成,即相对于基准列,将各列曲柄转角 θi 表示成基准列曲柄转角 θ
的函数; 3) 确定往复惯性力的矢量方向。 各列往复惯性力的方向均以本列指向外止点的方向作为正矢量方向, 旋转惯性力沿着曲柄方向指向外为正矢量方向,并将各列的惯性力按此矢量方向合成。 本文以两列立式且曲柄错角 δ = 90 的压缩机为例,讨论惯性力与惯性力矩的合成,其多列压缩机惯 性力及力矩的计算方法完全相同。图 1 表示了这种压缩机运动机构的简图:
摘
要
论文针对多列活塞式压缩机惯性力和力矩合成出现的问题,给出了惯性力合成时必须依据的准则,并以 两列压缩机为例,详细介绍了惯性力和力矩的计算,为多列压缩机的计算提供了参考。
关键词
活塞式压缩机,惯性力平衡,相位角
文章引用: 钱新春, 屈宗长. 活塞式压缩机惯性力平衡分析与计算[J]. 机械工程与技术, 2017, 6(2): 128-132. https:///10.12677/met.2017.62018
Open Access
1. 前言
活塞式压缩机由于活塞速度周期性的变化必然会产生往复惯性力, 而旋转质量不平衡也会引起旋转惯 性力。在多列压缩机中,由于曲拐不在同一平面上,还会存在惯性力矩。这些惯性力和力矩如果在机器 内部不能完全平衡,必然会传到机器外部,引起机器的振动。振动不仅会消耗能量,影响压缩机的正常 工作,还会影响到仪器仪表的寿命以及导致基础及建筑物的损害。严重时会引起机器的共振,毁坏设备 或缩短使用寿命。 文献[1] [2]分别对三列立式压缩机和对置三列压缩机惯性力及力矩平衡及计算进行了详细的分析与 研究,并且采用空间几何图形对其离心惯性力及力矩进行了分析。文献[4]对四列氮氢气压缩机惯性力平 衡进行了分析与计算。 但现有的压缩机惯性力的研究中,往往仅仅针对不同类型、不同结构进行惯性力平衡研究。而多列压 缩机由于列数较多,且气缸之间的夹角 γ 不同、各列曲柄之间的错角 δ 不同、压缩机的旋转方向也不同, 特别要使用空间图形表达离心惯性力及力矩的计算就显得更为复杂[3]。 惯性力计算中首先是各列的相位角难以确定, 往往会在多列惯性力合力及合力矩分析中出现差错, 特 别在多列离心惯性力合力及合力矩的计算中又无法应用图形表达,所以给多列惯性力及力矩分析带来困 惑。 本文针对多列往复惯性力、离心惯性力及力矩的特点,给出合成的规律,对于如何选取各列的相位角 问题给出计算准则,特别对离心惯性力及力矩的合成给出计算方法。在活塞式压缩机中,由于多列切向 力的合成方法与惯性力合成方法相同,所以此惯性力的合成方法也极易推广到多列压缩机切向力合成的 计算中。
(
)
∑ Frx —各列垂直于气缸中心线方向(水平方向)的分力,其值为
mr rω 2 sin θ + sin θ + 90 = mr rω 2 [sin θ + cos θ ]
= Frx ∑
(
)
旋转惯性力的合力为
= Fr =
(∑ F ) + (∑ F )
2 ry rx 2 2 r
2
cos θ − sin θ ) + ( cos θ + sin θ ) ( m rω ) (
2 2
(13)
= 2mr rω 2
旋转惯性的合力与 Y 轴的夹角 ϕ 为
∑ Frx arctg sin θ + cos θ = ϕ arctg = cos θ − sin θ ∑ Fry
arctg θ + 45 = tgθ + 45 =
(14)
上式说明,此种结构的旋转惯性力的合力与 Y 轴的夹角恒较第一列曲柄超前 450。 对于旋转惯性力矩, 则先将每列的旋转惯性力投影到垂直轴 Y 和水平轴 X, 再对几何中心(S-S)求矩, 两列分别在质心平面的两侧,即旋转惯性力的合力矩为: 在垂直平面内的旋转惯性力矩为
Mechanical Engineering and Technology 机械工程与技术, 2017, 6(2), 128-132 Published Online June 2017 in Hans. /journal/met https:///10.12677/met.2017.62018
th th th
Received: May 25 , 2017; accepted: Jun. 7 , 2017; published: Jun. 14 , 2017
