FF三因子模型在上海A股市场实证分析
中国股票市场的三因子模型

中国股票市场的三因子模型中国股票市场的三因子模型一、引言股票市场是经济社会中最重要的金融市场之一,也是资本运作和投资的重要平台。
对于股票投资者来说,了解股票市场的运行机制和影响因素,是进行投资决策的基础。
三因子模型是衡量股票收益率波动的一种重要方法,也被广泛应用于中国股票市场的研究。
二、三因子模型的基本原理三因子模型是基于市场效应、公司规模和市场账面市值比来解释股票收益率波动的模型。
市场效应指的是整个股票市场的整体表现对个股收益率的影响,市场规模和公司规模对个股收益率也有显著影响,而市场账面市值比则反映了公司的价值与市场估值之间的差异。
通过三因子模型,可以更全面地分析和解释股票市场的波动性。
三、中国股票市场的市场效应市场效应是指股票市场整体表现对个股收益率的影响力。
在中国股票市场中,市场效应受到政策法规、宏观经济情况以及市场情绪等多种因素的影响。
例如,政策发布对市场影响巨大,一些行业的政策利好或政策调整都会直接影响相关上市公司的股价。
此外,宏观经济指标如GDP增长率、通胀率等也会对市场效应产生重要影响。
最后,市场情绪因素如投资者心理、市场预期等也会对股票市场的波动性产生较大影响。
四、中国股票市场的公司规模因素公司规模是指上市公司的市值大小对股票收益率的影响。
在中国股票市场中,大公司往往比小公司更有优势,因为大公司通常在经营、研发和市场开拓等方面有更多资源和能力。
因此,大公司的股票收益率一般会相对稳定和较高,而小公司则存在较大的风险和不确定性。
在投资决策中,投资者需要根据公司规模因素来选择合适的股票,以降低投资风险。
五、中国股票市场的市场账面市值比市场账面市值比是指公司价值与市场估值之间的差异对个股收益率的影响。
在中国股票市场中,账面市值比被广泛应用于估值分析和价值投资。
当公司的账面市值比较低时,说明其市值相对较低,有较大的投资价值;反之,当公司的账面市值比较高时,说明其市值相对较高,风险也相对较大。
中国股票市场的三因子模型新

中国股票市场的三因子模型¹范龙振,余世典(复旦大学管理学院,上海200433)摘要:通过对中国股票市场从1995年7月到2000年6月所有A股股票月收益率的研究,发现股票市场具有显著的市值效应、账面市值比效应、市盈率效应和价格效应.这些效应不能用市场B值来解释,但再加上两个因子:市值因子和账面市值比因子,可以很好地解释这些效应.这个三因子模型也能够很好地解释中国股票市场众多指数的差异.关键词:Fama-Macbeth回归;收益率;股票市场;因子效应中图分类号:F830.91文献标识码:A文章编号:1000-5781(2002)06-0537-10Three-factor model in China stock marketFA N Long-zhen,Y U Sh-i dian(School of Management,Fudan University,Shanghai200433,China)Abstract:With the monthly stock returns,prices and corporate financial statements data from July1995 to June2000,the size effect,book_to_market effect,E/P ratio effect,and price effect are found to be obvious in China stock market.These effects can not be e xplained by their market B c s,but if two other factors:size factor and book_to_market factor are added,the three_factor model of Fama_French c s ex-plains the effects quite well in China stock market.The three_fac tor model can also e xplain the different behaviors of stock indexes in the China stock market.Key words:Fama-Macbeth regression;monthly return;stock market;fac tor effect0引言中国的两个证券交易所成立至今已逾10年,不少学者认为市场的交易行为在各项法规的不断完善之下日趋理性化,但中国这一新兴的证券市场能否用现代金融理论来解释,在一定假定下给出的金融模型能否应用到我国的金融市场,与国外成熟的同类市场相比,究竟有多少相似和差异?这还是一个难以回答的问题.本文选择中国股票市场的所有A股股票作为研究对象,以国外相关的研究作参考,研究我国股票市场影响股票回报率的一些相关因素,这些因素包括市值、账面市值比、价格、市盈率、现金红利收益率等.近年来,国外有大量关于资本市场的实证研究,一些结果至今还很难用令人信服的理论来解释.比较著名的有,Banz1981年发现股票的市场价值(market equity value)能够反映不同股票历史平均收益率的差别,小市值股票的平均历史回报率要高于大市值股票的历史平均回报率[1].市值对回报率的解释作用被称为市值效应(size ef-fect).Bhandari1988年认为公司的资本结构(finan-cial leverage)也能部分地解释股票收益率的差异,负债资产比越高的股票,平均回报率越大[2]. Rosenberg等1985年发现美国股票市场股票的历第17卷第6期2002年12月系统工程学报JOURNAL OF SYSTE MS E NGINEERINGVol.17No.6Dec.,2002¹收稿日期:2002-01-14;修订日期:2002-09-18.史平均收益率与发行该股票的公司的账面市值比(book_to_market value of equity)正相关.Chan、Hamao 和Lakonishok1991年发现在日本股票市场上也有同样的账面市值比效应.Fama和French1992年对美国股票市场决定不同股票回报率差异的因素有一个比较全面的研究.其研究发现,股票的市场B 值不能解释不同股票回报率的差异,而上市公司的市值、账面市值比、市盈率可以解释股票回报率的差异[3].Fama和French1993年指出,这些能解释股票回报率差异的因素具有很强的相关性,并且可以建立一个三因子模型解释股票回报率.模型认为,一个投资组合(包括单个股票)在扣除无风险利率后的期望回报率可由它对3个因子的暴露来解释,这3个因子是:市场溢酬,市值因子(SMB),账面市值比因子(HML)[4].这些实证发现对金融理论提出新的挑战,并促进了金融理论的发展,其后有很多文章从理论上探讨怎样解释这些现象.Fama和French倾向于把SMB、H ML看作风险因子[4,5],而其它观点认为它们只能算作公司的某种特征,不能看作风险因子[6,8,9,11].这些现象的发现对投资者投资决策具有重大意义[10,12)14].BARRA模型吸收了这些研究成果,成为美国股票市场及国际市场最为成功的风险管理和投资决策模型.同时BARRA和S&P共同推出一系列指数,反映市值、账面市值比差异,供被动的投资者作为投资标的,供主动投资者作为参考标准.本文以在中国两个交易所上市的A股股票为研究对象,考察可以解释不同股票收益率差异的各种因素.1数据处理和Fama_Macbeth回归结果我国股票交易所从建立至今不过10来年,在1995年以前,上市公司数量有限,另外市场的效率、信息的反映程度比较差,个股缺乏个性,往往表现为齐涨齐跌.从这两方面考虑,选定研究的时间区间从1995年7月至2000年6月,股票价格、收益率和公司财务资料来自于由香港理工大学中国会计与金融研究中心设计,深圳市国泰安信息技术有限公司开发的中国股票市场研究数据库(CSMAR).收益率资料已经对分红、配股、增发等做出了调整.公司的总市值和A股市值以及公司财务资料均来自该数据库.根据国外有关研究结果,结合对中国股票市场的认识,首先选定如下几个因素进行分析:总市值(公司全部股票市值,记为ME1)、流通市值(A 股市值,记为ME2)、股票交易价格(记为P)、账面市值比(账面净资产除以股票总市值,记为B E/ ME)、反映资本结构的账面总资产与账面股东权益价值比(公司账面资产价值除以股东权益账面价值,记为A/BE)、公司总资产账面价值和股东权益市场价值之比(记为A/ME)、市盈率的倒数(记为E/P)、红利率(记为D/P).使用市盈率的倒数而不是市盈率可以较好地处理公司净利润接近于0的情况.首先对单个因素对股票回报率的影响进行分析.以总市值为例,回归方程如下R it= t+b t ln(ME1it)+E it1[i[n(1)即对某一个月,假定知道上市公司每个股票的回报率R it(共有n个股票),还知道每个公司的总市值ME1it,就可以通过回归方程(1)估计出当月 t,b t.由于公司的财务资料每年公布一次,为一致起见,公司的总市值、流通市值、股票价格、账面总资产与账面股东权益价值比(A/BE)、市盈率等都是每年的6月末调整一次.ME1t,ME2t,P t分别是时间t之前的第1个6月末的总市值、流通A股市值、交易价格.(BE/ME)t、(A/BE)t、(E/P)t、(A/ME)t、(D/P)t分别是调整时上一年末公司股东权益账面价值和公司股东市场价值之比、公司总资产账面价值和股东权益账面价值之比、公司利润与股票价格的比值之比、公司总资产账面价值和股东权益市场价值之比、每股红利与每股价格之比.之所以这样做是因为年终财务报表一年公布一次,并且大部分在第2年的3月份以后,但在6月末前基本上已经全部公布.这样选取因素的取值可以保证这些因素的取值在每月的月初全是可以知道的,即解释月回报率的变量在每月开始时已经知道,这样的因素选取具有投资和预测意义.计算出每月的b t以后,得到b t的一个时间序列(t=1,2,,,m),然后计算出它们的时间序列均值、标准差、T-统计值,计算公式如下b=1mE mt=1b t(2))538)系统工程学报第17卷第6期st D b=1m E mi=1(b t- b)2(3)T b=m bst D b(4)这种计算b的均值、标准差及T统计值的方法称为Fama_Mecbath回归方法[7],根据Fama_Mecbath 的看法,在一定假定下,T统计值可以用来检验因素对回报率是否有显著影响.在作市盈率对价格的影响分析时,考虑到投资者对利润为零或者是负值的股票的看法与其他股票不同,把E/P划分成两部分考虑,利润大于0时,E/P不变,记为E+/P,利润小于0时,统统归为一类,定义它的取值为1,称作E/P哑元变量(dummy variable),回归方程为R it=A t+B1t(E+P)it+B2t(EPdummy)it+E it(5)估计出每个因素对回报率是否有显著影响后,下面再来看这些单个看来有较强影响的因素放在一起对市场回报率的影响如何.假定要考虑总市值和账面市值比一起对股票回报率的影响,可以利用回归方程R it=A t+B1t ln(ME1it)+B2t ln(BE it/ME it)+E it(6)求出每个月的B1t,B2t,然后利用式(2))(4)计算出平均值、标准差和T统计值,现在计算出的值与单个回归计算出的平均值和T统计值一般不同.原因在于不同因素具有一定的相互影响.表1给出了股票回报率对于这些因素的回归系数B的时间序列平均值和T统计值.表1各个因素对股票回报率的Fama_Macbeth回归结果ln(ME1)ln(ME2)ln(BE/ME)ln(A/ME)ln(A/BE)ln(P)E(+)/P E/P dummy D/PSingle_factor regressions-0.011-0.0050.0170.0120.002-0.020.1090.0210.059 (-3.540)(-1.340)(-2.204)(-2.145)(-0.606)(-2.242)(-1.742)(-2.52)(-0.714)Multiple_factor regressions-0.010.017(-3.122)(-2.212)-0.0110.012(-3.424)(-2.029)-0.0120.001(-3.748)(-0.38)-0.009-0.017(-3.102)(-1.907)-0.0130.1750.021(-4.326)(-2.914)(-2.461)-0.0120.167 (-3.830)(-2.208) -0.0140.012-0.011(-4.413)(-1.392)(-1.630)-0.0130.150.020.069 (-4.381)(-2.688)(-2.48)(-1.115) -0.011-0.0140.1440.0140.008 (-4.145)(-1.593)(-2.541)(-2.128)(-0.153)0.002-0.0160.0780.009-0.044(-0.539)(-1.948)-1.34-1.496(-0.820) -0.0140.001-0.003-0.0120.0530.0050.013 (-5.691)(-0.366)(-1.021)(-1.325)(-1.041)(-0.926)(-0.227)注:每一行分别是回归系数的平均值和T统计值,T统计值出现在括号中.在多因子回归中,如果某一行中有几组取值,表示回归分析是对这几个因素同时进行的.股票市值的单位为万元.由表1可知,从单个因素对股票回报率的影响来看,流通市值对股票回报率的影响是负的,但影响不显著.总市值对股票回报率的影响也是负的,影响是显著的.这说明市值越大的股票,回报率平均表现越不好.同时还可以看出,与流通市值比较,总市值更能反映股票回报率差异.因此在以后的分析中,以总市值代表一个企业的市值因素.从价格的单因素影响来看,价格越高的股票,)539)2002年12月范龙振等:中国股票市场的三因子模型股票的平均回报率越差,T统计值绝对值大于2.说明价格因素对回报率有显著的影响,由于价格对回报的影响可能有非线性因素,下面还要对价格作进一步的观察.账面市值比也是影响股票回报率的重要因素,相对于市场价值,账面值越大的股票,回报率也越高,考虑到可能的非线性影响,还应作进一步的分析.市盈率的影响对股票价格也有显著的影响,市盈率较大的股票,回报率表现较差.同时也看到利润为负的股票,其平均回报率相当高.在公司的资本结构中,负债较多的股票,表现为AE/BE较小,其平均回报率也较高.其影响也是显著的.但它和A/ME一起对市场的影响已经包含在BE/ME中.从单因素的分析看,红利率对市场的影响几乎为0.在两因素的回归中,总市值和市盈率放在一起对回报率都有显著的影响,总市值和账面市值比在一起对市场也有显著的影响.价格和总市值放在一起两者的影响都有所减弱,但影响是显著的.市值和红利率一起分析时,两者对市场都有显著的影响,并且红利率的影响是显著的,红利越大的股票,收益率越高.从多因素回归分析来看,除总市值的影响非常显著外,其他因素的影响都有所减弱.说明总市值是影响回报率差异的一个非常重要的因子,是其他几个因素无法替代的,而价格、账面市值比、市盈率、红利率等对回报率的影响有着密切的相互联系.2各因素影响的动态组合分析从Fama_Macbeth回归结果中,可以发现一些因素对股票平均回报率确实有明显的解释作用.这些因子包括总市值、帐面市值比、市盈率和价格.为了更准确地分析它们对回报率的影响,分别按每个因素把所有上市公司的股票划分成约10个不同组合,通过这些资产组合平均回报率及其它特征的对比,来直接反映每个因素的影响.进行非线性分析的方法如下:把上海股票市场交易的所有股票按照某因素F(分别代表总市值、帐面市值比和价格)大小从小到大分成10个小组,每个小组含有的股票数量基本相同.把每个小组的股票做成一个资产组合,资产组合中每个股票的权重就是它在每个月初的总市值,然后计算出每个资产组合的回报率.资产组合每年6月末重新划分一次,重新划分的主要原因是各个股票的因素F的取值大小顺序发生了变化.这样就计算出了动态资产组合1到10的月回报率的时间序列数据,然后计算这10个资产组合的时间序列平均收益率、标准差、T统计量值、平均账面市值比、平均总市值以及每个资产组合的B值.具体计算方法如下:平均值、标准差、T统计量值的计算见式(2))(4).各个资产组合的市场B值采用中国所有上市公司A股指数(所有A股股票回报率的加权平均,以总市值作为权重)作为市场资产组合(market portfolio),把它的月回报率R Mt和各个资产组合的月回报率R p t作回归得到回归方程为R pt=A p+B p R Mt+E p t(7)表2说明市值越大的资产组合,平均回报率越小,市值最小的资产组合和市值最大的资产组合的月平均回报率相差3.1%.但这10组的账面市值比也与市值有关,高市值的股票,平均账面市值比小,但这10个资产组合的B值与市值看不出关系.可以认为中国股票市场有着明显的市值效应,但市值效应可能与它们的账面市值比效应有关,但不能用它们的市场B值解释,说明CAPM理论不能反映回报率的市值效应.表3说明账面市值比越大的资产组合,平均回报率越大,但并不是明显的线性关系.账面市值比组合与市值无明显关系,也看不出与B值的关系.可以认为中国股票市场有着明显的账面市值比效应,但账面市值比效应与市值无关,也不能用它们的市场B值解释.C APM理论不能反映回报率的账面市值比效应.表4说明价格越大的资产组合,平均回报率越小,但并不是明显的线性关系.价格组合效应与账面市值比有明显关系,价格越大,账面市值比越小,与市值无明显关系,也看不出与B值的关系.可以认为中国股票市场有着明显的价格效应,其效应与面值无明显关系,也不能用它们的市场B 值解释.)540)系统工程学报第17卷第6期由于投资者对利润接近于0或者利润为负的股票的看法明显不同于其它股票,在每年的6月末,单独把上年利润为负的股票放在一个小组,其它的股票按上年E/P的大小从小到大组成10个小组,每个小组形成一个动态投资组合.表5给出了这11个投资组合的平均收益率、标准差及其他特征.表5说明除第0组以外,E/P越大的资产组合,即市盈率越小的股票,平均回报率越大,第0组由净利润为负的股票组成,其表现与一般正利润的股票不同,平均回报率也最高.市盈率效应与账面市值比有一定关系,从第3组起,市盈率越低的股票,账面市值比也越高,平均回报率越高.第1、第2组和第3组不是这种关系是因为这些股票的净利润接近于0,其表现与正常利润的股票不同,这是一种复杂的非线性关系.市盈率效应与B 也有一些关系,市盈率越小,其B值相对较大.表2按总市值从小到大组成的资产组合的平均回报率及其特征序号12345678910 mean0.0470.0370.0310.0330.0340.030.0280.0210.0250.016 std.0.1120.0970.0970.0890.10.0960.0990.0910.0910.095 t_value 3.282 2.918 2.478 2.825 2.604 2.438 2.166 1.825 2.132 1.338 BM(avg)0.2680.2860.2730.2510.2480.2540.2760.2640.2290.246 Ln(Size)(avg) 6.49 6.714 6.8797.097.2877.4717.6987.8918.2399.085 B 1.0240.9390.9580.889 1.029 1.016 1.0440.9580.976 1.028表3按账面市值比从小到大组成的资产组合的平均回报率及其特征序号12345678910 mean0.0170.0240.0220.0260.0240.0270.0370.0370.0430.035 std.0.0920.0940.0940.0950.0930.0940.0970.1030.0990.104 t_value 1.423 1.967 1.84 2.166 1.995 2.223 2.995 2.8 3.32 2.576 BM(avg)0.150.1880.1940.2180.2370.2660.2710.2970.35101451 Ln(Size)(avg)7.7387.4157.4477.5037.4527.4297.397.4397.4077.57 B0.9520.9670.9190.9690.9560.982 1.014 1.05 1.0290.987表4按价格从小到大组成的资产组合的平均回报率及其特征序号12345678910 mean0.040.0360.040.0340.0280.0290.0220.030.0190.023 std.0.1110.10.0970.1040.0980.0970.0950.10.090.1 t_value 2.802 2.796 3.163 2.519 2.212 2.346 1.763 2.13 1.615 1.777 BM(avg)0.3920.3390.2810.2850.2450.2220.2220.20.1780.133 Ln(Size)(avg)7.5327.3517.2967.1797.2937.2577.437.67.7068.187 B0.9780.992 1.001 1.0750.9830.9690.972 1.010.9070.986)541)2002年12月范龙振等:中国股票市场的三因子模型表5按E/P从小到大组成的资产组合的平均回报率及其特征序号012345678910 mean0.0310.0250.0250.0220.0270.0250.0290.0360.030.0280.036 std.0.1010.0980.1010.0940.0980.0970.0980.10.10.0940.103 t_value 2.376 1.961 1.907 1.844 2.175 2.018 2.339 2.753 2.52 2.316 2.689 BM(avg)0.280.2890.2650.2340.230.2440.2340.2520.270.2840.293 Ln(Size)(avg)7.1857.3417.4497.4457.3017.4567.4227.5097.577.5827.965 B0.8690.8790.980.9570.9720.98 1.021 1.0650.990.98 1.071注:第0组由净利润为负的股票组成.3市值因子和账面市值比因子以及它们的解释能力Fama和French在1993年的论文中指出,很多CAPM所不能解释的异常现象都是相互关联的,并且可以用一个三因素模型解释.模型反映,一个投资组合(包括单个股票)的超额回报率可由3个因子的回报率来解释,这3个因子是:¹市场超额回报率(R M-R»),其中R M为市场资产组合的回报率,R f为无风险利率;º市值因子(SMB);»账面市值比因子(HML).写成期望回报率形式是E(R p t)-R»=b p(E(R Mt)-R»)+s p E(SMB t)+h p E(HML t)(8)用回报率表达为R pt-R»=b p(R Mt-R»)+s p(SMB t)+h p(HML t)+E pt(9)其中,E(E p t)=0.他们认为该模型实质上可以理解为Merton(1973)的ICAPM或者Ross(1976)的APT模型的三因素版本.由前两部分的工作,可以知道在解释股票月收益率的各个因素中,市值效应和账面市值比效应是两个最重要的效应.因为无论市值与哪一个因素或几个因素在一起回归,几乎都表现出显著的影响,而账面市值比几乎也是这样,并且其他因素的影响与账面市值比表现出一定的相关性.下面首先从数据资料中提取出市值因子和账面价值比因子.首先介绍取得SMB和HML因子序列的方法.在每年的6月末,对所有股票进行交叉分类.先进行大小分类,根据股票市值的大小把股票分成两类,股票市值大的分为一类(B类),小的分为另一类(S类).两类股票的个数相等.同样根据账面市值比高低把股票分为3类,高类(H类)、中类(M 类)和低类(L类).分类的标准是把所有股票中账面市值比最高的30%归为高(H)类,中间的40%归为中(M)类,最低的30%归为低(L)类.然后把根据市值的分类和根据账面市值比的分类进行交叉,就得到了6个小组:S/L组、S/M组、S/H组、B/L组、B/M组和B/H组.每个小组根据股票市值形成一个资产组合,资产组合仍记成S/L,S/M, S/H,B/L,B/M,B/H.分类和资产组合每年的6月末更新一次.表6给出了这些资产组合的月平均回报率、标准差和T统计量值.表6市值和账面市值比交叉分类的资产组合的平均回报率及其特征组别S/L S/M S/H B/L B/M B/H mean/% 2.95 3.93 4.41 2.12 2.08 4.06 std0.095960.094650.102720.092420.095760.11272 t_value 2.38376 3.21467 3.32305 1.77571 1.68433 2.79155从表6可以发现规模效应和账面市值比效应的交叉影响.在类似的规模下,例如假定都是小市值公司(S),投资组合的收益率随着账面市值比从低到高增加而增加;而在账面市值比为同一类时,由小市值公司组成的投资组合的平均月收益率要高于由大市值公司组成的组合的收益率.)542)系统工程学报第17卷第6期最后,根据这6个资产组合的回报率提炼出市值因子SMB和账面市值比因子HML的时间序列取值(1995年7月至2000年6月).SMB,HML的计算方法为SMB=(S/L+S/M+S/H)/3-(B/L+B/M+B/H)/3(10) HML=(S/H+B/H)/2-(S/L+B/L)/2(11)根据SMB和HML的构造方法,两者的相关性应该较弱,把它们与市场超额回报率作比较,见表7A、7B.表7A R M-R f、SM B、HML的相关系数项目SM B HML R M-R»SM B1HML-0.24441R M-R»-0.038510.1418311表7B R M-R f、SM B、HML的平均回报率及其标准差项目SM B HML R M-R»R Mmean/%1.011.701.421.92 std0.049830.058510.084310.08427t_value1.567352.248851.306931.76541从表7A可以看出,3个因子:市场超额回报率、市值因子和账面价值比因子相关系数较小.从表7B可看出,SMB和HML因子的T统计值比市场超额回报率的T统计值还要大.HML的平均回报率大于市场平均超额回报率.由前面的分析已经知道,不同资产组合的平均回报率的不同并不能完全由它们的市场B值来解释.如果要看资产组合的回报率由市场B值的解释程度,需要考察回归方程R pt-R»t=A p+B p(R Mt-R»t)+E t(12)如果资产组合的超额回报率完全由市场B解释,式(12)的常数项应该为0.把前面第2节构造的41个资产组合的超额回报率与市场超额回报率按式(12)作回归,其中每个月的无风险利率取自当月的1年期银行储蓄存款利率.结果(篇幅所限,略)表明41个回归式中所有的常数项都是正值,并且大部分的T统计值都很显著,同时所有的B值的T 统计值都是显著的.说明B尽管可以部分地解释这些资产组合的回报率的变化(其T统计值显著),但不能完全解释各个资产组合的回报率,还有其他因子可以反映资产组合回报率的变化.现在把SMB和HML作为两个因子与市场超额回报率一起来解释这些资产组合的回报率,即按式(9)对各个资产组合超额回报率作时间序列回归分析,回归方程如下R pt-R»=A p+B p(R Mt-R»)+s p(SMB t)+h p(HML t)+E pt(13)如果3因子模型能够完全解释回报率的变化,常数项A p应该为0.否则如果常数项为正,并且显著的不为0,说明还有其他因子影响到组合的回报率.市值组合、账面市值比组合、市盈率组合及价格组合的回归结果分别见表8)11.表8市值组合的三因子模型回归结果序号A p B p s p h p t( p)t(b p)t(s p)t(h p)A_Rsq S.E 10.0091.0501.4300.1753.02135.70519.2414.1320.9700.021 20.0001.0621.072-0.0030.11429.61611.837-0.0580.9480.026 30.0051.0620.877-0.0371.68235.41811.581-0.8530.9600.022 40.0020.9570.7200.0400.60532.6129.7110.9410.9540.021 50.0020.9870.5740.1100.65539.3629.0583.0530.9680.018 60.0011.0590.319-0.0170.17125.4613.033-0.2890.9170.030 70.0031.1100.1630.1000.86927.0111.5711.6890.9280.030 80.0051.000-0.016-0.0471.69935.346-0.227-1.1440.9530.020 90.0030.9790.0060.0260.89133.1890.0800.6070.9490.021 100.0011.021-0.405-0.0390.77251.047-8.018-1.3400.9770.014)543)2002年12月范龙振等:中国股票市场的三因子模型表9账面市值比组合的三因子模型回归结果序号A p B p s p h p t( p)t(b p)t(s p)t(h p)A_Rsq S.E 10.0021.0400.371-0.5390.76240.7705.758-14.7090.9630.018 20.0020.9740.485-0.4440.73331.9406.295-10.1220.9420.022 3-0.0011.0220.494-0.273-0.33243.5488.331-8.0880.9680.017 4-0.0011.0030.527-0.221-0.43637.8167.862-5.8010.9590.019 50.0091.1530.165-0.1481.88523.5331.334-2.0990.8990.035 60.0041.0170.4390.1771.08627.0704.6223.2730.9350.027 70.0001.0530.7580.252-0.08726.5797.5754.4200.9390.028 80.0011.0250.5670.4560.37035.6967.81711.0570.9690.021 90.0011.0260.4470.4950.52535.4366.11011.8940.9680.021 100.0000.9600.4760.771-0.00225.1524.93914.0540.9520.027表10市盈率组合的三因子模型的回归结果序号A p B p s p h p t( p)t(b p)t(s p)t(h p)A_Rsq S.E 0-0.0081.0361.5750.377-1.19614.6308.8043.7080.8680.051 1-0.0100.9411.1940.045-2.55823.04811.5760.7680.9250.029 2-0.0031.0460.809-0.168-1.04833.53610.274-3.7370.9530.022 3-0.0031.0520.568-0.076-0.65523.8485.093-1.1990.9090.032 4-0.0011.0190.721-0.121-0.39831.1248.722-2.5780.9450.024 50.0031.1140.500-0.0451.03738.7576.891-1.0950.9630.021 60.0041.0870.381-0.0470.87522.5023.127-0.6770.8960.035 70.0060.9740.3690.0511.74926.5643.9810.9600.9270.026 80.0031.0310.2410.1161.00932.1872.9802.5170.9490.023 90.0101.002-0.1680.1802.41223.895-1.5882.9850.9110.030 100.0101.046-0.4220.3832.48725.075-4.0036.3910.9260.030表11价格组合的三因子模型回归结果序号Ap Bps p h p t( p)t(b p)t(s p)t(h p)A_Rsq S.E1-0.0070.9621.1880.759-1.46918.4919.03610.1460.9270.037 2-0.0020.9800.7980.516-0.57034.38211.08412.6100.9700.020 30.0031.0580.6000.3781.02533.7807.5828.4020.9630.023 40.0061.0180.4480.1521.88829.1975.0873.0390.9430.025 50.0031.1270.3960.0070.73022.8083.1740.0960.9010.036 60.0041.0300.491-0.1101.16332.8166.191-2.4350.9480.023 7-0.0020.9900.515-0.197-0.53129.2106.023-4.0500.9340.024 80.0021.0130.316-0.3210.74435.8524.426-7.9030.9530.020 90.0040.992-0.004-0.2861.37732.322-0.050-6.4920.9420.022 100.0141.0780.319-0.5493.33323.940-2.805-8.4840.9010.032从表8至表11可以看出,加入市值因子SMB 和账面市值比因子后可以大大改善对这些资产组合的解释能力,常数项和其T统计值都有显著下降.在41个资产组合中,只有5个资产组合的常数项的T统计值是显著的,由于其他资产组合的回归常数项已经在0左右,有的是正值有的是负值,基本上可以认为三因子模型可以解释这些资产组合的回报率.4三因子模型与中国股票指数在中国股票市场上,有很多股票指数用来反映股票市场的变化.在上海股票市场有上证综合指数、A股指数、30指数等.在深圳股票市场有深证综合指数、A-股指数、成分指数等.还有基金指数和各种行业指数.下面看三因子模型能否很好地解释这些指数的变化和不同.用这些指数的)544)系统工程学报第17卷第6期超额回报率与三因子模型按照式(13)作回归,结果如表12和表13.表12三因子模型对上海股票市场指数的解释股票指数A p B p s p h p t( p)t(b p)t(s p)t(h p)A_Rsq S.E 上证指数0.0000.891-0.049-0.1620.14827.714-0.599-3.4980.9230.023上证A股0.0000.897-0.042-0.1490.14037.643-0.690-4.3630.9570.017上证工业-0.0010.8830.019-0.079-0.37024.0940.206-1.4950.9030.026上海商业0.0000.8770.157-0.277-0.09920.0971.424-4.4240.8610.031上海地产-0.0030.907-0.443-0.177-0.50314.693-2.843-1.9910.7750.044公共事业0.0130.856-0.659-0.0272.18313.518-4.122-0.3020.7580.046上证综合-0.0020.9290.207-0.350-0.71530.1052.659-7.8920.9330.022上证300.0040.889-0.538-0.1530.83516.862-3.712-1.5780.8470.032表13三因子模型对深圳股票市场指数的解释股票指数A p B p s p h p t( p)t(b p)t(s p)t(h p)A_Rsq S.E 成分指数-0.0031.050-0.3730.322-0.46818.504-2.6033.9460.8680.041成分A股-0.0021.074-0.3810.318-0.30517.132-2.4043.5270.8480.045深证工业-0.0061.042-0.2330.431-0.88815.822-1.4044.5570.8380.047深证商业-0.0131.1600.2550.476-0.9447.9730.6942.2760.5740.105深证金融0.0051.082-0.923-0.0510.4609.347-3.000-0.3050.6270.070深证地产-0.0290.9880.2410.507-3.25610.6271.0273.7960.7250.067公共事业-0.0171.107-0.1520.618-2.08212.661-0.6864.9160.7860.063深证基金-0.0430.6760.5320.366-3.2204.8211.5661.8330.4270.090深证A股-0.0081.0320.2250.306-1.97125.1072.1715.1730.9270.030在这17个指数中,两个公用股指不能完全由三因子模型解释,深圳地产类指数也不能完全由三因子模型解释.地产股指的回归的常数项都是负的.说明地产股在过去几年表现较差,同时也可以看出上海股市房地产企业与深圳股市的房地产企业有显著不同.根据它们对市值因子和账面市值比因子的暴露的不同,可以知道,上海股票市场上市的企业多是大公司,账面市值比也较低,而深圳正好相反.比较两个市场的A股指数,可以看到上海股票市场的市场风险较小,而深圳股票市场的市场风险较大.与深圳股票市场相比,上海股票市场的上市公司市值稍大,而相对于市值,账面价值较低.除这3个方面的原因导致两个市场的差异之外,深圳A股指数在过去5年表现相对较差.同时看到深圳成分指数更符合三因子模型.两个市场的成分指数与各自的A股指数相比,最大的区别在于市值不同,即成分指数市值更大,其他方面差别不大,说明两个市场的成分指数比较好地反映了市场.深圳基金指数具有最大的回归常数项绝对值,最小的市场B值,最小的市值和较大的账面市值比.说明基金的投资组合由很多的小市值股票构成,股票的市值相对账面价值较低,从回归常数项来看,基金的表现比市场平均差得多,基金的运作不能得到投资者的认可.5结论根据国外股票市场的分析结果,结合对我国股票市场的认识,对中国股票市场的市值效应、账面市值比效应、价格效应、市盈率效应、资本结构效应等利用Fama_Macbeth方法进行了分析,然后对有显著影响的市值效应、账面市值比效应、价格效应、市盈率效应再利用动态资产组合的方式详细进行考察,进一步看出这些效应的影响程度,影响的非线性性,及这些效应与其他因素的关系.最后试图用多因子模型解释这些效应.从分析结果)545)2002年12月范龙振等:中国股票市场的三因子模型。
Fama-French三因子模型对我国饮料制造行业股票的影响分析
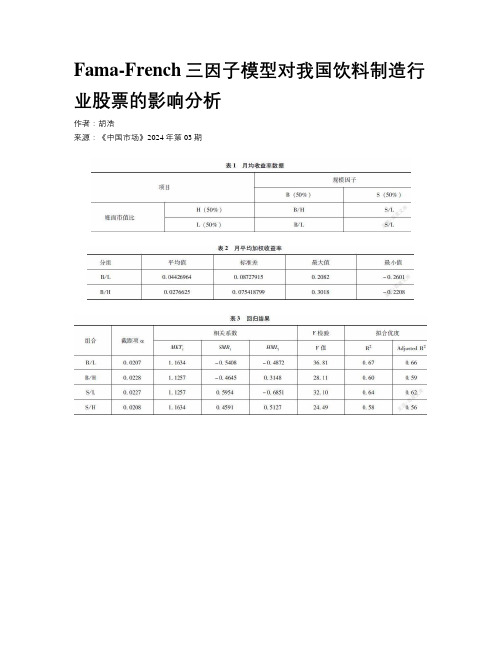
Fama-French三因子模型对我国饮料制造行业股票的影响分析作者:***来源:《中国市场》2024年第03期摘要:饮料制造板块的行情向来是A股市场投资者关注的焦点。
文章以沪深两市中20家代表性的饮料制造相关企业作为研究对象,按照流通市值大小和账面市值比大小将其分为4组,使用Fama-French三因子模型进行相关的实证检验和回归分析。
实验结果表明:三因子模型的三个因子对饮料制造股票组合收益率有较好的解释力,板块收益率的波动变化受市场波动的敏感性高;对于大市值饮料制造企业,其风险报酬率更高;小规模、高账面市值比的股票的超额收益率最高,该组合属于成长型股票,建议投资者高度关注。
关键词:饮料制造行业;Fama-French三因子模型;账面市值比中图分类号:F713.54文献标识码:A文章编号:1005-6432(2024)03-0044-05DOI:10.13939/ki.zgsc.2024.03.0111引言饮料制造行业的规模在中国股票市场占据前列,截至2022年8月,在A股市场饮料制造行业总市值仅次于银行和电气设备板块,同时饮料制造行业也带动了其他行业的发展,如原料、造纸业、设备、机械、生物工程制品(酶、酵母)、物流运输业等,酒文化也在其中传承,其在中国经济发展过程中也发挥着举足轻重的作用。
国家统计局数据显示,2022年1—4月,饮料类商品零售额同比增长10.4%,达到938亿元。
伴随着经济的稳定增长,国民消费水平的提升,消费结构的优化与升级,我国饮料制造市场以平稳的趋势迅速发展。
越来越多的投资者关注饮料制造行业的发展趋势,但若想在饮料制造行业投资中取得超额收益,需要对行业股票收益率做出评价,从而得出合理的投资策略。
对资本市场的研究向来是金融学领域研究的热点,而资本资产定价理论作为资本市场研究的经典方向,诞生了许多相关理论。
1964年WilliamSharpe等人提出CAPM模型后,EugeneF.Fama和KennethR.French发现,虽然CAPM模型对预测投资组合的收益发挥着一定的作用,但是许多研究者的实证结果显示,CAPM模型对某些反常情况的解释力很一般。
CAPM扩展模型在上证A股市场的实证检验

CAPM扩展模型在上证A股市场的实证检验吴强;刘奕汝【摘要】将流动性因子引入FF三因子模型,提出CAPM四因子扩展模型并针对上海A股市场进行实证检验.结果表明:市场超额收益率因子高度显著,市值因子次之,再次是账面市值比因子,流动性因子不够显著.CAPM三因子和四因子扩展模型均能够解释资产组合超额收益率85%以上的变异,具有较强解释能力,在上海A股市场具有适用性.【期刊名称】《中南林业科技大学学报(社会科学版)》【年(卷),期】2014(008)005【总页数】5页(P69-73)【关键词】CAPM;公司规模;账面市值比【作者】吴强;刘奕汝【作者单位】长江大学工程技术学院,湖北荆州434020;中南林业科技大学,湖南长沙410004;广东外语外贸大学,广东广州510006【正文语种】中文【中图分类】F832.51993年,美国学者E.Fama与K.French(1993)将公司规模、公司账面价值与股票总价值的比值(简称账面价值比)两个因素因素引入资本资产定价模型(Capital Asset Pricing Model,简称CAPM),提出CAPM扩展模型即FF三因子模型[1]。
流动性是指在基本不改变当前资产价格的前提下,以较低的成本迅速完成大量交易的可能性,流动性是证券市场生命力所在,在证券市场微观结构的研究中占据重要地位。
为了检验流动性对于股票资产组合超额收益率波动的影响是否显著,文章将换手率作为流动性因子引入模型,提出CAPM四因子扩展模型并对其在上证A股市场的适用性进行检验。
2005年9月,中国证监会发布《上市公司股权分置改革管理办法》,将A股市场上市公司的股份分为流通股与非流通股,此举对我国证券市场发展影响深远。
然而自从股权分置改革以来,有关CAPM扩展模型实证检验的研究成果尚不多见。
本文选取股权分置改革以来的上证A股相关数据,针对CAPM四因子扩展模型适用性问题进行实证检验。
按照E.Fama和K.French (1996)的研究结论,市场收益率、公司规模和账面市值比三个因子能够完全解释股票收益率的变异[2]。
上海股票市场的FF三因子模型

上海股票市场的FF三因子模型
孟庆顺
【期刊名称】《北华大学学报(社会科学版)》
【年(卷),期】2004(005)003
【摘要】FF三因子模型是法玛和弗兰切在1993年提出的资产定价理论,本文研究它对于上海股市的适用性.针对上证180指数样本股建立三因子模型,并进行了检验,结果表明:FF三因子模型对于上海股市是基本适用的.
【总页数】2页(P79-封三)
【作者】孟庆顺
【作者单位】吉林大学,数量经济研究中心,吉林,长春,130012
【正文语种】中文
【中图分类】F224.0
【相关文献】
1.股票市场CAPM和三因子模型分析——兼议中国股市的未来发展 [J], 李泉;陈雪花
2.中国股票市场的三因子定价模型实证研究 [J], 冯叔君;刘卓
3.中国股票市场的三因子时变风险溢价模型研究 [J], 陈学胜
4.上海股票市场风险因子数量研究——基于APT模型的分析 [J], 李福贵
5.基于流动性溢价视角下FF三因子模型在我国股票市场中的调整研究 [J], 王建勇;因版权原因,仅展示原文概要,查看原文内容请购买。
三因子模型选股策略在我国证券市场的应用

三因子模型选股策略在我国证券市场的应用摘要:三因子模型是由Eugene Fama和Kenneth French于1993年提出的,该模型认为股票的收益率由市场风险、公司规模和公司估值三个因子共同决定。
该模型在国际上已得到广泛的应用,而在我国证券市场的实际应用也已经开始起步。
本文将对三因子模型的原理及其在我国证券市场的应用进行深入探讨,并分析其效果与局限性。
一、引言作为投资者,如何在众多的股票中选择出表现良好的股票是一个很大的挑战。
为解决这个问题,学术界提出了许多股票选择模型,其中三因子模型因其理论基础扎实、实证效果显著被广泛应用于全球证券市场。
而在我国,近年来也有投资者开始借鉴该模型进行股票投资,并取得了一定的收益。
我们有必要对三因子模型在我国证券市场的应用情况进行深入的研究。
二、三因子模型的基本原理1. 市场风险因子市场风险因子是指股票的收益与市场整体的收益之间的关系。
如果一个股票的收益与市场整体的收益高度相关,那么这个股票的市场风险就较高。
而从风险与收益的关系来看,市场风险通常是与预期收益率正相关的。
2. 公司规模因子公司规模因子是指公司市值的大小对股票收益率的影响。
研究发现,在市场上,相对较小规模的公司通常会有更高的收益率。
这一现象可能是因为小公司的投资风险相对较高,因此投资者需要得到更高的回报来承担这一风险。
3. 公司估值因子公司估值因子是指一些估值指标对股票收益率的影响。
市盈率、市净率等指标。
研究发现,通常情况下,估值较低的公司往往具有较高的收益率。
这是因为市场通常会低估这些公司的价值,而导致它们的股价较为低廉。
三、三因子模型在我国证券市场的应用近年来,我国证券市场开始有投资者尝试应用三因子模型进行股票投资,并且取得了一定的效果。
这里我们以A股市场为例,对三因子模型在我国证券市场的应用进行分析。
1. 数据准备我们需要选取一定数量的股票作为研究对象,然后获取这些股票的历史交易数据。
这些数据将作为我们对三因子模型进行实证分析的基础。
上证A股市场FF三因子模型适用性研究的开题报告

上证A股市场FF三因子模型适用性研究的开题报告一、选题背景和研究意义随着我国经济的快速发展,证券市场的发展得到了空前的发展。
作为我国证券市场的重要组成部分,股票市场的投资人群日益增多,市场的交易总额也日益增加。
在股票投资方面,投资人不仅需要对特定股票进行分析,还需要了解市场的整体情况,从而制定与之对应的投资策略,获取更稳定的投资回报。
因此,在目前阶段,研究股票市场整体情况及其影响因素,能够帮助投资人更好地掌握市场的投资规律,并能制定相应的投资策略,更有效地管理投资风险,使投资回报得到进一步提升。
而三因子模型是目前市场上广泛使用的多元回归模型之一,研究其在我国A股市场中的适用性,是一项具有重要实际应用价值的研究。
二、研究目的和内容本研究旨在研究上证A股市场FF三因子模型适用性,并通过实证研究,对研究结果进行解释和分析,从而探讨如何更好地运用此模型,指导股票投资人的投资决策。
具体研究内容包括:1. 上证A股市场中FF三因子的构建及其经济学解释。
2. 上证A股市场中FF三因子对各行业和股票的回报的解释能力。
3. 上证A股市场中FF三因子与其他因素的相关性确认。
4. 上证A股市场中FF三因子的利用,指导股票投资方向和投资策略。
三、研究方法和可行性分析研究方法:采用多元线性回归分析法,对上证A股市场中FF三因子进行实证分析。
数据来源:采用Wind等数据平台的上证A股市场历史数据。
可行性分析:本研究所用的数据来源可靠,相关理论基础有所积累,相关文献资料充足,研究方法成熟,因此具备一定的可行性和可信度。
四、预期研究结果1. 确认上证A股市场中FF三因子模型的适用性。
2. 通过实证分析发现FF三因子对A股市场中不同行业和不同股票的回报能力的差异。
3. 通过实证分析发现FF三因子与其他因素的相关性。
4. 提出运用FF三因子指导股票投资方向和投资策略的具体方法。
中国股市三因子资产定价模型实证研究

中国股市三因子资产定价模型实证研究中国股市三因子资产定价模型实证研究引言股票市场是衡量一个国家经济状况的重要指标之一,对于投资者和经济决策者而言,了解股市运行规律和因素对于制定合理的投资策略和经济政策至关重要。
资产定价模型则是研究股市运行规律的重要工具之一,通过分析一系列因素对于股票报酬的影响,从而进行股价的预测和定价。
本文旨在通过实证研究,探讨中国股市中三因子资产定价模型的有效性和适用性。
一、资产定价模型简介资产定价模型是用来评估资产价格的数学模型,通过分析一系列因素对资产报酬的影响,进而进行资产定价和投资决策。
经典的资产定价模型主要有CAPM模型和三因子模型。
CAPM模型是由美国学者Sharpe、Lintner和Mossin等提出,它假设了市场风险是投资风险的唯一来源,股票的收益可以通过市场投资组合和无风险利率来解释,并且收益与风险成正比。
三因子模型的核心思想在于,股票的回报不仅与整个市场的回报有关,还与市场因子、规模因子和账面市值比因子等因素相关联。
其中,市场因子是指市场组合的回报,规模因子是指股票的市值大小,账面市值比因子则是指公司的净资产与市值的比值。
二、中国股市的特点在研究中国股市的资产定价模型之前,我们首先需要了解中国股市的特点。
中国股市自1990年代初开始发展起步,相比于发达国家的股市,中国股市在市场机制和资本运作方面仍然存在许多不完善的地方。
首先,中国股市存在着高度的国家干预,政府的政策和行为对市场运行有着直接的影响力。
例如,政府在限制外资进入、控制股指下跌以及干预公司上市等方面具有较大的权力。
其次,中国股市的整体风险相对较大,市场波动较为频繁且剧烈。
这主要是由于中国经济转型期的不确定性以及投资者心理的波动导致的。
此外,中国股市中的公司类型较多,包括国有企业、民营企业和外资企业等。
这些不同类型的企业在经营模式、盈利能力和市值等方面存在着差异,从而对股票报酬产生影响。
三、中国股市三因子资产定价模型实证研究基于中国股市的特点,我们构建了中国股市的三因子资产定价模型,该模型包括市场因子、规模因子和账面市值比因子,通过收集中国股市历史数据并运用回归分析等统计方法进行实证研究。
