Stress intensity factor evaluation for cracked chevron notched brazilian disc specimens
材料科学与工程专业英语词汇

材料科学与工程专业英语词汇1. 物理化学物理化学是研究物质结构、性质、变化规律及其机理的基础科学,是材料科学与工程的重要理论基础之一。
物理化学主要包括以下几个方面:热力学:研究物质状态和过程中能量转换和守恒的规律。
动力学:研究物质变化过程中速率和机理的规律。
电化学:研究电流和物质变化之间的相互作用和关系。
光化学:研究光和物质变化之间的相互作用和关系。
表面化学:研究物质表面或界面处发生的现象和规律。
结构化学:研究物质分子或晶体结构及其与性质之间的关系。
统计力学:用统计方法处理大量微观粒子行为,从而解释宏观物理现象。
中文英文物理化学physical chemistry热力学thermodynamics动力学kinetics电化学electrochemistry光化学photochemistry表面化学surface chemistry结构化学structural chemistry统计力学statistical mechanics状态方程equation of state熵entropy自由能free energy化学势chemical potential相平衡phase equilibrium化学平衡chemical equilibrium反应速率reaction rate反应级数reaction order反应机理reaction mechanism活化能activation energy催化剂catalyst电池battery电极electrode电解质electrolyte电位potential电流密度current density法拉第定律Faraday's law腐蚀corrosion中文英文光敏材料photosensitive material光致变色photochromism光致发光photoluminescence光催化photocatalysis表面张力surface tension润湿wetting吸附adsorption膜membrane分子轨道理论molecular orbital theory晶体结构crystal structure点阵lattice空间群space group对称元素symmetry element对称操作symmetry operationX射线衍射X-ray diffraction2. 量子与统计力学量子与统计力学是物理学的两个重要分支,是材料科学与工程的重要理论基础之一。
101基于MSC MARC的表面裂纹扩展特性的仿真_2010MSC年会论文002-刘青峰

基于MSC MARC的表面裂纹扩展特性的仿真刘青峰1,谢基龙2(1.海军后勤技术装备研究所,北京100072;2.北京交通大学机械与电子控制工程学院,北京100044)摘要:基于MSC Marc软件,本文通过编程实现了参数化、模块化建模与自动化分析;采用模块化有限元建模技术和接触技术仿真半椭圆表面裂纹(前缘),采用在裂纹前缘形成辐射状奇异单元网格的建模方法和接触技术来施加边界条件的方法,实现裂纹前缘奇异应力场和裂纹模型远场应力的模拟。
在此基础上,运用裂纹虚拟扩展技术,计算裂纹前缘的J积分, 通过线弹性有限元理论,换算出裂纹前缘的K因子分布,对裂纹前缘离散节点实行正交扩展,通过拟合裂纹前缘,实现了裂纹连续扩展仿真。
仿真结果与试验结果基本吻合,说明本文所采用的方法具有很好的实用性。
关键词:接触技术;奇异单元;裂纹前缘;半椭圆表面裂纹;MSC MarcSimulation Research of Continual Extension Rule of 3D Surface CrackUsing MSC MARC SoftwareLIU Qingfeng1,XIE Jilong2(1.Navy Logistic Tech.&Equipment Institute of PLA,Beijing 100072,China;2.School of Mechanical and Electronic Control Engineering,Beijing Jiaotong University,Beijing 100044,China) Abstract:The automatization of parameterization and modularized modeling and analysis are realized through program using MSC Marc software. The modularized finite element modeling and contact techniques were adopted to simulate the semi-ellipse surface crack. Radial singular unit meshes in the crack front were use to simulate the singular stress field of the crack front. At the same time, the boundary conditions of crack model by finite element contact technique were applied to simulate the far field stress of the crack model. In addition, the crack virtual extension technique was used to calculate the J integral on crack front. Then the stress intensity factor distribution can be transformed based on the linear elastic finite element theories. On the other side, the crack front was dispersed to realize orthogonal extension and the new crack front is fitted to get continual extension simulation. the extension of semi-ellipse surface crack was simulated. The result was in accordance with the fracture data of the sample with beach markings, the model of semi-ellipse surface crack extension simulation built in the paper was verified to be reasonable and feasible.Keywords:contact technique;singular unit;crack front;semi-ellipse surface crack;MSC Marc 国内外对于裂纹的研究,多数集中在理论推导和试验上[1],只能通过理论或经验公式指导工程结构的可靠性设计。
英国BS金属与非金属材料标准名称
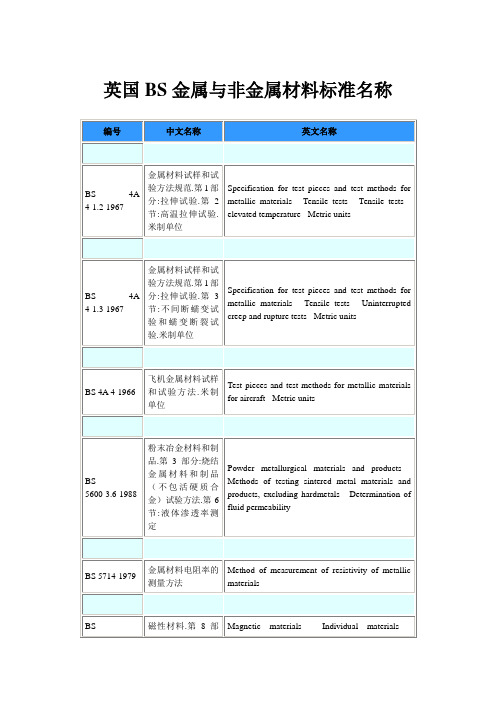
-
BS 7252-10-1997
外科植物入用金属 Metallic materials for surgical implants 材料.第 10 部分:煅 Specification for wrought titanium 5-aluminium 制钛 5-铝 2.5-铁合 2,5-iron alloy 金规范
BS
断 裂 机 械 韧 性 试 Fracture mechanics toughness tests - Method for
7448-4-1997
验 . 金 属 材 料 稳 定 determination of fracture resistance curves and 裂纹延伸的抗断裂 initiation values for stable crack extension in 曲线和初始值的测 metallic materials 定方法
BS 7252-6-1997
外科植入物用金属 Metallic materials for surgical implants for wrought 材料.可锻钴-镍-铬 Specification cobalt-nickel-chromium-molybdenum alloy -钼合金规范
BS 7252-7-1994
BS 7448-3-2005
断裂机械韧性试 验.应力强度因子 大于 3.0 MPa m0.5 s-1 的增长速度下 金属材料断裂韧性 的测定方法
Fracture mechanics toughness tests - Method for determination of fracture toughness of metallic materials at rates of increase in stress intensity factor greater than 3.0 MPa m0.5 s-1
ANSYS2020官方示例清单

ANSYS2020官⽅⽰例清单技术展⽰:⽰例问题Technology Showcase: Example Problems1、Brake Squeal Analysis:制动器噪声分析解决刹车噪声问题。
重点介绍了三种分析⽅法:线性⾮预应⼒模态、部分⾮线性预应⼒模态和全⾮线性预应⼒模态。
该问题演⽰了滑动摩擦接触,并使⽤复特征解算器预测不稳定模态。
2、Nonlinear Analysis of a 2-D Hyperelastic Seal Using Rezoning:⼆维超弹性密封的重分区⾮线性分析⽤单元分裂法对⼆维超弹性密封组件进⾏了重新划分和重新划分的⾮线性分析。
该问题显⽰了如何使⽤多个垂直重新分区步骤来确保分析的收敛和完成。
3、Fluid-Pressure-Penetration Analysis of a Sealing System:密封系统的流体压⼒渗透分析分析了流体压⼒渗透对密封系统的影响。
使⽤密封主要是为了防⽌流体(液体、固体或⽓体)在两个或多个区域之间的转移。
4、Ring-Gear Forging Simulation with Rezoning:基于重分区的齿圈锻造模拟证明了在⾦属成形过程的⼆维模拟中重新分区的有效性和有⽤性。
重新分区有助于⾮线性有限元模拟的收敛性,在这种情况下,单元变形过⼤。
5、Delamination of a Stiffened Composite Panel Under a Compressive Load:复合材料加筋板在压缩载荷下的分层使⽤实体壳单元技术对分层复合结构进⾏建模。
该问题通过接触单元的脱粘能⼒来模拟界⾯脱层。
6、Thermal Stress Analysis of a Cooled Turbine Blade:涡轮冷却叶⽚的热应⼒分析说明如何容易地设置和执⾏冷却涡轮叶⽚的热应⼒分析。
该问题利⽤表⾯效应能⼒模拟固体区域的对流载荷,并利⽤⼀维流体流动能⼒获得对流载荷的⾼精度热解。
基于结构应力法的车体结构疲劳裂纹扩展与剩余寿命评估

基于结构应力法的车体结构疲劳裂纹扩展与剩余寿命评估杨海宾;朱涛;肖守讷;阳光武;杨冰【摘要】为了弥补名义应力法不能针对具有初始裂纹的焊接结构进行评估的不足,采用结构应力法,在断裂力学的基础上推导了考虑裂纹扩展增量的焊缝裂纹扩展计算方法.以复铰式100%0低地板有轨电车为研究对象,采用名义应力法确定了典型工况下车体疲劳强度薄弱焊缝的位置,并基于结构应力法提取了该位置的膜应力和弯曲应力,并应用焊缝裂纹扩展计算方法对车体薄弱位置的焊缝进行了剩余寿命评估.研究结果表明:初始裂纹的存在导致车体寿命远低于设计寿命(1E7),但仍然具有一定的服役空间,可以利用焊缝裂纹扩展计算方法对含有缺陷的结构进行剩余寿命评估,并根据计算结果制定相应的维修策略.【期刊名称】《铁道机车车辆》【年(卷),期】2019(039)001【总页数】7页(P15-20,77)【关键词】名义应力;结构应力;裂纹扩展计算;车体结构;剩余寿命【作者】杨海宾;朱涛;肖守讷;阳光武;杨冰【作者单位】西南交通大学牵引动力国家重点实验室,成都610031;西南交通大学牵引动力国家重点实验室,成都610031;西南交通大学牵引动力国家重点实验室,成都610031;西南交通大学牵引动力国家重点实验室,成都610031;西南交通大学牵引动力国家重点实验室,成都610031【正文语种】中文【中图分类】U270.1+2目前,针对轨道交通车辆车体焊接结构疲劳评估,普遍采用基于疲劳强度值和P-S-N曲线的名义应力法,这种方法往往依赖于接头类型和载荷形式,当面对复杂结构时,精确度便会降低[1]。
密西根大学的董平沙教授提出了基于结构应力的主S-N曲线法,很好的解决了这个问题[2-3]。
对于焊接结构,不可避免的会存在缺陷,这些缺陷很可能成为裂纹的源头,导致结构的使用寿命和承载能力降低,对于服役多年的结构往往也会出现许多疲劳裂纹[4]。
如果能模拟这些裂纹的扩展行为,便能对具有裂纹缺陷的焊接结构的服役能力进行计算并指导车辆的阶段性维修。
API_579-1ASME_FFS-1_Fitness-For-Service_Standard

– Part 5 - Assessment of Local Thin Areas, assessment procedures for gouges have been relocated to Part 12
API 579-1/ASME FFS-1 Fitness-For-Service Standard
Presentation Overview
• Introduction • Joint API/ASME Fitness-For-Service Standards Committee • New Joint API and ASME FFS Standard • Overview of API 579-1/ASME FFS-1 • Balloting of API 579-1/ASME FFS-1 • Technical Basis and Validation of API 579-1/ASME FFS-1 • Relationships to Other FFS Standards • What’s next
• Membership includes international participation from France, UK, Japan, Canada, others…
5
New Joint API and ASME FFS Standard
• API 579 will form the basis of the new joint API/ASME standard that will be produced by the API/ASME joint committee
A Simplified Evaluation OfStress Intensity Factor For A Small Diameter Pipe Penetrating A ThickPlate
c – half crack surface length a/c –aspect ratio a/t – normalized crack depth t – material thickness
INTRODUCTION
Recent discoveries of stress corrosion cracking in pressure vessel components has driven interest in developing better fracture mechanics based methods for determining remaining service life of reactor components [1]-[4]. Crack growth predictions are paramount to this goal and a stress intensity factor (SIF) history is an integral part of a crack growth model. Accuracy is of utmost importance because typical stress corrosion crack growth models amplify error in SIF history. The evaluation of a reactor component to obtain a SIF history can be cumbersome and a simplified method that proves to be accurate would greatly speed up the process.
Cornell University, Ithaca, NY
受拉FRP加固X80钢板中表面裂纹应力强度因子的数值分析
受拉FRP加固X80钢板中表面裂纹应力强度因子的数值分析赵传宇;黄培彦;罗毅【摘要】半椭圆表面裂纹是金属结构中比较常见的一种缺陷,在外界因素作用下容易发生扩展,甚至导致结构破坏,而采用纤维增强复合材料(FRP)等新材料对其进行加固维修可以大幅度提高其使用寿命.文中应用Abaqus有限元软件,对受拉FRP加固X80钢板中半椭圆表面裂纹的应力强度因子进行数值分析,并给出了加固条件下应力强度因子的半经验表达式.结果表明,在均匀拉伸载荷作用下,对于应力强度因子及加固效果,裂纹形状比的影响较大,裂纹相对深度有一定影响.【期刊名称】《华南理工大学学报(自然科学版)》【年(卷),期】2013(041)008【总页数】6页(P109-114)【关键词】表面裂纹;纤维增强复合材料;应力强度因子;钢板;加固【作者】赵传宇;黄培彦;罗毅【作者单位】华南理工大学土木与交通学院,广东广州510640;华南理工大学土木与交通学院,广东广州510640;华南理工大学亚热带建筑科学国家重点实验室,广东广州510640;华南理工大学土木与交通学院,广东广州510640【正文语种】中文【中图分类】O346.1;U446.1随着社会的发展,钢结构在各类基础设施工程中得到了广泛的应用,如石油天然气管道、桥梁、海洋平台等.在长期的使用过程中,受环境条件和外界荷载的影响,钢结构中会不可避免地产生一些缺陷,如表面裂纹.表面裂纹的扩展会给工程设施带来很大的安全隐患.近年来,国内外学者对表面裂纹问题进行了较多的研究工作[1-6],而且,采用纤维增强复合材料(FRP)加固修复含有裂纹构件的技术也取得了一些进展[7-9].其中,Nicholas等[10]通过实验和有限元分析对FRP加固含贯穿裂纹的钢结构进行了研究,结果表明粘贴FRP加固可以有效地降低裂纹的扩展速率,试件的疲劳寿命提高了74%以上.笔者所在课题组则对受弯FRP加固钢板中半椭圆型表面裂纹的应力强度因子进行了数值分析[11],提出了在弯曲载荷作用下该类表面裂纹问题的应力强度因子的数值计算方法.在文献[11]的基础上,文中利用大型有限元软件Abaqus对受拉FRP加固钢板中三维半椭圆表面裂纹的应力强度因子进行有限元分析.1 有限元分析模型以含有表面裂纹的高强管线钢材X80[12]钢板为研究对象,在高度为H、宽度为W、厚度为B的钢板中心部位,有一半椭圆形三维表面裂纹,裂纹长度为2c、深度为a、离心角为θ,如图1所示.在钢板有裂纹的一面采用笔者所在课题组发明的新型FRP片材——碳纤维薄板(CFL)[13]予以满贴加固,CFL的计算厚度为tf,如图2所示.在钢板的两端施加荷载为σ的均布拉应力.由于上述研究对象具有严格的对称性,为了减少计算量,加快计算速度,取研究对象的1/4作为有限元分析模型,同时再对两个对称面上同时施加对称约束,如图3所示.考虑到CFL单元与裂纹尖端单元的兼容性问题,有限元模型中CFL和钢板全部采用三维实体单元.文中假定钢板与CFL之间不产生滑移或剪切破坏,故CFL和钢板之间采用共用结点连结,即不考虑胶层厚度.图1 带表面裂纹的受拉钢板Fig.1 Steel plate with surface crack under tensile load图2 CFL加固后的钢板Fig.2 Steel plate strengthened with CFL图3 有限元分析模型Fig.3 Meshes of the FEM model为了得到精确的计算结果,裂纹尖端划分为11层单元,每层12个单元,沿裂纹前沿的1/4的椭圆曲线共划分为20份,即裂纹尖端共有20组单元.紧靠裂纹前沿的单元即第1层单元为楔形单元,另外10层单元为六面体单元[14-15].裂纹尖端共计2640个单元,整个模型共有25932个单元.2 三维表面裂纹的应力强度因子2.1 未加固钢板中表面裂纹的应力强度因子为了验证上述有限元分析模型及计算方法的准确性,先对未加固钢板中三维半椭圆形表面裂纹的应力强度因子KI进行数值分析,并与Newman-Raju公式[16]的计算结果进行比较.有限元计算模型中各参数的设置如下:H=90mm,W=70 mm,B=8 mm,σ=100 MPa;X80钢板的弹性模量Es=206 GPa,泊松比νs=0.3;裂纹形状比a/c分别取为 0.4、0.6、0.8;裂纹相对厚度分别取为a/B=0.1,0.2,0.3.由于Abaqus有限元软件是通过J积分来求解应力强度因子,而在本研究中,裂纹尖端共划分为11层单元,故裂纹前沿每个点上相应地可以得到11个J积分,从而可以得到11个应力强度因子.有研究结果表明,通常情况下,靠近内层的计算结果波动较大,靠近外层的计算结果逐渐趋于稳定.在默认情况下,Abaqus按顺序从最内层开始输出结果,因此,为了保证结果的准确性,沿裂纹前沿每个点上,至少要输出6个应力强度因子值,同时应选取外层较稳定的计算值作为最终结果.当 a/c=0.4,a/B 分别为 0.1、0.2、0.3,以及当a/B=0.2,a/c分别为0.4、0.6、0.8 时,有限元计算结果与Newman-Raju公式的计算结果示于图4中.从图4可以看出,有限元计算结果与Newman-Raju公式的计算结果在总体上较为一致,5种参数的表面裂纹有限元计算结果的平均误差均在3%以内.因此,可以认为文中的有限元计算结果较为准确.图4 有限元与Newman-Raju公式的KI计算结果对比Fig.4 Comparison between computing values of KIby FEM and Newman-Raju Eq.然而,由图4可知,当θ=0 rad时,有限元计算结果与Newman-Raju公式的计算结果误差较大,如当 a/c=0.4,a/B=0.1 时的误差为 7.8%;当θ=1.57rad 时,两者的误差最小,如当 a/c=0.4,a/B=0.3时的误差仅为0.38%.也就是说,当裂纹相对深度a/B越小时,靠近钢板表面区域的应力强度因子计算结果的相对误差越大.这是由于Abaqus有限元软件在计算应力强度因子时,默认整个模型都处于平面应变状态下,而实际上在靠近钢板表面的区域接近于平面应力状态,因此造成θ=0 rad附近的计算结果的相对误差较大.2.2 CFL加固后表面裂纹的应力强度因子在有限元计算中,CFL的各参数取值为:弹性模量Ef=230GPa,泊松比νf=0.25,抗拉强度4850MPa,计算厚度 tf分别取为 0、0.2、0.4、0.6、0.8、1.0 mm.表面裂纹形状比 a/c分别取为0.4、0.6、0.8,裂纹相对厚度 a/B 分别为 0.1、0.2、0.3.当 a/B=0.2,a/c=0.6,tf分别为 0、0.2、0.4、0.6、0.8、1.0 时,CFL加固后表面裂纹的应力强度因子变化情况如图5所示.从图5中可以看出,经过CFL加固后,应力强度因子的数值普遍降低20%以上,加固效果相当明显.例如,当tf=0.2时,θ=0 rad所对应的应力强度因子降低幅度最大(54.9%),θ=1.57 rad所对应的应力强度因子降低较小(20.6%).也就是说,随着离心角θ的增大(从0rad到1.57rad变化),应力强度因子的降低幅度会减小,加固效果越来越小.这是因为加固后CFL限制了裂纹上、下表面之间的位移,因此,离钢板表面区域时越远,裂纹上、下表面受CFL的约束就越小.图5 表面裂纹应力强度因子KI的计算结果Fig.5 Computing values of KIforsurface crack从图5也可以看出,随着CFL计算厚度的增加,应力强度因子的降低幅度越来越大,但降低的速度逐渐变慢.当θ=0rad和θ=1.57rad时,应力强度因子随CFL计算厚度tf的变化情况如图6所示.由图6可知,当tf≥0.5 mm 后,KI降低较慢,并逐渐趋于平缓.这表明采用CFL加固可以显著降低表面裂纹的应力强度因子,但用量过多加固效果会变差,并造成材料的浪费.对于其他a/B和a/c值的计算结果也显示出类似的变化规律.图6 CFL计算厚度对应力强度因子的影响Fig.6 Effect of CFL computing thickness on stress intensity factors2.3 裂纹参数对KI的影响(1)a/c的影响当 a/B=0.2,a/c分别为 0.4、0.6、0.8 时,CFL(tf=0.2mm)加固后表面裂纹应力强度因子的计算曲线如图7所示.由图7可知,CFL的加固效果较好,但当裂纹形状比a/c增大时,加固效果会逐渐降低.例如,当θ=1.57rad 时,a/c=0.4 对应的加固效果为26.1%,a/c=0.6对应的加固效果则为20.6%,a/c=0.8对应的加固效果为16.1%,如图8所示.这是因为当a/B不变时,a/c越大,c越小,CFL与表面裂纹之间的相互作用区域越短,使CFL发挥的作用变小.而在θ=0 rad附近,因为Abaqus软件计算时自动假设整个试件都处于平面应变状态,从而造成误差较大,导致加固效果的降低并不明显.图7 a/c对CFL加固后KI的影响Fig.7 Effect of a/c on KIafter CFL strengthened(2)a/B的影响当 a/c=0.4,a/B 分别为 0.1、0.2、0.3 时,CFL(tf=0.2mm)加固后表面裂纹应力强度因子的计算曲线如图9所示.由图9可知,当a/B<0.3时,应力强度因子的降幅会随着离心角θ的增大而减小,加固效果降低;当a/B>0.3时(如图10所示),无论离心角θ如何变化,应力强度因子的降幅会随着a/B的增大而增加,加固效果增强.图8 θ=0,1.57rad时a/c对CFL加固后 KI的影响Fig.8 Effect of a/c on KIwhen θ=0 and 1.57rad after CFL strengthened图9 a/B对CFL加固后KI的影响Fig.9 Effect of a/B on KIafter CFL strengthened当离心角θ较大时,应力强度因子的降幅会先随着a/B的增大而减小,在a/B=0.3附近出现拐点,而后又随着a/B的增大而增大.例如,当θ=1.57rad 时,a/B=0.1时应力强度因子的降幅为32.1%,a/B=0.2 时为 26.1%,a/B=0.3 时为 24.8%,a/B=0.4 时为 25.9%,a/B=0.5 时为28.1%.探究其原因,可以认为当a/c不变时,a/B增大则a和c同时增大,当a影响较大时,裂纹深度的增加使CFL远离裂纹的尖端,CFL发挥作用小,使应力强度因子的降幅即加固效果降低;当c影响较大时,CFL与裂纹间的相互作用区域长,CFL发挥作用起来大,使加固效果增加.然而,在θ=0 rad附近,由于有限元计算时假设试件处于平面应变状态下,从而与实际的应力状态有较大差距,在该区域应力强度因子的变化规律暂时不予讨论.图10 θ=0,1.57rad时a/B对CFL加固后KI的影响Fig.10 Effect of a/B on KIwhen θ=0 and 1.57 rad after CFL strengthening3 加固试件中表面裂纹应力强度因子的表达式为了便于对FRP加固钢板中表面裂纹的应力强度因子计算,通过对大量的有限元计算结果的分析,并利用数学软件Matlab对其进行拟合,可得到KI的表达式如下:式中,σt为均布拉伸应力,F为修正因子,可由下式求出:式中,p=a/c,q=a/B,t=ln(1+tf),r=sinθ.式(1)的适用范围为:0 <a/c<1.0,0 <a/B <1.0,2c/W≤0.5,0rad≤θ≤1.57rad.将由式(1)和(2)求得的应力强度因子与有限元计算结果进行比较,可知两者的平均误差小于3%.这说明采用上述表达式计算FRP加固钢板中表面裂纹的应力强度因子是有效和可行的.4 结论应用大型通用软件Abaqus,对采用碳纤维薄板(CFL)加固的矩形钢板中三维半椭圆形表面裂纹的应力强度因子进行了数值分析,并对CFL的加固效果及其影响因素进行了初步探讨,得到如下结论:(1)采用CFL加固可以显著降低三维表面裂纹的应力强度因子,即加固效果显著.然而,随着CFL厚度的增加,加固效果的提升幅度逐渐减小;(2)裂纹形状比a/c对应力强度因子的降幅和加固效果的影响较大,而且a/c越大,加固效果越差;(3)裂纹相对深度a/B会影响加固效果.随着a/B的增大,加固效果先减弱后增强.(4)给出了FRP加固钢板中表面裂纹的应力强度因子的表达式.利用该表达式,可以方便地计算该类表面裂纹问题的应力强度因子.参考文献:[1]彭志刚,赵小兵,刘青锋,等.半椭圆表面裂纹前缘应力强度因子的计算[J].计算机仿真,2008,25(7):332-335.Peng Zhi-gang,Zhao Xiao-bing,Liu Qing-feng,et al.Calculation of stress intensity factor of semi-elliptical surface crack front[J].Computer Simulation,2008,25(7):332-335.[2]程长征,牛忠荣,叶建乔.边界元法计算浅表面裂纹应力强度因子[J].合肥工业大学学报:自然科学版,2009,32(4):503-507.Cheng Chang-zheng,Niu Zhong-rong,Ye Jian-qiao.Evaluation of the stress intensity factor of the crack close to the surface by the boundary element method [J].Journal of Hefei University of Technology:Natural Science Edition,2009,32(4):503-507.[3]Lin X B,Smith R A.Finite element modeling of fatigue crack growth of surface cracked plates:PartⅢ:Stress intensity factor and fatigue crack growth life[J].Engineering Fracture Mechanics,1999,63(5):503-522.[4]Miyazaki,Kanno K,Hosakl S,et al.Evaluation of environmentally assisted fatigue surface crack growth behavior in carbon steel [J].Pressure Vessels and Piping Division,1998,374:231-239.[5]Righiniotis T D,Lancaster E R,Hobbs R E.Stress intensity factors for a semi-elliptical surface crack in a T-shaped geometry.Part 1:Tension and Bending Results[J].Journal of Strain Analysis for Engineering Design,1999,34(3):147-155.[6]Hadi Khoramishad,Majid Reza Ayatollahi.Finite element analysis of a semi-elliptical external crack in a buried pipe[J].Transactions of the Canadian Society for Mechanical Engineering,2009,33(3):399-409.[7]张宁,岳清瑞,杨勇新,等.碳纤维布加固钢结构疲劳试验研究[J].工业建筑,2004,34(4):19-21.Zhang Ning,Yue Qing-rui,Yang Yong-xin,et al.Research on the fatigue tests of steel structure member reinforced with CFRP[J].Industrial Construction,2004,34(4):19-21.[8]Liu Hongbo,Riadh Al-Mahaidi.Experimental study of fatigue crack growth behaviour in adhesively reinforced steel structures[J].Composite Structures,2009,90(1):12-20.[9]Massimiliano Bocciarelli,Pierluigi Colombi,Giulia Fava,et al.Fatigue performance of tensile steel members strengthened with CFRP plates[J].Composite Structure,2009,87(4):334-343.[10]Nicholas G Tsouvalis,Lazarus S Mirisiotis,Dimitris N Dimou.Experimental and numerical study of the fatigue behaviour of composite patch reinforced cracked steel plates[J].International Journal of Fatigue,2009,31(10):1613-1627.[11]张术宽,黃培彦,赵传宇.CFL加固受弯钢板中表面裂纹应力强度因子的数值分析[J].华南理工大学学报:自然科学版,2012,40(4):162-168.Zhang Shu-kuan,Huang Pei-yan,Zhao Chuan-yu.Numerical analysis of stress intensity factor of surface crack in steel plate strengthened with CFL under bending load[J].Journal of South China University ofTechnology:Natural Science Edition,2012,40(4):162-168.[12]Briottet L,Batisse R,de Dinechin G de,et al.Recommendations on X80 steel for the design of hydrogen gas transmission pipelines [J].International Journal of Hydrogen Energy,2012,37(11):9423-9430.[13]黄培彦,曾竞成.纤维薄板及其应用:中国,ZL200410026742.8 [P].2006-08-23.[14]Dassault Systemes Simulia Corp.ABAQUS BenchmarksManual(6.10)[R].Pawtucket:[s.n.],2010.[15]Sharobeam M H,Landes J D.Numerical solutions for ductile fracture behavior of semi-elliptical surface crack[J].Engineering Fracture Mechanics,1999,63(2):131-145[16]Newman J C,Raju I S.Analyses of surface cracks in finite plates under tension or bending loads[R].USA:NASA TP,1979:1578。
TA16传热管的断裂韧度测试方法研究
TA16传热管的断裂韧度测试方法研究刘肖;王理;包陈;王浩;马娜【摘要】近年来,以蒸汽发生器传热管为代表的小尺寸管材的断裂韧度评价方法受到了日益关注.本文设计了一种可用于TA16传热管断裂韧性测试的含径向裂纹C 形试样,基于弹塑性有限元分析获得试样的应力强度因子K和J积分的计算式.采用规则化法完成了TA16传热管的断裂韧度试验,试验结果表明,不同试样得到的J阻力曲线和条件启裂韧度JQ的分散性均较小,JQ均值为32.875 MPa·mm,标准差为1.377 MPa· mm.%In recent years,the fracture toughness assessment for small size tubes repre sented by SG heat transfer tubes has received more and more attention.In this study,a type of radial cracked C-shaped specimen was designed to estimate the fracture toughness of TA16 heat transfer tubes.The expressions of stress intensity factor K and J integral were obtained based on elastic plastic finite element analyses.A group of radial cracked C-shaped specimens for TA16 heat transfer tubes were carried out by using normalization method.The test results show that small data dispersions of J resistance curves and conditional initiation toughness JQ are observed,the mean value of JQ is 32.875 MPa · mm,and the standard deviation is 1.377 MPa · mm.【期刊名称】《原子能科学技术》【年(卷),期】2018(052)003【总页数】7页(P427-433)【关键词】断裂韧度;J阻力曲线;含径向裂纹C形试样;规则化法;TA16传热管【作者】刘肖;王理;包陈;王浩;马娜【作者单位】中国核动力研究设计院反应堆燃料及材料重点实验室,四川成都610213;中国核动力研究设计院反应堆燃料及材料重点实验室,四川成都610213;西南交通大学力学与工程学院,四川成都610031;中国核动力研究设计院反应堆燃料及材料重点实验室,四川成都610213;中国核动力研究设计院反应堆燃料及材料重点实验室,四川成都610213【正文语种】中文【中图分类】TV313TA16钛合金以其比强度高、耐蚀性能优异及无磁性等特点,用于制造新型高效蒸汽发生器传热管,其规格为φ8 mm×1.5 mm。
论文写作与国际发表作业
1. IntroductionNowadays, more and more attention has been paid to the utilization of low-temperature flue gases (<120℃) released from several industry sectors (cement, steel, refineries), for its potential in reducing fossil fuel consumption and alleviating environmental problems. Organic Rankine Cycle (ORC) is proposed to recover low-grade energy and transform it into power. It is a proven technology, which allows the generation of electricity from low-temperature heat sources in a far more efficient way than conventional steam cycles [1,2].Much industrial flue gases may contain significant amount of moisture in vapor form (wet flue gases) due to many reasons such as flashing, washing, cleaning, and drying. The water dew point temperature of these fluegases could range between 55℃and 65℃. Therefore, a considerable amount of heat is available in the form of latent heat of water vapor in these gases and cannot be recovered if flue gases are not cooled down to temperatures lowerthan the flue-gas dew point. The recovery of this large amount of heat improves the overall efficiency of the recovery system [3].An important factor influencing latent heat recovery is the corrosion problem associated to the cooling when flue gases containsulfuric oxides (SO x), nitric oxides (NO x), and hydrochloric acid(HCl). However, many recovery technologies are already well developed and technicallyproven. Options include indirect contactcondensation recovery and direct contact condensation recovery [3]. In an indirect contact condenser, the heat is transferred between the two fluids (typically flue gases and working fluid) using an intervening wall (typically fin-and-tube heat exchanger). In this case, the heat-exchanger design requires using advanced materials su ch as ‘‘Te flon” or equivalent coating to withstand exposure to corrosion problems. In a direct contact condenser, heat is transferred between the two fluids (typically gas and water) without an intervening wall thus there are no heat-transfer surfaces exposed to corrosion, clogging, and fouling. The two fluids move in a counter-flow direction, with one of them dispersed as small particles in a vertical column.Many investigations were carried out about low-grade heat recovery using ORC. Comprehensive researches on appropriate working fluids for low-temperature applications have been investigated by many authors such as [4–6]. Others researchers havefocused on the parametric optimization and performance analysis of the ORC like [7–10]. [Research background]However, these studies deal with the indirect contact condensation recovery based on sensible heat extraction from fluegases with low moisture contents, or even though, with high moisture contents [11], but cooling the gases to a minimum safe temperature in order to prevent water vapor condensation and acid formation during gasflow. [Existing problem]. Theoriginality of thisstudy is to extend the ORC applications to low-grade gas heat sources with high moisture contents by pointing out the effect of water vapor condensation on cycle performance using the twocondensing heat recovery processes (direct and indirect heat exchange). [Research purpose]2.IntroductionSO2is widely known as a major pollutant that can cause variousissues to the environment and public health. Although multiplemethodologies have been developed to remedy such problems, a large amount of SO2 is still continuously emitted to theatmosphere every year. According to the estimation by publiclyavailable data sets and inventories, the global anthropogenicSO2released to the atmosphere in 2010 was over 100 Tg intotal, of which more than 50% came from coal combustion. Industrial processes, mostly supported by fossil fuel combustion, are leading sources for the release of SO2. Flue industrially generated SO2, and it is regarded as an effective wayto reduce SO2emission. By now, various FGD techniqueshave been developed, among which the lime/limestone processis the most commonly used one, owing to its stability and highefficiency.[Research background]. However, this process bears many drawbacks, including high capitalcosts, complex equipment, largeoccupation of land area, large consumption of fresh water, and formation of secondary pollutants. Application ofcarbonaceous materials in FGD provides an alternative with aseries of advantages in contrast to the lime/limestone process, such as low capital cost, regeneration, and capability to recoversulfur. Many studies have indicated that carbonaceous materials, including activated carbon, coke, semi-coke, and activated carbon fiberscan effectivelyremove SO2from flue gas with little negative impact on theenvironment. To date, great e ff orts have been devoted toimprove the feasibility and efficiency of carbonaceous materialsin desulfurization processes by optimizing the preparationmethodologies, parameters during desulfurization, and regeneration process.The properties of carbonaceous materials can be tailored byactivation. In previous studies, a large number of physical andchemical activation agents have been used on coal or othercarbonaceous precursors to achieve better adsorption capacitiesfor various adsorbates, but the knowledge is yet to expandon the selection of activation methods exclusively designed forremoval of SO2 from flue gas. [Existing problem]. In this paper, we employ a typeof low-cost carbonaceous material, semi-coke, to investigate the influence of activation methods on desulfurization capacity. Semi-coke is obtained from low-quality coal after going througha low-temperature carbonization process, duringwhich there isan enrichment of oxygenated functional groups and theformation of undeveloped pore structure of the semi-cokecaused by incomplete cracking of the coal precursor. Thesefeatures of the semi-coke might be auspicious for application indesulfurization. For better utilization, an activation process byphysical or chemical agents is usually carried out afterward. Inthis study, the semi-coke is respectively treated with CO2, KOH, ZnCl2, and H3PO4, all of which are widely usedactivation agents in the industrial preparation of activatedcarbonaceous materials.The influences of temperature and flue gas compositions are conducted, which reveal that theremoval of SO2 in the presence of O2and H2O is an integratedprocess of adsorption and oxidation, with H2SO4as the finalproduct. [Research purpose]In order to gain further insight into the fundamentalmechanisms, the adsorption and desorption behaviors of thesamples are analyzed by detailed characterizations of physicaland chemical properties. Eventually, attempts are made todiscuss possible reactions that occur in the adsorption anddesorption processes, during which some key steps for desulfurization by activated semi-coke are identified.[content arrangement]3.IntroductionFatigue is one of the major causes for failure of structuralmembers, especially in pipeline steel subjected to a cyclic load. Fatigue failure may occur because of changes in stress caused by frequent stop-and-start working pressure or outside forces, such as land movement and so on during operation [1 –4]. Hence, fatigue is a major concern in the evaluation of pipeline integrity. Generally, the total fatigue life mainly depends on fatigue crack initiation and propagation [5]. However, fatigue crack growth life is dominant in the total life of pipelines because fracture caused by notches and cracks is the primary failure mode of pipelines under the condition of cyclic loading [6]. Consequently, it is important and has prominent practical significance to study fatigue crack growth behavior.For the past decades, many researchers have carried out extensive work to study fatigue crack growth behavior of pipeline steel [7,8]. Among them, the relationship between fatigue crack growth rate (da/dN) and the stress intensity factor range( Δ K) was described by the well-known Paris equation [9],which means a straight line in the log – log fit for the da/dN –Δ K plots. Nevertheless, some r esearches indicated the fatigue crack propagation curves of some materials are changed in the slope of the da/dN –Δ K plots, such as dual-phase steel andtitanium alloy [10,11]. Thus, it is not clear that whether Paris equation still can describethe non-linear fatigue crack propagation curve exactly. Furthermore, a n ew empirical model, αβ model is presented by A.M.L. Adib to fit non-linear da/dN –Δ K relationship of Titanium alloys [12].[Research background].However, whether αβ model can describe the fatigue crack propagation behaviorof dual-phase steel more adequately is unknown. Therefore, in order to predict fatigue crack growth life, it is very necessary to find an appropriate method allowing for considering non-linear da/dN –Δ K relationships.[Existing problem]In this work, the non-linear fatigue crack propagation curve of a bainite/ferrite dual-phase X80 pipeline steel at differentstress ratios (R = σ min / σ max) was examined. Paris equation was compared with αβ model through describing fatigue crack propagation behavior. In addition, the effects of R- ratio on the location of transition point in fatigue crack propagation curve were also analyzed. This study provided beneficial experimental data for safe designs of gas transmission pipelines.[Research purpose ]。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
K 2 = G "E'
E E'= .
(1 - v 2)
Where CBE' is the dimensionless compliance value for the CCNBD specimen and Y*(ct) is the dimensionless SIF values for the CCNBD specimens. Therefore if the compliance values for the CCNBD specimens can be derived, the corresponding SIF value will then be obtained. Generally two models can be used to derive the compliance value for a chevron notched geometry based on the compliance value of its corresponding straight through notched specimen. Namely these two models are: Hypothesis I--Munz's identical compliance changing rate model and Hypothesis II--Bluhm's slice compliance superimposition model.
HYPOTHESIS I AND Y*(~) EVALUATION
for plane stress condition, for plane strain condition.
(3) As a first approximation, Munz [9] assumed that the change in dimensionless compliance with a crack extension da (dot) for the chevron notch specimen is identical to that for a straight through specimen provided the other geometrical values are identical, i.e. d(CcN • BE') dot (4) d(Csv" BE') dot (8)
Technical Note
Stress Intensity Factor Evaluation for Cracked Chevron Notched Brazilian Disc Specimens
c. x u t
R. J. FOWELLt
INTRODUCTION
Recently cracked Brazilian discs, including Cracked Straight Through Brazilian Discs (CSTBD) and Cracked Chevron Notched Brazilian Discs (CCNBD) (Fig. 1), are being used in rock fracture research [1-3]. The advantages of using cracked Brazilian disc geometries for rock fracture investigation are being identified. It has been concluded [4] that these geometries can be developed to be simple and ideal configurations for rock fracture toughness measurement under Mode I, Mode II or mixed Mode I and Mode II fracture conditions, rock fracture strength locus test and rock fracture initiation and crack propagation investigations (single or mixed mode). The CSTBD fracture problem was first studied by Libatskii in 1967 [5] and then actively investigated by the following researchers [5-7]. A recent study [6] based both on theoretical evaluation by dislocation and complex stress function methods, and numerical calibration by finite element and boundary element methods has given accurate solutions to the CSTBD fracture problem for any fracture mode or mixed mode conditions for any crack length. This provides the foundations to solve the fracture problems for the CCNBD geometry.
for.
C O M P L I A N C E M E T H O D IN C C N B D S I F E V A L U A T I O N
For chevron notched specimens, the theoretical SIF soluபைடு நூலகம்ion method is normally based on the compliance method in combination with the solution of the
Int. J. Rock Mech. Min. Sci. & Geomech. Abstr. Vol. 31, No. 2, pp. 157-162, 1994
Pergamon
Copyright© 1994 Elsevier Science Ltd Printed in Great Britain. All rights reserved 0148-9062/94 $7.00 + 0.00
=
[-d(CBE')
•
2T.'2 ]
L
4'fl(ot)
B,/-R'Y*(~)
(7)
p2 dC 2_-~ - d---a
(2)
where b is the width of the crack front. Under linear elastic fracture mechanics (LEFM) conditions, the SIF value of a crack problem, K, can be related to G in a simple form:
Y P
/
/ N
\
I l
\ \ I I
(a)
(b)
Fig. 1. CSTBD and CCNBD specimen geometries. 157
(c)
158
XU and FOWELL:
TECHNICAL NOTE
corresponding straight through notched specimens. A specimen compliance is defined as the reverse of the specimen stiffness, i.e.
C =u/P
(1)
and ot(=a/R), O~o(=ao/R), otl(=az/R) and %(=B/R) are dimensionless expressions for the specimen geometrical dimensions. Substituting equation (6) back into equation (4) will yield:
where P is the external load, and u the related displacement, loading point displacement (LPD) for example, as shown in Fig. 2. Combined with the definition of strain energy release rate G, the relation between C and G can be derived. When the crack with length a propagates stably for an increment da, the change in the compliance value of the specimen is dC, then the relation can be expressed as: G
tDepartment of Mining and Mineral Engineering, University of Leeds, Leeds, LS2 9JT, U.K.
A single CCNBD specimen geometry was first used by Shetty in 1985 [7] for the Mode I fracture toughness measurement of ceramic materials. The stress intensity factor (SIF) solution for this geometry was solely obtained by numerical calibration. When CCNBD was introduced into rock fracture research in the late 1980s [3, 8], one single geometry was again proposed and the SIF solution was obtained in the same way. However it was soon found that in rock fracture research, one single geometry was far too limited for practical application as the availability of rock core and specimen preparation equipment vary greatly. Therefore the SIF solutions for a complete set of different CCNBD specimen geometries needed to be given so that CCNBD users can select their own geometry according to their practical situation. Obviously it is impossible to use numerical methods to calibrate all the possible CCNBD specimen geometries and therefore a theoretical evaluation method has to be derived. The correctness of the theoretical approach can be calibrated based on some typical CCNBD geometries and the error in the method can then be compensated
