SSI效应对隔震结构地震响应的影响分析
考虑SSI效应的核电结构水平与竖向地震响应的耦合效应研究

结'构'工'程'师 ()*+,)+*-./012033*4
56.7!" (+88.3 93:7#$%&
考虑 00U效应的核电结构水平与竖向 地震响应的耦合效应研究
周志光% '郭'晶%'魏晓冬%'张建国#
%7同济大学土木工程学院上海 #$$$=# #7上海城投原水有限公司上海 #$%#\$
收稿日期 #$%; <$& <%& 基金项目 国家自然科学基金项目பைடு நூலகம்\%";&!\; 上海市高峰学科项目 ' ! 作者简介 周志光男副教授主要从事工程结构抗震消能及隔震电厂结构及设备抗震等的研究 />-2.D1D?6+B)601@273E+7,0
*试验研究*
*&!*
结构工程师第 !" 卷增刊'
>?引?言
到目前为止!大多数的核电厂在设计的时候 没有充分考虑竖向地震的影响" 日本福岛第一核 电厂0紧急应变中心1 建筑物采用由铅芯橡胶支 座'天然橡胶支座及滑动支座组成的隔震体系!在 #$%% 年东日本大地震中!该系统有效地降低了结 构的水 平 响 应! 但 是 竖 向 响 应 被 放 大 了! 竖 向 aKI为 $7"" #!一楼和二楼楼层的竖向响应分别 被放大了 %Ck和 !=k!相应的楼层竖向反应谱也 比竖向地震动的反应谱高(%) " 这表明!使用传统 隔震支座!地震响应的水平分量可以显著减少!但 是激励的竖向分量却会直接传递到结构中" 这一 现象对于核电站这类结构就显得尤为重要!因为 这类结构内部的专业设备和机器不仅昂贵!而且 对安全操作至关重要" 因此研究核电结构在竖向 地震分量下的响应显得非常重要(#) "
考虑SSI效应的层间隔震结构在三维地震下的响应研究
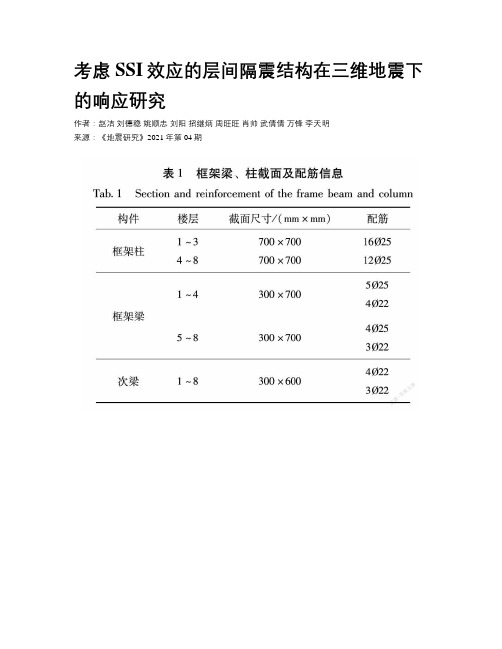
考虑SSI效应的层间隔震结构在三维地震下的响应研究作者:赵洁刘德稳姚顺忠刘阳招继炳周旺旺肖帅武倩倩万锋李天明来源:《地震研究》2021年第04期摘要:為探讨三维地震下层间隔震结构考虑土-结构相互作用(SSI效应)时的地震响应,建立了考虑SSI效应的层间隔震结构模型,分别输入一维、二维、三维地震动,比较层间隔震结构在不同维度地震波输入工况下的地震响应。
针对三维地震动输入下隔震支座拉压应力超限问题,添加三维隔震装置,并与传统水平隔震结构地震响应结果进行对比分析。
结果表明:三维地震动输入下的结构地震响应大于一维和二维;加入三维隔震支座后,竖向地震动被有效隔离,结构地震响应减小,优化了支座受力,支座拉压破坏问题得以解决,地基土体应力小于设置传统水平隔震支座下的土体应力,对地基和基础设计有利。
关键词:三维地震动;三维隔震;SSI效应;层间隔震中图分类号:TV352.1文献标识码:A文章编号:1000-0666(2021)04-0665-080引言层间隔震是在基础隔震技术上发展的一种新型隔震技术,基础隔震具有显著隔震效果(袁正国,周宪伟,2006),但层间隔震更具有研究空间。
东京汐留住友大厦采用的就是层间隔震结构,通过在结构中部设置隔震层有效降低了地震响应(末冈利之等,2008)。
现有的隔震设计和理论分析大多建立于刚性地基的假定之上,不能真实反映结构与地基在地震动作用下的能量传递机制(薛素铎等,2013)。
张之颖等(2007)研究了SSI效应对基础隔震体系的动力特性和地震响应造成的影响。
Spyrakos等(2009a,b)研究了SSI效应对隔震结构固有频率和阻尼产生的影响。
李昌平等(2013)推导了计算考虑SSI效应的隔震结构分析模型的周期和阻尼的公式。
张尚荣等(2014)推导了考虑SSI效应的层间隔震结构分析模型动力特性相关参数的表达式。
翁大根等(2015)针对建立在软弱地基上的隔震结构提出了由隔震支座与阻尼器组成的联合隔震方案。
基于SSI的桥梁地震脆弱性发展概述

基于SSI的桥梁地震脆弱性发展概述摘要:本文首先介绍地震脆弱性研究的发展,而后介绍ssi方法的研究与变革,然后介绍基于ssi的桥梁地震脆弱性曲线的发展与展望。
针对传统方法存在的问题,将ssi方法与基于脆弱性分析的桥梁抗震设计理论结合起来,介绍了基于ssi的桥梁抗震脆弱性分析方法。
关键词:地震脆弱性分析;土—结构相互作用(ssi);fema440;反应谱方法abstract: this paper firstly introduces the development of seismic vulnerability analysis and the research and change of ssi method, then it introduces the development and prospect of the seismic vulnerability line of bridges based on the ssi method. this paper will combine the bridge seismic design theory based on vulnerability analysis with ssi method against the problems of traditional methods. it introduces the seismic vulnerability analysis method of bridges.key words: the seismic vulnerability analysis;soil-structure interaction(ssi); fema440; response spectrum method中图分类号:u442.55 文献标识码:a 文章编号:桥梁脆弱性分析也称为桥梁易损性分析,是通过绘制桥梁结构的脆弱性曲线来判别桥梁脆弱性的一种方法。
考虑地基土体参数空间变异性隔震结构的SSI效应可靠性分析

第 36 卷第 5 期2023 年10 月振 动 工 程 学 报Journal of Vibration EngineeringVol. 36 No. 5Oct. 2023考虑地基土体参数空间变异性隔震结构的SSI效应可靠性分析方泓杰1,刘禹彤2,张丰宇1,吴应雄1(1.福州大学土木工程学院,福建福州 350108; 2.深圳市华阳国际工程设计股份有限公司,广东深圳 518000)摘要: 土体弹性模量的空间变异性不仅影响输入地震波的特性,考虑SSI效应后还会增加隔震结构动力响应的随机性,影响结构的可靠度。
为探究土体弹性模量的空间变异性对隔震结构地震动力响应的影响,将随机场模拟技术与有限元分析结合,实现基于蒙特卡罗模拟的动力“非侵入”随机有限元计算。
以典型大底盘隔震结构振动台试验为例,进行确定性与随机有限元分析,计算结构相关响应参数,并使用AIC(Akaike Information Criterion)准则判定响应参数的最优边际分布。
结果表明:考虑土体参数空间变异性后,不均匀软土对低频率地震波幅值的放大效应比均质软土更加明显,傅氏谱的峰值增大约14.2%,且谱值分布整体向低频集中;确定性分析低估了SSI效应对隔震结构隔震层加速度的放大作用及隔震层以上楼层的位移响应;经AIC准则检验,使用正态或对数正态分布描述数据的分布并不总是可靠的,需判定最优的拟合边际分布,从而为结构隔震提供更加合理的设计依据。
关键词: 层间隔震; SSI效应;地基空间变异性;随机有限元法中图分类号: TU352.12; TU317.1 文献标志码: A 文章编号: 1004-4523(2023)05-1380-10DOI:10.16385/ki.issn.1004-4523.2023.05.022引言考虑桩⁃土⁃结构相互作用(SSI效应)时,地基土体特性对于结构动力响应的影响不容忽视,其主要体现在土体对地表峰值加速度的放大[1]及系统自振周期的延长[2]两方面。
SSI效应对邵华大桥动力特性及地震响应影响分析

SSI效应对邵华大桥动力特性及地震响应影响分析作者:陈亮辉来源:《卷宗》2018年第30期摘要:本文主要通过等代土弹簧m法来初步研究SSI效应对邵华大桥的动力特征及地震响应影响,通过midas试算考虑SSI效应和没考虑SSI效应的两个模型,分析计算结果对比的出SSI效应对邵华大桥的结构响应影响趋势。
理解SSI效应在结构地震响应分析中的影响程度。
关键词:等代土弹簧法;自锚式悬索桥;动力特性分析地震波通过对土体传播再通过土体与结构相互作用传递给结构,使结构产生震动响应。
从地震波对结构作用的路径可以看出,考虑土-结构相互作用(Soil Structure Interaction)对结构地震响应的影响是必须的。
SSI影响结构整体变形、应力和动力特性,而且影响程度取决于土体的力学性质和结构的刚度、质量有关。
本文主要用m法来模拟SSI效应,按规范《2008公路桥梁抗震设计细则》中建议用等代土弹簧法考虑SSI效应的方法,模拟SSI效用对邵华大桥的结构动力响应影响,分析SSI效应对结构动力特性变化及地震响应结果的影响。
1 结构模型邵华大桥位于湖南省湘潭市岳塘区,本桥主桥为(44.76+168+228+45+44.68)m独塔自锚式悬索桥,主梁采用混合梁,主跨采用钢箱梁,锚跨和副跨采用混凝土,桥面全宽39.5米。
用Midas Civil建立模型,其中索单元采用受拉单元模拟外,其余结构采用梁单元模拟。
支座单元采用滞后系统来模拟,刚混连接段采用组合截面,对于m法的模拟采用节点弹性支承来模拟。
1.1 计算方法与公式推导KH,KZ分别为等代土弹簧的水平刚度和竖向刚度,为土层厚度,为桩的计算宽度。
1.2 参数计算全桥桩位所在土质基本为单层微风化泥质粉砂岩,根据规范《公路桥涵地基与基础设计规范》给定范围并考虑动力影响放大两倍后,m和m0取值为20000KN/m4,由规范算出bp取值,各取值由下表列出。
2 地震动输入及计算结果分析通过规范查找出邵华大桥所在桥址的地震动峰值加速度为0.05g,反应谱特征周期0.35s,地震基本烈度以VII度设防,地震波选用1952,Hollywood Storage P.E.,270 Deg,该波峰值发生13.3s左右出现峰值为0.0592g,接近桥址场地地震峰值,持续时间78.62s。
考虑SSI_效应的框架-摇摆墙结构响应数值计算研究

第 39 卷第 3 期2023 年6 月结构工程师Structural Engineers Vol. 39 , No. 3Jun. 2023考虑SSI效应的框架-摇摆墙结构响应数值计算研究何东毅1,*李培振1,2(1.同济大学结构防灾减灾工程系,上海 200092; 2.同济大学土木工程防灾国家重点实验室,上海 200092)摘要采用理论模型计算了考虑土-结构相互作用(SSI)效应的框架-摇摆墙结构的地震响应。
所提出的模型可以在结构初步设计完成后,进行结构响应及参数设定的分析验证。
根据所提出的理论模型,对固定地基的框架结构(RF)、考虑SSI效应的框架结构(SF)、固定地基的框架-摇摆墙结构(RW)以及考虑SSI效应的框架-摇摆墙结构(SW)四种模型进行了时域分析,并考虑了5种不同的土性。
结果表明,SSI效应会增大框架-摇摆墙结构的响应,框架-摇摆墙结构对土体条件变化的敏感度比框架结构更高。
因此,在框架-摇摆墙结构的抗震设计中,需要考虑SSI效应。
如果不能准确地确定地基特性,可能会导致对响应的错误评估。
关键词土-结构相互作用,框架-摇摆墙结构,动力时程分析Numerical Study on Response of Rocking Wall-Frame StructuresConsidering Soil-Structure InteractionHE Dongyi1,*LI Peizhen1,2(1.Department of Disaster Mitigation for Structure,Tongji University, Shanghai 200092, China;2.State Key Laboratory for Disaster Reduction in Civil Engineering,Tongji University, Shanghai 200092, China)Abstract In this paper, a theoretical model is used to calculate the seismic response of a rocking wall-frame structure considering soil-structure interaction (SSI). The proposed model can be used to analyze and verify the structural response and parameter setting after the preliminary design of the structure completed. In this paper,four models of frame structure on the fixed foundation (RF),the flexible foundation with SSI effect (RW), rocking wall-frame structure on the fixed foundation (SF) and the flexible foundation with SSI effect (SW)are analyzed in time domain. Five different soil properties are considered. The results show that SSI effect may increase the response of the rocking wall-frame structure, and with the rocking wall attached, the structure is more sensitive to soil condition changes than the frame structure. Therefore,SSI effect must be considered in the seismic design of the rocking wall-frame structure. If the foundation characteristics cannot be accurately determined, it may lead to the wrong evaluation of the response.Keywords soil-structure interaction, rocking wall-frame structure, dynamic time history analysis0 引言土与结构相互作用(Soil-Structure Interaction,简称SSI)是地震工程长久以来一直讨论的话题。
考虑SSI效应的输电塔-线耦合系统抗震可靠度分析

第50 卷第 11 期2023年11 月Vol.50,No.11Nov. 2023湖南大学学报(自然科学版)Journal of Hunan University(Natural Sciences)考虑SSI效应的输电塔-线耦合系统抗震可靠度分析王磊1,李正良1,2,王涛3,4†[1.重庆大学土木工程学院,重庆 400045;2.山地城镇建设与新技术教育部重点实验室(重庆大学),重庆 400045;3.哈尔滨工业大学交通科学与工程学院,黑龙江哈尔滨 150040;4.哈尔滨工业大学哈尔滨工业大学重庆研究院,重庆 401151]摘要:为研究输电塔在土结相互作用(Soil Structure Interactions, SSI)和塔-线耦合作用影响下的抗震可靠度,提出了考虑SSI效应的输电塔-线耦合系统抗震可靠度分析方法. 建立考虑SSI效应的输电塔-线耦合系统简化力学模型,推导其在随机地震作用下的运动方程. 基于随机函数-谱表示方法模拟随机地震动加速度时程,对耦合系统进行随机地震动力响应分析. 以基于GF-偏差点集的样本分数矩最大熵法估计随机地震响应极值分布,并求解耦合系统抗震可靠度. 选取工程中某特高压输电塔-线体系作为研究对象,对本文方法的有效性进行验证. 结果表明,当塔底地基土为软弱土时,考虑SSI效应后,塔顶位移响应极值增大约46.59%,加速度响应极值增大约17.43%,结构失效概率增加约70.32%. 考虑塔-线耦合作用后,塔顶位移响应极值减小约0.51%,加速度响应极值增大约1.74%,结构失效概率减小约15.71%. 对于考虑SSI效应的输电塔-线耦合系统,塔底地基土越软,塔顶位移与加速度响应极值越大. 与蒙特卡洛法相比,本文方法求解的结构失效概率最大误差仅为9.97%,具有较高的精度和计算效率.关键词:输电塔;土结相互作用;塔线耦合作用;抗震可靠度;分数矩中图分类号:TM753;文献标志码:ASeismic Reliability Analysis of Transmission Tower-line Coupling SystemConsidering SSI EffectWANG Lei1,LI Zhengliang1,2,WANG Tao3,4†[1.School of Civil Engineering, Chongqing University, Chongqing 400045, China;2.Key Laboratory of New Technology for Construction of Cities in Mountain Area (Chongqing University), Ministry of Education,Chongqing 400045, China;3.School of Transportation Science and Engineering, Harbin Institute of Technology, Harbin 150040, China;4.Chongqing Research Institute of Harbin Institute of Technology,Harbin Institute of Technology,Chongqing 401151, China]∗收稿日期:2022-12-28基金项目:国家自然科学基金国际(地区)合作与交流项目(51611140123), International(Regional)Cooperation and Exchang Program of the National Natural Science Foundation of China (51611140123);国家电网有限公司科技项目(5200-202156071A-0-0-00),Science and Technology Project of State Grid Corporation(5200-202156071A-0-0-00)作者简介:王磊(1999―),男,河南安阳人,重庆大学博士研究生† 通信联系人,E-mail:***************.cn文章编号:1674-2974(2023)11-0192-12DOI:10.16339/ki.hdxbzkb.2023138第 11 期王磊等:考虑SSI效应的输电塔-线耦合系统抗震可靠度分析Abstract:To investigate the seismic reliability of transmission towers under the influence of Soil Structure Interactions (SSI) and tower-line coupling effect, a seismic reliability analysis method of transmission tower-line coupling system considering the SSI effect was proposed. Firstly, a simplified mechanical model of the transmission tower-line coupling system considering the SSI effect was developed,and the dynamic equation under stochastic seismic excitation was derived. Secondly, the random function-spectrum representation model was used to generate random seismic acceleration time-history samples,and the seismic dynamic response of the coupling system was analyzed. Thirdly,the maximum entropy and fractional moments based on GF-discrepancy points were used to predict the distribution function of the extreme-value variable of random seismic response, and the coupling system’s seismic reliability was solved. Finally, the effectiveness of the proposed method was verified through a transmission tower-line system from an actual project. The results show that: When the foundation soil category is type Ⅳ, after considering the SSI effect,the maximum vertex displacement and acceleration increase by 46.59% and 17.43%,respectively, and the failure probability increases by 70.32%. When considering the tower-line coupling effect, the maximum vertex displacement is reduced by 0.51%, the maximum vertex acceleration increases by 1.74%, and the failure probability is reduced by 15.71%;For the transmission tower-line coupling system considering the SSI effect,the foundation soil becomes softer,and the maximum vertex displacement and acceleration become larger. Compared with results using Monte Carlo Simulation (MCS), the maximum relative error of the proposed method is 9.97%. The proposed method has high accuracy and efficiency.Key words:transmission tower;soil structure interactions;tower-line coupling effect;seismic reliability;frac⁃tional moment输电线路作为重要的生命线工程,其安全运行是保证国家经济发展与人民幸福生活的基础. 随着我国电力行业的快速发展,电网布设范围更加广泛,输电线路不可避免地跨越地震频发区[1]. 近年来,国内外已有多起地震引发的输电线路破坏事故[2],这些事故不仅影响人们的正常生活,也使各国经济遭受巨大损失. 因此,为保障电力系统正常运行以及地震灾后恢复,有必要对输电线路的抗震性能展开研究.在以往输电塔设计中,通常假设地基土为刚性,导线作用则等效为静力荷载施加于塔体,当输电线路承受地震荷载时,上述假设下的结构计算响应与实际情况之间往往有较大误差[3]. 在输电塔抗震设计中,若忽略土结相互作用以及塔线耦合作用,可能会低估结构响应,造成工程安全隐患. 为此,国内外学者对考虑两种作用的输电塔结构抗震分析进行了大量的研究,并提出了相应的力学模型[4-8]. 然而,上述研究多为确定性分析,实际地震动过程具有很强的随机性,考虑到地震不确定性,从概率的角度对考虑SSI效应的输电塔-线耦合系统进行抗震可靠度分析,对结构抗震设计及地震风险评估都具有重要意义.1984年,Peyrot等[9]提出了基于可靠度的输电塔设计,此后,各国学者对输电线路的可靠度展开研究. Natarajan等[10]将风荷载与构件抗力视为随机变量,对输电塔体系进行可靠度分析.俞登科等[11]基于等效随机静风荷载模型,考虑荷载随机性,采用矩方法分析特高压输电塔的抗风体系可靠度.熊铁华等[12]建立覆冰荷载作用下输电塔失效模式的识别方法,并将所有的失效模式组成一个串联系统,计算覆冰荷载下输电塔-线体系可靠度.孔伟等[13]考虑覆冰厚度和风速的随机性,对大风覆冰工况下的输电塔可靠度进行分析.熊铁华等[14]则将覆冰厚度、风速以及材料强度均视为随机变量,采用响应面法模拟输电杆塔构件极限状态方程,并对构件可靠度进行求解. 白海峰等[15]提出一种输电塔风致疲劳可靠度分析及疲劳寿命的预测方法. 以上研究主要关注风荷载以及覆冰荷载作用下的输电塔可靠度分析. 此外,亦有学者对输电塔抗震可靠度展开研究,例如,刘玉龙等[16]根据实测资料,得到地震反应谱法中特征周期和地震影响系数最大值的概率分布及相关系数,考虑以上两参数随机性,对输电塔进行抗震可靠度分析.黄帅等[17]运用正交展开方法得到随机地震动,193湖南大学学报(自然科学版)2023 年并基于概率密度演化理论,进行输电塔顺线方向的抗震可靠度分析. 总体而言,学者对输电塔抗震可靠度的研究仍然较少,考虑SSI 效应的塔-线体系抗震可靠度更鲜有涉及.本文提出了随机地震激励下考虑SSI 效应的输电塔-线耦合系统抗震可靠度分析方法. 首先,建立耦合系统的简化力学模型;其次,以随机函数-谱表示方法生成随机地震动,并基于简化力学模型计算结构响应极值;最后,采用基于GF-偏差点集的样本分数矩最大熵法重构等价极值事件概率密度函数,并求解系统抗震可靠度. 以一实际算例证明了本文方法具有较高的精度和计算效率.1 考虑SSI 效应的输电塔-线耦合系统简化力学模型1.1 输电塔-线体系简化模型现有输电塔-线体系简化模型中,较为典型的是如图1所示的输电塔-线体系多质点力学模型[4]. 该模型将输电塔简化为串联多自由度体系,导线简化为集中质点,导线在塔-线体系侧向振动和纵向振动中分别等效为锤链和悬索. 如图1(b )所示,在塔-线体系侧向振动模型中,输电塔可简化为N 个集中质点,即m 1,m 2,…,m j ,…,m N ,单层导线可简化为2个锤链,即m A i 、m B i ,若塔-线体系具有n 层导线,则该模型具有2n +N 个自由度,其振动为弹性-重力耦联振动.经推导,可得输电塔-线体系随机地震作用下的侧向振动运动方程为:Mu+Cu +Ku =-MIu g (1)式中:u 为侧向振动位移向量;u 为速度向量;u 为加速度向量;u g 为随机地震动加速度;I 为单位向量;M 、K 和C 分别为质量矩阵、刚度矩阵和阻尼矩阵.刚度矩阵K 可表示为:K =éëêùûúK L K LT K TLT K T (2a )式中:K L =diag [K 1L ⋯K i L ⋯K n L ]2n ×2n(2b )K LT =éëêêêêêêùûúúúúúú0⋯0000K 1LT ⋮⋮⋮⋮⋮⋮0⋯00K i LT 00⋮⋮⋮⋮⋮⋮0⋯K n LT 0002n ×N(2c )K T =éëêêêêêêùûúúúúúúk'1.1⋯k 1.j ⋯k 1.N ⋮⋮⋮k j .1⋯k'j .j ⋯k j .N ⋮⋮⋮k N .1⋯k N .j⋯k'N .N N ×N(2d )K i L=éëêùûúk iAAk i AB k i BAk i BB (2e )K iLT =éëêê0-()m A i +m B i g h +h 2ùûúúT(2f )式中:k i AA =m A ig h 1(2g )k i BB =m A i gh 1+()m A i +m B i g h +h 2(2h )k i AB=k i BA =-m A igh 1(2i )k ′j ,j =k j ,j +()mA i+m B i gh +h 2(2j )式中:h 为绝缘子长度;h 1与h 2定义见图1;k j ,j 为输电塔刚度系数,可采用输电塔-线体系空间有限元模型,通过自由度静态缩聚的方法获得.式(1)中,质量矩阵M 采用集中质量矩阵,阻尼矩阵C 采用瑞雷阻尼矩阵,其表达式分别为:M =diag [m A1 m B1⋯m A i m B i ⋯m A n m B n m 1⋯m j ⋯m N ](3)C =αM +βK(4)式中:α=2ξω1ω2/(ω1+ω2);β=2ξ/(ω1+ω2);ξ为阻尼比;ω1、ω2为输电塔前两阶频率,可由输电塔空间有限元模型模态分析得到.1.2 下部结构简化模型本文将塔底基础简化为具有等效质量m 0和等效转动惯量I 0的集中质点.在土结相互作用的计算中,(a )纵向振动(b )侧向振动图1 输电塔-线体系简化模型Fig.1 Simplified model of tower-line system194第 11 期王磊等:考虑SSI效应的输电塔-线耦合系统抗震可靠度分析集中参数模型计算简单,应用方便,本文采用S-R(Swaying-Rocking)模型来考虑地震作用下地基土对结构动力响应的影响,且不考虑结构竖向振动. 该模型在基础平动方向和转动方向均设置弹簧和阻尼器,弹簧及阻尼参数由阻抗函数确定[18]:K S=8ρV2S r2-v,C S=4.6ρV S r22-v(5)K R=8ρV2S r33()1-v,C R=0.4ρV S r41-v(6)式中:K S、K R分别为水平振动和摇摆振动的刚度阻抗;C S、C R为相应的阻尼阻抗;ρ为土体质量密度;v为土体泊松比;V S为土体剪切波速;r为基础底板等效半径,若等效基础为圆形基础,等效面积为A0,等效转动惯量为I0,则对于平动,r=(A0/π)1/2,对于转动,r=(4I0/π)1/4. 参考《建筑与市政工程抗震通用规范》(GB 55002―2021)[19],假设3种地基土体参数如表1所示.1.3 耦合系统运动方程如图2所示,将塔-线体系的多质点模型、基础简化模型和下部地基的弹簧-阻尼模型结合,可建立考虑SSI效应的塔-线耦合系统简化力学模型.基于式(1),可得考虑基础位移的塔-线体系多质点模型侧向振动运动方程:M(u+I u0+hθ0)+Cu+Ku=-MIu g(7)式中:u0与θ0分别为基础相对地面的平动加速度和转动加速度;矩阵h计算式见式(11g);其他符号的含义同式(1).建立基础塔-线体系多质点模型的水平力平衡方程和关于过基础形心轴的力矩平衡方程:∑k=12n+N m k()uk+u g+u0+h kθ0+m0(u g+u0)+V0=0(8)∑k=12n+N m k(u k+u g+u0+h kθ0)h k+(∑k=02n+N I k)θ0+M0=0(9)式中:m k、h k、ük和I k分别代表塔-线体系中第k个质点的质量、离地高度、相对加速度以及绕基础形心轴的转动惯量;m0为基础等效质量;I0为基础等效转动惯量;V0和M0分别为地基土与基础之间的相互作用的剪力和力矩,其可表示如下[20]:éëêùûúV0M0=éëêêùûúúK S00K Réëêùûúu0θ0+éëêêùûúúC S00C Réëêêùûúúu0θ0(10)式中:u0与θ0分别为基础相对地面的平动位移和转动位移;K S、C S由式(5)确定;K R、C R由式(6)确定.联立式(7)~式(10),可得考虑SSI效应的塔-线耦合系统运动方程:M Z U(t)+C Z U(t)+K Z U(t)=P(t)(11a)式中:M Z=éëêêêêêêùûúúúúúúM m mhm T m0+∑k=12n+N m k∑k=12n+N m k h k()mh T∑k=12n+N m k h k∑k=02n+N()Ik+m k h2k(11b)K Z=éëêêêêùûúúúúK0()2n+N×10()2n+N×101×()2n+N K S001×()2n+N0K R(11c)C Z=éëêêêêùûúúúúC0()2n+N×10()2n+N×101×()2n+N C S001×()2n+N0C R(11d)P(t)=-[m A1m B1⋯m A i m B i⋯m A n m B n m1⋯m j⋯mN∑k=12n+N m k∑k=12n+N m k h k]T u g(t)(11e)表1 土体参数Tab.1 Parameters of different soil types土体类型Ⅳ(软弱土)Ⅲ(中软土)Ⅱ(中硬土)剪切波速/(m∙s-1)100200400土层泊松比0.490.400.30土体密度/(kg∙m-3)1 8001 9002 000图2 考虑SSI效应的输电塔-线耦合系统简化力学模型Fig.2 Simplified mechanical model of transmission tower-linecoupling system considering SSI effect195湖南大学学报(自然科学版)2023 年矩阵m 与h 计算式如下:m =[m A1 m B1⋯m A i m B i ⋯m A n m B n m 1⋯m j ⋯m N ]T(11f )h =[h A1 h B1⋯h A i h B i ⋯h A n h B n h 1⋯h j ⋯h N ]T(11g )2 考虑SSI 效应的输电塔-线耦合系统抗震可靠度分析方法2.1 抗震可靠度分析的等价极值事件对一考虑荷载不确定性的结构体系,其动力响应可表示为包含荷载不确定参数Θ的随机过程. 对于本文提出的考虑SSI 效应的输电塔-线耦合系统简化力学模型,动力位移响应U i (Θ,t )控制下的结构整体失效概率可表示为:P f =1-Pr{∩i =1n ()U i ()Θ,t <U ∗ ∀t ∈(0,T)}(12)式中:Pr 表示概率;U *为位移阈值;T 为荷载持续时间. 对式(12)直接求解较为困难,可基于等价极值事件的思想[21],构造一个等价极值事件:U e =max1≤i ≤n{max t ∈()0,T{|U i(Θ,t )|}}(13)式(12)可转化为:P f =1-Pr {U e <U ∗}(14)若等价极值事件U e 的概率密度函数为f U e(u ),则结构失效概率可进一步表示为:P f =∫U*∞f U e()u d u(15)本文基于随机函数-谱表示方法模拟随机地震动,采用基于GF-偏差点集的样本分数矩最大熵法估计等价极值事件U e 的概率密度函数,进而分析考虑SSI 效应的塔-线耦合系统抗震可靠度.2.2 基于随机函数-谱表示方法的平稳随机地震动过程基于随机过程的演变谱表示理论,平稳随机地震动过程üg (t)可表示为[22]:u g (t )=∑k =1N 2S U ()ωk Δω[cos ()ωk t X k +]sin ()ωk t Y k(16)式中:{X k ,Y k }为一组标准正交随机变量;ωk 为圆频率;Δω为频率间隔;ωk =k Δω,k =1,2,…,N ;S U (ωk )为随机地震动过程üg (t)的双边功率谱密度函数.基于式(16)的随机过程演变谱表示方法,文献[22]用随机函数来构造标准正交随机变量,降低了问题维度,提高了随机过程的模拟效率. 当采用单个随机变量构造随机函数时,有[22]:X ˉn =2cos (nΘ+α)Yˉn =2sin (nΘ+α),n =1,2,⋯,N(17)式中:随机变量Θ服从区间[-π,π]上的均匀分布;α为常数,可取π/4. 通过一定的选点方法得到随机变量Θ的样本值,代入式(17),得到一组随机数{X ˉn ,Y ˉn },n =1,2,…,N ,由{X ˉn ,Y ˉn }与式(16)中{X k ,Y k }的映射关系,得到一组正交随机数{X k ,Y k },k =1,2,…,N ,代入 式(16),即可获得平稳随机地震动过程üg (t )基于随机函数-谱表示的结果.2.3 基于GF-偏差点集的样本分数矩最大熵法传统的分数矩最大熵法采用单变量降维进行分数矩估计[23],其计算精度受功能函数形式的影响,难以广泛地适用于复杂工程问题. 因此,本文发展了一类基于GF-偏差点集的样本分数矩最大熵法,进行考虑SSI 效应的输电塔-线耦合系统抗震可靠度分析.2.3.1 基于GF-偏差点集的极值变量分数矩估计对于式(13)定义的等价极值事件U e ,其α阶分数矩可表示如下:M αU e=∫Ωu a f U e()u d u(18)式中:α为任意实数;f U e(u )为变量U e 的概率密度函数;Ω为变量U e 分布域.将变量u a 在常数c 处进行泰勒(Taylor )展开可得:u a=∑i =0∞()αic α-i(u -c )i(19)式中:()αi=α()α-1⋯()α-i +1i ()i -1⋯1为二项式组合系数.对等式(19)两边求取期望得:E [Ua e]=∑i =0∞()αic α-i E [(U e -c)i](20)由式(20)可知,变量的任意阶分数矩包含了无穷整数矩信息,因此,少量分数矩即可刻画变量的概率分布特征,包括尾部信息.根据式(18),变量U e 的各阶分数矩可采用样本值进行估计,即M αU e=1N ∑i =1N [u ()i ]α(21)式中:u (i )(i =1,2,…,N )为变量U e 的样本点.196第 11 期王磊等:考虑SSI 效应的输电塔-线耦合系统抗震可靠度分析为了精确地估计变量U e 的分数矩,本文采用文献[24]提出的GF-偏差点集选取样本点. 具体地,若Ψn ={u q =(u q ,1,u q ,2,…,u q ,k ), q =1,2,…,n }为一个k 维点集,则其GF-偏差定义为:D GF (Ψn )=max 1≤i ≤k{D F ,i (Ψn)}(22)式中:D F ,i(Ψn)=sup u ∈R|F n ,i(u )-F i(u )|为第i 个随机变量U i 的边缘偏差,其中 F i (u )为U i 的边缘概率分布函数,F n ,i(u )为考虑赋得概率影响的边缘经验分布函数,其算式为:F n ,i (u )=∑q =1nP q ⋅I {}u q ,i ≤u (23)式中:u q ,i 是u q 的第i 个分量;P q 是点u q 的赋得概率. GF 偏差越小,点集越佳. 有关GF-偏差点集的详细内容可参考文献[24].2.3.2 样本分数矩最大熵法对于变量U e ,若其概率密度函数为f U e(u ),其信息熵定义为:H [U e ]=-∫f U e()u ln f U e(u )d u(24)以变量U e 的熵取最大值为目标函数,以其分数矩M αkU e,k =1,2,…,m 为约束条件,可建立优化模型[23]:ìíîïïïïïïïïïïïïFind : f U e()u max : H []U e =-∫f U e ()u ln f U e()u d u s.t. ∫f U e()u d u =1 ∫u αk f U e ()u d u =M αkU e()k =1,⋯,m (25)引入Lagrange 乘子,将上述优化模型转化为无约束优化模型,定义Lagrange 函数如下:L [λ,α,f U e(u)]=-∫f U e ()u ln f U e(u )d u - (λ0-1)éëê∫f U e()u d u -1ùûú- ∑k =1mλk éëê∫u αkf U e()u d u -M αkU eùûú(26)式中:λ=[λ0,λ1,⋯,λm ]T为Lagrange 乘子向量;α=[α0,α1,⋯,αm]T为分数矩的阶次向量.上述无约束优化问题在其最优解处需满足∂L [λ,α,f U e(u)]/∂(f U e(u ))=0,从而可得f U e(u )的估计表达式:f U e(u )=exp (-λ0-∑k =1mλk u αk)(27)式中:λ0为信息熵概率密度函数归一化参数,其计算式如下.λ0=ln éëêê∫exp (-∑k =1mλk u αk)d u ùûúú(28)K-L 偏差可衡量真实概率密度函数f U e(u )和估计式f U e(u )之间的差异,以K-L 偏差最小作为优化目标,可建立熵概率密度参数的无约束优化模型[23]:ìíîïïïïFind :α=[]α1,α2,⋯,αm T , λ=[]λ1,λ2,⋯,λm Tmin :ln éëêêùûúú∫exp ()-∑k =1m λk u αkd u +∑k =1m λk M αkU e(29)通过数值算法求解式(29)的优化问题,得到参数λ与α的最优解,将计算结果代入式(27),可求得变量U e 的概率密度函数的估计式.3 算例分析3.1 工程概况本文以某特高压交流输变电线路的直线塔为 研究对象,考虑SSI 效应和塔-线耦合作用,对其抗震可靠度进行分析. 直线塔总高108 m ,呼高60 m ,塔腿根开20.2 m ,其平面尺寸如图3所示. 输电线路挡距为600 m ,单跨线路含有4层8根导、地线.导、地线通过悬垂绝缘子与输电塔相连,导、地线悬垂绝缘子长度分别为13 m 和0.6 m ,导线单位长度质量为2.06 kg/m ,地线单位长度质量为1.747 kg/m. 塔底基础为独立基础,各塔腿下的独立基础尺寸为6 m×6 m×1.2 m.3.1.1 上部结构简化塔-线体系有限元模型如图4所示,将输电塔简化为11个集中质点,输电塔各集中质点的高度和质量如表2所示.每层导、地线简化为2个锤链,由于悬垂绝缘子的重量较大不能忽略,导、地线的上下锤链质量不同,上锤链质量m B 等于导、地线一半质量加上悬垂绝缘子质量,下锤链质量m A 等于导、地线一半的质量.经计算,对于地线,m B =1 148 kg ,m A =1 048 kg ;对于导线,m B =7 236 kg ,m A =1 236 kg.为求解输电塔刚度系数k j ,j 和输电塔前2阶频率197湖南大学学报(自然科学版)2023 年ω1、ω2,运用有限元软件ANSYS 建立输电塔-线体系有限元模型(图4). 塔体杆件采用BEAM188梁单元模拟,因杆件连接方式均为法兰连接,将杆件密度均除以0.75来考虑该连接对质量的影响;输电线和绝缘子均采用LINK10杆单元来模拟,输电线远端和输电塔底端均采用固结模拟.3.1.2 下部结构简化将塔脚下4个独立基础等效为一个圆形基础,耦合系统简化力学模型中基础等效集中质点的位置取圆形基础的圆心,如图5所示. 等效基础面积A 0取独立基础底面积之和,截面惯性矩I 0取独立基础对塔基对称轴的惯性矩之和,计算得基础等效质量m 0=449 280 kg ,等效面积A 0=144 m 2,等效惯性矩I 0=47 232 806.4 kg·m 2,基础平动等效半径为6.77 m ,基础转动等效半径为11.78 m. 将不同地基土土体参数及基础等效半径代入式(5)和式(6),可得土体等效刚度和等效阻尼,如表3所示. 由表3可知,土体越软,其等效刚度和等效阻尼值越小.3.2 随机地震动模拟基于随机函数-谱表示方法,模拟随机地震动加速度时程. 考虑Clough-Penzien 谱[25]:图4 塔-线体系有限元模型Fig.4 Finite element model of the transmissiontower-line system图3 直线塔平面尺寸(单位:mm )Fig.3 Dimension of the suspension tower (unit :mm )表2 直线塔计算参数Tab.2 Calculate parameters of the suspension tower集中质点1234567891011高度/m 19.531.540.548.555.064.573.081.590.699.2108.0质量/kg 29 19820 25310 6288 9487 75317 8977 2199 51213 4534 53016 842图5 塔底等效基础Fig.5 Equivalent foundation of the transmission tower表3 土体等效刚度和等效阻尼Tab.3 Equivalent stiffness coefficient and dampingcoefficient of soil土体类型ⅣⅢⅡK S6.456×1082.573×1091.019×1010K R1.539×10115.522×10111.993×1012C S2.513×1075.007×1079.921×107C R2.719×1094.878×1098.803×109198第 11 期王磊等:考虑SSI 效应的输电塔-线耦合系统抗震可靠度分析S (ω)=ω4g +4ξ2g ω2g ω2()ω2-ω2g2+4ξ2gω2gω2×ω4()ω2-ω2f2+4ξ2fω2fω2S 0(30)式中:S (ω)为双边功率谱;ωg 、ξg 分别为场地土的卓越圆频率和阻尼比;ωf 、ξf 分别为基岩的卓越圆频率和阻尼比;S 0为谱强度因子,其计算式如下.S 0=a 2maxr 2éëêêùûúúπωg ()2ξg +12ξg(31)式中:a max 为地震动峰值加速度;r 为峰值因子.本算例中,考虑抗震设防烈度8度,场地类别Ⅳ类,设计地震分组为第2组,设计基本地震加速度0.2g . 基于文献[26],本文的功率谱参数选取如下: ωg =8.38 rad/s ,ξg =0.90,ωf =0.838 rad/s ,ξf =0.90,r =2.60,a max =200 cm/s 2. 在地震动随机过程的谱表达中,参数ωu =240 rad/s ,Δω=0.15 rad/s ,N =1 601,T =20 s ,Δt =0.01 s ,满足Δt <π/ωu .基于GF-偏差点集选取式(17)中随机变量Θ的样本点,选点总数为500. 根据式(17)的结果及映射方式,得到式(16)中标准正交随机变量的确定性取值,并模拟生成500条随机地震动加速度时程样本.图6为随机地震动加速度时程代表样本;图7为样本均值和标准差,其吻合度良好;图8为样本均值功率谱与目标值,其吻合程度也较为理想.3.3 典型随机地震动样本的耦合系统动力响应分析采用随机函数-谱表示方法模拟生成随机地震动后,将随机地震动加速度沿垂直于导线方向作用于耦合系统. 采用第1节所述方法,考虑地基土类型为Ⅳ类(软弱土),分别建立单塔、单塔地基、塔-线、塔-线地基4种体系的侧向振动简化模型. 基于图6,采用Newmark-β积分法进行动力时程分析. 各体系塔顶位移与加速度最大值的结果如表4所示,图9和图10分别为不同体系塔顶位移和加速度时程曲线.图6 随机地震动加速度时程代表样本Fig.6 Representative sample of stochastic seismicacceleration process(a )均值(b )标准差图7 样本均值和标准差Fig.7 The mean and standard deviation of samples图8 样本均值功率谱与目标值Fig.8 The mean power spectral density of samplesand target values表4 塔顶位移与加速度最大值(不同体系)Tab.4 The maximum value of vertex displacement andacceleration (different systems )体系单塔单塔地基塔-线塔-线地基X max /m0.254 80.373 50.253 50.364 2位移差值/%―46.59-0.5142.94a max /(m·s -2)10.496 912.326 410.679 712.318 3加速度差值/%―17.431.7417.35199湖南大学学报(自然科学版)2023 年由表4和图9可知,当塔底地基土为软弱土时,单塔考虑SSI 效应后,塔顶最大位移增大46.59%,且塔顶位移时程曲线形状与单塔体系明显不同;单塔考虑塔-线耦合作用后,塔顶最大位移减小0.51%,位移时程曲线形状与单塔体系基本相同. 在随机地震作用下,当地基土较软时,土结相互作用对输电塔的位移响应影响较大,在塔体抗震设计中不易忽视,而塔-线耦合作用对位移响应影响较小,且导线有一定的减震作用.由表4和图10可知,当塔底地基土为软弱土时,单塔考虑SSI 效应后,塔顶最大加速度增大17.43%;单塔考虑塔-线耦合作用后,塔顶最大加速度增大1.74%. 在随机地震作用下,当地基土较软时,土结相互作用对输电塔的加速度响应影响较大,而塔-线耦合作用对加速度响应影响较小.3.4 典型随机地震动样本下不同土体类型对耦合系统动力响应的影响考虑不同的地基土工况,基于图6随机地震动加速度时程代表样本,对耦合系统进行动力时程分析. 表5为不同工况下,耦合系统塔顶位移与加速度的最大值结果,图11和图12分别为不同工况耦合系统塔顶位移和加速度的时程曲线,其中固定端代表塔底地基土为刚性.图11 塔顶位移时程曲线(不同工况)Fig.11 Time history curves of the vertex displacement oftransmission tower (different conditions)图12 塔顶加速度时程曲线(不同工况)Fig.12 Time history curves of the vertex acceleration oftransmission tower (different conditions )表5 塔顶位移与加速度最大值(不同工况)Tab.5 The maximum value of vertex displacement andacceleration (different conditions )工况固定端中硬土中软土软弱土X max /m0.253 50.256 40.262 00.364 2位移差值/%―1.143.3543.67a max /(m·s -2)10.679 710.845 311.273 912.318 3加速度差值/%―1.555.5615.34图9 塔顶位移时程曲线(不同体系)Fig.9 Time history curves of the vertex displacement oftransmission tower (different systems)图10 塔顶加速度时程曲线(不同体系)Fig.10 Time history curves of the vertex acceleration oftransmission tower (different systems )200第 11 期王磊等:考虑SSI效应的输电塔-线耦合系统抗震可靠度分析由表5可知,地基土越软,塔顶位移及加速度响应最大值越大. 观察图11和图12可知,在0~5 s内,不同工况下塔顶位移和加速度响应形状基本一致,幅值也基本相同;在5~20 s内,不同工况下塔顶位移响应时程曲线波形基本一致,但幅值明显不同,地基土越软,幅值越大;在5~20 s内,4种工况的塔顶加速度响应也有明显差别.3.5 耦合系统抗震可靠度分析考虑地基土为软弱土,以输电塔位移响应为控制变量进行耦合系统抗震可靠度分析,塔顶位移响应极值为本文构造的等价极值事件. 以500条随机函数-谱表示方法生成的随机地震动加速度时程样本计算塔顶位移响应极值,采用样本分数矩最大熵法构建极值变量概率密度函数,并基于式(15)求解结构失效概率. 采用单纯形算法求解式(29)的无约束优化问题,在MATLAB中,分别设置拉格朗日乘子λ与分数矩指数α的初始值为随机数“1 000×rand()”和“rand()”. 此外,本文进行106次蒙特卡洛模拟(Monte Carlo Simulation,MCS)计算,用于验证建议方法的有效性. 塔顶位移响应极值的概率密度函数(Probability Density Function,PDF)如图13所示. 不同体系极值变量的PDF如图14所示. 《110~750 kV 架空输电线路设计规范》(GB 50545―2010)[27]规定了悬垂直线自立式铁塔的计算挠度限值为3h/1 000,其中h为杆塔最长腿基础顶面起至计算点高度,计算得塔顶位移阈值为0.324 m,基于构建的概率密度函数求解系统失效概率,计算结果如表6所示.由图13可知,采用本文方法得到的塔顶位移响应极值的概率密度函数与MCS结果吻合良好,尾部刻画精确. 此外,由表6可知,采用本文方法计算的结构失效概率与MCS结果相接近,最大相对误差为9.97%. 且相较于一百万次MCS法,建议方法仅需500次结构分析便可精确求解失效概率,具有较高的计算效率.由图14可知,若塔下地基土为软弱土,当考虑SSI效应时,塔顶位移极值的概率密度函数峰值减小,曲线明显右移,这说明塔顶位移响应增大,系统失效概率上升;而考虑塔-线耦合作用时,概率密度函数峰值增大,曲线轻微左移,这说明塔顶位移响应减小,系统失效概率下降.图15为各体系失效概率相对于单塔的变化幅度.由图15可见,基于本文方法的计算结果,相对于单塔体系,单塔地基、塔-线、塔-线地基的失效概率变化幅度分别为96.72%、-15.71%、70.32%;基于MCS的计算结果,对应的失效概率变化幅度分别为88.48%、-13.61%、68.17%. 由此可知,对于输电塔抗震可靠度,若以塔体位移为控制变量,当塔底地基土较软时,土结相互作用将增加结构失效概率,且幅度较大;而塔-线耦合作用将减小结构失效概率,但幅度较小.(a)单塔(b)塔-线(c)单塔地基(d)塔-线地基图13 塔顶位移响应极值的PDF Fig.13 PDF of extreme value of the vertex displacement oftransmission tower图14 不同体系极值变量的PDF Fig.14 PDF of extreme variable of different systems oftransmission tower表6 不同体系的失效概率Tab.6 Failure probabilities of different systems体系单塔单塔地基塔-线塔-线地基本文方法0.090 0450.177 1430.075 9000.153 367MCS0.097 5870.183 9320.084 3020.164 111相对误差/%7.733.699.976.54201。
隔震结构的抗震效果分析

隔震结构的抗震效果分析郑斌;陈倩【摘要】通过对隔震结构的动力分析和结构特性测试,了解了隔震结构的抗震性能和机理,为隔震设计和应用提供了理论依据,而隔震建筑经历实际地震时的观测数据验证了隔震结构良好的抗震效果。
%According to the dynamic analysis of the isolated structure and the structural feature tests, the study introduces the seismic performance and the mechanism of the isolated structure, provides the theoretic reference for the isolated design and the application, and proves the isolated structure has better seismic effect according to the observatory data of the isolated buildings during factual earthquakes.【期刊名称】《山西建筑》【年(卷),期】2012(038)020【总页数】2页(P38-39)【关键词】隔震结构;抗震;动力分析;结构特性【作者】郑斌;陈倩【作者单位】浙江科技学院土木工程系,浙江杭州310023;浙江科技学院土木工程系,浙江杭州310023【正文语种】中文【中图分类】TU3180 引言相比传统抗震建筑,隔震建筑不仅在震时体现了其优越的抗震性能,也由于其上部结构只产生相对缓慢的平移,而在保护一些重要历史文物、个人财产等方面起到了重要作用,同时还能有效预防二次灾害的发生,并且震后仅需更换隔震装置,建筑物便可重新使用,对震后的恢复工作极为有利。
1 隔震结构动力分析1.1 隔震结构动力分析模型对于基础隔震结构,可将其上部结构视为刚性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Ef e t f So l S r c ur nt r c i n o r h a e f c s o i- t u t e I e a to n Ead S r c u e S s e s ns fI o a e t u t r y t m
Ab t a t Th o g n l z n h a a o h k n a l d lt s s o s l t d s r c u e o i e r u d s r c : r u h a a y i g t e d t fs a i g t b e mo e e t fio a e t u t r n fx d g o n
构 楼 层 加 速 度 反 应 有 明 显 影 响 ,S 效 应 使 隔 震 结 构 按 层 加 速度 放 大 倍 数 较 刚性 地 基 时增 大 。楼 层 加 速 度 组 成 SI
分 量 中隔 震 层 转动 引起 的摆 动 分 量是 导 致 土 性 地 基 上 隔 震 结 构 楼 层 加 速 度 反 应 增 大 的主 要 因 素之 一 。 关 键 词 : 动 台模 型 试 验 ;隔震 结构 ;土一 构相 互 作 用 ;地 震 振 结 中图 分 类 号 : TU3 1 1 文献标识码 : A 文 章 编 号 : 0 52 1 (0 1 0— 8 60 1 0— 6 5 2 1 )60 4 —6
S I效 应 对 隔震 结 构 地 震 响应 的 影 响 分 析 S
于 旭h 宰金 珉 庄 海 洋。
(.南 京 工 程 学 院 建筑 工 程 学 院 , 京 ,2 0 0 ;.南 京 工 业 大 学 土 木 工 程 学 院 , 京 , 1 1 7 1 南 1 09 2 南 2 1 6)
f u d to t n o s l t d s r c u e a e g e t t e p a a u f f u d to to S s l r t a o n a i n mo i f io a e t u t r r r a . h e k v l e o o n a i n mo i n i ma l h n o e t a ft e fe i l h t o h r e f d,a d t e s e t a o o e to o n a i n mo i n i d fe e t e n h p c r 1 mp n n ff u d to to i r n .Efe t f S n a — c s f f c so Io c S c l r to mp i c t n f c o so l o s o o a e t u t r r i n fc n ,a d t e a c l r t n a l i e e a i n a l i a i a t r f o r fi l t d s r c u e a es g i a t n h c e e a i mp i — f o f s i o f c to a t r ff o s i g e t rt a h s n f e r u d b s .On fma n f c o sl a i g t h c a i n f c o so l r s r a e h n t o e o i d g o n a e o x e o i a t r e d n o t e a -
Yu X u ,ZaiJi m i n ng。 ,Zh n H ai an ua g y g。
( .D p rme to ii E g e r g Na j gI si t f c n lg , nig 1 0 9 Chn ; 1 e at n f vl n i e i , ni n t u eo h oo y Na j ,2 0 0 , ia C n n n t Te n 2 e a t n f ii E gn e ig Na j g Unv r i f e h oo y Na j g 2 1 6 , hn ) .D p r me to vl n ie r , ni ie s y o c n lg , ni , 1 1 7 C ia C n n t T n
摘 要 : 过 对 刚 性 地 基 和 土 性 地 基 上 隔 震 结 构 体 系振 动 台 模 型 试 验 的数 据 进 行 对 比 分 析 , 究 了土一 构 动 力 相 通 研 结 互 作 用 ( S ) 隔震 结 构 地 震 响 应 的影 响规 律 。研 究 结 果 表 明 :S 效 应 对 隔 震 结 构 基 底 地 震 动 影 响 较 大 , 震 S I对 SI 隔 结 构 基 底 地 震 动 的峰 值 小 于 自由 场地 震 动 的 峰 值 , 频 谱 组 成 与 自由 场 地 震 动 不 完 全相 同。S I 应对 隔 震 结 其 S效
t n a t q a e r s o s fioa e tu t r r t d e . Th e ut h w h tefcs o S n i a d e rh u k e p n e o s lt d s r cu ea es u id c e r s ls s o t a fe t fS Io
第 4 卷第 6 3 期
21 年 1 01 2月
南
京
航
空
航
天
大
学
学
报
V0 . 3 No 6 14 .
De . 201 c 1
J u n lo n ig Unv r i fAe o a t s& Asr n u is o r a fNa j ie st o r n u i n y c to a tc
b s n ol r u d b s ,t eefc sp te n f olsr cu eit r cin( SI nd n mi h r c e i— a ea ds i g o n a e h fe t at r so i tu t r n e a to S )o y a cc a a trs s —
