R语言 Markov Switching马尔科夫转化模型 附代码数据
马尔可夫链蒙特卡洛方法及其r实现

马尔可夫链蒙特卡洛方法及其r实现马尔可夫链蒙特卡洛(Markov Chain Monte Carlo,MCMC)方法是一种统计推断方法,主要用于解决难以直接计算的问题。
它的基本思想是通过构造一个马尔可夫链,使其平稳分布为所要求解的分布,然后通过迭代这个马尔可夫链来得到所要求解的分布的样本。
在R语言中,我们可以使用`rstan`包来实现MCMC方法。
下面是一个简单的例子,说明如何使用MCMC方法来估计一个简单模型的参数。
首先,你需要安装和加载`rstan`包:```r("rstan")library(rstan)```然后,定义一个Stan模型。
这里我们使用一个简单的线性回归模型作为例子:model_code <- "data {int<lower=0> N; // number of data pointsvector[N] y; // response variablevector[N] x; // predictor variable};parameters {real mu; // mean of yreal beta; // slope of the regression line};model {y ~ normal(mu, 1); // normal distribution for ymu ~ normal(0, 1); // normal distribution for mu beta ~ normal(0, 1); // normal distribution for beta };"```接着,使用`stan`函数来拟合模型:Generate some fake dataN <- 100 number of data pointsx <- rnorm(N) predictor variabley <- 3x + rnorm(N) response variable with added noiseFit the model using MCMC methodfit <- stan(model_code, data = list(N = N, y = y, x = x))```最后,你可以使用`print`函数来查看模型拟合的结果:```rprint(fit)```这只是一个非常简单的例子。
马尔可夫区制转换向量自回归模型

马尔可夫区制转换向量自回归模型随着大数据时代的到来,统计学和数据科学领域的研究和应用也取得了长足的发展。
马尔可夫区制转换向量自回归模型(Markov regime-switching vector autoregressive model)作为一种重要的时间序列模型,在金融市场预测、宏观经济分析等领域得到了广泛的应用。
本文将对马尔可夫区制转换向量自回归模型进行介绍和分析,包括其基本概念、模型假设、参数估计方法等内容。
一、马尔可夫区制转换向量自回归模型的基本概念马尔可夫区制转换向量自回归模型是一种描述时间序列变量之间动态关系的模型,它考虑了不同时间段内数据的不同特征,并能够在不同状态下描述不同的关系。
具体来说,该模型假设时间序列在不同的时间段内处于不同的状态(或区域),而状态之间的转换满足马尔可夫链的性质,即未来状态的转换仅与当前状态有关,与过去状态无关。
二、马尔可夫区制转换向量自回归模型的模型假设马尔可夫区制转换向量自回归模型的主要假设包括以下几点:1. 状态转移性:时间序列的状态转移满足马尔可夫链的性质,未来状态的转移仅与当前状态相关。
2. 向量自回归性:时间序列变量之间的关系可以用向量自回归模型描述,即当前时间点的向量可以由过去时间点的向量线性组合而成。
3. 区制转换性:时间序列的状态在不同时期具有不同的动态特征,模型需要考虑不同状态下的向量自回归关系。
以上假设为马尔可夫区制转换向量自回归模型的基本假设,这些假设使得模型能够较好地描述时间序列数据的动态演化。
三、马尔可夫区制转换向量自回归模型的参数估计方法马尔可夫区制转换向量自回归模型的参数估计是一个重要且复杂的问题,一般可以通过以下几种方法进行估计:1. 极大似然估计:假设时间序列的概率分布形式,通过最大化似然函数来得到模型参数的估计值。
这种方法需要对概率分布进行合理的假设,并且通常需要通过迭代算法来求解。
2. 贝叶斯方法:利用贝叶斯统计理论,结合先验分布和似然函数,通过马尔科夫链蒙特卡洛(MCMC)等方法得到模型参数的后验分布,进而得到参数的估计值。
r语言马科维茨模型求股票收益率

r语言马科维茨模型求股票收益率(原创实用版)目录1.R 语言简介2.马科维茨模型简介3.使用 R 语言实现马科维茨模型4.应用马科维茨模型求股票收益率5.总结正文1.R 语言简介R 语言是一种功能强大的数据处理和统计分析语言,广泛应用于各个领域,如金融、生物、社会科学等。
R 语言的优势在于其丰富的库和扩展包,可以方便地处理和分析各种类型的数据。
2.马科维茨模型简介马科维茨模型是一种用于投资组合优化的经典模型,由美国经济学家哈里·马科维茨于 1952 年提出。
该模型主要通过计算投资组合的预期收益率和标准差,以最大化收益或最小化风险为目标,为投资者提供有效的投资建议。
3.使用 R 语言实现马科维茨模型在 R 语言中,可以使用诸如“portfolio”和“mvtnorm”等库来实现马科维茨模型。
以下是一个简单的示例:首先,安装并加载所需的库:```Rinstall.packages("portfolio")install.packages("mvtnorm")library(portfolio)library(mvtnorm)```然后,设置投资组合的权重和资产收益率:```Rweights <- c(0.5, 0.3, 0.2)returns <- c(0.1, 0.05, -0.02)```接下来,使用马科维茨模型计算投资组合的预期收益率和标准差:```Rmv_optimal_portfolio <- mvtnorm(returns, weights=weights, type="mean")mv_optimal_portfolio$meanmv_optimal_portfolio$var```4.应用马科维茨模型求股票收益率在实际应用中,我们可以使用马科维茨模型来计算股票的预期收益率。
例如,假设我们有三只股票,其收益率分别为 0.1、0.05 和 -0.02,权重分别为 0.5、0.3 和 0.2。
【原创】R语言数据可视化分析报告(附代码数据)
Vis 3这个图形是用另一个数据集菱形建立的,也是内置在ggplot2包中的数据集。
library(ggthemes)
ggplot(diamonds)+geom_density(aes(price,fill=cut,color=cut),alpha=0.4,size=0.5)+labs(title='Diamond Price Density',x='Diamond Price (USD)',y='Density')+theme_economist()
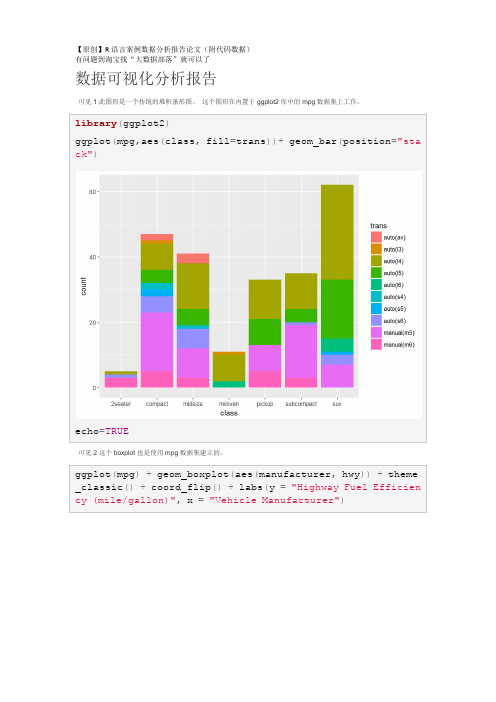
library(ggplot2)
ggplot(mpg,aes(class,fill=trans))+geom_bar(position="stack")
echo=TRUE
可见2这个boxplot也是使用mpg数据集建立的。
ggplot(mpg)+geom_boxplot(aes(manufacturer,hwy))+theme_classic()+coord_flip()+labs(y="Highway Fuel Efficiency (mile/gallon)",x="Vehicle Manufacturer")
echo=TRUE
另外,我正在使用ggplot2软件包来将线性模型拟合到框架内的所有数据上。
ggplot(iris,aes(Sepal.Length,Petal.Length))+geom_point()+geom_smooth(method=lm)+theme_minimal()+theme(panel.grid.major=element_line(size=1),panel.grid.minor=element_line(size=0.7))+labs(title='relationship between Petal and Sepal Length',x='Iris Sepal Length',y='Iris Petal Length')
马尔可夫区制转移模型r语言代码 概述及解释说明

马尔可夫区制转移模型r语言代码概述及解释说明1. 引言1.1 概述马尔可夫区制转移模型是一种常用的数学工具,用于描述系统在不同状态之间的转移规律。
它基于随机过程理论,可以应用于各个领域的研究和实践中。
在本文中,我们将介绍马尔可夫链的概念以及区制转移模型的定义和特点,并重点关注R语言在该模型中的应用。
通过R语言代码的实现,我们可以有效地建立马尔可夫矩阵和状态空间模型,并进行模型训练与参数估计。
1.2 文章结构本文分为五个部分,每个部分都有特定的目标和内容。
以下是各个部分的概要:- 第一部分为引言部分,主要介绍了文章的背景和目的,以及整体结构。
- 第二部分详细介绍了马尔可夫链的概念,并对区制转移模型进行了定义和特点解释。
- 第三部分着重介绍了R语言在马尔可夫区制转移模型中的应用,并逐步讲解了实现过程。
- 第四部分通过选择一个具体案例并导入相关数据集,展示了如何使用R语言代码进行马尔可夫区制转移模型分析。
- 第五部分为结论与展望部分,总结了本文的研究成果,并提出了目前存在的问题以及未来的改进方向。
1.3 目的本文旨在介绍马尔可夫区制转移模型的原理和R语言代码实现过程,帮助读者深入了解该模型,并能够运用R语言进行相关数据分析。
通过实例分析和结果解释,读者可以更好地理解该模型的应用价值和意义。
此外,本文还将探讨当前马尔可夫区制转移模型存在的问题,并展望未来的改进方向,以期为后续研究提供参考。
2. 马尔可夫区制转移模型概述及原理解释2.1 马尔可夫链概念介绍马尔可夫链是一种随机过程,它具有马尔可夫性质,即未来的状态只依赖于当前状态而与过去的状态无关。
马尔可夫链由一组离散的状态以及这些状态之间的转移概率所定义。
在时间步长递进的过程中,通过转移概率可以预测和描述系统从一个状态到另一个状态的演变过程。
2.2 区制转移模型定义和特点区制转移模型是马尔可夫链的一种扩展形式,在传统马尔可夫链中只有一个全局的转移矩阵,而在区制转移模型中,根据不同的时间或空间划分将系统分为多个子区域,并针对每个子区域建立相应的转移矩阵。
【原创】R语言使用马尔可夫链Markov Chain, MC来模拟抵押违约数据分析报告论文(代码+数据)

咨询QQ:3025393450有问题百度搜索“”就可以了欢迎登陆官网:/datablogR语言使用马尔可夫链Markov Chain, MC来模拟抵押违约数据分析报告来源:大数据部落| 有问题百度一下“”就可以了原文/?p=3603这篇文章的目的是将我学习的材料与我的日常工作和R相结合。
如果我们有一些根据固定概率随时间在状态之间切换的对象,我们可以使用马尔可夫链 * 来模拟该对象的长期行为。
一个很好的例子是抵押贷款。
在任何给定的时间点,贷款都有违约概率,保持最新付款或全额偿还。
总的来说,我们将这些称为“转移概率”。
假设这些概率在贷款期限内是固定的**。
咨询QQ:3025393450有问题百度搜索“”就可以了欢迎登陆官网:/datablog举个例子,我们将看一下传统的固定利率30年期抵押贷款。
让我们假设每个当前贷款的时间T有75%的可能性保持最新,10%的违约机会,15%的机会在T + 1时间内获得回报。
这些转换概率在上图中列出。
显然,一旦贷款违约或获得偿还,它将保持默认或支付。
我们称这些国家为“吸收国家”。
咨询QQ:3025393450有问题百度搜索“”就可以了欢迎登陆官网:/datablog由于我们知道转移概率,我们所需要的只是贷款的初始分配,我们可以预测在30年期间任何给定点的每个州的贷款百分比。
假设我们从T = 0开始,有100个当前贷款,0个违约和已付清贷款。
在时间T + 1,我们知道(根据我们的转换概率),这100个中的75个将保持最新的付款。
但是,15笔贷款将被清偿,10笔贷款将被违约。
由于我们假设转移概率在贷款期限内是不变的,我们可以用它们来查找当前贷款的时间t = 2。
在目前T + 1的75笔贷款中,56.25笔贷款将保持在T + 2(75 * .75 = 56.25)。
咨询QQ:3025393450有问题百度搜索“”就可以了欢迎登陆官网:/datablog如果我们重复这个过程28次(在代码中完成)并绘制点,我们得到上面绘制的时间序列。
马尔可夫区制转换向量自回归模型

马尔可夫区制转换向量自回归模型马尔可夫区制转换向量自回归模型(Vector Autoregression Model with Markov Regime Switching, VAR-MS),结合了马尔可夫区制转换模型和向量自回归模型的特点,可用于对多变量时间序列数据进行建模和预测。
传统的向量自回归模型(Vector Autoregression Model, VAR)假设观测数据具有平稳性,且变量之间的关系是线性的。
然而,在实际的金融、经济和社会领域中,经常会出现时间序列数据在不同时间段呈现不同的模式或状态,如金融市场的牛熊转换、经济周期的波动等。
为了更准确地捕捉这种转变过程,VAR-MS模型引入了马尔可夫区制转换的思想。
马尔可夫区制转换是指时间序列数据的状态在不同的时间段随机地发生转换。
这种转换可以用马尔可夫链来表示,其中每个时间段被定义为一个状态,而状态之间的转换概率由状态转移矩阵表示。
在VAR-MS模型中,时间序列数据被整体分为多个区域,并假设每个区域内的数据服从一个固定的向量自回归模型。
根据当前的状态,根据转移概率矩阵,模型会在不同的区域之间进行切换。
VAR-MS模型可以用以下的数学表达式表示:Y_t = μ_Z + A_ZY_{t-1} + ε_t其中,Y_t是一个n维向量,表示时间t时刻的观测数据;μ_Z是一个n维向量,表示在状态为Z时的截距项;A_Z是一个n×n的矩阵,表示在状态为Z时的系数矩阵;ε_t是一个n维向量,表示误差项,满足ε_t ∼ N(0, Σ_Z),其中Σ_Z是在状态为Z时的协方差矩阵。
VAR-MS模型的参数估计通常采用最大似然估计或贝叶斯估计方法。
在实际应用中,首先需要通过一些判别方法(如似然比检验或信息准则)来确定马尔可夫区制转换的状态数。
然后,使用EM算法或Gibbs采样等方法来估计模型的参数和状态序列。
VAR-MS模型在金融和经济领域具有广泛的应用。
R语言案例_隐马尔科夫链模型

. 2
. 3
陆银波
隐马氏(HMM)
简介 模型讨论 一些应用 总结
引入 模型设定
. Outline
. 1 简介 引入 模型设定 模型讨论 估计 自相关性 预测 检验 一些应用 应用1: 地震 应用2:股票收益率 应用3:反应时间
. . . . . .
. 2
. 3
陆银波
隐马氏(HMM)
.
.
.
.
.
.
陆银波
隐马氏(HMM)
简介 模型讨论 一些应用 总结
估计 自相关性 预测 检验
. Fact . 在平稳分布的假定下,观测值边际分布为混合分布;混合比例为初 始状态分布均值,方差等各级矩均易求得。 . . Fact . cov(g(Ot ), g(Ot+k )) = cov(g(Ot ), g(Ot+k )|Xt , Xt+k )Pr(Xt )Pr(Xt+k |Xt )= E(g(Ot )|Xt )E(g(Ot+k )|Xt+k )Pr(Xt )Ak Xt Xt+k − ... .
. 问题1 . 已 . 知模型参数,计算似然函数 . 问题2 . 估 . 计最优模型参数(最大似然) . 问题3 . 已知模型参数,估计最优状态序列Xi .
.
.
.
.
.
.
陆银波
隐马氏(HMM)
简介 模型讨论 一些应用 总结
估计 自相关性 预测 检验
. 3个问题
. 问题1 . 已 . 知模型参数,计算似然函数 . 问题2 . 估 . 计最优模型参数(最大似然) . 问题3 . 已知模型参数,估计最优状态序列Xi .
