线段长短的比较ppt(冀教版七上)优质课件PPT
合集下载
冀教版七年级上册数学《线段长短的比较》PPT教学课件

尺规作图。 无刻度直尺和圆规的作用分别是什么?
做一做
请利用无刻度直尺和圆规画出一条与已知线段长度相等的线段。
在数学中,我们常限定用无刻度的直尺和圆规作图,这就是
尺规作图。
直尺可以画出直线、 射线、线段
圆规可以画圆,画弧, 也可截取长度
做一做
a
A aB
C
如图,我们可以用直尺画射线AC,再用圆规在射线AC上截取AB=a, 这就是“作一条线段等于已知线段”的尺规作图。
思考
如下图,图中共有几个角?它们之间有什么关系?
C B
∠BOC ∠AOB
∠AOC
O
A
思考
C B
O 图中:
A
∠AOC是∠AOB与∠BOC的和,记作∠AOC=∠AOB+∠BOC.
∠AOB是∠AOC与∠BOC的差,记作∠AOB = ∠AOC—∠BOC.
类似地,∠AOC—∠AOB=
∠BOC
.
探究
如下图,借助三角尺画出 15°、 75°的角。用一副三角尺,你还 能画出哪些度数的角?试一试.
(填“>”“<”或“=”). 其中蕴含的数学道理是_____两__点__之__间__线__段__最__短________.
A
B
C
规律小结
1、画线段:可通过直尺和圆规作已知长度的线段; 2、比较:度量法,可直接使用刻度尺测量线段的长度进行比较; 叠合法, 将一线段“移动”,使其一端点与另一线段的一端点重合, 两线段的另一端点均在同一射线上. 3、距离:两点之间,线段最短。
如图,如果∠AOC=∠DOB,那么∠AOD与∠COB相等
吗?说明理由.
A
因为 ∠AOC=∠DOB,
C
所以 ∠AOC + ∠COD =∠DOB + ∠COD , O D
做一做
请利用无刻度直尺和圆规画出一条与已知线段长度相等的线段。
在数学中,我们常限定用无刻度的直尺和圆规作图,这就是
尺规作图。
直尺可以画出直线、 射线、线段
圆规可以画圆,画弧, 也可截取长度
做一做
a
A aB
C
如图,我们可以用直尺画射线AC,再用圆规在射线AC上截取AB=a, 这就是“作一条线段等于已知线段”的尺规作图。
思考
如下图,图中共有几个角?它们之间有什么关系?
C B
∠BOC ∠AOB
∠AOC
O
A
思考
C B
O 图中:
A
∠AOC是∠AOB与∠BOC的和,记作∠AOC=∠AOB+∠BOC.
∠AOB是∠AOC与∠BOC的差,记作∠AOB = ∠AOC—∠BOC.
类似地,∠AOC—∠AOB=
∠BOC
.
探究
如下图,借助三角尺画出 15°、 75°的角。用一副三角尺,你还 能画出哪些度数的角?试一试.
(填“>”“<”或“=”). 其中蕴含的数学道理是_____两__点__之__间__线__段__最__短________.
A
B
C
规律小结
1、画线段:可通过直尺和圆规作已知长度的线段; 2、比较:度量法,可直接使用刻度尺测量线段的长度进行比较; 叠合法, 将一线段“移动”,使其一端点与另一线段的一端点重合, 两线段的另一端点均在同一射线上. 3、距离:两点之间,线段最短。
如图,如果∠AOC=∠DOB,那么∠AOD与∠COB相等
吗?说明理由.
A
因为 ∠AOC=∠DOB,
C
所以 ∠AOC + ∠COD =∠DOB + ∠COD , O D
线段长短的比较ppt(冀教版七上)PPT优选课件

B
所以线段AB就是所要画的线段。
观察思考
A
M
B
点M把线段AB分成_相_等_的两条线段AM和BM,
点M叫做线段AB的_中_点_。
若AM= MB = 1 AB,则有点M是线段AB的中点 2
反过来,若点M是线段AB的中点,则
有AM=BM= 1 AB。 2
例2
如图:在一条直线上顺次取A、B、C三点,使AB=5cm, BC=2cm,并且取线段AC的中点O。
离和最小,请你确定引水站的位置,并说明
理由 解:
m
P
赵庄A· ·
·B李庄
答:点P就是引水站的位置
1、判断题
(1)两条线段能比较大小,而直线是不能
比较大小的. ( √ )
(2)线段是图形,而线段的长度是一个数
量.
(√ )
(3)线段的大小比较方法只有度量法一
种.
(×)
2、如图,B、C为线段AD上的两点,C 为线段AD的中点,AC=5厘米,BD=6 厘米,求线段AB的长.
7厘米
10厘米
A
BC
D
你会叠合法比较线段AB与CD的长
短吗?
A
B
情况
C
D
一
A(C)
DB AB>CD
二
A(C)
B(D)
AB=CD
三 A (C)
B
D
AB<CD
例1:如图,已知线段a, 试画出线段AB ,
使得AB=a
a
解: 1 、画射线AC;
2 、在射线AC上截 取AB=a
以点A为圆心, a为半径画弧, 交射线AC于点
A
B·
·
C
D
解:BC=BD-CD
所以线段AB就是所要画的线段。
观察思考
A
M
B
点M把线段AB分成_相_等_的两条线段AM和BM,
点M叫做线段AB的_中_点_。
若AM= MB = 1 AB,则有点M是线段AB的中点 2
反过来,若点M是线段AB的中点,则
有AM=BM= 1 AB。 2
例2
如图:在一条直线上顺次取A、B、C三点,使AB=5cm, BC=2cm,并且取线段AC的中点O。
离和最小,请你确定引水站的位置,并说明
理由 解:
m
P
赵庄A· ·
·B李庄
答:点P就是引水站的位置
1、判断题
(1)两条线段能比较大小,而直线是不能
比较大小的. ( √ )
(2)线段是图形,而线段的长度是一个数
量.
(√ )
(3)线段的大小比较方法只有度量法一
种.
(×)
2、如图,B、C为线段AD上的两点,C 为线段AD的中点,AC=5厘米,BD=6 厘米,求线段AB的长.
7厘米
10厘米
A
BC
D
你会叠合法比较线段AB与CD的长
短吗?
A
B
情况
C
D
一
A(C)
DB AB>CD
二
A(C)
B(D)
AB=CD
三 A (C)
B
D
AB<CD
例1:如图,已知线段a, 试画出线段AB ,
使得AB=a
a
解: 1 、画射线AC;
2 、在射线AC上截 取AB=a
以点A为圆心, a为半径画弧, 交射线AC于点
A
B·
·
C
D
解:BC=BD-CD
《线段长短的比较》课件2(15页)(冀教版七年级上)

若点D在线段AB外,即线段CD大于
A
B
线段AB
记作 CD > AB
C
D
中点的概念:
• 线段AB上一点M,把线段AB分成两条 线段AM与MB,如果线段AM与线段MB
相等,那么点M就叫做线段AB的中点。
A
M
B
AM = BM =-1 AB
2 AB = 2AM = 2MB
1.有一根绳子,不借助刻度尺,你能找到它的中点吗?
说一说
已知线段 AB,CD, 比较线段 AB,CD的长短
方法1 测量线段的长度
A
B 方法2 (叠合法)将线段CD放到线
段 AB 上,使点C和点A重合,点D和
点B在重合点的同侧。
C
D 若点D在线段AB上,即线段CD小于线段AB
A
B
记作 CD < AB
若点D与点B重合,即线段CD与线段AB相等
C
D
记作 CD = AB
C
在直线l上顺次取A、B、C三点,AB=6,
BC=4,再取AC中点O,求:
1)AO的长; 2)OB的长; 3)OC的长。
这节课你的收获是什么?
作业: P119 1 ~ 4
是线段DB的( B )
A.
3 4
B.
2 3
C.
1 2
D.
3 2
在直线ι上取两点 ,在ι两旁各取一个点,这些点能确定
的直线条数应该是 ( ) D
A. 4条 B. 5条 C. 6条 D. 4条或6条
已知:如图,M是线段AB的中点,B在线段AC上, 且AB=2㎝,BC=2AB,求BC和AM的长度。
A
BM
2.支撑一根质量均匀,水平放置的木棒,如果要使它平衡, 支点应选在什么位置?
冀教版-数学-七年级上册-2.3 线段的长度 配套课件

4.5
●
●
A B 0
1
2
3
4
5
6
7
数的角度
8
9 10
3.3
●
●
C0 1
2
3D 4
5
6
7
8
9 10
∴ AB>CD
方法2:叠合法(用平移法比较) 形的角度
●
●
●
A
B
∴ AB>CD
●
●
C
D
观察下图中的几条线段,估 计一下,哪一条最长,哪一 条最短?
a d
b c
问题2:如何画线段等于已知线段
如图,已知线段MN你能用直尺和 圆规准确地画一条与MN相等的线 段吗?
①
·A
②
③
·B
④
⑤
你来做一做
在纸上任意点两点,用线联接它们,量 一下它们的长短,比较一下谁最短?
基本事实: 两点之间的所有连线中,
线段最短.
1.按要求画图,填空:
(1)画一条线段BC=2cm; (2)延长BC到D,使CD=BC; (3)反向延长BC到A,使AC= 2BC,则AB=______cm,AD= _____cm.
2.3线段的长度
知识海洋,追逐梦想.
快乐学习,快乐成长.
姚明和潘长江谁的个子高? 小明和小亮谁的个子高?
你哪有 我高啊!
小 明
我比你 高!
同么们学办量的们法比争一比你取一执量有消?什他
服了吧!
喔,原 来你比 我高!
小
亮
小
明
小 亮
问题1: 如何比较下面两条线段的长短?
●
●
●
●
A
冀教版-数学-七年级上册-2.3 线段的长度 参考课件
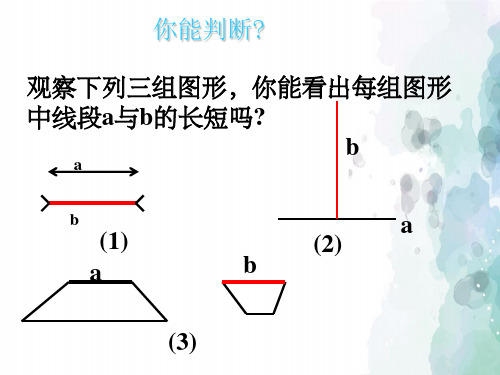
你能判断?
观察下列三组图形,你能看出每组图形 中线段a与b的长短吗?
b
a
b
(1)
a
a (2) b
(3)
2.3线段的长短
生活中长短的比较
怎样比较两个同学的高矮?
叠合法
度量法
思考:
我们能否借助于比较两位同学身高的 方法来比较两条线段的长短呢?
比较线段AB和CD的大小
方法(一)
度量法
A 3cm
B C 2.3cm D
练一练
1.下列说法正确的是( D ) A.过A、B两点的直线长是A、B两点间的距离 B.线段AB就是A、B两点间的距离 C.乘火车从杭州到上海要走210千米,这就是说
杭州站与上海站间的距离为210千米 D. 连结A、B两点的所有线中,其中最短的线的长度
就是A、B两点间的距离 2、课本71页A组1 3、课本71页B组1,单元本28页11 4、已知AB=5cm,BC=3cm,那AC两点间的距离是
先画一条线段,再画一条与它相等的线段, 怎么画?你能想出几种方法?
用圆规和直尺作一条线段等于已知线段
已知线段a,用直尺和圆规画一条线段等于已知线段。
① 画射线AB; ② 以A为圆心,a的长为半径画弧,交射线AB于点C。
注:尺规作图中: 1、直尺只能用来画直线,不能 量距离。 2、要求做出图形,说明结果, 并保留作图痕迹
a AC
B
线段AC即为所求线 段。
动手做一做
课本第70页 做一做 (1)、(2)
一个人过马路到对面的商店去。提 问:为什么有些人要直穿草坪过马 路到对面,却不愿走人行横道呢?
10
A·
12
7
·
15
B
基本事实:两点之间的所有连线中,
观察下列三组图形,你能看出每组图形 中线段a与b的长短吗?
b
a
b
(1)
a
a (2) b
(3)
2.3线段的长短
生活中长短的比较
怎样比较两个同学的高矮?
叠合法
度量法
思考:
我们能否借助于比较两位同学身高的 方法来比较两条线段的长短呢?
比较线段AB和CD的大小
方法(一)
度量法
A 3cm
B C 2.3cm D
练一练
1.下列说法正确的是( D ) A.过A、B两点的直线长是A、B两点间的距离 B.线段AB就是A、B两点间的距离 C.乘火车从杭州到上海要走210千米,这就是说
杭州站与上海站间的距离为210千米 D. 连结A、B两点的所有线中,其中最短的线的长度
就是A、B两点间的距离 2、课本71页A组1 3、课本71页B组1,单元本28页11 4、已知AB=5cm,BC=3cm,那AC两点间的距离是
先画一条线段,再画一条与它相等的线段, 怎么画?你能想出几种方法?
用圆规和直尺作一条线段等于已知线段
已知线段a,用直尺和圆规画一条线段等于已知线段。
① 画射线AB; ② 以A为圆心,a的长为半径画弧,交射线AB于点C。
注:尺规作图中: 1、直尺只能用来画直线,不能 量距离。 2、要求做出图形,说明结果, 并保留作图痕迹
a AC
B
线段AC即为所求线 段。
动手做一做
课本第70页 做一做 (1)、(2)
一个人过马路到对面的商店去。提 问:为什么有些人要直穿草坪过马 路到对面,却不愿走人行横道呢?
10
A·
12
7
·
15
B
基本事实:两点之间的所有连线中,
2.3线段的长短课件2023-2024学年冀教版七年级数学上册

2 两点之间的距离
定义:两点之间线段的长度,叫做两点之间的距离. 基本事实 两点之间的所有连线中,线段最短.
感悟新知
例2 下列说法正确的是( A ) A.两点之间线段的长度,叫做两点之间的距离 B.两点之间的线段叫做两点之间的距离 C.运动场一圈是300 m,表示起点与终点之间的距 离是300 m D.AB=2 cm,BC=5 cm,则AC=7 cm
于重合端点的同一侧,从而比较出两条线段的短. 2.线段长短的表示方法: 如果线段AB与CD相等,记作AB=CD; 如果线段AB小于CD,记作AB<CD; 如果线段AB大于CD,记作AB>CD.
感悟新知
例1 如图所示,分别比较线段AB与AC,AD与AE,AD 与AC的长短. 分析:比较线段的长短时,可用度量法 或叠合法,估测法在两条线段的长短很 明显的情况下使用,但不够精确. 解:AB>AC;AD>AE;AD=AC.
感悟新知
3.已知线段AB=20 cm,C是平面上任意一点,则 AC+BC( D )
A.等于20 cm
B.大于20 cm
C.小于20 cm
D.不小于20 cm
课堂小结线段的长短Biblioteka 线段的长短比较度量法
尺规作图
叠合法
两点之间线段最短
距离即线段PA与PB的长,结合两点之间 线段最短可求.
PP
解:连接AB,交MN于点P,则这个货站应建在点P处
1.【母题:教材P71练习】【2022·柳州】 如图,从学校A到书店B有①②③④四条 路线,其中最短的路线是( B ) A.① B.② C.③ D.④
感悟新知
2.如图所示,AB+BC__>______AC(填“>”“=” 或“<”),理由是两__点__之__间__线__段__最__短____.
定义:两点之间线段的长度,叫做两点之间的距离. 基本事实 两点之间的所有连线中,线段最短.
感悟新知
例2 下列说法正确的是( A ) A.两点之间线段的长度,叫做两点之间的距离 B.两点之间的线段叫做两点之间的距离 C.运动场一圈是300 m,表示起点与终点之间的距 离是300 m D.AB=2 cm,BC=5 cm,则AC=7 cm
于重合端点的同一侧,从而比较出两条线段的短. 2.线段长短的表示方法: 如果线段AB与CD相等,记作AB=CD; 如果线段AB小于CD,记作AB<CD; 如果线段AB大于CD,记作AB>CD.
感悟新知
例1 如图所示,分别比较线段AB与AC,AD与AE,AD 与AC的长短. 分析:比较线段的长短时,可用度量法 或叠合法,估测法在两条线段的长短很 明显的情况下使用,但不够精确. 解:AB>AC;AD>AE;AD=AC.
感悟新知
3.已知线段AB=20 cm,C是平面上任意一点,则 AC+BC( D )
A.等于20 cm
B.大于20 cm
C.小于20 cm
D.不小于20 cm
课堂小结线段的长短Biblioteka 线段的长短比较度量法
尺规作图
叠合法
两点之间线段最短
距离即线段PA与PB的长,结合两点之间 线段最短可求.
PP
解:连接AB,交MN于点P,则这个货站应建在点P处
1.【母题:教材P71练习】【2022·柳州】 如图,从学校A到书店B有①②③④四条 路线,其中最短的路线是( B ) A.① B.② C.③ D.④
感悟新知
2.如图所示,AB+BC__>______AC(填“>”“=” 或“<”),理由是两__点__之__间__线__段__最__短____.
冀教版数学七上23《线段的长短》ppt课件

1、判断题
√
√
×
试一试:如图,在一条河的两岸有李庄和赵庄,两村协议,共同投资在河旁修建一个引水站向两村引水,为了省钱,需要使引水站到两村的距离和最小,请你确定引水站的位置,并说明理由 ·李庄 ·
经过两点有且只有一条直线
线段、射线、直线中____可以度量长度,所以只有____才可以比较长短。
线段
线段
我比你高!
你哪有我高啊!
服了吧!
喔,原来你比我高!
如何比较两个人的身高
从中你得到什么启发来比较两条线段的长短
观察法
第一种方法是:度量法, 即用一把尺量出两条线段的长度, 再进行比较。
线段的比较:
考考你的眼力
A
B
C
D
线段AB和线段CD哪一条长
7厘米
10厘米
第二种方法是:叠合法 先把两条线段的一端重合,另一端 落在同侧,根据另一端落下的位置 来比较长短.
①
②
③
A
B
B
A
A
B
AB>CD
AB=EF
AB<MN
画在黑板上的两条线段是无法移动的,在没有度量工具的情况下,请大家想想办法,如何来比较它们的长短?
·
P
答:点P就是引水站的位置
解:
m
赵庄
A
B
小结
本节课你最大的收获是什么?
2.两点之间的所有连线中,线段最短。
3.两点之间线段的长度,叫做这两点之间的距离。
1.线段长短的比较方法: (1)估测法 (2)度量法 (3)叠合法
作业:P71 A组1、2、 B组1、2
2.3 线段长短的比较
(1)
A
(2)
√
√
×
试一试:如图,在一条河的两岸有李庄和赵庄,两村协议,共同投资在河旁修建一个引水站向两村引水,为了省钱,需要使引水站到两村的距离和最小,请你确定引水站的位置,并说明理由 ·李庄 ·
经过两点有且只有一条直线
线段、射线、直线中____可以度量长度,所以只有____才可以比较长短。
线段
线段
我比你高!
你哪有我高啊!
服了吧!
喔,原来你比我高!
如何比较两个人的身高
从中你得到什么启发来比较两条线段的长短
观察法
第一种方法是:度量法, 即用一把尺量出两条线段的长度, 再进行比较。
线段的比较:
考考你的眼力
A
B
C
D
线段AB和线段CD哪一条长
7厘米
10厘米
第二种方法是:叠合法 先把两条线段的一端重合,另一端 落在同侧,根据另一端落下的位置 来比较长短.
①
②
③
A
B
B
A
A
B
AB>CD
AB=EF
AB<MN
画在黑板上的两条线段是无法移动的,在没有度量工具的情况下,请大家想想办法,如何来比较它们的长短?
·
P
答:点P就是引水站的位置
解:
m
赵庄
A
B
小结
本节课你最大的收获是什么?
2.两点之间的所有连线中,线段最短。
3.两点之间线段的长度,叫做这两点之间的距离。
1.线段长短的比较方法: (1)估测法 (2)度量法 (3)叠合法
作业:P71 A组1、2、 B组1、2
2.3 线段长短的比较
(1)
A
(2)
冀教版2024新版七年级数学上册2.3 线段长短的比较 课件

课堂小结
线段长短的比较
度量法 叠合法
线段长短 的比较
线段的基本事实及 两点之间的距离
两点之间,线段最短.
尺规作图
•
•
A
B
新知探究
•
•
A
B
经过比较,我们可以得到一个关于线段的基本事实: 两点之间的所有连线中,线段最短.
简单说成:两点之间,线段最短.
连接两点间的线段的长度,叫做这两点之间的距离.
练一练
把一条弯曲的河道改直,可以缩短行程,这样做的依据是( A ) A.两点之间,线段最短 B.经过两点有且只有一条直线 C.线段可以比较大小 D.线段有两个端点
课堂练习
3.已知线段AB=20 cm,C是平面上任意一点,则AC+
BC( D ) A.等于20 cm
B.大于20 cm
C.小于20 cm
D.不小于20 cm
课堂练习
4.如图,在三角形ABC中,比较线段AC和AB长短的方法可行 的有___②__③__④___.(填序号) ①凭感觉估计; ②用直尺度量出AB和AC的长度; ③用圆规将线段AB叠放到线段AC上,观察点B的位置; ④沿点A折叠,使AB和AC重合,观察点B的位置.
A
B
C(A)
D
AB<CD
A
B
C(A) (B)D
AB>CD
新知探究
归 纳: 1. 点 A 与点 C 重合,若点 B 落在C,D之间,那么 AB < CD. 2. 点 A 与点 C 重合,若点 B 与点 D 重合 , 那么 AB = CD. 3. 点 A 与点 C 重合,若点 B 落在 CD 的延长线上,那么 AB > CD.
2.可以将两根绳子叠合在一起,就可以比较出来.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 小明到小英家有三条路可走,如图,你认为走 哪条路最近? (1)
A
(2)
B
(3)
答:走第(2)条路最短。
两点之间的所有连线中线段最短。
两点之间线段的长度,叫做
这两点之间的距离。
试一试:
如图,在一条河的两岸有李庄和赵庄,两村协
议,共同投资在河旁修建一个引水站向两村
引水,为了省钱,需要使引水站到两村的距
B
所以线段AB就是所要画的线段。
观察思考
A
M
B
点M把线段AB分成_相_等_的两条线段AM和BM,
点M叫做线段AB的_中_点_。
若AM= MB = 1 AB,则有点M是线段AB的中点 2
反过来,若点M是线段AB的中点,则
有AM=BM= 1 AB。 2
例2
如图:在一条直线上顺次取A、B、C三点,使AB=5cm, BC=2cm,并且取线段AC的中点O。
7厘米
10厘米
A
BC
D
你会叠合法比较线段AB与CD的长
短吗?
A
B
情况
C
D
一
A(C)
DB AB>CD
二
A(C)
B(D)
AB=CD
三 A (C)
B
D
AB<CD
例1:如图,已知线段a, 试画出线段AB ,
使得AB=a
a
解: 1 、画射线AC;
2 、在射线AC上截 取AB=a
以点A为圆心, a为半径画弧, 交射线AC于点
A
B·
·
C
D
解:BC=BD-CD
= BD-AC
=6-5
=1(厘米)
AB=AC- BC=5-1=4(厘米)
所以线段AB的长是4厘米
3、 如果点P在线段AB上,那么下列各 等式
AP=BP;BP=
1 2
AB
;AB
=2AP;
AP+BP=AB,其中,能判断P是线段
AB的中点的有 3 个
Thank you
感谢聆听 批评指导
4.2线段长短的比较
下面图形中,哪些是直线、射 线和线段?
(1) (2)
(3)
O
(4)
(5)
C
A
B
a
A
b D
答:图(1)(2) 是直线,
图(3)是射 线
图(4)(5) 是线段
你哪有 我高啊
! 1.70
小 明
我比你 高! 1.68
小 华
服了吧 !
小 明
喔,原 来你比 我高!
小 华
线段AB和线段CD哪一条长?
C
D
M
AC=AB + BC =2 AB =2 BC
即AB=BC= 1 2
AC
=
1 2
BD
2、如图,点C在线段上,线段AC=6㎝ ,BC=4㎝,M、N分别是线段AC,BC的 中点,线段MN的长度是 5㎝
C
A
B
M
N
3、已知线段AB=AC,请判断点A是否为线段BC的
中点?
B
C
B
A
C
所以点A不一定是线段BC的中点 A
离和最小,请你确定引水站的位置,并说明
理由 解:
m
P
赵庄A· ·
·B李庄
答:点P就是引水站的位置
1、判断题
(1)两条线段能比较大小,而直线是不能
比较大小的. ( √ )
(2)线段是图形,而线段的长度是一个数
量.
(√ )
(3)线段的大小比较方法只有度量法一
种.
(×)
2、如图,B、C为线段AD上的两点,C 为线段AD的中点,AC=5厘米,BD=6 厘米,求线段AB的长.
A
OB
C
求 AC= 7cm OC= 3.5cm OB= 1.5cm
解: AC=AB+BC=5+2=7(cm) AO=OC= 1 AC=3.5(cm) OB=OC-BC=3.25-2=1.5cm(或OB=AB-AO=5-3.5=1.5(cm))
二、练习
1、根据图填空 已知:AB=BC=CD
A·
B
汇报人:XXX 汇报日期:20XX年XX月XX日
感谢您的观看!本教学内容具有更强的时代性和丰富性,更适合学习需要和特点。为了 方便学习和使用,本文档的下载后可以随意修改,调整和打印。欢迎下载!
2021/02/01
16
