横截面上有轴力和弯矩
二建考试必备-建筑结构与设备(7) 杆件的基本变形与组合变形

第二节杆件的基本变形与组合变形一、轴向拉伸与压缩1.轴力与轴向变形轴向拉(压)杆件横截面上的内力只有轴力,轴力可采用截面法求得。
轴力的正负号一般规定为:拉力为正,压力为负。
轴力沿杆轴方向的变化采用轴力图表示。
依据平面假设,轴向拉(压)杆件的变形沿整个横截面是均匀的,因而应力在横截面上也是均匀分布的(图3-8)。
横截面上应力的计算式为:式中N 一轴力;A ―横截面面积。
在弹性变形范围内,轴向拉(压)杆的伸长(缩短)量与杆所受轴力、杆的长度成正比,与杆的抗拉(压)刚度EA 成反比,即【例3-4】计算图3-9(a)时所示轴向受力杆件的内力,作出内力图,并判断整个杆件的变形是伸长还是缩短。
E A=常数。
在BC段内任一截面处截开,取右侧部分为隔离体(图3-9b ) ,由平衡条件可得:同理,在AB 段内任一截面处截开,取右侧部分为隔离体(图3 -9c),由平衡条件可得因整个杆件的EA=常数,AB 段的杆长虽为BC 段的一半,但其所受的拉力为BC 段的3 . 5 / 1 . 5 ≈2 . 3 倍,因此AB 段的伸长量大于BC 段的缩短量,整个杆件的变形是伸长的。
2.温度改变的影响自然界中的物体普遍存在热胀冷缩的现象,杆件结构也是一样。
例如图 3 -10 ( a )所示的杆件,若其温度升高Δt,因没有多余约束(即为静定),故杆件可以自由地伸缩,并不会产生内力或反力。
在温度改变作用下,杆件的伸长量△l 与杆长l及温度改变量△t 成正比,即:式中α——材料的线膨胀系数。
对于图3 一10 ( b )的杆件,若温度升高△t,由于杆件两端固定(即为超静定),阻止了杆件的自由伸缩,这样杆内将产生温度应力。
显然,如果该杆温度升高(△t>0 ) ,则杆内将产生压力;若温度降低(△t < 0 ),则杆内将产生拉力。
二、剪切当杆件的某一截面受一对相距很近,方向相反的横向力作用时,杆件在该截面处将发生剪切变形。
例如图3-11所示的螺栓连接件,当钢板受拉力P 作用时,螺栓将在截面m-m处承受剪力,并产生剪切变形。
专升本《材料力学》_试卷_答案
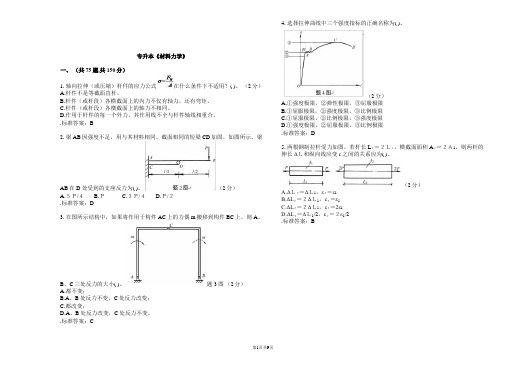
专升本《材料力学》一、(共75题,共150分)1. 轴向拉伸(或压缩)杆件的应力公式在什么条件下不适用?( )。
(2分)A.杆件不是等截面直杆。
B.杆件(或杆段)各横截面上的内力不仅有轴力,还有弯矩。
C.杆件(或杆段)各横截面上的轴力不相同。
D.作用于杆件的每一个外力,其作用线不全与杆件轴线相重合。
.标准答案:B2. 梁AB因强度不足,用与其材料相同、截面相同的短梁CD加固,如图所示。
梁AB在D 处受到的支座反力为( )。
(2分)A.5P/4B.PC.3P/4D.P/2.标准答案:D3. 在图所示结构中,如果将作用于构件AC上的力偶m搬移到构件BC上,则A、B、C三处反力的大小( )。
题3图(2分)A.都不变;B.A、B处反力不变,C 处反力改变;C.都改变;D.A、B处反力改变,C处反力不变。
.标准答案:C 4. 选择拉伸曲线中三个强度指标的正确名称为( )。
(2分)A.①强度极限,②弹性极限,③屈服极限B.①屈服极限,②强度极限,③比例极限C.①屈服极限,②比例极限,③强度极限D.①强度极限,②屈服极限,③比例极限.标准答案:D5. 两根钢制拉杆受力如图,若杆长L2=2L1,横截面面积A2=2A1,则两杆的伸长ΔL和纵向线应变ε之间的关系应为( )。
(2分)A.ΔL2=ΔL1,ε2=ε1B.ΔL2=2ΔL1,ε2=ε1C.ΔL2=2ΔL1,ε2=2ε1D.ΔL2=ΔL1/2,ε2=2ε1/2.标准答案:B6. 图所示受扭圆轴,正确的扭矩图为图( )。
(2分)A..标准答案:C7. 梁在集中力作用的截面处,它的内力图为( )。
(2分)A.Q图有突变,M 图光滑连续B.Q图有突变,M 图有转折C.M图有突变,Q 图光滑连续D.M图有突变,Q 图有转折.标准答案:B8. 梁的剪力图和弯矩图如图所示,则梁上的荷载为( )。
(2分)A.AB段无荷载,B 截面有集中力B.AB段有集中力,BC 段有均布力C.AB段有均布力,B 截面有集中力偶D.AB段有均布力,A 截面有集中力偶.标准答案:D 9. 变截面梁AB如图所示。
材料力学第5章-剪力图与弯矩图

第5章 梁的强度问题
剪力方程与弯矩方程
建立剪力方程和弯矩方程的方法与过程,实际上与前面所 介绍的确定指定横截面上的剪力和弯矩的方法和过程是相似的 ,所不同的,现在的指定横截面是坐标为x的横截面。
需要特别注意的是,在剪力方程和弯矩方程中,x是变量, 而FQ(x)和M(x)则是x的函数。
第5章 梁的强度问题
剪力方程与弯矩方程
例题2
MO=2FPl
FP
B
A
C
l
l
悬臂梁在B、C两处分别承受集中力FP和集中力偶M=2FPl
的作用。梁的全长为2l。 试写出:梁的剪力方程和弯矩方程。
第5章 梁的强度问题
剪力方程与弯矩方程
y
MO=2FPl
O
A
C
l
FP
B l
解:1.确定控制面和分段
本例将通过考察截开截面的右
边部分平衡建立剪力方程和弯矩方 程,因此可以不必确定左端的约束 力。
本章首先介绍如何建立剪力方程和弯矩方程;讨论载荷、 剪力、弯矩之间的微分关系;怎样根据载荷、剪力、弯矩之间 的微分关系绘制剪力图与弯矩图;然后应用平衡、变形协调以 及物性关系,建立确定弯曲的应力和变形公式;最后介绍弯曲 强度设计方法。
第5章 梁的强度问题
工程中的弯曲构件 梁的内力及其与外力的相互关系 剪力方程与弯矩方程 载荷集度、剪力、弯矩之间的微分关系 剪力图与弯矩图 刚架的内力与内力图 结论与讨论(1)
根据以上分析,不难得到结论: 杆件各截面上内力变化规律随着外力的 变化而改变。
第5章 梁的强度问题
梁的内力及其与外力的相互关系
所谓剪力和弯矩变化规律是指表示剪力和弯矩变 化的函数或变化的图线。这表明,如果在两个外力 作用点之间的梁上没有其他外力作用,则这一段梁 所有横截面上的剪力和弯矩可以用同一个数学方程 或者同一图线描述。
建筑力学试题库

建筑力学试题库LEKIBM standardization office【IBM5AB- LEKIBMK08- LEKIBM2C】建筑力学试题库一、单项选择题1.只限物体任何方向移动,不限制物体转动的支座称(A )支座。
2.A:固定铰 B:可动铰 C:固定端 D:光滑面 2.物体受五个互不平行的力作用而平衡,其力多边形是( C )39A.三角形B.四边形C.五边形D.六边形3.、平面力偶系合成的结果是一个( B )。
4.A:合力B:合力偶C:主矩D:主矢和主矩5..在集中力作用下( D )发生突变。
6.A.轴力图; B.扭矩图; C.弯矩图; D.剪力图。
7..在均布荷载作用段,梁的剪力图一定是( B )。
8.A.水平线; B.斜直线; C.抛物线; D.折线。
9.低碳钢的强度极限强度发生拉伸过程中的( D )阶段。
10.A弹性 B屈服(C)强化(D)颈缩11.下列结论中 C 是正确的。
12.A 材料力学主要研究各种材料的力学问题。
13.B 材料力学主要研究各种材料的力学性质。
14.C 材料力学主要研究杆件受力后变形与破坏的规律。
15.D 材料力学主要研究各类杆件中力与材料的关系16.下列结论中哪些是正确的?答: D 。
(1)杆件的某个横截面上,若轴力N为正(既为拉力),则各点的正应力σ也均为正(既均为拉应力)。
(2)杆件的某个横截面上,若各点的正应力σ均为正,则轴力N也必为正。
(3)杆件的某个横截面上,若轴力N不为零,则各点的正应力σ也均不为零。
(4)杆件的某个横截面上,若各点的正应力σ均不为零,则轴力N也必定不为零。
( A)(1)。
(B)(2)。
(C)(3),(4)。
(D) 全对。
17.变截面杆如图示,设F1、F2、F3分别表示杆件中截面1-1,2-2,3-3上的内力,则下列结论中 D 是正确的。
A F1≠F2,F2≠F3。
B F1=F2,F2>F3。
18.C F1=F2, F2=F3 。
圆杆横截面积为,截面惯性矩,同时受到轴力,扭矩和弯矩的共同作用,则按第四强度理论

圆杆横截面积为,截面惯性矩,同时受到轴力,扭矩和弯矩的共同作用,则按第四强
度理论
圆杆在受到轴力、扭矩和弯矩的共同作用时按照第四强度理论的性质如何分析。
第四强度理论是指在杆件受到轴力、扭矩和弯矩的共同作用时,杆件的承载能力可以用下列方程来表示:
P^2+M^2/S^2+Q^2/I^2≤F^2/S^2
其中,P是轴力,M是扭矩,Q是弯矩,S是截面抗压强度,I 是截面惯性矩,F是截面抗拉强度。
根据这个方程,我们可以计算出杆件在受到轴力、扭矩和弯矩的共同作用时的承载能力。
如果轴力、扭矩和弯矩的和小于等于F^2/S^2,则该杆件可以承受这些载荷;否则,杆件可能会受损或断裂。
在实际应用中,第四强度理论可以用来计算杆件在受到轴力、扭矩和弯矩的共同作用时的极限承载能力,并进而用来设计杆件的尺寸和材料,以确保其在使用过程中的安全性。
华南理工 网络 材料力学作业1

参考答案:×问题解析:3图示桁架中3杆的内力为0。
()参考答案:√1.图示扭转杆固定端截面的扭矩为15kN-M。
()参考答案:√问题解析:2.等截面圆轴作匀速转动,转速n=200r/min,传递的功率为60kw,作用在轴上的外力偶矩为2864.7N.m。
()参考答案:√1.梁AB受力如图所示,截面1-1剪力和弯矩分别为FS1=-qa, M1=-qa2/2 。
()答题:对. 错. (已提交)参考答案:√问题解析:2.图示简支梁,其正确的弯矩图如图所示。
()参考答案:×问题解析:3.图示受力梁的支座约束力、剪力图、弯矩图均正确。
()参考答案:√1.图示杆件的内力有轴力和扭矩。
()答题:对. 错. (已提交)参考答案:×问题解析:2.图示杆件的内力有轴力和弯矩。
()答题:对. 错. (已提交)参考答案:×问题解析:1.静定轴向拉(压)杆横截面上的应力与杆件材料的力学性能有关。
()参考答案:×问题解析:2.已知变截面圆杆受力如图所示,d=38mm,D=65mm,AB段和BC段横截面的应力是相同的。
()参考答案:×问题解析:3.边长为200mm的正方形杆件受力如图示,杆件横截面上最大压应力为 7.5MPa。
()参考答案:√1.拉压杆的最大切应力发生在与轴线成450的斜截面上,且。
()参考答案:√1.边长为200mm的正方形杆件受力如图示(同题2图),材料可认为符合胡克定律,其弹性模量E=10GPa,杆件总变形为1.05mm。
()参考答案:√问题解析:2.轴向拉(压)杆,受力和变形关系满足胡克定律,即。
()参考答案:×问题解析:3.变截面直杆受力如图所示,可用公式求杆的总伸长量。
参考答案:×1.图示的杆系结构中,按强度条件计算,最危险的杆件是4杆。
()参考答案:×1.图示两端固定的等截面直杆,其横截面面积为A,该杆受轴力FP作用。
《建筑力学》机考网考题库及答案

《建筑⼒学》机考⽹考题库及答案《建筑⼒学》机考⽹考题库及答案⼀、单项选择题1.若刚体在⼆个⼒作⽤下处于平衡,则此⼆个⼒必( )。
D.⼤⼩相等,⽅向相反,作⽤在同⼀直线2.由两个物体组成的物体系统,共具有( )独⽴的平衡⽅程。
D.63.静定结构的⼏何组成特征是( )。
B.体系⼏何不变且⽆多余约束4.低碳钢的拉伸过程中,胡克定律在( )范围内成⽴。
A.弹性阶段5.约束反⼒中含有⼒偶的⽀座为( )。
B.固定端⽀座7.截⾯法求杆件截⾯内⼒的三个主要步骤顺序为( )。
D.取分离体、画受⼒图、列平衡⽅程8.在⼀对( )位于杆件的纵向平⾯内的⼒偶作⽤下,杆‘件将产⽣弯曲变形,杆的轴线由直线弯曲成曲线。
B.⼤⼩相等、⽅向相反9.低碳钢的拉伸过程中,( )阶段的特点是应⼒⼏乎不变。
B.屈服1.约束反⼒中能确定约束反⼒⽅向的约束为( )。
D.光滑接触⾯2.平⾯平⾏⼒系有( )个独⽴的平衡⽅程,可⽤来求解未知量。
C.23.三个刚⽚⽤( )两两相连,组成⼏何不变体系。
A.不在同⼀直线的三个单铰4.⼒的作⽤线都互相平⾏的平⾯⼒系是( )。
C.平⾯平⾏⼒系5.结点法计算静定平⾯桁架,其所取脱离体上的未知轴⼒数⼀般不超过( )个。
B.27.轴向拉(压)时,杆件横截⾯上的正应⼒( )分布。
A.均匀8.在图乘法中,欲求某点的⽔平位移,则应在该点虚设( )。
B.⽔平向单位⼒3.静定结构的⼏何组成特征是( )。
B.体系⼏何不变且⽆多余约束5.图⽰构件为T形截⾯,其形⼼轴最有可能的是( )。
C Z3 、6.位移法的基本未知量是( )。
C.结点位移7.作刚架内⼒图时规定,弯矩图画在杆件的( )。
c.受拉⼀侧9.利⽤正应⼒强度条件,可进⾏( )三个⽅⾯的计算。
C.强度校核、选择截⾯尺⼨、计算允许荷载10.在图乘法中,欲求某点的转⾓,则应在该点虚设( )。
D.单位⼒偶6.在梁的强度计算中,必须满⾜( )强度条件。
材料力学全部习题解答

弹性模量
b
E 2 2 0 M P a 2 2 0 1 0 9P a 2 2 0 G P a 0 .1 0 0 0
s
屈服极限 s 240MPa
强度极限 b 445MPa
伸长率 ll010000m ax2800
由于 280;故0该50 材0料属于塑性材料;
13
解:1由图得
弹性模量 E0 3.550110063700GPa
A x l10.938m m
节点A铅直位移
A ytan 4 l150co sl4 2503.589m m
23
解:1 建立平衡方程 由平衡方程
MB 0 FN1aFN22aF2a
FN 2 FN1
得: FN12F1N22F
l1
l2
2.建立补充方程
3 强度计算 联立方程1和方
程(2);得
从变形图中可以看出;变形几何关
l
l0
断面收缩率
AAA110000d22d22d2121000065.1900
由于 2故.4 属6 % 于 塑5 性% 材料;
15
解:杆件上的正应力为
F A
4F D2 -d2
材料的许用应力为
要求
s
ns
由此得
D 4Fns d2 19.87mm
s
取杆的外径为
D19.87m m
16
FN1 FN 2
Iz= I( za) I( zR ) =1 a2 4
2R4 a4 R 4 =
64 12 4
27
Z
解 a沿截面顶端建立坐标轴z;,y轴不变; 图示截面对z,轴的形心及惯性矩为
0 .1
0 .5
y d A 0 .3 5 y d y2 0 .0 5 y d y
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
屋架
qy
qz
x
z
y
Mechanic of Materials
§8.1 组合变形和叠加原理
2、拉(压)弯组合变形:同时发生轴向拉伸(压缩) 与弯曲
拉弯组合变形工程实例1
目录
§8.1 组合变形和叠加原理
P
Mechanic of Materials
大桥桥墩
压弯组合变形工程实例2
q
gh
§8.1 组合变形和叠加原理
Mechanic of Materials
补充:斜弯曲
y
Mz
Mz x
My z
z
3)两组应力叠加,如图示
危险点B 、D
B
Mz Wz
My Wy
D
Mz Wz
My Wy
Mz
My
z
y My
x
y B
x My Mz D 中性轴z
补充:斜弯曲
(-) (-) (-) (-)
φ
Mechanic of Materials
令: K
M
cos
Iz
y0
M
sin
Iy
z0
0
+++++++
3
2
1
Mz 6
5
4
z'
中性轴 过原点
cos
Iz
y0
sin
Iy
z0
0
φ
9
8
K
7
- - - - φ- - - -
My
y0 I z sin tan z0 I y cos
M
2 y
M
2 z
Pz在 x截面上所引起的弯矩为:
=Px
M y Pz x P sin x M sin
(-) (-) (-) (-)
φ
Mechanic of Materials
补充:斜弯曲
⑶应力分析判危险点:危险面上应力最大的点。
①斜弯曲构件上任意一点的应力是由弯矩M z、My共同产
弯扭组合变形工程实例1
Mechanic of Materials
§8.1 组合变形和叠加原理
简易手摇绞车 的转轴
P
P
弯扭组合变形实例2
辘轳从深 井中提水
§8.1 组合变形和叠加原理
Mechanic of Materials
偏心拉伸实例
美国距 纽约55 英里远 的布里 奇波特 市曾发 生高层 建筑倒 塌事件。 28人丧 命。
生的,而且都是正应力,可代数相加:
x
y'
B
3
A D
12
C z' 4
P 5 6
z
8 9z
7 y'
ox Py
+++++++
(+) (+) (+) (+)
3
2
Mz 6
5
z ' 1
4
φ
9
8φ K
7
-- ---- - -
My
l Py
M
P
K
Mz Iz
yK
My Iy
zK
M cos
M sin
2.斜弯曲(组合)变形强度计算四步曲
(-) (-) (-) (-)
φ
Mechanic of Materials
x
B
3
A D
12
C z' 4
P 5 6
z
8 9z
7 y'
ox Py
l Py
(+) (+) (+) (+)
++++++& ' 1
4
9
8
K
7
-- ---- - -
y'
⑴外力分析判变形 PZ P sin Py P cos
F
P
P
FFF
T
T
§8.1 组合变形和叠加原理
另:斜弯曲 (双向弯曲,即两个平面内的弯曲)
Mechanic of Materials
§8.1 组合变形和叠加原理 一 、组合变形实例
Mechanic of Materials
1、斜弯曲:(双向弯曲,即两个平面内的弯曲)
屋面
檩条
q
屋架
屋面
q
qz
檩条
q
y
x
+++++++
B
3
3
2
1
A D
12
C z' 4
P 5 6
z
8 9z
7 y'
o x Mz Py
6
5
4
φ
9
8φ K
7
-- ---- - -
My
(+) (+) (+) (+)
z'
M
P
l Py
Py在x截面上所引起的弯矩为:
合成弯矩:
M Z Py x P cos x
M cos
M
Mechanic of Materials
第二十二讲目录
第八章 组合变形
§8.1 组合变形和叠加原理 §8.2 拉伸或压缩与弯曲的组合
目录
Mechanic of Materials
§8.1 组合变形和叠加原理
一、组合变形慨念:
在复杂外载作用下,构件的变形会包含几种基本变形,当 几种基本变形所对应的应力属同一量级时,不能忽略,这类构 件的变形称为——组合变形。
§8.1 组合变形和叠加原理
Mechanic of Materials
§8.1 组合变形和叠加原理
Mechanic of Materials
补充:斜弯曲
1.受力特点:外力与轴线垂直,不沿形心主轴 变形特点:发生双向弯曲。
Mechanic of Materials
平面弯曲
zPy
斜弯曲
补充:斜弯曲
My Wy
max
Mz Wz
My Wy
②三大应用 a.校核强度。 b.截面设计 c.求许可载荷.
(-) (-) (-) (-)
Mechanic of Materials
补充:斜弯曲
y ' 3.中性轴:应力为零的点的轨迹。设动点坐标(yo,zo)
(+) (+) (+) (+)
Iz yK I y zK
M
cos
Iz
yK
sin
Iy
zK
Mechanic of Materials
补充:斜弯曲
Mz 1)由Mz(Py)产生
的应力分布 z
2)由My (Pz)产生的 应力分布
My z
y
x Mz 中性轴z y
x My 中性轴y
如图 P与y轴夹φ锐角,P y使其绕z 轴在xoy平面内弯曲(上下 弯);Pz 使其绕y 轴在xoz平面内弯曲(前后弯)。
(-) (-) (-) (-)
φ
Mechanic of Materials
补充:斜弯曲
⑵内力分析判危险面:两弯矩的合成弯矩达到最大值时的
y ' 横截面、横截面横向尺寸最小的面。
B A
z ''
C
y D ''
Pz o x
z
Py
l Py
(+) (+) (+) (+)
+++++++
B
z A
''
C
D
-- ---- - -
y ''
② 危险点的应力 ⑷强度计算:
max
Mz Wz
My Wy
max
Mz Wz
My Wy
①强度条件
max
Mz Wz
H
Mechanic of Materials
b l=1m
H h
q= 0
0h
栏水坝(挡土墙)
压弯组合变形工程实例3
h
G1 G2
D
烟囱
§8.1 组合变形和叠加原理 3、弯扭组合变形:同时发生弯曲与扭转
Mechanic of Materials
y 400
800
250
FT2
z
A
C
FT2
FT1
B D
x FT1
