统考总积分的计算方法
2022届高考数学(理)大一轮复习教师用书:第三章第五节定积分与微积分基本定理 Word版含解析

第五节定积分与微积分基本定理突破点(一) 求定积分基础联通 抓主干学问的“源”与“流”1.定积分的定义一般地,假如函数f (x )在区间[a ,b ]上连续,用分点a =x 0<x 1<…<x i -1<x i <…<x n =b ,将区间[a ,b ]等分成n 个小区间,在每个小区间[x i -1,x i ]上任取一点ξi (i =1,2,…,n ),作和式∑i =1nf (ξi )Δx =∑i =1nb -an f (ξi ),当n →∞时,上述和式无限接近某个常数,这个常数叫做函数f (x )在区间[a ,b ]上的定积分,记作⎠⎛ab f (x )d x .2.定积分的相关概念在⎠⎛ab f (x )d x 中,a 与b 分别叫做积分下限与积分上限,区间[a ,b ]叫做积分区间,函数f (x )叫做被积函数,x 叫做积分变量,f (x )d x 叫做被积式.3.定积分的性质(1)⎠⎛a b kf (x )d x =k ⎠⎛ab f (x )d x (k 为常数);(2)⎠⎛a b [f 1(x )±f 2(x )]d x =⎠⎛a b f 1(x )d x ±⎠⎛ab f 2(x )d x ;(3)⎠⎛ab f (x )d x =⎠⎛ac f (x )d x +⎠⎛cb f (x )d x (其中a <c <b ).4.微积分基本定理假如f (x )是区间[a ,b ]上的连续函数,并且F ′(x )=f (x ),那么⎠⎛ab f (x )d x =F (b )-F (a ).其中F (x )叫做f (x )的一个原函数.为了便利,我们经常把F (b )-F (a )记为F (x )b a ,即⎠⎛ab f (x )d x =F (x )b a =F (b )-F (a ).考点贯穿 抓高考命题的“形”与“神”利用微积分基本定理求定积分[例1] 计算下列定积分: (1)⎠⎛1(-x 2+2x )d x ;(2)⎠⎛0π(sin x -cos x )d x ;(3)⎠⎛12⎝⎛⎭⎫e 2x +1x d x ; (4) 20⎰π1-sin 2x d x .[解] (1)⎠⎛01(-x 2+2x )d x =⎠⎛01(-x 2)d x +⎠⎛012x d x =-13x 3⎪⎪⎪10+x 2|10=-13+1=23. (2)⎠⎛0π(sin x -cos x )d x =⎠⎛0πsin x d x -⎠⎛0πcos x d x=(-cos x )|π0-sin x|π0=2.(3)⎠⎛12⎝⎛⎭⎫e 2x +1x d x =⎠⎛12e 2x d x +⎠⎛121xd x =12e 2x | 21+ln x|21=12e 4-12e 2+ln 2-ln 1 =12e 4-12e 2+ln 2. (4)20⎰π1-sin 2x d x =20⎰π|sin x -cos x |d x =40⎰π (cos x -sin x )d x +24⎰ππ (sin x -cos x )d x=(sin x +cos x )⎪⎪⎪⎪π4+(-cos x -sin x ) ⎪⎪⎪π2π4=2-1+(-1+2)=22-2.[方法技巧]利用微积分基本定理求定积分的步骤(1)把被积函数变形为幂函数、正弦函数、余弦函数、指数函数与常数的积的和或差. (2)把定积分用定积分性质变形为求被积函数为上述函数的定积分. (3)分别用求导公式找到一个相应的原函数.(4)利用微积分基本定理求出各个定积分的值. (5)计算原始定积分的值.利用定积分的几何意义求定积分[例2] 利用定积分的几何意义计算下列定积分:(1)⎠⎛011-(x -1)2d x ;本节主要包括2个学问点: 1.求定积分; 2.定积分的应用.(2)⎠⎛5-5 (3x 3+4sin x )d x .[解] (1)依据定积分的几何意义,可知⎠⎛011-(x -1)2d x 表示的是圆(x -1)2+y 2=1的面积的14(如图所示的阴影部分).故⎠⎛011-(x -1)2d x =π4.(2) ⎠⎛5-5 (3x 3+4sin x )d x 表示直线x =-5,x =5,y =0和曲线y =3x 3+4sin x 所围成的曲边梯形面积的代数和,且在x 轴上方的面积取正号,在x 轴下方的面积取负号.设y =f (x )=3x 3+4sin x ,则f (-x )=3(-x )3+4sin(-x )=-(3x 3+4sin x )=-f (x ),又f (0)=0, 所以f (x )=3x 3+4sin x 在[-5,5]上是奇函数,所以⎠⎛0-5 (3x 3+4sin x )d x =-⎠⎛05(3x 3+4sin x )d x ,所以⎠⎛5-5(3x 3+4sin x )d x =⎠⎛0-5(3x 3+4sin x )d x +⎠⎛05(3x 3+4sin x )d x =0.[方法技巧]1.利用定积分几何意义求定积分的策略当被积函数的原函数不易求,而被积函数的图象与直线x =a ,x =b ,y =0所围成的曲边梯形的面积易求时,利用定积分的几何意义求定积分.2.两个常用结论设函数f (x )在闭区间[-a ,a]上连续,则由定积分的几何意义和奇、偶函数图象的对称性可得两个结论: (1)若f (x )是偶函数,则⎠⎛a-a f (x )d x =2⎠⎛0af (x )d x ; (2)若f (x )是奇函数,则⎠⎛a-a f (x )d x =0.力量练通 抓应用体验的“得”与“失” 1.[考点一]⎠⎛1-1(x -1)d x =( )A .2B .-2 C.13D.12解析:选B ⎠⎛1-1 (x -1)d x =⎝⎛⎭⎫x 22-x 1-1=⎝⎛⎭⎫12-1-⎝⎛⎭⎫12+1=-2. 2.[考点一]20⎰πsin 2x2d x =( )A .0 B.π4-12 C.π4-14D.π4-1 解析:选B ∫20⎰πsin 2x2d x =20⎰π1-cos x 2d x =12x -12sin x ⎪⎪⎪⎪π20=π4-12.3.[考点一]设f (x )=⎩⎪⎨⎪⎧x 2,x ∈[0,1],1x ,x ∈(1,e](其中e 为自然对数的底数),则⎠⎛0e f (x )d x 的值为( )A.43 B .2 C .1 D.23解析:选A 依据定积分的性质,可知⎠⎛0e f (x )d x 可以分为两段,则⎠⎛0e f (x )d x =⎠⎛01x 2d x +⎠⎛1e 1xd x =13x 3⎪⎪⎪10+ln x ⎪⎪⎪e=13+1=43. 4.[考点二]⎠⎛12-x 2+4x -3d x =________.解析:依据定积分的几何意义,可知⎠⎛12-x 2+4x -3d x 表示圆(x -2)2+y 2=1与x =1,x =2及y =0所围成的圆的面积的14,即⎠⎛12-x 2+4x -3d x =π4.答案:π45.[考点二]⎠⎛-11[1-x 2-sin x ]d x =________. 解析:令1-x 2=y ,则x 2+y 2=1(y ≥0),该方程表示以(0,0)为圆心,1为半径的圆的一半.所以⎠⎛-111-x 2d x 表示圆x 2+y 2=1与x 轴所围成的上半圆的面积,因此⎠⎛-11-11-x 2d x =π2.又由于⎠⎛-11sin x d x =(-cos x )⎪⎪⎪1-1=-cos 1-[-cos(-1)]=0,所以⎠⎛1-1[1-x 2-sin x ]d x =π2.答案:π2突破点(二) 定积分的应用基础联通 抓主干学问的“源”与“流”1.定积分与曲边梯形面积的关系 如图:设阴影部分面积为S.图形阴影部分面积S =⎠⎛ab f (x )d xS =-⎠⎛ab f (x )d xS =⎠⎛a c f (x )d x -⎠⎛cb f (x )d xS =⎠⎛ab f (x )d x -⎠⎛ab g(x )d x=⎠⎛ab [f (x )-g(x )]d x2.求变速运动的路程做变速运动的物体在时间[a ,b ]上所经过的路程s ,等于其速度函数v =v (t )(v (t )≥0)在时间区间[a ,b]上的定积分,即s =⎠⎛ab v (t )d t .具体步骤为:①找出速度函数v =v (t ),作出图形.②观看v =v (t )的图形是否满足v (t )≥0.③若v (t )≥0,则相应的时间段[a ,b ]上的路程为s =⎠⎛ab v (t )d t ;若v (t )<0,则相应的时间段[a ,b ]上的路程为s =⎪⎪⎪⎪⎠⎛ab v (t )d t =-⎠⎛ab v (t )d t .考点贯穿 抓高考命题的“形”与“神”利用定积分求平面图形的面积[例1] 由曲线y =x ,直线y =x -2及y 轴所围成的图形的面积为( ) A.103 B .4 C.163D .6[解析] 作出曲线y =x 和直线y =x -2的草图(如图所示),所求面积为阴影部分的面积.由⎩⎪⎨⎪⎧y =x ,y =x -2得交点A(4,2). 因此y =x 与y =x -2及y 轴所围成的图形的面积为⎠⎛04[]x -(x -2)d x =⎠⎛04(x -x +2)d x =23x 32-12x 2+2x 4=23×8-12×16+2×4=163.[答案] C [方法技巧]利用定积分求平面图形面积的步骤 (1)依据题意画出图形;(2)借助图形确定出被积函数,求出交点坐标,确定积分的上、下限; (3)把曲边梯形的面积表示成若干个定积分的和; (4)计算定积分,写出答案.定积分在物理中的应用[例2] (1)一辆汽车在高速大路上行驶,由于遇到紧急状况而刹车,以速度v (t )=7-3t +251+t(t 的单位:s ,v 的单位:m/s)行驶至停止.在此期间汽车连续行驶的距离(单位:m)是( )A .1+25ln 5B .8+25ln 113C .4+25ln 5D .4+50ln 2(2)一物体在力F (x )=⎩⎪⎨⎪⎧5,0≤x ≤2,3x +4,x >2(单位:N)的作用下沿与力F 相同的方向,从x =0处运动到x =4(单位:m)处,则力F (x )做的功为________J.[解析] (1)由v (t )=7-3t +251+t=0,可得t =4⎝⎛⎭⎫t =-83舍去,因此汽车从刹车到停止一共行驶了4 s ,此期间行驶的距离为⎠⎛04v (t )d t =⎠⎛04⎝⎛⎭⎫7-3t +251+t d t =⎣⎡⎦⎤7t -32t 2+25ln (1+t )40=4+25ln 5. (2)由题意知,力F (x )所做的功为 W =⎠⎛04F (x )d x =⎠⎛025d x +⎠⎛24(3x +4)d x=5x|20+⎝⎛⎭⎫32x 2+4x ⎪⎪⎪42=5×2+⎣⎡⎦⎤32×42+4×4-⎝⎛⎭⎫32×22+4×2=36(J). [答案] (1)C (2)36 [方法技巧]定积分在物理中的两个应用(1)求物体做变速直线运动的路程:假如物体做变速直线运动,且其速度为v =v (t )(v (t )≥0),那么从时刻t =a 到t =b 所经过的路程s =∫b a v (t )d t .(2)求变力做功:一物体在变力F (x )的作用下,沿着与F (x )相同方向从x =a 移动到x =b 时,力F (x )所做的功是W =∫b a F (x )d x .力量练通 抓应用体验的“得”与“失”1.[考点二]若x (单位:m)表示位移的大小,一物体在力F (x )=x(单位:N )的作用下沿与力F (x )相同的方向运动了4 m ,力F (x )做功为( )A .8 JB .12 JC .15 J D.163 J解析:选D 由题意得W =⎠⎛04x d x =23x 32⎪⎪⎪40=163J. 2.[考点一]曲线y =2x 与直线y =x -1及x =4所围成的封闭图形的面积为( )A .2ln 2B .2-ln 2C .4-ln 2D .4-2ln 2解析:选D 由曲线y =2x 与直线y =x -1联立,解得x =-1,x=2,如图所示,故所求图形的面积为S =∫42⎝⎛⎭⎫x -1-2x d x =12x 2-x -2ln x |42=4-2ln 2. 3.[考点一](2022·衡阳一模)如图,阴影部分的面积是( )A .32B .16 C.323 D.83解析:选C 由题意得,阴影部分的面积S =⎠⎛1-3 (3-x 2-2x )d x =⎝⎛⎭⎫3x -13x 3-x 2⎪⎪⎪1-31-3=323. 4.由抛物线y =x 2-1,直线x =0,x =2及x 轴围成的图形面积为________.解析:如图所示,由x 2-1=0,得抛物线与x 轴的交点分别为(-1,0)和(1,0). 所以S =⎠⎛02|x 2-1|d x =⎠⎛01(1-x 2)d x +⎠⎛12(x 2-1)d x= ⎪⎪⎝⎛⎭⎫x -x 3310+⎪⎪⎝⎛⎭⎫x 33-x 21=⎝⎛⎭⎫1-13+⎣⎡⎦⎤83-2-⎝⎛⎭⎫13-1 =2. 答案:25.[考点二]物体A 以速度v =3t 2+1(t 的单位:s ,v 的单位:m/s )在始终线上运动,在此直线上与物体A 动身的同时,物体B 在物体A 的正前方5 m 处以v =10t (t 的单位:s ,v 的单位:m/s )的速度与A 同向运动,当两物体相遇时,相遇地与物体A 的动身地的距离是________m.解析:设b s 后两物体相遇,则⎠⎛0b(3t 2+1)d t -⎠⎛0b10t d t =5,即b 3+b -5b 2=5,(b 2+1)(b -5)=0,解得b=5,此时物体A 离动身地的距离为⎠⎛05(3t 2+1)d t =(t 3+t )|50=53+5=130(m). 答案:130近五年全国卷对本节内容未直接考查[课时达标检测] 重点保分课时——一练小题夯双基,二练题点过高考 [练基础小题——强化运算力量] 1.⎠⎛01e x d x 的值等于( )A .eB .1-eC .e -1D.12(e -1)解析:选C ⎠⎛01e x d x =e x |10=e 1-e 0=e -1.2.已知t 是常数,若⎠⎛0t (2x -2)d x =8,则t =( )A .1B .-2C .-2或4D .4解析:选D 由⎠⎛0t (2x -2)d x =8得,(x 2-2x )|t 0=t 2-2t =8,解得t =4或t =-2(舍去).3.从空中自由下落的一物体,在第一秒末恰经过电视塔顶,在其次秒末物体落地,已知自由落体的运动速度为v =g t (g 为常数),则电视塔高为( )A .12g B .g C .32g D .2g解析:选C 由题意知电视塔高为⎠⎛12g t d t =12g t 2|21=2g -12g =32g.4.由曲线y =x 2,y =x 围成的封闭图形的面积为( ) A .16 B .13 C .23D .1解析:选B 由⎩⎪⎨⎪⎧y =x 2,y =x ,得交点为(0,0)和(1,1),故所求面积(如图阴影部分的面积)为⎠⎛1(x -x 2)d x =⎝ ⎛⎭⎪⎫23x 3232-13x 3)|10=13. 5.20⎰π2sin ⎝⎛⎭⎫x +π4d x =________. 解析:依题意得20⎰π2sin ⎝⎛⎭⎫x +π4d x =20⎰π(sin x +cos x )d x =(sin x -cos x ) ⎪⎪⎪⎪π2=⎝⎛⎭⎫sin π2-cos π2-(sin 0-cos 0)=2.答案:2[练常考题点——检验高考力量] 一、选择题1.定积分|x 2-2x |d x =( )A .5B .6C .7D .8解析:选D ∵|x 2-2x |=⎩⎪⎨⎪⎧x 2-2x ,-2≤x <0,-x 2+2x ,0≤x ≤2,∴⎠⎛2-2|x 2-2x |d x =⎠⎛0-2(x 2-2x )d x +⎠⎛02(-x 2+2x )d x =⎝⎛⎭⎫13x 3-x 2|0-2+⎝⎛⎭⎫-13x 3+x 2|20=8.2.(2021·河北五校联考 )若f (x )=⎩⎪⎨⎪⎧lg x ,x >0,x +⎠⎛0a 3t 2d t ,x ≤0,f (f (1))=1,则a 的值为( )A .1B .2C .-1D .-2解析:选A 由于f (1)=lg 1=0,f (0)=⎠⎛0a 3t 2d t =t 3|a 0=a 3,所以由f (f (1))=1得a 3=1,所以a =1. 3.若S 1=⎠⎛121x d x ,S 2=⎠⎛12(ln x +1)d x ,S 3=⎠⎛12x d x ,则S 1,S 2,S 3的大小关系为( )A .S 1<S 2<S 3B .S 2<S 1<S 3C .S 1<S 3<S 2D .S 3<S 1<S 2解析:选A 如图,分别画出对应图形,比较围成图形的面积,易知选A.4.(2021·贵阳监测)若由曲线f (x )=x 与y 轴及直线y =m (m >0)围成的图形的面积为83,则m 的值为( )A .2B .3C .1D .8解析:选A 由题意得,围成的图形的面积S =⎠⎛0m2(m -x )d x =⎝⎛⎭⎫mx -23x 32⎪⎪⎪m2am 20=m 3-23m 3=83,解得m =2.5.设变力F (x )(单位:N )作用在质点M 上,使M 沿x 轴正方向从x =1 m 处运动到x =10 m 处,已知F (x )=x 2+1且方向和x 轴正方向相同,则变力F (x )对质点M 所做的功为( )A .1 JB .10 JC .342 JD .432 J解析:选C 变力F (x )=x 2+1使质点M 沿x 轴正方向从x =1运动到x =10所做的功W =∫101F (x )d x =∫101(x 2+1)d x =⎝⎛⎭⎫13x 3+x |101=342(J). 6.若函数f (x ),g(x )满足⎠⎛1-1f (x )g(x )d x =0,则称f (x ),g(x )为区间[-1,1]上的一组正交函数.给出三组函数:①f (x )=sin 12x ,g(x )=cos 12x ;②f (x )=x +1,g(x )=x -1;③f (x )=x ,g(x )=x 2.其中为区间[-1,1]上的正交函数的组数为( )A .0B .1C .2D .3解析:选C 对于①,⎠⎛1-1sin 12x cos 12x d x =⎠⎛1-112sin x d x =0,所以①是区间[-1,1]上的一组正交函数;对于②,⎠⎛1-1 (x +1)(x -1)d x =⎠⎛1-1 (x 2-1)d x ≠0,所以②不是区间[-1,1]上的一组正交函数;对于③,⎠⎛1-1x ·x 2d x =⎠⎛1-1x 3d x =0,所以③是区间[-1,1]上的一组正交函数.选C.二、填空题7.若函数f (x )=x +1x ,则⎠⎛1e f (x )d x =________.解析:⎠⎛1e ⎝⎛⎭⎫x +1x d x =⎝⎛⎭⎫x22+ln x |e 1=e 2+12. 答案:e 2+128.(2021·洛阳统考)函数f (x )=⎩⎪⎨⎪⎧x +1,-1≤x <0,e x ,0≤x ≤1的图象与直线x =1及x 轴所围成的封闭图形的面积为________.解析:由题意知所求面积为⎠⎛0-1(x +1)d x +⎠⎛01e x d x =⎝⎛⎭⎫12x 2+x |0-1+e x |10=-⎝⎛⎭⎫12-1+(e -1)=e -12. 答案:e -129.⎠⎛1e 1x d x +⎠⎛2-24-x 2d x =________;解析:⎠⎛1e 1xd x =ln x |e 1=1-0=1,由于⎠⎛2-24-x 2d x 表示的是圆x 2+y 2=4在x 轴上方的面积,故⎠⎛2-24-x 2d x =12π×22=2π.所以原式=2π+1.答案:2π+110.如图,由曲线y =x 2和直线y =t 2(0<t <1),x =1,x =0所围成的图形(阴影部分)的面积的最小值是________.解析:设图中阴影部分的面积为S(t ),则S(t )=⎠⎛0t (t 2-x 2)d x +⎠⎛t1(x 2-t 2)d x =43t 3-t 2+13.由S ′(t )=2t (2t -1)=0,得t =12为S(t )在区间(0,1)上的最小值点,此时S(t )min =S ⎝⎛⎭⎫12=14. 答案:14三、解答题11.已知f (x )为二次函数,且f (-1)=2,f ′(0)=0,⎠⎛01f (x )d x =-2.(1)求f (x )的解析式;(2)求f (x )在[-1,1]上的最大值与最小值. 解:(1)设f (x )=a x 2+b x +c(a ≠0), 则f ′(x )=2a x +b. 由f (-1)=2,f ′(0)=0,得 ⎩⎪⎨⎪⎧a -b +c =2,b =0,即⎩⎪⎨⎪⎧c =2-a ,b =0,∴f (x )=a x 2+2-a.又⎠⎛01f (x )d x =⎠⎛01(a x 2+2-a)d x=⎣⎡⎦⎤13ax 3+(2-a )x ⎪⎪⎪1=2-23a =-2.∴a =6,从而f (x )=6x 2-4. (2)∵f (x )=6x 2-4,x ∈[-1,1]. ∴当x =0时,f (x )min =-4; 当x =±1时,f (x )max =2.12.已知函数f (x )=x 3-x 2+x +1,求其在点(1,2)处的切线与函数g(x )=x 2围成的图形的面积. 解:∵(1,2)为曲线f (x )=x 3-x 2+x +1上的点, 设过点(1,2)处的切线的斜率为k ,则k =f ′(1)=(3x 2-2x +1)⎪⎪⎪x=1=2, ∴过点(1,2)处的切线方程为y -2=2(x -1),即y =2x .y =2x 与函数g(x )=x 2围成的图形如图:由⎩⎪⎨⎪⎧y =x 2,y =2x可得交点A(2,4),O(0,0), 故y =2x 与函数g(x )=x 2围成的图形的面积 S =⎠⎛02(2x -x 2)d x =⎝⎛⎭⎫x 2-13x 3| 20=4-83=43.。
艺体教师考核方案

艺体教师考核⽅案艺体教师考核⽅案 ⼀、⽅案的内容 ⽅案的内容多是上级对下级或涉及⾯⽐较⼤的⼯作,⼀般都⽤带“⽂件头”形式下发,所以不⽤落款,只有标题、成⽂时间和正⽂三部分内容。
1、标题 ⽅案的标题有两种写法:⼀个是“三要素”写法,即由发⽂机关、计划内容和⽂种三部分组成,如《北华⼤学五年发展规划总体⽅案》;⼀个是“两要素”写法,即省略发⽂机关,但这个发⽂机关必须在领头的“批⽰性通知”(⽂件头)的标题中体现出来,如《治理采掘⼯业危机,实现良性循环⽅案》。
成⽂时间,为郑重起⻅,⽅案的成⽂时间⼀般不省略,⽽且要注在标题下。
2、正⽂ ⽅案的正⽂⼀般有两种写法:⼀是常规写法,即按“指导⽅针”、“主要⺫标(重点)”、“实施步骤”、“政策措施”及“要求”⼏个部分来写,这个较固定的程序适合于⼀般常规性单项⼯作;⼆是变项写法,即根据实际需要加项或减项的写法,适合于特殊性的单项⼯作。
但不管哪种写法,“主要⺫标”、“实施步骤”、“政策措施”这三项必不可少的,实际写作时的称呼可以不同,如把“主要⺫标”称为“⺫标和任务”或“⺫标和对策”等,把“政策措施”称为“实施办法”或“组织措施”等。
在“主要⺫标”⼀项中,⼀般还要分总体⺫标和具体⺫标;“实施步骤”⼀般还要分基本步骤或阶段和关键步骤,关键步骤⾥还有重点⼯作项⺫;“政策措施”的内容⾥⼀般还要分“政策保证”、“组织保证”和“具体措施”等。
⽅案也可以是下级或具体责任⼈为落实和实施某项具体⼯作⽽形成的⽂件,然后报上级或主管领导批准实施。
写法要求同上。
⼆、艺体教师考核⽅案 ⽅案是计划中内容最为复杂的⼀种。
由于⼀些具有某种职能的具体⼯作⽐较复杂,不作全⾯部署不⾜以说明问题,因⽽公⽂内容构成势必要繁琐⼀些,⼀般有指导思想、主要⺫标、⼯作重点、实施步骤、政策措施、具体要求等项⺫。
下⾯是⼩编整理的艺体教师考核⽅案,欢迎阅读与收藏。
艺体教师考核⽅案1 为评价教职⼯履职情况,落实师德师⻛第⼀标准,突出教育教学实绩,引导教师潜⼼教书育⼈,发挥年度考核的导向和激励作⽤,根据有关⽂件精神,结合我校实际,特制定本⽅案。
学校教师工作考核制度

学校教师工作考核制度为调动教职工的工作积极性,真正发挥年度考核的评价、激励和导向作用,制定本制度。
一、德(7分)(一)因违反教师职业道德以及违反从教行为“八严禁”等相关规定,受到市县教育局通报的,分别扣5分、3分;受到教管办通报批评的每次扣1分。
(二)拒不接受教管办、学校安排工作的,每次扣1-5分。
(三)因违反教师职业道德以及违反从教行为“八严禁”等相关规定,经学校查处尚未造成严重影响的,每次扣1-2分。
(四)学生或家长评教,满意度测评95%以上为满分,每增一个百分点加0.2分。
(五)无故不参加上级培训的每次扣0.5分,不参加校本研训的每次扣0.2分,完不成研训任务的每次扣0.1分(六)值班、上课发现学生睡觉等违纪现象不及时制止和教育的每人次扣0.1分,完不成值班任务的每次扣0.1分。
本项项为倒扣分项,如有减分从总分中扣除。
二、能(15分)(一)备课(6分)根据《XX学校教学常规要求》,进行纸质备课、纸质备课按1:1:1的比例分三档分别计4分、3.5分、3分;无该项目的教师按最低档计分、检查时应上交不上交的教师不得分。
(二)上课(3分)根据学校安排公开课(录课)打分进行量化系数修正后按1:1:1的比例分三档计入课堂能力分值,分别是3分、2.5分、2分。
无该项目的或因特殊情况未参加的教师,此项不得分。
(三)作业(2分)根据作业检查量化进行系数修正后按1:1:1的比例分三档计入考核,分别计2分、1.5分、1分。
无该项目的教师按最低档计分、检查时应上交不上交的教师不得分。
(十)听评课(2分)。
教导处根据个人填写的听评课和课例研修记录卡和签到表计算节数。
学期结束时,每人至少听课10节,质量和数量各计一半分,没完成的按实有节数换算成分值加入。
(十一)学习笔记、计划与总结(各0.5分,共计1分)根据学习笔记完成情况按1:1:1的比例分别分三档分别计0.5分、0.4分、0.3分。
计划总结按1:1比例,各占0.25分. 根据计划、总结分别完成情况按1:1:1的比例分别分三档计0.25分、0.2分、0.15分。
中小学年度考核办法(2023版)

***学校教职工年度考核办法第一部分总则(2023.12.26)一、指导思想为全面公开、公正、公平的对教职工工作进行综合评定,使年度考核更加准确地反映教师工作的实绩,以此调动广大教职工教育教学、教研的积极性,参照《甘肃省事业单位人员年度考评办法》、《古浪县教师职称申报办法》《土门教育工作站教职工年度考核办法》,以二十大精神为指导,全面贯彻党的教育方针,全面、综合、多元考评教师的德、能、勤、绩、廉。
结合我校实际,特修订本办法。
学校年度考核按高级教师、一级教师、二级教师分类考核,按照教师定量积分高低排序名次,分别确定优秀、合格、不合格三个等次,优秀占同级考核人数的15%。
二、基本原则坚持“公开、公平、公正”原则。
充分发扬民主,确保教职工有知情权、参与权、监督权,保障教职工的合法权益。
三、考核对象***学校在册的全体教职工四、考核内容及分值考核内容主要包括德、能、勤、绩、廉五个方面(重点考核教育教学工作实绩)总分100分:德:主要考核教师遵守教育法律法规、《中小学教师职业道德规范》。
通过民主测评从德、勤、廉等方面对教师日常工作进行评议,满分为10分,以测评小组评议结果为准。
(10%)能:主要考核业务能力、创新能力以及知识更新情况,任课教师周教学工作量,满分为30分。
(30%)勤:主要考核工作态度、敬业精神和平时考勤情况,满分为5分。
(5%)绩:主要考核完成工作任务、效率,以及教学质量的高低,满分为50分。
(50%)廉:主要考核廉政从教、廉洁自律等情况,满分为5分。
(5%)第二部分考核细则第一、加分项一、德(10%)(一)民主测评。
通过民主测评从德、勤、廉等方面对教师日常工作进行评议,满分为10分,以测评小组评议结果为准。
(二)有以下行为者评优一票否决。
1.违反《中小学教师违反职业道德行为处理办法》的通知(国务院[2014]1号)内容规定者;2.违反中央八项规定及省、市、县委相关规定者;3.违反市纪委监察局文件《关于进一步严明党员干部操办婚丧嫁娶婚庆事宜纪律通知》*纪发[2015]28号文件内容规定者;4.违反县纪委《关于严禁党员干部“升学宴”、“谢师宴”的通知》古纪发[2015]22号文件内容规定者;5.学生户外教学活动时间,未采取防范措施,或安全教育不力,导致不良后果的。
综合成绩计算细则及评分参考标准【模板】
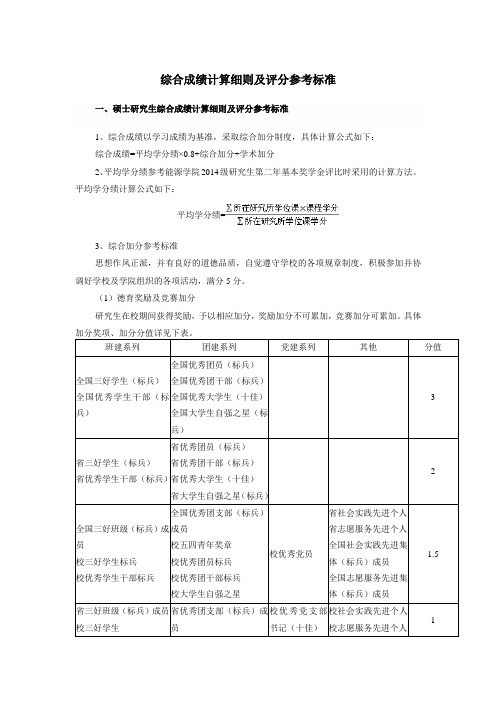
综合成绩计算细则及评分参考标准平均学分绩计算公式如下:平均学分绩=注:需提供获奖证书(2)科技竞赛注:能源学院2015年研究生国家奖学金评定时参考的各级竞赛项目,依据《XX大学大学生科技竞赛活动管理办法》进行相关认定,科技竞赛需第一完成人。
注:1)可获得加分的文章需满足下列两个条件:必须与课题或研究生教育相关;第一作者及第一作者通信地址为XX大学;作者署名里面必须有自己的导师或所在课题组其他老师。
2)如果学生为第二作者,其导师为第一作者时,按第一作者计算,其余情况按正常排序。
3)从研究生入学至奖学金评定截止日期之间的成果为有效成果,可获得加分。
论文以实际发表日期为准,若能提供论文已被录用的证明也可加分。
4)论文分级由对应研究所(中心)主管教师等组成的评审团最终决定。
注:1)可获得加分的专利需满足下列两个条件:必须与课题或研究生教育相关;2)第一作者及第一申请单位为XX大学;研究生的申请专利,如果学生为第二作者,其导师为第一作者时,按第一作者计算,其余情况按正常排序。
注:需提供获奖证书(2)竞赛类获奖加分(不可兼得,取最高一项)注:能源学院2015年研究生国家奖学金评定时参考的各级竞赛项目,依据《XX大学大学生科技竞赛活动管理办法》进行相关认定,科技竞赛需第一完成人。
(3)其他类型加分注:需提供授权证书,本人为第一作者。
4、发表论文加分占65%或更多(可累计加分)注:(1)可获得加分的文章需满足下列条件:①必须与课题或研究生教育相关;②学校署名必须为XX大学,作者署名里面必须有自己的导师。
(2)博士研究生发表学术论文,本人为第一作者。
如果学生为第二作者,其导师为第一作者时,按第一作者计算。
(3)发明专利只认定已授权的,受理不予计算,可获得加分的专利必须与课题或研究生教育相关。
(3)从博士研究生入学至奖学金评定截止日期之间的成果为有效成果,可获得加分。
论文必须已经实际发表方可计为有效成果。
(4)论文分级由对应研究所(中心)主管教师等组成的评审团最终决定。
中学高一年级督查考核积分细则(3篇)

中学高一年级督查考核积分细则是根据学校制定的考核政策和要求来制定的。
以下是一种可能的细则参考:1. 学业表现积分:- 平时考试成绩:每次考试根据成绩排名给予相应积分。
- 期末考试成绩:根据成绩排名给予相应积分。
- 作业完成情况:按时完成作业、作业质量、参与课堂讨论等表现给予积分。
2. 学科竞赛积分:- 参加学科竞赛并获奖:根据获奖等级给予相应积分。
- 学科竞赛参赛表现:参加学科竞赛并取得好成绩的给予积分。
3. 综合素质积分:- 学生干部任职情况:根据担任学生干部的职位等级给予相应积分。
- 社团活动参与情况:积极参与学校社团活动,表现优秀者给予积分。
- 社会实践参与情况:积极参与学校组织的社会实践活动,表现优秀者给予积分。
4. 日常表现积分:- 课堂纪律:上课守纪律、尊重师长、课堂参与等表现给予积分。
- 活动秩序:参加学校组织的活动,秩序良好,遵守规则者给予积分。
- 操行评价:根据班主任的评价,以及是否有违纪情况给予相应积分。
以上只是一个示例,具体的细则可能根据学校和地方的要求而有所不同。
学校应该根据实际情况,结合学生的特点和需求,制定合理的细则,以激励和引导学生全面发展。
中学高一年级督查考核积分细则(2)一、考核对象高一所有教学人员二、考核内容(一)计划评估标准⑴制定或上交不及时,扣____分。
(2)未制定计划,扣____分。
(3)未按时完成学校、年级组相关材料的扣____分。
(二)备课评估标准使用陈旧教案或网上下载教案,或以电子教案代替书面教案,没有二次备课,发现一次扣____分。
(三)上课评估标准(1)上课迟到、早退或中途离开课堂一次扣____分,旷课____次扣____分。
(2)上课时有学生看小说、玩手机、听音乐、睡觉、东张西望每人次扣____分。
(3)体育课上、下课时需到位集中,不集中上下课,发现一次扣____分。
(4)充分使用好“五粮课”积分表,未积分的每节课扣____分。
(5)早读课无教学目标的每次扣____分。
总分计算方法

总分计算方法在各种考试、评估、竞赛等场合中,总分计算方法是一个非常重要的概念。
它可以用来确定一个人或一个团队在某个特定领域的综合表现,从而作出相应的评判。
本文将详细介绍总分计算方法的步骤和注意事项,并结合实际例子进行说明,帮助读者更好地理解和应用这一概念。
一、明确评分项和权重在进行总分计算之前,首先需要明确评分项和它们的权重。
评分项是指用来评估被评价对象表现的各个方面,而权重则是各个评分项在总分中占比的大小。
例如,在评价一个学生的综合表现时,可能会包括学习成绩、课堂参与度、习惯品行等评分项,而这些评分项的权重可以根据实际情况来确定,比如学习成绩占60%、课堂参与度占30%、习惯品行占10%。
二、设定评分标准评分标准是对每个评分项进行具体量化的规定,用来区分不同表现层次。
在设定评分标准时,需要充分考虑到被评价对象的实际情况,同时保证标准的客观性和公平性。
以学习成绩为例,可以根据百分制进行评分,90分以上为优秀,80-89分为良好,70-79分为中等,60-69分为及格,60分以下为不及格。
三、进行评分在明确了评分项、权重和评分标准之后,就可以开始进行评分了。
针对每个评分项,根据被评价对象的具体表现进行评分,并将评分结果转化为相应的分数。
例如,一个学生的学习成绩为85分,那么可以根据设定的评分标准将其转化为相应的分数,比如80分。
四、求得各项得分在进行评分后,需要对各项得分进行计算。
将每个评分项的得分乘以其相应的权重,然后相加,即可得到一个人或团队在该领域的总分。
例如,在前述例子中,学习成绩的权重为60%,得分为80分,则该学生在学习成绩评分项上的得分为80 * 60% = 48分。
五、计算总分最后,将各项得分相加,即可得到被评价对象的总分。
例如,如果还有其他评分项,比如课堂参与度得分为90分,占30%权重,习惯品行得分为95分,占10%权重,那么该学生的总分为48分+ 90 * 30% + 95 * 10% = 48分+ 27分+ 9.5分= 84.5分。
统考版2022届高考数学一轮复习第三章3.3定积分与微积分基本定理课时作业理含解析

课时作业17 定积分与微积分基本定理[基础达标]一、选择题1.[2021·某某某某一中月考]⎠⎜⎛-11|x|d x 等于( )A .0B .1C .2D .122.[2021·某某黄冈调研]⎠⎜⎛-44⎣⎢⎡⎦⎥⎤cos ⎝ ⎛⎭⎪⎫x +π2+16-x 2d x =( )A .8πB .4πC .2πD .π3.已知f(x)为偶函数且⎠⎜⎛06f(x)d x =8,则⎠⎜⎛-66f(x)d x 等于( ) A .0B .4C .8D .164.[2021·某某内江适应性测试]由曲线y =x 2+1,直线y =-x +3,x 轴正半轴与y 轴正半轴围成的图形的面积为( )A .3B .103C .73D .835.[2019·某某八市重点高中第二次联合测评]已知函数f(x)=⎩⎪⎨⎪⎧x ,1<x ≤4,x|x|,-1≤x ≤1,则⎠⎜⎛-14f(x)d x =( )4326.若⎠⎜⎛01(x 2+mx)d x =0,则实数m 的值为( )A .-13B .-23C .-1D .-27.[2021·某某模拟]若f(x)=⎩⎨⎧lg x ,x>0,x +⎠⎜⎛0a 3t 2d t ,x ≤0,f(f(1))=1,则a 的值为( )A .1B .2C .-1D .-28.[2021·某某模拟]汽车以v =(3t +2)m /s 做变速运动时,在第1s 至第2s 之间的1s 内经过的路程是( )A .5mB .112mC .6mD .132m9.[2021·某某某某模拟]已知⎠⎜⎛1e⎝ ⎛⎭⎪⎫1x -m d x =3-e2,则m 的值为( )A .e -14eB .12C .-12D .-1 10.[2021·某某某某适应性测试]如图,函数y =-x 2+2x +1与y =1的图象相交,形成一个闭合图形(图中的阴影部分),则该闭合图形的面积是()3二、填空题11.[2021·某某市高三摸底测试]20π⎰(-2sin x)d x =________.12.[2021·某某株洲质检]若⎠⎜⎛0T x 2d x =9,则常数T 的值为________.13.[2021·某某八所重点中学联考]若函数f(x)=ln (e x +1)+ax为偶函数,则⎠⎜⎛1e⎝ ⎛⎭⎪⎫1x -x a d x=________.14.[2021·某某某某中学调研]曲线y =x 3-3x 和直线y =x 所围成的图形的面积是________. [能力挑战]15.一物体受到与它运动方向相反的力F(x)=110e x +x 的作用,则它从x =0运动到x =1时F(x)所做的功等于( )A .e10+25B .e 10-25C .-e 10+25D .-e 10-2516.[2021·某某某某长郡中学第一次适应性考试]已知函数f(x)=⎩⎪⎨⎪⎧ -x +2,x ≤2,1-(x -3)2,2<x ≤4,则412⎰f(x)d x 的值为( )A .9+4π8B .1+4π4C .1+π2D .3+2π417.[2019·某某某某第二次模拟]如图,图形由部分正弦曲线y =sin x 与余弦曲线y =cos x及矩形ABCD 组成,向矩形ABCD 内掷一粒豆子(大小忽略不计),若豆子落在矩形ABCD 内的任一位置是等可能的,则豆子落在阴影部分的概率为________.课时作业171.解析:如图,由定积分的几何意义可知⎠⎜⎛-11|x|d x 表示图中阴影部分的面积,故⎠⎜⎛-11|x|d x =2×⎝ ⎛⎭⎪⎫12×1×1=1. 答案:B2.解析:cos ⎝ ⎛⎭⎪⎫x +π2=-sin x .令y =16-x 2,两边平方,得y 2=16-x 2(y ≥0),则有x 2+y 2=16(y ≥0),所以函数y =16-x 2在[-4,4]上的图象是圆x 2+y 2=16的上半部分,所以⎠⎜⎛-4416-x 2d x =12×π×42=8π.所以⎠⎜⎛-44⎣⎢⎡⎦⎥⎤cos ⎝ ⎛⎭⎪⎫x +π2+16-x 2d x =⎠⎜⎛-44(16-x 2-sin x)d x =⎠⎜⎛-4416-x 2d x -⎠⎜⎛-44sin x d x =8π+cos x ⎪⎪⎪⎪4-4=8π,故选A 项.答案:A3.解析:原式=⎠⎜⎛-60f(x)d x +⎠⎜⎛06f(x)d x ,因为原函数为偶函数,即在y 轴两侧的图象对称.所以对应的面积相等,即⎠⎜⎛-66-6f(x)d x =2⎠⎜⎛06f(x)d x =8×2=16.答案:D 4.解析:由题意可知题中曲线与坐标轴围成的图形如图中阴影部分所示,由⎩⎪⎨⎪⎧y =x 2+1,y =-x +3,解得⎩⎪⎨⎪⎧ x =-2,y =5(舍去)或⎩⎪⎨⎪⎧x =1,y =2,则A (1,2),结合图形可知,所求的面积为⎠⎜⎛01(x 2+1)d x+12×22=⎝ ⎛⎭⎪⎫13x 3+x ⎪⎪⎪⎪1+2=103,选B 项.答案:B5.解析:函数f (x )=⎩⎪⎨⎪⎧x ,1<x ≤4,x |x |,-1≤x ≤1,则⎠⎜⎛-14f(x)d x =⎠⎜⎛-11x|x|d x +⎠⎜⎛14x d x =0+23x 32⎪⎪⎪⎪41=143. 故选B 项. 答案:B6.解析:由题意知⎠⎜⎛01(x 2+mx)d x =⎝ ⎛⎭⎪⎫x 33+mx 22⎪⎪⎪⎪10=13+m 2=0,得m =-23. 答案:B7.解析:因为f (1)=lg1=0,f (0)=⎠⎜⎛0a 3t 2d t =t 3⎪⎪⎪⎪a0=a 3,所以由f(f(1))=1得a 3=1,所以a =1.答案:A8.解析:根据题意,汽车以v =(3t +2)m/s 做变速运动时,汽车在第1s 至第2s 之间的1s 内经过的路程s =⎠⎜⎛12(3t +2)d t =⎝ ⎛⎭⎪⎫3t 22+2t ⎪⎪⎪⎪21=132m ,故选D .答案:D9.解析:由微积分基本定理得⎠⎜⎛1e ⎝ ⎛⎭⎪⎫1x -m d x =(ln x -mx)⎪⎪⎪⎪e 1=m +1-m e ,结合题意得m +1-m e =3-e 2,解得m =12.故选B .答案:B10.解析:由⎩⎪⎨⎪⎧y =-x 2+2x +1,y =1,得x 1=0,x 2=2,所以闭合图形的面积S =⎠⎜⎛02(-x 2+2x +1-1)d x =⎠⎜⎛02(-x 2+2x)d x =⎝ ⎛⎭⎪⎫-x 33+x 2⎪⎪⎪⎪20=-83+4=43.答案:B11.解析:由定积分的概念及微积分基本定理,得20π⎰(-2sin x)d x =2cos x ⎪⎪⎪⎪π20=-2.答案:-212.解析:⎠⎜⎛0T x 2d x =⎝ ⎛⎭⎪⎫13x 3⎪⎪⎪⎪T0=13T 3=9,所以T =3.答案:313.解析:∵f (x )=ln(e x +1)+ax为偶函数,∴f (1)=f (-1),ln(e +1)+a =ln ⎝ ⎛⎭⎪⎫1e +1-a ,解得a =-12,∴⎠⎜⎛1e ⎝ ⎛⎭⎪⎫1x -x a d x =⎠⎜⎛1e ⎝ ⎛⎭⎪⎫1x +2x d x =(ln x +x 2)⎪⎪⎪⎪e 1=e 2.答案:e 214.解析:由⎩⎪⎨⎪⎧y =x 3-3x ,y =x 得交点的坐标分别为(0,0),(2,2),(-2,-2),作出草图如图,可知曲线y =x 3-3x 和直线y =x 围成图形的面积S =2⎠⎜⎛02[x -(x 3-3x )]d x =2⎠⎜⎛02(4x -x 3)d x =2⎝ ⎛⎭⎪⎫2x 2-14x 4⎪⎪⎪⎪20=2×(8-4)=8.答案:815.解析:由题意知W =-⎠⎜⎛01⎝ ⎛⎭⎪⎫110e x+x d x=-⎝ ⎛⎭⎪⎫110e x +12x 2⎪⎪⎪⎪10=-e 10-25.答案:D16.解析:因为f (x )=⎩⎪⎨⎪⎧-x +2,x ≤2,1-(x -3)2,2<x ≤4,所以412()f x dx ⎰=212(x 2)x d ⎰-++⎠⎜⎛241-(x -3)2d x ,212(x 2)x d ⎰-+=⎝ ⎛⎭⎪⎫-12x 2+2x ⎪⎪⎪⎪212=⎝ ⎛⎭⎪⎫-12×22+2×2-⎣⎢⎡⎦⎥⎤-12×⎝ ⎛⎭⎪⎫122+2×12=98,⎠⎜⎛241-(x -3)2d x 的几何意义为以(3,0)为圆心,1为半径的圆在x 轴上方的面积,因而(⎠⎜⎛241-(x -3)2d x)=12×π×12=π2,所以412()f x dx ⎰=212(x 2)x d ⎰-++⎠⎜⎛241-(x -3)2d x =98+π2=9+4π8,故选A 项. 答案:A17.解析:根据题意,可得阴影部分的面积为24ππ⎰(sin x -cos x)d x +2ππ⎰sin x d x =(-cos x -sin x)⎪⎪⎪⎪π2π4+(-cos x)⎪⎪⎪⎪ππ2=2,又矩形ABCD 的面积为4π,所以由几何概型的概率计算公式得豆子落在阴影部分的概率是24π.答案:24π。
