2K01高数(上)试题A

合集下载

2001年普通高等学校招生全国统一考试理科数学(全国卷)

2001年普通高等学校招生全国统一考试数学（理工农医类）本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分。

第I 卷1至2页。

第II 卷3至9页。

共150分。

考试时间120分钟。

第I 卷（选择题 60分）注意事项：1．答第I 卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。

2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试题卷上。

3．考试结束，监考人将本试卷和答题卡一并收回。

参考公式：三角函数的积化和差公式()()[]βαβαβα-++=sin sin 21cos sin ()()[]βαβαβα--+=sin sin 21sin cos()()[]βαβαβα-++=cos cos 21cos cos()()[]βαβαβα--+-=cos cos 21sin sin正棱台、圆台的侧面积公式()l c c S +'=21台侧其中c '、c 分别表示上、下底面周长，l 表示斜高或母线长台体的体积公式()h S S S S V +'+'=31台体其中S '、S 分别表示上、下底面积，h 表示高一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1．若sin cos 0θθ>，则θ在A ．第一、二象限B ．第一、三象限C ．第一、四象限D ．第二、四象限2．过点(1,1)A -，(1,1)B -且圆心在直线20x y +-=上的圆的标准方程是A ．22(3)(1)4x y -++= B ．22(3)(1)4x y ++-=C ．22(1)(1)4x y -+-=D ．22(1)(1)4x y +++=3．设{}n a 是递增等差数列，前三项的和为12，前三项的积为48，则它的首项是A ．1B ．2C ．4D ．64．若定义在区间(1,0)-内的函数2()log (1)a f x x =+满足()0f x >，则a 的取值范围是A ．10,2⎛⎫ ⎪⎝⎭B ．10,2⎛⎤ ⎥⎝⎦C ．1,2⎛⎫+∞⎪⎝⎭D ．()0,+∞5．极坐标方程2sin()4πρθ=+的图形是6．函数cos 1(0)y x x π=+-≤≤的反函数是A ．arccos(1)(02)y x x =--≤≤B ．arccos(1)(02)y x x π=--≤≤C ．arccos(1)(02)y x x =-≤≤D ．arccos(1)(02)y x x π=+-≤≤7．若椭圆经过原点，且焦点为1(1,0)F ，2(3,0)F ，则其离心率为A ．34B ．23C ．12D ．148．若04παβ<<<，sin cos a αβ+=，sin cos b ββ+=，则A ．a b <B ．a b >C ．1ab <D ．2ab >9．在正三棱柱111ABC A B C -中，若1AB =，则AB 与1C B 所成的角的大小为A ．60°B ．90°C ．105°D ．75°10．设()f x ，()g x 都是单调函数，有如下四个命题： ①若()f x 单调递增，()g x 单调递增，则()()f x g x 单调递增； ②若()f x 单调递增，()g x 单调递减，则()()f x g x 单调递增； ③若()f x 单调递减，()g x 单调递增，则()()f x g x 单调递减； ④若()f x 单调递减，()g x 单调递减，则()()f x g x 单调递减．其中，正确的命题是A ．①③B ．①④C ．②③D ．②④11．一间民房的屋顶有如图三种不同的盖法：①单向倾斜；②双向倾斜；③四向倾斜．记三种盖法屋顶面积分别为1P ，2P ，3P ．若屋顶斜面与水平面所成的角都是α，则A ．321P P P >>B ．321P P P >=C ．321P P P =>D ．321P P P ==12．如图，小圆圈表示网络的结点，结点之间的连线表示它们有网线相联，连线标注的数字表示该段网线单位时间内可以通过的最大信息量，现从结点A 向结点B 传递信息，信息可以分开沿不同的路线同时传递，则单位时间内传递的最大信息量为 A ．26B ．24C ．20D ．19第Ⅱ卷（非选择题共90分）注意事项：用钢笔或圆珠笔直接答在答题卡上．二、填空题：本大题共4小题，每小题4分，共20分，把答案填在题中横线上．13．若一个圆锥的轴截面是等边三角形，则这个圆锥的侧面积是．14．双曲线221916x y -=的两个焦点为1F ，2F ，点P 在双曲线上．若12PF PF ⊥，则P 点到x 的距离为．15．设数列{}n a 是公比为q 的等比数列，n S 是它的前n 项和．若{}n S 是等差数列，则q ＝．16．圆周上有n 个等分点(1)n >，以其中三个点为顶点的直角三角形的个数为．三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤．17．（本小题满分10分）如图，在底面是直角梯形的四棱锥S ABCD -中，90ABC ∠=，SA ⊥面ABCD ，1SA AB BC ===，12AD =．（1）求四棱锥S ABCD -的体积；（2）求面SCD 与面SBA 所成的二面角的正切值．SADCB18．（本小题满分12分）已知复数31(1)z i i =-．（1）求1arg z 及1||z ；（2）当复数z 满足||1z =，求1||z z -的最大值．19．（本小题满分12分）设抛物线22(0)y px p =>的焦点为F ，经过F 的直线交抛物线于A ，B 两点，点C 在抛物线的准线上，且BC ∥x 轴．证明：直线AC 经过原点O ．20．（本小题满分12分）已知i ，m ，n 是正整数，且1i m n ≤≤<．（1）证明：i i i im n n P m P <；（2）证明：(1)(1)nmm n +>+．21．（本小题满分12分）从社会效益和经济效益出发，某地投入资金进行生态环境建设，并以此发展旅游产业．根据规划，本年度投入800万元，以后每年投入将比上年减少15．本年度当地旅游业收入估计为400万元，由于该项建设对旅游业的促进作用，预计今后旅游业收入每年会比上年增加14．（1）设n 年内（本年度为第一年）总投入为n a 万元，旅游业总收入为n b 万元．写出n a ，n b 的表达式；（2）至少经过几年旅游业的总收入才能超过总投入？22．（本小题满分12分）设()f x 是定义在R 上的偶函数，其图像关于直线1x =对称，对任意121,0,2x x ⎡⎤∈⎢⎥⎣⎦，都有1212()()()f x x f x f x +=．（1）求1()2f 及1()4f ；（2）证明()f x 是周期函数；（3）记1(2)2n a f n n=+，求lim(ln )n n a →∞．参考解答及评分标准说明：一. 本解答指出了每题要考查的主要知识和能力，并给出了一种或几种解法供参考，如果考生物解法与本解答不同，可根据试题的主要考查内容比照评分标准制订相应的评分细则．二. 对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定部分的给分，但不得超过该部分正确解答得分数的一半；如果后继部分的解答有较严重的错误，就不再给分．三. 解答右端所注分数，表示考生正确做到这一步应得的累加分数．四. 只给整数分数．选择题和填空题不给中间分．一.选择题：本题考查基本知识和基本运算．每小题5分，满分60分．（1）B （2）C （3）B （4）A （5）C （6）A （7）C （8）A （9）B （10）C （11）D （12）D 二.填空题：本题考查基本知识和基本运算．每小题4分，满分16分．（13）2π （14）516（15）1 （16）2n (n －1) 三.解答题：（17）本小题考查线面关系和棱锥体积计算，以及空间想象能力和逻辑推理能力．满分12分．解：（Ⅰ）直角梯形ABCD 的面积是M 底面()43125.0121=⨯+=⋅+=AB AD BC ， ……2分 ∴ 四棱锥S —ABCD 的体积是⨯⨯=SA V 31M 底面43131⨯⨯=41=． ……4分（Ⅱ）延长BA 、CD 相交于点E ，连结SE 则SE 是所求二面角的棱．……6分∵ AD ∥BC ，BC = 2AD ， ∴ EA = AB = SA ，∴ SE ⊥SB ，∵ SA ⊥面ABCD ，得SEB ⊥面EBC ，EB 是交线，又BC ⊥EB ，∴ BC ⊥面SEB ，故SB 是CS 在面SEB 上的射影，∴ CS ⊥SE ，所以∠BSC 是所求二面角的平面角． ……10分 ∵ 22AB SA SB +=2=，BC =1，BC ⊥SB ，∴ tan ∠BSC =22=SB BC ．即所求二面角的正切值为22． ……12分（18）本小题考查复数基本性质和基本运算，以及分析问题和解决问题的能力．满分12分．解：（Ⅰ）z 1 = i (1－i ) 3 = 2－2i ，将z 1化为三角形式，得⎪⎭⎫⎝⎛+=47sin47cos 221ππi z ， ∴ 47arg 1π=z ，221=z ． ……6分（Ⅱ）设z = cos α＋i sin α，则z －z 1 = ( cos α－2)＋(sin α＋2) i ， ()()22212sin 2cos ++-=-ααz zsin 249+=(4πα-)， ……9分当sin(4πα-) = 1时，21z z -取得最大值249+．从而得到1z z -的最大值为122+． ……12分（19）本小题考查抛物线的概念和性质，直线的方程和性质，运算能力和逻辑推理能力．满分12分．证明一：因为抛物线y 2 =2px (p ＞0)的焦点为F (2p，0)，所以经过点F 的直线的方程可设为2pmy x +=； ……4分代入抛物线方程得y 2 －2pmy －p 2 = 0，若记A (x 1，y 1)，B (x 2，y 2)，则y 1，y 2是该方程的两个根，所以y 1y 2 = －p 2． ……8分因为BC ∥x 轴，且点c 在准线x = －2p 上，所以点c 的坐标为（－2p，y 2），故直线CO 的斜率为111222x y y p p y k ==-=．即k 也是直线OA 的斜率，所以直线AC 经过原点O ． ……12分证明二：如图，记x 轴与抛物线准线l 的交点为E ，过A 作AD ⊥l ，D 是垂足．则AD ∥FE ∥BC ． ……2分连结AC ，与EF 相交于点N ，则ABBF AC CN AD EN ==，，ABAF BCNF = ……6分根据抛物线的几何性质，AD AF =，BC BF =， ……8分∴ NF ABBC AF ABBF AD EN =⋅=⋅=，即点N 是EF 的中点，与抛物线的顶点O 重合，所以直线AC 经过原点O ．…12分（20）本小题考查排列、组合、二项式定理、不等式的基本知识和逻辑推理能力．满分12分．（Ⅰ）证明：对于1＜i ≤m 有 im p = m ·…·(m －i ＋1)，⋅-⋅=m m m m m p i im 1…m i m 1+-⋅，同理 ⋅-⋅=n n n n np i i n 1…n i n 1+-⋅， ……4分由于 m ＜n ，对整数k = 1，2…，i －1，有mkm n k n ->-，所以 i im i i n mp n p >，即im i i n i p n p m >． ……6分（Ⅱ）证明由二项式定理有()inni i nC m m ∑==+01， ()i m mi i mC n n ∑==+01， ……8分由 (Ⅰ)知i n i p m ＞im i p n (1＜i ≤m ＜n ＝，而 !i p C i m im=，!i p C in in =， ……10分所以， im i i n i C n C m >(1＜i ≤m ＜n ＝．因此，∑∑==>mi imi mi i niC n Cm 22．又 10==m n C n C m ，mn nC mC m n ==11，()n i m C m in i≤<>0．∴∑∑==>mi imi ni iniC n Cm 0．即 (1＋m )n ＞(1＋n )m ． ……12分（21）本小题主要考查建立函数关系式、数列求和、不等式等基础知识；考查综合运用数学知识解决实际问题的能力．满分12分．解：（Ⅰ）第1年投入为800万元，第2年投入为800×（1－51）万元，……，第n 年投入为800×（1－51）n －1万元．所以，n 年内的总投入为a n = 800＋800×（1－51）＋…＋800×（1－51）n －1∑=--⨯=nk k 11)511(800= 4000×[1－(54)n]； ……3分第1年旅游业收入为400万元，第2年旅游业收入为400×（1＋41）万元，……，第n 年旅游业收入为400×（1＋41）n －1万元．所以，n 年内的旅游业总收入为b n = 400＋400×（1＋41）＋…＋400×（1＋41）n －1∑=-⨯=nk k 11)45(400= 1600×[ (54)n－1]． ……6分（Ⅱ）设至少经过n 年旅游业的总收入才能超过总投入，由此b n －a n ＞0，即 1600×[（45）n －1]－4000×[1－（54）n ]＞0．化简得 5×（54）n ＋2×（54）n －7＞0， ……9分设=x （54）n ，代入上式得5x 2－7x ＋2＞0，解此不等式，得52<x ，x ＞1(舍去)．即（54）n ＜52，由此得 n ≥5．答：至少经过5年旅游业的总收入才能超过总投入． ……12分（22）本小题主要考查函数的概念、图像，函数的奇偶性和周期性以及数列极限等基础知识；考查运算能力和逻辑思维能力．满分14分．（Ⅰ）解：因为对x 1，x 2∈[0，21]，都有f (x 1＋x 2) = f (x 1) · f (x 2)，所以=)(x f f (2x ) · f (2x )≥0，x ∈[0，1]．∵ =)1(f f (2121+) = f (21) ·f (21) = [f (21)]2，f (21)=f (4141+) = f (41) · f (41) = [f (41)]2． ……3分0)1(>=a f ，∴ f (21)21a =，f (41)41a =． ……6分（Ⅱ）证明：依题设y = f (x )关于直线x = 1对称，故 f (x ) = f (1＋1－x )，即f (x ) = f (2－x )，x ∈R ． ……8分又由f (x )是偶函数知f (－x ) = f (x ) ，x ∈R ， ∴ f (－x ) = f (2－x ) ，x ∈R ，将上式中－x 以x 代换，得f (x ) = f (x ＋2)，x ∈R ．这表明f (x )是R 上的周期函数，且2是它的一个周期． ……10分（Ⅲ）解：由（Ⅰ）知f (x )≥0，x ∈[0，1]．∵ f (21)= f (n ·n 21) = f (n 21＋（n －1）·n 21) = f (n 21) · f (（n －1）·n 21)= f (n 21) · f (n 21) · … ·f (n 21)= [ f (n21)]n，f (21) = 21a ，∴ f (n21) = n a 21．∵ f (x )的一个周期是2，∴ f (2n ＋n 21) = f (n21)，因此a n = n a 21， ……12分∴ ()∞→∞→=n n n a lim ln lim (a nln 21) = 0． ……14分。

理科二类高等数学(上.下)参考答案

理科二类《高等数学》（上）习题参考答案第一章函数与极限习题一一、1.．224>-<<-x x 或；2．[]a a -1,； 3．1525++⋅x x ； 4．奇函数； 5．0，1，1，0； 6．4231,,,--e e e e ．二(略)三、1．1； 2．0； 3．21； 4．4．四、1,1,1,-不存在．五、1,1-==b a 六、都不存在．七、;32.4;221.3;1.2;0.1 5．-2； 6.e . 八、2.6,0.5,2.4,32.3,21.2,2.1-.九(略)习题二一、()()[]1,0.5,1,1.4,,22,1.3,2.2,.1-+∞⋃e 第一二、41=a ．三、1.6,1.5,.4,ln .3,.2,2ln .163e a e .四、1．为可去间断点1=x ，为无穷间断点2=x ；2．为跳跃间断点1=x ．五、()()+∞⋃∞-,00,.六、七、(略);八、为跳跃间断点0=x ；为无穷间断点1=x .第一章测验题一、1., 2., 3., 4., 5.D C C A B .二、[]2.5,22.4,2,0.3,2.2,2.12+-x x . 三、112211.,2.1,3.,4.3,6.6e e -.四、x x x x p ++=232)(.五、11,2,1,.2x x x x =-===处连续为可去间断点为无穷间断点．六、.3,21==b a 七*、(略)第二章导数与微分习题一一、)0(.2,)(,)(2,)(.1000f x f x f x f ''''；)(),(1.3000000x x x y y x x x y y --=--=- 二、,0()2,0,0x e x f x x x x ⎧>⎪'=<⎨⎪=⎩不存在三、)(2)(a ag a f ='. 四、处连续且可导0=x . 五*、()()10,21a a >>.习题二一、1．3622ln 2-++x x x ； 2．1； 3．2ln 1x x-； )2(42,)2(42.422ππππππ-=---=-x y x y ；)(4)(2.5222x f x x f ''+'．二、2)1()sin 3(cos sin cos 2.1x x e x x e x x +-+-； x x x x x x x x c o s s i n l n c o s 2s i n .2+-+；211arcsin 2.3xx -⋅；12ln (ln )4.n x n x x --；a a x x x ax a a a 21211sec ln .5+⋅+-；21sec 222116.3ln3ln ;8.sec tan xx y y y e x x x -⎡'''===⎢⎣三、()[]{}()[]()x f x f f x f f f '⋅'⋅'.1, )()(2.222x x x x x e f e e e f xe '+四、00,,11)12()(222=≠⎪⎪⎩⎪⎪⎨⎧+-='x x x e x x f x . 五、(略) 六*、[]222()2()()(ln )()(ln )(ln )()()ln x x x x f x f x y f a a a f a a a a a f x a f x a ''''''''=+++习题三一、2ln 82.3,)2(323.2,11.1--=-+a x ab b y e y, 63114.1(,,sin(31),arctan ,ln ln 263x x y x c e c x c e c x c -=-+++++. 二、1．[]2(1)cos()(1)cos()1y x y xy x xy xy -+++； 2．)()(2)()(22y f x x yf x f y y f x '+'--；三、1．)sin ln (cos sin xxx x x x +⋅； 2．⎥⎦⎤⎢⎣⎡-----+-+------)5(51)4(54)3(53)2(5211)5()4()3()2()1(5432x x x x x x x x x x ．四、1．t t cos -； 2．)(1t f ''；五、1．dx x x x x ⎥⎦⎤⎢⎣⎡--+-2222211cot )1(2)11ln(sin ；2．dx xye x xy xye y y x y x ++--+；六、212x +. 第二章测验题一、,1.3,1.2,)1(21.1arctan =⋅+--y dx e x x x π)1()1(4)1()1(21)1(2.43442x f x f x x f x f x x x f '+''+⎥⎦⎤⎢⎣⎡'； 2ln 21.5-．二、..3,.2,.1C D D三、1．3322)2(42y yy y xe y xe ye e +++-； 2．214t t +； 3．0；4．[]2()sin ()cos ,0(0),()1,0[(0)1]2x g x x g x xx x a g f x x g '⎧+-+⎪≠⎪⎪''==⎨⎪=''⎪+⎪⎩第三章微分中值定理与导数的应用习题一一、1．不满足，2πξ=； 2．1； 3．满足，914； 4．4,1--．二、三、四、(略)．五、111., 2.0,3.,4.3,5.ln ,6.1,22a -六*、(略)．习题二一、1．单减，凹的； 2．(),29,23.4,0,0.34,1-==x y 5. ac b 32<.二、单减区间为]([],02,-∞⋃+∞；单增区间为[]0,2 三、拐点为()7,1-；凹区间为)[∞+,1；凸区间为[]1,0．四、0,3,3,1==-==d c b a 五、(略) 六、极大值17)1(=-f ；极小值47)3(-=f ；七、为极大值3)3(,2==πf a . 八、(略)第三章测验题一、1.; 2.; 3.; 4.; 5..B B A C A二、()0.5;,.4;2,1.3;4.2;1.1=>±x 凹的三、1.3;0.2;61.1-; 4.∞四、3;0; 1.a b c =-== 五*、83(,)55第四章不定积分习题一一、1．dx x f )(，C x f +)(，)(x f ，C x f +)(； 2．C ； 3．C x +2； 4．32x ； 5．)11(1x e x -； 6．21x-．二、1．C x x +-arctan ； 2．C x e x +-2；3．C x x +-sec tan ； 4．C x +tan 21； 5．C x x x e x+---tan cot ； 6．427)7(4xx +．三、1ln +=x y四、12)(2+-=x x x G 习题二一、1．C e x x ++-tan tan ； 2．C x f +--)1(212； 3．C x F ++)12(；4．C x f +--）2cos 3(31．二、1．C x +|ln ln |ln ； 2．C x ++-|1cos |ln 2； 3．C e x +arctan ；4．C x +--21)32(312； 5．C x x x +---------999897)1(991)1(491)1(971；6．C e x x ++1； 7．C x x +-32)cos (sin 23； 8．C e x x ++-)1ln(；9．C x x ++-)9ln(292122； 10．C x x +-5cos 101cos 21； 11．C e e x x +--)arctan(； 12．C x+-arcsin 1； 13．C x x ++21； 14．C e x +-1arctan 2；15．C xx x x +-+-21arcsin ；习题三一、1．C x e x ++-)1(；2．C x xf +)(； 3．C x f x f x +'-'')()(； 4．C e xe x x +-2．二、1．C x x x x +++-)1ln(6161arctan 31223； 2．C x x x x +++-|cos |ln tan 212；3．C x x x x x ++-2ln 2ln 2； 4．C x x x x++++-)6ln 6ln 3(ln 123；5．C x x e x ++-)22(33323； 6．C x x x++)ln sin ln (cos 2；7．C x x x x x +--+2arcsin 12)(arcsin 22； 8．C x x x x ++-sin 4cos )24(；三、C x x x +-++21)arcsin 1(．四、C x x x x ++-+arctan 22)1ln(2．习题四1． C x x x x +-+-+-arctan 21)1ln(41|1|ln 21||ln 22． C x ++-|1csc |ln 3．C x x x +++++-+|11|ln 313)1(233332 4． C x x ++66)1(ln5．C x +2tan arctan2126． arcsin x c第五章定积分习题一一、1．>， 2．>; 二、（提示：用定积分性质6证）三、（略）四、1．412x x +； 2．81221213x x x x +-+； 3．3； 4．21； 5．28-x ； 6．]41,0(； 7．yx e y 2cos 22．五、)(x f 在0=x 处有极小值0)0(=f ．六、1．6π； 2．4； 3．38．七、1．1； 2．2 八*、4π．习题二一、1．)(sin x f ； 2．)0(arctan )1(arctan f f -； 3．)]()([2122a F b F -； 4．3243π；5．0； 6．)()(a x f b x f +-+； 7．8； 8．0二、1．34-π； 2．32ln 22+； 3．a )13(-； 4．34； 5．22； 6．214-π； 7．)11(2e -； 8．)2(51-πe ．三、四（略）五、（提示：令x t -=2π）；4π六*、(提示：用分部积分法) 七*、(提示：用分部积分法)习题三一、B二、1．π； 2．2π．3．22p ωω+; 4．∞ 第六章定积分的应用一、1．332； 2．2ln 23-； 3．21-+e e ； 4．23a π； 5．π45；二、2e 三、π7128；π564四、π103；五*、A b a ==,0《高等数学（下）与线性代数》习题参考答案第六章微分方程习题一一、判断题1、×；2、√；3、√；4、×；5、× 二、填空题1、2)(ln 21)(x x f =；2、x cxe y -=；3、x y 2=；4、x x x y 91ln 31-=；5、C t x +=)(ln ϕ三、1、C y x =⋅tan tan ； 2、C e e y x =-⋅+)1()1( 四、22sec )1(=⋅+y e x五、1、Cx y x =-332； 2、223x y y -= 六、)ln 41(x x y -= 七、1、)(sin C x ey x+=-； 2、322Cy y x +=； 3、)cos 1(1x y --=ππ 八、⎪⎪⎭⎫ ⎝⎛-+=-t m ke k m k t k k v 2122121 九、x x e e xf 2323)(-=习题二一、选择题 1、（C ）； 2、（B ）； 3、（D ）； 4、（C ）； 5、（B ）； 6、（A ）； 7、（D ）二、填空题1、3221)3(C x C x C e x y x +++-=；2、22121C x x e C y x +--=； 3、)1ln(1+-=ax ay三、1、x x e C e C y 221-+=；2、x C x C y sin cos 21+=；3、x C x C e C e C y x x sin cos 4321+++=-；4、x e y x 5sin 32-= 四、⎪⎭⎫ ⎝⎛-+=+-++-tk k tk k k eek k v x 1221222424122014五、)sin (cos 21)(x e x x x ++=ϕ 六、xe x c x x c y xcos 5sin 2cos 2cos 21++⋅= 第八章多元函数微分学习题一一、 1、yyx +-112； 2、},0,0|),{(2y x y x y x ≥≥≥； 3、1，-4； 4、⎪⎪⎭⎫ ⎝⎛++++xy xy xy xy x 1)1ln()1(，12)1(-+x xy x ； 5、22812y x -，22812x y -，xy 16-．二、1．D ； 2．A ；3．D ；4．B ；5．A三、 1．（1）)ln(21xy x x z =∂∂，)ln(21xy y y z =∂∂；（2）1-=∂∂z yx z y x u ，x x z y u zy ln 1=∂∂，x x z y z u z yln 2-=∂∂ 2.12222222222222222223.z xy z xyx x y y x y z y xx y x y ∂∂==-∂+∂+∂-=∂∂+（）（）（）4．xdz yx xdy zx dx yzx du yz yz yz ln ln 1++=-5．dy dx 3231+习题二一、1、)()(y x f xy y x yf +'++，)()()()(y x f xy y x f y x y x f +''++'+++；2、2242232f y x f y x ''+'； 3、dy f f dx f f ⎪⎪⎭⎫ ⎝⎛+''-''-12121； 4、y x y x -+； 5、x y z z z -ln ln ，yyz xy z ln 2-二、 1、C ； 2、A ； 3、C ； 4、B ； 5、C 三、 1、321f yz f y f x u '+'+'=∂∂，32f xz f x yu '+'=∂∂，3f xy z u '=∂∂ 3、212f x f y x z '+'=∂∂，22122211124)(2f xy f y x f xy f yx z''-''-+''+'=∂∂∂ 7、)()(1)](1)[(v g u f v g u f x z ''+'+'=∂∂，)()(1)](1)[(v g u f v g u f y z ''+'+'-=∂∂8、3322312211122cos 2cos sin f e e f x f e x f x f xzy x y x y x ''+⋅'+⋅''+⋅''+⋅'-=∂∂+++； 332232313122sin cos sin cos f e f y e f e f x e y x f yx zy x y x y x y x ''+''⋅-'+''⋅+''-=∂∂∂++++ 习题三一、1、A ；2、C ；3、C 二、1、极小值：2)1,21(ef -=--．2、当0222<-a b ，且0<a 时，有唯一极小值；当0222<-a b ，且0>a 时，有唯一极大值．3、32p ，3p． 4、在点)1,1(-处有极小值：-2；极大值：6．第九章重积分习题一、1.()2ab a b +； 2．⎰⎰e e y dx y x f dy ),(10； 3．)1(214--e ； 4．⎰⎰θππθsec 2034)(rdr r f d ；1210cos sin 5.(cos ,sin )d f r r rdr πθθθθθ+⎰⎰二、1. 2. 3. 4. 5.C A B D C三、1.[36,100]ππ； 62.55； 1.3--e e ； 4．49； 5．2643π； 6．38；《线性代数》习题参考答案习题一一、填空题1．)1(-n n ；2．+； 3．0（提示：由根与系数的关系：0=++γβα）； 4．-600； 5．)1)(1(++cd ab ．二、计算题 1．n n nb a 1)1(--+； 2．1)]()1([---+n a x a n x ；3．∑=+ni in a a a a 121)11( （提示：先第1行乘（-1）加到第2、3、…、n 行上；再第j 列乘ja a 1加到第1列）； 4．6； 5．1)2]()2([---+n a x a n x ．三、证明题（略）习题二一、填空题1．21； 2．E ； 3．)(21E A -，)3(41E A --； 4．⎪⎪⎭⎫⎝⎛--0011A B ； 5．⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----8500320000520021； 6．⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛n a a a 11121 ．二、选择题1．③；2．③；3．②；4．③；5．②；6．①；7．③；8．③．三、计算题1．⎪⎪⎭⎫ ⎝⎛---3/253/8122； 2．⎪⎪⎪⎭⎫ ⎝⎛201030102； 3．-16； 4．0≠k ，⎪⎪⎪⎭⎫ ⎝⎛-=-1/110/100011k k A ．四、证明题（略）习题三一、1．2； 2．)()(b A R A R =； 3．1≠λ且2-≠λ； 4．04321=+++a a a a ．二、1．④； 2．④； 3．④；4．①； 5．④三、⎪⎪⎪⎭⎫ ⎝⎛---011101110；四、（1）1=k ；（2）2-=k ；（3）1≠k 且2-≠k ．五、（1）2,1-≠λ ；（2）2-=λ；（3）1=λ．六、2-≠b 时，方程组无解；2-=b ，无论a 取什么值时，方程组有无穷多解．当8-=a 时，⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛001110210124214321k k x x x x ；当8-≠a 时，⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛001110214321k x x x x ．证明题（略）．习题四一、1．5=t ； 2．至少有一个向量； 3．321,,ααα ；4．2≤r ；5．t s r -= 二、1．④； 2．③； 3．③； 4．③； 5．② 三、321,,ααα为极大无关组，323214,3ααααααα+-=-+=四、（1）4-=α且0≠β ；（2）4-≠α ；（3）4-=α且321)12(,0αααβ++-==c c b 五、⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=54326543c x 六、1-≠a 时，向量组A 、B 等价．证明题略．习题五一、1．1或-1 ；2．E ；3．18 ；4．11=λ（二重），212-=λ；5．125 ； 6．4=λ ； 7．2524232221y y y y y ---- ；8．2<t ；9．可逆；10．232221455y y y -+二、1．②； 2．③； 3．④； 4．②； 5．④ 三、⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-===23132212343102313221,5,4P y x 四、⎪⎪⎪⎭⎫⎝⎛------=244354332A 五、⎪⎪⎪⎭⎫ ⎝⎛-=022********A六、当3=x 时，A 可对角化．证明题略．。

高等数学1(上册)试题答案及复习要点汇总(完整版)

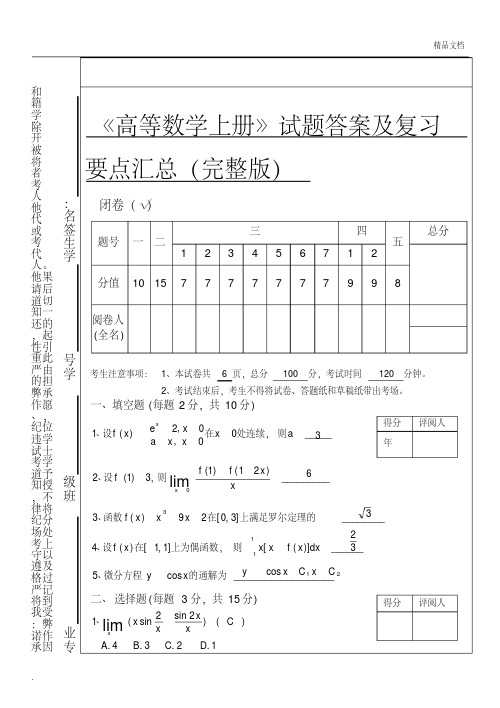
xe x e x 0 3
0 cos2 d (令 x 1 sin )
2
2e3 1 4
12. 解：由 f (0) 0 ，知 g(0) 0 。
x
1
f ( u ) du
xt u
g ( x ) f ( xt )dt 0
0
x
(x
x
xf ( x ) f (u)du
g ( x)
0
x2
x
( x 0)
f (u )du
2
1
代入初始条件 y(0)
y (0) 1，得
3 4 3 )e4 x 4
通解 y x ( 1 x 3 )e4x 44
C1e2 x
C 2e4x
五、证明题 (8 分 )
得分评阅人
1、设 f ( x )在 [0，1]上连续，证明：
2 f (sin x)dx 2 f (cos x)dx
0
0
证令x
t，则 dx dt
2
2 f (sin x )dx
0
0
2
2
当x
1 时 f ( x) 取极小值，极小值为 f ( 1 )
11 e
2
22
2x
2x
f (x ) 4e
4 xe
令f (x ) 0得 x 1
当 x 1时， f ( x ) 0，当 x 1时， f ( x ) 0 拐点为 (1，e 2 )
得分评阅人
.
精品文档
2、求微分方程 y 6 y 8 y ( x 1) e4 x 的通解 .
.
3、设y (cos x ) sin x，求 dy.
解两边取对数得 ln y sin x ln cos x

2000年高考数学(理科)真题及答案[全国卷I]

2000年普通高等学校招生全国统一考试数学(理工农医类)本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分。

第I 卷1至2页。

第II 卷3至9页。

共150分。

考试时间120分钟。

第I 卷(选择题 60分)注意事项：1、答第I 卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。

2、每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试题卷上。

3、考试结束，监考人将本试卷和答题卡一并收回。

选择题：本大题共12小题；第每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

(1)设集合A 和B 都是自然数集合N ，映射f:A →B 把集合A 中的元素n映射到集合B 中的元素2n +n ，则在映射f 下，象20的原象是(A)2 (B)3 (C)4 (D)5i 3对应的向量按顺时针方向旋转3π，i 33+2，3， 6，(4)已知sin α>sin β，那么下列命题成立的是(A)若α、β是第一象限角，则cos α>cos β(B)若α、β是第二象限角，则tg α>tg β(C)若α、β是第三象限角，则cos α>cos β(D)若α、β是第四象限角，则tg α>tg β(5)函数y=-x cos x 的部分图象是(6)《中华人民共和国个人所得税法》规定，公民全月工资、薪金所得不超过 800元的部分不必纳税，超过800元的部分为全月应纳税所得额。

此项税款按下表分段累进计算：<div align="center"> 全月应纳税所得额税率不超过500元的部分 5%超过500元至2000元的部分 10%超过2000元至5000元的部分 15%… …</div>某人一月份应交纳此项税款26.78元，则他的当月工资、薪金所得介于800~900元 (B)900~1200元(C)1200~1500元 (D)1500~2800元(7)若a >b >1，)2lg(),lg (lg 21,lg lg ba R Q P +=+=⋅=βαβα,则(A)R<P<Q (B)P<Q< R(C)Q< P<R (D)P< R<Q(8)以极坐标系中的点(1,1)为圆心，1为半径的圆的方程是(A))4cos(2πθ-=p (B))4sin(2πθ-=p (C))1sin(2-=θp (D))1sin(2-=θp(9)一个圆柱的侧面展开图是一个正方形，这个圆柱的全面积与侧面积的比是(A) (B) (C) (D)(10)过原点的直线与圆相切，若切点在第三象限，则该直线的方程是(A) (B) (C) (D)(11)过抛物线的焦点F 作一条直线交抛物线于P 、Q 两点，若线段PF 与FQ 的长分别是p 、q ，则等于(A)2a(B)(C)4a(D)(12)如图，OA是圆锥底面中心O到母线的垂线，OA绕轴旋转一周所得曲面将圆锥分成体积相等的两部分，则母线与轴的夹角为2000年普通高等学校招生全国统一考试数学(理工农医类)第II卷(非选择题90分)注意事项：第II卷共7页，用钢笔或圆珠笔直接答在试题卷中。

2009-2010学年第一学期高等数学(1)期末试卷及其答案

2009 至 2010学年度第 1 期高等数学（1）课程考试试题册（A ）试题使用对象：2009级理工科各专业本科学生命题人：考试用时 120 分钟答题方式采用：闭卷说明：1.答题请使用黑色或蓝色的钢笔、圆珠笔在答题纸上书写工整.2.考生应在答题纸上答题，在此卷上答题作废.一. 填空题（每小题3分，本题15分）. 1. 11lim(sinsin )x x x x x→∞+=（）. 2. 微分 tan ()x de f x dx -⎰＝（）. 3. 曲线x e y x -=在点（0，1）处的切线方程是（）. 4.设连续函数)(x f 满足：)(x f = 2xx +1()f x dx ⎰，则)(x f =（）.5. 微分方程22250d y dyy dx dx-+=的通解为（）. 二. 单项选择题（每小题3分，本题15分）.1. 0sin 3limln(13)x xx →=+（）. A. 0 B. 1 C. 1/2 D. 32.下列广义积分收敛的是（）. A.sin xdx +∞⎰B.20xedx +∞-⎰C.1dx x+∞⎰D. 0dx +∞⎰3.下列变量中，（）是无穷小量. A. )1(ln →x x B. )0(1ln+→x x C. )0(cosx →x D. )2(422→--x x x 4. 定积分22sin 1x x x ππ-+⎰dx =（）. A. 2 B. -1 C. 0 D. 15．已知(),()1x y f e f x x '==-,0x dy dx=则=（）.A. 1B. eC. 2D. 0 三.计算题（每小题7分，本题共49分）.21. 求极限 2011lim()tan x x x x→-. 2. 设cot (1tan )()2sin x b x f x arc ax x ⎧⎪+⎪=⎨⎪⎪⎩000x x x <=> 在0=x 处连续，求b a ,的值.3. 已知⎩⎨⎧+=-=)sin (cos )cos (sin t t t a y t t t a x ，求 22dx y d 在 2t π= 处的值.4. 计算积分π⎰dx .5. 计算积分 2(1)xxe x +⎰dx . 6. 已知()1f π=，(()())sin 3f x f x xdx π''+=⎰，求(0)f .7. 求解微分方程sin dy y xdx x x+=，1x y π==.四. 应用题（本题10分）.设抛物线2y ax bx c =++通过点(0,0)，且当[0,1]x ∈时，0y ≥. 试确定,,a b c 的值，使得该抛物线与直线1,0x y ==所围图形的面积为49，且使该图形绕x 轴旋转而成的旋转体的体积最小.五. 证明题（1小题5分，2小题6分，本题共11分）.1. 若函数)(x f 在闭区间],[b a 上连续，在开区间),(b a 内可导，且0)()(==b f a f . 证明：至少有一点),(b a ∈ξ，使得0)()(='+ξξξf f .2. （1）设0>x ，证明：11ln(1)1x x+>+. （2）证明：当1x >时，函数1(1)xy x=+单调递增.2009 至 2010 学年度第 1 期高等数学（上）课程考试试题(A)参考答案一. 填空题（每小题3分，本题15分）.1. 12. tan ()x e f x dx -3. 1=y4. +x 243x 5. (cos2sin2)x y e a x b x =+，,a b 为任意常数. 二. 单项选择题（每小题3分，本题15分）.1.B2. B3. A4. C5. D 三.计算题（每小题7分，本题共49分）. 1.解： 220011tan lim()limtan tan x x x xx x xx x →→--= 2分 300tan lim limtan x x x x xx x →→-= 4分 222200sec 1tan 1lim lim 333x x x x x x →→-=== 7分 2. 1tan 0lim ()lim (1tan )xx x f x b x --→→=+b e = ２分sin lim ()lim x x arc axf x a x++→→== ４分因为 )(x f 在0=x 处连续, 所以0lim ()lim ()(0)x x f x f x f -+→→==即 2be a == ，所以 2,l n a b ==7分3.(sin sin cos )cos dya t t t t at t dt=-++= (cos cos sin )sin dxa t t t t at t dt=-+= 2分 cos cot sin dy at t t dx at t == 4分 2223(cot )csc 1()sin sin d y t t dx x t at t at t'-===-' 6分4所以 2222t d y dx a ππ==-7分 4. 解：原式 1/20(sin )cos x x dx π=⎰2分/21/21/20/2(sin )cos (sin )(cos )x xdx x x dx πππ=+-⎰⎰5分3/2/23/20/222(sin )(sin )33x x πππ=-43=7分 5. 21(1)1x xxe dx xe d x x=-++⎰⎰ 2分 1(())11x x xe d xe x x =--++⎰ ()11x x xxe e xe dx x x +=--++⎰ 6分1x x xe e dx x =-++⎰1x xxe e c x =-+++1x e c x=++ 7分6. 0(()())sin ()sin ()sin f x f x xdx f x xdx f x xdx πππ''''+=+⎰⎰⎰（1） 1分而()sin sin ()f x xdx xdf x ππ'''=⎰⎰()sin ()sin f x x f x d x ππ''=-⎰()cos cos ()f x xdx xdf x ππ'=-=-⎰⎰(()cos ()cos )f x xf x d x ππ=--⎰(()cos (0)cos0)()(sin )f f f x x dx πππ=--+-⎰()(0)()sin f f f x xdx ππ=+-⎰（2） 6分把（2），()1f π=代入（1），原式为 31(0)f =+，得(0)2f = 7分7. 解：对于0dy y dx x +=，分离变量 d y d x y x=-，积分得1ln ln y x c =-+， cy x=3分令 ()u x y x =，则 ()sin u x xx x'=，()sin u x x '=，积分得()cos u x c x =-，方程通解 cos c x y x-=，代入,1x y π==，解出 1c π=-，特解 1cos x y xπ--=. 7分四. 应用题（本题10分）.1. 解：2y ax bx c =++通过点(0,0)，得0c =，所以2y ax bx =+. 1分抛物线与直线1,0x y ==所围图形的面积为120()S ax bx dx =+⎰321011()32ax bx =+ 32a b =+=49，869a b -= (1) 4分图形绕x 轴旋转而成的旋转体的体积1220()V ax bx dx π=+⎰1243220(2)a x abx b x dx π=++⎰4252310121()543abx a x b x π=++22()523a ab b π=++2286186(())52939a a a a π--=++222418(())1358139a a π=++ (2) 7 分 44()()13581a V x π'=+, 令()0V x '=，得 1355813a =-=-，从而2b =. 10分五. 证明题（1小题5分，2小题6分，本题共11分）.1. 证明：()()F x xf x =， 2分由题意()F x 在闭区间],[b a 上连续，在开区间),(b a 内可导， ()()()F x f x xf x ''=+，()()0F a F b ==. 由罗尔定理知，至少存在一点(,)a b ξ∈，使()()()0F f f ξξξξ''=+=. …5分2. 证明：（1）令()ln f x x =，当0x >时，显然()f x 在[,1]x x +上连续，在(,1)x x +上可导，1()f x x'=，由Lagrange 中值定理知，存在(,1)x x ξ∈+，使得 1ln(1)ln 11ln(1)(1)1x x x x x xξ+-+==>+-+ 3分6（2）令1(1)xy x=+，则ln [ln(1)ln ]y x x x =+-，方程两边同时对x 求导1111ln(1)()1y x y x x x'=++-+，11(ln(1))1y y x x '=+-+ 由（1）知，0y '>，1(1)xy x=+单调递增. 6分。

2000~2001年上海高考数学试题

2001年上海高考数学试题一、填空题1.(理)设函数f(x)=，则满足41)(=x f 的x 值为 . (文) 设函数x x f 9log )(=, 则满足21)(=x f 的x 值为 .2.(理)设数列的通项为a n =2n －7(n ∈N*)，则|a 1|＋|a 2|……＋|a 15|= . (文) 设数列的首项,且满足,则a 1＋a 2……＋a 17= . 3.设P 为双曲线－y 2=1上一动点，O 为坐标原点，M 为线段OP 的中点，则点M 的轨迹方程为 . 4.设集合A={x|2lgx=lg(8x —15)，x ∈R}B={x|cos＞0，x ∈R}，则A∩B 的元素个数为个. 5.抛物线x 2－4y －3=0的焦点坐标为 .6.设数列是公比q ＞0的等比数列，S n 是它的前n 项和.S n ＝7，则此数列的首项a 1的取值范围是 .7.某餐厅供应客饭，每位顾客可以在餐厅提供的菜肴中任选2荤2素共4种不同的品种.现在餐厅准备了5种不同的荤菜，若要保证每位顾客有200种以上不同的选择，则餐厅至少还需要准备不同的素菜品种种.（结果用数值表示）8.(理)在代数式(4x 2－2x －5)(1+)5的展开式中，常数项为 .(文) 在代数式62)1(x x -的展开式中，常数项为 .9.设x=sinα，α∈［－，］，则arccosx 的取值范围为 .10.(理)直线y=2x －与曲线（φ为参数）的交点坐标为 .11.已知两个圆：x 2+y 2=1①与x 2+(y －3)2=1②，则又①式减去②式可得上述两圆的对称轴方程.将上述命题在曲线的情况下加以推广，即要求得到一个更一般的命题，而已知命题应成为所推广命题的一个特例，推广的命题为.12. 据报道，我国目前已成为世界上受荒漠化危害最严重的国家之一.下左图表示我国土地沙化总面积在上个世纪五六十年代、七八十年代、九十年代的变化情况.由图中的相关信息，可将上述有关年代中，我国年平均土地沙化面积在下右图中图示为.二、选择题13.a=3是直线ax+2y+3a=0和直线3x+(a－1)y=a－7平行且不重合的（）A.充分非必要条件B.必要非充分条件C.充要条件D.既非充分也非必要条件14.如图在平行六面体ABCD－A1B1C1D1中，M为AC与BD的交点，若＝、＝、＝，则下列向量中与相等的向量是（）A.－＋＋B.＋＋C.－＋D.－－＋15.已知a、b为两条不同的直线，α、β为两个不同的平面，且a⊥α，b⊥β，则下列命题中的假命题是（）A. 若a∥b，则α∥βB.若α⊥β，则a⊥bC.若a、b相交，则α、β相交D.若α、β相交，则a、b相交16. 用计算器验算函数y=（x＞1）的若干个值，可以猜想下列命题中的真命题只能是（）A. y=在（1，+∞）上是单调减函数B. y=，x∈（1，+∞）的至于为（0，C. y=，x∈（1，+∞）有最小值D.=0 ，n∈N三、解答题17.已知a、b、c是△ABC中∠A、∠B、∠C的对边，S是△ABC的面积，若a=4，b=5，S=5，求c的长度.18.设F1、F2为椭圆＝1的两个焦点，P为椭圆上的一点.已知P、F1、F2是一个直角三角形的三个顶点，且|PF1|＞|PF2|,求的值.19.在棱长为a的正方体OABC－O'A'B'C'中，E、F分别是棱AB、BC上的动点，且AE=BF. （1）求证：A'F⊥C'E；（2）当三棱锥B'－BEF的体积取得最大值时，求二面角B'－EF－B的大小.（结果用反三角函数表示）20.(理)对任意一个非零复数z，定义集合M z={ω|ω=z2n-1，n∈N*}.（1）设a是方程x+＝的一个根，试用列举法表示集合M a.若在M a中任取两个数，求其和为零的概率P；（2）设复数ω∈M z，求证MωM z .(文) 对任意一个非零复数z，定义集合M z={ω|ω=z n，n∈N*}.（1）设a是方程1=+xx的一个根，试用列举法表示集合M a.若在M a中任取两个数，求其和为零的概率P；（2）设集合M z中只有3个元素,试写出满足条件的一个z的值,并说明理由 .21. 用水清洗一堆蔬菜上残留的农药，对用一定量的水清洗一次的效果作如下假定：用1个单位量的水可洗掉蔬菜上残留农药用量的，用水越多洗掉的农药量也越多，但总还有农药残留在蔬菜上.设用x单位量的水清洗一次以后，蔬菜上残留的农药与本次清洗前残留有农药量之比为函数f（x）.（1）试规定f（0）的值，并解释其实际意义；（2）试根据假定写出函数f（x）应该满足的条件和具有的性质；（3）设f（x）=，现有a（a＞0）单位量的水，可以清洗一次，也可以把水平均分成2份后清洗两次.试问用哪种方案清洗后蔬菜上的农药量比较少？说明理由22. 对任意函数f（x），x∈D，可按图示构造一个数列发生器，其工作原理如下：①输入数据x0∈D，经数列发生器输出x1=f（x0）；②x1D，则数列发生器结束工作；若x1∈D，则将x1反馈回输入端，再输出x2=f（x1），并依此规律继续下去.现定义f（x）=.（1）若输出x0=，则由数列发生器产生数列{x n}.请写出数列{x n}的所有项；（2）若要数列发生器产生一个无穷的常数数列，试求输出的初始数据x0的值；（3）(理)若输出x0时，产生的无穷数列{x n}满足：对任意正整数n均有x n＜x n+1，求x0的取值范围.(文)是否存在x0,,在输入数据x0时, 该数列发生器产生一个各项均为负数的无穷数列?若存在,求出x0的值;若不存在,请说明理由.2000年全国普通高等学校招生统一考试上海数学试卷一、填空题（本大题满分48分）本大题共有12题，只要求直接填写结果，每个空格填对得4分，否则一律得零分。

2001年高考数学(理科)真题及答案[全国卷I]

2001年全国普通高等学校招生全国统一考试数学(理工农医类)一．选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．(1)若0cos sin >θθ，则θ在(A)第一、二象限 (B)第一、三象限 (C)第一、四象限 (D)第二、四象限 (2)过点A(1，-1)，B(-1，1)且园心在直线x+y-2=0上的圆珠笔的方程是 (A)(x-3)2+(y+1)2=4 (B)(x+3)2+(y-1)2=4 (C)(x-1)2+(y-1)2=4 (B)(x+1)2+(y+1)2=4(3)设{a n }是递增等差数列，前三项的和为12，前三项的积为48，则它的首项是 (A)1 (B)2 (C)4 (D)6(4)若定义在区间(-1，0)内的函数f (x )= log 2a (x ＋ 1)满足f (x )＞ 0，则 a 的取值范围是(A)(0，21) (B) (0，21] (C) (21，+∞) (D) (0，+∞)(5)极坐标方程)4sin 2πθρ+=的图形是(6)函数)0(1cos ≤≤-+=x x y π的反函数是(A) )20)(1arccos(≤≤--=x x y (B) )20)(1arccos(≤≤--=x x y π (C) )20)(1arccos(≤≤-=x x y (D) )20)(1arccos(≤≤-+=x x y π (7)若椭圆经过原点，且焦点为F 1(1，0)，F 2(3，0)，则其离心率为(A) 43(B) 32 (C) 21 (D) 41(8)若ba =+=+<<<ββααπβαcos sin ,cos sin ,40，则(A)a <b (A)a >b(A)ab <1(D)ab >2(9)在正三棱柱ABC －A 1 B 1C 1中，若AB =2BB 1，则AB 与C 1B 所成的角的大小为(A)60°(B)90°(C)105°(D)75°(10)设f(x)、g(x)都是单调函数，有如下四个命题：①若f(x)单调速增，g(x)单调速增，则f(x)-g(x))单调递增;②若f(x)单调速增，g(x)单调速减，则f(x)-g(x))单调递增;③若f(x)单调速减，g(x)单调速增，则f(x)-g(x))单调递减;④若f(x)单调速减，g(x)单调速减，则f(x)-g(x))单调递减;其中，正确的命题是(A)①③(B)①④(C)②③(D)②④(11)一间民房的屋顶有如图三种不同的盖法：①单向倾斜；②双向倾斜；③四向倾斜．记三种盖法屋顶面积分别为P1、P2、P3．若屋顶斜面与水平面所成的角都是α，则(A)P3>P2>P1 (B) P3>P2=P1(C) P3=P2>P1(D) P3=P2=P1(12)如图，小圆圈表示网络的结点，结点之间的连线表承它们有网线相联．连线标注的数字表示该段网线单位时间内可以通过的最大信息量．现从结点A向结点B传递信息，信息可以分开沿不同的路线同时传递．则单位时间内传递的最大信息量为(A)26(B)24(C)20(D)19二．填空题：本大题共4小题，每小题4分，共16分．把答案填在题中横线上．(13)若一个圆锥的轴截面是等边三角形，其面积为3，则这个圆锥的侧面积是_________．(14)双曲线116922=+yx的两个焦点为F1、F2，点P在双曲线上．若PF⊥PF2，则点P到x轴的距离为_________。

大一上学期(第一学期)高数期末考试题(有答案)

大一上学期(第一学期)高数期末考试题(有答案)------------------------------------------作者xxxx------------------------------------------日期xxxx大一上学期高数期末考试一、单项选择题 (本大题有4小题, 每小题4分, 共16分) 1. )(0),sin (cos )(　处有则在设=+=x x x x x f .（A ）(0)2f '= （B ）(0)1f '=（C ）(0)0f '= （D ）()f x 不可导.2. ）时（　，则当，设133)(11)(3→-=+-=x x x x xx βα.（A ）()()x x αβ与是同阶无穷小，但不是等价无穷小；（B ）()()x x αβ与是等价无穷小；（C ）()x α是比()x β高阶的无穷小；（D ）()x β是比()x α高阶的无穷小.3. 若()()()02xF x t x f t dt=-⎰，其中()f x 在区间上(1,1)-二阶可导且'>()0f x ，则（）.（A ）函数()F x 必在0x =处取得极大值；（B ）函数()F x 必在0x =处取得极小值；（C ）函数()F x 在0x =处没有极值，但点(0,(0))F 为曲线()y F x =的拐点；（D ）函数()F x 在0x =处没有极值，点(0,(0))F 也不是曲线()y F x =的拐点。

4.)()( , )(2)( )(1=+=⎰x f dt t f x x f x f 则是连续函数，且设（A ）22x （B ）222x+（C ）1x - （D ）2x +.二、填空题（本大题有4小题，每小题4分，共16分） 5. =+→xx x sin 2)31(l i m .6. ,)(cos 的一个原函数是已知x f x x =⋅⎰x x xx f d cos )(则 .7.lim(cos cos cos )→∞-+++=22221n n nnnn ππππ .8. =-+⎰21212211arcsin －dx xx x .三、解答题（本大题有5小题，每小题8分，共40分）9. 设函数=()y y x 由方程sin()1x ye xy ++=确定，求'()y x 以及'(0)y .10. .d )1(177x x x x ⎰+-求11. ．　求，，设⎰--⎪⎩⎪⎨⎧≤<-≤=1 32)(1020)(dx x f x x x x xe x f x12. 设函数)(x f 连续，=⎰10()()g x f xt dt，且→=0()limx f x A x ，A 为常数.求'()g x 并讨论'()g x 在=0x 处的连续性.13. 求微分方程2ln xy y x x '+=满足=-1(1)9y 的解.四、解答题（本大题10分）14. 已知上半平面内一曲线)0()(≥=x x y y ，过点(,)01，且曲线上任一点M x y (,)00处切线斜率数值上等于此曲线与x 轴、y 轴、直线x x =0所围成面积的2倍与该点纵坐标之和，求此曲线方程. 五、解答题（本大题10分）15. 过坐标原点作曲线x y ln =的切线，该切线与曲线x y ln =及x 轴围成平面图形D.(1) 求D 的面积A ；(2) 求D 绕直线x = e 旋转一周所得旋转体的体积V . 六、证明题（本大题有2小题，每小题4分，共8分）16. 设函数)(x f 在[]0,1上连续且单调递减，证明对任意的[,]∈01q ，1()()≥⎰⎰qf x d x q f x dx.17. 设函数)(x f 在[]π,0上连续，且0)(0=⎰πx d x f ，cos )(0=⎰πdx x x f .证明：在()π,0内至少存在两个不同的点21,ξξ，使.0)()(21==ξξf f （提示：设⎰=xdxx f x F 0)()(）解答一、单项选择题(本大题有4小题, 每小题4分, 共16分) 1、D 2、A 3、C 4、C二、填空题（本大题有4小题，每小题4分，共16分）5. 6e . 6.c x x +2)cos (21　.7. 2π. 8.3π.三、解答题（本大题有5小题，每小题8分，共40分） 9. 解：方程两边求导(1)cos()()0x ye y xy xy y +''+++=cos()()cos()x y x ye y xy y x e x xy +++'=-+0,0x y ==，(0)1y '=-10. 解：767u x x dx du == 1(1)112()7(1)71u du duu u u u -==-++⎰⎰原式 1(ln ||2ln |1|)7u u c =-++ 7712ln ||ln |1|77x x C =-++11. 解：1033()x f x dx xe dx ---=+⎰⎰⎰3()x xd e --=-+⎰⎰00232cos (1sin )x x xe e d x πθθθ----⎡⎤=--+-=⎣⎦⎰令3214e π=--12. 解：由(0)0f =，知(0)0g =。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

济南大学2k01
高等数学（上）试题(A)
一、填空题：（本题共5小题，满分20分）
1、)2ln()(2x x x f -+=的定义域是。

2、
3
22
31lim
2
-+-+→x x x x 的值等于。

3、若=)(x f ⎩⎨⎧≤+>020
x ,a x x ,e x 是),(+∞-∞上的连续函数，则 a = 。

4、设函数 x s i n
x )x (f = 则=')(f 2
π。

5、定积分=⎰
++-dx x
x
1
12
1sin 1 。

二、选择题：（本题共10小题，满分 40分）将选择的正确答案的代号填在横线上，每小
１．设()x f 在()b a ,内连续，且()b a x ,0∈，则在点0x 处（）
(Ａ)．()x f 的极限存在，且可导； (Ｂ)．()x f 的极限存在，但不一定可导； (Ｃ)．()x f 的极限不存在，但可导； (Ｄ)．()x f 的极限不一定存在； 2、已知a 是大于零的常数，)1ln()(2x
a
x f -+=，则)0(f '的值应是
（A ）a ln ；（B ） a ln - ；（C ）
a ln 21；（D ）2
1 3、方程0133
=+-x x 在区间（0，1）内
（A ）无实根；（B ）有唯一实根；（C ）有两个实根；（D ）有三个实根 4、设3)2)(2(x x y -+=，则
（A ）2=x 是该函数的极值点；
（B ） 2=x 是该函数所表示曲线的拐点横坐标；（C ）2-=x 是该函数的极大值点；
（D ）1-=x 是该函数的极小值点.
5、曲线2,1,1
===
x y x
y 所围图形绕x 轴旋转体积为( ) (A) dx x
⎰2121π (B) dx x ⎰2
021π
(C) dx x ⎰-202)1(ππ ( D) dx x
⎰-2
12)1(ππ
6、f(x )在x 邻域内存在二阶连续导数，且000
<=-''→k x
x )
x (f lim
x x 则
(A). f （x ）图形在x=x 0邻域内是凹的；(B).f （x ）图形在x=x 0邻域内是凸的；
(C)．（f （x 0），x 0）是曲线的拐点； (D). x=x 0是f （x ）的极值点； 7.设()x f 是可导函数,x ∆是自变量在x 处的增量,则()()=∆-∆+→∆x
x f x x f
x 22
lim
（）
(A .) ()[]2
x f '； ( B). ()x f '2； ( C). ()()x f x f '2； (D)．不存在； 8、设函数)(x f 在()+∞∞-,上连续，则⎰
])([dx x f d 等于（）
(A) )(x f ， (B) ,)(C x f +， (C) dx x f )( (D) dx x f )('。

9、⎰
>=a a dx x f x I
023)0()( 则（）
（A ）⎰=2
;)(a dx x xf I
（B ）⎰=a dx x xf I 0
;)(
（C ）⎰=2
0;)(21a dx x xf I （D ）⎰=a
dx x xf I 0
;)(21
10、设x
x e
e x
f 11
11)(-+=
则0=x 是)(x f 的（）
（.A ）连续点（.B ）可去间断点（.C ）第二类间断点（.D ）跳跃间断点三、计算下列各题：（本题共5小题，满分25分） 1、x
x x
x sin cos 1lim 0-→
2、设()
⎩⎨⎧-=+=t
t y t x arctan 1ln 2，求：dx dy
3、计算dx x )1ln(2
⎰
+
4、计算dx x x ⎰+-1
0244
四、（7分）求由曲线：0,,===x ex y e y x 围成图形的面积；
五、（7分）试求单位球的内接正圆锥体，其体积为最大时的高与体积。

（如图）
六、（6分）设)(,0x f b a <<在],[b a 上可导，试证明存在)(b a <<ξξ使得：
a
b
f a f b f ln )()()(ξξ'=-。