济南大学2013高数B(二)期末
0910高等数学B( 二)试题答案济南大学

解
所求直线的一个方向向量 n (3, 7,5)
所求直线方程为 x 3 y0 z 1 3 7 5
2.设函数 z f ( x , y )是由方程 x 2 y 2 z 2 4z 给出, 则全微分 dz ;xdx ydy
2 n 1 x n arctan x ( 1) 2n 1 n 0
见教材P282
二、选择题 (每小题2分,共10分) 1、 f ( x, y )在点 ( x0 , y0 ) 可微是两个偏导数 f x ( x0 , y0 ), f y ( x0 , y0 )
都存在的 [ A. C.
(1)
n 1
n 1
n ; n 1 3
解 (1) 记 un sin
而级数
n 1
3
n
,
vn
3
n
.
因为 limsin
n
3
n
3
n
1
3
n
收敛,故原级数收敛.
n 1
un1 n1 3 1 lim n . ( 2) lim n u n 3 n 3 n
2 z u z v 2x 3x z 2 ln(3 x 2 y ) 2 x u x v x y y (3 x 2 y )
2. 计算
D
yd , 其中D 是抛物线
及直线
y 2 y2 x
所围成的闭区域. 解: 为计算简便, 先对 x 后对 y 积分, 则
济南大学高等数学下历年考题答案

得f x ( x, x) f x ( x, x) x 2
y( x) -2e 2 x f ( x, x) x 2e 2 x
一阶线性微分方程
P( x) 2
Q( x ) x 2e 2 x
P ( x ) dx
ye
P ( x ) dx
[C Q( x )e
B( x, y )
在 整 个 xoy面 内2 xydx x 2dy是 某 个 函 数 的 全 微 分
取积分路径,如图:
则u( x, y )
2
( x, y)
( 0, 0 )
2
2 xydx x dy
2
2 2
OA
xy dx x ydy xy dx x ydy
2
AB
A( x ,0)
2 xdv 2 ydv 0 (由对称性)
上式 dv
2
0
d
1 rdr 2 dz 0 r 2
1
1
3、计算曲面积分 I x 2 dydz y 2 dzdx ( z x)dxdy ,其中 为抛物面 z
1
) ( x n1 )
n 0
(
1 x ) (1 x ) 2 1 x
1
( x 6 y)dxdy,其中 D 是由 y x
D
y 5x 和 x 1 ,
y 5x
所围成的闭区域.
dx ( x 6 y )dy 0
x
1
5x
y x
0
1
2. ( 2 xy3 y 2 cos x )dx (1 2 y sinx 3 x 2 y 2 )dy ,其中
2013-2014高数IIB试卷A
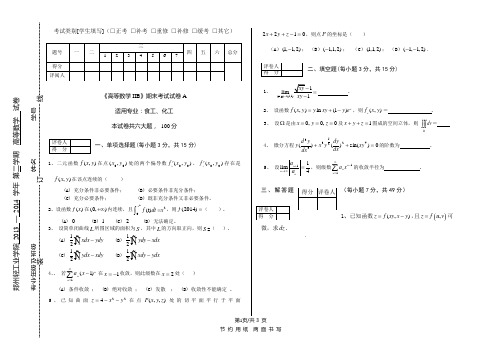
第1页/共3 页 考试类别[学生填写](□正考 □补考 □重修 □补修 □缓考 □其它)《高等数学IIB 》期末考试试卷A适用专业:食工、化工 本试卷共六大题, 100分一、单项选择题(每小题3分,共15分)1、二元函数),(y x f 在点),(00y x 处的两个偏导数),(00y xf x ',),(00y x f y '存在是),(y x f 在该点连续的( )(A) 充分条件非必要条件; (B) 必要条件非充分条件;(C) 充分必要条件; (D) 既非充分条件又非必要条件。
2、设函数()f x 在(0,)+∞内连续,且22(t)x f dt x =⎰,则(2014)f =( ).(A) 0 (B) 1 (C) 2 (D) 无法确定。
3、 设简单闭曲线L 所围区域的面积为S ,其中L 的方向取正向,则S =( ). (A)12L xdx ydy -⎰Ñ (B) 12L ydy xdx -⎰Ñ (C) 12L ydx xdy -⎰Ñ (D) 12L xdy ydx -⎰Ñ4、、 若∑∞=-1)1(n n nx a在1-=x 收敛,则此级数在2=x 处( )(A) 条件收敛 ; (B) 绝对收敛 ; (C) 发散 ; (D) 收敛性不能确定 。
5、已知曲面224yx z --=在点(,,)P x y z 处的切平面平行于平面0122=-++z y x ,则点P 的坐标是( )(A )(1,1,2)-; (B )(1,1,2)-; (C )(1,1,2); (D )(1,1,2)--.二、填空题(每小题3分,共15分)1、 (x,y)(1,1)lim→= .2、 设函数(,)ln (1)xf x y y xy y e =+-,则(,)x f x y = .3、 设Ω是由0,0,0x y z ===及1x y z ++=围成的空间立体,则dv Ω⎰⎰⎰=4、 微分方程0)sin()()(4225333=++xy dx dy y x dxy d y 的阶数为 .5、 设11lim 4n n na a +→∞=,则级数11n n n a x ∞-=∑的收敛半径为 .三、解答题(每小题7分,共49分)1、 已知函数(,)z f xy x y =-,且(),z f u v =可微,求dz ..线 订 装郑州轻工业学 2013 — 2014 学年 第二学期 高等数学 试卷专业年级及班级 姓名 学号第2页/共3 页2、交换积分次序10xydx dy y⎰⎰,并求其值.3、计算曲线积分⎰,其中L 为ln y x =上点(1,0)与点(,1)e 间的弧段.4、计算2 2Ly dx xydy +⎰,其中L :2y x =从()0,0O 到()1,1A .5. 判定级数2123n n n n ∞=∑的敛散性..6.计算二重积分()22Dx y dxdy +⎰⎰,其中D :221x y +≤.7.求微分方程56x y y y e '''-+=通解第3页/共3 页四、解答题(本题9分)求幂级数2121n n x n +∞=+∑的收敛域及和函数五、应用题(本题满分9分)计算由曲面22x y z +=与2z =所围成立体的体积.六、证明题(本题满分3分)设函数()f x 在[0,1]上连续, 证明1112001()()[()]2xdx f x f y dy f x dx =⎰⎰⎰.线订装第4页/共3 页。
济南大学高数试题及答案

济南大学高数试题及答案一、选择题(每题5分,共30分)1. 函数f(x)=x^2在区间[0,1]上的定积分值是:A. 0.5B. 1C. 0D. 22. 极限lim(x→0)(sin(x)/x)的值是:A. 0B. 1C. -1D. 无法确定3. 以下哪个函数是奇函数?A. f(x) = x^2B. f(x) = x^3C. f(x) = sin(x)D. f(x) = cos(x)4. 曲线y=x^3在点(1,1)处的切线斜率是:A. 0B. 1C. 3D. 275. 以下哪个选项是二阶可导的?A. f(x) = |x|B. f(x) = x^(1/3)C. f(x) = e^xD. f(x) = ln(x)6. 以下哪个级数收敛?A. 1 - 1/2 + 1/3 - 1/4 + ...B. 1 + 2 + 3 + 4 + ...C. 1 - 1/2 + 1/4 - 1/8 + ...D. 1 + 1/2 + 1/4 + 1/8 + ...二、填空题(每题5分,共20分)1. 函数f(x)=2x+3的反函数是______。
2. 定积分∫(0到1) x dx的值是______。
3. 函数f(x)=x^2-4x+3的极小值点是______。
4. 曲线y=x^2在点(2,4)处的法线方程是______。
三、解答题(每题10分,共50分)1. 求函数f(x)=x^3-3x^2+2在区间[0,3]上的最大值和最小值。
2. 计算定积分∫(0到π/2) sin(x) dx。
3. 求函数f(x)=x^3-6x^2+11x-6的单调区间。
4. 证明函数f(x)=x^2-2x在区间[1,2]上是增函数。
5. 求曲线y=x^2-4x+3在点(2,-1)处的切线方程。
答案:一、选择题1. A2. B3. B4. C5. C6. C二、填空题1. f^(-1)(x) = (x-3)/22. 0.53. x=34. y=-x+6三、解答题1. 最大值:f(3)=2,最小值:f(1)=-22. ∫(0到π/2) sin(x) dx = 13. 单调递增区间:(2,+∞),单调递减区间:(-∞,2)4. 证明略5. 切线方程:y=2x-5。
0809高等数学B(二)试题答案 济南大学

不趋于0, 因此这个级数发散.
注意: lim u n 0 并非级数收敛的充分条件.
n
例如, 调和级数 虽然 但此级数发散 .
事实上 , 假设调和级数收敛于 S , 则
1 1 1 1 1 n 但 S 2n S n n 1 n 2 n 3 2n 2 n 2
3.
点(0,0)是z xy的 (
B
).
z
(A)极值点;(B).驻点但不是极值点; (C)是极值点但不是驻点;(D)以上都不对 分析:
O
y
z x y 0, 得驻点 (0,0). 令 zy x 0
x
D {( x, y ) a x a, x y a}, D1 {( x, y ) 0 x a, x y a}, 则 ( x y cos x sin y ) dx d y A
当 x 2 1, 2 当 x 1,
时级数收敛 时级数发散
故收敛半径为 R 1.
1 当x 1 时,级数为 , 此级数发散; n 1 2n
收敛域为 1,1.
4.
解:
x 求幂级数 的收敛域及和函数. n 1 2 n
2n
在( 1,1)内, 有
2n
x1 2n x 2 n 1 t dt t dt 0 s ( x) 0 t n 1 2 n n 1 n 1 x
tn
(x 1) n
(1)( x 1) n .
n 0
x 1 1
即 2 x 0.
一.选择题(每小题3分,共15分) xy ,则极限 lim f ( x, y ) ( 1. f ( x, y ) 2 2 x0 x y y 0
2013年山东省专升本高等数学(专业课)专题二检测题答案

2013年山东省本科生入学考试高等数学(专业课)答案专题二:导数与微分检测题标准答案一、单项选择题:每小题2分,共10分.1.C2.A3.C4.D5.B二、填空题:每小题2分,共10分.6.y=0和x=-17.e y/(1-xe y)dx8.π/6+31/29.x=21/2/210.(-1)n-1·[(n-1)!/(1+x)n]三、计算题:每小题5分,共20分.11. 已知f(x)=arcsin[(㏑cosx)1/2],求dy/dx.解:由题意得,f(x)是由y=arcsinu,u=v1/2,v=㏑w和w=cosx 复合而成,故根据复合函数求导的链式法则得:f'(x)= dy/dx=(dy/du)·(du/dv)·(dv/dw)·(dw/dx)=1/(1-u2)1/2·1/2(v1/2)·1/w·(-sinx)=1/(1-㏑cosx)1/2·1/2(㏑cosx)1/2·1/cosx·(-sinx)=(-2tanx)/[㏑cosx(1-㏑cosx)]1/2.12. 设由方程y=F(x2+y2)+F(x+y),确定隐函数y=y(x),又F(x)可导,且F'(2)=1/2,F'(4)=1,y(0)=2,求dy/dx┃x=0.解:方程两边同时对x求导,得:dy/dx=y'=F'(x2+y2)(2x+2yy')+F'(x+y)(1+y'),整理,得:dy/dx= y'=[2x F'(x2+y2)+ F'(x+y)]/[1-2yF'(x2+y2)- F'(x+y)]∴dy/dx┃x=0=F'(2)/[1-4F'(4)-F'(2)]=(1/2)/(1-4-1/2)=(1/2)/(-7/2)=-1/7.13. 已知y=┃㏑┃x┃┃在x=1和x=-1处的连续性与可导性. 解:由题意得,原函数可化为y=f(x)={ ㏑x ,x≥1{ -㏑x ,0<x<1{-㏑(-x),-1<x<0{ ㏑(-x),x≤-1 (1).该分段函数在x=1处的连续性:lim x→1-f(x)= lim x→1-(-㏑x)= lim x→1-(-㏑1)=0;lim x→1+f(x)= lim x→1+(㏑x)= lim x→1+(㏑1)=0,∵lim x→1-f(x)= lim x→1+f(x),∴该分段函数在x=1处连续. (2).该分段函数在x=1处的可导性:f-'(1)= lim x→1-{[f(x)-f(1)]/(x-1)}= lim x→1-{[(-㏑x)-(㏑1)]/(x-1)}= lim x→1-[(-㏑x)/(x-1)]=- lim x→1-[1/(x-1)·㏑x]=- lim x→1-(㏑x)[1/(x-1)]= - lim x→1-㏑[1+(x-1)] [1/(x-1)]=-1.f+'(1)= lim x→1+{[f(x)-f(1)]/ (x-1)}= lim x→1+{[(㏑x)-0]/(x-1)}= lim x→1+[㏑x/(x-1)]= lim x→1+㏑[1+(x-1)] [1/(x-1)]=1.∵f-'(1)≠f+'(1),∴该分段函数在x=1处不可导. (3). 该分段函数在x=-1处的连续性:lim x→-1-f(x)= lim x→-1-㏑(-x)= lim x→-1-㏑(1)=0;lim x→-1+ f(x)=- lim x→-1+㏑(-x)=- lim x→-1+㏑(1)=0,∵lim x→-1-f(x)= lim x→-1+ f(x),∴该分段函数在x=-1处连续.(4). 该分段函数在x=-1处的可导性:f-'(-1)=lim x→-1-{[f(x)-f(-1)]/(x+1)}= lim x→-1-{[㏑(-x)-0]/(x+1)}= lim x→-1-[㏑(-x)/(x+1)]= lim x→-1-㏑[1-(x+1)][-1/(x+1)]·(-1)=㏑e-1=-1.f+'(-1)=lim x→-1+{[f(x)-f(-1)]/(x+1)}= lim x→-1+{[-㏑(-x)-0]/(x+1)}=- lim x→-1+ [㏑(-x)/(x+1)]=- lim x→-1+㏑[1-(x+1)][-1/(x+1)]·(-1)=-㏑e-1=1.∵f-'(-1)≠f+'(-1),∴该分段函数在x=-1亦处不可导. 综上所述,该函数y=┃㏑┃x┃┃在x=1和x=-1处都连续,在x=1和x=-1处都不可导.14.求曲线x2/3+y2/3=a2/3在点(21/2/4a,21/2/4a)处的切线方程和法线方程.解:方程两边同时对x求导,得:2/3x-1/3+2/3y-1/3·y'=0,解得:y'=-(y/x)1/3即dy/dx=-(y/x)1/3∴dy/dx┃(21/2/4a,21/2/4a)=-1,即该点处的切线斜率为-1,故该点处的切线方程为y-(21/2/4)a=-[x-(21/2/4)a],整理得:x+y-(21/2/2)a=0.该点处的法线斜率为1,故该点处的法线方程为y-21/2/4a= x-(21/2/4)a,整理得:x-y=0.因此该点处的切线方程为x+y-(21/2/2)a=0,该点处的法线方程为x-y=0.四、证明应用题:每小题5分,共10分.15.解:由题意可知该函数的定义域为R,∴y'=6x-3x2=3x (2-x)=-3x(x-2),y"=6-6x=-6(x-1).令y'=0,得:x1=0,x2=2;令y"=0,得:x3=1.由y'>0,得:0<x<2;由y'<0,得:x<0或x>2;由y">0,得:x<1;由y"<0,得:x>1.当x变化时,y'、y"和y的变化如下表所示:由表格可知:极小值为f(0)=0;极大值为f(2)=4.因此函数在(-∞,0)和(2,+∞)上单调递减;在(0,2)上单调递增;极小值为0,极大值为4;上凸区间(凹区间)为(-∞,1);下凸区间为(1,+∞);拐点为(1,2).16.证明:由题意,可对f(x)在闭区间[a,c],[c,b]上分别应用拉格朗日中值定理,得:f'(ζ1)=[f(c)-(a)]/(c-a),ζ1∈(a,c);f'(ζ2)=[f(b)-(c)]/(b-c),ζ2∈(b,c).∵A、B、C三点在同一直线上,∴[f(c)-(a)]/(c-a)=[f(b)-(c)]/(b-c)=[f(b)-(a)]/(b-a)故f'(ζ1)= f'(ζ2),因此f'(x)在[ζ1,ζ2]上满足罗尔定理的条件,于是至少存在一点ζ∈(ζ1,ζ2)∈(a,b),使得f"(ζ)=0.。
12高数B2考卷参考答案

围成。(8分)
解:
,
故:
八、设 连续,且: ,求: 。(8分)
解:对: 两边求导得:
再求导: ,初始条件: ,
特征方程和特征根: ,ห้องสมุดไป่ตู้
所以,通解:
设特解形式为: ,可解得: ,
由: ,得最后特解为:
七、求微分方程: 的通解。(8分)
解:原方程变形为: ,令: ,则: ,
,
由于生产条件的限制,设备总产量为: ,求两种设备的产量 及价格
,使总利润最大。(10分)
解:即求:
做函数:
由: ,得: ,
。
代入原方程并整理得: ,
两边积分得: ,即:
原方程的解为: 。
六、求幂级数: 的收敛区域与和函数。
解:由于级数在 上收敛,
所以当: 时,有:
九、某设备厂生产两种设备,设备A、B的需求函数分别为: ,
其中 为单价(单位:万元/台), 为产量(或销售量,单位:台),已知
生产 台A设备和生产 台B设备的总成本为:
山东省济南市2013届高三数学上学期期末考试 理 新人教B版

2013年1月高三教学质量调研考试学本试题分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共4页. 考试时间120分钟。
满分150分,考试结束后,将本试卷和答题卡一并交回.注意事项:1.答题前,考生务必用0.5毫米黑色签字笔将自己的姓名、座号、考生号、县区和科类写在答题卡和试卷规定的位置上.2. 第Ⅰ卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其它答案标号,答案不能答在试卷上.3. 第Ⅱ卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸、修正带.不按以上要求作答的答案无效.4.填空题请直接填写答案,解答题应写出文字说明、证明过程或演算步骤.第I 卷(选择题 共60分)一、选择题:(本大题共12个小题,每小题5分,共60分.每小题给出的四个选项中只有一项是符合题目要求的)1. 设全集U R =,集合2{|230}M x x x =+-≤,{|14}N x x =-≤≤,则MN 等于A .{|14}x x ≤≤B .}31|{≤≤-x xC .{|34}x x -≤≤D .{|11}x x -≤≤2. 复数12ii+-表示复平面内的点位于 A .第一象限 B .第二象限 C .第三象限 D .第四象限3. 设0.30.33,log 3,log a b c e π===则,,a b c 的大小关系是A .a b c <<B .c b a <<C .b a c <<D .c a b << 4. 将函数 ()sin(2)6f x x π=+的图象向右平移6π个单位后,所得的图象对应的解析式为A .y =sin 2xB .y =cos2xC .y =2sin(2)3x π+D .y =sin(2)6x π- 5. 已知函数1()()2x xf x e e -=-, 则()f x 的图象 A. 关于原点对称 B .关于y 轴对称 C .关于x 轴对称 D. 关于直线y x =对称6. 一个锥体的主视图和左视图如图所示,下面选项中,不可能是该锥体的俯视图的是7. 已知椭圆方程22143x y +=,双曲线22221(0,0)x y a b a b-=>>的焦点是椭圆的顶点, 顶点是椭圆的焦点,则双曲线的离心率为23 C. 2D. 38. 设实数,x y 满足不等式组 1103300x y x y x +-≤⎧⎪-+≤⎨⎪≥⎩,则 2z x y =+的最大值为A. 13B. 19C. 24D. 299. 已知等比数列{}n a 满足213562,4a a a a =⋅=,则3a 的值为A.12B. 1C. 2D. 1410. 非零向量,a b 使得||||||a b a b +=-成立的一个充分非必要条件是A. //a bB. 20a b +=C.||||a ba b =D. a b = 11. 设函数()2xf x =,则如图所示的函数图象对应的函数是A. ()||y f x =B. ()||y f x =-C. ()||y f x =--D. ()||y f x =- 12. 已知定义在R 上的函数()f x ,对任意x R ∈,都有()()()63f x f x f +=+成立,若函数()1y f x =+的图象关于直线1x =-对称,则()2013f =A.0B.2013C.3D.2013-第Ⅱ卷(非选择题 共90分)二、填空题:(本大题共4个小题,每小题4分,共16分) 13.221x dx =⎰;14. 已知程序框图如右图所示,则输出的i = ;15. 若圆C 以抛物线24y x =的焦点为圆心,截此抛物线的准线所得弦长为6,则该圆 的标准方程是 ; 16. 根据下面一组等式开始1S =结束3i =100S ≥i 输出2i i =+S S i =⨯是否123456712354561578+9+10=3411121314156516171819202111122232425262728175S S S S S S S ==+==++==+=++++==+++++==++++++=可得 13521n S S S S -++++= .三、解答题:(本大题共6小题,共74分) 17. (本小题满分12分)在ABC ∆中,角C B A ,,的对边分别为.,,c b a 且满足()2cos cos .b c A a C -= (1)求角A 的大小;(2)若2,b c ==||AB AC +.18. (本小题满分12分)已知等差数列{}n a 的前n 项和为n S ,365,36a S ==, (1)求数列{}n a 的通项公式;(2) 设2n an b =,求数列{}n b 的前n 项和n T .19. (本小题满分12分)设函数()sin x f x e x =(1)求函数()f x 单调递增区间;(2)当[0,]x π∈时,求函数()f x 的最大值和最小值.(第20题)20. (本小题满分12分)已知四棱锥P ABCD -的底面是直角梯形,1//,,12AB CD AD AB AD AB CD ⊥===,PD ABCD ⊥面,2PD =E 是PC 的中点(1)证明://BE PAD 面; (2)求二面角E BD C --的大小.21. (本小题满分13分)已知椭圆22221(0)x y a b a b+=>>过点()0,1,其长轴、焦距和短轴的长的平方依次成等差数列.直线l 与x 轴正半轴和y 轴分别交于点Q 、P ,与椭圆分别交于点M 、N ,各点均不重合且满足12,PM MQ PN NQ λλ== (1)求椭圆的标准方程;(2)若123λλ+=-,试证明:直线l 过定点并求此定点.22. (本小题满分13分)设函数()2ln f x x ax x =+-.(1)若1a =,试求函数()f x 的单调区间;(2)过坐标原点O 作曲线)(x f y =的切线,证明:切点的横坐标为1; (3)令()()x f x g x e=,若函数()g x 在区间(0,1]上是减函数,求a 的取值范围.2013届高三教学质量调研考试理科数学参考答案一、 选择题:1.D2. A3. B4. D5. A6.C7.C8.A9.B 10.B 11.C 12.A二、填空题:(本大题共4个小题,每小题4分,共16分) 13.7314. 9 15. 22(1)13x y -+=; 16. 4n 三、解答题: 17. 解:(1)由正弦定理可得:2sin cos sin cos cos sin ,B A C A C A =+ -----3分2sin cos sin()sin B A A C B ∴=+= -------5分1sin 0,cos .2B A ≠∴=.3A π∴=--------------------8分 222(2)2cos AB AC AB AC AB ACA +=++7=+ --------11分7AB AC ∴+=-----12分18. 解: (1)设{}n a 的公差为d , 36535a S =⎧∴⎨=⎩;则1125656362a d a d +=⎧⎪⎨⨯+=⎪⎩------3分 即112556a d a d +=⎧⎨+=⎩,解得112a d =⎧⎨=⎩, -------6分*12(1)21,()n a n n n N ∴=+-=-∈. ------8分(2) 2122na n nb -==135212222n n T -∴=++++--------------10分2(14)2(41)143n n --==------12分19.解:(1)'()(sin cos )xf x e x x =+ ------- --------------------------------2分2sin()4x e x π=+ -----4分'()0,sin()0.4f x x π≥∴+≥ --------6分322,22,444k x k k x k ππππππππ∴≤+≤+-≤≤+即 3()2,2,44f x k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦单调增区间为--------8分(2)[]0,,x π∈3310,,44x x πππ⎡⎤⎡⎤∈∈⎢⎥⎢⎥⎣⎦⎣⎦由()知,是单调增区间,是单调减区间----10分3432(0)0,()0,(),42f f f e πππ===所以43max 22)43(ππe f f ==,0)()0(min ===πf f f --------12分 20. (本小题满分12分)证明:取PD 的中点为,F 连接,EF,21,//CD EF CD EF =------------2分又,,//CD 21AB //AB EF AB EF CD AB =∴=,且 FyzxBE //,ABEF AF ∴∴是平行四边形,---------4分BE PAD AF PAD BE //PAD.⊄⊂∴又面,面,面-------6分(2)建系:以DA ,DB ,DP 分别为x 轴、y 轴、z 轴,),2,0,0(),0,2,0(),0,1,1(P C B 则(0,1,2E -------7分(1,1,0),(1,0,2DB BE ==-------------------------------8分(,,)n x y z =设平面EDB 的法向量为002x y x z +=⎧⎪⎨-+=⎪⎩(,)(1,n x x x ∴=-=- -----10分令 x=1,则(1,1,n ∴=-又因为ABCD (0,0,1),m=平面的法向量为,22=二面角C BD E --为.450 ---12分 21.解:(1)设椭圆方程为)0(12222>>=+b a by a x ,焦距为2c , -------1分由题意知 b =1,且2222222)()()(c b a =+,又222a b c =+得32=a . -------------3分所以椭圆的方程为1322=+y x ---------5分(2) 由题意设),(),,(),0,(),,0(22110y x N y x M x Q m P ,设l 方程为)(m y t x -=, 由MQ PM 1λ=知),(),(110111y x x m y x --=-λ ∴111λy m y -=-,由题意1≠λ,∴111-=y mλ -----------------7分 同理由2PN NQ λ=知221my λ=- ∵321-=+λλ,∴0)(2121=++y y m y y (*)------8分联立⎩⎨⎧-==+)(3322m y t x y x 得032)3(22222=-+-+m t y mt y t∴需0)3)(3(4422242>-+-=∆m t t t m (**)且有33,32222212221+-=+=+t m t y y t mt y y (***) -------10分(***)代入(*)得023222=⋅+-mt m m t ,∴1)(2=mt ,由题意<mt ,∴1-=mt (满足(**)),----------12分得l 方程为1+=ty x ,过定点(1,0),即P 为定点.---------------13分22.解: (1)1a =时, 2()(0)f x x x lnx x =+-> -------1分1'()21f x x x ∴=+-(21)(1)x x x -+=---------3分()()110,,'0,,,'022x f x x f x ⎛⎫⎛⎫∈<∈+∞> ⎪ ⎪⎝⎭⎝⎭()f x 的减区间为10,2⎛⎫ ⎪⎝⎭,增区间1,2⎛⎫+∞ ⎪⎝⎭ -------5分(2)设切点为()(),M t f t ,()1'2f x x ax x=+- 切线的斜率12k t a t=+-,又切线过原点()f t k t =()22212ln 211ln 0f t t a t at t t at t t t t=+-+-=+-∴-+=,即:-------------7分1t =满足方程21ln 0t t -+=,由21,ln y x y x =-=图像可知21ln 0x x -+=有唯一解1x =,切点的横坐标为1; -----8分或者设()21ln t t t ϕ=-+,()1'20t t tϕ=+>()()0+t ϕ∞在,递增,且()1=0ϕ,方程21ln 0t t -+=有唯一解--------9分 (3)()()()''xf x f xg x e -=,若函数()g x 在区间(0,1]上是减函数,则()()()(0,1],'0,:'x g x f x f x ∀∈≤≤即,所以()212ln 10x x x a x x-+-+-≥---(*)------------10分()()212ln 1h x x x x a x x =-+-+-设()()()222122111'222x x x h x x a a x x x-++=---+=--+ 若2a ≤,则()'0,h x ≤()h x 在(]0,1递减,()()10h x h ≥=即不等式()()',(0,1],f x f x x ≤∀∈恒成立----------------------11分若2a >,()()232112122'20x x x x x x x ϕϕ=---∴=++> ()x ϕ在(]0,1上递增,()()12x ϕϕ≤=-()()000,1,x x a ϕ∃∈=-使得()()0,1,x x x a ϕ∈>-,即()'0h x >,()(]0,1h x x 在上递增,()()10h x h ≤=这与(]0,1x ∀∈,()212ln 10x x x a x x -+-+-≥矛盾 ----------------------------12分综上所述,2a ≤ -----------------------------------------13分解法二:()()()''x f x f x g x e -=,若函数()g x 在区间(0,1]上是减函数, 则()()()(0,1],'0,:'x g x f x f x ∀∈≤≤即,所以()212ln 10x x x a x x -+-+-≥-----------------10分 显然1x =,不等式成立当()0,1x ∈时,212ln 1x x x x a x -+-≤-恒成立 -------------------------------------11分设()()()22221112ln 21ln ,'11x x x x x x x x x h x h x x x -+--+--+-==-- 设()()()()()223121121ln ,'210x x x x x x x x x x x ϕϕ-+=-+--+-=-+> ()x ϕ在()0,1上递增,()()10x ϕϕ<= 所以()'0h x <-----------------------------12分()h x 在()0,1上递减,()()221112ln 111lim lim 2221x x x x x x h x h x x x x →→-+-⎛⎫>==-+++= ⎪-⎝⎭所以 2a ≤ ----------------------------------------------------------------13分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
∫∫
D
1 + x 2 + y 2 dxdy , D 为圆 x 2 + y 2 = 1 所围在第一象限中的区域.
4. 求函数 u = xy + yz + zx 在点 (2,1,3) 沿着从该点到点 (5,5,15) 的方向导数.
∞
5. 计算级数
∞
3. 已知级数
1
∑u
n =1
n
的部分和 S n =
n ,则 ∑ u n = _______ . 2n + 1 n =1
(B) 重合 (C) 相交但不垂直 (D) 垂直
(
)
(A) 平行但不重合
∞
5. 若
∑a
n =1
nபைடு நூலகம்
( x − 1) n 在 x = 3 处发散,则它在 x = −1 处
(
)
第 1 页, 共 1 页
五、证明题(每小题 7 分,共 7 分) ⎧ xy ⎪ 证明 f ( x, y ) = ⎨ x 2 + y 2 ⎪0 ⎩ ( x, y ) ≠ (0, 0) ( x, y ) = (0, 0)
在 (0,0) 点偏导数存在,但不可微.
2. 设 D 为 x 2 + y 2 ≤ a 2 ,
∫∫
D
3
a 2 − x 2 − y 2 dxdy = π ,则 a =
3 2 3 4 1 2
(A)
1
(B)
(C)
3
(D)
3
3. 在点 P 处函数 f ( x, y ) 的全微分 df 存在的充分条件为 (A) f x , f y 均存在 (C) f 的全部一阶偏导数均连续 4. 两平面 (B) f 连续 (D) f 连续且 f x , f y 均存在
(
)
x y z + + = 1 , 2 x + 3 y − 4 z = 1 的位置关系是 2 3 4
→ →
→
5. 若 a , b 为同向的单位向量,则它们的数量积 a ⋅ b = ___________.
2. 判别级数
(−1)n n 的敛散性,若收敛则说明条件收敛还是绝对收敛. ∑ n −1 n= 2
∞ 2
二、选择题(每小题 2 分,共 10 分)
1. 设平面方程为 By + Cz + D = 0 ,且 B , C , D ≠ 0 ,则平面 (A)平行于 x 轴 (B) 平行于 y 轴 (C) 经过 y 轴 (D) 经过 x 轴 ( ) ( ) 3. 求曲线 z = x 绕 z 轴旋转一周而成的曲面与平面 z = 1 所围成立体的体积 V .
2
三、计算题(每小题 8 分,共 40 分)
1. 设 z = z ( x, y ) 是由方程 x 2 + y 2 + z 2 = 2 z 所确定的隐函数,计算 ∂z , ∂ z 的值. 2
∂x ∂x
注:请将答案全部答在答题纸上,直接答在试卷上无效 。 ……………… ………………注:请将答案全部答在答题纸上,直接答在试卷上无效 注:请将答案全部答在答题纸上,直接答在试卷上无效。 ………………
∞
∑ (n + 1)( x − 1)
n =0
n
的收敛域及和函数.
四、解答题(每小题 11 分,共 33 分)
1. 求过点(-3,2,5)且与平面 x − 4 z − 3 = 0 和 2 x − y − 5 z − 1 = 0 的交线平行的直线方程.
4. 将
∫ dx ∫
0
→
x
0
f ( x, y )dy 交换积分次序为 __________________ .
2. 计算 3. 计算
∫∫ ( x + 6 y)dxdy, D : y = x, y = 5x, x = 1 所围成的区域.
D
一、填空题(每小题 2 分,共 10 分)
1. z = x y 在点 (1,1) 处的 dz = _______________ . 2. 设函数 f ( x, y ) = 2 x 2 + ax + xy 2 + 2 y 在点 (1,−1) 取得极值,则常数 a = _____ .
…………………………………………装…………………………订…………………………线…………………………………………………
济南大学 2011~2012 学年第二学期课程考试试卷(A 卷)
课 程 高等数学 B(二) 考试时间 2012 年 6 月 27 日
(A)发散
(B)条件收敛
(C)绝对收敛
(D) 不能确定
