机械原理习题答案第十章
机械原理习题册答案

参考答案 第一章 绪论一,填空题1.1 能量,物料,信息1.2运动,动力 1.3制造,运动,装配 二、选择题2.1 D 2.2 B 三,简答题第二章 机械的结构分析二、综合题1.n = 7 ,p l = 9 ,p h = 121927323=-⨯-⨯=--=h l P P n F从图中可以看出该机构有2个原动件,而由于原动件数与机构的自由度数相等,故该机构具有确定的运动。
2. (a )D 、E 处分别为复合铰链(2个铰链的复合);B 处滚子的运动为局部自由度;构件F 、G 及其联接用的转动副会带来虚约束。
n = 8 ,p l = 11 ,p h = 1111128323=-⨯-⨯=--=h l P P n F3. (c )n = 6 ,p l = 7 ,p h = 313726323=-⨯-⨯=--=h l P P n F(e )n = 7 ,p l = 10 ,p h = 0101027323=-⨯-⨯=--=h l P P n F 4. (a )n = 5 ,p l = 7 ,p h = 010725323=-⨯-⨯=--=h l P P n FⅡ级组 Ⅱ级组 因为该机构是由最高级别为Ⅱ级组的基本杆组构成的,所以为Ⅱ级机构。
(c )n = 5 ,p l = 7 ,p h = 010725323=-⨯-⨯=--=h l P P n FⅢ级组因为该机构是由最高级别为Ⅲ级组的基本杆组构成的,所以为Ⅲ级机构。
5. n = 7 ,p l =10 ,p h = 0101027323=-⨯-⨯=--=h l P P n FⅡ级组 Ⅲ级组当以构件AB 为原动件时,该机构为Ⅲ级机构。
Ⅱ级组 Ⅱ级组 Ⅱ级组当以构件FG 为原动件时,该机构为Ⅱ级机构。
可见同一机构,若所取的原动件不同,则有可能成为不同级别的机构。
6. (a )n = 3 ,p l = 4 ,p h = 101423323=-⨯-⨯=--=h l P P n F因为机构的自由度为0,说明它根本不能运动。
中南大学 机械原理 第十章作业答案

判断题(每2)
9、满足正确啮合条件的一对齿轮一定能连续传动( ) 10、斜齿圆柱齿轮只能实现平行轴传动。( )
11、正传动的一对齿轮必定都是正变位齿轮( )。
12、法向齿距就是基圆齿距( )。 13、两个齿轮的模数、齿数相等,但压力角不等,则此两齿轮的齿廓形状不同 ( )。
14、齿轮上齿厚等于齿槽宽的圆称为分度圆( )。 15、直齿圆柱轮传动中,节圆总是大于分度圆( )。 16、图示中的C、C‘、C“ 为由同一基圆上所生成的几条渐开线。其任意两条渐 开线(不论是同向还是反向)沿公法线方向对应两点之间的距离处处相等(即: A1B1=A2B2;A1C1=A2C2及B1C1=B2C2)。( ) C A2 A1 C' C" B1 C1 B2 C2
分度圆上曲率半径
r sin
r 2 rb2
基圆上曲率半径 齿顶圆上曲率半径 齿厚和齿槽宽:
ρb1 =0
ρb2 =0
ρb1 =55.76
ρb2 =90.6
p S1= S2=e1=e2= =7.85mm 2
30、一对渐开线外啮合直齿圆柱齿轮机构,两轮的分度圆半径分 别为 r1=30mm ,r2=54mm ,α = 20°,试求(12分)
da1=260mm
db1≈234.92mm
db2≈422.86mm
Z1=50
分度圆上压力角 基圆上压力角 α1 =20° αb1 =0° αa1 =25.4° ρ1 =42.75
Z2=90
α2 =20° αb2 =0° αa2 =23.2° ρ 2 =76.95
齿顶圆上压力角
rb a arccos ra
A、一定 B、不一定 C、一定不
机械原理作业参考答案-第10章-孙桓-第8版-A

2)短齿制
* ha 0.8
c * 0 .3
20
则
故,当 当
* 2(ha c* ) 2 (0.8 0.3) z 36.48 1 cos 1 cos 20
z 36 时,基圆直径大于齿根圆直径;
z 37 时,基圆直径小于齿根圆直径;
《机械原理》(第8版)--孙桓等主编, 高等教育出版社
1)正常齿制
c* 0.25
20
* 2(ha c* ) 2 (1 0.25) 41.4543 则 z 1 cos 1 cos20
故,当 z 41 当
时,基圆直径大于齿根圆直径;
z 42 时,基圆直径小于齿根圆直径;
《机械原理》(第8版)--孙桓等主编, 高等教育出版社
《机械原理》(第8版)--孙桓等主编, 高等教育出版社
《机械原理》(第8版)--孙桓等主编, 高等教育出版社
《机械原理》(第8版)--孙桓等主编, 高等教育出版社
《机械原理》(第8版)--孙桓等主编, 高等教育出版社
《机械原理》(第8版)--孙桓等主编, 高等教育出版社
(4) 蜗杆和蜗轮旋向相同,且蜗杆导程角与蜗轮 螺旋角相等。
z1m 导程角为 arctan d 1
S m / 2 Sb rb 2 rb 2inv rb 2rbinv z r mz / 2
L1 (k 1) pb sb (k 1)m cos rb 2rb inv z m mz cos (k 1)m cos cos 2 inv 2 2 m cos (k 0.5) z inv
2) 两轮分度圆直径
西工大教材-机械原理各章习题及答案
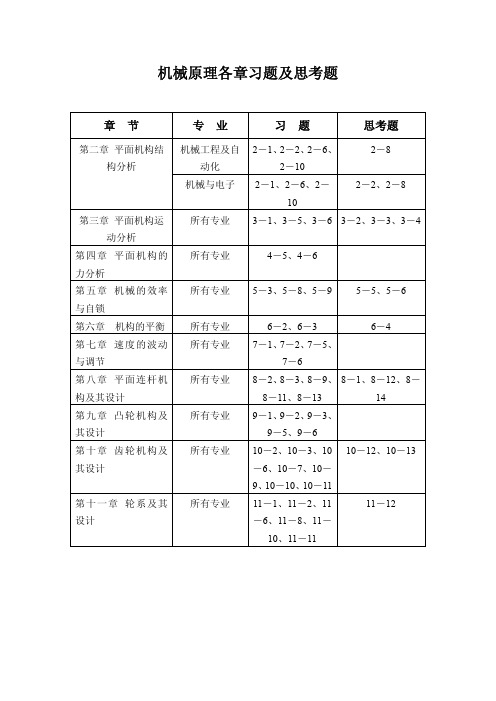
电动机所需的功率为
p = ρ • v /η = 5500 ×1.2 ×10−3 / 0.822 = 8.029(KW )
5-8 在图示斜面机构中,设已知摩擦面间的摩擦系数 f=0.2。求在 G 力作用下(反行程),此斜面 机构的临界自锁条件和在此条件下正行程(在 F 力作用下)的效率。 解 1)反行程的自锁条件 在外行程(图 a),根据滑块的平衡条件:
解 1 ) 取 比 例 尺 μ 1 = 1mm/mm 绘 制 机 构 运 动 简 图 ( 图 b )
(a)
2 )计算该机构的自由度
n=7
pι=9
ph=2(算齿轮副,因为凸轮与齿轮为一体) p’=
F’= F=3n-2pe-ph
=3x7-2x8-2 =1
G7
D 64 C
EF
3
9
B
2
8
A
ω1
b)
2-6 试计算如图所示各机构的自由度。图 a、d 为齿轮一连杆组合机构;图 b 为凸轮一连杆组合 机构(图中在 D 处为铰连在一起的两个滑块);图 c 为一精压机机构。并问在图 d 所示机构中, 齿轮 3 与 5 和齿条 7 与齿轮 5 的啮合高副所提供的约束数目是否相同?为什么?
C3 重合点继续求解。
解 1)速度分析(图 b)取重合点 B2 与 B3,有
方向 大小 ?
v vv vB3 = vB2 + vB3B2 ⊥ BD ⊥ AB // CD ω1lAB ?
D
C
3 d3
ω3
4
ω3 90°
2
B(B1、B2、B3)
ω1
A1 ϕ = 90°
机械原理第八版第十章答案

机械原理第八版第十章答案【篇一:机械原理第八版答案与解析】1、如图a所示为一简易冲床的初拟设计方案,设计者的思路是:动力由齿轮1输入,使轴a连续回转;而固装在轴a上的凸轮2与杠杆3组成的凸轮机构将使冲头4上下运动以达到冲压的目的。
试绘出其机构运动简图(各尺寸由图上量取),分析其是否能实现设计意图?并提出修改方案。
解 1)取比例尺?l绘制其机构运动简图(图b)。
2)分析其是否能实现设计意图。
图 a)由图b可知,n?3,pl?4,ph?1,p??0,f??0 故:f?3n?(2pl?ph?p?)?f??3?3?(2?4?1?0)?0?0因此,此简单冲床根本不能运动(即由构件3、4与机架5和运动副b、c、d组成不能运动的刚性桁架),故需要增加机构的自由度。
图 b)3)提出修改方案(图c)。
为了使此机构能运动,应增加机构的自由度(其方法是:可以在机构的适当位置增加一个活动构件和一个低副,或者用一个高副去代替一个低副,其修改方案很多,图c给出了其中两种方案)。
图 c1)图 c2)2、试画出图示平面机构的运动简图,并计算其自由度。
图a)解:n?3,pl?4,ph?0,f?3n?2pl?ph?1图 b)解:n?4,pl?5,ph?1,f?3n?2pl?ph?13、计算图示平面机构的自由度。
将其中的高副化为低副。
机构中的原动件用圆弧箭头表示。
3-1解3-1:n?7,pl?10,ph?0,f?3n?2pl?ph?1,c、e复合铰链。
3-2解3-2:n?8,pl?11,ph?1,f?3n?2pl?ph?1,局部自由度3-3 解3-3:n?9,pl?12,ph?2,f?3n?2pl?ph?14、试计算图示精压机的自由度解:n?10,pl?15,ph?0解:n?11,pl?17,ph?0p??2pl??p?h?3n??2?5?0?3?3?1p??2pl??p?h?3n??2?10?3?6?2f??0f??0f?3n?(2pl?ph?p?)?f?f?3n?(2pl?ph?p?)?f??3?10?(2?15?0?1)?0?1 ?3?11?(2?17?0?2)?0?1(其中e、d及h均为复合铰链)(其中c、f、k均为复合铰链)5、图示为一内燃机的机构简图,试计算其自由度,并分析组成此机构的基本杆组。
机械原理课后答案第十章作业

由df ≥db ,有: z′≥2(ha*+2 c*) / (1 - cosα) =41.45(不能圆整)
∴ 当齿根圆与基圆重合时,z′=41.45; 当 z ≥ 42时,齿根圆大于基圆。
10-5 已知一对渐开线标准外啮合圆柱齿轮传动,其模数 m=10mm,
解:1)确定传动类型
a = m ( z1+z2 ) /2 = 10 ( 12+12 ) /2 =120 < a′= 130mm 故此传动应为 正 传动。
2)确定两轮变位系数 α′ = arccos(a cosα/ a′) = arccos(120 cos20°/ 130) = 29.83° x1 + x2 = (z1+z2) (invα′-invα) / (2tanα)
10-2 设有一渐开线标准齿轮 z=20,m=8mm,α=20°,ha* =1,试
求:1)其齿廓曲线在分度圆及齿顶圆上的曲率半径ρ、ρa 及齿顶圆压
力角αa ;2)齿顶圆齿厚 s a 及基圆齿厚 s b ;3)若齿顶变尖( s a =0)时,
齿顶圆半径 ra′又应为多少?并完成图示各尺寸的标注。 解:1)求ρ、αa 、ρa d = m z =8×20=160(mm) da= d +2 ha=(z+2ha*)m=(20+2×1)×8= 176(mm) db= d cosα= 160cos20°= 160×0.9397= 150.35(mm) ρ= rb tanα= 75.175 tan20°= 75.175×0.3640= 27.36(mm) αa =arccos( rb/ra )= arccos( 75.175/88 ) = arccos0.8543=31.32° ρa = rb tanαa =75.175tan31.32°= 75.175×0.6085=45.74(mm) 2)求s a 及s b sa=s(ra/r)-2ra(invαa-invα)= 8π/2×88/80-176×(inv31.32°-inv20°)
机械原理课后答案第十章作业解读

法、端面齿距:pn =πmn =25.14(mm)
3)计算重合度
pt =πmn / cosβ =26.19(mm)当
量 齿 数: zv1 = z1 / cos 3β=22.61 zv2 = z2 / cos 3β=45.21 αt =arctan(tanαn / cosβ) = arctan(tan20°/ cos16.26°) =20.764° αat1 = arccos(db1/da1 ) = arccos(155.84/182.67 ) =31.447° αat2 = arccos(db2/da2 ) = arccos(311.69/349.33 ) =26.843° εα= [z1(tanαat1-tanαt )+z2 (tanαat2 – tanαt )] /(2π) =[20(tan31.447°-tan20.764°)+40(tan26.843°–tan20.764°)]/(2π) =1.59 εβ=B sinβ/πmn = 30 sin16.26°/8π=0.332
3)计算几何尺寸 分度圆分离系数:y = (a′-a) / m = 1 齿顶高变动系数:σ= x1 + x2 - y =0.249 齿 顶 高: ha1 = ha2 = ( ha* + x - σ ) m= 13.755(mm) 齿 根 高: hf1 = hf2 = ( ha* + c* - x) m = 6.255(mm) 分 度 圆 直 径: d1 = d2 = m z1 = 120 (mm) 齿 顶 圆 直 径: da1= da2= d1 +2ha1= 147.51 (mm) 齿 根 圆 直 径: df1= df2= d1 - 2hf1= 107.49 (mm) 基 圆 直 径: db1 = db2 = d1 cosα= 112.763(mm) 分 度 圆 齿 厚: s1= s2 = (π/2 + 2 x tanα) m = 20.254 (mm)
机械原理课后习题答案
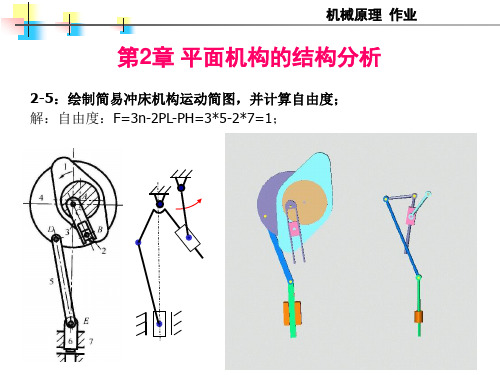
inva )
=6.8mm
分度圆半径r=mz/2=10*18/2=90mm
齿槽宽:ea=2π ra/z-sa
分度圆齿厚s=π m/2=15.7mm
=28.1mm
齿顶圆半径ra=r+ha*m=90+10=100mm
基圆半径rb=rcosα=90cos200=84.57mm
inv200=0.0148
齿顶圆压力角
第2章 平面机构的结构分析
2-7:计算自由度,指出所有的复合铰链、局部自由度和虚约束,判定运动 是否确定; 解:自由度:
a) F=3n-2PL-PH=3*3-2*4=1;确定 b) F=3n-2PL-PH=3*6-2*8=2;不确定 c) F=3n-2PL-PH=3*4-2*5-1=1;确定 d) F=3n-2PL-PH=3*4-2*5-1=1;确定
从而lAB+lBC, lBC-lAB可求得,最后确定lAB和lBC; 设计步骤:
①取一点A,并定D点; ②以D为圆心,作圆; 根据CD摆角15°定C1,C2点; ③ 量取lAC1,lAC2
lAB+lBC=430 lBC-lAB=348
C2 15° 15°C1
B A
lAB=41
A
B1
D
lBC=389
B2
虚约束
局部自由度
复合铰链
a)
b)
c)
d)
机械原理 作业
第2章 平面机构的结构分析
2-8:计算自由度;确定机构所含杆组的数目与级别;确定机构级别。画出 瞬时替代机构; 解:自由度:
a) F=3n-2PL-PH=3*7-2*10=1;Ⅱ级 b) F=3n-2PL-PH=3*6-2*8-1=1;Ⅲ级
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
10-1 试求出题10-1图中机构的最小传动角和最大压力角。
解:(a )、4583.0120
25
30sin max =+=+=
BC AB l e l α 所以最大压力角︒==28.274583.0arcsin max α 最小传动角︒=︒-︒=-︒=72.6228.279090max min αγ (b )、最大压力角︒=0max α
最小传动角︒=︒-︒=-︒=9009090max min αγ
10-2 标出题10-2图所示机构在图示位置的传动角。
解:(a)对于该机构,在滑块C处有一传动角c γ,如图所示;在滑块D处也有一传动角D γ,如图所示。
(b)从动件4受到的驱动力是由构件3提供的。
构件4的速度v 很好确定,而构件3作用于构件4的驱动力的方向的确定应当按照下面的步骤进行:①根据构件3上受有三个力、三个力应当汇交于一点可以确定出构件4作用在构件3上的力;②根据作用力和反作用力的关系,确定出构件3作用在构件4上的力的方向。
max
α︒=0αB '
题10-1图
F
v D
γ
)
(a D
F D
v
图示机构在图示位置的传动角γ分别如图中所示。
10-5 标出题10-5图中各个凸轮机构在图示位置时的压力角。
凸轮为主动件。
解:图中各个凸轮机构在图示位置时的压力角α如图所示。
)
(b n
n
n
︒
=0αααv
v v
n
n
n
n α
题10-5图
10-6 在题10-6图中,凸轮为主动件,画出凸轮逆时针转过30º时机构的压力角。
解:利用反转法,即将凸轮固定、机架和从动件沿与凸轮转向相反的方向运动,固定铰链点A 从点A “反转”到点A ’,从动件从AB 运动到A ’B ’,再由点B ’的速度方向和从动件的受力方向确定出凸轮逆时针转过30º时机构的压力角α,如图所示。
原教材6-8 在题6-8图中凸轮为半径为R 的圆盘,凸轮为主动件。
(1) 写出机构的压力角α与凸轮转角之间的关系; (2)
讨论如果][αα≥,应采用什么改进设计的措施?
解:(1)、当凸轮转动任意角δ时,其压力角α如图所示。
由图中几何关系有
r
r R e e +-=
δ
αcos sin
所以机构的压力角α与凸轮转角δ之间的关系为
)cos arcsin(
r
r R e e +-=δ
α
(2)、如果][αα≥,则应减小偏距e ,增大圆盘半径R 和滚子半径r r 。
10-10 在题10-1图所示的机构中,以构件1为主动件机构是否会出现死点位置?以构件3为主动件,机构是否会出现死点位置?画出机构的死点位置,并标明机构的主动件是哪一个构件。
题6-8图
解:在图示机构中,当以构件1为主动件时,机构不会出现死点位置;当以构件3为主动件时,机构会出现死点位置,其死点位置分别如下图示。
10-12 利用移动副的自锁条件推出:螺旋副中以轴向载荷Q 为主动力时(即:反行程),螺旋副的自锁条件为式ϕλ≤。
题10-1图
2
B )
(
a B
解:当反程时,载荷Q为主动力,P为阻力。
由移动副自锁的条件,反程驱动力Q与接触面法线n---n的夹角λ必须小于或等于斜面与滑块之间的摩擦角ϕ,即
λ≤
ϕ
例10-2在图10-17a所示的机构中,已知各构件的尺寸及机构的位置,各转动副处的摩擦圆半径、移动副及凸轮高副处的摩擦角ϕ,凸轮为主动件,顺时针转动,作用在构件4上的工作阻力Q的大小。
试求图示位置:
(1)各运动副的反力;
M。
(2)需施加于凸轮1上的驱动力矩
1
解:选取长度比例尺μL(m/mm)作机构运动简图。
(1)确定各运动副中反力的方向。
由主动件凸轮的转向,确定出机构中各个构件之间的相对运动方向,如图10-17a所示。
分析各个构件受到的运动副反力和外力。
构件1受到的力有R 51、R 21、1M ;构件2受到的力有R 52、R 12、R 32;构件3受到的力有R 23、R 43;构件4受到的力有R 34、R 54、Q 。
先确定凸轮高副处点B 的反力R 12的方向,与移动副反力方向确定方法相同,该力方向与接触点处的相对速度V B2B1的方向成900
+ϕ角。
再由R 51应切于运动副A 处的摩擦圆,与R 21大小相等方向相反,且对A 之矩的方向与ω1
方向相反,确定出R 51的方向。
R 51与R 21形成一个力偶与M 1平衡;
由于连杆3为受拉二力构件,其在D 、E 两转动副处所受两力R 23及R 43应切于该两处摩擦圆,大小相等方向相反,在一条直线上。
同时,根据相对转速3432,ωω的方向,可确定出R 23及R 43的作用线和方向,亦即铰链点D 、E 的摩擦圆的内公切线。
;
图10-17 凸轮连杆机构考虑摩擦的机构力分析
反力R 52应切于运动副C 处的摩擦圆,且对C 之矩的方向应与ω25的方向相反,同时构件2受有的三个力R 12、R 52、R 32应汇交于一点,由此可确定出R 52的方向线;
滑块4所受反力R 54应与V 45的方向成900
+ϕ角,它受到的三个力R 34、R 54及Q 也应汇交于一点,于是可定出R 54的方向线。
依照以上的步骤和方法,确定出各个运动副反力的作用线和方向,如图10-17(b )所示。
(2)求各运动副处的反力大小。
分别取构件2、4为分离体,列出力平衡方程式为
构件2 0523212=++R R R
构件4 05434=++Q R R
而 32234334R R R R -==-=
根据上述力方程式,选取力比例尺μF (N/mm),从已知力Q 画起,作出力多边形,如图10-17(C )所示。
由图可得各总反力
F i i R R μ=
其中 i R 为力多边形中第i 个力的图上长度(mm)。
(3)求需施加于凸轮1上的驱动力矩1M 。
由凸轮1的平衡条件可得
()Nm l R l R M L
F L μμμ21211==
式中 l 为R 21与R 51两方向线的图上距离,单位为mm 。
10-17 题10-17图所示为按μL =0.001m/mm 画的机构运动简图,滑块3为原动件,驱动力P=80N 。
各转动副处的摩擦圆如图中所示,滑块与导路之间的摩擦角ϕ=0
20 ,试求在图示位置, 构件AB 上所能克服的阻力矩M Q 的大小和方向。
解:首先确定各个运动副中的反力的方向如图所示。
选取构件3为分离体,再选取力比例尺F μ,作出其力多边形,如图所示。
在力多边形中,量得力23R 的长为18mm ,力P 的长为20mm , 所以N P R 728020
18
201823=⨯==
构件2为二力杆,所以N R R R R 7223321221==== 最后得构件AB 上所能克服的阻力矩M Q 的大小为
m N l R M l Q ⋅=⨯⨯==72.0001.0107221μ
阻力矩M Q 的方向为逆时针方向,如图所示。
10-18 题10-18图所示为按μL =0.001m/mm 绘制的机构运动简图。
已知圆盘1与杠杆2接触处的摩擦角ϕ=0
30 ,各转动副处的摩擦圆如图中所示,悬挂点D 处的摩擦忽略不计。
设重物 Q=150N ,试求出在图示位置时,需加在偏心圆盘上的驱动力矩M 1的大小。
解:首先确定各个运动副中的反力的方向如图所示。
选取构件2为分离体,再选取力
比例尺F μ,作出其力多边形,如图所示。
题10-17图
N Q R 23115013
20132012=⨯==
依据作用力与反作用的关系,得N R R 2311221== 最后得需加在偏心圆盘上的驱动力矩M 1的大小为
m N l R M l ⋅=⨯⨯==2.3001.014231211μ
例10-6图10-19所示为斜面压榨机。
确定在以Q 为主动力的行程中机构的自锁条件。
设所有移动副的摩擦角均为ϕ。
解:首先利用考虑摩擦机构力分析的步骤和方法,求出驱动力Q 与工作阻力P 之间的关系
)2cot(ϕα-=P Q
理想驱动力为αcot 0P Q = 效率为
α
ϕαηtan )
2tan(0'-=
=
Q Q 令0'≤η得自锁条件:ϕα2≤。
10-20 题10-20图所示机构,作用于构件3上的P 为驱动力,作用于构件1上的Q 为生产阻力。
各转动副处的摩擦圆如图中所示;各移动副处的摩擦系数均为 f ,各构件惯性力、重力忽略不计。
(1)机构处于死点位置时,连杆2与水平线之间的夹角θ为多大? (2) 机构自锁时,连杆2与水平线之间的夹角θ为多大?
图10-19 斜面压榨机力分析
解:(1)、机构处于死点位置时,其传动角为零度。
所以连杆2与水平线之间的夹角θ为
︒90。
(2)、机构自锁时,应有
ϕβθ≤+-︒)(90
即)(90ϕβθ+-︒≥ 式中:AB
r
l ρβ2arcsin =,f arctan =ϕ。
r ρ为摩擦圆的半径,AB l 为连杆AB 的杆长。
所以最后得
)arctan 2(arcsin
90f l AB
r
+-︒≥ρθ。
