第二节 光的衍射现象
合集下载
第二章 光的衍射

四、单缝衍射图样的特点
(1)条纹最大值光强不相等、 中央最大、其余皆小 , I10< 5%I0. 2 中央: 2 b (2)角宽度: =sin k
k
b
2 中央:l f b 线宽度: l =f 其余:l f b
令:I0=A02=1 则可由
Ip=Ap2=A0 2 [
sin( b ) sin
b ) sin (
k0
]
2
k0
得: A12=0.0451 A22=0.0162 A32=0.0083 A42=0.0050 A52=0.0034 A62=0.0024 A72=0.0018
sin 0.610
1
R
sin 1.116
2
sin 1.619 R R
3
(3)次最大的位置;
sin 0.819
10
R
sin 1.333
20
R
sin 1.847
30
R
中央亮斑的光强占总光强的84%,其余 光强共占16% .
四、讨论:
1 2 3 4
sinθ sinθ sinθ
10 20
30
sinθ
k0
=±1.43 =±2.46 =±3.47 ( …… 1 =± (k )
0
( ) b ( ) b
3 ≈± 2 b 3 ≈± 2 b 5/2 7 ) ≈± 2 b b
k0 = 1,2,
2 b
2.4 菲涅耳衍射(圆孔和圆屏)
一、圆孔衍射
光的衍射现象ppt课件

[教学难点]
菲涅耳半波带、光栅方程、光栅光谱
.
1
光的衍射
.
2
一、光的衍射现象
衍射——光绕过障碍物偏离直线传播而进入几何阴影
区,并在屏上出现光强不均匀分布的现象。同光的干涉 现象一样,是光的本质特性之一。
.
3
不同宽度的单缝衍射图样
.
4
单缝衍射
.
5
圆孔衍射
日常生活中为什么我们很容易观察到声波、无线电波的衍射, 而难以观察到光波的衍射呢?这是由于声波和无线电波的波长较 长(约几百米),自然界中存在这样尺度的障碍物或空隙(如墙、 山秋和建筑物等),容易表现出衍射现象;而光波的波长很短 (4000-7600Å ),自然界中通常不存在如此小的障碍物或空隙,光 主要表现出直线传播的特性。
如何从理论上解释光的衍射现象呢?
.
8
二、Huygens-Fresnel原理
.
9
惠更斯 — 菲涅耳原理 惠更斯 波阵面上各点都看成是子波波源
能定性解释光的传播方向问题
菲涅耳 波场中各点的强度由各子波在该点 的相干叠加决定
能定量解释衍射图样中的强度分布
波前上每个面元d都可以看成是新的振动中 心,它们发出次波。在空间某一点P的振动是 所有这些次波在该点的相干迭加。
相 邻 小 环 带 在 P 0 贡 献 的 振 动 位 相 差 m ,振 动 .的 合 成 用 矢 量 图 来 表 示
29
其余的半波带同样处理,并考虑到倾斜因子 f ( ) 的影响, 半径将逐渐收缩,形成螺旋线
uur
M 1 Am
m
u ur
A1
u ur
u ur
A3
o u ur A 2
高中物理-选修3-4-《光的衍射》PPT课件

四、双缝干涉与单缝衍射的比较.
15
【课堂训练与检测】 见学案“典题分类剖析”
【作业布置】 1、见学案“课后演练提升” 2、见学案“课时作业”
.
16
1、单缝衍射 1)单缝衍射现象
用平行光照射狭缝,在屏上产生一条与缝 宽相当的亮条纹。但是,当缝调到很窄时, 尽管亮条纹的亮度有所降低,但是宽度反 而增大了。
激
调 节
光
狭
束
缝
宽
窄
.
像屏
5
2)图样特征 (1)单色光的衍射条纹? 亮暗相间,中央条纹亮度大; 分布不均匀,中央条纹宽度大; (2)白光的衍射条纹? 中间是白色亮条纹,两边是彩色条纹;
不 同 点
条纹 距离
条纹 间距
条纹宽度相等 各相邻条纹等间距
条纹宽度不等, 中央最宽
各相邻条纹间距 不等
衍 射 的
亮度
清晰条纹,亮度基 本相等
中央条纹最亮, 两边变暗
比 较
相同点
波特有的现象,属于波的叠加; 都有明暗相间的条纹
.
14
【课堂小结】
一、产生明显衍射现象的条件——
障碍物或孔的尺寸跟波长相近或者比光的波长还要小
(其中最靠近中央的色光是紫色,最远离中央的 是红光)
.
6
1)缝越窄,亮纹的亮度_降__低___,
但条纹宽度__变_宽___。
2)入射光的波长越短,条纹宽度__越_窄___。
.
7
2、圆孔衍射
1)圆孔衍射现象
S
用点光源照射圆孔,
在屏上产生一个圆形
亮斑。但是,当圆孔
缩小到一定程度时,
光所达到的范围会远
远超过它沿直线传播
第二章 光的衍射

· Q
θ
r
面元dS发出的各次波的 面元dS发出的各次波的 和位相满足: dE(p) 和位相满足:
~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~
· p
1. S上各面元位相相同; 上各面元位相相同 上各面元位相相同;
S(波前 波前) 波前 设初相为零
2. 次波在 点引起的振动的振幅 次波在P点引起的振动的 点引起的振动的振幅 成反比; 与r成反比; 成反比 3. 次波在 点的位相由光程 决定。 次波在P点的位相由光程∆决定 点的位相由光程 决定。
b 2 b b b sinu , 由 I = I0 可得到以下结果: 可得到以下结果: u
1.主最大(中央明纹中心)位置: 1.主最大(中央明纹中心)位置: 主最大 单缝衍射 sin u = 1 →I = I0 = Imax θ = 0处 u = 0 → , u 即为几何光学像点位置
1. 波面在 点产生的振动 波面在P点产生的振动
A(Q) dE( p) ∝ K(θ) cos(ω −kr) dS t r A(Q)取决于波面上Q点处的强度。 点处的强度。 ( )
K(θ):方向因子
θ ≥ 90o,K = 0
θ ↑→ θ )↓ ↑→K( ↓
θ = 0, K=Kmax ,
( K(θ)A Q) dE( p) = C dS ⋅ cos(ωt −kr) r ( K(θ) A Q) cos(ω −kr)dS t EP = ∫∫ dE = C∫∫ S S r ——菲涅耳衍射积分 菲涅耳衍射积分
圆孔的衍射图样: 圆孔的衍射图样:
屏上 图形: 图形:
孔的投影 菲涅耳衍射 夫琅禾费衍射
二、圆屏衍射
P点合振幅为: 点合振幅为: 点合振幅为 A = ak+1 −ak+2 +ak+3 −ak+4 +... P
光的衍射(教学课件)(完整版)

只通过一条窄缝,则在光屏上可以看到(
)
A.与原来相同的明暗相间的条纹,只是明条纹比原来暗些
B.与原来不相同的明暗相间的条纹,而中央明条纹变宽些
C.只有一条与缝宽对应的明条纹
D.无条纹,只存在一片红光
答案:B
考点二:光的干涉和衍射的比较
解析:双缝为相干光源的干涉,单缝为光的衍射,且干涉和衍射的图样
不同。衍射图样和干涉图样的异同点:中央都出现明条纹,但衍射图样
(1)孔较大时——屏上出现清晰的光斑
ASLeabharlann 几乎沿直线传播学习任务一:光的衍射
4.圆孔衍射
(2) 孔较小时—
—屏上出现衍射花
样(亮暗相间的不
等间距的圆环,这
些圆环的范围远远
超过了光沿直线传
播所能照明的范围)
以中央最亮的光斑为圆心的逐
渐变暗的不等距的同心圆
学习任务一:光的衍射
4.圆孔衍射
(3)圆孔衍射图样的两个特点
答案:A
考点二:光的干涉和衍射的比较
解析:干涉条纹是等间距的条纹,因此题图a、b是干涉图样,题图c、d
是衍射图样,故A项正确,B项错误;由公式Δx=
λ可知,条纹宽的入射光
的波长长,所以题图a图样的光的波长比题图b图样的光的波长长,故C项
错误;图c的衍射现象比图d的衍射现象更明显,因此题图c图样的光的波
中央明条纹较宽,两侧都出现明暗相间的条纹,干涉图样为等间隔的明
暗相间的条纹,而衍射图样两侧为不等间隔的明暗相间的条纹,且亮度
迅速减弱,所以选项B正确。
祝你学业有成
2024年5月2日星期四1时48分21秒
S
学习任务一:光的衍射
2.光的明显衍射条件
)
A.与原来相同的明暗相间的条纹,只是明条纹比原来暗些
B.与原来不相同的明暗相间的条纹,而中央明条纹变宽些
C.只有一条与缝宽对应的明条纹
D.无条纹,只存在一片红光
答案:B
考点二:光的干涉和衍射的比较
解析:双缝为相干光源的干涉,单缝为光的衍射,且干涉和衍射的图样
不同。衍射图样和干涉图样的异同点:中央都出现明条纹,但衍射图样
(1)孔较大时——屏上出现清晰的光斑
ASLeabharlann 几乎沿直线传播学习任务一:光的衍射
4.圆孔衍射
(2) 孔较小时—
—屏上出现衍射花
样(亮暗相间的不
等间距的圆环,这
些圆环的范围远远
超过了光沿直线传
播所能照明的范围)
以中央最亮的光斑为圆心的逐
渐变暗的不等距的同心圆
学习任务一:光的衍射
4.圆孔衍射
(3)圆孔衍射图样的两个特点
答案:A
考点二:光的干涉和衍射的比较
解析:干涉条纹是等间距的条纹,因此题图a、b是干涉图样,题图c、d
是衍射图样,故A项正确,B项错误;由公式Δx=
λ可知,条纹宽的入射光
的波长长,所以题图a图样的光的波长比题图b图样的光的波长长,故C项
错误;图c的衍射现象比图d的衍射现象更明显,因此题图c图样的光的波
中央明条纹较宽,两侧都出现明暗相间的条纹,干涉图样为等间隔的明
暗相间的条纹,而衍射图样两侧为不等间隔的明暗相间的条纹,且亮度
迅速减弱,所以选项B正确。
祝你学业有成
2024年5月2日星期四1时48分21秒
S
学习任务一:光的衍射
2.光的明显衍射条件
2-1光的衍射现象
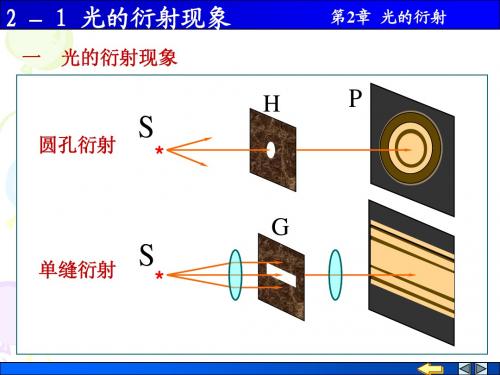
用惠更斯原理证明.
N I A N
R
N
N A2
A3
B1 B2
rB r
B3 Ⅰ
Ⅱ
r
i I i A1 d Ⅰ i A B1 B2 B3 Ⅱ
R
时刻 t
时刻 t+△t
2 – 1 光的衍射现象
N N N I A
第2章 光的衍射 N B1 B2
rB r
i I i A1 d Ⅰ i A B1 B2 B3 Ⅱ
A2
A3
i
r
ds
~ I P AP
2
光波的复振幅表示
2 – 1 光的衍射现象
四
第2章 光的衍射
菲涅尔衍射和夫琅禾费衍射 菲涅尔衍射 夫琅禾费 衍射
S
缝
P
缝
光源、屏与缝相距有限远 在夫 实琅 验禾 中费 实衍 现射
光源、屏与缝相距无限远
S
L1
R
L2
P
S
S :波阵面上面元
(子波波源) 并与
s 子波在 P点引起的振动振幅 r
有关 .
菲涅尔指出 衍射图中的强度分布是因为衍射时, 波场中各点的强度由各子波在该点的相干叠加决定. P 点振动是各子波在此产生的振动的叠加 .
2 – 1 光的衍射现象
e θ ds r
第2章 光的衍射
子波面 ds 传播到P点引起振动!
积分方法:
用
cos i sin e
将波函数写成 复指数式.
i
K ( )ds 2 cos( t r) . p dA r K ( ) 2 dA c cos( t r )ds r c系数,Κ (1 cos )(倾斜因子)
N I A N
R
N
N A2
A3
B1 B2
rB r
B3 Ⅰ
Ⅱ
r
i I i A1 d Ⅰ i A B1 B2 B3 Ⅱ
R
时刻 t
时刻 t+△t
2 – 1 光的衍射现象
N N N I A
第2章 光的衍射 N B1 B2
rB r
i I i A1 d Ⅰ i A B1 B2 B3 Ⅱ
A2
A3
i
r
ds
~ I P AP
2
光波的复振幅表示
2 – 1 光的衍射现象
四
第2章 光的衍射
菲涅尔衍射和夫琅禾费衍射 菲涅尔衍射 夫琅禾费 衍射
S
缝
P
缝
光源、屏与缝相距有限远 在夫 实琅 验禾 中费 实衍 现射
光源、屏与缝相距无限远
S
L1
R
L2
P
S
S :波阵面上面元
(子波波源) 并与
s 子波在 P点引起的振动振幅 r
有关 .
菲涅尔指出 衍射图中的强度分布是因为衍射时, 波场中各点的强度由各子波在该点的相干叠加决定. P 点振动是各子波在此产生的振动的叠加 .
2 – 1 光的衍射现象
e θ ds r
第2章 光的衍射
子波面 ds 传播到P点引起振动!
积分方法:
用
cos i sin e
将波函数写成 复指数式.
i
K ( )ds 2 cos( t r) . p dA r K ( ) 2 dA c cos( t r )ds r c系数,Κ (1 cos )(倾斜因子)
光的衍射 课件

个数越多,衍射条纹的宽度越窄,亮度越大。
一、光的直线传播是一种特殊情况
光的直线传播是一种特殊情况,具体从以下两个方面去理解: 1.多数情况下,光照到较大的障碍物或小孔上时是按沿直线传 播的规律传播的,在它们的后面留下阴影或光斑。如果障碍物、缝 或小孔都小到与照射光的波长差不多或更小时,光就表现出明显的 衍射现象,在它们的后面形成泊松亮斑、明暗相间的条纹或圆环。 2.光是一种波,衍射是它基本的传播方式,但在一般情况下,由于 障碍物都比较大(比起光的波长来说),衍射现象很不明显。光的传 播可近似地看做是沿直线传播。所以,光的直线传播只是特殊情况。
二、光的双缝干涉与单缝衍射的比较
种
类
单缝衍射
双缝干涉
项目
产生 条件
只要狭缝足够小,任何光都 频率相同的两列光波相
能发生
遇叠加
不 条纹 同 宽度
条纹宽度不等,中央最宽
条纹宽度相等
点 条纹 间距
各相邻条纹间距不等
各相邻条纹等间距
亮度 相同点
中央条纹最亮,两边变暗 清晰条纹,亮度基本相等 干涉、衍射都是波特有的现象,属于波的叠加;干涉、 衍射都有明暗相间的条纹
光的衍射
1.光的衍射现象 光在传播过程中,遇到障碍物或小孔时,光将偏离直线传播的途
径而绕到障碍物后面传播的现象。 2.常见的光的衍射现象 (1)单缝衍射:单色光通过狭缝时,在屏幕上出现明暗相间的条纹,
中央为亮条纹,中央条纹最宽最亮,其余条纹变窄变暗;白光通过狭缝 时,在屏上出现彩色条纹,中央为白色条纹。
类型 光的衍射现象
【例题】在单缝衍射实验中,下列说法中正确的是( ) A.将入射光由黄色换成绿色,衍射条纹间距变窄 B.使单缝宽度变小,衍射条纹间距变窄 C.换用波长较长的光照射,衍射条纹间距变宽 D.增大单缝到屏的距离,衍射条纹间距变宽
一、光的直线传播是一种特殊情况
光的直线传播是一种特殊情况,具体从以下两个方面去理解: 1.多数情况下,光照到较大的障碍物或小孔上时是按沿直线传 播的规律传播的,在它们的后面留下阴影或光斑。如果障碍物、缝 或小孔都小到与照射光的波长差不多或更小时,光就表现出明显的 衍射现象,在它们的后面形成泊松亮斑、明暗相间的条纹或圆环。 2.光是一种波,衍射是它基本的传播方式,但在一般情况下,由于 障碍物都比较大(比起光的波长来说),衍射现象很不明显。光的传 播可近似地看做是沿直线传播。所以,光的直线传播只是特殊情况。
二、光的双缝干涉与单缝衍射的比较
种
类
单缝衍射
双缝干涉
项目
产生 条件
只要狭缝足够小,任何光都 频率相同的两列光波相
能发生
遇叠加
不 条纹 同 宽度
条纹宽度不等,中央最宽
条纹宽度相等
点 条纹 间距
各相邻条纹间距不等
各相邻条纹等间距
亮度 相同点
中央条纹最亮,两边变暗 清晰条纹,亮度基本相等 干涉、衍射都是波特有的现象,属于波的叠加;干涉、 衍射都有明暗相间的条纹
光的衍射
1.光的衍射现象 光在传播过程中,遇到障碍物或小孔时,光将偏离直线传播的途
径而绕到障碍物后面传播的现象。 2.常见的光的衍射现象 (1)单缝衍射:单色光通过狭缝时,在屏幕上出现明暗相间的条纹,
中央为亮条纹,中央条纹最宽最亮,其余条纹变窄变暗;白光通过狭缝 时,在屏上出现彩色条纹,中央为白色条纹。
类型 光的衍射现象
【例题】在单缝衍射实验中,下列说法中正确的是( ) A.将入射光由黄色换成绿色,衍射条纹间距变窄 B.使单缝宽度变小,衍射条纹间距变窄 C.换用波长较长的光照射,衍射条纹间距变宽 D.增大单缝到屏的距离,衍射条纹间距变宽
大学物理--第二章--光的衍射
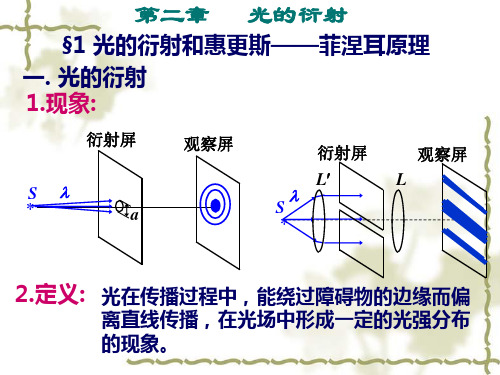
缝平面 透镜L a
p · 0
f
解:(1) 中央明纹的宽度
6 107 3 x 2 f 2 0.4 0 . 8 10 (m) 3 a 0.6 10
(2)根据单缝衍射的明纹位置公式
1 k ax / f x ( 2k 1) f, k 1,2,3 … 2a 2 3 3 7 0.6 10 1.4 10 / 0.4 6 10 1 / 2 3 P点所在位置为第三级明条纹,
微向上平移时,屏幕上的衍射图样。 (A)向上平移; (C)不动; (B) 向下平移; (D)条纹间距变大。
L
C
S
例.若有一波长为 =600nm 的单色平行光, 垂直 入射到缝宽 a =0.6mm 的单缝上,缝后有一焦距 f = 40 cm 透镜。 试求: (1)屏上中央明纹的宽度; (2)若在屏上 P 点观察到一明纹,op=1.4mm 问 P 点处是第几级明纹,对 P 点而言狭缝处波面可分成几 个半波带? 观察屏
D 分辨本领 R 1.22
1
D R
望远镜: 不可选择,可 D R
显微镜: D不会很大,可 R 电子显微镜l~10-3 nm,最小分辨距离10-1 nm,放大倍数可达几万~几百万倍。
在夫琅和费单缝衍射中,对于给定的入 射光,当缝宽度变小时,除中央亮纹的 中心位置不变外,各级衍射条纹。
A
S2¤
§4
一. 光栅
光栅衍射
1. 光栅—大量等宽等间距的平行狭缝(或反射面) 构成的光学元件。 广义上,任何装置,只要能起到等宽 2. 种类:
等间隔地分割波阵面的作用,均为衍 射光栅。
透射光栅 反射光栅
3. 结构:
p · 0
f
解:(1) 中央明纹的宽度
6 107 3 x 2 f 2 0.4 0 . 8 10 (m) 3 a 0.6 10
(2)根据单缝衍射的明纹位置公式
1 k ax / f x ( 2k 1) f, k 1,2,3 … 2a 2 3 3 7 0.6 10 1.4 10 / 0.4 6 10 1 / 2 3 P点所在位置为第三级明条纹,
微向上平移时,屏幕上的衍射图样。 (A)向上平移; (C)不动; (B) 向下平移; (D)条纹间距变大。
L
C
S
例.若有一波长为 =600nm 的单色平行光, 垂直 入射到缝宽 a =0.6mm 的单缝上,缝后有一焦距 f = 40 cm 透镜。 试求: (1)屏上中央明纹的宽度; (2)若在屏上 P 点观察到一明纹,op=1.4mm 问 P 点处是第几级明纹,对 P 点而言狭缝处波面可分成几 个半波带? 观察屏
D 分辨本领 R 1.22
1
D R
望远镜: 不可选择,可 D R
显微镜: D不会很大,可 R 电子显微镜l~10-3 nm,最小分辨距离10-1 nm,放大倍数可达几万~几百万倍。
在夫琅和费单缝衍射中,对于给定的入 射光,当缝宽度变小时,除中央亮纹的 中心位置不变外,各级衍射条纹。
A
S2¤
§4
一. 光栅
光栅衍射
1. 光栅—大量等宽等间距的平行狭缝(或反射面) 构成的光学元件。 广义上,任何装置,只要能起到等宽 2. 种类:
等间隔地分割波阵面的作用,均为衍 射光栅。
透射光栅 反射光栅
3. 结构:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第k 级明纹 角宽度 j k λ a 请写出线宽度
讨论
(1) j 0 2j 1 2 λ a 波长越长,缝宽越小,条纹宽度越宽。 (2) λ a 0 j 0 0 波动光学退化到几何光学。 (3) λ a 1 j 0 π 观察屏上不出现暗纹。
(4) 缝位置变化不影响条纹位置分布
·
解: a s in j 1
sin j 1 tan j 1
x f
a
x f 500 540 10 6 0.64m m
a
0.42
例二
波长为λ=589nm的钠黄光通过单缝后在距离缝1m处产生衍射 图样,若两个第一极小值之间的距离为2mm,求单缝的宽度。
解: x f
a
2x 2m m
a f 103 589 10 6 0.589m m
x
1
2.3 夫琅禾费圆孔衍射实验
衍射屏 L
1
孔径为D
f
相对光强曲线
中央亮斑 (艾里斑)
经圆孔衍射后,一个点光源对应一个艾里斑
特点: 1.中央亮纹很亮,称为艾里斑,集中了衍射中的光能量的84%; 2.第一暗纹,衍射角为1,1为中央亮纹的半角宽度, 21为中 央亮纹的张角。
说明 (1) 得到的暗纹和中央明纹位置精确,其它明纹位置只是近似 (2) 单缝衍射和双缝干涉条纹比较。
单缝衍射条纹
双缝干涉条纹
单缝衍射明纹角宽度和线宽度
角宽度 相邻两暗纹中心对应的衍射角之差
线宽度 观察屏上相邻两暗纹中心的间距
透镜
观测屏
x2
j1
x1
x1
j1 o
x0
j0
x1
衍射屏
f
中央明纹 角宽度 j 0 2j 1 2 λ a 线宽度 x 0 2 f ta n j 1 2 fj 1 2 f λ a
B
f A
( 单缝夫琅禾费衍射典型装置 )
(5) 一定,改变a,对同一级(k值定)条纹,a,缝越细,
衍射越明显,最大衍射角=900
a,缝宽到一定程度,无衍射现象,为直线传播
例 如图示,设有一波长为 的单色平面波沿着与缝平面的法 线成 角的方向入射到宽为 a 的单缝 AB 上。
求 各级暗条纹对应的衍射角 j 所满足的条件。 解 在狭缝两个边缘处,衍射角为 j 的两光的光程差为
2
a
其他相邻两点的光线的
光程差都是 2
j
A
A1
A2
C
B
2
(d)同理,波带AA1与A1A2上对应点所发出的两光线的光程差
总是2 ,其他任何相邻两波带上对应点发出光束的光程差总
是 。
2
(e) 2
j
相邻两波带发出的光束
A
两两抵消。
a
A1
A2
C
(f)P点亮与暗,只考虑
B
2
两两波带抵消后,余下波 带发出光束的多少。
第二节 光的衍射现象
一、光的衍射 二、单缝衍射实验 三、圆孔衍射实验 四、光栅衍射实验
光的衍射现象
光绕过障碍物传播的现象
(剃须刀边缘衍射)
a 直线传播
a 衍射现象
2.1 惠更斯---菲涅尔原理
波所到之处各点都可以看作是发射子波的波源,在以后任一时 刻,这些子波的包络面就是在该时刻的波面——惠更斯原理。
a (sin φ sin θ )
对于暗纹有 k
a sin θ A
则 a (sin φ sin θ ) k sin φ k sin θ
a (k 1,2,3, )
φ θ
B a sin φ
例一
已知:设有一观测单缝衍射的装置,其缝宽a=0.42mm,采用 的单色光为λ=540nm的汞光,设透镜的焦距f=50cm(即单缝 到屏的距离),求中央明纹中心到第一暗纹之间的距离。
A1
A2
C
a sin j 2k
2
k
B
2
k 1,2
重点
a s in j k
内容
单缝衍射条纹特点
①在中央明纹两侧对称分布平行于狭缝。 ②中央亮条纹的亮度很大,其他次亮纹的亮度很小,依次衰减。
③中央亮条纹的宽度是次亮纹的两倍。 ④a越小(λ一定),φ1越大,衍射越明显。 ⑤用白光照射单缝,中央为白色条纹,其它条纹为彩色条纹。
L
P
a
o
f
(2)与光轴成φ角的平行光
半波带法
(a)将最两端两光束的光程差
BC 分成若干个间距,
每个间距宽为λ/2。
a
(b)做平行于AC的平行线, 交AB于A1,A2……,
半波带 A A 1 A 1 A 2 A 2 A 3
j
A
A1
A2
C
B
2
(c)这样,A点与A1点发出光线 的光程差
A1与A2两点的光程差也是
光学仪器均有口径,每个像点均是圆孔的夫琅和 费衍射斑。
f
1.22
D
由瑞利判据,可分辨的两物点对望远镜张的最小角度为
例:观察一发光波长为λ=500nm 的双星,双星的视角为 6 . 1 1 0 7 r a d 则望远镜的镜筒直径至少为多少m?
解: a 1.22
1 10 9 nm 1m
圆孔第一暗纹的衍射角满足下式:
艾里斑的半角宽度
1
1.22
D
D为圆孔直径
例: 在夫琅禾费圆孔衍射中,用波长500nm的单色光分别照 射直径为0.10mm和1.0mm的圆孔上,若透镜的焦距为0.50m, 求接收屏上艾里斑的半径。
r1
1.22
f
a1
1.5 10 3 m
r2
1.22
f
a1
1.5 10 4 m
瑞利判据:对于两个等光强的非相干物点,如果一个像斑中
心恰好落在另一像斑的边缘(第一暗纹处),则此两像被认为 是刚好能分辨。此时两像斑中心角距离为最小分辨角
1
1.22
D
几何光学 波动光学
物点 物点
一一对应 一分辨 1
不可分辨 1
1
1.22
D
光学仪器的分辨本领
分三种情况讨论:
①AB恰好分成偶数个半波带——P点是暗条纹。
②AB恰好分成奇数个半波带——P点是亮条纹(但是亮度 比零级中央亮条纹小得多,只是一个半波带贡献的结果)。
③AB不是整数个半波带——P点是亮条纹(亮度介于①与 ②之间)。
j
A
BC A B sin j a sin j
单缝衍射的暗条纹
a
菲涅尔作出补 充:同一波前上 各点发出的子波, 经传播在空间某 点相遇,也可相 互干涉——惠更 斯—菲涅尔原理。
A.J.菲涅耳
两类衍射:
1、菲涅耳衍射:非平行光。
2、夫朗和费衍射: 平行光。
2.2 夫琅禾费单缝衍射实验
单缝衍射实验装置
L2 L1
P
S
aj
o
f
D
(1)平行光轴的一束平行光
n 1 r1 n 2 r2 0
射电望远镜
波多黎各射电望远镜305
讨论
(1) j 0 2j 1 2 λ a 波长越长,缝宽越小,条纹宽度越宽。 (2) λ a 0 j 0 0 波动光学退化到几何光学。 (3) λ a 1 j 0 π 观察屏上不出现暗纹。
(4) 缝位置变化不影响条纹位置分布
·
解: a s in j 1
sin j 1 tan j 1
x f
a
x f 500 540 10 6 0.64m m
a
0.42
例二
波长为λ=589nm的钠黄光通过单缝后在距离缝1m处产生衍射 图样,若两个第一极小值之间的距离为2mm,求单缝的宽度。
解: x f
a
2x 2m m
a f 103 589 10 6 0.589m m
x
1
2.3 夫琅禾费圆孔衍射实验
衍射屏 L
1
孔径为D
f
相对光强曲线
中央亮斑 (艾里斑)
经圆孔衍射后,一个点光源对应一个艾里斑
特点: 1.中央亮纹很亮,称为艾里斑,集中了衍射中的光能量的84%; 2.第一暗纹,衍射角为1,1为中央亮纹的半角宽度, 21为中 央亮纹的张角。
说明 (1) 得到的暗纹和中央明纹位置精确,其它明纹位置只是近似 (2) 单缝衍射和双缝干涉条纹比较。
单缝衍射条纹
双缝干涉条纹
单缝衍射明纹角宽度和线宽度
角宽度 相邻两暗纹中心对应的衍射角之差
线宽度 观察屏上相邻两暗纹中心的间距
透镜
观测屏
x2
j1
x1
x1
j1 o
x0
j0
x1
衍射屏
f
中央明纹 角宽度 j 0 2j 1 2 λ a 线宽度 x 0 2 f ta n j 1 2 fj 1 2 f λ a
B
f A
( 单缝夫琅禾费衍射典型装置 )
(5) 一定,改变a,对同一级(k值定)条纹,a,缝越细,
衍射越明显,最大衍射角=900
a,缝宽到一定程度,无衍射现象,为直线传播
例 如图示,设有一波长为 的单色平面波沿着与缝平面的法 线成 角的方向入射到宽为 a 的单缝 AB 上。
求 各级暗条纹对应的衍射角 j 所满足的条件。 解 在狭缝两个边缘处,衍射角为 j 的两光的光程差为
2
a
其他相邻两点的光线的
光程差都是 2
j
A
A1
A2
C
B
2
(d)同理,波带AA1与A1A2上对应点所发出的两光线的光程差
总是2 ,其他任何相邻两波带上对应点发出光束的光程差总
是 。
2
(e) 2
j
相邻两波带发出的光束
A
两两抵消。
a
A1
A2
C
(f)P点亮与暗,只考虑
B
2
两两波带抵消后,余下波 带发出光束的多少。
第二节 光的衍射现象
一、光的衍射 二、单缝衍射实验 三、圆孔衍射实验 四、光栅衍射实验
光的衍射现象
光绕过障碍物传播的现象
(剃须刀边缘衍射)
a 直线传播
a 衍射现象
2.1 惠更斯---菲涅尔原理
波所到之处各点都可以看作是发射子波的波源,在以后任一时 刻,这些子波的包络面就是在该时刻的波面——惠更斯原理。
a (sin φ sin θ )
对于暗纹有 k
a sin θ A
则 a (sin φ sin θ ) k sin φ k sin θ
a (k 1,2,3, )
φ θ
B a sin φ
例一
已知:设有一观测单缝衍射的装置,其缝宽a=0.42mm,采用 的单色光为λ=540nm的汞光,设透镜的焦距f=50cm(即单缝 到屏的距离),求中央明纹中心到第一暗纹之间的距离。
A1
A2
C
a sin j 2k
2
k
B
2
k 1,2
重点
a s in j k
内容
单缝衍射条纹特点
①在中央明纹两侧对称分布平行于狭缝。 ②中央亮条纹的亮度很大,其他次亮纹的亮度很小,依次衰减。
③中央亮条纹的宽度是次亮纹的两倍。 ④a越小(λ一定),φ1越大,衍射越明显。 ⑤用白光照射单缝,中央为白色条纹,其它条纹为彩色条纹。
L
P
a
o
f
(2)与光轴成φ角的平行光
半波带法
(a)将最两端两光束的光程差
BC 分成若干个间距,
每个间距宽为λ/2。
a
(b)做平行于AC的平行线, 交AB于A1,A2……,
半波带 A A 1 A 1 A 2 A 2 A 3
j
A
A1
A2
C
B
2
(c)这样,A点与A1点发出光线 的光程差
A1与A2两点的光程差也是
光学仪器均有口径,每个像点均是圆孔的夫琅和 费衍射斑。
f
1.22
D
由瑞利判据,可分辨的两物点对望远镜张的最小角度为
例:观察一发光波长为λ=500nm 的双星,双星的视角为 6 . 1 1 0 7 r a d 则望远镜的镜筒直径至少为多少m?
解: a 1.22
1 10 9 nm 1m
圆孔第一暗纹的衍射角满足下式:
艾里斑的半角宽度
1
1.22
D
D为圆孔直径
例: 在夫琅禾费圆孔衍射中,用波长500nm的单色光分别照 射直径为0.10mm和1.0mm的圆孔上,若透镜的焦距为0.50m, 求接收屏上艾里斑的半径。
r1
1.22
f
a1
1.5 10 3 m
r2
1.22
f
a1
1.5 10 4 m
瑞利判据:对于两个等光强的非相干物点,如果一个像斑中
心恰好落在另一像斑的边缘(第一暗纹处),则此两像被认为 是刚好能分辨。此时两像斑中心角距离为最小分辨角
1
1.22
D
几何光学 波动光学
物点 物点
一一对应 一分辨 1
不可分辨 1
1
1.22
D
光学仪器的分辨本领
分三种情况讨论:
①AB恰好分成偶数个半波带——P点是暗条纹。
②AB恰好分成奇数个半波带——P点是亮条纹(但是亮度 比零级中央亮条纹小得多,只是一个半波带贡献的结果)。
③AB不是整数个半波带——P点是亮条纹(亮度介于①与 ②之间)。
j
A
BC A B sin j a sin j
单缝衍射的暗条纹
a
菲涅尔作出补 充:同一波前上 各点发出的子波, 经传播在空间某 点相遇,也可相 互干涉——惠更 斯—菲涅尔原理。
A.J.菲涅耳
两类衍射:
1、菲涅耳衍射:非平行光。
2、夫朗和费衍射: 平行光。
2.2 夫琅禾费单缝衍射实验
单缝衍射实验装置
L2 L1
P
S
aj
o
f
D
(1)平行光轴的一束平行光
n 1 r1 n 2 r2 0
射电望远镜
波多黎各射电望远镜305
