决策树例题
决策树案例及答案

案例:假设有一工程项目,管理人员要根据天气状况决定开工方案。
如果开工后天气好,可以给国家创收30000元;如果开工后天气差,将给国家带来损失10000元;如果不开工,讲给国家带来损失1000元,。
已知开工后天气好的概率是0.6,开工后天气差的概率是0.4.请用
决策树方案进行决策。
状方、、态案天气好天气坏
0.60.4
开工30000 (期望收益=30000*0.6 )-10000 (期望收益=-10000*0.4 )爪开工-1000 (期望收益=-1000*0.6 )-1000 (期望收益=-1000*0.4 )第二步,绘制决策树
(1) 计算期望收益并标注在决策树上
开工方案下,预期收益值=30000*0.6+ (-10000) *0.4=14000
不开工方案下,预期损失值=-1000
(2) 比较两个方案并减去期望收益较小的方案枝
30000*0. 6
概率枝-10000*0-4
-1000*0.6
-1 000*0.4
概率枝▲18000 .▲-4000▲-600
A-400。
案例试题—决策树
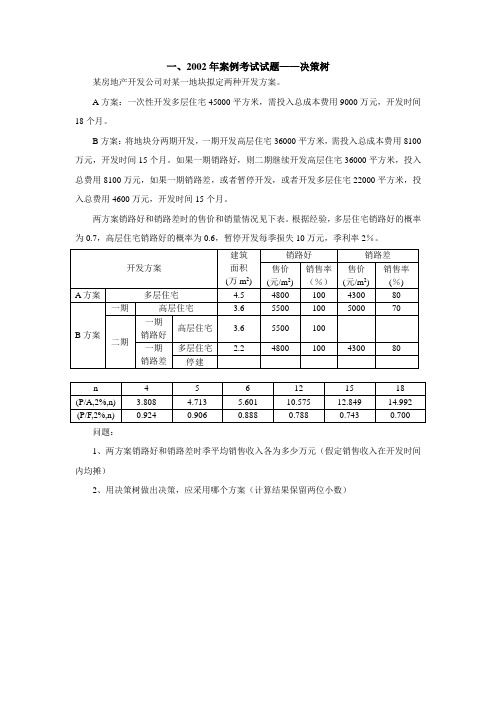
一、2002年案例考试试题——决策树某房地产开发公司对某一地块拟定两种开发方案。
A方案:一次性开发多层住宅45000平方米,需投入总成本费用9000万元,开发时间18个月。
B方案:将地块分两期开发,一期开发高层住宅36000平方米,需投入总成本费用8100万元,开发时间15个月。
如果一期销路好,则二期继续开发高层住宅36000平方米,投入总费用8100万元,如果一期销路差,或者暂停开发,或者开发多层住宅22000平方米,投入总费用4600万元,开发时间15个月。
两方案销路好和销路差时的售价和销量情况见下表。
根据经验,多层住宅销路好的概率为0.7,高层住宅销路好的概率为0.6,暂停开发每季损失10万元,季利率2%。
问题:1、两方案销路好和销路差时季平均销售收入各为多少万元(假定销售收入在开发时间内均摊)2、用决策树做出决策,应采用哪个方案(计算结果保留两位小数)答案:1、A方案开发多层住宅:销路好4.5×4800×100%÷6=3600(万元)销路差4.5×4300×80%÷6=2580(万元)B方案一期开发高层住宅:销路好3.6×5500×100%÷5=3960(万元)销路差3.6×5000×70%÷5=2520(万元)B方案二期开发高层住宅:3.6×5500×100%÷5=3960(万元)开发多层住宅:销路好2.2×4800×100%÷5=2112(万元)销路差2.2×4300×80%÷5=1513.6(万元)2、机会点①净现值的期望值:(3600×0.7+2580×0.3)×(P/A,2%,6)-9000=(3600×0.7+2580×0.3)×5.601-9000=9449.69(万元)等额年金:9449.69×(A/P,2%,6)=9449.69×1/5.601=1687.14(万元)机会点③净现值的期望值:3960×(P/A,2%,5)×1.0-8100=3960×4.713×1.0-8100=10563.48(万元)等额年金:10563.48×(A/P,2%,5)=10563.48×1/4.713=2241.35(万元)机会点④净现值的期望值:-10×(P/A,2%,5)=-10×4.713=-47.13(万元)等额年金:-47.13×(A/P,2%,5)=-47.13×1/4.713=-10.00(万元)机会点⑤净现值的期望值:(2112×0.7+1513.6×0.3)×(P/A,2%,5)-4600=(2112×0.7+1513.6×0.3)×4.713-4600=4507.78(万元)等额年金:4507.78×(A/P,2%,5)=4507.78×1/4.713=956.46(万元)根据计算结果判断,B方案在一期开发高层住宅销路差的情况下,二期应改为开发多层住宅。
管理学决策树习题及答案

注意答卷要求:1.统一代号:P为利润,C为成本,Q为收入,EP为期望利润2.画决策树时一定按照标准的决策树图形画,不要自创图形3.决策点和状态点做好数字编号4.决策树上要标出损益值某企业似开发新产品,现在有两个可行性方案需要决策。
I开发新产品A,需要追加投资180万元,经营期限为5年。
此间,产品销路好可获利170万元;销路一般可获利90万元;销路差可获利-6万元。
三种情况的概率分别为30%,50%,20%。
II.开发新产品B,需要追加投资60万元,经营期限为4年。
此间,产品销路好可获利100万元;销路一般可获利50万元;销路差可获利20万元。
三种情况的概率分别为60%,30%,10%。
(1)画出决策树17090-61005020(2)计算各点的期望值,并做出最优决策求出各方案的期望值:方案A=170×0.3×5+90×0.5×5+(-6)×0.2×5=770(万元)方案B=100×0.6×4+50×0.3×4+20×0.1×4=308(万元)求出各方案的净收益值:方案A=770-180=590(万元)方案B=308-60=248(万元)因为590大于248大于0所以方案A最优。
某企业为提高其产品在市场上的竞争力,现拟定三种改革方案:(1)公司组织技术人员逐渐改进技术,使用期是10年;(2)购买先进技术,这样前期投入相对较大,使用期是10年;(3)前四年先组织技术人员逐渐改进,四年后再决定是否需要购买先进技术,四年后买入技术相对第一年便宜一些,收益与前四年一样。
预计该种产品前四年畅销的概率为0.7,滞销的概率为0.3。
如果前四年畅销,后六年畅销的概率为0.9;若前四年滞销,后六年滞销的概率为0.1。
相关的收益数据如表所示。
(1)画出决策树(2)计算各点的期望值,并做出最优决策投资收益表单位:万元解(1)画出决策树,R为总决策,R1为二级决策。
决策树决策表练习题与参考答案

1.某厂对一部分职工重新分配工作,分配原则是:
⑴年龄不满20岁,文化程度是小学者脱产学习,文化程度是中学者当电工;
⑵年龄满20岁但不足50岁,文化程度是小学或中学者,男性当钳工,女性当车工;文化程度是大专者,当技术员。
⑶年龄满50岁及50岁以上,文化程度是小学或中学者当材料员,文化程度是大专者当技术员。
优化后的决策表如下:
2、试画出某企业库存量监控处理的判断树。
若库存量≤0,按缺货处理;若库存量≤库存下限,按下限报警处理;若库存量>库存下限,而又≤储备定额,则按订货处理;若库存量>库存下限,而又>储备定额,则按正常处理;若库存量≥库存上限,又>储备定额,则按上限报警处理。
3某货运站收费标准如下:
若收件地点在本省,则快件6元/公斤,慢件4元/公斤;
若收件地点在外省,则在25公斤以内(包括25公斤),快件8元/公斤,慢件6元/公斤;而超过25公斤时,快件10元/公斤,慢件8元/公斤;
画出决策表和决策树:
决策表:
优化后的结果如下所示:决策树:
收费
本省
外省快件
慢件
快件
慢件
≤25斤
>25斤
≤25斤
>25斤
6元
4元
8元
10元
6元
8元
地点规格重量收费金额
欢迎您的下载,
资料仅供参考!
致力为企业和个人提供合同协议,策划案计划书,学习资料等等
打造全网一站式需求。
决策树习题练习(答案)

决策树习题练习答案1.某投资者预投资兴建一工厂,建设方案有两种:①大规模投资300万元;②小规模投资160万元。
两个方案的生产期均为10年,其每年的损益值及销售状态的规律见表15。
试用决策树法选择最优方案。
【解】(1)绘制决策树,见图1;(2)计算各状态点的期望收益值节点②:[]10300340()⨯⨯⨯-=1000.7+(-20)0.3万元 节点③:[]10160320()⨯⨯⨯-=600.7+200.3万元 将各状态点的期望收益值标在圆圈上方。
(3)决策比较节点②与节点③的期望收益值可知,大规模投资方案优于小规模投资方案,故应选择大规模投资方案,用符号“//”在决策树上“剪去”被淘汰的方案。
表1 各年损益值及销售状态2.某项目有两个备选方案A和B,两个方案的寿命期均为10年,生产的产品也完全相同,但投资额及年净收益均不相同。
A方案的投资额为500万元,其年净收益在产品销售好时为150万元,,销售差时为50万元;B方案的投资额为300万元,其年净收益在产品销路好时为100万元,销路差时为10万元,根据市场预测,在项目寿命期内,产品销路好时的可能性为70%,销路差的可能性为30%,试根据以上资料对方案进行比选。
已知标准折现率i c=10%。
【解】(1)首先画出决策树此题中有一个决策点,两个备用方案,每个方案又面临着两种状态,因此可以画出其决策树如图18。
(2)然后计算各个机会点的期望值机会点②的期望值=150(P/A,10%,10)×0.7+(-50)(P/A,10%,10)×0.3=533(万元)机会点③的期望值=100(P/A,10%,10)×0.7+10(P/A,10%,10)×0.3=448.5(万元)最后计算各个备选方案净现值的期望值。
方案A的净现值的期望值=533-500=33(万元)方案B的净现值的期望值=448.5-300=148.5(万元)因此,应该优先选择方案B。
人工智能决策树例题经典案例

人工智能决策树例题经典案例一、经典案例:天气预测决策树在天气预测中有广泛应用,下面是一个关于是否适宜进行户外运动的示例:1. 数据收集:- 温度:高(>30℃)/中(20℃-30℃)/低(<20℃)- 降水:是/否- 风力:高/中/低- 天气状况:晴朗/多云/阴天/雨/暴雨- 应该户外运动:是/否2. 构建决策树:- 根据温度将数据分为三个分支:高温、中温、低温- 在每个分支中,继续根据降水、风力和天气状况进行划分,最终得到是否适宜户外运动的决策3. 决策树示例:温度/ / \高温中温低温/ | | \ |降水无降水风力适宜/ \ | | / \是否高中低| |不适宜适宜- 如果温度是高温且有降水,则不适宜户外运动- 如果温度是高温且无降水,则根据风力判断,如果风力是高,则不适宜户外运动,如果风力是中或低,则适宜户外运动 - 如果温度是中温,则不论降水和风力如何,都适宜户外运动- 如果温度是低温,则需要考虑风力,如果风力是高,则适宜户外运动,如果风力是中或低,则不适宜户外运动4. 参考内容:决策树的构建和应用:决策树通过对输入特征进行划分,构建了一棵树形结构,用于解决分类或回归问题。
构建决策树主要包括数据预处理、特征选择、划分策略和停止条件等步骤。
特征选择可以使用信息增益、基尼指数等算法,划分策略可以使用二叉划分或多叉划分,停止条件可以是叶子节点纯度达到一定阈值或达到预定的树深度。
决策树的应用包括数据分类、特征选择和预测等任务。
天气预测案例中的决策树:将天气预测问题转化为分类问题,通过构建决策树,可以得到识别是否适宜户外运动的规则。
决策树的决策路径可以用流程图或树状图表示,帮助理解和解释决策过程。
决策树的节点表示特征值,分支表示判断条件,叶子节点表示分类结果。
决策树的生成算法可以基于启发式规则或数学模型,如ID3、C4.5、CART等。
决策树的优缺点:决策树具有可解释性强、易于理解和实现、能处理非线性关系等优点。
决策树练习题-多级决策树

E(5)=1.0×(-30)×7= -210 (万元)
4
前三年的期望收入=0.7×100×3+0.3×(-30)×3=183(万元)
5
E(1)=183+0.7×609+0.3×(-210)-300=246.3 (万元)
6
02
03
对于节点2即改建车间
E(6)=0.9×40×7+0.1×10×7=259 (万元)
Hale Waihona Puke 01通过比较各期望收益,选择方案。
03
方案3为最佳方案。
02
E(3)=302.3> E(1)246.3 > E(2)155.3
销路好0.7
销路好0.7
销路差0.3
销 路差0.3
销路差0.3
销路差1.0
销路差0.1
销路差0.1
销路差1.0
销路差0.1
销路差0.1
销路差1.0
销路好0.9
销路好0.9
销路好0.9
销路好0.9
100
-30
-30
40
10
10
10
10
100
-30
40
前三年
后七年
扩 建
不 扩 建
E(4)=0.9×100×7+0.1×(-30)×7=609
E(5)=1.0×(-30)×7= -210
前三年的期望收入= 0.7×100×3+0.3×(-30)×3=183
E(1)=183+0.7×609+0.3×(-210)-300=246.3
决策树计算题
某工厂为生产一种新产品,制定三个基建方案。一是新建车间生产;二是改建原有车间进行生产;三是先改建,生产3年后当产品销路好时再进行扩建。新建和改建车间所需投资分别是300万元和140万元,若要在改建的基础上扩建车间,还需要追加投资140万元,产品生产期定为10年。
临床决策树例题经典案例医学

临床决策树例题经典案例医学
临床决策树是一种基于概率和逻辑的推理模型,用于帮助医生根据患者的症状和体征做出诊断和治疗决策。
以下是一个经典的临床决策树案例:
假设有一位患者因胸痛和呼吸困难而就诊。
医生可以使用临床决策树来评估患者患急性心肌梗死的风险。
1. 首先,医生需要收集患者的病史和体格检查结果。
例如,患者是否有高血压、糖尿病、吸烟等危险因素。
2. 然后,医生可以使用临床决策树来评估患者患急性心肌梗死的风险。
临床决策树通常由一系列的问题组成,每个问题的答案都会导致不同的分支,每个分支都代表不同的风险水平。
3. 医生可以根据患者的回答选择相应的分支,最终得出患者患急性心肌梗死的风险水平。
4. 根据患者的风险水平,医生可以制定相应的治疗方案。
例如,对于高风险患者,医生可能需要紧急进行冠状动脉造影和支架植入术;对于低风险患者,医生可能只需要药物治疗和密切观察。
通过使用临床决策树,医生可以更加准确地评估患者的病情,并制定更加个性化的治疗方案。
这有助于提高患者的治疗效果和生活质量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.为什么使用决策树分析?
当项目需要做出某种决策、选择某种解决方案或者确定是否存在某种风险时,决策树(decision making tree)提供了一种形象化的、基于数据分析和论证的科学方法,这种方法通过严密地逻辑推导和逐级逼近地数据计算,从决策点开始,按照所分析问题的各种发展的可能性不断产生分枝,并确定每个分支发生的可能性大小以及发生后导致的货币价值多少,计算出各分枝的损益期望值,然后根据期望值中最大者(如求极小,则为最小者)作为选择的依据,从而为确定项目、选择方案或分析风险做出理性而科学的决策。
2.决策树分析有哪些作用?
决策树分析清楚显示出项目所有可供选择的行动方案,行动方案之间的关系,行动方案的后果,后果发生的概率,以及每种方案的损益期望值;
使纷繁复杂的决策问题变得简单、明了,并且有理有据;
用数据说话,形成科学的决策,避免单纯凭经验、凭想象而导致的决策上的失误。
3.怎么用?
(1)决策树包含了决策点,通常用方格或方块表示,在该点表示决策者必须做出某种选择;机会点,用圆圈表示,通常表示有机会存在。
先画一个方框作为出发点,叫做决策点;
(2)从决策点向右引出若干条支线(树枝线),每条支线代表一个方案,叫做方案枝;
(3)在每个方案枝的末端画一个圆圈,叫做状态点;
(4)估计每个方案发生的概率,并把它注明在在该种方案的分支上,称为概率枝;
(5)估计每个方案发生后产生的损益值,收益用正值表示,损失用负值表示;
(6)计算每个方案的期望价值,期望价值=损益值x该方案的概率;
(7)如果问题只需要一级决策,在概率枝末端画△表示终点,并写上各个自然状态的损益值;
(8)如果是多级决策,则用决策点□代替终点△重复上述步骤继续画出决策树,如图1所示。
(9)计算决策期望值,决策期望值=由此决策而发生的所有方案期望价值之和;
(10)根据决策期望值做出决策。
4.例题:
某承包商向某工程投标,计划采取两种策略:一种是投高标,中标机会为0.2,不中标机会为0.8;另一种是投低标,中标与不中标机会均为0.5。
投标不中时,则损失投标准备费5万元。
根据下表数据,用决策树做出决策。
方案效果可能获利
(万元)
概率
高标
好500 0.3 一般300 0.5 赔-100 0.2
低标
好350 0.2 一般200 0.6 赔-150 0.2
计算的结果表明,
高标:500×0.3+300×0.5-100×0.2=280万,280×0.2-5×0.8=52万;
低标: 350×0.2+200×0.6-150×0.2=160万,160×0.5-5×0.5=77.5万;
最大损益期望值为77.5万,也就是上说若投高标,可能最多只能赚到52万,而若投低标则有可能赚到77.5万,故应采取低标策略。
感谢下载!
欢迎您的下载,资料仅供参考。
