轧制参数计算模型及其应用(一)
轧制力能参数范文

轧制力能参数范文轧制力是指钢铁、金属等材料在轧制过程中受到的切削力或变形力。
轧制力的参数对轧制过程的控制和优化具有重要的意义。
下面将从轧制力的定义、计算、调节和影响因素等方面,详细介绍轧制力的参数。
一、轧制力的定义轧制力是指轧制机综合作用下金属材料所受的力。
在轧制过程中,轧辊通过对金属材料的压制、切割、牵引等方式对其进行变形。
这些力的大小和方向决定了轧制过程中金属材料的变形途径、变形程度和质量。
二、轧制力的计算1.平面轧制力计算公式在平面轧制过程中,轧制力的大小可以通过以下公式进行计算:F=kAε其中,F为轧制力,k为表征轧制过程的特性参数,A为金属材料的截面积,ε为金属材料的应变。
该公式表明,轧制力与材料的截面积和应变呈正比关系,同时受到轧制过程特性参数k的影响。
2.缺口轧制力计算公式在缺口轧制过程中,轧制力的大小可以通过以下公式进行计算:F=kAl其中,F为轧制力,k为表征轧制过程的特性参数,A为金属材料的截面积,l为两辊缺口的长度。
该公式表明,轧制力与材料的截面积和缺口长度呈正比关系,同时受到轧制过程特性参数k的影响。
三、轧制力的调节为了获得良好的轧制质量和提高生产效率,需要对轧制力进行调节。
常见的调节方法包括调节轧辊力、调节辊缝尺寸、调节轧机速度等。
1.调节轧辊力通过调节轧辊的力大小和方向,可以改变轧制力的大小和分布,从而达到控制变形的目的。
调节轧辊力可以通过改变轧辊的压下力和牵引力来实现。
2.调节辊缝尺寸通过调节辊缝的宽度和间隙,可以改变轧制力的大小和分布。
辊缝的宽度和间隙对轧制力的影响较大。
辊缝宽度小,间隙大,轧制力较大;辊缝宽度大,间隙小,轧制力较小。
3.调节轧机速度通过调节轧机的转速和进给速度,可以改变轧制力的大小和分布。
提高轧机速度可以减小轧制力,但同时也会增加摩擦力和能量消耗。
四、轧制力的影响因素轧制力的大小受到多种因素的影响,主要包括材料的物理力学性质、工艺参数和轧机设备的调整情况。
轧制力的计算范文

轧制力的计算范文轧制力是指在金属轧制过程中,金属带材或板材所受到的压力。
轧制力的计算非常重要,它能够帮助我们预测并控制轧制过程中的变形和应变,以获得所需的产品质量。
下面将详细介绍轧制力的计算方法。
1.塑性力学方法:在轧制过程中,金属材料会发生变形,塑性力学方法通过考虑材料的弹性、塑性和流变行为,从宏观和微观两个角度对轧制力进行计算。
宏观力学方法的基本假设是轧制过程中金属材料的体积守恒。
根据这个假设,轧制力可以通过以下公式进行计算:F=σ×A其中,F是轧制力,σ是金属带材或板材在轧制过程中所受到的应力,A是轧制区截面的面积。
金属材料的应力可以通过以下公式进行计算:σ=K×ε^n其中,K是比例常数,ε是真应变(真实变形),n是流变指数。
这些参数可以通过实验和理论分析来确定。
微观力学方法考虑了金属材料的结晶学和滑移机制。
它使用了位错理论和格点模型来计算轧制力。
这种方法需要对材料的晶体结构和力学性质进行深入研究和分析。
2.能量方法:能量方法的基本假设是轧制力是使金属材料的能量损失等于所用的能量传递速率的比例常数。
根据这个假设,轧制力可以通过以下公式进行计算:F=ΔE/Δt其中,ΔE是金属材料在轧制过程中的能量损失,Δt是时间。
能量损失可以通过测量轧制区的温度变化来计算,或者使用热力学和热传导理论进行估计。
需要注意的是,轧制力的计算方法多种多样,不同的金属材料和轧制过程可能需要不同的计算方法。
此外,实际的轧制力还受到很多其他因素的影响,如润滑条件、辊形状、辊缩径等。
总结起来,轧制力的计算是金属轧制过程中的重要问题。
通过正确地计算轧制力,我们能够更好地控制产品的变形和应变,提高产品的质量。
同时,轧制力的计算也为轧制设备的设计和优化提供了重要的理论依据。
经典轧制力模型理论解析 (带钢冷轧模型理论学习笔记)

经典轧制力模型理论解析(带钢冷轧模型理论学习笔记)中冶南方工程技术有限公司上海分公司2005年11月9日序号文章名称页数1 一、奥罗曼(E.Orowan)理论 62 二、布兰德-福特(D.R.Bland &H.Ford)轧制力近似计算理论163 三、斯通(M.D.Stone)的计算轧制力公式 554 四、布兰德-福特(D.R.Bland &H.Ford)轧制力及轧制转矩数学模型离散计算方法5 五、用离散算法对轧制程序表的试算题266 六、斯通轧制力与轧制转矩公式近似计算 37 七、M.D.Stone公式近似计算法试算例题188 八、冷轧轧辊辊缝中摩擦形成理论31在带钢冷轧机的轧制工艺设计、机械设备设计和轧钢生产过程控制应用软件的设计与开发。
都需要利用轧制力模型做计算。
那么,当前广为人们使用的轧制力模型是前人为我们留下的宝贵财富。
只有对那些成果深入地理解,才能认清当前应用的各种轧制模型的脉络,提高对模型的鉴别力和有所前进。
最先用微分方程式描述沿轧辊与带钢交界面的接触弧上的轧制力分布的是卡尔曼(T.Karmann),即所谓卡尔曼方程,发表在1925年的《应用数学与力学》杂志上。
卡尔曼方程虽然用解析方法不能得解,但是对于随后的学者发展可用于工程的轧制力模型具有重要意义,如史密斯和采利可夫,他们各自利用不同假定和简化得到卡尔曼方程的实用解。
贴近当前应用的,多采用在奥罗万(E.Orowan)理论的基础上,和由卡尔曼确立方程式的分析方法,布兰德-福特(D.R.Bland & H.Ford)发展了广为应用的轧制力模型;斯通(M.D.Stone)提出了轧制力计算比较简便的斯通公式。
本文将对奥罗万理论、布兰德-福特轧制力模型和斯通公式做详细解析。
带钢冷轧生产过程是个复杂的多参数作用的过程,有多项不确定性因素,从物理和数学的观点来说会是十分复杂的。
因此,研制可实用的轧制力模型,通常要对过程条件和控制参数做些基本假定和简化如下:1.轧件为连续介质,体积(或密度)基本不变。
轧钢机械(第二章力能参数)(精)

©xuyong
20
§2 接触弧上的单位压力及影响因素
二、轧制时接触弧上px的微分方程式 1、T.Karman px的微分方程式(1925年)
L L
©xuyong
大压下量
小压下量
30
§3 轧制时接触弧上的平均单位压力
, pm= n’n”n”nB
这里介绍几种常用的计算公式
一、采利柯夫公式
三大步: 解Karman方程,求px表达式; 沿接触弧分段积分,求总压力P; 总压力除以面积得pm。
pm= n’K
31
©xuyong
©xuyong
§1 轧制力计算的基本思路与理论
四、金属塑性变形条件——塑性方程式 1、屈服准则 • 屈雷斯卡(H.Trasca)屈服准则 • 蜜赛斯(R.von.Misse)屈服准则
欲使处于应力状态的物体中的某一点进入 塑性状 态,必须使得该点的单位弹性形状变化位能达到材料 所允许的极限值,并且该极限数值与应力状态无关, 而是一个常值。
24
©xuyong
§2 接触弧上的单位压力及影响因素
三、影响单位压力的因素 2、变形阻力的确定 • 金尼克曲线; • 库克曲线; • 北京钢院曲线; • 其他曲线或经验公式。
25
©xuyong
§2 接触弧上的单位压力及影响因素
三、影响单位压力的因素 3、影响应力状态的因素
接触弧上单位摩擦力分布的影响 干摩擦理论 粘着摩擦理论 结论: μ↑则 p↑
轧制摩擦角

轧制摩擦角
标题:轧制摩擦角的理论与应用
一、引言
在金属加工行业中,轧制是一种常见的材料塑性变形方式。
而轧制摩擦角则是影响轧制过程的重要参数之一,它对轧制力、轧制温度、轧制速度等都有显著的影响。
二、轧制摩擦角的定义
轧制摩擦角是指在轧制过程中,工作辊和轧件之间接触面的法线与相对滑动方向之间的夹角。
它是衡量轧制过程中摩擦力大小的一个重要参数。
三、轧制摩擦角的计算
轧制摩擦角的计算公式为:tanφ=(τf-τs)/σb,其中,φ为轧制摩擦角,τf为轧制面间的最大静摩擦系数,τs为轧制面间的切向应力,σb为轧件的屈服强度。
四、轧制摩擦角的影响因素
1. 轧制条件:如轧制速度、轧制压力、轧制温度等都会影响轧制摩擦角的大小。
2. 材料性质:如材料的硬度、韧性和表面粗糙度等也会影响轧制摩擦角的大小。
3. 润滑条件:良好的润滑可以降低轧制摩擦角,提高轧制效率。
五、轧制摩擦角的应用
1. 在实际生产中,通过控制轧制摩擦角,可以有效改善轧制产品的质量和产量。
2. 通过对轧制摩擦角的研究,可以优化轧制工艺,提高生产效率。
3. 在设计和选择轧机设备时,也需要考虑到轧制摩擦角的影响。
六、结论
总的来说,轧制摩擦角是决定轧制效果的关键参数之一。
理解并掌握其基本原理和应用,对于提高轧制工艺水平,提升产品质量具有重要意义。
七、参考文献
[待添加]。
轧制过程数学模型

1轧制过程数学模型1.1轧制工艺参数模型随着科学技术的发展,计算机已广泛应用于轧钢生产过程的控制,促使轧钢生产向自动化、高速和优质方向发展。
电子计算机在线控制生产过程,不仅仅只是电子计算机本身的硬件和软件的作用,更重要的是控制系统和各种各样的数学模型,正因为有适合轧钢生产的各种数学模型,才有可能实现电子计算机对整个轧钢生产各个环节的控制,获得高精度的产品。
线材连轧生产过程的主要内容基本上可归纳为尺寸变化和温度变化两大类性质极不相同但又相互紧密联系的物理过程,涉及的数学模型主要是轧制工艺参数的制定、各环节的温降变化、产品质量控制及实现线材连轧生产的可靠性等。
在线材连轧生产过程中,准确地计算(预估)各个环节的温度变化是实现计算机控制的重要前提,这是因为轧件各道次的变形阻力、轧制压力、轧制力矩的准确确定与温度是分不开的,而各机架轧制压力的预估精度将直接关系到设备的使用安全等。
下面分别讨论线材连轧生产过程中的温降模型、变形阻力模型、轧制力与轧制力矩模型。
1.1.1延伸系数及孔型尺寸计算模型在制订棒线材轧制工艺时,当坯料和产品断面面积F 0和F n 给定之后,总延伸系数∑μ就可唯一确定:nn n i i n i F FF F F F F F F F 011211021===-+∑ μμμμμ 其中:n ——总轧制道次;μi ——某一道次的延伸系数; F i ——某一道次的轧件断面面积。
椭圆孔示意图mB R F +-=)sin (2θθRB 2arcsin2=θ ⎪⎭⎫ ⎝⎛--=2cos 12θR h m对于圆孔,轧件断面面积可通过下式计算:圆孔示意图απθ2-=αθtan 422R R F +=1.1.2前滑模型孔型轧制时的前滑率计算可采用筱篬或斋藤提出的实验模型。
两者都认为前滑仅是轧件、孔型几何尺寸的函数。
斋藤模型以平均工作辊径定义前滑,当道次变形量较小时会出现负前滑的计算结果;筱篬模型改用孔型槽底处的最小辊径定义前滑,即前滑S f 为:S f =V 1/V R -1 (1.1) 其中:V 1 ,V R ——轧件出口速度及孔型槽底处的轧辊线速度。
轧制过程数学模型

1轧制过程数学模型1.1轧制工艺参数模型随着科学技术的发展,计算机已广泛应用于轧钢生产过程的控制,促使轧钢生产向自动化、高速和优质方向发展。
电子计算机在线控制生产过程,不仅仅只是电子计算机本身的硬件和软件的作用,更重要的是控制系统和各种各样的数学模型,正因为有适合轧钢生产的各种数学模型,才有可能实现电子计算机对整个轧钢生产各个环节的控制,获得高精度的产品。
线材连轧生产过程的主要内容基本上可归纳为尺寸变化和温度变化两大类性质极不相同但又相互紧密联系的物理过程,涉及的数学模型主要是轧制工艺参数的制定、各环节的温降变化、产品质量控制及实现线材连轧生产的可靠性等。
在线材连轧生产过程中,准确地计算(预估)各个环节的温度变化是实现计算机控制的重要前提,这是因为轧件各道次的变形阻力、轧制压力、轧制力矩的准确确定与温度是分不开的,而各机架轧制压力的预估精度将直接关系到设备的使用安全等。
下面分别讨论线材连轧生产过程中的温降模型、变形阻力模型、轧制力与轧制力矩模型。
1.1.1延伸系数及孔型尺寸计算模型在制订棒线材轧制工艺时,当坯料和产品断面面积F 0和F n 给定之后,总延伸系数∑μ就可唯一确定:nn n i i n i F FF F F F F F F F 011211021===-+∑ μμμμμ 其中:n ——总轧制道次;μi ——某一道次的延伸系数; F i ——某一道次的轧件断面面积。
椭圆孔示意图mB R F +-=)sin (2θθRB 2arcsin2=θ ⎪⎭⎫ ⎝⎛--=2cos 12θR h m对于圆孔,轧件断面面积可通过下式计算:圆孔示意图απθ2-=αθtan 422R R F +=1.1.2前滑模型孔型轧制时的前滑率计算可采用筱篬或斋藤提出的实验模型。
两者都认为前滑仅是轧件、孔型几何尺寸的函数。
斋藤模型以平均工作辊径定义前滑,当道次变形量较小时会出现负前滑的计算结果;筱篬模型改用孔型槽底处的最小辊径定义前滑,即前滑S f 为:S f =V 1/V R -1 (1.1) 其中:V 1 ,V R ——轧件出口速度及孔型槽底处的轧辊线速度。
轧制模拟mscmarc
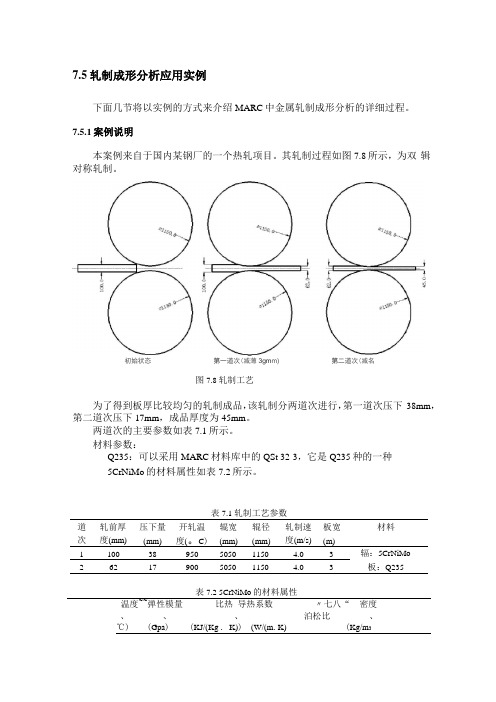
7.5轧制成形分析应用实例下面几节将以实例的方式来介绍MARC中金属轧制成形分析的详细过程。
7.5.1案例说明本案例来自于国内某钢厂的一个热轧项目。
其轧制过程如图7.8所示,为双辑对称轧制。
初始状态第一道次(减薄3gm m) 第二道次(减名图7.8轧制工艺为了得到板厚比较均匀的轧制成品,该轧制分两道次进行,第一道次压下38mm,第二道次压下17mm,成品厚度为45mm。
两道次的主要参数如表7.1所示。
材料参数:Q235:可以采用MARC材料库中的QSt 32-3,它是Q235种的一种5CrNiMo的材料属性如表7.2所示。
表7.1轧制工艺参数道轧前厚压下量开轧温辊宽辊径轧制速板宽材料次度(mm) (mm) 度(。
C)(mm) (mm) 度(m/s) (m)1 100 38 950 5050 1150 4.0 3 辐:5CrNiMo2 62 17 900 5050 1150 4.03 板:Q235表7.2 5CrNiMo的材料属性温度~~弹性模量比热导热系数〃七八“密度、、、泊松比、℃)(Gpa) (KJ/(Kg . K)) (W/(m.K) (Kg/m3-100 217000 371 45.10 213000 451 45.120 212000 461 45,1 ……0.3 7850100 207000 496 45.1200 199000 533 44.1300 192000 568 41.9400 184000 611 39.4500 175000 677 37.9600 164000 778 34.41500 78120 778 34.4板和辊之间的摩擦系数为0.3。
分析目的为:(1)分析轧制过程中工件和轧辊的温度分布;轧辊刚度足够,不用考虑其变形(2)计算轧制力(3)分析轧制过程中的应力分布情况(4)分析板厚和板形7.5.2模型的简化在提出的几个分析目的中,轧制温度和轧制力是可以在二维模型中计算得到的;因此,可以先进行二维的分析;三维应力分布、板厚、板形只能在三维模型中进行查看。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
轧制参数计算模型及其应用(一)
轧制参数计算模型及其应用
概述
轧制参数计算模型是一种用于计算轧机工艺参数的数学模型,通过模
拟折弯、伸拉和扭转等过程,计算出轧制板材的几何形状和力学性能。
该模型在轧机设计、质量控制和工艺优化等方面具有广泛应用。
模型构建
材料模型
轧制板材的力学性能由材料性能决定,因此必须首先确定材料模型。
常用的材料模型有等效应力模型和本构模型。
轧制力学模型
轧制力学模型可分为几何模型和力学模型。
几何模型是指轧制板材的
形状和尺寸模型,力学模型是指轧制板材的应力、应变和塑性变形模型。
数值模拟方法
常用的数值模拟方法有有限元法、边界元法和有限差分法。
其中,有
限元法是最常用的方法,具有高精度、高效率和高稳定性等优点。
应用
轧机设计
轧机设计中需要确定轧制力学参数,以控制轧制板材的形状和力学性能。
轧制参数计算模型可以提供合理的轧制参数,以满足不同尺寸、
材质和工艺需求。
质量控制
轧制板材的质量受多种因素影响,如轧制力、轧制速度和冷却方式等。
轧制参数计算模型可以提供轧制板材的几何形状和力学性能参数,以
确定轧制质量是否符合要求。
工艺优化
轧制工艺中的轧制参数可以影响轧制板材的形状、尺寸和力学性能。
轧制参数计算模型可以提供不同轧制参数对轧制板材性能的影响程度,以优化轧制工艺,提高生产效率和产品质量。
结论
轧制参数计算模型是一种重要的数学模型,可以为轧机设计、质量控
制和工艺优化等方面提供重要参考,促进轧制生产技术的发展和进步。
发展方向
随着轧制技术的不断发展和进步,轧制参数计算模型也在不断完善和
提高。
未来,轧制参数计算模型的发展方向主要包括以下几个方面:
•更精确的材料模型,使得轧制参数计算模型能够更好地预测轧制板材的性能特征;
•更高效的数值计算方法,以提高计算效率并降低计算成本;
•精细化的轧制力学模型,以更真实地模拟轧制板材的变形和应力分布;
•基于机器学习和人工智能的轧制参数计算模型,使得模型能够“自学习”,更好地适应复杂的轧制工艺。
总结
轧制参数计算模型是一种基于力学原理和数值计算方法构建的数学模型,通过计算出轧制板材的几何形状和力学性能,为轧机设计、质量
控制和工艺优化等提供重要参考。
未来,随着轧制技术的不断发展和
进步,轧制参数计算模型也将朝着更精确、更高效和更智能化的方向
发展。
