光明市的菜篮子工程
光明市的菜篮子工程

光明市的菜篮子工程一、问题重述光明市是一个人口不到15万人的小城市,根据该市的蔬菜种植情况分别在花市A、城乡路口B和下塘街C设三个收购点。
清晨5点前菜农将蔬菜送至各收购点,再由各收购点分送到全市的8个菜市场。
该市道路情况、各路段距离(单位:100m)及各收购点、菜市场1..8的具体位置如图1:图1:该市道路情况、各路段距离及收购点、菜市场具体位置按常年情况,,、,、,三个收购点每天收购量分别为200、170和160(单位:100kg),各菜市场的每天需求量及发生供应短缺时带来的损失(元/100kg)见表1。
设从收购点至各菜市场蔬菜调运费用为1元/(100kg*100m)。
表1:各菜市场的每天需求量及发生供应短缺是带来的损失菜市场每天需求(100kg) 短缺损失(元/100kg)1 75 102 60 83 80 54 70 105 100 106 55 87 90 58 80 8 (a)为该市设计一个从各收购点至各菜市场的定点供应方案,使用于蔬菜调运及预期的短期损失最小。
(b)若规定各菜市场短缺量一律不超过需求量的20%,重新设计定点供应方案。
(c)为满足城市居民的蔬菜供应,光明市的领导规划增加蔬菜种植面积,试问增加的蔬菜每天应分别向A、B、C三个采购点各供应多少最经济合理。
二、模型的基本假设1、只考虑运输费用和短缺费用,不考虑装卸等其他费用。
2、假设运输的蔬菜路途中没有损耗。
3、假设各市场蔬菜只来源于三个收购站,无其他来源且三个收购站所收购蔬菜全部运往8个菜市场。
4、假设规划增加蔬菜种植面积后,蔬菜供应总量恰好能满足8个菜市场的需求量。
三、符号说明x:第i个收购点向j市场供给的数量(i=1,2,3;j=1,2 …,8)。
ijx:第j(j=1,2 … 8)个市场因供给量小于需求量的单位短缺损失。
4jp:第i个收购点向j 市场供给的单位运费(i=1,2,3;j=1,2 …,8)。
ijb:第i(i=1,2,3,4)个收购点供应量。
2024年一季度经济运行分析统计会议领导讲话稿(三篇)

2024年一季度经济运行分析统计会议领导讲话稿在高速开发区段的建设过程中,征拆与服务工作面临严峻挑战。
花安高速开发区段因中途线路调整,导致所有征拆工作需重新展开,造成了巨大的经济损失,群众工作亦显得尤为艰难。
幺铺收费站的建设协调工作亦面临重重困难。
作为建设业主的花安公司,在推进幺铺收费站项目时,需与省公路局、省高管处等多个部门协调交通管制、封闭施工等事宜。
加之施工现场存在超高压线路横跨的复杂情况,还需与超高压管理局及南方电网相关运检公司进行安全施工事宜的协调。
跨行业的协调工作,无疑增加了项目推进的难度,对重点项目的实施速度产生了显著影响。
我区作为非建制县(区),在金融管理体制上存在明显不足。
金融管理机构的不健全,使得我们在统筹、协调金融工作时,不得不严重依赖市级部门的支持,这导致了工作力度的薄弱。
加之人员编制严重不足,金融办自成立以来,除主任一职外,无其他正式编制,现有工作人员均为借调人员,亟需解决编制问题,以确保工作的顺利开展。
固定资产投资方面,我区也面临着高缺口的问题。
目前,固定资产投资仅完成了全年目标的____%,与时间进度相比,存在____亿元的缺口,这是主要指标中最大的缺口。
针对上述问题,我们制定了以下工作打算:一、强化征管,狠抓财政收入。
我们将把完成收入任务作为工作的重中之重,采取有力措施,以____收入为中心,加强对经济形势的研判和财政收入预算执行的分析,坚持全年收入目标任务不动摇。
加强税收征管,加大税收稽查和税源培育力度,抓好重点税源,加强非税收入清缴,确保应收尽收,以完成收入任务。
二、强化管理,规范财政支出。
我们将坚持厉行节约的原则,充分发挥财政投资评审和政府采购的积极作用,严格控制预算追加和“____”支出,提高财政资金的使用效益。
按照公共财政和统筹发展的要求,盘活资金存量,用好资金增量,集中财力办大事。
我们还将探索建立绩效评价办法和评价指标体系,对重大支出项目的预算执行情况进行考核评价,以提升财政资金的绩效水平。
深圳市人民政府办公厅关于推动现代农业高质量发展的实施意见

深圳市人民政府办公厅关于推动现代农业高质量发展的实施意见文章属性•【制定机关】深圳市人民政府办公厅•【公布日期】2023.05.24•【字号】深府办〔2023〕6号•【施行日期】2023.05.24•【效力等级】地方规范性文件•【时效性】现行有效•【主题分类】农业管理正文深圳市人民政府办公厅关于推动现代农业高质量发展的实施意见深府办〔2023〕6号各区人民政府,市有关单位:习近平总书记指出,农业强国是社会主义现代化强国的根基,推进农业现代化是实现高质量发展的必然要求。
为贯彻落实《中共中央国务院关于支持深圳建设中国特色社会主义先行示范区的意见》《国务院关于印发“十四五”推进农业农村现代化规划的通知》(国发〔2021〕25号)、《国务院关于促进乡村产业振兴的指导意见》(国发〔2019〕12号)、《广东省人民政府关于印发广东省推进农业农村现代化“十四五”规划的通知》(粤府〔2021〕56号)等文件精神,经市政府同意,现就推动我市现代农业高质量发展提出如下实施意见。
一、总体要求(一)指导思想。
以习近平新时代中国特色社会主义思想为指导,深入学习贯彻党的二十大精神,树立“大农业观、大食物观”,落实建设农业强国、保障“粮食安全”、守住耕地红线、推动种业振兴等重大部署,以及加强农业科技和装备支撑、构建多元化食物供给体系、培育现代农业服务业新体系等工作要求,抢抓“双区”建设、“双改”示范等重大国家战略机遇,加快推动“农业科技创新先行示范区”“深圳国际食品谷”建设,促进“科技链、产业链、民生供应链、质量监管链、资金链”五链融合,探索深圳特色的新产业新业态新模式发展路径,全面提升“研发、生产、加工、制造、流通、服务”全产业链融合发展价值,进一步满足社会消费升级需求,实现现代农业产业高质量发展。
(二)总体目标。
建立健全现代农业产业高质量发展体制机制,优化完善民生供应体系,有效服务和支撑引领广东农业强省及国家农业强国建设,到2030年把“大农业、大食物”培育发展成为我市经济建设与高质量发展的基础性保障产业。
运筹学菜蓝子工程

运筹学菜蓝子工程3.1 光明市的菜篮子工程方案(a)设Xij:第i个收购点向第j个菜市场运输蔬菜的数量(i=1,2,3;j=1,…,8);蔬菜调运总费用为P短缺损失总费用为Q则蔬菜运输和短缺损失的总费用Z:Z=P+Q适当改变符号x(i,j)为:x(1,j)记为xj,x(2,j)记为yj,x(3,j)记为zj,那么各菜市场的短缺量分别为(75-x1-y1-z1)、(60-x2-y2-z2)、(80-x3-y3-z3)、(70-x4-y4-z4)、(100-x5-y5-z5)、(55-x6-y6-z6)、(90-x7-y7-z7)、(80-x8-y8-z8),那么短缺损失为10(75-x1-y1-z1)+8(60-x2-y2-z2)+5(80-x3-y3-z3)+10(70-x4-y4-z4)+10(100-x5-y5-z5)+8(55-x6-y6-z6)+5(90-x7-y7-z7)+8(80-x8-y8-z8)运费为4*x1+8*x2+8*x3+19*x4+11*x5+6*x6+22*x7+20*x8+14*y1 +7*y2+7*y3+16*y4+12*y5+16*y6+23*y7+17*y8+20*z1+19*z2+11*z3+14* z4+6* z5+15*z6+5*z7+10*z8那么总费用即为Z=-6*x1+3*x3+9*x4+x5-2*x6+17*x7+12*x8+4*y1-y2+2*y3+6*y4+2*y5+8*y6+18*y7+9*y8+10*z1+11*z2+6*z3+4*z4-4*z5+7*z6+2*z8+486 0约束条件:x1+x2+...+x8=200y1+y2+…+y8=170z1+z2+…+z8=160x1+y1+z1<=75x2+y2+z2<=60x3+y3+z3<=80x4+y4+z4<=70x5+y5+z5<=100x6+y6+z6<=55x7+y7+z7<=90x8+y8+z8<=80x(i,j)>=0,i=1,2,3;j=1,2,…,8运用lingo求解min=-6*x1+3*x3+9*x4+x5-2*x6+17*x7+12*x8+4*y1-y2+2*y3+6*y4+2*y5+8*y6+18*y7+9*y8+10*z1+11*z2+6*z3+4*z4-4*z5+7*z6 +2*z8+4860;x1+x2+x3+x4+x5+x6+x7+x8=200;y1+y2+y3+y4+y5+y6+y7+y8=170;z1+z2+z3+z4+z5+z6+z7+z8=160;x1+y1+z1<=75;x2+y2+z2<=60;x3+y3+z3<=80;x4+y4+z4<=70;x5+y5+z5<=100;x6+y6+z6<=55;x7+y7+z7<=90;x8+y8+z8<=80;求解结果:Global optimal solution found.Objective value:4610.000Total solver iterations: 9Variable Value Reduced CostX1 75.00000 0.000000X3 40.00000 0.000000X4 0.000000 2.000000X5 30.00000 0.000000X6 55.00000 0.000000X7 0.000000 12.000005.000000Y1 0.000000 11.00000Y2 60.00000 0.000000Y3 40.00000 0.000000Y4 70.00000 0.000000Y5 0.000000 2.000000Y6 0.000000 11.00000Y7 0.000000 14.00000Y8 0.000000 3.000000Z1 0.000000 21.00000Z2 0.000000 16.000008.000000Z4 0.000000 2.000000Z5 70.00000 0.000000Z6 0.000000 14.00000Z8 0.000000 0.000000X2 0.000000 0.000000Z7 90.00000 0.000000Row Slack or Surplus Dual Price1 4610.000 -1.0000002 0.000000 -7.0000003 0.000000-6.0000004 0.000000 -2.0000005 0.000000 13.000006 0.0000007.0000007 0.000000 4.0000008 0.000000 0.0000009 0.000000 6.00000010 0.000000 9.00000011 0.000000 2.00000012 80.00000 0.000000结果分析:在该题目的假设下,最经济合理的蔬菜定点供应方案是:收购点A每天向菜市场1运送蔬菜75千克,向3运送40千克,向5运送30千克,向6运送55千克;收购点B每天向菜市场2运送蔬菜60千克,向菜市场3运送蔬菜40千克,向菜市场4运送蔬菜70千克;收购点C每天向菜市场5运送蔬菜70千克,向菜市场7运送蔬菜90千克;在这种情况下使用于蔬菜调运及预期的短缺损失为:4610元。
光明市的菜篮子工程 实验报告
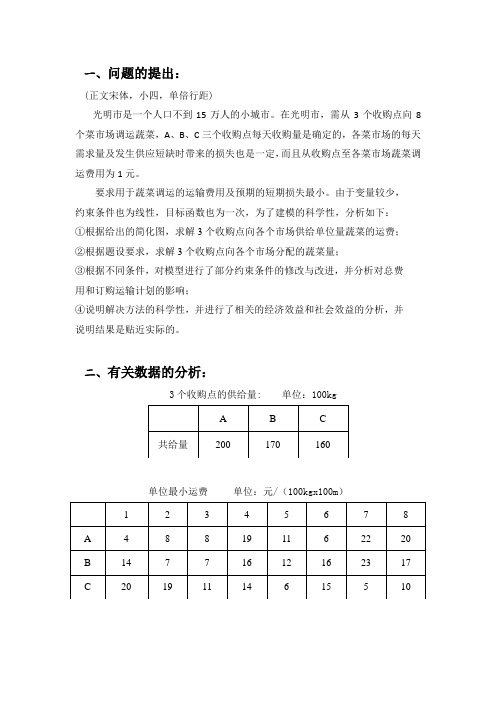
一、问题的提出:(正文宋体,小四,单倍行距)光明市是一个人口不到15万人的小城市。
在光明市,需从3个收购点向8个菜市场调运蔬菜,A、B、C三个收购点每天收购量是确定的,各菜市场的每天需求量及发生供应短缺时带来的损失也是一定,而且从收购点至各菜市场蔬菜调运费用为1元。
要求用于蔬菜调运的运输费用及预期的短期损失最小。
由于变量较少,约束条件也为线性,目标函数也为一次,为了建模的科学性,分析如下:①根据给出的简化图,求解3个收购点向各个市场供给单位量蔬菜的运费;②根据题设要求,求解3个收购点向各个市场分配的蔬菜量;③根据不同条件,对模型进行了部分约束条件的修改与改进,并分析对总费用和订购运输计划的影响;④说明解决方法的科学性,并进行了相关的经济效益和社会效益的分析,并说明结果是贴近实际的。
二、有关数据的分析:3个收购点的供给量: 单位:100kg单位最小运费单位:元/(100kgx100m)各市场每单位短缺损失与每天需求量三、建立模型模型的基本假设①只考虑运输和短缺费用,不考虑装卸等其它费用。
②假设运输的蔬菜在路途中没有损耗。
③假设各个市场的蔬菜只来源于三个收购站,而且并无其他来源。
④假设各收购站供应蔬菜同质且单位运价相同。
⑤假设各收购站可以作为中转站1、模型的决策变量确定决策变量:xij :第i 个收购点向j 市场提供的数量 cij :第i 个收购点向j 市场提供的单位运费 ai : 第i 个收购点供应量 bj : 第j 个市场需求量dj: 第j 个市场因供给量小于需求量的单位短缺损失2、模型的目标函数确定目标函数总费用Z 来表示,总费用包括两项: 蔬菜调运费Q ,各市场供给量小于需求量的短缺损失P ,即:Z=P+Q其中P= 8311)j ij j j i (b x d ==-∑∑ Q= iji j ij x c ∑∑==3181(1)目标函数min Z=j ij j j d x (b )3181∑∑-=+ij i j ij x c ∑∑==3181(2)目标函数min Z=dj x (b ij j j )3181∑∑-=+ij i j ij x c ∑∑==3181(3)目标函数min Z=8311)j ij j j i (b x d ==-∑∑+ij i j ij x c ∑∑==31813、模型的约束条件确定约束条件为:①3个收购点的蔬菜全部供给给8个市场 (i=1,2,3) ②3个收购点分别向每个市场供应的总量不超过每个市场的需求量(j=1, (8)③变量非负性限制 (i=1,2,3,j=1,…,8) (1) 约束条件i j ija x<=∑=81(i=1,2,3)j i ijb x≤∑=31(j=1, (7)0≥ij x (i=1,2,3,j=1,…,7) (2) 约束条件i j ija x=∑=81(i=1,2,3)31ijj i xb =≤∑(j=1, (8)310.8ijj i xb =≥∑(j=1, (8)0≥ij x (i=1,2,3,j=1,…,8) (3) 约束条件i i j ijt a x+=∑=81(i=1,2,3)31ijj i xb =≤∑(j=1, (8)0≥ij x (i=1,2,3,j=1,…,8) t i ≥0(i=1,2,3)四、求解结果及分析(1)为该市设计一个从各收购点至各菜市场的定点供应方案,使用于蔬菜调运及预期的短期损失最小。
2024年菜篮子工程实施方案专题模板(2篇)

2024年菜篮子工程实施方案专题模板摘要:本文旨在制定2024年菜篮子工程的实施方案,以保障我国粮食和重要农产品的供应稳定性,并促进农业发展和农民收入增长。
本文提供了一个专题模板,包括背景介绍、目标设定、工作重点和具体措施等内容。
通过制定和执行本实施方案,我们有信心实现菜篮子工程的目标,并为全面建设社会主义现代化国家奠定坚实的基础。
一、背景介绍1.1 菜篮子工程的意义和目标1.2 国内外农业发展形势的分析1.3 我国粮食和重要农产品供应的现状和问题二、目标设定2.1 2024年菜篮子工程的总体目标2.2 具体目标的分解和量化指标三、工作重点3.1 粮食生产的保障和提质增效3.2 重要农产品的供应保障3.3 农业科技创新和现代农业发展的促进3.4 农村地区的基础设施建设和农民收入增长四、具体措施4.1 加强农业基础设施建设4.1.1 提升农田水利设施建设水平4.1.2 完善农产品流通网络4.1.3 加强农机设备更新和维护4.2 推进农业科技创新4.2.1 加大科技投入,推动农业科技成果转化4.2.2 鼓励农业企业和科研机构合作4.2.3 提升农业生产管理水平,优化资源配置4.3 加强农产品质量安全监管4.3.1 建立健全农产品质量追溯体系4.3.2 加强农产品质量监测和抽检4.3.3 加强农产品质量标准制定和执行4.4 提升农民收入水平4.4.1 加强农业产业化经营,培育新型农业经营主体4.4.2 订单农业和农产品深加工的发展4.4.3 加强农民培训和技能提升五、预期效果和考核指标5.1 预期效果的具体描述5.2 相关考核指标的设定和测评方法结论:通过制定和执行本实施方案,我们有信心实现2024年菜篮子工程的目标,并为全面建设社会主义现代化国家奠定坚实的基础。
我们将加强各项具体措施的落实,加大政府支持力度,促进农业发展和农民收入增长,确保菜篮子工程取得持续稳定的成果。
2024年菜篮子工程实施方案专题模板(二)菜篮子工程是指为了维护国家粮食和农产品市场稳定供应,优化农业生产结构,提升农产品质量和安全水平,保障人民群众基本生活需求,加强对市场价格的宏观调控而采取的一系列措施的总称。
关于加快都市现代农业发展的意见

关于加快都市现代农业发展的意见为深入贯彻市第十一次党代会精神,全面落实市委、市政府对农业农村工作的总体部署,加快都市现代农业发展,现提出如下意见:一、总体要求以农业供给侧结构性改革为主题,深化现代农业产业体系、生产体系和经营体系建设,大力推动农业生产供给、生态涵养、生活服务协调发展,加快推进农业变产业、园区变景区、产品变精品、劳动变活动,全面提升农业一二三产业融合发展水平。
二、主要任务(一)实施绿色农业安全供给工程。
将“菜篮子”市长负责制延伸至县(市)区长负责制,实施“菜篮子”产品生产绩效管理,开展鲜活农产品调控目录制度试点工作,每年新增2万亩设施农业面积、10万吨蔬菜产量;实施粮食绿色增效、畜牧绿色低碳循环、渔业绿色健康养殖模式攻关三大行动,稳定300万吨粮食和100万吨畜禽蛋奶水产品产能。
扶优扶强长丰草莓、合肥西(甜)瓜、大圩(同大、黄麓)葡萄、樱桃、油桃等优势水果产业,提升水果品质。
突出品牌引领,延伸产业链条,大力发展农产品加工业,强化主食加工、方便食品、休闲食品、冷冻食品等优势产业集群建设。
加强农产品质量安全监管,增加优质农产品供给,“三品一标”认证率每年提高2个百分点,规模以上新型农业经营主体率先实现质量安全可追溯。
(二)实施农业生活休闲服务工程。
把丰富城乡居民生活作为都市现代农业发展的重要方向,鼓励各地依托农村绿水青山、田园风光、乡土文化等物质与非物质资源,以农业园区、美丽乡村建设为载体,有规划地开发休闲农庄、乡村酒店、采摘农园、特色民宿、自驾露营、户外运动等乡村休闲度假产品,扶持发展休闲度假、旅游观光、养生养老、创意农业、农耕体验、乡村手工艺、订制认养等新型农业业态,建设一批农业主题公园、农业嘉年华、教育农园、摄影基地、特色小镇、渔人码头、运动垂钓示范基地。
采取以奖代补、先建后补等方式,择优扶持一批休闲农业精品节庆活动和休闲农业精品村,繁荣农业节庆经济,促进休闲农业消费。
深入挖掘、保护和开发具有合肥地域特色的优秀农耕文化。
某市的菜篮子工程运筹学案例分析PPT课件(31张)

图3-3
菜市场 1 2 3 4 5 6 7 8
表3 - 45
每天需求(100kg) 短缺损失(元/100kg)
75
10
60
8
80
5
70ቤተ መጻሕፍቲ ባይዱ
10
100
10
55
8
90
5
80
8
(a)为该市设计一个从各收购点至各菜市场的定点供应方案,使用于蔬 菜调运及预期的短期损失最小。 (b)若规定各菜市场短缺量一律不超过需求量的20%,重新设计定点供 应方案。 (c)为满足城市居民的蔬菜供应,光明市的领导规划增加蔬菜种植面积, 试问增加的蔬菜每天应分别向A、B、C三个采购点各供应多少最经济合 理。
问题分析:
要求用于蔬菜调运的运输费用及预期的短期损失最小。 由于变量较少,约束条件也为线性,目标函数也为一次, 为了建模的科学性,分析如下:
①根据给出的简化图,求解3个收购点向各个市场供给单 位量蔬菜的运费; ②根据题设要求,求解3个收购点向各个市场分配的蔬菜 量; ③根据不同条件,对模型进行了部分约束条件的修改与改 进,并分析对总费用和订购运输计划的影响; ④说明解决方法的科学性,并进行了相关的经济效益和社 会效益的分析,并说明结果是贴近实际的。
10x41+8x42+5x43+10x44+10x45+8x46+5x47+8 x48 ;
问题(a):为该市设计一个从各收购 点至各菜市场的定点供应方案,使用 于蔬菜调运及预期的短期损失最小。
目标函数:
Min Z=
4x11+8x12+8x13+19x14+11x15+6x16+22x17+20x18+ 14x21+7x22+7x23+16x24+12x25+16x26+23x27+17x 28+20x31+19x23+11x33+14x34+6x35+15x36+5x37+1 0x38+10x41+8x42+5x43+10x44+10x45+8x46+5x47+8 x ;48
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
光明市的菜篮子工程 Prepared on 24 November 2020光明市的菜篮子工程摘要本文研究的是蔬菜市场为满足不同条件的最优调配方案问题,用了Froyd 算法、线性规划建立了一系列数学规划模型,并用MATLAB和LINGO软件编程实现。
关于问题一:用Froyd算法结合MATLAB编程求出收购点至个菜市场的最短距离,以用于蔬菜调运及预期的短缺损失为最小为目标建立线性规划模型。
用LINGO编程求得日均费用最少为4610元。
关于问题二:在模型一的基础增加各菜市场短缺量一律不超过需求量的20%的约束条件,用LINGO编程求得最少日均费用以及最优供应方案。
费用最少为4806元,供应方安见正文。
关于问题三:在模型一的基础上,改为以供货充足、费用最小为目标,建立模型三,用LINGO编程求得日均费用为4770元,增产的蔬菜每天应分给C 收购点8000Kg。
关键字:蔬菜市场调配方案 Froyd算法线性规划一、问题的重述海江市是一个人口不到20万人的小城市。
根据该市的蔬菜种植情况,分别在菜市场(A),菜市场(B)和菜市场(C)设三个收购点,再由各收购点分送到全市的8个菜市场,该市道路情况,各路段距离(单位:100m)及各收购点,菜市场①⑧的具体位置见图.按常年情况,A,B,C三个收购点每天收购量分别为30000,25000和20000(单位:100 kg),各菜市场的每天需求量及发生供应短缺时带来的损失(元/100kg)见表3.设从收购点至各菜市场蔬菜调运费为1元/.① 7 ②5 4 8 3 7A 7 6 B⑥ 6 8 55 4 7 117 4 ③7 5 66 ⑤ 3 5 ④8 6 610 C 10 ⑧5 11⑦表3(a)为该市设计一个从收购点至个菜市场的定点供应方案,使用于蔬菜调运及预期的短缺损失为最小;(b)若规定各菜市场短缺量一律不超过需求量的20%,重新设计定点供应方案;(c)为满足城市居民的蔬菜供应,光明市的领导规划增加蔬菜种植面积,试问增产的蔬菜每天应分别向A,B,C三个采购点供应多少最经济合理。
二、符号说明()D i=……从A到i(各个菜市场)的最短距离1,28Ai()1,28D i=……从B到i(各个菜市场)的最短距离Bi()1,28D i=……从C到i(各个菜市场)的最短距离Ci()S i=……从A到i(各个菜市场)的运货量1,28Ai()S i=……从B到i(各个菜市场)的运货量1,28Bi()S i=……从C到i(各个菜市场)的运货量1,28CiP总调运费Q短缺损失R总费用三模型假设1、假设日需求量与缺货损失费用不变。
2、假设在蔬菜调配的过程中无意外发生。
3、假设新增产的蔬菜能够满足缺货量。
四模型的建立与求解问题一为了使用于蔬菜调运及预期的短缺损失为最小,即调运费用与缺货损失之和最小。
首先考虑调运费用P,P为距离与送货量的积,因为与送货距离相关,我们必须先求出A、B、C三个采购点至各个菜市场的最短距离。
采用Froyd算法,结合MATLAB 编程实现。
其次考虑缺货损失Q ,以题中要求为约束条件,损失最低位目标建立线性规划模型,用LINGO 编程求解。
由图和表格的信息知,建立一个线性规划模型,使得蔬菜调运及预期的短缺损失为最小。
调运总费用P 为:若使调运总费用最少,则应保证A 、B 、C 三个收购点到8个菜市场的路程最短,最短路线的求解过程如图一:图一:求解过程图分析上图可知,该路线为无向网络,就该图而言,网络弧集为:E=[(v1,v2),(v1,v4),(v1,v5),(v2,v1),(v2,v3),(v2,v5),(v2,v6),(v3,v2),.(v3,v6),(v3,v8),(v 3,v9),(v4,v1),(v4,v5).(v4,v7),(v4,v10),(v5,v1),(v5,v2),(v5,v4),(v5,v6),(v5,v7),(v5,v8),(v6,v2),(v6,v3),(v6,v5),(v6,v8),(v7,v4),(v7,v5),(v7,v8),(v7,v11),(v8,v3),(v8,v5),(v8,v6),(v8,v7),(v8,v9),(v8,v 11),(v9,v3),(v9,v8),(v9,v11),(v9,v13),(v9,v15),(v10,v4),(v10,v11),(v10,v12),(v10,v14),(v11,v7),(v11,v8),(v11,v9)(v11,v10),(v11,v12),(v12,v10),(v12,v11),(v12,v13),(v12,v14),(v13,v 9),(v13,v12),(v13,v14),(v14,v10),(v14,v12),(v14,v13),(v15,v9)] 下面来确定网络权矩阵: W=()n nij w其中ii w =ij l ,当(i v ,j v )属于E 时,ij l 为弧(i v ,j v )的权 ii w =0,i=1,2,3……nij w =inf,当(i v ,j v )不属于E 时。
(inf 为无穷大,n 为网络结点个数)按上述规定,该网络的权矩阵为:0 7 inf 5 4 inf inf inf inf inf inf inf inf inf inf 7 0 7 inf 8 3 inf inf inf inf inf inf inf inf inf inf 7 0 inf inf 6 inf 7 11 inf inf inf inf inf inf5 inf inf 06 inf 5 inf inf7 inf inf inf inf inf 48 inf 6 0 7 4 8 inf inf inf inf inf inf inf inf 3 6 inf 7 0 inf 5 inf inf inf inf inf inf inf inf inf inf 5 4 inf 0 4 inf inf 7 inf inf inf inf inf inf 7 inf 8 5 4 0 6 inf 5 inf inf inf inf inf inf 11 inf inf inf inf 6 0 inf 3 inf 6 inf 5 inf inf inf 7 inf inf inf inf inf 0 6 8 inf 10 inf inf inf inf inf inf inf 7 5 3 6 0 6 inf inf inf inf inf inf inf inf inf inf inf inf 8 6 0 10 5 inf inf inf inf inf inf inf inf inf 6 inf inf 10 0 11 inf inf inf inf inf inf inf inf inf inf 10 inf 5 11 0 inf inf inf inf inf inf inf inf inf 5 inf inf inf inf inf 0 因为上述网络有15个结点,故网络的权矩阵均为15阶矩阵。
现在给出网络最短路线的Froyd 算法: (1) d1=w.(w 为所给网络的n 阶权矩阵) (2) dk=()ij n n dk ⨯,k=2,3,…,p.其中ij dk =min[(1)is d k -+(1)sj d k -,i,j=1,2,…,n. 计算次数的确定:当ij w ≥0时,p 由下式确定:p ≥ln(n-1)/ln2,这样的dp 就确定了网络各点间的最短距离。
此处n=15,解出≥ 故只需要取p=4即可,即算到d4即可。
按照Froyd 算法:d1=d,d2=fld(15,d1),d3=fld(15,d2), d4=(fld(15,d3),算的d4为:0 7 14 5 4 10 8 12 18 12 15 20 24 22 23 7 0 7 12 8 3 12 8 14 19 13 19 20 24 19 14 7 0 16 13 6 11 7 11 18 12 18 17 23 16 5 12 16 0 6 13 5 9 15 7 12 15 21 17 20 4 8 13 6 0 7 4 8 14 13 11 17 20 22 19 10 3 6 13 7 0 9 5 11 16 10 16 17 21 16 8 12 11 5 4 9 0 4 10 12 7 13 16 18 15 12 8 7 9 8 5 4 0 6 11 5 11 12 16 11 18 14 11 15 14 11 10 6 0 9 3 9 6 14 5 12 19 18 7 13 16 12 11 9 0 6 8 15 10 14 15 13 12 12 11 10 7 5 3 6 0 6 9 11 820 19 18 15 17 16 13 11 9 8 6 0 10 5 1424 20 17 21 20 17 16 12 6 15 9 10 0 11 1122 24 23 17 22 21 18 16 14 10 11 5 11 0 1923 19 16 20 19 16 15 11 5 14 8 14 11 19 0d4即为该网络的距离矩阵,距离矩阵的第i行指明了iv到其他各点的最短距离。
根据上述矩阵,分别找出A,B,C到①、②、③、④、⑤、⑥、⑦、⑧的最短距离,见表一:表一:收购点到菜市场的最短距离调运量的限制:短缺损失费为:()()()()()()()()1112223334445556667778881075860580107010100855590880A B CA B CA B CA B CA B CA B CA B CA B CQ S S SS S SS S SS S SS S SS S SS S SS S S=⨯-++⎡⎤⎣⎦+⨯-+++⎡⎤⎣⎦⨯-+++⎡⎤⎣⎦⨯-+++⎡⎤⎣⎦⨯-+++⎡⎤⎣⎦⨯-+++⎡⎤⎣⎦⨯-+++⎡⎤⎣⎦⨯-++⎡⎤⎣⎦总费用为:R P Q=+由以上约束条件,用LINGO 软件进行线性规划求解(源程序及完整运行结果见附录),部分运行结果如下:Global optimal solution found.Objective value:Infeasibilities:Total solver iterations: 10Model Class: LPTotal variables: 26Nonlinear variables: 0Integer variables: 0Total constraints: 22Nonlinear constraints: 0Total nonzeros: 124Nonlinear nonzeros: 0Variable Value Reduced Cost PQSA1SA2SA3SA4SA5SA6SA7SA8SB1SB2SB3SB4SB5SB6SB7SB8SC1SC2SC3SC4SC5SC6SC7SC8从上述运行结果中可以得出调运方案为:在此种方案下,蔬菜调运及预期的短缺损失为最小,最小金额为4610元。
