人工智能概论课件 第2章 知识表示(导论)
合集下载
人工智能 第2章 知识表示
2.1.1 知识的概念
按知识的作用范围划分
➢ 常识性知识 ➢ 领域性知识
按知识的确定性划分
➢ 确定知识 ➢ 不确定知识
按知识的作用及表示来划分
➢ 事实性知识 ➢ 规则性知识 ➢ 控制性知识 ➢ 元知识
按人类的思维及认识方法划分
➢ 逻辑性知识 ➢ 形象性知识
2.1.2 知识表示的概念
知识表示就是研究用机器表述上述知识的可行性、有效性的一 般方法，可以看成将知识符号化，即编码成某种数据结构，并输 入到计算机的过程和方法，即：
规则库: 用于描述相应领域内知识的产生式集合。
2. 综合数据库
综合数据库(事实库、上下文、黑板等)：用于存放输 入的事实、从外部数据库输入的事实以及中间结果（事 实）和最后结果的工作区。
2.3.2 产生式系统的基本结构
3. 推理机
推理机:用来控制和协调规则库与综合数据库的 运行，包含了推理方式和控制策略。
一阶谓词逻辑表示法的缺点：
效率低
由于推理是根据形式逻辑进行的，把推理演算和知识含义截然分开， 抛弃了表达内容所含的语义信息，往往是推理过程太冗长，降低系统 效率。另外，谓词表示越细，表示越清楚，推理越慢、效率越低。
灵活性差
不便于表达和加入启发性知识和元知识。不便于表达不确定性的指示， 但人类的知识大都具有不确定性和模糊性，这使得它表示知识的范围 受到了限制。
R10：IF 该动物是哺乳动物 AND 是食肉动物 AND 是黄褐色 AND 身上有黑色条纹 THEN 该动物是虎
R11： IF 该动物是有蹄类动物 AND 有长脖子 AND 有长腿 AND 身上有暗斑点 THEN 该动物是长颈鹿
R12：IF 该动物有蹄类动物 AND 身上有黑色条纹 THEN 该动物是斑马
人工智能导论-第2章知识表示和知识图谱
产生式表示法：
产生式表示法又称为产生式规则（Production Rule）表示法。美国数学家波斯特（E.POST）在1934年首先提出“产生式”，它根据串代替规则提出了一种称为波斯特机的计算模型，模型中的每条规则称为产生式。
框架表示法：
以一个通用的数据结构的形式存储以往的经验。这样的数据结构就是框架（frame），框架提供了一个结构，一种组织。
(三)任务实施
1、对于犯罪行为的新闻报道中都会提到犯罪意图、犯罪结果、证人指控等信息，这些信息可以用一个犯罪框架来表示。
2、试着构造一个描述学校图书馆的框架。
3、用产生式表示：如果一个人出现腹痛、腹泻及呕吐的症状，那么得肠胃炎的可能性有8成。
4、知识图谱在搜索引擎中的应用
（四）归纳总结
通过案例阅读，了解知识图谱的相关概念，知道知识图谱的简单应用。
信息技术飞速发展，不断推动着互联网技术的变革，互联网的核心性技术Web经历了网页链接到数据链接的变革后，正逐渐向大规模的语义网络演变。语义网络将知识采用网络的形式表示，它将经过加工和推理的知识以图形的方式提供给用户，而实现智能化语义检索的基础和桥梁就是知识图谱。
二、教学目标
知识目标
能力目标
1、了解知识、知识表示、知识图谱的概念
(三)任务实施
试着为自己绘制一个社交网络的知识图谱。
（四）归纳总结
通过本节课的学习，了解知识图谱的表示方法。
五、六节归纳
知识图谱的应用：
（1）智能问答
（2）智能推荐
（3）金融领域
知识图谱的总结与展望：
虽然现在知识图谱很多，但大部分还处于初级阶段，只是侧重于简单事实，对于常识的覆盖十分有限，依然面临众多挑战和难题，如：知识库的自动扩展、异构知识处理、推理规则学习、跨语言检索等。总体而言，知识图谱技术的落地应用前景是光明的，但是也需要充分意识到知识图谱面临的巨大挑战。
产生式表示法又称为产生式规则（Production Rule）表示法。美国数学家波斯特（E.POST）在1934年首先提出“产生式”，它根据串代替规则提出了一种称为波斯特机的计算模型，模型中的每条规则称为产生式。
框架表示法：
以一个通用的数据结构的形式存储以往的经验。这样的数据结构就是框架（frame），框架提供了一个结构，一种组织。
(三)任务实施
1、对于犯罪行为的新闻报道中都会提到犯罪意图、犯罪结果、证人指控等信息，这些信息可以用一个犯罪框架来表示。
2、试着构造一个描述学校图书馆的框架。
3、用产生式表示：如果一个人出现腹痛、腹泻及呕吐的症状，那么得肠胃炎的可能性有8成。
4、知识图谱在搜索引擎中的应用
（四）归纳总结
通过案例阅读，了解知识图谱的相关概念，知道知识图谱的简单应用。
信息技术飞速发展，不断推动着互联网技术的变革，互联网的核心性技术Web经历了网页链接到数据链接的变革后，正逐渐向大规模的语义网络演变。语义网络将知识采用网络的形式表示，它将经过加工和推理的知识以图形的方式提供给用户，而实现智能化语义检索的基础和桥梁就是知识图谱。
二、教学目标
知识目标
能力目标
1、了解知识、知识表示、知识图谱的概念
(三)任务实施
试着为自己绘制一个社交网络的知识图谱。
（四）归纳总结
通过本节课的学习，了解知识图谱的表示方法。
五、六节归纳
知识图谱的应用：
（1）智能问答
（2）智能推荐
（3）金融领域
知识图谱的总结与展望：
虽然现在知识图谱很多，但大部分还处于初级阶段，只是侧重于简单事实，对于常识的覆盖十分有限，依然面临众多挑战和难题，如：知识库的自动扩展、异构知识处理、推理规则学习、跨语言检索等。总体而言，知识图谱技术的落地应用前景是光明的，但是也需要充分意识到知识图谱面临的巨大挑战。
人工智能_知识表示ppt课件
D n { x 1 ,( x 2 ,,x n )|x 1 ,x 2 ,,x n D }
则称P是一个n元谓词，记为
P(x1,x2,…,xn)
其中，x1,x2,…,xn为个体，可以是个体常量、变元和函数。
例如：GREATER(x,6)
x大于6
STUDENT(wanghong )
王红是一名学生
TEACHER(father(zhang)) 张的父亲是一位教师
知识表示的要求（难度很大）
表示能力：能否正确、有效地将问题求解所需的各种知识表示出来
表示范围的广泛性
领域知识表示的高效性
对非确定性知识表示的支持程度
可利用性：利用这些知识进行推理，可以求得待解决问题的解
对推理的适应性：推理是根据已知事实利用知识导出结果的过程
对高效算法的支持程度：知识表示要有较高的处理效率
一阶谓词逻辑表示的逻辑基础 ----命题与真值
命题的定义： 断言：一个陈述句称为一个断言 命题：具有真假意义的断言成为命题
可以用大写字母表示命题，如：
A: 天在下雨。 B: 天晴 C: 人是会死的 D: 他在哭
命题的真值： T：表示命题的意义为真 F：表示命题的意义为假
表达单一意义的命题称为“原子命题”。 命题逻辑就是研究命题和命题之间关系的符号逻辑系统。
辖域：指位于量词后面的单个谓词或者用括弧括起来的合式公式
约束变元：辖域内与量词中同名的变元称为约束变元
自由变元：不受约束的变元称为自由变元
例子：(x)(P(x，y)→Q(x，y))VR(x，y)
其中，(P(x，y)→Q(x，y))是(x)的辖域
辖域内的变元x是受( x)约束的变元
R(x，y)中的x和所有的y都是自由变元
人工智能知识表示方法ppt课件
2024/2/15
2.2.2 谓词逻辑表示知识举例
例3
用谓词逻辑表示下列知识： 人人爱劳动。 自然数都是大于零的整数。 所有整数，不是偶数就是奇数。
第一步
定义谓词如下： MAN(x)：x是人 LOVE(x，y)：x爱y N(x): x是自然数 I(x):x是整数 E(x): x是偶数 O(x): x是奇数 GZ(x): x大于零
效率低,过程冗长 灵活性差，不确定知识
组合爆炸
优点
缺点
2024/2/15
返回
2.3 产生式表示法1943年由美国数学家Fra bibliotek.Post提出。
产生式知识 表示方法
它使用类似文法的规则。用该方法求解 问题时的思路与人类很相似。目前大部 分的专家系统都采用产生式系统的结构 来构建。
2024/2/15
产生式系统的组成
例1
张三是学生，李四也是学生。
第一步
定义谓词如下： ISStudent(x)：x是一个学生 张三是个体 李四也是个体
第二步
将个体代入谓词中，得到 ISStudent(张三)， ISStudent(李四)
第三步
根据语义，用逻辑连接符连接 ISStudent(张三) ∧ISStudent(李四)
2024/2/15
能否在同一层次上和不同层次上模块化
是否适于推理
知识和元知识能否用统一的形式表示
是否适于计算机处理
是否适合于加入启发信息
是否有高效的求解算法 能否表示不精确知识
过程性表示还是说明性表示 表示方法是否自然
2024/2/15
返回
2.2 一阶谓词逻辑表示法
一阶谓词逻 辑表示法
一种重要的知识表示方法，它以数理逻辑 为基础，是到目前为止能够表达人类思维 和推理的一种最精确的形式语言。它的表 现方式和人类自然语言非常接近，它能够 被计算机进行精确推理。
2.2.2 谓词逻辑表示知识举例
例3
用谓词逻辑表示下列知识： 人人爱劳动。 自然数都是大于零的整数。 所有整数，不是偶数就是奇数。
第一步
定义谓词如下： MAN(x)：x是人 LOVE(x，y)：x爱y N(x): x是自然数 I(x):x是整数 E(x): x是偶数 O(x): x是奇数 GZ(x): x大于零
效率低,过程冗长 灵活性差，不确定知识
组合爆炸
优点
缺点
2024/2/15
返回
2.3 产生式表示法1943年由美国数学家Fra bibliotek.Post提出。
产生式知识 表示方法
它使用类似文法的规则。用该方法求解 问题时的思路与人类很相似。目前大部 分的专家系统都采用产生式系统的结构 来构建。
2024/2/15
产生式系统的组成
例1
张三是学生，李四也是学生。
第一步
定义谓词如下： ISStudent(x)：x是一个学生 张三是个体 李四也是个体
第二步
将个体代入谓词中，得到 ISStudent(张三)， ISStudent(李四)
第三步
根据语义，用逻辑连接符连接 ISStudent(张三) ∧ISStudent(李四)
2024/2/15
能否在同一层次上和不同层次上模块化
是否适于推理
知识和元知识能否用统一的形式表示
是否适于计算机处理
是否适合于加入启发信息
是否有高效的求解算法 能否表示不精确知识
过程性表示还是说明性表示 表示方法是否自然
2024/2/15
返回
2.2 一阶谓词逻辑表示法
一阶谓词逻 辑表示法
一种重要的知识表示方法，它以数理逻辑 为基础，是到目前为止能够表达人类思维 和推理的一种最精确的形式语言。它的表 现方式和人类自然语言非常接近，它能够 被计算机进行精确推理。
人工智能_人工智能导论课件第2章知识表示导论
P：老李是小李的父亲
P：李白是诗人 Q：杜甫也是诗人
13
2.2.2 谓词
谓词的一般形式： P (x1, x2,…, xn)
个体 x1, x2,…, xn ：某个独立存在的事物或者某个抽象 的概念； 谓词名 P：刻画个体的性质、状态或个体间的关系。
（1）个体是常量：一个或者一组指定的个体。
“老张是一个教师”：一元谓词 Teacher (Zhang)
Human（Zhugeliang）
{ 1, 2 }
Die（Zhugeliang）
T规则
29
2.2.4 谓词公式的性质
谓词逻辑的其他推理规则：
④ 反证法： P Q，当且仅当 P Q F ，即Q为P
的逻辑结论，当且仅当 P Q 是不可满足的。
… ，P 的逻辑结论，当且仅当 定理：Q为 P ， ， P 1 2 n
2
第2章 知识表示
2.1 知识与知识表示的概念
2.2 一阶谓词逻辑表示法
2.3 产生式表示法 2.4 框架表示法
3
第2章 知识表示
2.1
知识与知识表示的概念
2.2 一阶谓词逻辑表示法
2.3 产生式表示法
2.4 框架表示法
4
2.1.1 知识的概念
知识：在长期的生活及社会实践中、在科学研究及实验 中积累起来的对客观世界的认识与经验。 知识：把有关信息关联在一起所形成的信息结构。 知识反映了客观世界中事物之间的关系，不同事物或者 信息关联形式：“如果„„，则„„” 相同事物间的不同关系形成了不同的知识。
“5>3” ：二元谓词 Greater (5, 3) “Smith作为一个工程师为IBM工作”： 三元谓词 Works (Smith, IBM, engineer)
人工智能导论 课件 PPT -第2章知识表示
产生式的基本形式
（2）规则型知识的产生式表示 规则描述的是事物间的因果关系。含义是：如果…则…，规则型 知识的产生式表示基本形式是：
P→Q 或者 IF P THEN Q 其中，P是生产式的前提，用于指出该生产式是否可用的条件；Q 是一组结论或操作，用于指出当前提P所指示的条件被满足时，应 该得出的结论或应该执行的操作。整个产生式的含义是：如果前 提P被满足，则可推出结论Q或执行Q所规定的操作。
产生式系统
规则集
控制器 匹配排序 冲突裁决
匹配
检索 产生式系统结构与工作过程
综合数据库
产生式系统
【例2.1】 建立一个动物识别系统的规则库，用以识别虎、 豹、斑马、长颈鹿、企鹅、鸵鸟、信天翁等7种动物。
框架表示法
框架
我们无法把过去的经验一一都存在脑子里，而只能以一个通用 的数据结构的形式存储以往的经验。这样的数据结构就是框架 （frame），框架提供了一个结构，一种组织。在这个结构或组织 中，新的资料可以用从过去的经验中得到的概念来分析和解释。 实例框架：对于一个框架，当人们把观察或认识到的具体细节填 入后，就得到了该框架的一个具体实例，框架的这种具体实例被 称为实例框架。 框架系统：在框架理论中，框架是知识的基本单位，把一组有关 的框架连结起来便形成一个框架系统。
人工智能导论
知识表示和知识图谱
2.1知识表示
人类之所以有智能行为是因为他们拥有知识，智能活动过程 其实就是一个获得并运用知识的过程，要使机器系统具有人的智 能能力（人工智能AI），则必须以人的知识为基础，知识是人工 智能的基石。但人类的知识要用适当的模式表示出来，才能够存 储到计算机中并被识别运用，本节将对人工智能中常用的几种知 识表示方法进行介绍，为后续学习奠定基础。
人工智能导论-第2章-2 知识图谱
(实体1-关系-实体2)：中国-首都-北京 (实体-属性-属性值)：北京-人口-2069万
7
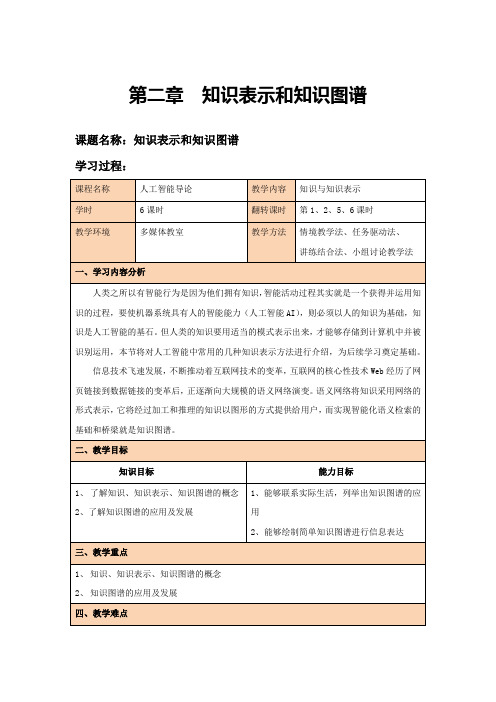
2.5.3 知识图谱的表示
知识图谱也可被看作是一张图，图中的节点表示实体 或概念，而图中的边则由属性或关系构成。
法国
英国
963万平 方公里
面积
13.6亿亿
人口 首都
中国
国家
……
面积
美国
人口 首都
937万平 方公里
人工智能导论
Introduction of Artificial Intelligence
人工智能导论
Introduction of Artificial Intelligence
第 2 章-2 知识图谱
第2章 知识表示与知识图谱
第2章 知识表示与知识图谱
2.1 知识与知识表示的概.4 框架表示法 2.5 知识图谱
3.1亿亿
1.6万平 方公里
面积 北京 人口 纬度
经度
2069万
北纬 39°54′
东经 116°25′
华盛顿
经度
面积
纬度
西经 77°02′25′
178平 方公里
北纬 9°53′
8
2.5.4知识图谱的架构
1. 知识图谱的逻辑结构：模式层与数据层。 数据层主要是由一系列的事实组成，而知识以事实为单 位进行存储。 模式层构建在数据层之上，是知识图谱的核心。 2. 知识图谱的体系架构
5
2.6 知识图谱
由于互联网内容的大规模、异质多元、组织结构松散 的特点，给人们有效获取信息和知识提出了挑战。
谷歌于2012年5月16日首先发布 知识图谱（Knowledge Graph）。
知识图谱是一种互联网环境下的知识表示方法。 知识图谱的目的是为了提高搜索引擎的能力，改善用
7
2.5.3 知识图谱的表示
知识图谱也可被看作是一张图，图中的节点表示实体 或概念，而图中的边则由属性或关系构成。
法国
英国
963万平 方公里
面积
13.6亿亿
人口 首都
中国
国家
……
面积
美国
人口 首都
937万平 方公里
人工智能导论
Introduction of Artificial Intelligence
人工智能导论
Introduction of Artificial Intelligence
第 2 章-2 知识图谱
第2章 知识表示与知识图谱
第2章 知识表示与知识图谱
2.1 知识与知识表示的概.4 框架表示法 2.5 知识图谱
3.1亿亿
1.6万平 方公里
面积 北京 人口 纬度
经度
2069万
北纬 39°54′
东经 116°25′
华盛顿
经度
面积
纬度
西经 77°02′25′
178平 方公里
北纬 9°53′
8
2.5.4知识图谱的架构
1. 知识图谱的逻辑结构：模式层与数据层。 数据层主要是由一系列的事实组成，而知识以事实为单 位进行存储。 模式层构建在数据层之上，是知识图谱的核心。 2. 知识图谱的体系架构
5
2.6 知识图谱
由于互联网内容的大规模、异质多元、组织结构松散 的特点，给人们有效获取信息和知识提出了挑战。
谷歌于2012年5月16日首先发布 知识图谱（Knowledge Graph）。
知识图谱是一种互联网环境下的知识表示方法。 知识图谱的目的是为了提高搜索引擎的能力，改善用
920091-人工智能导论(第4版)-第2章 知识表示(导论)
中的任何个体y都是朋友。
▪ ( x)( y) F(x, y) 表示在个体域中存在个体x与个体y，
x与y是朋友。
▪ ( x)( y) F(x, y) 表示对于个体域中的任何两个个体x
和y，x与y都是朋友。
20
2.2.3 谓词公式
全称量词和存在量词出现的次序将影响命题的意思。 例如：
▪ ( x)( y)(Employee(x) → Manager(y, x)) :
Introduction of Artificial Intelligence
第 2 章 知识表示
教材：
王万良《人工智能导论》（第4版） 高等教育出版社，2017.7
第2章 知识表示
人类的智能活动主要是获得并运用知识。知识是智 能的基础。为了使计算机具有智能，能模拟人类的 智能行为，就必须使它具有知识。但知识需要用适 当的模式表示出来才能存储到计算机中去，因此， 知识的表示成为人工智能中一个十分重要的研究课 题。 本章将首先介绍知识与知识表示的概念，然后介绍 一阶谓词逻辑、产生式、框架、语义网络等当前人 工智能中应用比较广泛的知识表示方法，为后面介 绍推理方法、专家系统等奠定基础。
词演算表达式的每个常量、变量、谓词和函数符号的 指派。
Friends (george, x) Friends (george, susie) T Friends (george, kate) F
对于每一个解释，谓词公式都可求出一个真值（T 或F）。
24
2.2.4 谓词公式的性质
2. 谓词公式的永真性、可满足性、不可满足性
③ 经验引起的不确定性
④ 不完全性引起的不确定性
7
2.1.2 知识的特性
3. 可表示性与可利用性
▪ ( x)( y) F(x, y) 表示在个体域中存在个体x与个体y，
x与y是朋友。
▪ ( x)( y) F(x, y) 表示对于个体域中的任何两个个体x
和y，x与y都是朋友。
20
2.2.3 谓词公式
全称量词和存在量词出现的次序将影响命题的意思。 例如：
▪ ( x)( y)(Employee(x) → Manager(y, x)) :
Introduction of Artificial Intelligence
第 2 章 知识表示
教材：
王万良《人工智能导论》（第4版） 高等教育出版社，2017.7
第2章 知识表示
人类的智能活动主要是获得并运用知识。知识是智 能的基础。为了使计算机具有智能，能模拟人类的 智能行为，就必须使它具有知识。但知识需要用适 当的模式表示出来才能存储到计算机中去，因此， 知识的表示成为人工智能中一个十分重要的研究课 题。 本章将首先介绍知识与知识表示的概念，然后介绍 一阶谓词逻辑、产生式、框架、语义网络等当前人 工智能中应用比较广泛的知识表示方法，为后面介 绍推理方法、专家系统等奠定基础。
词演算表达式的每个常量、变量、谓词和函数符号的 指派。
Friends (george, x) Friends (george, susie) T Friends (george, kate) F
对于每一个解释，谓词公式都可求出一个真值（T 或F）。
24
2.2.4 谓词公式的性质
2. 谓词公式的永真性、可满足性、不可满足性
③ 经验引起的不确定性
④ 不完全性引起的不确定性
7
2.1.2 知识的特性
3. 可表示性与可利用性
《人工智能应用概论》课件第2章-知识表示
2 2.2.1知识表示具体实现
匹配流程： 初始信息：黑斑点、长脖子、长腿、乳汁、有蹄
第一次匹配： R2: IF 分泌乳汁 THEN 哺乳动物 --> 哺乳动物
第二次匹配： R7: IF 哺乳动物 AND 有蹄 THEN 有蹄类动物 --> 有蹄、哺乳动物
（关系，对象1，对象2，置信度） 例如：（情侣，小明，小红，0.7） 意思：小明和小红是情侣关系的概率是70%
2 2.1.3知识表示概念
(2)产生式系统 把一组产生式放在一起，让它们互相配合，协 同作用，一个产生式生成的结论可以供另一个 产生式作为已知事实使用，以求得问题的解决， 这样的系统称为产生式系统。
2 2.1.3知识表示概念
不确定性知识：推论中有一定概率发生的事件， 表示为 IF P THEN Q（置信度） 例如：IF 打雷 THEN 雨（0.9） 意思：如果打雷了，有90%的几率会下雨 （对象，属性，值，置信度） 例如：（手机，待机时间，10H，0.8） 意思：手机待机时间10小时的概率是80%
2 2.1.3知识表示概念
知识表示的完整过程
2 2.1.4知识表示发展历程 不同阶段时期，产生不同的知识表示概念
2 2.1.4知识表示发展历程
1.数据连接阶段 20世纪40年代，知识表示更多通过数据之间的关联所表示，还没形成一个相对统一的概念模型。
2.图形表示的信息阶段 随着1956年达特茅斯会议的召开，面向人工智能的表示方法从20世纪五六十年代就开始了，科 学家提出通过符号的形式表示知识，也就是‘一阶谓词逻辑表示’
同期为了表示过程性知识，1975年由夏克从框架发展出”脚本”表示方法，这种表示方式可以描 述事件及时间顺序，并成为基于示例的推理CBR（case-based reasoning）的基础之一，与框架 表示法类似
人工智能课件第二章 知识表示(修改)
19
• 接上一页
TABLE(a)
TABLE(a)
SETWODN(b) TABLE(b) GOTO( b,c) TABLE(b)
=======>状态5 ON(box,b) =======>状态6 ON(box,b)
EMPTY(robot)
EMPTY(robot)
AT(robot , a)
AT(robot ,b)
则称P是一个n元谓词，记为P(x1,x2,…,xn)，其中， x1,x2,…,xn为个体。
7
定义2.2 设D是个体域，f：Dn→D是一个映射，则称 f是D上的一个n元函数，记作f(x1,x2,…,xn) 其中，x1,x2,…,xn为个体。
• 谓词与函数的区别： 谓词是D到{T，F}的映射，函数是D到D的映射； 谓词的真值是T和F，函数的值（无真值）是D中 的元素； 谓词可独立存在，函数只能作为谓词的个体。
5
二、谓词逻辑表示法
1. 基本概念
• 命题：具有真假意义的断言称为命题。 • 命题的真值：
T：表示命题的意义为真 F：表示命题的意义为假 • 命题真值的说明： 一个命题不能同时既为真又为假 一个命题可在一定条件下为真，而在另一条件下为假
6
• 论域：由所讨论对象的全体构成的集合。 • 个体：论域中的元素。 • 谓词：在谓词逻辑中命题是用形如P(x1,x2,…,xn)的谓词
是一种“一直往前走”不回头的方式，该方式是利用问 题给定的局部知识来决定选用的规则，就像动物识别系统一 样，选取一条与综合数据库进行匹配，然后作用到综合数据 库，再选取一条新的规则进行匹配，此时在选择上不再考虑 已经用过的规则了。
动物有暗斑点，有长脖子，有长腿，有奶，有蹄
• 该例子的部分推理网络如下：
人工智能概论第2章-知识表示
按照作用的层次，知识还可以分成以下两类： （1）对象级知识 （2）元级知识
知识表示的方法按其表示的特征可分为两类： （1）叙述性表示 （2）过程性表示
所谓表示就是为描述世界所作的一组约定，是把 知识符号化的过程、知识的表示与知识的获取、 管理、处理、解释等有直接的关系。
首先，将适用的算符作用于初始状态，以产生新的状态； 然后，再把一些适用的算符作用于新的状态；这样继续下 去，直到产生的状态为目标状态为止。 最后，就得到了问题的一个解，这个解是从初始状态到目 标状态所用算符构成的序列。
产生式可表示的知识种类及其基本形式 1.可表示的知识种类 2.产生式的基本形式 3.产生式与谓词逻辑中蕴涵式的区别
同构变换可使问题更明确，更便于求解。同构问题的解答 等价于原始问题的解答。
同态变换可使问题更加简化，易于求解。原始问题有解， 则同态问题有解，同态问题无解，则原始问题无解。
它们之间是蕴含关系，通过同构或同态变换，可以将原始 问题转化为比较清晰、简单的同构或同态问题。
2.2 状态空间表示法
2.7.1 状态空间表示法的构成
(3) 状态空间 由表示一个问题的全部状态及一切可用算符构
成的集合称为该问题的状态空间。
(4) 问题的解 从问题的初始状态集S出发，经过一系列的算
符运算，到达目标状态。由初始状态到目标状 态所用算符的序列就构成了问题的一个解。
2.2.2 状态空间方法表示问题时的步骤
2.7.1 状态空间表示法的构成
状态空间表示法就是以“状态空间”的形式对问 题进行表示。
(1) 状态：状态是描述问题求解过程中不同时刻状 况的数据结构。
(2) 算符：引起状态中某些分量发生变化，从而使 问题由一个状态变为另一个状态的操作称为算符。 算符可分为走步、过程、规则、数学算子、运算 符号或逻辑符号等。
人工智能导论第二章
第二章 知识表示方法
• 2.1 知识和知识表示 • 2.2 状态空间表示 • 2.3 问题归约表示 • 2.4 谓词逻辑表示 • 2.5 语义网络表示 • 2.6 产生式表示 • 2.7 框架表示 • 2.8 面向对象表示
2021/2/28
人工智能导论第二章-
1
产生式
2.6 产生式表示
• 产生式通常用于表示事实、规则以及它们 的不确定性度量，适合于表示事实性知识 和规则性知识。
THEN 该动物是食肉动物
r7： IF 该动物是哺乳动物 AND 有蹄 THEN 该动物是有蹄类动物
r 8： IF 该动物是哺乳动物 AND 是反刍动物
THEN 该动物是有蹄类动物
2021/2/28
人工智能导论第二章- 刘珊
12
规则库
2.6 产生式表示
r9： IF 该动物是哺乳动物 AND 是食肉动物 AND 是黄褐色
2021/2/28
人工智能导论第二章- 刘珊
5
产生式的形式描述及语义
——巴科斯范式BNF
2.6 产生式表示
<产生式>::= <前提> <结论> <前 提> :: = <简单条件>|<复合条件> <结 论> :: = <事实>|<操作> <复合条件> :: = <简单条件>AND<简单条件>[AND<简单
AND 身上有暗斑点
THEN 该动物是金钱豹
r10：IF 该动物是哺乳动物 AND 是食肉动物 AND 是黄褐色 AND 身上有黑色条纹 THEN 该动物是虎
r11： IF 该动物是有蹄类动物 AND 有长脖子 AND 有长腿 AND 身上有暗斑点 THEN 该动物是长颈鹿
• 2.1 知识和知识表示 • 2.2 状态空间表示 • 2.3 问题归约表示 • 2.4 谓词逻辑表示 • 2.5 语义网络表示 • 2.6 产生式表示 • 2.7 框架表示 • 2.8 面向对象表示
2021/2/28
人工智能导论第二章-
1
产生式
2.6 产生式表示
• 产生式通常用于表示事实、规则以及它们 的不确定性度量，适合于表示事实性知识 和规则性知识。
THEN 该动物是食肉动物
r7： IF 该动物是哺乳动物 AND 有蹄 THEN 该动物是有蹄类动物
r 8： IF 该动物是哺乳动物 AND 是反刍动物
THEN 该动物是有蹄类动物
2021/2/28
人工智能导论第二章- 刘珊
12
规则库
2.6 产生式表示
r9： IF 该动物是哺乳动物 AND 是食肉动物 AND 是黄褐色
2021/2/28
人工智能导论第二章- 刘珊
5
产生式的形式描述及语义
——巴科斯范式BNF
2.6 产生式表示
<产生式>::= <前提> <结论> <前 提> :: = <简单条件>|<复合条件> <结 论> :: = <事实>|<操作> <复合条件> :: = <简单条件>AND<简单条件>[AND<简单
AND 身上有暗斑点
THEN 该动物是金钱豹
r10：IF 该动物是哺乳动物 AND 是食肉动物 AND 是黄褐色 AND 身上有黑色条纹 THEN 该动物是虎
r11： IF 该动物是有蹄类动物 AND 有长脖子 AND 有长腿 AND 身上有暗斑点 THEN 该动物是长颈鹿
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
9
第2章 知识表示
2.1 知识与知识表示的概念
✓ 2.2 一阶谓词逻辑表示法
2.3 产生式表示法 2.4 框架表示法
10
2.2 一阶谓词逻辑表示法
11Байду номын сангаас
2.2 一阶谓词逻辑表示法
2.2.1 命题 2.2.2 谓词 2.2.3 谓词公式 2.2.4 谓词公式的性质 2.2.5 一阶谓词逻辑知识表示方法 2.2.6 一阶谓词逻辑表示法的特点
▪ 知识的可利用性: 知识可以被利用。
8
2.1.3 知识的表示
知识表示（knowledge representation）：将人类知识形 式化或者模型化。
知识表示是对知识的一种描述，或者说是一组约定，一 种计算机可以接受的用于描述知识的数据结构。
选择知识表示方法的原则： （1）充分表示领域知识。 （2）有利于对知识的利用。 （3）便于对知识的组织、维护与管理。 （4）便于理解与实现。
“如果头痛“且真流”涕与“，假则”有之可间能的患中了间感状冒态”
① 随机性引起的不确定性
小李很高
② 模糊性引起的不确定性
③ 经验引起的不确定性
④ 不完全性引起的不确定性
7
2.1.2 知识的特性
3. 可表示性与可利用性
▪ 知识的可表示性: 知识可以用适当形式表示出来，如 用语言、文字、图形、神经网络等。
命题逻辑表示法：无法把它所描述的事物的结构及逻辑特 征反映出来，也不能把不同事物间的共同特征表述出来。
P：老李是小李的父亲
P：李白是诗人 Q：杜甫也是诗人
13
2.2.2 谓词
谓词的一般形式： P (x1, x2,…, xn)
▪ 个体 x1, x2,…, xn ：某个独立存在的事物或者某个抽象 的概念；
例如： “雪是白色的”—— 事实 “如果头痛且流涕，则有可能患了感冒 —— 规则
5
2.1.2 知识的特性
1.相对正确性 任何知识都是在一定的条件及环境下产生的，在
这种条件及环境下才是正确的。 1+1=2 （十进制） 1+1=10 (二进制）
6
2.1.2 知识的特性
知识状态：“真”
2. 不确定性
“假”
2
第2章 知识表示
2.1 知识与知识表示的概念 2.2 一阶谓词逻辑表示法 2.3 产生式表示法 2.4 框架表示法
3
第2章 知识表示
✓ 2.1 知识与知识表示的概念
2.2 一阶谓词逻辑表示法 2.3 产生式表示法 2.4 框架表示法
4
2.1.1 知识的概念
知识：在长信期息关的联生形活式及：“社如会果实……践，则中…、…”在科学研究及实验 中积累起来如的果大对雁客向观南世飞，界则的冬认天就识要与来经临了验。。 知识：把有关信息关联在一起所形成的信息结构。 知识反映了客观世界中事物之间的关系，不同事物或者 相同事物间的不同关系形成了不同的知识。
15
2.2.3 谓词公式
1. 连接词（连词）
“机器人不在2号房间”：﹁ Inroom (robot, r2)
（1）﹁： ““李否明定打”篮（球或ne踢ga足tio球n”）：或 “非”。
Plays (Liming, basketball) ∨ Plays (Liming, football)
（2）∨： “析取”（disjunction）——或。
Introduction of Artificial Intelligence
第 2 章 知识表示
教材：
王万良《人工智能导论》（第4版） 高等教育出版社，2017.7
第2章 知识表示
人类的智能活动主要是获得并运用知识。知识是智 能的基础。为了使计算机具有智能，能模拟人类的 智能行为，就必须使它具有知识。但知识需要用适 当的模式表示出来才能存储到计算机中去，因此， 知识的表示成为人工智能中一个十分重要的研究课 题。 本章将首先介绍知识与知识表示的概念，然后介绍 一阶谓词逻辑、产生式、框架、语义网络等当前人 工智能中应用比较广泛的知识表示方法，为后面介 绍推理方法、专家系统等奠定基础。
12
2.2.1 命题
命题（propositi例on如）：3一<个5 非真即假的陈述句。
▪ 若命题的意义为真，称它的真值为真，记为 T。 ▪ 若命题的意义为假，称它的真值为假，记为 F。
▪ 一个命题可在一种例条如件：下太为阳真从，西在边另升一起种条件下为假。
P例：:北1＋京1是＝中1华0 人民共和国的首都 命题逻辑：研究命题及命题之间关系的符号逻辑系统。
域中的所有（或任一个）个体 x ”。
“所有的机器人都是灰色的”：
( x)[ROBOT (x) → COLOR (x，GRAY)] （2）存在量词（existential quantifier）（ x）：“在
14
2.2.2 谓词
（2）个体是变元（变量）：没有指定的一个或者一组个
体。
“x<5” ：Less(x, 5)
（3）个体是函数：一个个体到另一个个体的映射。 ▪ “小李的父亲是教师”：Teacher (father (Li) )
（4）个体是谓词 ▪ “Smith作为一个工程师为IBM工作”：
二阶谓词 Works (engineer (Smith), IBM)
▪ 谓词名 P：刻画个体的性质、状态或个体间的关系。
（1）个体是常量：一个或者一组指定的个体。
▪ “老张是一个教师”：一元谓词 Teacher (Zhang) ▪ “5>3” ：二元谓词 Greater (5, 3) ▪ “Smith作为一个工程师为IBM工作”：
三元谓词 Works (Smith, IBM, engineer)
（3）∧： “合取”（conjunction）——与。
“我喜欢音乐和绘画”： Like (I, music) ∧ Like (I, painting)
16
2.2.3 谓词公式
1. 连接词（连词） （4）→：“蕴含”(implication)或 “条
件”(“如co果nd刘iti华on跑)。得最快，那么他取得冠军。” ：
RUNS (Liuhua，faster)→WINS (Liuhua ，champion)
（5） ：“等价”（equivalence）或“双条件”
（bicondition）。
P Q: “P当且仅当Q”。
17
2.2.3 谓词公式
1. 连接词（连词）
谓词逻辑真值表
18
2.2.3 谓词公式
2. 量词（quantifier） （1）全称量词（universal quantifier）（ x）：“对个体
第2章 知识表示
2.1 知识与知识表示的概念
✓ 2.2 一阶谓词逻辑表示法
2.3 产生式表示法 2.4 框架表示法
10
2.2 一阶谓词逻辑表示法
11Байду номын сангаас
2.2 一阶谓词逻辑表示法
2.2.1 命题 2.2.2 谓词 2.2.3 谓词公式 2.2.4 谓词公式的性质 2.2.5 一阶谓词逻辑知识表示方法 2.2.6 一阶谓词逻辑表示法的特点
▪ 知识的可利用性: 知识可以被利用。
8
2.1.3 知识的表示
知识表示（knowledge representation）：将人类知识形 式化或者模型化。
知识表示是对知识的一种描述，或者说是一组约定，一 种计算机可以接受的用于描述知识的数据结构。
选择知识表示方法的原则： （1）充分表示领域知识。 （2）有利于对知识的利用。 （3）便于对知识的组织、维护与管理。 （4）便于理解与实现。
“如果头痛“且真流”涕与“，假则”有之可间能的患中了间感状冒态”
① 随机性引起的不确定性
小李很高
② 模糊性引起的不确定性
③ 经验引起的不确定性
④ 不完全性引起的不确定性
7
2.1.2 知识的特性
3. 可表示性与可利用性
▪ 知识的可表示性: 知识可以用适当形式表示出来，如 用语言、文字、图形、神经网络等。
命题逻辑表示法：无法把它所描述的事物的结构及逻辑特 征反映出来，也不能把不同事物间的共同特征表述出来。
P：老李是小李的父亲
P：李白是诗人 Q：杜甫也是诗人
13
2.2.2 谓词
谓词的一般形式： P (x1, x2,…, xn)
▪ 个体 x1, x2,…, xn ：某个独立存在的事物或者某个抽象 的概念；
例如： “雪是白色的”—— 事实 “如果头痛且流涕，则有可能患了感冒 —— 规则
5
2.1.2 知识的特性
1.相对正确性 任何知识都是在一定的条件及环境下产生的，在
这种条件及环境下才是正确的。 1+1=2 （十进制） 1+1=10 (二进制）
6
2.1.2 知识的特性
知识状态：“真”
2. 不确定性
“假”
2
第2章 知识表示
2.1 知识与知识表示的概念 2.2 一阶谓词逻辑表示法 2.3 产生式表示法 2.4 框架表示法
3
第2章 知识表示
✓ 2.1 知识与知识表示的概念
2.2 一阶谓词逻辑表示法 2.3 产生式表示法 2.4 框架表示法
4
2.1.1 知识的概念
知识：在长信期息关的联生形活式及：“社如会果实……践，则中…、…”在科学研究及实验 中积累起来如的果大对雁客向观南世飞，界则的冬认天就识要与来经临了验。。 知识：把有关信息关联在一起所形成的信息结构。 知识反映了客观世界中事物之间的关系，不同事物或者 相同事物间的不同关系形成了不同的知识。
15
2.2.3 谓词公式
1. 连接词（连词）
“机器人不在2号房间”：﹁ Inroom (robot, r2)
（1）﹁： ““李否明定打”篮（球或ne踢ga足tio球n”）：或 “非”。
Plays (Liming, basketball) ∨ Plays (Liming, football)
（2）∨： “析取”（disjunction）——或。
Introduction of Artificial Intelligence
第 2 章 知识表示
教材：
王万良《人工智能导论》（第4版） 高等教育出版社，2017.7
第2章 知识表示
人类的智能活动主要是获得并运用知识。知识是智 能的基础。为了使计算机具有智能，能模拟人类的 智能行为，就必须使它具有知识。但知识需要用适 当的模式表示出来才能存储到计算机中去，因此， 知识的表示成为人工智能中一个十分重要的研究课 题。 本章将首先介绍知识与知识表示的概念，然后介绍 一阶谓词逻辑、产生式、框架、语义网络等当前人 工智能中应用比较广泛的知识表示方法，为后面介 绍推理方法、专家系统等奠定基础。
12
2.2.1 命题
命题（propositi例on如）：3一<个5 非真即假的陈述句。
▪ 若命题的意义为真，称它的真值为真，记为 T。 ▪ 若命题的意义为假，称它的真值为假，记为 F。
▪ 一个命题可在一种例条如件：下太为阳真从，西在边另升一起种条件下为假。
P例：:北1＋京1是＝中1华0 人民共和国的首都 命题逻辑：研究命题及命题之间关系的符号逻辑系统。
域中的所有（或任一个）个体 x ”。
“所有的机器人都是灰色的”：
( x)[ROBOT (x) → COLOR (x，GRAY)] （2）存在量词（existential quantifier）（ x）：“在
14
2.2.2 谓词
（2）个体是变元（变量）：没有指定的一个或者一组个
体。
“x<5” ：Less(x, 5)
（3）个体是函数：一个个体到另一个个体的映射。 ▪ “小李的父亲是教师”：Teacher (father (Li) )
（4）个体是谓词 ▪ “Smith作为一个工程师为IBM工作”：
二阶谓词 Works (engineer (Smith), IBM)
▪ 谓词名 P：刻画个体的性质、状态或个体间的关系。
（1）个体是常量：一个或者一组指定的个体。
▪ “老张是一个教师”：一元谓词 Teacher (Zhang) ▪ “5>3” ：二元谓词 Greater (5, 3) ▪ “Smith作为一个工程师为IBM工作”：
三元谓词 Works (Smith, IBM, engineer)
（3）∧： “合取”（conjunction）——与。
“我喜欢音乐和绘画”： Like (I, music) ∧ Like (I, painting)
16
2.2.3 谓词公式
1. 连接词（连词） （4）→：“蕴含”(implication)或 “条
件”(“如co果nd刘iti华on跑)。得最快，那么他取得冠军。” ：
RUNS (Liuhua，faster)→WINS (Liuhua ，champion)
（5） ：“等价”（equivalence）或“双条件”
（bicondition）。
P Q: “P当且仅当Q”。
17
2.2.3 谓词公式
1. 连接词（连词）
谓词逻辑真值表
18
2.2.3 谓词公式
2. 量词（quantifier） （1）全称量词（universal quantifier）（ x）：“对个体