中考数学压轴题-抛物线与圆(含答案)
二次函数与圆的综合题(中考数学必考压轴题)
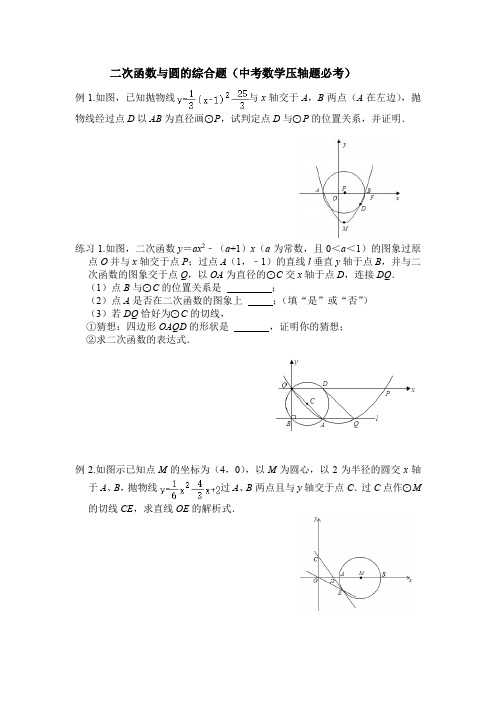
二次函数与圆的综合题(中考数学压轴题必考)例1.如图,已知抛物线与x轴交于A,B两点(A在左边),抛物线经过点D以AB为直径画⊙P,试判定点D与⊙P的位置关系,并证明.练习1.如图,二次函数y=ax2﹣(a+1)x(a为常数,且0<a<1)的图象过原点O并与x轴交于点P;过点A(1,﹣1)的直线l垂直y轴于点B,并与二次函数的图象交于点Q,以OA为直径的⊙C交x轴于点D,连接DQ.(1)点B与⊙C的位置关系是;(2)点A是否在二次函数的图象上;(填“是”或“否”)(3)若DQ恰好为⊙C的切线,①猜想:四边形OAQD的形状是,证明你的猜想;②求二次函数的表达式.例2.如图示已知点M的坐标为(4,0),以M为圆心,以2为半径的圆交x轴于A、B,抛物线过A、B两点且与y轴交于点C.过C点作⊙M 的切线CE,求直线OE的解析式.练习2.平面直角坐标系中,已知A(﹣4,0),B(1,0),且以AB为直径的圆交y轴的正半轴,设平行于x轴的直线交抛物线y=﹣x2﹣x+2于E,F两点,问:是否存在以线段EF为直径的圆,恰好与x轴相切?若存在,求出该圆的半径;若不存在,请说明理由.练习3.如图,抛物线y=﹣x2﹣x+2与x轴交于A(﹣4,0),B(2,0),与y 轴交于点C(0,2).以AB为直径作⊙M,直线经过点E(﹣1,﹣5),并且与⊙M相切,求该直线的解析式.练习4.如图,抛物线y=﹣x2+x+2.经过A、B、C三点,A点坐标为(4,0),B点坐标为(﹣1,0),以AB的中点P为圆心,AB为直径作⊙P的正半轴交于点C,M为抛物线的顶点,试说明直线MC与⊙P的位置关系,并证明你的结论.练习5.如图,抛物线与x轴交于A、B两点,与y轴交于C点.以AB为直径作⊙M.(1)求出M的坐标并证明点C在⊙M上;(2)若P为抛物线上一动点,求出当CP与⊙M相切时P的坐标;练习6.在平面直角坐标系中,已知A(﹣4,0),B(1,0),且以AB为直径的圆交y轴的正半轴于点C,过点C作圆的切线交x轴于点D.(1)求点C的坐标和过A,B,C三点的抛物线的析式;(2)求点D的坐标:(3)设平行于x轴的直线交抛物线于E,F两点,问:是否存在以线段EF为直径的圆,恰好与x轴相切?若存在,求出该圆的半径,若不存在,请说明理由.练习7.如图,在平面直角坐标系中,已知OA=n,OC=m,⊙M与y轴相切于点C,与x轴交于A,B两点,∠ACD=90°,抛物线y=ax2+bx+c经过A,B,C三点.(1)求证:∠OCA=∠OBC;(2)若A(x1,0),B(x2,0),且x1,x2满足x1+x2=5,x1•x2=4,求点C 的坐标和抛物线的解析式;(3)若△ACD≌△ABD,在四边形ABDC内有一点P,且点P到四边形四个顶点的距离之和P A+PB+PC+PD最小,求此时距离之和的最小值及P点的坐标(用含n的式子表示).练习8.已知二次函数y=mx2+(m﹣3)x﹣3(m>0)(1)求证:它的图象与x轴必有两个交点;(2)这条抛物线与x轴交于两点A、B(A在B左),与y轴交于点C,顶点为D,sin∠ABD=,⊙M过A、B、C三点,求⊙M的面积;(3)在(2)的条件下,抛物线上是否存在点P,使P A是⊙M的切线?若存在,求出P点的坐标,若不存在,说明理由.例3.如图,抛物线y=ax2+bx+c(a,b,c是常数,a≠0)的对称轴为y轴,且经过(0,0)和(,)两点,点P在该抛物线上运动,以点P为圆心的⊙P总经过定点A(0,2).(1)求a,b,c的值;(2)求证:在点P运动的过程中,⊙P始终与x轴相交;(3)设⊙P与x轴相交于M(x1,0),N(x2,0)(x1<x2)两点,当△AMN 为等腰三角形时,求圆心P的纵坐标.练习9.已知:如图,抛物线y=ax2+bx+1的图象关于y轴对称,且抛物线过点(2,2),点P为抛物线上的动点,以点P为圆心的⊙P与x轴相切,当点P运动对,⊙P始终经过y轴上的一个定点E.(1)求抛物线的解析式;(2)当⊙P的半径为时,⊙P与y轴交于M、N两点,求MN的长;(3)求定点E到直线y=kx﹣8k的距离的最大值.练习10.已知:直线y=﹣x﹣4分别交x、y轴于A、C两点,抛物线y=ax2+bx (a>0)经过A、O两点,且顶点B的纵坐标为﹣2(1)判断点B是否在直线AC上,并求该抛物线的函数关系式;(2)以点B关于x轴的对称点D为圆心,以OD为半径作⊙D,试判断直线AC与⊙D的位置关系,并说明理由;(3)若E为⊙D的优弧AO上一动点(不与A、O重合),连接AE、OE,问在抛物线上是否存在点P,使∠POA:∠AEO=2:3?若存在,请求出所有满足条件的点P的坐标;若不存在,请说明理由.练习11.已知A是x轴正半轴上一个动点,以线段OA为直径作⊙B,圆心为点B,直径OA=m,线段EF是⊙B的一条弦,EF∥x轴,点C为劣弧EF的中点,过点E作DE垂直于EF,交抛物线C1:y=ax2+bx(a>0)于点G,抛物线经过点O和点A.(1)求证:DG=m;(2)拖动点A,如果抛物线C1与⊙B除点O和点A外有且只有一个交点,求b的值;(3)拖动点A,抛物线C1交⊙B于点O、E、F、A,①求证:DE=m﹣;②直接写出FC2的值(用a,m的代数式表示)练习13.如图,在平面直角坐标系中,以点C(1,1)为圆心,2为半径作圆,交x轴于A.B两点,开口向下的抛物线经过点A,B,且其顶点P在⊙C上.(1)求∠ACB的大小;(2)写出A,B两点的坐标;(3)由圆与抛物线的对称性可知抛物线的顶点P的坐标为(1,3),求出抛物线的解析式;(4)在该抛物线上是否存在一点D点,使线段OP与CD互相平分?若存在,求出点D的坐标;若不存在,请说明理由.例4.如图1,抛物线y=ax2+3ax(a为常数,a<0)与x轴交于O,A两点,点B 为抛物线的顶点,点D是线段OA上的一个动点,连接BD并延长与过O,A,B三点的⊙P相交于点C,过点C作⊙P的切线交x轴于点E.(1)①求点A的坐标;②求证:CE=DE;(2)如图2,连接AB,AC,BE,BO,当,∠CAE=∠OBE时,①求证:AB2=AC•BE;②求的值.练习14.如图1,已知圆O的圆心为原点,半径为2,与坐标轴交于A,C,D,E 四点,B为OD中点.(1)求过A,B,C三点的抛物线解析式;(2)如图2,连接BC,AC.点P在第一象限且为圆O上一动点,连接BP,交AC于点M,交OC于点N,当MC2=MN•MB时,求M点的坐标;(3)如图3,若抛物线与圆O的另外两个交点分别为H,F,请判断四边形CFEH的形状,并说明理由.练习15.如图,二次函数与x轴的一个交点A的坐标为(﹣3,0),以点A为圆心作圆A,与该二次函数的图象相交于点B,C,点B,C的横坐标分别为﹣2,﹣5,连接AB,AC,并且满足AB⊥AC.过点B作BM⊥x轴于点M,过点C作CN⊥x轴于点N.(1)求该二次函数的关系式;(2)经过点B作直线BD,在A点右侧与x轴交于点D,与二次函数的图象交于点E,使得∠ADB=∠ABM,连接AE,求证:AE=AD;(3)若直线y=kx+1与圆A相切,请求出k的值.例5.已知抛物线y=ax2+bx+5(a≠0)经过A(5,0),B(6,1)两点,且与y 轴交于点C.(1)求抛物线y=ax2+bx+5(a≠0)的函数关系式;(2)如图1,连接AC,E为线段AC上一点且横坐标为1,⊙P是△OAE外接圆,求圆心P点的坐标;(3)如图2,连接AC,E为线段AC上任意一点(不与A、C重合)经过A、E、O三点的圆交直线AB于点F;①点E在运动过程中四边形OEAF的面积是否为定值?如果是,请求出这个定值;如果不是,请说明理由;②求出当△AEF的面积取得最大值时,点E的坐标.练习16.如图1,已知抛物线y=﹣x2+bx+c经过点A(1,0),B(﹣5,0)两点,且与y轴交于点C.(1)求b,c的值.(2)在第二象限的抛物线上,是否存在一点P,使得△PBC的面积最大?求出点P的坐标及△PBC的面积最大值.若不存在,请说明理由.(3)如图2,点E为线段BC上一个动点(不与B,C重合),经过B、E、O 三点的圆与过点B且垂直于BC的直线交于点F,当△OEF面积取得最小值时,求点E坐标.练习17.如图1,抛物线y=+bx+c与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C,顶点为D.(1)求抛物线的解析式;(2)如图2,以AB为直径在x轴上方画半圆交y轴于点E,圆心为G,P为半圆上一动点,连接DP,点Q为PD的中点.①判断点C、D与⊙G的位置关系,并说明原因;②当点P沿半圆从点B运动到点A时,求线段AQ的最小值.练习18.如图1,二次函数y=ax2﹣3ax+b(a、b为参数,其中a<0)的图象与x 轴交于A、B两点,与y轴交于点C,顶点为D.(1)若b=﹣10a,求tan∠CBA的值(结果用含a的式子表示);(2)若△ABC是等腰三角形,直线AD与y轴交于点P,且AP:DP=2:3.求抛物线的解析式;(3)如图2,已知b=﹣4a,E、F分别是CA和CB上的动点,且EF=AB,若以EF为直径的圆经过点C,并交x轴于M、N两点,求MN的最大值.课后练习1.抛物线y=ax2+bx﹣4交x轴于A(﹣2,0),B(4,0)两点,交y轴于点C,点P是介于B、C之间的抛物线上的动点(包括B、C两点),点E是△ABP 的外接圆圆心.(1)求抛物线的解析式;(2)如图1,当P为抛物线的顶点时,求圆心E的坐标;(3)如图2,作PH⊥x轴于点H,延长PH交⊙E于点Q,当P从C点出发,沿该抛物线运动到B点,求点Q在这个运动过程中的路径长.2.如图,在正方形OABC中,AB=4,点E是线段OA(不含端点)边上一动点,作△ABE的外接圆交AC于点D.抛物线y=ax2﹣x+c过点O,E.(1)求证:∠BDE=90°;(2)如图1,若抛物线恰好经过点B,求此时点D的坐标;(3)如图2,AC与BE交于点F.①请问点E在运动的过程中,CF•AD是定值吗?如果是,请求出这个值,如果不是,请说明理由;②若,求点E坐标及a的值.。
2024广东中考数学压轴题

2024广东中考数学压轴题一、在直角坐标系中,抛物线y = ax2 + bx + c与x轴交于点A(-3,0)和B(1,0),且与y 轴交于点C(0,3)。
下列说法正确的是:A. a > 0B. b < 0C. c = 0D. 抛物线的对称轴是直线x = -1(答案:D)二、已知三角形ABC的三边长为a,b,c,且满足a2 + b2 + c2 = 10a + 6b + 8c - 50。
则下列判断三角形ABC的形状中,正确的是:A. 等腰三角形B. 等边三角形C. 直角三角形D. 等腰直角三角形(答案:D)三、函数y = (x - 1)/(x + 2)中,当x的值增大时,y的值会:A. 一直增大B. 一直减小C. 在某个区间内增大,在另一个区间内减小D. 保持不变(答案:C)四、已知四边形ABCD是平行四边形,且AB = 6,BC = 8,对角线AC与BD相交于点O,则下列关于O点到AB和BC的距离d1和d2的说法正确的是:A. d1 + d2 = 14B. d1 × d2 = 24C. d1/d2 = AB/BCD. d12 + d22 = AB2 + BC2(答案:B)五、圆O的半径为5,点P在圆O外,且OP = 8。
过点P作圆O的两条切线,分别与圆O 相切于点A和B。
则弦AB的长度为:A. 6B. 4√3C. 5√2D. 2√15(答案:A)六、在数轴上,点A表示的数为-2,点B表示的数为3。
若点C表示的数为x,且满足AC + BC = 8,则x的值为:A. -3或4B. -4或3C. -3或-1D. 2或-5(答案:B)七、已知二次函数y = ax2 + bx + c的图像经过点(1,0),(2,0)和(3,4)。
下列说法正确的是:A. a > 0B. b < 0C. c = 0D. 函数的顶点在x轴上(答案:A)八、正方形ABCD的边长为4,点E在边AB上,且AE = 1。
2023年九年级数学中考专题:二次函数与圆综合压轴题(含简单答案)

2023年九年级数学中考专题:二次函数与圆综合压轴题1.如图1,在平面直角坐标系中,O为坐标原点,已知抛物线与x轴交于,两点,与y轴交于点C.(1)求抛物线解析式;(2)如图2,M是抛物线顶点,的外接圆与x轴的另一交点为D,与y轴的另一交点为E.①求;②若点N是第一象限内抛物线上的一个动点,在射线上是否存在点P,使得与相似?如果存在,请求出点P的坐标;(3)点Q是拋物线对称轴上一动点,若为锐角,且,请直接写出点Q 纵坐标的取值范围.2.【概念学习】在平面直角坐标系中,对于已知的点和图形,给出如下定义:如果图形上存在一点,使得当时,,则称点为图形的一个“垂近点”.(1)【初步理解】若图形为线段,,,在点、、、中,是线段的“垂近点”的为________;(2)【知识应用】若图形为以坐标原点为圆心,2为半径的圆,直线与轴交于点、与轴交于点,如果线段上的点都是的“垂近点”,求的取值范围;(3)若图形为抛物线,以点为中心,半径为的四边形,轴,轴,如果正四边形上存在“垂近点”,直接写出的取值范围.3.在平面直角坐标系xOy中,已知抛物线y=x2﹣2x﹣3与x轴交于A、B两点,与y 轴交于C点,D为抛物线顶点.(1)连接AD,交y轴于点E,P是抛物线上的一个动点.①如图一,点P是第一象限的抛物线上的一点,连接PD交x轴于F,连接,若,求点P的坐标.②如图二,点P在第四象限的抛物线上,连接AP、BE交于点G,若,则w 有最大值还是最小值?w的最值是多少?(2)如图三,点P是第四象限抛物线上的一点,过A、B、P三点作圆N,过点作轴,垂足为I,交圆N于点M,点在运动过程中,线段是否变化?若有变化,求出MI的取值范围;若不变,求出其定值.(3)点Q是抛物线对称轴上一动点,连接OQ、AQ,设AOQ外接圆圆心为H,当的值最大时,请直接写出点H的坐标.4.如图1,在平面直角坐标系中,已知抛物线y=ax2+bx-4(a≠0)经过点A(-2,0)和点B(4,0).(1)求这条抛物线所对应的函数表达式;(2)点P为抛物线上第一象限内一点,若S△ABC=2S△PBC,求点P的坐标;(3)如图2,点D是第二象限内抛物线上一点,过点D作DF⊥x轴,垂足为F,△ABD 的外接圆与DF相交于点E.试问:线段EF的长是否为定值?如果是,请求出这个定值;如果不是,请说明理由.5.如图,抛物线经过点,,直线AC的解析式为,且与y轴相交于点C,若点E是直线AB上的一个动点,过点E作轴交AC于点F.(1)求抛物线的解析式;(2)点H是y轴上一动点,连结EH,HF,当点E运动到什么位置时,四边形EAFH 是矩形?求出此时点E,H的坐标;(3)在(2)的前提下,以点E为圆心,EH长为半径作圆,点M为上以动点,求的最小值.6.已知二次函数的图象经过点A(2,0),B(,0),C(0,4),点为二次函数第二象限内抛物线上一动点,轴于点,交直线于点,以为直径的圆⊙M与交于点.(1)求这个二次函数的关系式;(2)当三角形周长最大时.求此时点点坐标及三角形的周长;(3)在(2)的条件下,点N为⊙M上一动点,连接BN,点Q为BN的中点,连接HQ,求HQ的取值范围.7.如图,在平面直角坐标系中,抛物线,y与轴交于A、B两点,与轴交于点C.(1)求点A、B、C的坐标;(2)如图1,连接BC,点D是抛物线上一点,若∠DCB=∠ABC,求点D的坐标;(3)如图2,若点P在以点O为圆心,OA长为半径作的圆上,连接BP、CP,请你直接写出CP+BP的最小值.8.如图,在平面直角坐标系中,半径为1的圆的圆心在坐标原点,且与两坐标轴分别交于、、、四点,点坐标为.抛物线与轴交于点,与直线交于点、,且、分别与圆相切于点和点.(1)求抛物线的解析式.(2)过点作圆的切线交的延长线于点,判断点是否在抛物线上,说明理由.(3)抛物线对称轴交轴于点,连接并延长交于点,求点的坐标.9.如图,在平面直角坐标系中,抛物线交y轴于点,交x轴于两点.(1)求此抛物线的解析式;(2)已知点P是抛物线上的一个动点,且位于A、C两点之间,问:当点P运动到什么位置时,的面积最大?并求出此时P点的坐标和的最大面积;(3)过点B作线段的垂线交抛物线于点D,如果以点C为圆心的圆与直线相切,请判断抛物线的对称轴l与有怎样的位置关系,并给出证明.10.如图,直线与x轴交于点B,与y轴交于点C,抛物线经过B、C两点,且与x轴交于另一点A.(1)求抛物线的解析式.(2)点P是线段BC下方的抛物线上的动点(不与点B、C重合),过P作PD∥y轴交BC 于点D,以PD为直径的圆交BC于另一点E,求DE的最大值及此时点P的坐标;(3)当(2)中的DE取最大值时,将△PDE绕点D旋转,当点P落在坐标轴上时,求点E的坐标.11.直角坐标系xOy中,有反比例函数上的一动点P,以点P为圆心的圆始终与y轴相切,设切点为A(1)如图1,⊙P运动到与x轴相切时,求OP2的值.(2)设圆P运动时与x轴相交,交点为B、C,如图2,当四边形ABCP是菱形时,①求出A、B、C三点的坐标.②设一抛物线过A、B、C三点,在该抛物线上是否存在点Q,使△QBP的面积是菱形ABCP 面积的?若存在,求出所有满足条件的Q点的坐标;若不存在,说明理由.12.已知:如图,在平面直角坐标系xOy中,以点P(2,)为圆心的圆与y轴相切于点A,与x轴相交于B、C两点(点B在点C的左边).(1)求经过A、B、C三点的抛物线的解析式;(2)在(1)中的抛物线上是否存在点M,使△MBP的面积是菱形ABCP面积的.如果存在,请直接写出所有满足条件的M点的坐标;如果若不存在,请说明理由;(3)如果一个动点D自点P出发,先到达y轴上的某点,再到达x轴上某点,最后运动到(1)中抛物线的顶点Q处,求使点D运动的总路径最短的路径的长.13.已知,如图,二次函数y=﹣x2+bx+c的图象经过点A(﹣1,0),B(3,0),点E为二次函数第一象限内抛物线上一动点,EH⊥x轴于点H,交直线BC于点F,以EF为直径的圆⊙M与BC交于点R.(1)求这个二次函数关系式.(2)当△EFR周长最大时.①求此时点E点坐标及△EFR周长.②点P为⊙M上一动点,连接BP,点Q为BP的中点,连接HQ,求HQ的最大值.14.如图所示,对称轴为直线的抛物线与轴交于、两点,与轴交于点,点在抛物线对称轴上并且位于轴的下方,以点为圆心作过、两点的圆,恰好使得弧的长为周长的.(1)求该抛物线的解析式;(2)求的半径和圆心的坐标,并判断抛物线的顶点与的位置关系;(3)在抛物线上是否存在一点,使得?若存在,求出所有符合条件的点的坐标;若不存在,请说明理由.15.已知抛物线y=ax2+bx+5(a≠0)经过A(5,0),B(6,1)两点,且与y轴交于点C.(1)求抛物线y=ax2+bx+5(a≠0)的函数关系式;(2)如图1,连接AC,E为线段AC上一点且横坐标为1,⊙P是△OAE外接圆,求圆心P 点的坐标;(3)如图2,连接AC,E为线段AC上任意一点(不与A、C重合)经过A、E、O三点的圆交直线AB于点F;①点E在运动过程中四边形OEAF的面积是否为定值?如果是,请求出这个定值;如果不是,请说明理由;②求出当△AEF的面积取得最大值时,点E的坐标.16.如图1,已知圆O的圆心为原点,半径为2,与坐标轴交于A,C,D,E四点,B 为OD中点.(1)求过A,B,C三点的抛物线解析式;(2)如图2,连接BC,AC.点P在第一象限且为圆O上一动点,连接BP,交AC于点M,交OC于点N,当MC2=MN•MB时,求M点的坐标;(3)如图3,若抛物线与圆O的另外两个交点分别为H,F,请判断四边形CFEH的形状,并说明理由.17.已知一次函数:与轴交于点,与轴交于点.抛物线(、为常数)过定点,连接,点为线段上一动点.(1)求出点的坐标;(2)过作于点,于点,设点横坐标为,长度为,试求关于的函数解析式;(3)①当,时,该抛物线上存在唯一的点使,求此时抛物线的解析式;②过点作交线段于点,连接并延长交的外接圆于点,当点在上移动时,求的最大值.18.已知抛物线经过,,三个点.(1)求抛物线的解析式;(2)如图1,作的外接圆,为上方半圆上一点,当时,求的长;(3)如图2,直线与抛物线交于,两点,与轴交于点,作轴的平行线,分别与线段、抛物线交于,两点(点与点,不重合),点为射线上一点,当与相似时,求的最大面积.参考答案:1.(1)(2)①;②存在,或或或(3)或2.(1),;(2);(3)或时,正方形上存在抛物线的“垂近点”.3.(1)①,②w有最小值,w的最值是(2)不变,(3)或4.(1);(2);(3)为定值.5.(1);(2),;(3)6.(1);(2)F(,4),△EFD的周长为;(3).7.(1),,;(2),;(3)8.(1);(2)点在抛物线上;(3)9.(1);(2),;(3)相交,10.(1)y=x2﹣x﹣2;(2)m=2时,DE有最大值,此时P;(3),或E或11.(1)16;(2)①A(0,),B(2,0),C(6,0);②存在,满足条件的Q点有(0,),(14,),(8,)和(6,0).12.(1).(2)存在,点M的坐标为(0,),(3,0),(4,),(7,).(3).13.(1)y=﹣x2+2x+3;(2)①E(,),周长为+;②HQ的最大值大为:+.14.(1)(2)2,,点在上(3)存在,,,15.(1)抛物线解析式为y=x2﹣x+5(2)圆心P点的坐标为(,)(3)①四边形OEAF的面积是定值,这个定值为;②当△OEF的面积取得最小值时,E点坐标为(,)16.(1)y=﹣x2+x+2;(2)M(,);(3)四边形CFEH是矩形.17.(1);(2)();(3)①;②18.(1);(2);(3).。
中考数学压轴题--有关圆的压轴题汇编含答案Word版

2020中考数学押题--有关圆的压轴题汇编含答案(53页)1.如图,在M e 中,»AB 所对的圆心角为120o ,已知圆的半径为2cm ,并建立如图所示的直角坐标系. (1)求圆心M 的坐标; (2)求经过A B C ,,三点的抛物线的解析式;(3)点D 是弦AB 所对的优弧上一动点,求四边形ACBD 的最大面积; (4)在(2)中的抛物线上是否存在一点P ,使PAB△和ABC △相似?若存在,求出点P 的坐标;若不存在,请说明理由.[解] (1)如图(1),连结MA MB ,. 则120AMB ∠=o 60CMB ∴∠=o ,30OBM ∠=o .112OM MB ∴==,(01)M ∴,. (2)由A B C ,,三点的特殊性与对称性, 知经过A B C ,,三点的抛物线的解析式为2y ax c =+.1OC MC MO =-=Q ,223OB MB OM =-=,(01)(30)C B ∴-,,,.113c a ∴=-=,2113y x ∴=-.(3)ABC ABD ACBD S S S =+Q △△四边形,又ABC S △与AB 均为定值,∴当ABD △边AB 上的高最大时,ABD S △最大,此时点D 为M e 与y 轴的交点,如图1.211143cm 222ABC ABD ACBD S S S AB OC AB OD AB CD ∴=+=+==△△四边形···. (4)方法1:如图2,ABC Q △为等腰三角形,303ABABC BC∠==o ,,ABC PAB ∴△∽△等价于302336PAB PB AB PA PB ∠=====o ,,.设()P x y ,且0x >,则cos3033323x PAAO =-=-=o ·,sin 303y PA ==o ·. 又(233)P Q ,的坐标满足2113y x =-,∴在抛物线2113y x =-上,存在点(233)P ,,使ABC PAB △∽△. y xAM O BCy xB C A MP 图2O yxAM OBCD图1由抛物线的对称性,知点(233)-,也符合题意.∴存在点P ,它的坐标为(233),或(233)-,. 方法2:如图(3),当ABC PAB △∽△时,30PAB BAC ∠=∠=o ,又由(1)知30MAB ∠=o ,∴点P 在直线AM 上.设直线AM 的解析式为y kx b =+,将(30)(01)A M -,,,代入,解得31.k b ⎧=⎪⎨⎪=⎩,∴直线AM 的解析式为31y x =+. 解方程组231113y x y x ⎧=+⎪⎪⎨⎪=-⎪⎩,得(233)P ,. 又tan 3233PBx ∠==-Q ,60PBx ∴∠=o .30P ∴∠=o ,ABC PAB ∴△∽△.∴在抛物线2113y x =-上,存在点(233)P ,,使ABC PAB △∽△. 由抛物线的对称性,知点(233)-,也符合题意.∴存在点P ,它的坐标为(233),或(233)-,. 方法3:如图3,ABC Q △为等腰三角形,且3ABBC=,设()P x y ,则 图3 ABC PAB △∽△等价于23PB AB ==,36PA AB ==.当0x >时,得2222(3)23(3) 6.x y x y ⎧-+=⎪⎨⎪++=⎩,解得(233)P ,. 又Q (233)P ,的坐标满足2113y x =-,∴在抛物线2113y x =-上,存在点(233)P ,,使ABC PAB △∽△. 由抛物线的对称性,知点(233)-,也符合题意.∴存在点P ,它的坐标为(233),或(233)-,. [点评]本题是一道综合性很强也是传统型的压轴题,涉及了函数、方程、相似、圆等大量初中数学的重点知识,解这类问题要求学生必须稳固的掌握各个领域的数学知识,须注意的是在第4小问中涉及了相似三角形的问题,很有可能会有多解的情况出现,此时就要求学生拥有较强的数形结合思想去探索结论的存在性。
圆与二次函数结合型压轴题专题(解析版)--2024年中考数学重难点

圆与二次函数结合型压轴题专题通用的解题思路:一、点在圆上的使用技巧:①没告诉半径,利用圆上的点到圆心的距离等于半径可以表示出半径的长度;②告诉半径,圆上的点到圆心的距离等于半径这个等量关系可以求出一个参数。
二、判断直线与圆的位置关系的标准流程:第一步,利用圆上的点到圆心的距离等于半径表示出半径r ,第二步,表示出圆心到直线的距离d ,第三步,比较半径r 和距离d 的大小:若半径r >距离d ,则直线与圆相交,若半径r =距离d ,则直线与圆相切,若半径r <距离d ,则直线与圆相离。
三、记直线l 被圆C 截得的弦长为|AB |的常用方法弦长公式:AB =2r 2-d 21(长沙中考)如图,抛物线y =ax 2+bx +c (a ,b ,c 是常数,a ≠0)的对称轴为y 轴,且经过(0,0)和(a ,116)两点,点P 在该抛物线上运动,以点P 为圆心的⊙P 总经过定点A (0,2).(1)求a ,b ,c 的值;(2)求证:在点P 运动的过程中,⊙P 始终与x 轴相交;(3)设⊙P 与x 轴相交于M (x 1,0),N (x 2,0)(x 1<x 2)两点,当△AMN 为等腰三角形时,求圆心P 的纵坐标.【解答】解:(1)∵抛物线y =ax 2+bx +c (a ,b ,c 是常数,a ≠0)的对称轴为y 轴,且经过(0,0)和(a ,116)两点,∴抛物线的一般式为:y =ax 2,∴116=a (a )2,解得:a =±14,∵图象开口向上,∴a =14,∴抛物线解析式为:y =14x 2,故a =14,b =c =0;(2)设P (x ,y ),⊙P 的半径r =x 2+y -2 2,又∵y =14x 2,则r =x 2+14x 2-2 2,化简得:r =116x 4+4>14x 2,∴点P 在运动过程中,⊙P 始终与x 轴相交;(3)设P (t ,14t 2),∵r 2-y 2=4,∴MH =NH =2,∴M (t -2,0),N (t +2,0),A (0,2),∵△AMN 为等腰三角形,∴AM =AN ,AM =MN ,AN =MN ,(t -2)2+(2-0)2=(t +2)2+(2-0)2,∴t =0,(t -2)2+(2-0)2=42,∴t =2±23,(t +2)2+(2-0)2=42,∴t =-2±23,①当t =0时,P 的纵坐标为0,②当t =2±23时,P Y =14(2±23)2=4±23,∴P 的纵坐标为4±23,③当t =-2±23时,P Y =14(2±23)2=4±23,∴P 的纵坐标为4±23,综上所述,P 的纵坐标为:0或4+23或4-23.2(岳麓区校级月考)如图,已知直线l :y =-1和抛物线L :y =ax 2+bx +c (a ≠0),抛物线L 的顶点为原点,且经过点A 2a ,14,直线y =kx +1与y 轴交于点F ,与抛物线L 交于点B (x 1,y 1),C (x 2,y 2),且x 1<x 2.(1)求抛物线L 的解析式;(2)点P 是抛物线L 上一动点.①以点P 为圆心,PF 为半径作⊙P ,试判断⊙P 与直线l 的位置关系,并说明理由;②若点Q (2,3),当|PQ -PF |的值最大时,求点P 的坐标;(3)求证:无论k 为何值,直线l 总是与以BC 为直径的圆相切.【解答】解:(1)抛物线的表达式为:y =ax 2,将点A 坐标代入上式得:14=a (2a )2,解得:a =14,故抛物线的表达式为:y =14x 2⋯①;(2)①点F (0,1),设:点P (m ,14m 2),则PF =m 2+14m 2-1 2=14m 2+1,而点P 到直线l 的距离为:14m 2+1,则⊙P 与直线l 的位置关系为相切;②当点P 、Q 、F 三点共线时,|PQ -PF |最大,将点FQ 的坐标代入一次函数表达式:y =kx +b 并解得:直线FQ 的函数表达式为:y =x +1⋯②,联立①②并解得:x =2±22,故点P 的坐标为:(2+22,3+22)或(2-22,3-22);(3)将抛物线的表达式与直线y =kx +1联立并整理得:x 2-4kx -4=0,则x 1+x 2=4k ,x 1x 2=-4,则y 1+y 2=k (x 1+x 2)+2=4k 2+2,则x 2-x 1=x 1+x 2 2-4x 1x 2=4,设直线BC 的倾斜角为α,则tan α=k ,则cosα=1k 2+1,则BC =x 2-x 1k 2+1=4(k 2+1),则12BC =2k 2+2,设BC 的中点为M (2k ,2k 2+1),则点M 到直线l 的距离为:2k 2+2,故直线l 总是与以BC 为直径的圆相切.3在平面直角坐标系xOy 中,已知二次函数y =14x 2+mx +n 的图象经过点A (2,0)和点B (1,-34),直线l 经过抛物线的顶点且与y 轴垂直,垂足为Q .(1)求该二次函数的表达式;(2)设抛物线上有一动点P 从点B 处出发沿抛物线向上运动,其纵坐标y 1随时间t (t ≥0)的变化规律为y 1=-34+2t .现以线段OP 为直径作⊙C .①当点P 在起始位置点B 处时,试判断直线l 与⊙C 的位置关系,并说明理由;在点P 运动的过程中,直线l 与⊙C 是否始终保持这种位置关系?请说明你的理由.②若在点P 开始运动的同时,直线l 也向上平行移动,且垂足Q 的纵坐标y 2随时间t 的变化规律为y 2=-1+3t ,则当t 在什么范围内变化时,直线l 与⊙C 相交?此时,若直线l 被⊙C 所截得的弦长为a ,试求a 2的最大值.【解答】解:(1)将点A (2,0)和点B (1,-34)分别代入y =14x 2+mx +n 中,得:14×4+2m +n =014+m +n =-34 ,解得:m =0n =-1 ,∴抛物线的解析式:y =14x 2-1;(2)①将P 点纵坐标代入(1)的解析式,得:14x 2-1=-34+2t ,x =8t +1,∴P (8t +1,-34+2t ),∴圆心C (8t +12,-38+t ),∴点C 到直线l 的距离:-38+t -(-1)=t +58;而OP 2=8t +1+(-34+2t )2,得OP =2t +54,半径OC =t +58;∴直线l 与⊙C 始终保持相切.②Ⅰ、由①可知,若直线l 与⊙C 相切,则:2t -58=t +58,t =54;∴当0<t <54时,直线l 与⊙C 相交;Ⅱ、∵0<t <54时,圆心C 到直线l 的距离为d =|2t -58|,又半径为r =t +58,∴a 2=4(r 2-d 2)=4[(t +58)2-|2t -58|2]=-12t 2+15t ,∴t =58时,a 的平方取得最大值为7516.4(长沙中考)如图半径分别为m ,n (0<m <n )的两圆⊙O 1和⊙O 2相交于P ,Q 两点,且点P (4,1),两圆同时与两坐标轴相切,⊙O 1与x 轴,y 轴分别切于点M ,点N ,⊙O 2与x 轴,y 轴分别切于点R ,点H .(1)求两圆的圆心O 1,O 2所在直线的解析式;(2)求两圆的圆心O 1,O 2之间的距离d ;(3)令四边形PO 1QO 2的面积为S 1,四边形RMO 1O 2的面积为S 2.试探究:是否存在一条经过P ,Q 两点、开口向下,且在x 轴上截得的线段长为s 1-s 2 2d 的抛物线?若存在,请求出此抛物线的解析式;若不存在,请说明理由.【解答】解:(1)由题意可知O 1(m ,m ),O 2(n ,n ),设过点O 1,O 2的直线解析式为y =kx +b ,则有:mk +b =m nk +b =n (0<m <n ),解得k =1b =0 ,∴所求直线的解析式为:y =x .(2)由相交两圆的性质,可知P 、Q 点关于O 1O 2对称.∵P (4,1),直线O 1O 2解析式为y =x ,∴Q (1,4).如解答图1,连接O 1Q .∵Q (1,4),O 1(m ,m ),根据两点间距离公式得到:O 1Q =m -1 2+m -4 2=2m 2-10m +17,又O 1Q 为小圆半径,即QO 1=m ,∴2m 2-10m +17=m ,化简得:m 2-10m +17=0①如解答图1,连接O 2Q ,同理可得:n 2-10n +17=0②由①,②式可知,m 、n 是一元二次方程x 2-10x +17=0③的两个根,解③得:x =5±22,∵0<m <n ,∴m =5-22,n =5+22.∵O 1(m ,m ),O 2(n ,n ),∴d =O 1O 2=m -n 2+m -n 2=8.(3)假设存在这样的抛物线,其解析式为y =ax 2+bx +c ,因为开口向下,所以a <0.如解答图2,连接PQ .由相交两圆性质可知,PQ ⊥O 1O 2.∵P (4,1),Q (1,4),∴PQ =4-1 2+1-4 2=32,又O 1O 2=8,∴S 1=12PQ •O 1O 2=12×32×8=122;又S 2=12(O 2R +O 1M )•MR =12(n +m )(n -m )=202;∴s 1-s 2 2d =122-202 2×8=1,即抛物线在x 轴上截得的线段长为1.∵抛物线过点P (4,1),Q (1,4),∴16a +4b +c =1a +b +c =4 ,解得b =-5a +1 c =5+4a,∴抛物线解析式为:y =ax 2-(5a +1)x +5+4a ,令y =0,则有:ax 2-(5a +1)x +5+4a =0,设两根为x 1,x 2,则有:x 1+x 2=5a +1a ,x 1x 2=5+4a a,∵在x 轴上截得的线段长为1,即|x 1-x 2|=1,∴(x 1-x 2)2=1,∴(x 1+x 2)2-4x 1x 2=1,即(5a +1a )2-4(5+4a a )=1,化简得:8a 2-10a +1=0,解得a =5±178,可见a 的两个根均大于0,这与抛物线开口向下(即a <0)矛盾,∴不存在这样的抛物线.5(广益)如图1,已知一次函数y =-x +4与反比例函数y =3x相交于P ,Q 两点(P 在Q 的右侧).(1)求P ,Q 的坐标并写出△OPQ 的面积;(2)如图2,已知M (m ,m ),N (n ,n ),其中(0<m <n ),若分别以M ,N 为圆心的圆均与x 轴相切,切点分别为A ,B ,并且点P 既在⊙M 上又在⊙N 上.①求直线MN 的解析式;②求出线段MN 的长度d ;(3)在(2)的前提上,记四边形PMQN 的面积为S 1,四边形AMNB 的面积为S 2,已知抛物线y =ax 2+bx +c 满足两个条件:①经过点P 和点Q ,②该抛物线截x 轴得到的线段长度为s 1-s 2 d,请求出抛物线二次项系数a 的值.【解答】解:(1)由题意得:y =-x +4y =3x.解这个方程组得:x 1=1y 1=3 ,x 2=3y 2=1 .∵P 在Q的右侧,∴P (3,1),Q (1,3).设直线PQ 交x 轴于点C ,如图,则C (4,0).∴OC =4.过点Q 作QE ⊥OC 于E ,过点P 作PF ⊥OC 于F ,则QE =3,PF =1.∴S △OPQ =S △OQC -S △OPC =12×OC ×QE -12OC ×PF =6-2=4.(2)①∵M (m ,m ),N (n ,n ),∴直线MN 的解析式为:y =x .②∵以M ,N 为圆心的圆均与x 轴相切,切点分别为A ,B ,∴MA ⊥AB ,NB ⊥AB .过点P 作PE ⊥MA 于E ,PF ⊥NB 与,过点M 作MG ⊥NB 于G ,如图,则∠NMG =45°.∴MN =2MG .∵M (m ,m ),N (n ,n ),P (3,1),∴MA =m ,NB =n ,PE =3-m ,PM =3-m 2+m -1 2,ME =m -1,PF =n -3,NF =n -1.∵点P 既在⊙M 上又在⊙N 上,∴PM =MA ,PN =NB .∴PM 2=MA 2,PN 2=NB 2.∴(3-m )2+(m -1)2=m 2,(n -3)2+(n -1)2=n 2.整理得:m 2-8m +10=0,n 2-8n +10=0.∴m ,n (0<m <n )是方程x 2-8x +10=0的两个根.∴m +n =8,mn =10.∴(n -m )2=(m +n )2-4mn =24.∴n -m =26.∵MG =AB =n -m ,∴MG =26.∴MN =2MG =43,∴d =43.(3)抛物线y =ax 2+bx +c 满足经过点P 和点Q ,∴a +b +c =39a +3b +c =1.∴b =-1-4a c =3a +4 .∵S 1=12PQ ×MN =12×22×43=46,S 2=12MA +MB ⋅AB =12m +n ×n -m =12×8×26=86,∴s 1-s 2 d =4643=2.设抛物线y =ax 2+bx +c 与x 轴的交点为(x 1,0),(x 2,0),∴|x 1-x 2|=2.∴x 1-x 2 2=2.∴x 1+x 2 2-4x 1⋅x 2=2.∵x 1,x 2是方程ax 2+bx +c =0的两个根,∴x 1+x 2=-b a ,x 1⋅x 2=c a .∴-b a 2-4×c a =2.∴-1-4a a 2-4×3a +4a=2.整理得:2a 2-8a +1=0.解得:a =4±14.∴抛物线二次项系数a 的值为:4+14或4-14.6已知:如图,抛物线y =ax 2+bx +c (a ≠O )经过X 轴上的两点A (x 1,0)、B (x 2,0)和y 轴上的点C (0,-32),⊙P 的圆心P 在y 轴上,且经过B 、C 两点,若b =3a ,AB =23,(1)求抛物线的解析式;(2)设D 在抛物线上,且C ,D 两点关于抛物线的对称轴对称,问直线BD 是否经过圆心P ,并说明理由;(3)设直线BD 交⊙P 于另一点E ,求经过E 点的⊙P 的切线的解析式.【解答】解:(1)∵轴上的点C (0,-32),∴c =-32,又∵b =3a ,AB =23,令ax 2+3ax -32=0,|x 1-x 2|=23,解得:a =23,b =233;∴抛物线的解析式是:y =23x 2+233x -32.(4分)(2)D (-3,-32),直线B D 为:y =33x -12,连接BP ,设⊙P 的半径为R ,R 2=32 2+32-R 2,R =1,P (0,-12),点P 的坐标满足直线BD 的解析式y =33x -12.∴直线B D 经过圆心P .(3)过点E 作EF ⊥y 轴于F ,得△OPB ≌△FPE ,E (-32,-1),设经过E 点⊙P 的切线L 交y 轴于点Q .则∠P EQ =90°,EF ⊥PQ ,∴P E 2=P F •PQ ,∴PQ =2,Q (0,-2.5),∴切线L 为:y =-3x -2.5.7(青竹湖)定义:如果一条直线与一条曲线有且只有一个交点,且曲线位于直线的同旁,称之为直线与曲线相切,这条直线叫做曲线的切线,直线与曲线的唯一交点叫做切点.(1)如图,在平面直角坐标系中,点O 为坐标原点,以点A (0,-3)为圆心,5为半径作圆A ,交x 轴的负半轴于点B ,求过点B 的圆A 的切线的解析式;(2)若抛物线y =ax 2(a ≠0)与直线y =kx +b (k ≠0)相切于点(2,2),求直线的解析式;(3)若函数y =14x 2+(n -k -1)x +m +k -2的图象与直线y =-x 相切,且当-1≤n ≤2时,m 的最小值为k ,求k 的值.【解答】解:(1)如图1,连接AB ,记过点B 的⊙A 切线交y 轴于点E ,∴AB =5,∠ABE =90°,∵A (0,-3),∠AOB =90°,∴OA =3,∴OB =AB 2-OA 2=52-32=4,∴B (-4,0),∵∠OAB =∠BAE ,∠AOB =∠ABE =90°,∴△OAB ∽△BAE ,∴AB AE =OA BA ,∴AE =AB ⋅BA OA =253,∴OE =AE -OA =253-3=163,∴E (0,163),设直线BE 解析式为:y =kx +163,∴-4k +163=0,解得:k =43,∴过点B 的⊙A 的切线的解析式为y =43x +163,方法二:设直线BE 的解析式为y =k (x +4),∴E (0,4k ),∴AB =5,AE =4k +3,BE =42+4k 2,由勾股定理可得,AB 2+BE 2=AE 2,∴25+16+16k 2=16k 2+9+24k ,∴k =43,∴过点B 的⊙A 的切线的解析式为y =43x +163;(2)∵抛物线y =ax 2经过点(2,2),∴4a =2,解得:a =12,∴抛物线解析式:y =12x 2,∵直线y =kx +b 经过点(2,2),∴2k +b =2,可得:b =2-2k ,∴直线解析式为:y =kx +2-2k ,∵直线与抛物线相切,∴关于x 的方程12x 2=kx +2-2k 有两个相等的实数根,方程整理得:x 2-2kx +4k -4=0,∴△=(-2k )2-4(4k -4)=0,解得:k 1=k 2=2,∴直线解析式为y =2x -2,(3)∵函数y =14x 2+(n -k -1)x +m +k -2的图象与直线y =-x 相切,∴关于x 的方程14x 2+(n -k -1)x +m +k -2=-x 有两个相等的实数根,方程整理得:14x 2+(n -k )x +m +k -2=0,∴△=(n -k )2-4×14(m +k -2)=0,整理得:m =(n -k )2-k +2,可看作m 关于n 的二次函数,对应抛物线开口向上,对称轴为直线x =k ,∵当-1≤n ≤2时,m 的最小值为k ,①如图2,当k <-1时,在-1≤n ≤2时m 随n 的增大而增大,∴n =-1时,m 取得最小值k ,∴(-1-k )2-k +2=k ,方程无解,②如图3,当-1≤k ≤2时,n =k 时,m 取得最小值k ,∴-k +2=k ,解得:k =1,③如图4,当k >2时,在-1≤n ≤2时m 随n 的增大而减小,∴n =2时,m 取得最小值k ,∴(2-k )2-k +2=k ,解得:k 1=3+3,k 2=3-3(舍去),综上所述,k 的值为1或3+3.8(麓山国际)如图,经过定点A 的直线y =k (x -2)+1(k <0)交抛物线y =-x 2+4x 于B ,C 两点(点C 在点B 的右侧),D 为抛物线的顶点.(1)直接写出点A 的坐标;(2)如图(1),若△ACD 的面积是△ABD 面积的两倍,求k 的值;(3)如图(2),以AC 为直径作⊙E ,若⊙E 与直线y =t 所截的弦长恒为定值,求t 的值.【解答】解:(1)∵A 为直线y =k (x -2)+1上的定点,∴A 的坐标与k 无关,∴x -2=0,∴x =2,此时y =1,∴点A 的坐标为(2,1);(2)∵y =-x 2+4x =-(x -2)2+4,∴顶点D 的坐标为(2,4),∵点A 的坐标为(2,1),∴AD ⊥x 轴.如图(1),分别过点B ,C 作直线AD 的垂线,垂足分别为M ,N ,设B ,C 的横坐标分别为x 1,x 2,∵△ACD 的面积是△ABD 面积的两倍,∴CN =2BM ,∴x 2-2=2(2-x 1),∴2x 1+x 2=6.联立y =x 2+4x y =kx -2k +1 ,得x 2+(k -4)x -2k +1=0,①解得x 1=4-k -k 2+122,x 2=4-k +k 2+122,∴2×4-k -k 2+122+4-k +k 2+122=6,化简得:k 2+12=-3k ,解得k =-62.另解:接上解,由①得x 1+x 2=4-k ,又由2x 1+x 2=6,得x 1=2+k .∴(2+k )2+(k -4)(2+k )-2k +1=0,解得k =±62.∵k <0,∴k =-62;(3)如图(2),设⊙E 与直线y =t 交于点G ,H ,点C 的坐标为(a ,-a 2+4a ).∵E 是AC 的中点,∴将线段AE 沿AC 方向平移与EC 重合,∴x E -x A =x C -x E ,y E -y A =y C -y E ,∴x E =12(x A +x C ),y E =12(y A +y C ).∴E (1+a 2,-a 2+4a +12).分别过点E ,A 作x 轴,y 轴的平行线交于点F ,在Rt △AEF 中,由勾股定理得:EA 2=1+a 2-2 2+-a 2+4a +12-1 2=a 2-1 2+-a 2+4a +12-1 2,过点E作PE⊥GH,垂足为P,连接EH,∴GH=2PH,EP2=-a2+4a+12-t 2,又∵AE=EH,∴GH2=4PH2=4(EH2-EP2)=4(EA2-EP2)=4[a2-12+-a2+4a+12-12--a2+4a+12-t2]=4[a24-a+1+-a2+4a+12-12-(-a2+4a+1)+1--a2+4a+122+t(-a2+4a+1)-t2]=4[(54-t)a2+(4t-5)a+1+t-t2].∵GH的长为定值,∴5 4-t=0,且4t-5=0,∴t=54.9(长郡)如图,在平面直角坐标系中,点M的坐标是(5,4),⊙M与y轴相切于点C,与x轴相交于A、B两点.(1)分别求A、B、C三点的坐标;(2)如图1,设经过A、B两点的抛物线解析式为y=14x-52+k,它的顶点为E,求证:直线EA与⊙M相切;(3)如图2,过点M作直线FG∥y轴,与圆分别交于F、G两点,点P为弧FB上任意一点(不与B、F重合),连接FP、AP,FN⊥BP的延长线于点N.请问AP-BPPN是否为定值,若为定值,请求出这个值,若不为定值,请说明理由.【解答】解:(1)如图1,连接CM、AM,连接ME交x轴于点D,则ME⊥x轴,∵⊙M与y轴相切于点C,点M的坐标是(5,4),∴CM⊥y轴,即C(0,4),⊙M的半径为5,∴AM=5,DM=4,∴AD=DB=AM2-DM2=52-42=3,∴OA=5-3=2,∴A(2,0),B(8,0);(2)证明:将A(2,0)代入y=14x-52+k中,可得k=-94,∴E(5,-94),∴DE=94,∴ME=DE+MD=94+4=254,则AE2=32+942=22516,MA2+AE2=52+22516=62516,ME2=254 2=62516,∴MA2+AE2=ME2,∴MA⊥AE,又∵MA为半径,∴直线EA与⊙M相切;(3)AP-BPPN为定值,理由如下:连接AF、BF,作FQ⊥AP于点Q,∵∠FPN为圆内接四边形ABPF的外角,∴∠FPN=∠FAB,又∵MF⊥AB,∴AF=BF,∴∠FAB=∠FBA=∠FPA,∴∠FPN=∠FPA,∵FQ⊥AP,FN⊥PN,∴FQ=FN,又∵FP=FP,∴Rt△FPQ≌Rt△FPN(HL),∴PQ=PN,又∵AF=BF,FQ=FN,∴Rt△AFQ≌Rt△BFN(HL),∴AQ=BN,∴AP-BPPN =AQ+PQ-BPPN=BP+PN+PQ-BPPN=2PNPN=2.10(长郡)如图1,抛物线y=14x2-2x与x轴交于O、A两点,点B为抛物线的顶点,连接OB.(1)求∠AOB的度数;(2)如图2,以点A为圆心,4为半径作⊙A,点M在⊙A上.连接OM、BM,①当△OBM是以OB为底的等腰三角形时,求点M的坐标;②如图3,取OM的中点N,连接BN,当点M在⊙A上运动时,求线段BN长度的取值范围.【解答】解:(1)令y=0,则14x2-2x=0,解得:x=0或8.∴A(8,0).∴OA=8.∵y=14x2-2x=14x-42-4,∴B(4,-4).过点B作BD⊥OA于点D,如图,则OD =4,BD =4,∴OD =BD ,∴∠AOB =∠OBD =45°;(2)①设⊙A 与x 轴交于点C ,则C (4,0).连接BC ,如图,∵B (4,-4),∴BC ⊥OA .∵CO =CB =4,∴△CBO 是以OB 为底的等腰三角形.∴点M 与点C 重合时,△MBO 是以OB 为底的等腰三角形.此时点M (4,0);过点A 作AM ⊥x 轴,交⊙A 于点M ,延长MA 交⊙A 于点E ,连接BE ,过点M 作MF ⊥y 轴于点F ,如图,则M (8,4),E (8,-4),F (0,4).∴MF =ME =8.∵B (4,-4),∴BE ∥x 轴.∴BE ⊥ME ,BE =4.∴∠BEM =∠MFO =90°,BE =OF =4.在△MOF 和△MBE 中,MF =ME∠MFO =∠BEM =90°OF =BE,∴△MOF ≌△MBE (SAS ).∴MO =MB .∴△MBO 是以OB 为底的等腰三角形.此时点M (8,4);综上,当△OBM 是以OB 为底的等腰三角形时,点M 的坐标为(4,0)或(8,4);②设⊙A 与x 轴交于点C ,则C (4,0).连接BC ,CN ,AM ,如图,AM=2.∵A(8,0),∴点C是OA的中点.∵N为OM的中点,∴CN是△OMA的中位线.∴CN=12当点M在⊙A上运动时,由三角形的三边的关系定理可知:BC-CN≤BN≤BC+CN.∵BC=4,∴4-2≤BN≤4+2.∴线段BN长度的取值范围为:2≤BN≤6.。
中考数学圆-经典压轴题(含答案)

初三中考数学与圆有关的压轴题1.如图,△ABC内接于⊙O,AB为⊙O的直径,D为的中点,过D作DF⊥AB于点E,交⊙O于点F,交弦BC于点G,连接CD,BF.(1)求证:△BFG≌△DCG;(2)若AC=10,BE=8,求BF的长;(3)在(2)的条件下,P为⊙O上一点,连接BP,CP,弦CP交直径AB于点H,若△BPH与△CPB相似,求CP的长.2.如图,AB为⊙O的直径,D是的中点,BC与AD,OD分别交于点E,F.(1)求证:OD∥AC;(2)求证:DC2=DE•DA;(3)若⊙O的直径AB=10,AC=6,求BF的长.3.如图1,以△ABC的边AB为直径作⊙O,交AC于点E,BD平分∠ABE交AC于F,交⊙O于点D,且∠BDE=∠CBE.(1)求证:BC是⊙O的切线;(2)如图2,延长ED交直线AB于点P,若P A=AO,DE=2,求的值及AO的长.4.如图,已知直角△ABC中,∠ABC=90°,BC为⊙O的直径,D为⊙O与斜边AC的交点,作∠ECB使得CA平分∠ECB,且CE⊥DE;DE与AB交与点F.(1)猜想并证明直线DE与⊙O的位置关系;(2)若DE=3,CE=4,求⊙O的半径;(3)记△BCD的面积为S1,△CDE的面积为S2,若S1:S2=3:2.求sin∠AFD的值.5.如图,AB是⊙O的直径,点C是⊙O上一点,过点C作⊙O的切线与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.(1)利用尺规作图,过点A作AD⊥CP于点D(保留作图痕迹,不写作法);(2)求证:△PCF是等腰三角形;(3)若tan∠ABC=,BE=7,求线段PC的长.6.如图,四边形ABCD内接于⊙O,对角线AC是⊙O的直径,过点C作AC的垂线交AD 的延长线于点E,F为CE的中点,连接BD,DF,BD与AC交于点P.(1)求证:DF是⊙O的切线;(2)若AC=2DE,求tan∠ABD的值;(3)若∠DPC=45°,PD2+PB2=8,求AC的长.7.如图,四边形ABCD内接于⊙O,AB=AC,∠BAD=90°,延长AD、BC交于点F.点E在BF上,且DE=EF.(1)求证:DE是⊙O的切线;(2)已知CE=3,EF=5,求AB的长;(3)在(2)的条件下,求图中阴影部分的面积.8.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,连接AD,过点D作DM⊥AC,垂足为M,AB、MD的延长线交于点N.(1)求证:MN是⊙O的切线;(2)求证:DN2=BN•(BN+AC);(3)若BC=6,cos C=,求DN的长.1【解答】解:(1)∵D是的中点,则,∵AB为⊙O的直径,DF⊥AB,∴,∴,∴BF=CD,又∵∠BFG=∠DCG,∠BGF=∠DGC,∴△BFG≌△DCG(AAS);(2)如图1,连接OD交BC于点M,∵D为的中点,∴OD⊥BC,∴BM=CM,∵OA=OB,∴OM是△ABC的中位线,∴OM=AC=5,∵,∴,∴OE=OM=5,∴OD=OB=OE+BE=5+8=13,∴EF=DE==12,∴BF===4;(3)如图2,∵弦CP交AB于点H,则点P与点C在直径的两侧,则∠CBP>∠HBP,∵△BPH与△CPB相似,∴∠ABP=∠PCB,又∵∠CPB=∠BPH,∴∠ACP=∠BCP,∵AB是直径,则∠ACB=∠APB=90°,∴∠ACP=∠BCP=45°,过点B作BN⊥PC于点N,由(2)得AB=26,在Rt△CBN中,CN=BN=BC=12,∵∠CAB=∠CPB,∴tan∠CAB=tan∠CPB=,即,故PN=5,∴PC=CN+PN=5+12=17.2【解答】解:(1)因为点D是弧BC的中点,所以∠CAD=∠BAD,即∠CAB=2∠BAD,而∠BOD=2∠BAD,所以∠CAB=∠BOD,所以DO∥AC;(2)∵D是的中点,∴∠CAD=∠DCB,∴△DCE∽△DAC,∴CD2=DE•DA;(3)∵AB为⊙O的直径∴∠ACB=90°,在Rt△ACB中,BC=.=8,∵OD∥AC,∴△BOF∽△BAC,∴,即=,∴BF=4.即BF的长为4.3【解答】(1)证明:如图1中,连接BE.∵AB是直径,∴∠AEB=90°,∴∠A+∠ABE=90°,∵∠A=∠D=∠EBC,∴∠ABE+∠EBC=90°,∴∠ABC=90°,∴AB⊥BC,∴BC是⊙O的切线;(2)如图2中,连接OD、BE.∵BD平分∠ABE,∴D是的中点,∴OD⊥AE,∵AE⊥BE,∴BE∥OD,∵P A=OA=OB,∴OP=2OB,∴==2,∴PD=2DE=4,∵△PDB∽∠P AE,∴=,∴PD•PE=P A•PB,∴.4【解答】解:(1)直线DE与⊙O相切,证明如下:连接OD,∵CA平分∠ECB,∴∠ECD=∠OCD,∵OD=OC,∴∠OCD=∠ODC,∴∠ODC=∠ECD,∴OD∥CE,∴OD⊥DE,∵D为⊙O与斜边AC的交点,∴直线DE与⊙O相切;(2)如图2,连接BD,OD,在Rt△CED中,DE=3,CE=4,∴DC==5,∵BD为直径,∴∠BDC=90°,∵CE⊥DE,∴∠E=90°∴∠BDC=∠E=90°,∵由(1)知∠ECD=∠DCB,∴△BDC∽△DEC,∴,即,∴BC=,即⊙O的半径为;(3)在四边形BODF中,∠FBO=∠FDO=90°,∴∠BFD+∠BOD=180°=∠BFD+∠AFD,∴∠BOD=∠AFD,∴sin∠BOD=sin∠AFD,∵△BDC∽△DEC,∴=,,∴,设BC=2,CD=2,∴BD===2,过点D作DG⊥BC于G,如图3,∵S△EDC=BC•DG=BD•CD,∴2×DG=2×2.∴DG=,在Rt△ODG中,sin∠GOD=,∴sin∠AFD=.5【解答】(1)解:如图,(2)证明:∵AD⊥PD,∴∠DAC+∠ACD=90°.又∵AB为⊙O的直径,∴∠ACB=90°.∴∠PCB+∠ACD=90°,∴∠DAC=∠PCB.又∵PD切⊙O于点C,∴OC⊥PD,∴OC∥AD,∴∠ACO=∠DAC.∵OC=OA,∴∠ACO=∠CAO,∴∠DAC=∠CAO,∴∠CAO=∠PCB.∵CE平分∠ACB,∴∠ACF=∠BCF,∴∠CAO+∠ACF=∠PCB+∠BCF,∴∠PFC=∠PCF,∴PC=PF,即△PCF是等腰三角形;(3)解:连接AE,∵CE平分∠ACB,∴=,∴AE=BE,∵AB是⊙O的直径,∴∠AEB=90°,∴△ABE是等腰直角三角形,∵BE=7,∴AB=BE=14,∵∠P AC=∠PCB,∠CPB=∠APC,∴△P AC∽△PCB,∴.又∵tan∠ABC=,∴,∴,设PC=4k,PB=3k,则在Rt△POC中,PO=3k+7,OC=7,∵PC2+OC2=OP2,∴(4k)2+72=(3k+7)2,∴k=6 (k=0不合题意,舍去).∴PC=4k=4×6=24.6、【解答】证明:(1)证明:如图,连接OD,∵AC是⊙O的直径,∴∠ADC=90°,∴∠EDC=90°,∵F是EC的中点,∴DF=FC,∴∠FDC=∠FCD,∵OD=OC,∴∠ODC=∠OCD,∵AC⊥CE,∴∠OCF=90°,∴∠ODF=∠ODC+∠FDC=∠OCD+∠FCD=∠OCF=90°,即DF⊥OD,∴DF是⊙O的切线;(2)∵∠CAE+∠E=90°,∠CAE+∠ACD=90°,∴∠E=∠ACD,又∠ACE=∠ADC=90°,∴△ACE∽△ADC,∴,即AC2=AD•AE.设DE=x,则AC=x,即(x)2=AD(AD+x).整理,得AD2+AD•x﹣20x2=0.解得AD=4x或AD=﹣5x(舍去).∴DC==2x.∴tan∠ABD=tan∠ACD===2;(3)如图,过点O作OG⊥BD于点G,由垂径定理,得BG=DG,设BG=DG=m,则PD=m+PG,PB=m﹣PG,∵PD2+PB2=8,∴(m+PG)2+(m﹣PG)2=8,整理,得2m2+2PG2=8,即m2+PG2=4.∵∠DPC=45°,∴OG=PG.∴OD2=DG2+OG2=m2+PG2=4,∴⊙O的半径为2.∴AC=4.7、【解答】证明:(1)连接BD,∵∠BAD=90°,∴BD是直径,∠ABF+∠F=90°,∵AB=AC,∴∠ABC=∠ACB,∵∠ACB=∠ADB,∴∠ADB=∠ABC,∴∠ADB+∠F=90°,∵DE=EF,∴∠F=∠EDF,∴∠ADB+∠EDF=90°,∴∠BDE=90°,∴DE⊥BD,又∵BD是直径,∴DE是⊙O的切线;(2)∵BD是直径,∴∠BCD=90°=∠DCE,∵CE=3,DE=EF=5,∴CD===4,∴DF===4,∵∠F+∠ADB=90°,∠ADB+∠ABD=90°,∴∠F=∠ABD,又∵∠BAD=∠DCF=90°,∴△DCF∽△DAB,∴,∴AB=2AD,∵∠ABD=∠F,∠BAD=∠BAD,∴△ABD∽△AFB,∴,∴==,∴AB=;(3)∵AB=,AB=2AD,∴AD=,∴BD===,∴BO=∵S阴影=×π×()2﹣×AB×AD=π﹣××,∴S阴影=π﹣.8、【解答】证明:(1)如图,连接OD,∵AB是直径,∴∠ADB=90°,又∵AB=AC,∴BD=CD,∠BAD=∠CAD,∵AO=BO,BD=CD,∴OD∥AC,∵DM⊥AC,∴OD⊥MN,又∵OD是半径,∴MN是⊙O的切线;(2)∵AB=AC,∴∠ABC=∠ACB,∵∠ABC+∠BAD=90°,∠ACB+∠CDM=90°,∴∠BAD=∠CDM,∵∠BDN=∠CDM,∴∠BAD=∠BDN,又∵∠N=∠N,∴△BDN∽△DAN,∴,∴DN2=BN•AN=BN•(BN+AB)=BN•(BN+AC);(3)∵BC=6,BD=CD,∴BD=CD=3,∵cos C==,∴AC=5,∴AB=5,∴AD===4,∵△BDN∽△DAN,∴==,∴BN=DN,DN=AN,∴BN=(AN)=AN,∵BN+AB=AN,∴AN+5=AN∴AN=,∴DN=AN=.。
中考数学 抛物线-压轴题
数学中考题精选----------抛物线1、在平面直角坐标系中,已知抛物线经过A (-4,0),B (0,-4),C (1)求抛物线的解析式;(2)若点M 为第三象限内抛物线上一动点,点M 的横坐标为m ,△AMB 的面积为S .求S 关于m 的函数关系式,并求出S 的最大值. (3)若点P 是抛物线上的动点,点Q 是直线y =-x 上的动点,判断有几个位置能够使得点P 、Q 、B 、O 直接写出相应的点Q 的坐标.2、已知抛物线y =-x 2+bx +c 经过点A (0,4),且抛物线的对称轴为直 线x =2. (1)求该抛物线的解析式; (2)若该抛物线的顶点为B ,在抛物线上是否存在点C ,使得A 、B 、O 、C 点构成的四边形为梯形?若存在,请求出点C (3)试问在抛物线上是否存在着点P ,使得以3为半径的⊙P 既与x 又与对称轴相交?若存在,请求出点P 的坐标,并求出对称轴被⊙P 的弦EF 的长度;若不存在,请说明理由.3、如图,已知抛物线y =ax 2+bx +c (a ≠0)的顶点坐标为Q (2,-1),且与y 轴交于点C (0,3),与x 轴交于A 、B 两点(点A 在点B 的右侧),点P 是该抛物线上一动点,从点C 沿抛物线向点A 运动(点P 与A 不重合),过点P 作PD ∥y 轴,交AC 于点D . (1)求该抛物线的函数关系式;(2)当△ADP 是直角三角形时,求点P 的坐标; (3)在题(2)的结论下,若点E 在x 轴上,点F 在抛物线上,问是否存在以A 、P 、E 、F 为顶点的平行四边形?若存在,求点F 的坐标;若不存在,请说明理由..4、如图,平面直角坐标系中,点A 、B 、C 在x 轴上,点D 、E 在y 轴上,OA =OD =2,OC =OE =4,DB ⊥DC ,直线AD 与经过B 、E 、C 三点的抛物线交于F 、G 两点,与其对称轴交于M .点,P 为线段FG 上一个动点(与F 、G 不重合),PQ ∥y 轴与抛物线交于点Q .(1)求经过B 、E 、C 三点的抛物线的解析式;(2)是否存在点P ,使得以P 、Q 、M 为顶点的三角形与△AOD 相似?若存在,求出满足条件的点P 的坐标;若不存在,请说明理由; (3)若抛物线的顶点为N ,连接QN ,探究四边形PMNQ 的形状:①能否成为菱形;②能否成为等腰梯形?若能,请直接写出点P 的坐标;若不能,请说明理由.5、如图,把抛物线y=-x2(虚线部分)向右平移1个单位长度,再向上平移1个单位长度,得到抛物线l1,抛物线l2与抛物线l1关于y轴对称.点A、O、B分别是抛物线l1、l2与x轴的交点,D、C分别是抛物线l1、l2的顶点,线段CD交y轴于点E.(1)分别写出抛物线l1与l2的解析式;(2)设P是抛物线l1上与D、O两点不重合的任意一点,Q点是P 点关于y轴的对称点,试判断以P、Q、C、D为顶点的四边形是什么特殊的四边形?说明你的理由.(3)在抛物线l1上是否存在点M,使得S△ABM =S四边形AOED ,如果存在,求出M点的坐标;如果不存在,请说明理由.6、已知二次函数y=ax2+bx+c的图象经过点A(3,0),B(2,-3),C(0,-3).(1)求此函数的解析式及图象的对称轴;(2)点P从B点出发以每秒0.1个单位的速度沿线段BC向C点运动,点Q从O点出发以相同的速度沿线段OA向A点运动,其中一个动点到达端点时,另一个也随之停止运动.设运动时间为t秒.①当t为何值时,四边形ABPQ为等腰梯形;②设PQ与对称轴的交点为M,过M点作x轴的平行线交AB于点N,设四边形ANPQ的面积为S,求面积S关于时间t的函数解析式,并指出t的取值范围;当t为何值时,S有最大值或最小值.说明理由.7、如图,二次函数y=-x2+ax+b的图象与x轴交于A(-21,0),B(2,0)两点,且与y轴交于点C.(1)求该抛物线的解析式,并判断△ABC的形状;(2)在x轴上方的抛物线上有一点D,且以A、C、D、B四点为顶点的四边形是等腰梯形,请直接写出D点的坐标;(3)在此抛物线上是否存在点P,使得以A、C、B、P四点为顶点的四边形是直角梯形?若存在,求出P点的坐标;若不存在,说明理由.8、如图,Rt△ABC的顶点坐标分别为A(0,3),B(-21,23),C(1,0),∠ABC=90°,BC与y轴的交点为D,D点坐标为(0,33),以点D为顶点、y轴为对称轴的抛物线过点B.(1)求该抛物线的解析式;(2)将△ABC沿AC折叠后得到点B的对应点B′,求证:四边形AOCB′是矩形,并判断点B′是否在(1)的抛物线上;(3)延长BA交抛物线于点E,在线段BE上取一点P,过P点作x轴的垂线,交抛物线于点F,是否存在这样的点P,使四边形PADF是平行四边形?若存在,求出点P的坐标,若不存在,说明理由.9、如图,矩形OABC 的两边OA 、OC 分别在x 轴和y 轴上,A (-3,0),过点C 的直线y =-2x +4与x 轴交于点D ,二次函数y =-21x 2+bx +c 的图象经过B 、C 两点. (1)求B 、C 两点的坐标;(2)求二次函数的解析式;(3)若点P 是CD 的中点,求证:AP ⊥CD ;(4)在二次函数的图象上是否存在这样的点M ,使以A 、P 、C 、M 为顶点的四边形为矩形?若存在,求出点M 的坐标;若不存在,请说明理由.10、如图,在平面直角坐标系中,以点A (-3,0)为圆心、5为半径的圆与x 轴相交于点B 、C 两点(点B 在点C 的左边),与y 轴相交于D 、M 两点(点D 在点M 的下方).(1)求以直线x =-3为对称轴、且经过D 、C 两点的抛物线的解析式;(2)若点P 是这条抛物线对称轴上的一个动点,求PC +PD 的取值范围;(3)若点E 为这条抛物线对称轴上的点,则在抛物线上是否存在这样的点F ,使得以点B 、C 、E 、F 为顶点的四边形是平行四边形?若存在,求出点F11、如图,已知抛物线y =ax 2-2ax -b (a >0)与x 轴的一个交点为B (-1,0),与y 轴的负半轴交于点C ,顶点为D .(1)直接写出抛物线的对称轴及抛物线与x 轴的另一个交点A 的坐标; (2)以AD 为直径的圆经过点C .①求抛物线的解析式;②点E 在抛物线的对称轴上,点F 在抛物线上,且以B ,A ,F ,E四点为顶点的四边形为平行四边形,求点F 的坐标.12、如图,已知抛物线与x 轴交于点A (-1,0)和点B (1,0),与y 轴交于点C (0,-2),直线x =m (m >1)与x 轴交于点D .(1)求该抛物线的解析式;(2)在直线x =m (m >1)上有一点P (点P 在第一象限),使得以P 、D 、B 为顶点的三角形与以B 、C 、O 为顶点的三角形相似,求点P 的坐标(用含m 的代数式表示);(3)在(2)成立的条件下,在抛物线上是否存在点Q ,使得四边形ABPQ 为平行四边形?若存在,请求出点Q 的坐标;若不存在,请说明理由.13、已知抛物线: x x y 22121+-= (1)求抛物线y 1的顶点坐标;(2)将抛物线y 1向右平移2个单位,再向上平移1个单位,得到抛物线y 2,求抛物线y 2的解析式;(3)如下图,抛物线y 2的顶点为P ,x 轴上有一动点M ,在y 1、y 2这两条抛物线上是否存在点N ,使O (原点)、P 、M 、N 四点构成以OP 为一边的平行四边形?若存在,求出N 点的坐标;若不存在,请说明理由.14如图,在水平地面点A 处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B .有人在直线AB 上点C (靠点B 一侧)竖直向上摆放无盖的圆柱形桶,试图让网球落入桶内.已知AB =4米,AC =3米,网球飞行最大高度OM =5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).(1)如果竖直摆放5个圆柱形桶时,网球能不能落入桶内? (2)当竖直摆放圆柱形桶多少个时,网球可以落入桶内?15、已知抛物线y =x 2+bx +c 交y 轴于点A ,点A 关于抛物线对称轴的对称点为B (3,-4),直线y =41x 与抛物线在第一象限的交点为C ,连结OB .(1)求抛物线的解析式;(2)如图(1),点P 在射线..OC ..上运动,连结BP ,设点P 的横坐标为x ,△OBP 的面积为y ,求y 与x 之间的函数关系式; (3)如图(2),点P 在直线..OC ..上运动,点Q 在抛物线上运动,试问点P 、Q 在运动过程中是否存在以O 、B 、P 、Q 为顶点的四边形是平行四边形的情况,若存在,请求出点P 的坐标;若不存在,请说明理由.图(1) 图(2) 备用图。
中考数学压轴题20题(含答案_)

中考数学压轴题复习20题1.在平面直角坐标系xO y 中,抛物线y =-41 m x2+45mx +m2-3m +2与x 轴的交点分别为原点O 和点A ,点B (2,n )在这条抛物线上.(1)求点B 的坐标;(2)点P 在线段OA 上,从O 点出发向A 点运动,过P 点作x 轴的垂线,与直线OB 交于点E ,延长PE 到点D ,使得ED =PE ,以PD 为斜边,在PD 右侧作等腰直角三角形PCD (当P 点运动时,C 点、D 点也随之运动).①当等腰直角三角形PCD 的顶点C 落在此抛物线上时,求OP 的长;②若P 点从O 点出发向A 点作匀速运动,速度为每秒1个单位,同时线段OA 上另一个点Q 从A 点出发向O 点作匀速运动,速度为每秒2个单位(当Q 点到达O 点时停止运动,P 点也同时停止运动).过Q 点作x 轴的垂线,与直线AB 交于点F ,延长QF 到点M ,使得FM =QF ,以QM 为斜边,在QM 的左侧作等腰直角三角形QMN (当Q 点运动时,M 点、N 点也随之运动).若P 点运动到t 秒时,两个等腰直角三角形分别有一条边恰好落在同一条直线上,求此刻t 的值.2.在平面直角坐标系中,矩形OACB 的顶点O 在坐标原点,顶点A 、B 分别在x 轴、y 轴的正半轴上,OA =3,OB =4,D 为边OB 的中点.(Ⅰ)若E 为边OA 上的一个动点,当△CDE 的周长最小时,求点E 的坐标;(Ⅱ)若E 、F 为边OA 上的两个动点,且EF =2,当四边形CDEF 的周长最小时,求点E 、F 的坐标.3.在平面直角坐标系中,已知抛物线y =-x2+bx +c 与x 轴交于点A 、B (点A 在点B 的左侧),与y 轴的正半轴交于点C ,顶点为E .(Ⅰ)若b =2,c =3,求此时抛物线顶点E 的坐标;(Ⅱ)将(Ⅰ)中的抛物线向下平移,若平移后,在四边形ABEC 中满足S △BCE=S △ABC,求此时直线BC的解析式;(Ⅲ)将(Ⅰ)中的抛物线作适当的平移,若平移后,在四边形ABEC 中满足S △BCE=2S △AOC,且顶点E 恰好落在直线y =-4x +3上,求此时抛物线的解析式.4.如图1,在Rt △ABC 中,∠ACB =90°,半径为1的圆A 与边AB 相交于点D ,与边AC 相交于点E ,连结DE 并延长,与线段BC 的延长线交于点P . (1)当∠B =30°时,连结AP ,若△AEP 与△BDP 相似,求CE 的长; (2)若CE =2,BD =BC ,求∠BPD 的正切值;(3)若tan ∠BPD =31,设CE =x ,△ABC 的周长为y ,求y 关于x 的函数关系式.5.已知:如图①,在平面直角坐标系xO y 中,边长为2的等边△OAB 的顶点B 在第一象限,顶点A 在x 轴的正半轴上.另一等腰△OCA 的顶点C 在第四象限,OC =AC ,∠C =120°.现有两动点P ,Q 分别从A ,O 两点同时出发,点Q 以每秒1个单位的速度沿OC 向点C 运动,点P 以每秒3个单位的速度沿A →O →B 运动,当其中一个点到达终点时,另一个点也随即停止. (1)求在运动过程中形成的△OPQ 的面积S 与运动的时间t 之间的函数关系,并写出自变量t 的取值范围; (2)在等边△OAB 的边上(点A 除外)存在点D ,使得△OCD 为等腰三角形,请直接写出所有符合条件的点D 的坐标;(3)如图②,现有∠MCN =60°,其两边分别与OB ,AB 交于点M ,N ,连接MN .将∠MCN 绕着C 点旋转(0°<旋转角<60°),使得M ,N 始终在边OB 和边AB 上.试判断在这一过程中,△BMN 的周长是否发生变化?若没变化,请求出其周长;若发生变化,请说明理由.6.已知抛物线y =ax2+bx +c (a >0)的图象经过点B (12,0)和C (0,-6),对称轴为x =2. (1)求该抛物线的解析式:(2)点D 在线段AB 上且AD =AC ,若动点P 从A 出发沿线段AB 以每秒1个单位长度的速度匀速运动,同时另一动点Q 以某一速度从C 出发沿线段CB 匀速运动,问是否存在某一时刻,使线段PQ 被直线CD 垂直平分?若存在,请求出此时的时间t (秒)和点Q 的运动速度;若不存在,请说明理由;AE C B P D 图2(备用) B PE C D A 图3(备用) A B C P E D 图1图②图①(3)在(2)的结论下,直线x =1上是否存在点M ,使△MPQ 为等腰三角形?若存在,请求出所有点M 的坐标;若不存在,请说明理由.7.如图,抛物线y =ax2+bx +1与x 轴交于两点A (-1,0),B (1,0),与y 轴交于点C . (1)求抛物线的解析式;(2)过点B 作BD ∥CA 与抛物线交于点D ,求四边形ACBD 的面积;(3)在x 轴下方的抛物线上是否存在点M ,过M 作MN ⊥x 轴于点N ,使以A 、M 、N 为顶点的三角形与△BCD 相似?若存在,则求出点M 的坐标;若不存在,请说明理由.8.如图,已知抛物线y =21x2+bx +c 与y 轴相交于C ,与x 轴相交于A 、B ,点A 的坐标为(2,0),点C 的坐标为(0,-1).(1)求抛物线的解析式;(2)点E 是线段AC 上一动点,过点E 作DE ⊥x 轴于点D ,连结DC ,当△DCE 的面积最大时,求点D 的坐标;(3)在直线BC 上是否存在一点P ,使△ACP 为等腰三角形,若存在,求点P 的坐标,若不存在,说明理由.9.如图,已知△ABC ∽△A 1B 1C 1,相似比为k (k >1),且△ABC 的三边长分别为a 、b 、c (a >b >c ),△A 1B 1C 1的三边长分别为a 1、b 1、c 1. (1)若c =a 1,求证:a =kc ;(2)若c =a 1,试给出符合条件的一对△ABC 和△A 1B 1C 1,使得a 、b 、c 和a 1、b 1、c 1都是正整数,并加以说明;(3)若b =a 1,c =b 1,是否存在△ABC 和△A 1B 1C 1,使得k =2?请说明理由.10.如图,Rt △ABC 内接于⊙O ,AC =BC ,∠BAC 的平分线AD 与⊙O 交于点D ,与BC 交于点E ,延长BD ,与AC 的延长线交于点F ,连结CD ,G 是CD 的中点,连结OG . (1)判断OG 与CD 的位置关系,写出你的结论并证明; (2)求证:AE =BF ; (3)若OG ·DE =3(2-2),求⊙O 的面积.11.已知:抛物线y =ax2+bx +c (a ≠0)的对称轴为x =-1,与x 轴交于A 、B 两点,与y 轴交于点C ,其中A (-3,0)、C (0,-2). (1)求这条抛物线的函数表达式.(2)已知在对称轴上存在一点P ,使得△PBC 的周长最小.请求出点P 的坐标.(3)若点D 是线段OC 上的一个动点(不与点O 、点C 重合).过点D 作DE ∥PC 交x 轴于点E ,连接PD 、PE .设CD 的长为m ,△PDE 的面积为S .求S 与m 之间的函数关系式.试说明S 是否存在最大值,若存在,请求出最大值;若不存在,请说明理由.12.(本小题满分12分)如图,BD 是⊙O 的直径,OA ⊥OB ,M 是劣弧上一点,过M 点作⊙O 的切线MP 交OA 的延长线于P 点,MD 与OA 交于N 点. (1)求证:PM =PN ; (2)若BD =4,P A =23AO ,过B 点作BC ∥MP 交⊙O 于C 点,求BC 的长. B C AA 1 a b cB 1C 1 a 1b 1c 1 A C B F D EO G13.如图,在平面直角坐标系中放置一矩形ABCO ,其顶点为A (0,1)、B (-33,1)、C (-33,0)、O (0,0).将此矩形沿着过E (-3,1)、F (-334,0)的直线EF 向右下方翻折,B 、C 的对应点分别为B ′、C ′.(1)求折痕所在直线EF 的解析式;(2)一抛物线经过B 、E 、B ′三点,求此二次函数解析式;(3)能否在直线EF 上求一点P ,使得△PBC 周长最小?如能,求出点P 的坐标;若不能,说明理由.14.已知:甲、乙两车分别从相距300(km )的M 、N回,图1、图2分别是它们离各自出发地的距离y (km )与行驶时间x (h )之间的函数图象. (1)试求线段AB所对应的函数关系式,并写出自变量的取值范围;(2)当它们行驶到与各自出发地的距离相等时,用了29h ,求乙车的速度; (3)在(2)的条件下,求它们在行驶的过程中相遇的时间.y h图1y h图215.如图1,在△ABC 中,AB =BC ,且BC ≠AC ,在△ABC 上画一条直线,若这条直线..既平分△ABC 的面积,又平分△ABC 的周长,我们称这条线为△ABC 的“等分积周线”. (1)请你在图1中用尺规作图作出一条△ABC 的“等分积周线”;(2)在图1中过点C 能否画出一条“等分积周线”?若能,说出确定的方法;若不能,请说明理由; (3)如图2,若AB =BC =5cm ,AC =6cm ,请你找出△ABC 的所有“等分积周线”,并简要说明确定的方法.16.如图,在Rt △ABC 中,∠C =90°,AC =3cm ,BC =4cm ,点P 以一定的速度沿AC 边由A 向C 运动,点Q 以1cm/s 的速度沿CB 边由C 向B 运动,设P 、Q 同时运动,且当一点运动到终点时,另一点也随之停止运动,设运动时间为t (s ). (1)若点P 以43cm/s 的速度运动 ①当PQ ∥AB 时,求t 的值;②在①的条件下,试判断以PQ 为直径的圆与直线AB 的位置关系,并说明理由.(2)若点P 以1cm/s 的速度运动,在整个运动过程中,以PQ 为直径的圆能否与直线AB 相切?若能,请求出运动时间t ;若不能,请说明理由.17.青海玉树发生7.1级强震后,为使人民的生命财产损失降到最低,部队官兵发扬了连续作战的作风。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考数学压轴题分类强化训练3-抛物线与圆
1、如图①②,在平面直角坐标系中,边长为2的等边△CDE 恰好与坐标系中的△OAB 重合,
现将△CDE 绕边AB 的中点G (G 点也是DE 的中点),按顺时针方向旋转180°到△C 1DE 的位置。
(1)求C 1点的坐标;
(2)求经过三点O 、A 、C 1的抛物线的解析式;
(3)如图③,⊙G 是以AB 为直径的圆,过B 点作⊙G 的切线与x 轴相交于点F ,求切线BF 的解析式; (4)抛物线上是否存在一点M ,使得3:16:=∆∆OAB AMF S S .若存在,请求出点M 的坐标;若不存在,请说明理由。
解(1)C 1(3,3)
(2)∵抛物线过原点O(0,0),设抛物线解析式为y =ax 2
+b x
把
A(2,0),C`(3,3)带入,得420
933
a b a b +=⎧⎪⎨+=⎪⎩ 解得a =3,b =-23
∴抛物线解析式为y =
3x 2-23
x (3)∵∠ABF=90°,∠BAF=60°,∴∠AFB=30°
又AB =2 ∴AF=4 ∴OF=2 ∴F (-2,0) 设直线BF 的解析式为y =k x +b
把B(1,3),F(-2,0)带入,得3
20
k b k b ⎧+=⎪⎨-+=⎪⎩ 解得k =33,b =233
∴直线BF 的解析式为y =
33x +23
3
(4)①当M 在x 轴上方时,存在M(x ,
3x 2-23
x )
S△AMF:S△OAB=[
12×4×(3x 2-23x )]:[1
2
×2×4]=16:3
得x 2
-2x -8=0,解得x 1=4,x
2=-2 当x 1=4时,y =
3×42
-23×4=83;
当x 1=-2时,y =
3×(-2)2
-23×(-2)=83
∴M 1(4,
83),M 2(-2,83
) ②当M 在x 轴下方时,不存在,设点M(x ,
33x 2-23
3
x ) S△AMF:S△OAB=[-
12×4×(33x 2-233x )]:[1
2
×2×4]=16:3
得x 2
-2x +8=0,b 2
-4a c <0 无实解 综上所述,存在点的坐标为M 1(4,
83),M 2(-2,83
). 2.已知:如图,在平面直角坐标系xOy 中,以点P (2,3)为圆心的圆与y 轴相切于 点A ,与x 轴相交于B 、C 两点(点B 在点C 的左边).
(1)求经过A 、B 、C 三点的抛物线的解析式;
(2)在(1)中的抛物线上是否存在点M ,使△MBP 的面积是菱形ABCP 面积的
2
1
.如果 存在,请直接写出所有满足条件的M 点的坐标;如果若不存在,请说明理由; (3)如果一个动点D 自点P 出发,先到达y 轴上的某点,再
到达x 轴上某点,最后运动到(1)中抛物线的顶点Q 处,求使点D 运动的总路径最短的路径的长..
解:(1)联结P A ,PB ,PC ,过点P 作PG ⊥BC 于点G .
∵⊙P 与y 轴相切于点A , ∴P A ⊥y 轴,
∵P (2,3),
∴OG =AP =2,PG =OA =3 ∴PB =PC =2. ∴BG =1.
∴CG =1,BC =2. ∴OB =1,OC =3.
∴ A (0,3),B (1,0),C (3,0)
根据题意设二次函数解析式为:(1)(3)y a x x =--,
∴(01)(03)3a --=,解得a =
3
3
. ∴二次函数的解析式为:23433y x x =
-+ (2)存在.点M 的坐标为(0,3),(3,0),(4,3),(7,83)
(3)∵23433y x x =
-+=33
)2(33)34(3322--=+-x x x ,
∴抛物线的顶点Q (2,3
3-
). 作点P 关于y 轴的对称点P ’,则P ’(-2,3).
联结P ’ Q ,则P ’ Q 是最短总路径, 根据勾股定理,可得P ’ Q =
83
3.如图,在直角坐标系xoy 中,已知点)3,2(P ,过P 作轴y PA ⊥交y 轴于点A ,以点P 为圆心PA 为半径作⊙P ,交x 轴于点C B ,,抛物线c bx ax y ++=2经过A ,B ,C 三点. (1)求点A ,B ,C 的坐标;
(2)求出该抛物线的解析式;
(3)抛物线上是否存在点Q ,使得四边形ABCP 的面积是BPQ ∆面积
的2倍?若存在,请求出所有满足条件的点;若不存在,请说明理由.
解:(1)过P 作BC PD ⊥交BC 于D ,
由题意得:2===PC PB PA ,3==OA PD
∴1==CD BD ,
∴1=OB
∴)3,0(A ,)0,1(B ,)0,3(C
y x
P
A
B
C
Q
O
(2)设该抛物线解析式为:)3)(1(--=x x a y ,则有
)30)(10(3--=a 解之得3
3=
a 故该抛物线的解析式为)3)(1(3
3
--=x x y (3)存在
∵︒=∠90BDP ,2,1==BP BD ∴2
1
cos ==
∠BP BD DBP ∴︒=∠60DBP ∴︒=∠60BPA
∴ABP ∆与BPC ∆都是等边三角形 ∴BCP ABP ABCP S S S ∆∆==22四边形 ∵)0,1(B ,)3,2(P
∴过P B ,两点的直线解析式为:33-=
x y
则可设经过点A 且与BP 平行的直线解析式为:13b x y +=
且有1033b +⨯=
解之得31=b 即33+=x y
解方程组⎪⎩
⎪
⎨⎧--=+=)3)(1(33
3
3x x y x y 得⎩⎨⎧==⎩⎨⎧==38730y x y x 或 也可设经过点C 且与BP 平行的直线解析式为:23b x y +=
且有2330b +=解之得332-=b 即333-=
x y
解方程组⎪⎩
⎪
⎨⎧--=-=)3)(1(33
3
33x x y x y 得⎩⎨⎧==⎩⎨⎧==3403y x y x 或 ∴)3,4(),0,3(),38,7(),3,0(Q
4.如图,在直角坐标系中,
以点A 为圆心,
以x 轴相交于点B C ,,
与y 轴相交于点D E ,.
(1)若抛物线2
13
y x bx c =++经过C D ,两点,求抛物线的解析式,并判断点B 是否在该抛物线上.
(2)在(1)中的抛物线的对称轴上求一点P ,使得PBD △的周长最小.
(3)设Q 为(1)中的抛物线的对称轴上的一点,在抛物线上是否存在这样的点M ,使得四边形BCQM 是平行四边形.若存在,求出点M 的坐标;若不存在,说明理由.
解:(1
)
OA =∵
AB AC ==
(B ∴
,C 又在Rt AOD △
中,AD =
OA =
3OD =
=∴, D ∴的坐标为(03)-,
又D C ,两点在抛物线上,
2
3103c c =-⎧⎪⎨++=⎪⎩g ∴
解得3
b c ⎧
=⎪
⎨⎪=-⎩ ∴
抛物线的解析式为:2133y x x =
-
当x =0y =, ∴
点(B 在抛物线上 (2
)2133y x x =
-
∵21
(43x =- ∴
抛物线21333
y x x =
--
的对称轴方程为x = 在抛物线的对称轴上存在点P ,使PBD △的周长最小.
BD ∵的长为定值 ∴要使PBD △周长最小只需PB PD +最小. 连结DC ,则DC 与对称轴的交点即为使PBD △周长最小的点. 设直线DC 的解析式为y mx n =+.
由30n n =-⎧⎪
⎨+=⎪⎩
得3
m n ⎧=⎪⎨⎪=-⎩
, ∴直线DC
的解析式为33y x =-
由33
y x x ⎧=-⎪⎨⎪=⎩
得2x y ⎧=⎪⎨=-⎪⎩ 故点P
的坐标为2)- (3
)存在,设)Q t
为抛物线对称轴x =
M 在抛物线上要使四边形
BCQM 为平行四边形,则BC QM ∥且BC QM =,点M 在对称轴的左侧.
于是,过点Q 作直线L BC ∥与抛物线交于点()m M x t , 由BC QM =
得QM =
从而m x =-12t =
故在抛物线上存在点(M ,使得四边形BCQM 为平行四边形.。
