实验2-利用SIMULINK进行制导弹道仿真
导弹最优导引律仿真分析(例子)
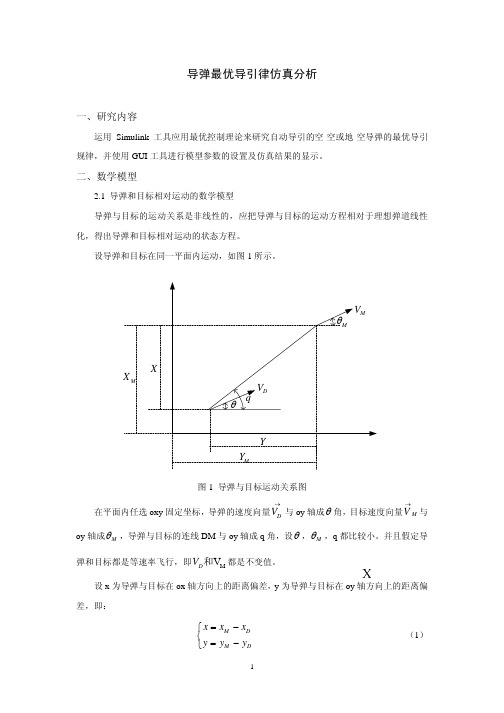
到限制,导弹结构能承受的最大过载也受到限制,所以控制信号 u 应该受到限制,因此,选
择下列形式的二次型指标函数
( ) ( ) ∫ ( ) J = 1 X T 2
tf
CX t f
+ 1 tf 2 t0
X T QX + U T RU dt
⎡c1 0 0 0 ⎤ ⎡0 0 0 0⎤
式中,
C
=
⎢ ⎢
0
c2
0
0
⎥ ⎥
,
Q
=
⎢⎢0
0
0
0⎥⎥
⎢0
⎢ ⎣
0
0 0
c3 0
0⎥
c4
⎥ ⎦
⎢0 0 0 0⎥ ⎢⎣0 0 0 0⎥⎦
2.2.2 最优导引律
(11)
完全考虑弹体二阶振荡环节时,假定目标不机动,导弹运动的状态方程见式(8),即
•
X = AX + Bu
(12)
⎡0 1 0 0 ⎤ ⎡ 0 ⎤
式中, A = ⎢⎢0 0 VD ⎢0 0 0
]
2(t f − t)2 + 6(t f − t)
ω
ω2
−
15 4ω
2
3
]
K3 (t) =
KDVD [(t f
− t)3
3 ω2 3 −
(t f
−t −
3 )2 ω
2(t f ω
− t)2
+
6(t f − t) ω2
−
15 4ω
2
3
]
最优导引方框图如图 3 所示。
6
u(σ )
KDω 2
+
1 s x4 1 s x3 VD +
基于Matlab/Simulink的火箭深弹水中弹道可视化仿真

爹 c o s
d£
㈩
=z0O , s c : i0 sn
t
积分初始条件取为空中弹道落点 C的弹道诸元 : £ c , cY y , C0 。 =t 时 = , c =X , = 上式是深弹在水 中任意时刻 的运动方程 ,随着 深弹在水 中的运动 , 角一直在改变 , 0 最后趋 于 9  ̄ 0, 所 以在一定时刻后 , 火箭深弹垂直 向下运动。当深弹 正面阻力与浮力 之和等于重力时 ,深弹 以一定 的速 度匀速下沉 , 此时的速度称为极限下沉速度 。 极限 速度可用下面公式计算
、
3 6 3 6 3 7 3 7 3 8 3 8 3 9 40 , 5 4O 1 4 5 40 45 40
1 2 13 3 514 3 51 5 3 5 3 0 16 3 0 35 3 013 3 01 4 3 015 I 6 3 517
距离 ( m)
距 离( ) m
关 键 词 : 箭 深 弹 ; db S lk 弹 道 仿 真 火 Ma a/i i ; mun 中图 分 类 号 :J ; P 9 . T 6 T 3 19 文 献 标识 码 : A 文 章 编 号 :6 2 5 5 2 1 0 — 0 3 0 1 7 — 4 X( 0 2)7 0 3 — 3
不同的射角人水后 , 在水中垂直段的射角均变为 9 。 0;
航 天大学 出版社 。0 9 20 .
Ba e nt e Ma lb/ muik Ro k t p h Ch r e Un e wa e s d o h t a Si l c e n De t a g d r t r
l ・ 6 以某 火箭 深弹 为例 ,初始射 角分别 为 4 。和 5 15 ・ 1o 行 弹道仿 真 和分 析 。 2进 曼1 . 3 31 速度 变 化规 律 . 火 箭 深 弹 以一 定 的初 速 和射 角 到 达水 面 ,进入 水 中, 深弹首先作减速运动 , 然后进人极限下潜段。 以某火箭深弹为例 , 以两种不 同的初始射角 , 经过仿 真 系统 得 到 的速 度变 化 图如 图 2所 示 。
基于SIMULINK的某型反坦克导弹平射弹道特性研究

0引言反坦克导弹是陆军反装甲作战的重要武器。
在反坦克导弹的设计阶段,弹道方案的充分论证、设计和分析是导弹成功研制的重要前提。
反坦克导弹目前已经发展第三代,具有“发射后不管”的特点,其外弹道特征与前两代反坦克导弹相比有较大差异。
平射弹道是第三代反坦克导弹打击近距离目标的一种基本弹道形式,研究第三代反坦克导弹平射弹道的特性,并设计出相应的弹道方案,对研制导弹的制导系统有着非常重要的意义。
1导弹质点弹道模型1.1导弹基本情况该型导弹为钝头圆柱外形、十字翼舵布局,弹径为127mm 。
外形如图1所示。
在进行弹道设计之前,已经完成了气动仿真和风洞试验工作,获得了相关气动力参数数据。
根据导弹结构、技战术指标和气动力参数,确定了最大攻角不超过40°,最大舵偏角不超过25°的指标。
1.2基本假设导弹的运动方程组是确定导弹外弹道方案的基础。
为了对导弹的主要外弹道特性进行研究,需要对导弹的受力状况作合理的简化,以达到能将导弹视为质点的目的[1]。
通常采用以下假设:①导弹绕弹体轴的转动是无惯性的,即假设转动惯量为0;②导弹控制系统能够理想控制,既无误差也无时间延迟;③不考虑横风等干扰因素对导弹的影响;④假设导弹处于“瞬时平衡”状态,认为导弹在任一瞬时都处于平衡状态。
该型导弹属于第三代反坦克导弹,有攻顶打击和侧面打击两种攻击方式。
攻顶方式适用于打击暴露状态下的装甲目标,一般情况下为首选方式。
但在某些时机下,例如对顶部有掩蔽的装甲目标、某些野战或永备工事、城市建筑物中的火力点进行攻击时,也需要导弹能够实施侧面打击。
侧面打击所对应弹道即为平射弹道。
平射弹道主要分为四个阶段:无控段、爬升段、定攻角飞行段和比例导引段。
导弹出筒后即进入无控段;发动机开始工作后即进入爬升段;当导弹按照爬升段的控制方案飞行至弹道顶点(即弹道倾角为0°时对应的位置)时,导弹进入定攻角飞行段;当目标进入捕获域时,导弹进入比例导引段,直至击中目标位置。
实验2-利用SIMULINK进行制导弹道仿真
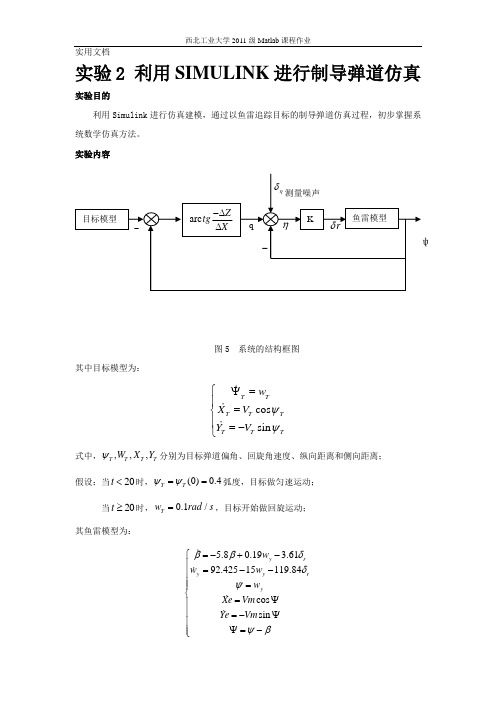
实验2 利用SIMULINK 进行制导弹道仿真 实验目的利用Simulink 进行仿真建模,通过以鱼雷追踪目标的制导弹道仿真过程,初步掌握系统数学仿真方法。
实验内容图5 系统的结构框图其中目标模型为:cos sin T T T T T T T T w X V Y V ψψ⎧ψ=⎪=⎨⎪=-⎩式中,,,,T T T T W X Y ψ分别为目标弹道偏角、回旋角速度、纵向距离和侧向距离;假设:当20t <时,(0)0.4T T ψψ==弧度,目标做匀速运动;当20t ≥时,0.1/T w rad s =,目标开始做回旋运动;其鱼雷模型为:5.80.19 3.6192.42515119.84cos sin y r y y ry w w w w Xe Vm Ye Vm ββδδψψβ⎧=-+-⎪=--⎪⎪=⎪⎨=ψ⎪⎪=-ψ⎪ψ=-⎪⎩式中,,,,,,,,y w r Vm Xe Ye βδψψ分别为鱼雷的侧滑角、回旋角速度、直舵角、航向角、弹道偏角、速度,地面坐标系中的X 轴和Z 轴坐标。
Vm=25m/s 。
鱼雷与目标的相对距离为,,T T X X Xe Y Z Ze ∆=-∆=-。
q 为地球视线角,q ηψ=-为雷体系中的提前角。
操舵规律,0.5,10r K K r δηδ=-=≤。
终端脱靶量定义为t f r =鱼雷模型仿真初值为:(0)(0)(0)(0)(0)(0)0.25/y w r Xe Ze Vm m s βδψ=======。
目标模型仿真初值为:(0)5/,(0)(0)1500,(0)0T T T T V m s X Z m w ====实验步骤由图5所示的系统控制结构图可知,该系统大致可以分为三个部分:目标模型,鱼雷模型以及观察模块。
1.根据目标模型和鱼雷模型的数学方程组,调用Simulink 工具箱模块库中的所需模块建立目标模型和鱼雷模型。
2.根据系统结构框图完成整个系统仿真模型的搭建,如图6 所示。
基于MATLAB/Simulink的弹道仿真模块化设计

The Incorporate Simulation of the M issile Traj ectory Based on M ATLAB/Simulink
ZHA()Jun-min.HE Ya—juan (N o.203 Research Institute of China O rdnance Industries.Xi’an 710065.China) Abstract:In this paper.the incorporate ballistic simulation model of missile trajectory is based on the Simulink toolbox in the M atlab language. Using this method,the dynamic system simulation becomes easy and visua1.increasing this model transplant. The relevant results are given tO a determ inate condition.the results have been validated. Key words{MATLAB/Simulink;sim ulation of missile trajectory;incorporate
Simulink完成某 型 号 制 导 导 弹 的 弹 道 模块 化 设
计 ,为 总体 性 能及控 制 系统 的分析 提供 平 台。
3 弹 道பைடு நூலகம் 真模 块 化 设 计
2 弹 道 仿 真 模 块 化 设 计 思 想
弹道 仿真模 块 的设 计 分 三 步 :(1)根 据 弹道 仿 真系 统 的 任 务 及 功 能 ,将 系 统 分 为 若 干 个 模 块 ,确定 各模块 的输 入输 出信 号流 ;(2)分别 构 建 各模 块 的 内容 ;(3)模 块封 装 ,闭合 大 回路 。
基于SIMULINK的某型反坦克导弹攻顶弹道方案设计研究

Ab s t r a c t :Ba l l i s t i c s s c h e me i s v e r y i mp o r t a n t i n r e s e a r c h i n g a n t i — t a n k mi s s i l e . T h i s p a p e r d e s i g n e d b a l l i s t i c s s c h e me o f a k i n d o f a n t i — t a n k mi s s i l e p r e l i mi n a r i l y a n d p r o p o s e d a k i n d o f b a l l i s t i c s s c h e me t h a t c a n a c h i e v e t o a t t a c k t o p a r mo r b a s e d o n t h e S I MUL I NK a n d f u n c t i o n s o f mo t i o n .a n d a n a l y s e s h o w he t c h a n g e d p a r a me t e r s i n f u n c t i o n s o f mo t i o n i n f l u e n c e he t a t t a c k i n g t o p a l T a o r a c c o r d i n g t o t h e r e s u l t o f s i mu l a t i o n .
摘要 : 在反坦克导弹的研制 中, 弹道方案的设计具有重要地位 。本文基 于 S I MU L I NK仿真平 台, 在导 弹外弹道运动 方程 的基础 上, 对某型反 坦克 导弹攻顶 弹道方案进行 了初步设 计, 提 出了一种能够 实现有 效攻顶打 击的弹道方案 , 并通过仿真结果分析 了各运 动
仿真技术试验(探测专业)——实验二 导弹的纵向运动仿真建模

西工大制导控制系统仿真技术 试验 实验二 导弹的纵向运动仿真建模一、实验目的与要求1.加深对导弹的纵向模型的理解;2.掌握Matlab/Simulink 仿真模型的建模步骤和注意事项; 3.在Matlab/SimuLink 环境下,进行导弹的纵向运动仿真建模;二、实验内容1、首先给出导弹的的简化纵向运动方程:◆ 质心动力学方程:cos sin sin cos dVmP X mg dtd mV P Y mg dt αθθαθ=--=+-◆ 绕质心转动转动动力学方程: zzz d J M dtω= ◆ 质心运动学方程:cos sin dxV dtdyV dt θθ==◆ 绕质心转动动力学方程: z d dtϑω= ◆ 补充几何关系方程: ϑαθ=+◆ 过载计算方程:cos y V d n g dtθθ=+ 式中: m 为导弹当前的质量;V 为导弹速度; P 为导弹推力; X 为导弹受到的阻力; Y 为导弹受到的升力;g 为重力加速度;z J 为导弹的z 轴的转动惯量;z ω为导弹俯仰角速度;y n 为导弹的法向过载;z M 为导弹受到气动俯仰力矩;ϑ为俯仰角;θ为弹道倾角; α为攻角。
2、下面给出导弹的弹体参数: ● 弹体参数:弹体质量:0m =250;转动惯量:315Jz =;参考面积:0.45S =参考长度: 2.5L =;发动机推力:1000P =;质量秒消耗量:0.46dm = ● 阻力计算公式:x X C qS =,其中:220x x x C C C αα=+,00.2x C =,20.0005x C α=● 升力计算公式:y Y C qS =,其中:z y y y z C C C δααδ=+,0.25y C α=,0.05z y C δ=● 俯仰力矩计算公式:z z M m qSL =,其中:z z z z z m m m δααδ=+,-0.1z m α=,-0.024z z m δ=3、下面给出导弹的控制系统:图 1 导弹的俯仰控制系统图中,控制系统的参数:Kwz = -0.05,Kpny = 0.1,Kiny = 2。
炮弹运动方程

最后,很感谢周老师这个学期来对我们的细心教导,使我们学到了很多东西,特别是MATLAB这个使用型的软件,对于我们以后工作一定有很大的帮助,在这里祝周老师工作顺利!天天开心!
Integrator:此为积分模块。
Scope:此为示波器,用于显示最后结果。
运行后可以得到如下结果:
四、实验感想
1、学会了使用Simulink工具箱对一些简单实际问题进行动态仿真,从而得到无法用计算得到的复杂结果,特别是用Scope显示的图形直观、形象、快速、易于理解。我很感兴趣,我还要继续深入地学习;
三、实验分析及结果
根据题目,用simulink仿真的图形如下:
注:0.0004905为2g/v02的值。
图中模块说明如下:
Constant:此为常数模块,在整个过程中都是9.81。
Product:此为乘法模块,可用于多个数相乘。
Gain:此为增益模块。
Math function:此为数学函数模块,可通过改变参数来调用不同的数学函数,上图中我们用了开根号(sqrt)和平方。
《
学院
信息科学技术学院
班3号
实验项目名称
炮弹运动方程仿真
指导
教师
周小云
一、实验目的
[1]学习由实际问题去建立数学模型的过程;
[2]学会借助于matlab软件的simulink工具箱进行动态仿真。
二、实验内容
且已知:v0=212m/s,y’(0)=150,y(0)=50,x’(0)=150,x(0)=50利用simulink对其过程进行仿真。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验2 利用SIMULINK 进行制导弹道仿真 实验目的
利用Simulink 进行仿真建模,通过以鱼雷追踪目标的制导弹道仿真过程,初步掌握系统数学仿真方法。
实验内容
图5 系统的结构框图
其中目标模型为:
cos sin T T T T T T
T T w X V Y V ψψ⎧ψ=⎪=⎨⎪=-⎩ 式中,,,,T T T T W X Y ψ分别为目标弹道偏角、回旋角速度、纵向距离和侧向距离;
假设:当20t <时,(0)0.4T T ψψ==弧度,目标做匀速运动;
当20t ≥时,0.1/T w rad s =,目标开始做回旋运动;
其鱼雷模型为:
5.80.19 3.6192.42515119.84cos sin y r y y r
y w w w w Xe Vm Ye Vm ββδδψψβ⎧=-+-⎪=--⎪⎪=⎪⎨=ψ⎪⎪=-ψ⎪ψ=-⎪⎩
式中,,,,,,,,y w r Vm Xe Ye βδψψ分别为鱼雷的侧滑角、回旋角速度、直舵角、航向角、弹道偏角、速度,地面坐标系中的X 轴和Z 轴坐标。
Vm=25m/s 。
鱼雷与目标的相对距离为,,T T X X Xe Y Z Ze ∆=-∆=-。
q 为地球视线角,q ηψ
=-为雷体系中的提前角。
操舵规律,0.5,10r K K r δηδ=-=≤。
终端脱靶量定义为
t f r =鱼雷模型仿真初值为:
(0)(0)(0)(0)(0)(0)0.25/y w r Xe Ze Vm m s βδψ=======。
目标模型仿真初值为:(0)5/,(0)(0)1500,(0)0T T T T V m s X Z m w ====
实验步骤
由图5所示的系统控制结构图可知,该系统大致可以分为三个部分:目标模型,鱼雷模型以及观察模块。
1.根据目标模型和鱼雷模型的数学方程组,调用Simulink 工具箱模块库中的所需模块建立目标模型和鱼雷模型。
2.根据系统结构框图完成整个系统仿真模型的搭建,如图6 所示。
3.设置各模块的参数,并按照题目给定的初值条件设置好各模块的初值。
4.设置仿真器的参数,这里选择起始时间为0s ,终止时间为100s ,变步长解法器ode45,最大步长为0.05,最小步长自动调整。
5.对已经建立好的系统仿真模型进行运行调试,并对仿真结果进行分析。
图6 系统仿真模型结构图
图7 目标的弹道曲线
图8 鱼雷追踪曲线为了绘制绘制鱼雷跟踪弹道曲线,运行以下程序代码:plot(xe,ze)
hold on
plot(xt,zt)
图9 鱼雷跟踪弹道曲线
实验结果分析
由上图可以发现利用Simulink 建立系统仿真模型可以实现鱼雷跟踪目标的功能,达到了预期的目的,验证了实验的正确性。
与此同时,由图9可以发现鱼雷跟踪目标后还会继续运行,与实际情况并不相符,为了更好的绘制绘制鱼雷跟踪弹道曲线,仿真结构图中结合了stop 模块用来使终端脱靶量即终端时刻所对应的最小距离22tf r x z =∆+∆以给出仿真结束的时间停止仿真。
通过反复的调试,观测工作空间tf r 的值发现终端脱靶量不可能为零,最小为3.3左右。
将tf r 设置为小于等于3.3时绘制的鱼雷跟踪目标弹道曲线如图10所示。
可见数学模型并不能完全深刻的描述出物理模型,所以仿真结果也与实际鱼雷弹道并不完全吻合,但作为一个仿真软件,在其精度允许范围内并不影响其仿真效果和实验的有效性和正确性。
图10 鱼雷跟踪弹道曲线。
