模电第五版童诗白答案
模电第五版课后答案

模电第五版课后答案第一章电路的基本概念和基本定律1.1 电路的基本概念1.电路是由电子元件、电源和连接线组成的。
2.电路分为直流电路和交流电路两种。
3.电子元件包括电阻、电容和电感等。
4.电路的连接方式有串联和并联。
1.2 电路的基本定律基尔霍夫定律•第一定律:电流在任一节点的进出代数和为零•第二定律:沿着任一回路,电动势之和等于电势降之和电阻定律•奥姆定律:电流通过一个电阻的大小与电阻两端的电压成正比,与电阻本身无关第二章基本电路分析方法和技巧2.1 基本电路分析方法1.求解线性方程组法2.叠加法3.超节点法2.2 基本电路分析技巧1.电流分配定理2.电压分配定理3.电流、电压与功率的关系第三章电路的时间特性3.1 RC电路的时域分析1.RC电路的充放电过程2.RC电路的阶跃响应3.RC电路的脉冲响应3.2 RL电路的时域分析1.RL电路的充放电过程2.RL电路的阶跃响应3.RL电路的脉冲响应第四章电路的频率特性4.1 交流电路的频率特性1.交流电路中的欧姆定律2.交流电路中的电流和电压的相位关系3.交流电路中的功率计算4.2 电阻、电容和电感的频率特性1.电阻的频率特性2.电容的频率特性3.电感的频率特性第五章运算放大电路5.1 差动放大器1.差动放大器的基本原理2.差模增益和共模增益3.差动放大器的共模抑制比5.2 频率和相位响应1.运算放大器的频率响应特性2.运算放大器的相位响应特性5.3 运放的应用电路1.非反馈放大电路2.反馈放大电路3.运放的综合应用以上是《模电第五版》课后答案的一些概要内容,希望对你的学习有所帮助。
详细的答案和解析请参考教材中的原文或者其他辅助教材。
祝你学习进步!。
《模拟电子技术基础》(童诗白)课后习题答案
模拟电子技术基础第 1 章常用半导体器件1.1选择合适答案填入空内。
(l)在本征半导体中加入( A )元素可形成N 型半导体,加入( C )元素可形成P 型半导体。
A.五价B. 四价C. 三价(2)当温度升高时,二极管的反向饱和电流将(A) 。
A.增大B.不变C.减小(3)工作在放大区的某三极管,如果当I B 从12 uA 增大到22 uA 时,I C 从l mA 变为2mA ,那么它的β约为( C ) 。
A.83B.91C.100(4)当场效应管的漏极直流电流I D 从2mA 变为4mA 时,它的低频跨导g m 将( A ) 。
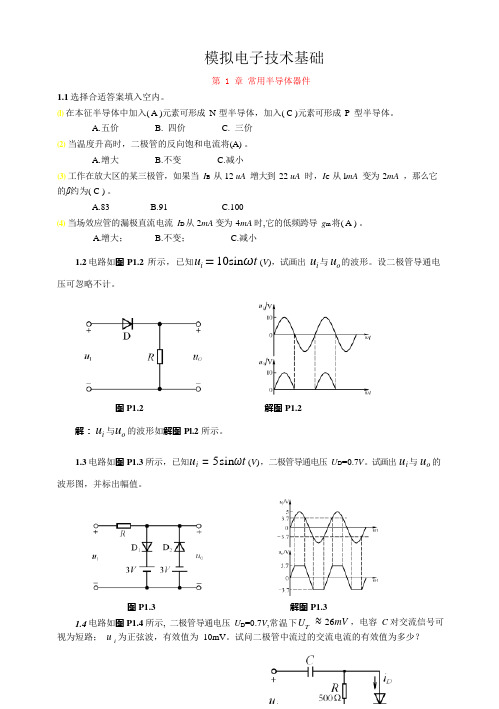
A.增大;B.不变;C.减小1.2电路如图P1.2 所示,已知u i = 10sinωt (V),试画出u i 与u o 的波形。
设二极管导通电压可忽略不计。
图P1.2 解图P1.2解:u i 与u o 的波形如解图Pl.2 所示。
1.3电路如图P1.3 所示,已知u i =5sinωt(V),二极管导通电压U D=0.7V。
试画出u i 与u o 的波形图,并标出幅值。
图P1.3 解图P1.31.4电路如图P1.4 所示, 二极管导通电压U D=0.7V,常温下U T≈ 26mV ,电容C 对交流信号可视为短路;u i 为正弦波,有效值为10mV。
试问二极管中流过的交流电流的有效值为多少?解:二极管的直流电流I D = (V −U D ) / R = 2.6mA其动态电阻:r D ≈U T / I D =10Ω图 P1.4故动态电流的有效值: I d = U i / r D ≈1mA1.5 现有两只稳压管,稳压值分别是 6V 和 8V ,正向导通电压为 0.7V 。
试问: (1)若将它们串联相接,则可得到几种稳压值?各为多少? (2)若将它们并联相接,则又可得到几种稳压值?各为多少?解:(1)串联相接可得 4 种:1.4V ;14V ;6.7V ;8.7V 。
(2)并联相接可得 2 种:0.7V ;6V 。
模电习题答案(第五版)

湖南人文科技学院 田汉平
27
湖南人文科技学院 田汉平
28
湖南人文科技学院 田汉平
29
湖南人文科技学院 田汉平
30
电子技术基础模拟部分 第五版
第五章作业题解答
田汉平
湖南人文科技学院通信与控制工程系
湖南人文科技学院 田汉平
2
湖南人文科技学院 田汉平
3
湖南人文科技学院 田汉平
4
湖南人文科技学院 田汉平
17
湖南人文科技学院 田汉平
18
湖南人文科技学院 田汉平
19
湖南人文科技学院 田汉平
20
湖南人文科技学院 田汉平
21
湖南人文科技学院 田汉平
22
湖南人文科技学院 田汉平
23
湖南人文科技学院 田汉平
24
湖南人文科技学院 田汉平
25
湖南人文科技学院 田汉平
26
湖南人文科技学院 田汉平
21
湖南人文科技学院 田汉平
22
湖南人文科技学院 田汉平
23
电子技术基础模拟部分 第五版
第三章作业题解答
田汉平
湖南人文科技学院通信与控制工程系
湖南人文科技学院 田汉平
2
湖南人文科技学院 田汉平
3
湖南人文科技学院 田汉平
4
湖南人文科技学院 田汉平
5
湖南人文科技学院 田汉平
6
湖南人文科技学院 田汉平
电子技术基础模拟部分 第五版
第一章作业题解答
田汉平
湖南人文科技学院通信与控制工程系
湖南人文科技学院 田汉平
2
湖南人文科技学院 田汉平
3
湖南人文科技学院 田汉平
模电第五版课后答案

模电第五版课后答案第一章简介1.1 什么是模拟电子技术?模拟电子技术是研究模拟电子元器件、电路和系统的原理和设计方法的一门学科。
它主要研究电子元器件和电路在连续信号情况下的原理和应用。
1.2 为什么学习模拟电子技术?学习模拟电子技术有以下几个原因:•模拟电子技术在许多领域中都有广泛的应用,比如通信、医疗设备、汽车电子等。
•模拟电子技术是电子技术的基础,掌握了模拟电子技术可以更好地理解和应用其他领域的电子技术。
•对于电子工程师来说,模拟电子技术是必备的基本技能。
第二章模拟电子元器件2.1 电阻器电阻器是一种常见的电子元器件,其主要功能是阻碍电流流过。
常见的电阻器有稳态电阻器、变阻器等。
2.2 电容器电容器是一种存储电荷的元器件。
电容器的主要特性有容量、介质、工作电压等。
2.3 电感器电感器是一种储存电能的元器件。
它主要由线圈组成,具有自感和互感等特性。
第三章模拟电路基础3.1 基本电路元件模拟电路基础中的基本电路元件包括电阻、电容、电感。
3.2 电路定理小结电路定理是研究电路行为和性质的基本理论。
常见的电路定理有欧姆定律、基尔霍夫定律、戴维南定理等。
第四章放大电路基础知识4.1 放大电路的基本概念放大电路是指通过放大输入信号的幅度来获得输出信号的电路。
放大电路常用于信号放大、功率放大等应用。
4.2 放大电路的分类放大电路可以分为线性放大电路和非线性放大电路两大类。
第五章放大电路的分析与设计5.1 放大电路的基本分析方法放大电路的基本分析方法包括小信号模型、频率响应等。
5.2 放大电路的设计方法放大电路的设计方法主要包括增益的设计、频率响应的设计等。
以上是《模电第五版》中第一章至第五章的课后答案摘要。
希望对你的学习有所帮助!。
模电第五版童诗白答案

第四章 集成运算放大电路自 测 题一、选择合适答案填入空内。
(1)集成运放电路采用直接耦合方式是因为 。
A .可获得很大的放大倍数 B . 可使温漂小 C .集成工艺难于制造大容量电容 (2)通用型集成运放适用于放大 。
A .高频信号 B . 低频信号 C . 任何频率信号(3)集成运放制造工艺使得同类半导体管的 。
A . 指标参数准确 B . 参数不受温度影响 C .参数一致性好(4)集成运放的输入级采用差分放大电路是因为可以 。
A .减小温漂 B . 增大放大倍数 C . 提高输入电阻(5)为增大电压放大倍数,集成运放的中间级多采用 。
A .共射放大电路 B . 共集放大电路 C .共基放大电路解:(1)C (2)B (3)C (4)A (5)A二、判断下列说法是否正确,用“√”或“×”表示判断结果填入括号内。
(1)运放的输入失调电压U I O 是两输入端电位之差。
( ) (2)运放的输入失调电流I I O 是两端电流之差。
( ) (3)运放的共模抑制比cdCMR A A K( ) (4)有源负载可以增大放大电路的输出电流。
( )(5)在输入信号作用时,偏置电路改变了各放大管的动态电流。
( ) 解:(1)× (2)√ (3)√ (4)√ (5)×三、电路如图T4.3所示,已知β1=β2=β3=100。
各管的U B E 均为0.7V ,试求I C 2的值。
图T4.3解:分析估算如下: 100BE1BE2CC =--=RU U V I R μAβCC B1C0B2C0E1E2CC1C0I I I I I I I I I I I I R +=+=+====1001C =≈⋅+=R R I I I ββμA四、电路如图T4.4所示。
图T4.4(1)说明电路是几级放大电路,各级分别是哪种形式的放大电路(共射、共集、差放……);(2)分别说明各级采用了哪些措施来改善其性能指标(如增大放大倍数、输入电阻……)。
童诗白《模拟电子技术基础》(第5版)笔记和课后习题考研真题

童诗白《模拟电子技术基础》(第5版)笔记和课后习题考研真题完整版>精研学习䋞>无偿试用20%资料
全国547所院校视频及题库全收集
考研全套>视频资料>课后答案>往年真题>职称考试
第1章常用半导体器件
1.1复习笔记
1.2课后习题详解
1.3名校考研真题详解
第2章基本放大电路
2.1复习笔记
2.2课后习题详解
2.3名校考研真题详解
第3章多级放大电路
3.1复习笔记
3.2课后习题详解
3.3名校考研真题详解
第4章放大电路的频率响应
4.1复习笔记
4.2课后习题详解
4.3名校考研真题详解
第5章放大电路中的反馈
5.1复习笔记
5.2课后习题详解
5.3名校考研真题详解
第6章信号的运算和处理
6.1复习笔记
6.2课后习题详解
6.3名校考研真题详解
第7章波形的发生和信号的转换
7.1复习笔记
7.2课后习题详解
7.3名校考研真题详解
第8章功率放大电路
8.1复习笔记
8.2课后习题详解
8.3名校考研真题详解
第9章直流电源
9.1复习笔记
9.2课后习题详解
9.3名校考研真题详解第10章模拟电子电路读图10.1复习笔记
10.2课后习题详解10.3名校考研真题详解。
模拟电子技术基础第5章放大电路地频率响应的题目解(童诗白)

第五章 放大电路的频率响应(童诗白)自 测 题一、选择正确答案填入空内。
(1)测试放大电路输出电压幅值与相位的变化,可以得到它的频率响应,条件是 。
A.输入电压幅值不变,改变频率B.输入电压频率不变,改变幅值C.输入电压的幅值与频率同时变化(2)放大电路在高频信号作用时放大倍数数值下降的原因是 ,而低频信号作用时放大倍数数值下降的原因是 。
A.耦合电容和旁路电容的存在B.半导体管极间电容和分布电容的存在。
C.半导体管的非线性特性D.放大电路的静态工作点不合适(3)当信号频率等于放大电路的f L 或f H 时,放大倍数的值约下降到中频时的 。
A.0.5倍B.0.7倍C.0.9倍 即增益下降 。
A.3dBB.4dBC.5dB(4)对于单管共射放大电路,当f = f L 时,oU 与i U 相位关系是 。
A.+45˚B.-90˚C.-135˚当f = f H 时,oU 与i U 的相位关系是 。
A.-45˚ B.-135˚ C.-225˚解:(1)A (2)B ,A (3)B A (4)C C二、电路如图T5.2所示。
已知:V C C =12V ;晶体管的C μ=4pF ,f T = 50MHz ,'bb r =100Ω, β0=80。
试求解:(1)中频电压放大倍数smu A ; (2)'πC ;(3)f H 和f L ;(4)画出波特图。
图T5.2解:(1)静态及动态的分析估算:∥178)(mA/V2.69k 27.1k 27.1k 17.1mV26)1(V 3mA 8.1)1(Aμ 6.22c m bee b'i s ismTEQ m b be i e b'bb'be EQe b'c CQ CC CEQ BQ EQ bBEQCC BQ -≈-⋅+=≈=Ω≈=Ω≈+=Ω≈+=≈-=≈+=≈-=R g r r R R R A U I g R r R r r r I r R I V U I I R U V I u ββ(2)估算'πC :pF1602)1(pF214π2)(π2μc m 'μTe b'0μπe b'0T ≈++=≈-≈+≈C R g C C C f r C C C r f πππββ(3)求解上限、下限截止频率:Hz14)π(21kHz 175π21567)()(i s L 'πH s b b'e b'b s b b'e b'≈+=≈=Ω≈+≈+=CR R f RC f R r r R R r r R ∥∥∥(4)在中频段的增益为dB 45lg 20sm ≈u A频率特性曲线如解图T5.2所示。
模拟电子技术基础课后习题答案(童诗白,华成英版,高教版)8章 波形的发生和信号的转换题解

基础课程教学资料第八章波形的发生和信号的转换自测题一、判断下列说法是否正确,用“√”或“×”表示判断结果。
(1)在图T8.1所示方框图中,若φF=180°,则只有当φA=±180°时,电路才能产生正弦波振荡。
()图T8.1(2)只要电路引入了正反馈,就一定会产生正弦波振荡。
()(3)凡是振荡电路中的集成运放均工作在线性区。
()(4)非正弦波振荡电路与正弦波振荡电路的振荡条件完全相同。
()解:(1)√(2)×(3)×(4)×二、改错:改正图T8.2所示各电路中的错误,使电路可能产生正弦波振荡。
要求不能改变放大电路的基本接法(共射、共基、共集)。
图T8.2解:(a)加集电极电阻R c及放大电路输入端的耦合电容。
(b)变压器副边与放大电路之间加耦合电容,改同铭端。
三、试将图T8.3所示电路合理连线,组成RC桥式正弦波振荡电路。
图T8.3解:④、⑤与⑨相连,③与⑧相连,①与⑥相连,②与⑦相连。
如解图T8.3所示。
解图T8.3四、已知图T8.4(a)所示方框图各点的波形如图(b)所示,填写各电路的名称。
电路1为,电路2为,电路3为,电路4为。
图T8.4解:正弦波振荡电路,同相输入过零比较器,反相输入积分运算电路,同相输入滞回比较器。
五、试分别求出图T8.5所示各电路的电压传输特性。
图T8.5解:图(a)所示电路为同相输入的过零比较器;图(b)所示电路为同相输入的滞回比较器,两个阈值电压为±U T=±0.5 U Z。
两个电路的电压传输特性如解图T8.5所示解图T8.5六、电路如图T8.6所示。
图T8.6(1)分别说明A 1和A 2各构成哪种基本电路;(2)求出u O 1与u O 的关系曲线u O 1=f (u O );(3)求出u O 与u O 1的运算关系式u O =f (u O 1);(4)定性画出u O 1与u O 的波形;(5)说明若要提高振荡频率,则可以改变哪些电路参数,如何改变。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2010年全国硕士研究生入学统一考试数学一试题一、选择题(1~8小题,每小题4分,共32分.下列每题给出的四个选项中,只有一个选项符合题目要求的,请将所选项前的字母填在答题纸...指定位置上.) (1) 极限2lim ()()xx x x a x b →∞⎡⎤=⎢⎥-+⎣⎦( ) (A) 1. (B) e . (C) a be -. (D) b ae-.(2) 设函数(,)z z x y =,由方程,0y z F x x ⎛⎫=⎪⎝⎭确定,其中F 为可微函数,且20F '≠,则z zxy x y∂∂+=∂∂( ) (A) x . (B) z . (C) x -. (D) z -.(3) 设,m n 是正整数,则反常积分()2ln 1mnx dx x-⎰的收敛性 ( )(A) 仅与m 的取值有关. (B)仅与n 的取值有关. (C) 与,m n 取值都有关. (D) 与,m n 取值都无关. (4) ()()2211limn nn i j nn i n j →∞===++∑∑ ( ) (A)()()120111xdx dy x y ++⎰⎰. (B) ()()100111x dx dy x y ++⎰⎰. (C)()()11111dx dy x y ++⎰⎰. (D) ()()1120111dx dy x y ++⎰⎰. (5) 设A 为m n ⨯矩阵,B 为n m ⨯矩阵,E 为m 阶单位矩阵,若AB E =,则 ( )(A) 秩()r A m =,秩()r B m =. (B) 秩()r A m =,秩()r B n =. (C) 秩()r A n =,秩()r B m =. (D) 秩()r A n =,秩()r B n =. (6) 设A 为4阶实对称矩阵,且2A A O +=,若A 的秩为3,则A 相似于 ( )(A) 1110⎛⎫⎪⎪ ⎪ ⎪⎝⎭. (B) 1110⎛⎫ ⎪⎪ ⎪- ⎪⎝⎭.(C) 1110⎛⎫ ⎪- ⎪ ⎪- ⎪⎝⎭. (D) 1110-⎛⎫ ⎪- ⎪ ⎪- ⎪⎝⎭. (7) 设随机变量X 的分布函数0,1(),0121,1x x F x x e x -<⎧⎪⎪=≤<⎨⎪-≥⎪⎩,则{}1P X == ( ) (A) 0. (B)12. (C) 112e --. (D) 11e --.(8) 设1()f x 为标准正态分布的概率密度,2()f x 为[]1,3-上均匀分布的概率密度,若12(),0()(),0af x x f x bf x x ≤⎧=⎨>⎩,(0,0)a b >>为概率密度,则,a b 应满足 ( ) (A) 234a b +=. (B) 324a b +=. (C) 1a b +=. (D) 2a b +=.二、填空题(9:14小题,每小题4分,共24分.请将答案写在答题纸...指定位置上.) (9) 设()20,ln 1,t tx e y u du -⎧=⎪⎨=+⎪⎩⎰ 求220t d y dx == . (10)2x xdx π=⎰ .(11) 已知曲线L 的方程为[]{}11,1y x x =- ∈-,起点是()1.0-,终点是()1,0,则曲线积分2Lxydx x dy +=⎰.(12) 设(){}22,,1x y z xy z Ω=+≤≤,则Ω的形心的竖坐标z = .(13) 设()()()1231,2,1,0,1,1,0,2,2,1,1,TTTa ααα=-==,若由123,,ααα生成的向量空间的维数是2,则a = .(14) 设随机变量X 的概率分布为{}!C P X k k ==,0,1,2,k =L ,则()2E X = .三、解答题(15~23小题,共94分.请将解答写在答题纸...指定位置上.解答应写出文字说明、证明过程或演算步骤.)求微分方程322xy y y xe '''-+=的通解. (16)(本题满分10分)求函数()()2221x t f x xt e dt -=-⎰的单调区间与极值.(17)(本题满分10分)(I)比较()1ln ln 1n t t dt +⎡⎤⎣⎦⎰与10ln nt t dt ⎰()1,2,n =L 的大小,说明理由;(II)记()1ln ln 1nn u t t dt =+⎡⎤⎣⎦⎰()1,2,n =L ,求极限lim n n u →∞. (18)(本题满分10分)求幂级数()121121n n n x n -∞=--∑的收敛域及和函数.(19)(本题满分10分)设P 为椭球面222:1S x y z yz ++-=上的动点,若S 在点P 处的切平面与xOy 面垂直,求点P 的轨迹C ,并计算曲面积分223244x y zI dS y z yz∑-=++-,其中∑是椭球面S 位于曲线C 上方的部分. (20)(本题满分11分)设110111a A b λλλ ⎛⎫⎛⎫ ⎪ ⎪= - 0= ⎪ ⎪ ⎪ ⎪1 1 ⎝⎭⎝⎭,,已知线性方程组Ax b =存在两个不同的解.( I ) 求λ,a ;( II ) 求方程组Ax b =的通解. (21)(本题满分11 分)已知二次型123(,,)T f x x x x Ax =在正交变换x Qy =下的标准形为2212y y +,且Q 的第三列为22T . ( I ) 求矩阵A ;( II ) 证明A E +为正定矩阵,其中E 为3阶单位矩阵. (22)(本题满分11分)设二维随机变量(,)X Y 的概率密度为2222(,)xxy y f x y Ae -+-=,x -∞<<+∞,y -∞<<+∞,求常数A 及条件概率密度|(|)Y X f y x .设总体X X1 2 3P1θ- 2θθ- 2θ其中参数()0,1θ∈未知,以i N 表示来自总体X 的简单随机样本(样本容量为n )中等于i 的个数(1,2,3i =).试求常数123,,a a a ,使31iii T a N ==∑为θ的无偏估计量,并求T 的方差.2010年全国硕士研究生入学统一考试数学一试题参考答案一、选择题(1)【答案】 (C).【解析】本题属于未定式求极限,极限为1∞型,故可以用“e 的抬起法”求解.()()2lim xx x x a x b →∞⎡⎤⎢⎥-+⎣⎦()()2ln lim x x x a x b x e ⋅-+→∞=()()2lim ln x x x x a x b e →∞⋅-+=, 其中又因为()()2222()()lim ln lim ln 1()()()()lim()()()lim()()x x x x x x x a x b x x x a x b x a x b x x x a x b x a x b a b x abxx a x b a b→∞→∞→∞→∞--+⋅=+-+-+⎡⎤--+⎣⎦=-+-+=-+=-⎡⎤⎣⎦故原式极限为a be-,所以应该选择(C).(2)【答案】 (B).【解析】122212122221x z y z y zF F F F F yF zF z x x x x x F F xF F x⎛⎫⎛⎫''''-+-⋅+⋅ ⎪ ⎪'''+∂⎝⎭⎝⎭=-=-==∂''''⋅,112211y z F F F z x y F F F x'⋅''∂=-=-=-∂'''⋅, 1212222yF zF yF F z z z x y z x y F F F ''''+⋅∂∂+=-==∂∂'''. (3) 【答案】 (D).【解析】0x =与1x =都是瑕点.应分成()()()22211212ln 1ln 1ln 1mm mnnnx x x xxx---=+⎰⎰,用比较判别法的极限形式,对于()2120ln 1m nx x-,由于121012[ln (1)]lim 11mnx n mx xx+→--=.显然,当1201n m<-<,则该反常积分收敛. 当120n m -≤,1210[ln (1)]lim mx nx x+→-存在,此时()2120ln 1mn x x -实际上不是反常积分,故收敛.故不论,m n 是什么正整数,()2120ln 1mnx dx x-总收敛.对于()2112ln 1mnx x-⎰,取01δ<<,不论,m n 是什么正整数,1211211[ln (1)]lim lim ln (1)(1)01(1)mnmx x x xx x x δδ--→→-=--=-, 所以()2112ln 1mnx dx x-⎰收敛,故选(D).(4)【答案】 (D). 【解析】()()222211111()nnn ni j i j n nn i n jn i n j =====++++∑∑∑∑22111()()n n j i n n j n i ===++∑∑ 12220211111lim lim ,11()nn n n j j n dy j n jn y n→∞→∞====+++∑∑⎰ 1011111lim lim ,11()nn n n i i n dx i n i n x n→∞→∞====+++∑∑⎰()()2222111111lim lim()()n nn nn n i j j i n n j n i n i n j →∞→∞=====++++∑∑∑∑ 221(lim )nn j n n j →∞==+∑1(lim )nn i nn i →∞=+∑ 1120011()()11dx dy x y =++⎰⎰()()11200111dx dy x y =++⎰⎰. (5)【答案】 (A).【解析】由于AB E =,故()()r AB r E m ==.又由于()(),()()r AB r A r AB r B ≤≤,故(),()m r A m r B ≤≤ ①由于A 为m n ⨯矩阵,B 为n m ⨯矩阵,故(),()r A m r B m ≤≤ ②由①、②可得(),()r A m r B m ==,故选A. (6)【答案】 (D).【解析】设λ为A 的特征值,由于2A A O +=,所以20λλ+=,即(1)0λλ+=,这样A 的特征值只能为-1或0. 由于A 为实对称矩阵,故A 可相似对角化,即A Λ:,()()3r A r =Λ=,因此,1110-⎛⎫ ⎪- ⎪Λ= ⎪- ⎪⎝⎭,即1110A -⎛⎫ ⎪- ⎪Λ= ⎪- ⎪⎝⎭:. (7) 【答案】 (C).【解析】离散型随机变量的分布函数是跳跃的阶梯形分段函数,连续型随机变量的分布函数是连续函数.观察本题中()F x 的形式,得到随机变量X 既不是离散型随机变量,也不是连续型随机变量,所以求随机变量在一点处的概率,只能利用分布函数的定义.根据分布函数的定义,函数在某一点的概率可以写成两个区间内概率的差,即{}{}{}()()1111111110122P X P X P X F F e e --==≤-<=--=--=-,故本题选(C).(8)【答案】 (A).【解析】根据题意知,()2212x f x e π-=(x -∞<<+∞),()21,1340,x f x ⎧ -≤≤⎪=⎨⎪ ⎩其它利用概率密度的性质:()1f x dx +∞-∞=⎰,故()()()()03121001312424a a f x dx af x dx bf x dx f x dxb dx b +∞+∞+∞-∞-∞-∞=+=+=+=⎰⎰⎰⎰⎰所以整理得到234a b +=,故本题应选(A).二、填空题 (9) 【答案】0.【解析】因为 ()()22ln 1ln 1ttt dy t e dx e-+==-+-, ()()()()22222ln 12ln 11tt t td te d y dt t e t e e dx dt dx t -+⎡⎤=⋅=-⋅-+⋅-⎢⎥+⎣⎦,所以2200t d y dx ==. (10)【答案】 4π-.x t =,2x t =,2dx tdt =,利用分部积分法,原式220cos 22cos 2sin t t tdt t tdt t d t πππ=⋅==⎰⎰⎰20002sin 2sin 4cos t t t tdt td t πππ⎡⎤=-=⎢⎥⎣⎦⎰⎰0004cos cos 4cos 4sin 4t t tdt t ππππππ⎡⎤=-=-=-⎢⎥⎣⎦⎰. (11) 【答案】0.【解析】12222LL L xydx x dy xydx x dy xydx x dy +=+++⎰⎰⎰()()()01221011x x dx x dx x x dx x dx -=+++-+-⎰⎰ ()()0122122xx dx x x dx -=++-⎰⎰01322310223223x x x x -⎛⎫⎛⎫=++- ⎪ ⎪⎝⎭⎝⎭211203223⎛⎫⎛⎫=--++-= ⎪ ⎪⎝⎭⎝⎭(12) 【答案】23. 【解析】()2221221211000211212021r rrz d rdr zdxdydz d rdr zdz dxdydz d rdr dz d r rdrππππθθθθΩΩ⎛⎫⎪⋅ ⎪⎝⎭==-⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰4211222r d r dr πθπ⎛⎫-⎪⎝⎭=⎰⎰126204122r r d πθπ⎛⎫- ⎪⎝⎭=⎰20112266322d πθπππ⋅===⎰. (13)【答案】6a =.【解析】因为由123,,ααα生成的向量空间维数为2,所以123(,,)2r ααα=. 对123(,,)ααα进行初等行变换:123112112112211013013(,,)1010130060202000a a a ααα⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪--⎪ ⎪ ⎪=→→ ⎪ ⎪ ⎪-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭所以6a =.(14) 【答案】2.【解析】利用离散型随机变量概率分布的性质,知{}001!k k CP X k Ce k ∞∞======∑∑,整理得到1C e -=,即 {}111!!k e P X k e k k --===.故X 服从参数为1的泊松分布,则()()1,1E X D X ==,根据方差的计算公式有()()()222112E X D X E X =+=+=⎡⎤⎣⎦. 三、解答题(15)【解析】对应齐次方程的特征方程为2320λλ-+=,解得特征根121,2λλ==,所以对应齐次方程的通解为212x xc y C e C e =+.设原方程的一个特解为*()xy x ax b e =+,则()()*22x y axax bx b e '=+++,()()*2422x y axax bx a b e ''=++++,代入原方程,解得1,2a b =-=-,故特解为*(2)xy x x e =--.故方程的通解为*212(2)x x xc y y y C e C e x x e =+=+-+.(16)【解析】因为22222222111()()x x x t t t f x x t e dt xe dt te dt ---=-=-⎰⎰⎰,所以2224423311()2222x x t x x t f x x e dt x ex ex e dt----'=+-=⎰⎰,令()0f x '=,则0,1x x ==±.又22421()24x t x f x e dt x e--''=+⎰,则21(0)20t f e dt -''=<⎰,所以2211111(0)(0)(1)22t t f t e dt e e ---=-=-=-⎰是极大值.而1(1)40f e -''±=>,所以(1)0f ±=为极小值.又因为当1x ≥时,()0f x '>;01x ≤<时,()0f x '<;10x -≤<时,()0f x '>;1x <-时,()0f x '<,所以()f x 的单调递减区间为(,1)(0,1)-∞-U ,()f x 的单调递增区间为(1,0)(1,)-+∞U .(17)【解析】 (I)当01x <<时0ln(1)x x <+<,故[]ln(1)nn t t +<,所以[]ln ln(1)ln nn t t t t +<,则[]11ln ln(1)ln nn t t dt t t dt +<⎰⎰()1,2,n =L .(II)()111101ln ln ln 1n n n t t dt t t dt td t n +=-⋅=-+⎰⎰⎰ ()211n =+,故由 ()1210ln 1n n u t t dt n <<=+⎰,根据夹逼定理得()210lim lim01n n n u n →∞→∞≤≤=+,所以lim 0n n u →∞=.(18)【解析】(I) (1)1222(1)1122(1)(1)2(1)121lim lim (1)(1)2121n n n n n n n n n nx x n n xx n n +-++--→∞→∞--⋅+-+=--⋅--222(21)21lim lim 2121n n n x n x x n n →∞→∞--==⋅=++, 所以,当21x <,即11x -<<时,原级数绝对收敛.当21x >时,原级数发散,因此幂级数的收敛半径1R =.当1x =±时,11211(1)(1)2121n n n n n x n n --∞∞==--⋅=--∑∑,由莱布尼兹判别法知,此级数收敛,故原级数的收敛域为[]1,1-.(II) 设1122111(1)(1)()2121n n nn n n S x x x x n n --∞∞-==⎛⎫--=⋅=⋅⋅ ⎪--⎝⎭∑∑,其中令 12111(1)()21n n n S x x n -∞-=-=⋅-∑()1,1x ∈-,所以有 12221111()(1)()n n n n n S x xx ∞∞---=='=-⋅=-∑∑ ()1,1x ∈-, 从而有 12211()1()1S x x x '==--+ ()1,1x ∈-,故 11201()(0)arctan 1xS x dx S x x =+=+⎰,()1,1x ∈-.1()S x 在1,1x =-上是连续的,所以()S x 在收敛域[]1,1-上是连续的.所以()arctan S x x x =⋅,[]1,1x ∈-.(19)【解析】 ( I )令()222,,1F x y z x y z yz =++--,故动点(),,P x y z 的切平面的法向量为()2,2,2x y z z y --,由切平面垂直xOy ,故所求曲线C 的方程为222120x y z yz z y ⎧++-=⎨-=⎩. ( II ) 由⎩⎨⎧=-=-++,02,1222y z yz z y x 消去z ,可得曲线C 在xOy 平面上的投影曲线所围成的xOy 上的区域223:{(,)|1}4D x y x y +≤,由()()x x yz z y x '='-++1222,由 dxdy zy yzz y dxdy y z x z dS 24412222--++=⎪⎪⎭⎫⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂+=,故(22323344DDDx y zI dS x dxdy xdxdy dxdy y z yz∑-==+=+++-⎰⎰⎰⎰33123Ddxdy ππ==⋅=. (20)【解析】因为方程组有两个不同的解,所以可以判断方程组增广矩阵的秩小于3,进而可以通过秩的关系求解方程组中未知参数,有以下两种方法.方法1:( I )已知Ax b =有2个不同的解,故()()3r A r A =<,对增广矩阵进行初等行变换,得111110101010111111a A a λλλλλλ⎛⎫⎛⎫ ⎪ ⎪=-→- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭22111111010101010110011a a λλλλλλλλλ⎛⎫⎛⎫⎪⎪→-→- ⎪ ⎪ ⎪ ⎪-----+⎝⎭⎝⎭当1λ=时,11111111000100010000000A a ⎛⎫⎛⎫⎪ ⎪→→ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,此时,()()r A r A ≠,故Ax b =无解(舍去).当1λ=-时,111102010002A a -⎛⎫ ⎪→- ⎪ ⎪+⎝⎭,由于()()3r A r A =<,所以2a =-,故1λ=- ,2a =-.方法2:已知Ax b =有2个不同的解,故()()3r A r A =<,因此0A =,即211010(1)(1)011A λλλλλ=-=-+=,知1λ=或-1.当1λ=时,()1()2r A r A =≠=,此时,Ax b =无解,因此1λ=-.由()()r A r A =,得2a =-.( II ) 对增广矩阵做初等行变换31012111211121020102010102111100000000A ⎛⎫- ⎪----⎛⎫⎛⎫ ⎪⎪ ⎪⎪=-→-→- ⎪ ⎪ ⎪ ⎪ ⎪- ⎪⎝⎭⎝⎭ ⎪ ⎪⎝⎭可知原方程组等价为1323212x x x ⎧-=⎪⎪⎨⎪=-⎪⎩,写成向量的形式,即123332110210x x x x ⎛⎫⎪⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪=+- ⎪ ⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭ ⎪ ⎪⎝⎭.因此Ax b =的通解为32110210x k ⎛⎫⎪⎛⎫ ⎪⎪ ⎪=+- ⎪ ⎪ ⎪ ⎪⎝⎭ ⎪ ⎪⎝⎭,其中k 为任意常数.(21)【解析】 ( I )由于二次型在正交变换x Qy =下的标准形为2212y y +,所以A 的特征值为1231,0λλλ===.由于Q 的第3列为2222T ⎛⎫ ⎪ ⎪⎝⎭,所以A 对应于30λ=的特征向量为22,0,22T⎛⎫⎪ ⎪⎝⎭,记为3α. 由于A 是实对称矩阵,所以对应于不同特征值的特征向量是相互正交的,设属于121λλ==的特征向量为()123,,Tx x x α=,则30T αα=,13220x x +=. 求得该方程组的基础解系为()()120,1,0,1,0,1TTαα==-,因此12,αα为属于特征值1λ=的两个线性无关的特征向量.由于12,αα是相互正交的,所以只需单位化:())1212120,1,0,1,0,12T Tααββαα====-. 取()1232022,,100202Q ββα⎛⎪⎪==⎝⎭,则110T Q AQ ⎛⎫ ⎪=Λ= ⎪ ⎪⎝⎭,且1TQ Q -=, 故 1102201011022TA Q Q ⎛⎫- ⎪ ⎪=Λ= ⎪ ⎪- ⎪⎝⎭.( II )A E +也是实对称矩阵,A 的特征值为1,1,0,所以A E +的特征值为2,2,1,由于A E +的特征值全大于零,故A E +是正定矩阵.(22)【解析】当给出二维正态随机变量的的概率密度(),f x y 后,要求条件概率密度|(|)Y X f y x ,可以根据条件概率公式|(,)(|)()Y X X f x y f y x f x =来进行计算.本题中还有待定参数,A 要根据概率密度的性质求解,具体方法如下.()()22222222()(),xxy y y x x xy x X f x f x y dy A e dy A e dy Ae e dy +∞+∞+∞+∞-+--------∞-∞-∞-∞====⎰⎰⎰⎰2,x A e x π-=-∞<<+∞.根据概率密度性质有()21x X f x dx A e dx A ππ+∞+∞--∞-∞===⎰,即1A π-=,故()2x X f x π-=,x -∞<<+∞.当x -∞<<+∞时,有条件概率密度()()()222222222(),,,x xy y x xy y x y Y X x X f x y f y x x y f x A eπππ-+--+----===-∞<<+∞-∞<<+∞.(23)【解析】()()()22123~,1,~,,~,N B n N B n N B n θθθθ--()()()()31122331i i i E T E a N a E N a E N a E N =⎛⎫==++ ⎪⎝⎭∑()()221231a n a n a n θθθθ=-+-+()()212132na n a a n a a θθ=+-+-.因为T 是θ的无偏估计量,所以()E T θ=,即得()()12132010na n a a n a a =⎧⎪-=⎨⎪-=⎩,整理得到10a =,21,a n =31a n=.所以统计量 ()()12323111110T N N N N N n N n n n n=⨯+⨯+⨯=⨯+=⨯-.注意到1(,1)N B n θ-:,故()()()11211D T D n N D N n n⎡⎤=⨯-=⨯⎢⎥⎣⎦()11n θθ=-.。
