光学赵凯华答案2
赵凯华光学非线性光学_2

绪论§4、非线性介质中的波方程光与物质的相互作用:电磁相互作用理论工具:Maxwell方程组+物质方程0t t ρ∇⋅=⎧⎪∇⋅=⎪⎪∂⎨∇×=−∂⎪⎪∂∇×=+⎪∂⎩D B BE D H j 000D B 0t εμμσρ=+⎧⎪=+⎪⎪⎨=⎪∂⎪∇⋅+=⎪∂⎩E PH Mj E j 绪论§4、非线性介质中的波方程考虑均匀、非导电、非磁性、无自由电荷的介质电极化强度波运动方程,0==j ρH B P E D 00,με=+=NLL P P P +=22200022t tμεεμ∂∂∇−=∂∂E PE ⇒绪论§5、非线性光学的主要机制•电子的贡献电子云的畸变电子能级布局数的改变•分子的振动与转动•分子的重新取向与重新分布•电致伸缩•热效应第二章非线性极化的宏观描述非线性极化的宏观描述(上)§1引言1.极化电介质在外场的作用下,由于静电感应,在介质内部产生反方向电场,但不足以抵消外电场。
a.无极分子正、负电荷中心重合分子本身电偶极矩为零。
外场导致正、负电荷中心发生相对位移分子本身电偶极矩不为零。
介质体现出总的极化强度。
ΕG=p G 0≠p G≠=∑p P G G 非线性极化的宏观描述(上)§1引言b.有极分子正负电荷中心不重合,分子本身有电偶极矩(1)无外场,热运动导致杂乱分布(2)外光场,导致单个电偶极矩取向相近介质表现出总的极化强度:EG0≠p G 0==∑p P G G 0≠=∑p P G G 非线性极化的宏观描述(上)§1引言宏观描述极化强度与外加电场之间的关系(1)各向同性介质:与方向相同,简单的正比关系(2)各向异性介质:与方向不平行,正比关系P G E GE P G G χ=()()()zE E E y E E E xE E E P z zz y zy x zx z yz y yy x yx z xz y xy x xx ˆˆˆχχχχχχχχχ++++++++=GP G E G§1引言2.非线性极化非线性极化是非线性光学现象的产生原因之一介质在外加光场的作用下产生非线性极化(气体、液体、固体、液晶、聚合物、等离子体等)•特殊性:不同的微观机制与过程电子能级、分子振动/转动、取向•共性:统一的宏观描述线性非线性:光场:频率、偏振等非线性极化:频率、偏振特性E P )1(χ=(1)(2)2(3)3P E E E χχχ=+++"§2介质对光场的非线性响应外加光场介质的电极化线性:非线性:介质极化是介质对外加光场的响应1.介质极化的线性响应函数1)因果性原理因:外加光场果:介质极化线性极化P E EP )1(χ="+++=3)3(2)2()1(E E E P χχχ非线性极化的宏观描述(上)§2介质对光场的非线性响应任意时间段的光场,都会对其后时刻的介质极化产生贡献:其中,是线性响应函数。
赵凯华光学1079186849178

返
回 上一页 下一页
绪
论
把量子论贯穿到整个辐射和吸收过程中,提出了杰出的光量子(光子)理论,圆满解释了光电效应, 并为后来的许多实验例如康普顿效应所证实。1924年德布罗意(L.V.de Broglie,1892- )创立了 物质波学说。他大胆地设想每一物质的粒子都和一定的波相联系 ,这一假设在1927年为戴维孙 (C.J.Davisson,1881-1958)和革末(L.H.Germer,1896-1971年)的电子束衍射实验所证实。 2.5现代光学时期 从本世纪六十年代起,特别在激光问世以后,由于光学与许多科学技术领域紧密结合、相互渗 透,一度沉寂的光学又焕发了青春,以空前的规模和速度飞速度飞速发展,它已成为现代物理学和 现代科学技术一块重要的前沿阵地,同时又派生了许多崭新的分支学科。 1958年肖络(A.L.Schawlow)和汤斯(C.H.Townes)等提出把微波量子放大器的原理推广到光 频率段中去,1960年梅曼(T.H.Maiman,1927- ),首先成功地制成了红宝石激光器。自此以后, 激光科学技术的发展突飞猛进,在激光物理、激光技术和激光技术和激光应用等各方面都取得了巨 大的进展。同时全息摄影术已在全息显微术、信息存贮、象差平衡、信息编码、全息干涉量度、声 波全息和红外全息等方面获得了越来越广泛的应用。光学纤维已发展成为一种新型的光学元件,为 光学窥视(传光传象)和光通讯的实现创造了条件,它已成为某些新型光学系统和某些特殊激光器 的组成部分。可以预期光计算机将成为新一代的计算机,想象中的光计算机,由于采取了光信息存 储,并充分吸收了光并行处理的特点,它的运算速度将会成千倍地增加,信息存储能力可望获得极 大的提高,甚至可能代替人脑的部分功能。总之,现代光学与其他科学和技术的结合,已在人们的 生产和生活中发挥着日益重大的作用和影响,正在成为人们认识自然、改造自然以及提高劳动生产 率的越来越强有力的武器。
实验六 原子光谱实验—氢氘光谱的测量.

实验六 原子光谱实验—氢氘光谱的测量一、 实验目的(1)熟悉光栅光谱仪的基本原理,了解它的性能和使用方法。
(2)熟悉测量氢-氘和其他原子光谱的方法。
(3)计算氢和氘原子核的质量比。
(4)了解并观察钠、汞原子的主要光谱线。
二、 实验原理(1) 测量公式的导出:根据玻尔(Bohr )原子理论,一个电子绕正电荷为Ze 、质量为M z 的原子核作圆周运动时,其能量是量子化的,可表示为2Z 22220242n1R hcZ n 1h )4(Z e 2E -=πεμπ-= (6-0) 其中ZZ M m mM +=μ 为核与电子的折合质量,ZZ 32042Z Z 32042Z M m 11R M m 11c h )4(me 2M m M c h )4(me 2R +=+πεπ=+πεπ=∞ 称为里德堡(Rydberg )常数,ε0为真空介电常数,m 为电子质量,h 和c 分别为普朗克常数和真空中的光速,n=1,2,3…,称为能级量子数,而常数1-32042m 10973731ch )4(me 2R =πεπ=∞ 为忽略原子核运动时(即认为原子核质量M Z 趋于无穷)的里德堡常数。
当原子从高能级向低能级跃迁时,便辐射出光子,并满足能量守恒:)m1n 1(hcZ R h 222Z --=ν 其中ν为光子频率,n 为上能级量子数,m 为下能级量子数。
对于氢原子,Z=1,并且对于落在可见区的巴耳末线系m=2(参见图6-0),此时发射出的光谱以波数表示为)n141(R c 1~2H -=ν=λ=ν n= 3,4,5,… (6-1)图6-0 氢原子能级图其中R H 为氢原子的里德堡常数:HH H 3204232042H M m 11R M m mM c h )4(e 2c h )4(e 2R +=+πεπ=πεμπ=∞ (6-2) 同理,对于氢的同位素氘,设核的质量为M D ,其里德堡常数为DD M m 11R R +=∞ (6-3) 将式(6-3)除以式(6-2),有D H HDM m 1M m 1R R ++= 解出M D /M H ,得 )1R R (m M 1R R M M HD H H DH D --= (6-4) 式中M H /m 为氢原子核质量与电子质量之比,采用公认值1836.5。
赵凯华光学mechanicalwave

线度与波长相比较,线度比波长小。
对一定波长的波,线度小,衍射现象明显 线度大,衍射现象不明显 30
波的衍射
水波通过窄缝时的衍射
31
衍射:受限的尺度与波长相比
广播和电视
障
哪个更容易
碍
收到?
物
容易听到男 士还是女士 说话声音?
32
2. 用惠更斯作图法导出光的折射定律 法线
¾ 作图步骤: ¾ 导出折射定律
几种波速:
纵波:u// =
E
ρ
E——弹性模量
横波:u⊥ =
G
ρ
弦上横波:u = T η
G ——切变模量
T ——弦线张力 η——弦线密度
流体内的波:u = B ρ
B ——容变模量
18
波动方程:
∂2ξ
∂x2
=
1 u2
∂2ξ
∂t 2
∇ 2ξ
=
1 u2
ξ
对于不同介质或不同波,波速 三维空间波动方程
u
值不同。
27
2、惠更斯原理 基本内容: 子波概念:波面上任一点都是新的振源——子波源
发出的波称为子波 子波面的包络面——新波前 t 时刻各子波波面的公共切面(包络面) 就是该时刻的新波面 作用:已知一波面就可求出任意时刻的波面
28
例: 波在各向同性介质中传播
t 时刻 t+Δt时刻
波面
波面
·
u
· ·
·
·
波传播方向
Δx)
Δx
−φ
(
x)
φ′( x) Δx + φ ( x) 所以 F
=
ES
⋅
∂2ξ
∂x2
⋅
赵凯华光学及习题答案 ppt课件

二、几何光学时期
<1500~1800,大约300年>
1、建立了光的反射定律和折射定律, 奠定了几何光学的基础
2、研制出了望远镜和显微镜等光学仪器 3、牛顿为代表的微粒说占据了统治地位 4、对折射定律的解释是错误的
n2 n1 v2n v1n
v 1t
v 1 t v 1 s in i1 v 2 t v 2s in i2 v 1 n
光的本性
光的两种互补性质: 传播过程中显示波动性 与其他物质相互作用时显示粒子性
光具有波粒二象性
赵凯华光学及习题答案
1、全息术、光学传递函数和激光的问世 是经典光学向现代光学过渡的标志
2、光学焕发了青春,以空前的规模和速度 飞速发展 1)智能光学仪器 2)全息术 3)光纤通信 4)光计算机 5)激光光谱学的实验方法
5)线光谱:光谱集中在一些分立的波长区 间的线状谱线,就叫线光谱。
dI
dIdLeabharlann d连续光谱1 2 3 线光谱
谱线宽度:每条线光谱在其半强度值处的波长间隔
称为谱线宽度, 越小表示光波的单色性越好.
光学的研究对象、分支与应用
光学是研究光的传播以及它和物质相互作用问题的学科
几何光学: 从光的直进、反射、折射等基本实验定律出发,研究成像
2)光强:通过单位面积的平均光功率,
或者说,光的平均能流密度
3)光强表达式:
SEH
EH
0E 0H
SEH
0 E2
0
, 分别是相对介电常数和相对磁率
0 , 分0 别是真空介电常数和真空磁率
在光频波段 1
1/ 00 c1/ 00
nc/
故
S 0 nE2 n E2
0
赵凯华光学optics_25

第二次课堂测验(25分钟)在光栅光谱仪中,所用光栅有2000条光缝,每缝宽a=0.5μm,光栅周期d=3μm,所用准直透镜和汇聚透镜的焦距f'=50c m,口径都足够大。
已知缝光源中有两条谱线λ1=6000Å和λ2=6010Å。
○1、画出光栅光谱仪的实验装置图(或者光路图)。
○2、当光源很窄时,该光谱仪能够分辨开这两条谱线?○3、在每缝的零级衍射包络中,可观察到几个干涉级别λ1的光谱线?○4、当光源缝宽S=0.2m m 时,该光谱仪在一级光谱中,能否分辨开这两条谱线?第49,50课时,共72课时-111-第49,50课时, 共72课时 - 112 - 解:○1如图所示;○2在波长λ处,k 级衍射条纹能够分辨的最小波长差为: cos cos k Nd d kN λλδλθθ==,做为上限,设k =1,可求得波长λ1 = 6000 Å 处能够分辨的最小波长差为:δλ=60002000=3 Å,因此波长距之10Å的λ2 = 6000 Å 谱线应能分辨;○3零级衍射包络的角半径θm满足:s i nθm=λa第k级缝间干涉主极大衍射角θk满足:s i nθk=kλd;可见,零级衍射包络的半角宽度内包含缝间干涉主极大数k为:k=ad=30.5=6。
但0级与λ2谱线重合,而6级缺级,所以只可观察到干涉级别为1,2,3,4,5的λ1谱线。
(注:在使用光谱仪的场合,±k级同属k级。
)○4对于谱线λ1=6000Å和λ2=6010Å,每线角半径约为:第49,50课时,共72课时-113-Δθ1=λN d≈0.62000×3=1×10-4r a d普线一级衍射角约满足:s i nθ≈λd=0.63=0.2,即c o sθ=1-0.22=0.9798,所以在6000Å附近谱线λ1=6000Å和λ2=6010Å的角距离应为:Δθ2=Δλd c o sθ=10×10-43×0.9798=3.4×10-4r a d>Δθ1,∴当光源缝宽无限窄时,上述一级谱线原本是可以区分的。
赵凯华光学optics_18
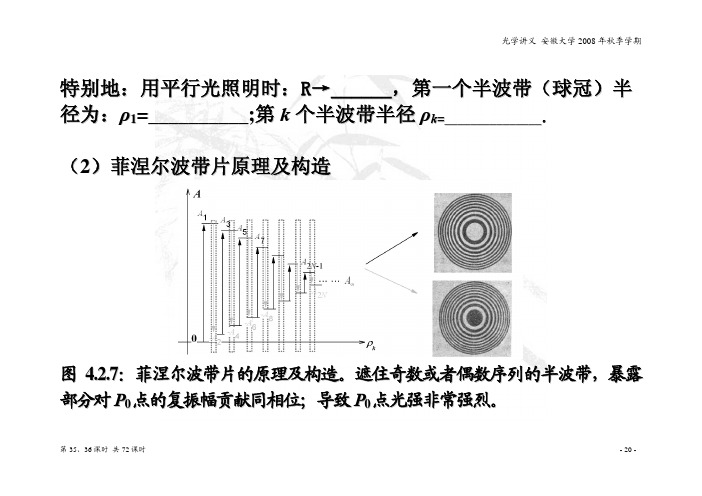
特别地:用平行光照明时:R→______,第一个半波带(球冠)半径为:ρ1=__________;第k个半波带半径ρk=_______________。
(2)菲涅尔波带片原理及构造
图4.2.7:菲涅尔波带片的原理及构造。
遮住奇数或者偶数序列的半波带,暴露部分对P0点的复振幅贡献同相位;导致P0点光强非常强烈。
第35、36课时共72课时- 20 -
(3)菲涅尔波带片的透镜性质1
如前所述,ρk2=k R bλ
(R+b),即
1
R+
1
b=
kλ
ρk=
λ
ρ1
图4.2.8:菲涅尔波带片的透镜性质1。
物体点O发出的发散球面波半径R和汇聚球面波半径b满足透镜的物象关系,此点可视为菲涅尔波带片的一个透镜性质。
第35、36课时共72课时- 21 -
(4)菲涅尔波带片的透镜性质2——多焦点和虚焦点
下面的讨论将表明,当平行光照射同一个菲涅尔波带片时,轴线上会出现多重亮点(多重实焦点)。
同样、也可以观察到多重虚焦点。
图4.2.9:菲涅尔半波带片除了主焦点外,还存在着负焦点。
该示意图阐述一个焦距为f的菲涅尔半波带片,同时还存在着焦距为f/3的副焦点。
同理该半波带片焦距为f/5、f/7、f/9…的副焦点也是存在的。
第35、36课时共72课时- 22 -。
赵凯华光学课件及习题答案

其物理意义:
可以通过比较两个振动的光程来考察 两个振动的步调差异。
1.5
在真空中波长为 λ 的单色光,在折射率为 n 的透明介质中从 P 沿某路径传到 Q,若 P、Q 两 点位相差为 5π,则路径 PQ 的光程为:
(1) 5λ (2) 5nλ (3) 2.5λ (4) 2.5nλ (5) 无法判断
i nsin i n sin i
2.2 全反射定律
◆ 当光线从光密媒质 射向光疏媒质时,折射 角大于入射角;当入射 角增大到某一临界值时, 折射光线消失,光线全 部反射,此现象叫全反 射。
全反射临界角:
ic s in1(n2/n1)
n 2 1 的空气对于 n1 1.5 的玻璃,临界角
ic 42
◆ 棱镜光谱仪中的色散元件色散 棱镜就是利用介质的这种性质, 将含有多种波长的复色光分散开 来。
光的可逆性原理:
当光线的方向反转时,它将逆着同一 路径传播,称为光的可逆性原理。
§3 惠更斯原理
波线
2.1 波的几何描述
波动:扰动在空间的传播 球面波波面 平面波
波面:
波面与波线
(1)在同一振源的波场中
光在均匀媒质里沿直线传播。 例:物体的影子, 针孔成像 例:海市蜃楼(mirage)
海市蜃楼(mirage)是一种折光现象,由于靠 近表面竖直方向上空气密度的剧烈变化,使 得一些远处的物体在一定区域形成图像以代 替其真实位置。这些图像是扭曲的,倒转的 或是摇摆的。
空气密度与气压、温度和水蒸气含量密切相关。
2、爱因斯坦提出了光子假说,成功地解释了 光电效应问题
3、光的某些行为象经典的“波动” 4、另一些行为却象经典的“粒子”
