晶体的电光效应及其应用
晶体的电光效应实验报告

晶体的电光效应实验报告晶体的电光效应实验报告引言:晶体是一种具有有序排列的原子、离子或分子的固体物质。
它们在光学、电子学和通信等领域中具有重要的应用。
本实验旨在探究晶体的电光效应,通过实验观察和数据分析,深入了解晶体在电场作用下的光学行为。
实验装置和步骤:实验装置包括:晶体样品、光源、电源、电极、偏振片等。
实验步骤如下:首先,将晶体样品放置在实验台上,并连接电源和电极;然后,使用光源照射晶体样品,并通过偏振片调节光的偏振方向;最后,记录观察到的光学现象,并根据实验数据进行分析和解释。
实验结果:在实验过程中,我们观察到了晶体的电光效应。
当电场施加到晶体上时,晶体的折射率发生了变化,导致光线的传播速度发生改变。
这种现象称为克尔效应。
通过调节电场的强度,我们发现晶体的折射率随电场的变化而变化,进一步验证了克尔效应。
此外,我们还观察到了晶体的双折射现象。
在无电场作用下,晶体的折射率相同,光线以相同的速度传播。
然而,在电场的作用下,晶体的折射率变化,光线被分成了两束,分别沿着不同的方向传播。
这种现象称为晶体的双折射现象,也是晶体的电光效应的重要表现形式之一。
数据分析:通过实验测量和数据分析,我们可以得出晶体的电光效应与电场强度之间存在一定的关系。
随着电场强度的增加,晶体的折射率也随之增加。
这种关系可以通过线性拟合得到一条直线,从而可以预测在不同电场强度下晶体的折射率。
此外,我们还可以通过实验数据计算晶体的电光系数。
电光系数是衡量晶体电光效应强弱的指标,它描述了晶体折射率随电场变化的程度。
通过实验测量晶体在不同电场下的折射率,并将其与电场强度进行对比,我们可以计算出晶体的电光系数。
讨论和结论:通过本实验,我们深入了解了晶体的电光效应。
晶体在电场作用下表现出的克尔效应和双折射现象,为我们理解晶体在光学领域的应用提供了重要的实验基础。
此外,我们还发现晶体的电光效应与电场强度之间存在一定的关系,并通过实验数据计算出晶体的电光系数。
研究性实验报告——晶体的电光效应1.

研究性实验报告——晶体的电光效应1.
实验目的:
通过实验,学习晶体的电光效应原理,掌握利用光学仪器测量晶体的电光性质的方法,并了解晶体的电光效应在光电技术中的应用。
实验原理:
当晶体被加上一个外部的电场时,它的介电常数会发生变化,从而会改变晶体的折射率。
这种现象被称为晶体的电光效应。
晶体的电光效应可以分为两种类型:平移效应和旋
转效应。
平移效应:当一个光束穿过一个加有电场的单轴晶体时,光束的振动方向会发生平移。
平移角度与电场的强度成正比。
旋转效应:当一个光束穿过一个加有电场的双轴晶体时,光束会因为双折射现象而沿
着不同的路径传播。
这种现象被称为旋转效应。
实验步骤:
1. 实验室管理员指导下,打开光路并将实验装置调整到最佳状态。
2. 将一块单轴晶体放在两根金属极板之间,接上稳压直流电源以施加电场。
3. 在透过晶体的光路中加入一束偏振光,并将光路调整到最佳状态。
使用光度计测
量被散射的光束的光密度与偏振角度之间的关系。
4. 按照同样的方法,使用双轴晶体来研究旋转效应。
5. 根据实验得到的数据,绘制光密度和电场强度之间的关系图,并分析它的形状和
趋势。
实验结果和分析:
从实验数据得到的图形中,我们可以看到光密度和电场强度之间的关系是非线性的,
并且在电场强度为一定值时,光密度会发生一个明显的跳跃现象。
这是因为在这个电场强
度下,晶体的介电常数发生了变化,导致光线发生了反射或折射。
这种现象可以应用于光
电调制器和光电开关等光学器件的设计和制造中。
结论:。
晶体的电光效应及其应用

制晶体的长厚比来降低半波电压,这是它的一个优点; ii) 横向运用中存在着自然双折射作用。由于自然双折
射(晶体的主折射率no、ne)受温度的影响严重,所以对相位
差的稳定性影响很大。
实验表明,KDP晶体的Δ (no-ne)/Δ T~1.1×10-5/℃,
单个下标。经过这些简化后,只计线性电光效应,可得如下 结果:
Δ Bi=γ ijEj
i = 1, 2, …, 6; j = 1, 2, 3
相应的矩阵形式为:
B1
B2
B3
B4
B5
B6
11
21 31
41
51
x2' x2'
s in c os
x3 x3'
经过理论推证,可得:
1 no2
2 63E3
s in
cos
x1'2
1 no2
2 63E3
s in
cos
x2'2
1 ne2
x3'2
2 63E3(cos2 sin2 )x1' x2' 1
得到,该转角与外加电场的大小无关,但转动方向与电场方 向有关。若取α =45°,折射率椭球方程为:
1 no2
63E3 x1'2
1 no2
63E3 x2'2
1 ne2
x3'2
1
或者写成:
3晶体的电光效应与电光调制_实验报告
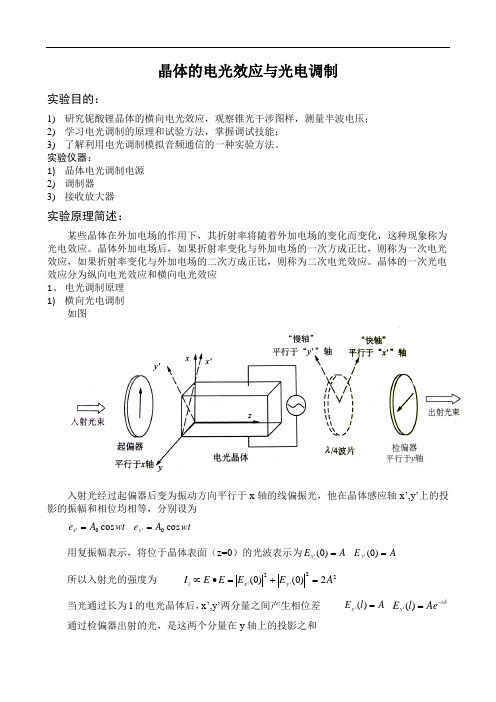
晶体的电光效应与光电调制实验目的:1) 研究铌酸锂晶体的横向电光效应,观察锥光干涉图样,测量半波电压; 2) 学习电光调制的原理和试验方法,掌握调试技能; 3) 了解利用电光调制模拟音频通信的一种实验方法。
实验仪器:1) 晶体电光调制电源 2) 调制器 3) 接收放大器实验原理简述:某些晶体在外加电场的作用下,其折射率将随着外加电场的变化而变化,这种现象称为光电效应。
晶体外加电场后,如果折射率变化与外加电场的一次方成正比,则称为一次电光效应,如果折射率变化与外加电场的二次方成正比,则称为二次电光效应。
晶体的一次光电效应分为纵向电光效应和横向电光效应 1、 电光调制原理 1) 横向光电调制如图入射光经过起偏器后变为振动方向平行于x 轴的线偏振光,他在晶体感应轴x ’,y’上的投影的振幅和相位均相等,分别设为wt A e x cos 0'= wt A e y cos 0'=用复振幅表示,将位于晶体表面(z=0)的光波表示为A E x =)0(' A E y =)0(' 所以入射光的强度为 22'2'2)0()0(A E E E E I y x i =+=•∝ 当光通过长为l 的电光晶体后,x’,y’两分量之间产生相位差 A l E x =)(' δi y Ae l E -=)('通过检偏器出射的光,是这两个分量在y 轴上的投影之和()1245cos )()('0-=︒=-δδi i y y eA e l E E其对应的输出光强I t 可写为 ()()[]2sin 2*2200δA E E I y y t =•∝由以上可知光强透过率为2sin 2δ==i t I I T 相位差的表达式 ()dlVr n l n ny x 2230''22λπλπδ=-=当相位差为π时 ⎪⎭⎫ ⎝⎛=l d r n V n 22302λ由以上各式可将透过率改写为 ()wt V V V V VT m sin 2sin 2sin 022+==ππππ可以看出改变V0或Vm ,输出特性将相应变化。
晶体的电光效应实验报告完整版

晶体的电光效应介质因电场作用而引起折射率变化的现象称为电光效应,介质折射率和电场的关系可表示为:+++=20bE aE n n (1)式中n 0是没有外加电场(E =0)时的折射率,a 和b 是常数,其中电场一次项引起的变化称为线性电光效应,由Pokels 于1893年发现,故也称为Pokels 效应;由电场的二次项引起的变化称为二次电光效应,由Kerr 在1875年发现,也称Kerr 效应,在无对称中心晶体中,一次效应比二次效应显著得多,所以通常讨论线性效应。
尽管电场引起折射率的变化很小,但可用干涉等方法精确地显示和测定,而且它有很短的响应时间,所以利用电光效应制成的电光器件在激光通信、激光测距、激光显示、高速摄影、信息处理等许多方面具有广泛的应用。
[实验目的]研究铌酸锂晶体的横向电光效应,观察锥光干涉图样,测量半波电压;学习电光调制的原理和实验方法,掌握调试技能;了解利用电光调制模拟音频光通信的一种实验方法;[实验原理]1. 晶体的电光效应 按光的电磁理论,光在介质中传播的速度为210)(−==µεn c c ,ε为介电系数,是对称的二阶张量,即ji ij εε=,由此建立的D 和E 的关系为:j j i i E D ε= (3,2,1,=j i ) (2)即: 333232131332322212323132121111E E E D E E E D E E E D εεεεεεεεε++=++=++=在各向同性的介质中,εεεε===332211,D 和E 成简单的线性关系,光在这类介质中以某一确定速度传播;但在各向异性的介质中,一般情况下各方向的折射率却不再相同,所以各偏振态的光传播速度也不同,将呈现双折射现象。
如果光在晶体中沿某方向传播时,各个方向的偏振光折射率都相等,则该方向称为晶体的光轴。
若晶体只含有一个这样的方向,则称为单轴晶体。
通常用折射率椭球来描述折射率与光的传播方向、振动方向的关系。
晶体电光效应实验报告

晶体电光效应实验报告晶体电光效应实验报告引言:晶体电光效应是指在外加电场作用下,晶体表面发生光学现象的现象。
这一现象在光电子学和光通信领域有着重要的应用,因此对其进行深入研究和实验探究是非常有意义的。
本实验旨在通过实际操作,观察晶体在电场下的光学变化,进一步了解晶体的电光性质。
实验材料和方法:实验所用材料为一块具有晶体结构的透明晶体样品,实验仪器包括电源、电压表、光源和光强测量仪。
实验步骤如下:1. 将晶体样品放置在实验台上,并确保其表面光洁无划痕。
2. 将电源与电压表连接,调节电源输出电压,并记录下不同电压下的数值。
3. 将光源对准晶体样品,调节光源亮度,并记录下不同亮度下的数值。
4. 使用光强测量仪测量不同电压和亮度下的光强,并记录下相应的数值。
实验结果和分析:根据实验数据,我们可以得到晶体在不同电场下的光学变化。
随着电场的增加,晶体的透光性会发生变化,即光强会有所改变。
通过观察实验数据,我们可以发现晶体的光强与电压呈现一定的关联性。
当电压较小时,光强基本保持不变;但当电压达到一定数值后,光强会出现明显的变化。
这说明晶体在电场作用下,会发生电光效应。
进一步分析实验结果,我们可以得出晶体电光效应的几个特点。
首先,晶体的电光效应是非线性的,即光强与电压之间的关系不是简单的比例关系。
其次,晶体的电光效应是可逆的,即当电压减小时,光强会恢复到初始状态。
这说明晶体的电光效应是与电场的存在和强度密切相关的。
晶体电光效应的机理可以通过晶体的结构来解释。
晶体是由离子或分子组成的有序排列的固体,其内部存在着电荷分布的不均匀性。
当外加电场作用于晶体时,电场会使晶体内部的电荷分布发生变化,从而导致晶体的光学性质发生变化。
具体来说,电场会引起晶体内部的电荷重新排列,导致晶体的折射率发生变化,从而影响光的传播和透射。
这就是晶体电光效应的基本机理。
结论:通过本次实验,我们观察到了晶体在电场作用下的光学变化,进一步了解了晶体的电光性质。
KDP晶体电光效应【重要 讲解清晰】

当入射沿 x1 方向偏振,进入晶体后即分解为沿 x1 ' 和 x2 ' 方向的两个垂直 偏振分量。它们在晶体内传播 L 光程分别为 n1 ' L 和 n2 ' L ,两偏振分量的相位 延迟分别为
2 2 L 1 3 n1 ' L (no no 63 E ) 2 2 2 L 1 3 2l n2 ' L (no no 63 E ) 2
41 , 52 , 63 0 ,而且 41 52 。加电场 E 后:
0 0 1 1 1 (0) 0 0 0 0 0 2 2 2 (0) 0 E1 3 3 3 (0) 0 0 0 0 E2 4 0 4 41 0 E 41 E1 5 0 41 0 3 41 E2 5 E 6 0 63 6 0 63 3
1 2 1 2 1 2 2 63 E x1 ' 2 63 E x2 ' 2 x3 ' 1 n n n e o o
(20) (19)
主折射率变为:
1 3 n ' n no 63 E 1 o 2 1 3 n2 ' no no 63 E 2 n ' ne 3
(17)
折射率方程变为:
1 1 ( x12 x2 2 ) 2 x3 2 2 41 ( E1 x2 x3 E2 x3 x1 ) 2 63 E3 x1 x2 1 2 no ne
(18)
电光效应及其应用

电光效应及其应用摘要:电光晶体在外加电场中,随电场强度变化改变折射率的现象称为电光效应。
利用电光效应进行的调制称为电光调制。
关键词:电光效应、电光调制、电致折射率变化1.电光效应某些晶体(固体或液体)在外加电场中,随着电场强度E 的改变,晶体的折射率会发生改变,这种现象称为电光效应。
通常将电场引起的折射率的变化用下式表示:+++=2000bE aE n n (1)式中a 和b 为常数,0n 为00=E 时的折射率。
由一次项0aE 引起折射率变化的效应,称为一次电光效应,也称线性电光效应或普克尔电光效应(pokells );由二次项引起折射率变化的效应,称为二次电光效应,也称平方电光效应或克尔效应(kerr )。
一次电光效应只存在于不具有对称中心的晶体中,二次电光效应则可能存在于任何物质中,一次效应要比二次效应显著。
光在各向异性晶体中传播时,因光的传播方向不同或者是电矢量的振动方向不同,光的折射率也不同。
通常用折射率椭球来描述折射率与光的传播方向、振动方向的关系,在主轴坐标中,折射率椭球方程为1232222212=++n z n y n x (2) 式中1n ,2n ,3n 为椭球三个主轴方向上的折射率,称为主折射率。
如图一所示,从折射率椭球的坐标原点O 出发,向任意方向作一直线OP ,令其代表光波的传播方向k 。
然后,通过O 垂直OP 作椭圆球的中心截面,该截面是一个椭圆,其长短半轴的长度OA 和OB 分别等于波法线沿OP ,电位移矢量振动方向分别与OA 和OB 平行的两个线偏振光的折射率n ′和n ′′。
显然k ,OA ,OB 三者互相垂直,如果光波的传播方向k 平行于x 轴,则两个线偏光波的折射率等于2n 和3n 。
同样当k 平行于y 轴和z 轴时,相应的光波折射率亦可知。
当晶体上加上电场后,折射率椭球的形状、大小、方位都发生变化,椭球的方程变为1222212213223233222222112=+++++n xy n xz n yz n z n y n x (3) 只考虑一次电光效应,上式与式(2)相应项的系数之差和电场强度的一次方成正比。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
②.光沿x2′(或x1′)方向传播
当外加电压平行于x3′轴方向,光沿x2′(或x1′)轴方 向传播时,γ63贡献的电光效应叫γ63的横向运用。这种工 作方式通常对晶体采取 45°-x3切割,即如图 5-3 所示, 晶片的长和宽与x1、x2轴成 45°方向。光沿晶体的[110]
因为γ63、E3不为零,只能是:
cos(2α)-sin(2α)=0
所以:
α=±45 故x3-切割晶片沿光轴方向外加电场后,感应折射率椭球 的三个主轴方向为原折射率椭球的三个主轴绕x3轴旋转45°
得到,该转角与外加电场的大小无关,但转动方向与电场方
向有关。若取α=45°,折射率椭球方程为:
1 no2
通过改变晶体的长厚比,可以降低横向运用的半波电压。但
由于横向运用必须采取补偿措施,结构复杂,对两块晶体的
加工精度要求很高,所以,一般只有在特别需要较低半波电
压的场合才采用。
图 5-4 补偿自然双折射的两种晶体配置
B. LiNbO3
LiNbO3(铌酸锂)以及与之同类型的LiTaO3(钽酸锂)、 BaTaO3(钽酸钡)等晶体,属于3m晶体点群,为单轴晶体。它 们在 0.4~5μm波长范围内的透过率高达98%,光学均匀性 好,不潮解,因此在光电子技术中经常采用。其主要缺点是 光损伤阈值较低。
1 no2
2 63E3
s in
cos
x1'2
1 no2
2 63E3
s in
cos
x2'2
1 ne2
x3'2
2 63E3(cos2 sin2 )x1' x2' 1
由于x1′,x2′,x3′为感应折射率椭球的三个主轴方向,
所以上式中的交叉项为零,即应有:
2 63E3 (cos2 sin 2 )x1' x2' 0
假设感应折射率椭球的新主轴方向为 x1'、x2'、x3' , 则 由 x1'、x2' 、x3' 构成的坐标系可由原坐标系(O-x1x2x3)绕x3轴
旋转α角得到,相应的坐标变换关系为:
x1 x2
x1' x1'
c os s in
x2' x2'
s in c os
x3 x3'
经过理论推证,可得:
相应于这种工作方式的晶片是从KDP型晶体上垂直于光
轴方向(x3轴)切割下来的, 通常称为x3 -切割晶片。在未 加电场时,光沿着x3方向传播不发生双折射。当平行于x3方
向加电场时,感应折射率椭球的表示式为:
B10 (x12 x22 ) B30 x32 2 63E3 x1x2 1
或者
x12 x22 no2
图 5-1 KDP型晶体外型图
(1) KDP型晶体的感应折射率椭球
KDP型晶体无外加电场时,折射率椭球为旋转椭球,在主 轴坐标系(折射率椭球主轴与晶轴重合)中,折射率椭球方程 为:
B10 (x12 x22 ) B30 x32 1
式中:
B10 1/ n12 1/ n02 B20; B30 1/ n32 1/ ne2; n0, ne
方向传播,晶体在电场方向上的厚度为d,在传播方向上的 长度为l
如前所述,当沿x3方向外加电压时,晶体的感应折射率 椭球的主轴方向系由原折射率椭球主轴绕x3轴旋转45°得 到,因此,光沿感应折射率椭球的主轴方向x2′传播时,相 应的两个特许线偏振光的折射率为n1′和n3′,该二光由晶
片射出时的相位差(“电光延迟”)为:
圆,变成现在的主轴在45°方向上的椭圆,如图 5-2 所示。
图 5-2 折射率椭球与x1Ox2面的交线
首先,将α=45°时的折射率椭球方程变换为:
1 no2
(1 no2 63E3 )x1'2
1 no2
(1 no2 63E3 )x2'2
1 ne2
x3'2
1
因为γ63的数量级是10-10cm/V,E3的数量级是104
x32 ne2
2 63E3x1x2
1
为了讨论晶体的电光效应,首先应确定感应折射率椭球 的形状,也就是找出感应折射率椭球的三个主轴方向及相应 的长度。为此,我们进一步考察感应折射率椭球的方程式。
可以看出,这个方程的x23项相对无外加电场时的折射
率椭球没有变化,说明感应折射率椭球的一个主轴与原折射
率椭球的x3轴重合,另外两个主轴方向可绕x3轴旋转得到。
n3' ne
以上讨论了x3-切割晶片在外加电场E3后,光学特性(折射
率)的变化情况。下面,具体讨论两种通光方向上光传播的双
折射特性。
①.光沿x3′方向传播
在外加电场平行于x3轴(光轴),而光也沿x3(x3′)轴 方向传播时,由γ63贡献的电光效应,叫γ63的纵向运用。
由第4章的讨论知道,在这种情况下,相应的两个特许 偏振分量的振动方向分别平行于感应折射率椭球的两个主
KDP(KH2PO4,磷酸二氢钾)晶体是水溶液培养的一种人工 晶体,由于它很容易生长成大块均匀晶体,在0.2~1.5 μm 波长范围内透明度很高,且抗激光破坏阈值很高,所以在光
KDP晶体是单轴晶体,属四方晶系。属于这一类型的晶体 还有ADP(磷酸二氢氨)、KD*P(磷酸二氘钾)等,它们同为42 m
晶体点群,其外形如图 5-1所示,光轴方向为x3轴方向。
V/cm,所以γ63E3<<1, 故可利用幂级数展开,并只取前两
项的关系,将上式变换成:
x1'2
no2
1
1 2
no2
63
E3
2
x2'2
no2
1
1 2
no2
63E3
2
x3'2 ne2
1
由此,得到感应折射率椭球的三个主折射率为:
n1'
no
1 2
no3 63 E3
n2'
no
1 2
no3
63 E3
第二块晶体变为o光,而且二晶体长度和温度环境相同,所
以, 由自然双折射和温度变化引起的相位差相互抵消。因
此,由第二块晶体射出的两光束间,只存在由电光效应引起
的相位差:
2
no3 63U
l d
相应的半波电压为:
U /2
2no3
63
d l
经比较得到:
(U / 2 )横
(U / 2 )纵
d l
显然,横向运用时的半波电压一般均比纵向运用时低,
相应的矩阵形式为:
B1
B2
B3
B4
B5
B6
11
21 31
41
51
61
12 22 32 42 52 62
13
23
33
43
53
63
E1
E2
E3
式中的(6×3)γ矩阵就是线性电光系数矩阵,它描述了
外加电场对晶体光学特性的线性效应。
2.
A. KDP
5.2 晶体的电光效应及应用
5.2.1 晶体的线性电光效应 5.2.2 晶体的二次电光效应 5.2.3 晶体电光效应的应用
5.2.1 晶体的线性电光效应
1.
如上所述,在主轴坐标系中,无外加电场晶体的折射率 椭球为:
B10 x12 B20 x22 B30 x32 1
外加电场后,由于线性电光效应,折射率椭球发生了变 化, 它应表示为一般折射率椭球的形式:
式可简化为:
B11x12 B22 x22 B33x32 2B23x2 x3 2B31x3x1 2B12 x1x2 1
经比较可见,外加电场后,晶体折射率椭球系数[Bij]
的变化为:
B11 B22
B11 B10 B22 B20
B33
B33
B30
B23 B23
B31 B31
因此:
B1 0
B2 0
B3 B4
0
41 E1
B5
41 E 2
B6 63 E3
由此,可得KDP型晶体的感应折射率椭球表示式:
B10 x12 B20 x22 B30 x32
2 41(E1x2 x3 E2 x3 x1 ) 2 63E3 x1x2 1
(2) 外加电场平行于光轴的电光效应
LiNbO3型晶体未加电场时的折射率椭球为旋转椭球,即:
B10 ( x12 x22 ) B30 x32 1
式中,B10 1/ n12 1/ no2 B20; B30 1/ n32 1/ ne2; 和 ne 分 别 为
B12 B21
考虑到[Bij]是二阶对称张量,将下标i和j交换其值
不变, 所以可将它的二重下标简化成单个下标, 其对应关 系为:
B11 B22 B33 B23 B31 B12
B1 B2 B3 B4 B5 B6
相应的[ΔBij]也可简化为有六个分量的矩阵:
B1
B2
B11
B22
B3
2
no3 63U
通常把这种由外加电压引起的二偏振分量间的相位差叫
由上式可见,γ63纵向运用所引起的电光延迟正比于外 加电压差为半个波长,相应的外加电压叫半波
电压,以Uπ或Uλ/2表示。由此可以求得半波电压为:
U/2
2no3 63
它只与材料特性和波长有关,在实际应用中,它是表征 晶体电光效应特性的一个很重要的物理参量。
