勾股定理的实际应用课件
合集下载
勾股定理数学优秀ppt课件

实际应用
在建筑、工程等领域,经常需要利用勾股定理求解直角三角形的边长问题,如计算梯子抵墙 时的长度等。
判断三角形类型问题
判断是否为直角三角形
01
若三角形三边满足勾股定理公式,则该三角形为直角三角形。
判断直角三角形的直角边和斜边
02
在直角三角形中,斜边是最长的一边,通过勾股定理可以判断
哪条边是斜边,哪条边是直角边。
06
总结回顾与展望未来
关键知识点总结回顾
勾股定理的定义和表达式
在直角三角形中,直角边的平方和等于斜边的平方,即a²+b²=c²。
勾股定理的证明方法
通过多种几何图形(如正方形、梯形等)的面积关系来证明勾股定 理。
勾股定理的应用场景
在几何、三角学、物理学等领域中广泛应用,如求解三角形边长、 角度、面积等问题。
勾股定理与其他数学定理关系探讨
与三角函数关系
勾股定理是三角函数的基础,通 过勾股定理可以推导出正弦、余 弦、正切等三角函数的基本关系。
与向量关系
在向量空间中,勾股定理可以表示 为两个向量的点积等于它们模长的 平方和,这进一步揭示了勾股定理 与向量的紧密联系。
与几何图形关系
勾股定理在几何图形中有着广泛的 应用,如求解直角三角形、矩形、 菱形等图形的边长、面积等问题。
勾股定理是数学中的基本定理之一, 也是几何学中的基础概念,对于理 解三角形、圆等几何形状的性质具 有重要意义。
历史发展及应用
历史发展
勾股定理最早可以追溯到古埃及时期,但最为著名的证明是由 古希腊数学家毕达哥拉斯学派给出的。在中国,商高在周朝时 期就提出了“勾三股四弦五”的勾股定理的特例。
应用
勾股定理在几何、三角、代数、物理等多个领域都有广泛应用, 如求解三角形边长、角度、面积等问题,以及力学、光学等领 域的计算。
在建筑、工程等领域,经常需要利用勾股定理求解直角三角形的边长问题,如计算梯子抵墙 时的长度等。
判断三角形类型问题
判断是否为直角三角形
01
若三角形三边满足勾股定理公式,则该三角形为直角三角形。
判断直角三角形的直角边和斜边
02
在直角三角形中,斜边是最长的一边,通过勾股定理可以判断
哪条边是斜边,哪条边是直角边。
06
总结回顾与展望未来
关键知识点总结回顾
勾股定理的定义和表达式
在直角三角形中,直角边的平方和等于斜边的平方,即a²+b²=c²。
勾股定理的证明方法
通过多种几何图形(如正方形、梯形等)的面积关系来证明勾股定 理。
勾股定理的应用场景
在几何、三角学、物理学等领域中广泛应用,如求解三角形边长、 角度、面积等问题。
勾股定理与其他数学定理关系探讨
与三角函数关系
勾股定理是三角函数的基础,通 过勾股定理可以推导出正弦、余 弦、正切等三角函数的基本关系。
与向量关系
在向量空间中,勾股定理可以表示 为两个向量的点积等于它们模长的 平方和,这进一步揭示了勾股定理 与向量的紧密联系。
与几何图形关系
勾股定理在几何图形中有着广泛的 应用,如求解直角三角形、矩形、 菱形等图形的边长、面积等问题。
勾股定理是数学中的基本定理之一, 也是几何学中的基础概念,对于理 解三角形、圆等几何形状的性质具 有重要意义。
历史发展及应用
历史发展
勾股定理最早可以追溯到古埃及时期,但最为著名的证明是由 古希腊数学家毕达哥拉斯学派给出的。在中国,商高在周朝时 期就提出了“勾三股四弦五”的勾股定理的特例。
应用
勾股定理在几何、三角、代数、物理等多个领域都有广泛应用, 如求解三角形边长、角度、面积等问题,以及力学、光学等领 域的计算。
初中数学《勾股定理及其应用》课件

A
c= a2 b2
股 c弦
b
a= c2 b2 b= c2 a2
C a勾B
拼图
运用勾股定理 可解决直角三角形中边的计算
例1 在 Rt△ABC中,∠C=90° ⑴已知a=6,b=8,则c1=0 __ ⑵已知a=9,c=41,则b4=0 __ ⑶已知c=25,b=15,则2a0=__ ⑷已知a=n2-1,b=2n,则nc2=+1____
2PBCD2=*P(DDC+PD)2=CD2+PD2+
∴ PB2+P2CC2D=*P2DBD2+2PD2=2(AD2+PD2)=
练一练 2PA2
练一练
M N
B 如图,已知:在Rt△ABC中, ∠ACB=90º,AC=12,BC=5,
AM=AC,BN=BC
则MN的长是__4__
A
C
练一练
折叠矩形ABCD的一边AD,点D
例3 已知:在△ABC中,AB=AC,
AB=17,BC=16,求△ABC的面 积A 。 解:作△ABC边BC上的高AD
∵ AB=AC ∴BD=DC=8
在Rt△ABD中,
AD2=AB2-BD2=BC=22=125 1B5C*AD=
120
运用勾股定理
可解决直角三角形中边的计算
例3 已知:在△ABC中,AB=AC,
AB=17,BC=16,求△ABC的面
积。
A
思考:若过C点作AB边
D
上的高CD,则如何求解?
B
C
运用勾股定理 可解决直角三角形中边的计算
例 4
B
A 如图,已知:△ABC中, AD是中线,AE⊥BC于E
⑴若AB=12,BC=10, AC=8 求:DE的长度
1勾股定理的应用PPT课件(华师大版)
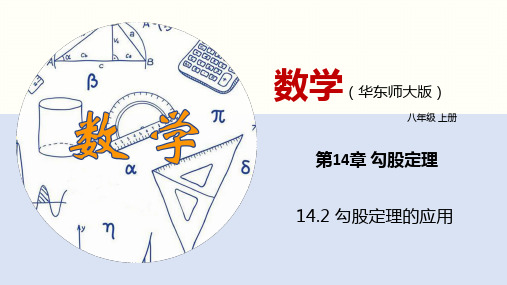
分析:由于车宽1.6米,所以卡车能否
通过,只要比较距厂门中线0.8米处的
高度与车高即可.如图所示,点D在离厂
门中线0.8米处,且CD⊥AB,与地面相
交于点H.
讲授新课
解:在Rt△OCD中,由勾股定理,可得
CD OC 2 OD2 12 0.82 0.6,
CH=CD+DH=0.6+2.3=2.9>2.5.
的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸
边的水面,请问这个水池的深度和这根芦苇的长度各是多少?
解: 设水池的水深AC为x尺,则这根芦苇长为AD=AB=(x+1)尺,
在直角三角形ABC中,BC=5尺
由勾股定理得:BC2+AC2=AB2
即
52+x2=(x+1)2
25+x2= x2+2x+1,
可见高度上有0.4米的余量,因此卡
车能通过厂门.
讲授新课
2、有一根高为16米的电线杆在A处断裂,如图所示,电线杆的
顶部C落在离电线杆底部B处8米远的地方,求电线杆断裂处A到
地面的距离.
根据题意可知在Rt△ABC中,
∠ABC =90°,BC=8米,AB+
AC=16米.若设AB=x米,则
AC=(16-x)米,然后根据勾股定理
90°.∴S四边形ABCD=S△ABC+S△ACD= AB·BC+
AC·AD= ×4×3+ ×5×12=36.
∵36×30=1080(元),
∴这块地全部种草的费用是1080元.
讲授新课
练一练
1、一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图所示
勾股定理的应用-课件

02
在实际应用中,可以利用勾股定 理来检验一个三角形是否为直角 三角形,从而确定角度和边长之 间的关系。
勾股定理的逆定理
勾股定理的逆定理是:如果一个三角 形的一组边长满足勾股定理,则这个 三角形一定是直角三角形。
通过勾股定理的逆定理,可以用来判 断一个三角形的角度和边长是否满足 直角三角形的条件,从而确定其是否 为直角三角形。
如何进一步推广和应用勾股定理
跨学科应用
01
鼓励将勾股定理应用于其他学科,以促进跨学科的学习和理解
。
创新教学方法
02
通过创新教学方法,例如使用数字化工具和互动游戏,提高学
生对勾股定理的兴趣和参与度。
实际应用
03
鼓励学生将勾股定理应用于实际问题解决中,例如在建筑、工
程和科学实验等领域。
THANKS
感谢观看
确定直角三角形
勾股定理可以用来确定一个三角形是 否为直角三角形,只需验证三边关系 是否满足勾股定理即可。
计算直角三角形边长
判断三角形的稳定性
勾股定理的应用可以帮助我们判断三 角形的稳定性,因为只有直角三角形 满足勾股定理,所以只有直角三角形 是稳定的。
已知直角三角形两条边的长度,可以 使用勾股定理计算第三边的长度。
。
在气象学中,勾股定理也被用于 计算气象气球上升的高度和速度 ,以了解大气层的结构和变化。
05
勾股定理的未来发展
勾股定理在现代数学中的应用
代数证明
勾股定理可以通过代数方法进行证明,这有助于学生更好地理解 代数和几何之间的联系。
三角函数
勾股定理与三角函数密切相关,通过应用勾股定理,可以解决一些 与三角函数相关的问题。
在海上导航中,勾股定理也用于确定船只的经度和纬度,以确保航行安全和准确 到达目的地。
在实际应用中,可以利用勾股定 理来检验一个三角形是否为直角 三角形,从而确定角度和边长之 间的关系。
勾股定理的逆定理
勾股定理的逆定理是:如果一个三角 形的一组边长满足勾股定理,则这个 三角形一定是直角三角形。
通过勾股定理的逆定理,可以用来判 断一个三角形的角度和边长是否满足 直角三角形的条件,从而确定其是否 为直角三角形。
如何进一步推广和应用勾股定理
跨学科应用
01
鼓励将勾股定理应用于其他学科,以促进跨学科的学习和理解
。
创新教学方法
02
通过创新教学方法,例如使用数字化工具和互动游戏,提高学
生对勾股定理的兴趣和参与度。
实际应用
03
鼓励学生将勾股定理应用于实际问题解决中,例如在建筑、工
程和科学实验等领域。
THANKS
感谢观看
确定直角三角形
勾股定理可以用来确定一个三角形是 否为直角三角形,只需验证三边关系 是否满足勾股定理即可。
计算直角三角形边长
判断三角形的稳定性
勾股定理的应用可以帮助我们判断三 角形的稳定性,因为只有直角三角形 满足勾股定理,所以只有直角三角形 是稳定的。
已知直角三角形两条边的长度,可以 使用勾股定理计算第三边的长度。
。
在气象学中,勾股定理也被用于 计算气象气球上升的高度和速度 ,以了解大气层的结构和变化。
05
勾股定理的未来发展
勾股定理在现代数学中的应用
代数证明
勾股定理可以通过代数方法进行证明,这有助于学生更好地理解 代数和几何之间的联系。
三角函数
勾股定理与三角函数密切相关,通过应用勾股定理,可以解决一些 与三角函数相关的问题。
在海上导航中,勾股定理也用于确定船只的经度和纬度,以确保航行安全和准确 到达目的地。
勾股定理的应用课件

勾股定理的发展
在后来的几千年中,勾股定理经历了许多数学家的研究和证明,不断得到完善和发展。如今, 勾股定理已经成为中学数学课程中的重要内容之一,也是数学竞赛中的常见考点之一。
勾股定理的证明方法
基础证明方法
勾股定理可以通过多种方法进行证明,其中最基础的方法是利用相似三角形的性质进行证明。此外,还有利用代 数方法、微积分方法和几何方法等证明方法。
03 结构分析
在建筑结构分析中,勾股定理用于计算结构的承 载力和稳定性,确保建筑物的安全可靠。
航空航天领域中的应用
01 飞机设计
在飞机设计中,勾股定理用于计算机翼的弯度和 长度,以及机身的垂直度和水平度。
02 航天器设计
在航天器设计中,勾股定理用于确定卫星轨道的 参数和火箭发射角度等。
03 导航定位
物理学领域
在物理学中,勾股定理也具有广泛的应用。例如,在力学中,勾股定理可以用于解决与力的合 成和分解相关的问题。在电磁学中,勾股定理可用于计算电磁波的传播路径和强度。 物理学中的许多现象和规律都与勾股定理有关,如光的反射和折射、电场和磁场等。
日常生活中的应用
勾股定理在日常生活中也有很多应用,如建筑测量、航海导 航、道路桥梁设计等。通过勾股定理可以确定建筑物的垂直 度和水平度,保证建筑物的安全性和稳定性。
勾股定理在日常生活中的应用案例
家具制作
在家具制作中,勾股定理 用于确定家具的尺寸和比 例,保证家具的美观和实 用性。
航海导航
在航海导航中,勾股定理 用于计算航行距离和方向 ,确保航行的准确性和安 全性。
音乐艺术
在音乐艺术中,勾股定理 用于确定音符的频率和音 高,保证音乐的和谐性和 美感。
如何提高勾股定理的应用能
勾股定理的表述
在后来的几千年中,勾股定理经历了许多数学家的研究和证明,不断得到完善和发展。如今, 勾股定理已经成为中学数学课程中的重要内容之一,也是数学竞赛中的常见考点之一。
勾股定理的证明方法
基础证明方法
勾股定理可以通过多种方法进行证明,其中最基础的方法是利用相似三角形的性质进行证明。此外,还有利用代 数方法、微积分方法和几何方法等证明方法。
03 结构分析
在建筑结构分析中,勾股定理用于计算结构的承 载力和稳定性,确保建筑物的安全可靠。
航空航天领域中的应用
01 飞机设计
在飞机设计中,勾股定理用于计算机翼的弯度和 长度,以及机身的垂直度和水平度。
02 航天器设计
在航天器设计中,勾股定理用于确定卫星轨道的 参数和火箭发射角度等。
03 导航定位
物理学领域
在物理学中,勾股定理也具有广泛的应用。例如,在力学中,勾股定理可以用于解决与力的合 成和分解相关的问题。在电磁学中,勾股定理可用于计算电磁波的传播路径和强度。 物理学中的许多现象和规律都与勾股定理有关,如光的反射和折射、电场和磁场等。
日常生活中的应用
勾股定理在日常生活中也有很多应用,如建筑测量、航海导 航、道路桥梁设计等。通过勾股定理可以确定建筑物的垂直 度和水平度,保证建筑物的安全性和稳定性。
勾股定理在日常生活中的应用案例
家具制作
在家具制作中,勾股定理 用于确定家具的尺寸和比 例,保证家具的美观和实 用性。
航海导航
在航海导航中,勾股定理 用于计算航行距离和方向 ,确保航行的准确性和安 全性。
音乐艺术
在音乐艺术中,勾股定理 用于确定音符的频率和音 高,保证音乐的和谐性和 美感。
如何提高勾股定理的应用能
勾股定理的表述
勾股定理的应用ppt课件

1.3 勾股定理的应用
● 考点清单解读 ● 重难题型突破
1.3 勾股定理的应用
返回目录
考 ■考点一 立体图形上的最短路线
点 清 1. 确定圆柱侧面上两点之间的最短距离,其步骤如下:
单 解
(1)将侧面展开为长方形;
读
(2)根据“两点之间线段最短”构造直角三角形;
(3)利用勾股定理求距离.
1.3 勾股定理的应用
单 解
一边与另两边的关系,求直角三角形的另两边时,可设未知
读 数,根据勾股定理建立方程,通过解方程解决问题.
1.3 勾股定理的应用
返回目录
考
对点典例剖析
点 清
典例2 如图,台风过后,一棵白杨树在某处折断,白杨
单 树的顶部落在离白杨树根部 8 m 处,已知白杨树高 16 m, 解
读 则白杨树是在离根部_____ m 的位置折断的.
1.3 勾股定理的应用
考 [答案] 6 点 清 单 解 读
返回目录
1.3 勾股定理的应用
返回目录
重 ■题型 勾股定理中的方案设计问题
难 题
例 一路上 A,B 两地(视为直线上的两点)相距 25
型 突
km,C,D为两村庄(视为两点),DA⊥AB
于点
A,CB⊥AB
破 于点 B(如图),已知 DA=10 km,CB=15 km,现要在路
AB 上建一个土特产收购站 E,使得 C,D 两村到收购站 E
的距离相等,请求出 E 站到 A 地的距离.
1.3 勾股定理的应用
返回目录
重 [答案] 解:由题意得 CE=DE,在 Rt△DAE和 Rt
难 题
△CBE
中
,DE2
=AD2
● 考点清单解读 ● 重难题型突破
1.3 勾股定理的应用
返回目录
考 ■考点一 立体图形上的最短路线
点 清 1. 确定圆柱侧面上两点之间的最短距离,其步骤如下:
单 解
(1)将侧面展开为长方形;
读
(2)根据“两点之间线段最短”构造直角三角形;
(3)利用勾股定理求距离.
1.3 勾股定理的应用
单 解
一边与另两边的关系,求直角三角形的另两边时,可设未知
读 数,根据勾股定理建立方程,通过解方程解决问题.
1.3 勾股定理的应用
返回目录
考
对点典例剖析
点 清
典例2 如图,台风过后,一棵白杨树在某处折断,白杨
单 树的顶部落在离白杨树根部 8 m 处,已知白杨树高 16 m, 解
读 则白杨树是在离根部_____ m 的位置折断的.
1.3 勾股定理的应用
考 [答案] 6 点 清 单 解 读
返回目录
1.3 勾股定理的应用
返回目录
重 ■题型 勾股定理中的方案设计问题
难 题
例 一路上 A,B 两地(视为直线上的两点)相距 25
型 突
km,C,D为两村庄(视为两点),DA⊥AB
于点
A,CB⊥AB
破 于点 B(如图),已知 DA=10 km,CB=15 km,现要在路
AB 上建一个土特产收购站 E,使得 C,D 两村到收购站 E
的距离相等,请求出 E 站到 A 地的距离.
1.3 勾股定理的应用
返回目录
重 [答案] 解:由题意得 CE=DE,在 Rt△DAE和 Rt
难 题
△CBE
中
,DE2
=AD2
八年级数学上册教学课件《勾股定理的应用》
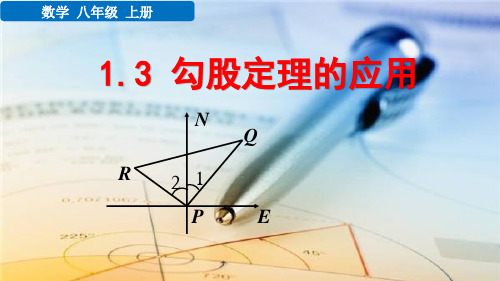
解:如图所示 在Rt△ABC中,利用勾股定理可得, AB 2=AC2+BC2 =20 2+102 =500
10
10
10
所以AB2=500.
李叔叔想要检测雕塑底座正面的AD边和BC边是否分别垂直于底边AB,但他随身只带了卷尺.(1)你能替他想办法完成任务吗?
D
A. B. C. D.
2.如图是医院、公园和超市的平面示意图,超市在医院的南偏东25°的方向,且到医院的距离为300 m,公园到医院的距离为400 m,若公园到超市的距离为500 m,则公园在医院的 ( )A.北偏东75°的方向上 B.北偏东65°的方向上C.北偏东55°的方向上 D.无法确定
B
3.如图,某探险队的A组由驻地O点出发,以12km/h的速度前进,同时,B组也由驻地O出发,以9km/h的速度向另一个方向前进,2h后同时停下来,这时A,B两组相距30km.此时,A,B两组行进的方向成直角吗?请说明理由.
解:因为出发2小时,A组行了12×2=24(km), B组行了9×2=18(km), 又因为A,B两组相距30km, 且有242+182=302, 所以A,B两组行进的方向成直角.
以小组为单位,研究蚂蚁在圆柱体的A点沿侧面爬行到B点的问题.
讨论 1.蚂蚁怎样沿圆柱体侧面从A点爬行到B点? 2.有最短路径吗?若有,哪条最短?你是怎样找到的?
B
A
我要从A点沿侧面爬行到B点,怎么爬呢?大家快帮我想想呀!
利用勾股定理解答最短路径问题
想一想 蚂蚁走哪一条路线最近?
在Rt△ABC中,AC===5,在△ACD中,AC2+CD2=52+122=169=AD2,所以△ACD是直角三角形,且∠ACD=90°.所以S四边形ABCD=SRt△ABC+SRt△ACD=6+30=36.
17.2 勾股定理的应用 课件(共17张PPT) 2024-2025学年人教版八年级数学下册

解 : 设水的深度为x尺 , 则这根芦苇的长 度为(x+1)尺 , 根据题意和勾股定理可列方 程为x2+52=(x+1)2 , 整理得2x+1=25 , 解得 x=12.所以水的深度为12尺,这根芦苇的长 度为13尺.
拓展延伸ቤተ መጻሕፍቲ ባይዱ
如图,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方
体的外表面爬到顶点B的最短距离是( B ).
探索新知
例1 一个门框的尺寸如图所示,一块长3 m,宽2.2 m的长方形 薄木板能否从门框内通过?为什么?
思考:
已知两直角边求斜边.
1.木板能横着或竖着从门框通过吗?
2.这个门框能通过的最大长度是多少?
3.怎样判定这块木板能否通过门框?
探索新知
例1 一个门框的尺寸如图所示,一块长3 m,宽2.2 m的长方形 薄木板能否从门框内通过?为什么?
A.3
B . 5 C.2
D.1
B
B
A
A
课堂小结
利用勾股定理解决实际问题的一般思路: ①正确理解实际问题的题意; ②建立对应的数学模型; ③解决相应的数学问题; ④将数学问题的结果“翻译”成实际问题的答案.
A
B
A′
O
亭亭多姿湖中立,突遭狂风吹一边.
A
离开原处六尺远,花贴湖面像睡莲.
请君动脑想一想,湖水在此深几尺? B
A′
解:设水深为h尺,Rt△ABC中, OB=h,AO=h+3,A′B=6. 由勾股定理得:A′O2=A′B2+BO2,即 O (h+3)2=h2+62, ∴h2+6h+9=h2+36,解得:h=4.5. 答:湖水深为4.5尺.
拓展延伸ቤተ መጻሕፍቲ ባይዱ
如图,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方
体的外表面爬到顶点B的最短距离是( B ).
探索新知
例1 一个门框的尺寸如图所示,一块长3 m,宽2.2 m的长方形 薄木板能否从门框内通过?为什么?
思考:
已知两直角边求斜边.
1.木板能横着或竖着从门框通过吗?
2.这个门框能通过的最大长度是多少?
3.怎样判定这块木板能否通过门框?
探索新知
例1 一个门框的尺寸如图所示,一块长3 m,宽2.2 m的长方形 薄木板能否从门框内通过?为什么?
A.3
B . 5 C.2
D.1
B
B
A
A
课堂小结
利用勾股定理解决实际问题的一般思路: ①正确理解实际问题的题意; ②建立对应的数学模型; ③解决相应的数学问题; ④将数学问题的结果“翻译”成实际问题的答案.
A
B
A′
O
亭亭多姿湖中立,突遭狂风吹一边.
A
离开原处六尺远,花贴湖面像睡莲.
请君动脑想一想,湖水在此深几尺? B
A′
解:设水深为h尺,Rt△ABC中, OB=h,AO=h+3,A′B=6. 由勾股定理得:A′O2=A′B2+BO2,即 O (h+3)2=h2+62, ∴h2+6h+9=h2+36,解得:h=4.5. 答:湖水深为4.5尺.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)
(2)
聪明的葛藤
有 一棵树直立在地上,树高2丈,粗3尺,有一 根葛藤从树根处缠绕而上,缠绕7周到达树顶, 请问这根葛藤条有多长?(1丈等于10尺)
C 20尺
A
3×7=21(尺)
B
如图,小颍同学折叠一个直角三角形 的纸片,使A与B重合,折痕为DE,若已知 AC=10cm,BC=6cm,你能求出CE的长吗?
A
C 5
B
假期中,王强和同学到某海岛上去玩探 宝游戏,按照探宝图,他们登陆后先往东 走8千米,又往北走2千米,遇到障碍后又 往西走3千米,在折向北走到6千米处往东 一拐,仅走1千米就找到宝藏,问登陆点A 到宝藏埋藏点B的距离是多少千米?
解:过B点向南作垂线, 连结AB,可得Rt△ABC 由题意可知:AC=6千米, BC=8千米 根据勾股定理 AB2=AC2+BC2 =62+82=100 ∴AB=10千米 A 8 C 1 6 3 2 B
S3
S4
S2
结论:
S1+S2+S3+S4 =S5+S6 =S7
S1
S5
S6
S7
探索1、一个门框的尺寸如图所示,一块
D C
长3m、宽2.2m的薄木板能否从门框内通 过?为什么?
2 2
解:连接AC,在Rt△ABC中根 据勾股定理:
2m
∵ AC AB BC 1 2 5
2 2
2
A
1m
B
AC 5 2.236
D B 解:连结BE
由已知可知:DE是AB的中垂线, ∴AE=BE 设AE=xcm,则EC=(10-x)cm 在Rt△ABC 中,根据勾股定理:
A E
C
BE2=BC2+EC2 x2=62+ (10-x)2 解得x=6.8 ∴EC=10-6.8=3.2cm
如图,有两棵树,一棵高 8m ,另一棵高 2m , 两树相距8m,一只小鸟从一棵树的树梢飞到另一 棵树的树梢,至少飞了 ( ) A.7m B.8m C.9m D.10m
乘风破浪 y=0
18m
5m
?
如图,大风将一根木 制旗杆吹裂,随时都 可能倒下,十分危急。 接警后“119”迅速 赶到现场,并决定从 断裂处将旗杆折断。 现在需要划出一个安 全警戒区域,那么你 能确定这个安全区域 的半径至少是多少米 吗?
一种盛饮料的圆柱形杯(如图),测得 内部底面直径为5㎝,高为12㎝,吸管 放进杯里,杯口外面露出5㎝,问吸管要 做多长?
C
A
B
如图,将一根25㎝长的细木棒放入长、 宽、高分别为 8㎝、 6㎝和 10㎝的长方体 无盖盒子中,则细木棒露在盒外面的最 短长度是多少㎝.(保留1位小数)
C
A
B
D
有一个圆柱,它的 高等于12厘米,底 面半径等于3厘米, 在圆柱下底面上的 A点有一只蚂蚁,它 想从点A爬到点B , 蚂蚁沿着圆柱侧面 爬行的最短路程是 多少? (π的值取3)
B
我怎 么走 会最 近呢?
A
B 高 12cm A A
9cm
B
长18cm (π的值取3)
∵ AB2=92+122=81+144=225= 152
∴ AB=15(cm) 蚂蚁爬行的最短路程是15厘米.
如图所示,现在有长方体木块的长3厘米,宽4 厘米,高24厘米。一只蜘蛛潜伏在一个顶点A 处,一只苍蝇在这个长方体上和蜘蛛相对的顶 点B处,蜘蛛急于想捉住苍蝇,沿着长方体的表 面向上爬,它要从点A爬到点B处,有无数条路 线,它们有长有短,蜘蛛究竟应该沿着怎样的 路线爬上去,所走的路程会最短。你能帮蜘蛛 找到最短路径吗? H
G F
B
D A C
如图,是一个三级台阶,它的每一级的长、宽和高 分别等于36cm,10cm和6cm,A和B是这个台阶的两个 相对的端点,A点上有一只小虫子,想到B点去吃可口 的食物。请你想一想,这只小虫子从A点出发,沿着台 阶面爬到B点,最短线路是多少?
A
.
A
.
B
C
B
数学奇闻
聪明的葛藤
葛藤是一种刁钻的植物,它自 己腰杆不硬,为了得到阳光的沐 浴,常常会选择高大的树木为依 托,缠绕其树干盘旋而上。如图 (1)所示。 葛藤又是一种聪明的植物, 它绕树干攀升的路线,总是沿着 最短路径——螺旋线前进的。若 将树干的侧面展开成一个平面, 如图( 2 ),可清楚的看出葛藤 在这个平面上是沿直线上升的。
A
8m
C
B
2m 8m
帮一帮农民
如图所示,要修一个种植蔬菜的育苗大棚, 棚宽 a=2m ,高 b=1.5m ,长 d=12m ,则修 盖在顶上的塑料薄膜需要的面积为多少?
b
c
a d
帮一帮消防员
一大楼发生火灾,消防车立即赶到距大楼 9 米处,升起云梯到失火的窗口,已知发 生火灾的窗口距地面有 14.2米,云梯底部 距地面 2.2 米,问云梯至少需要搭出多少 A 米可以够到失火的窗口?
B
E
C
D
与古人比一比 在我国古代数学著作 《九章算术》中记载了一道 有趣的问题,这个问题的意 思是:有一个水池,水面是 一个边长为10尺的正方形,在 水池的中央有一根新生的芦 苇,它高出水面1尺,如果把 这根芦苇垂直拉向岸边,它 的顶端恰好到达岸边的水面, 请问这个水池的深度和这根 芦苇的长度各是多少?
A 8
10
所以梯子的顶端下滑1m,它的底 端不是滑动1m.
C
B B
思考
如图,一个三米长的梯子 AB,斜靠在一竖直的墙 AO上,这时AO的距离为 2.5m,如果梯子的顶端A 沿墙下滑0.5m,那么梯子 底端B也外移0.5m吗?
A C
O
B
D
小明想知道学校旗杆的高,他发现旗杆 顶端的绳子垂到地面还多1米,当他把绳 子的下端拉开5米后,发现下端刚好接触 地面,求旗杆的高度。
C
1
D
B
5
x
A
……
小结:
实际问题 数学问题
构造直角三角形
(在直角三角形中已知 两边,可以 求出第三边。) (在直角三角形中,知道一边及 另两边关系,可以求出未知的两 边.)
学生活动 算趣题:“执竿进屋” 笨人执竿要进屋,无奈门框拦住竹, 横多四尺竖多二,没法急得放声哭。 有个邻居聪明者,教他斜竿对两角, 笨伯依言试一试,不多不少刚抵足。 借问竿长多少数,谁人算出我佩服。
探索2 如图,一架长为10m的梯子AB斜靠在
墙上,梯子的顶端距地面的垂直距离为8m.如果 梯子的顶端下滑1m,那么它的底端是否也滑动 1 m? A
18.1勾股定理
----实际应用
海伦市共合三角形ABC的三边为a,b,c , ∠C= 90° ,则 a,b,c 三者之间的关系 2 2 2 a b c 是 。
2 矩形的一边长是5,对角线是13,则它 的面积是 60 。
二.y=0 复习面积法证明勾股定理
已知S1=1,S2=3,S3=2,S4=4,求 S5、S6、S7的值
