2019年中考数学备考培优
2019年中考数学复习弧长扇形面积专项练习题C(培优附答案详解)

解:连接CO,∵AB=2,∴OB=1,∵AB是半圆的直径,∴∠ACB=90°,∵∠B=30°,∴∠A=60°,∴∠COB=120°,∴ = = π,故选B.
3.C
解: π(AA1+A1A2+A2A3+A3B)= π×AB,因此甲虫走的四段半圆的弧长正好和乙虫走的大半圆的弧长相等,因此两个同时到B点。故选C.
(2)连接AD、CD,求⊙D的半径及弧 的长.
(3)有一点E(6,0),判断点E与⊙D的位置关系.
18.已知A、B两点,求作:过A、B两点的⊙O及⊙O的内接正六边形ABCDEF.(要求用直尺和圆规作图,保留作图痕迹,不必写作法及证明.)
19.如图所示,已知圆锥底面半径r=10cm,母线长为40cm.
14.能完全覆盖边长为12的等边三角形的最小圆的半径为_______________.
15.边长为4cm的正方形ABCD绕它的顶点A旋转180°,顶点B所经过的路线长为(______)cm.
16.如图,半圆的直径AB=10,P为AB上一点,点C,D为半圆上的三等分点,则图中阴影部分的面积等于__.
17.如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:(1)在图中确定该圆弧所在圆的圆心D点的位置,并写出点D点坐标为.
(1)如图①,在点P的移动过程中,线段CD的长是否会发生变化?若不发生变化,请求出线段CD的长;若会发生变化,请说明理由;
(2)如图②,若点M、N为 的三等分点,点I为△DOC的外心.当点P从点M运动到N点时,点I所经过的路径长为__________.(直接写出结果)
22.如图,P是半径为 cm的⊙O外一点,PA,PB分别和⊙O切于点A,B,PA=PB=3cm,∠APB=60°,C是弧AB上一点,过C作⊙O的切线交PA,PB于点D,E.
2019年全国各地中考数学精选反比例函数培优题(附解析)

2019年全国各地中考数学精选反比例函数培优题(附解析)注意事项:认真阅读理解,结合历年的真题,总结经验,查找不足!重在审题,多思考,多理解!〔附答案〕1.〔2017甘肃兰州,15,4分〕如图,矩形ABCD 的对角线BD 经过坐标原点,矩形的边分别平行于坐标轴,点C 在反比例函数221k k y x++=的图象上。
假设点A 的坐标为〔-2,-2〕,那么k 的值为A 、1B 、-3C 、4D 、1或-32.〔2017四川乐山10,3分〕〔6〕,直线6y x =-交x 轴、y 轴于A 、B 两点,P 是反比例函数4(0)y x x=>图象上位于直线下方的一点,过点P 作x 轴的垂线,垂足为点M ,交AB 于点E ,过点P 作y 轴的垂线,垂足为点N ,交AB 于点F 。
那么AF BE ⋅= A 、8B 、6C 、4D、3〔2017山东东营,10,3分〕,如图直线l 和双曲线(0)ky k x=>交于A 、B 亮点,P 是线段AB 上的点〔不与A 、B 重合〕,过点A 、B 、P 分别向x 轴作垂线,垂足分别是C 、D 、E,连接OA 、OB 、OP,设△AOC 面积是S 1、△B OD 面积是S 2、△P OE 面积是S 3、那么〔〕 AS1<S2<S3BS1>S2>S3CS1=S2>S3DS1=S2<S34.〔2017四川南充市,7,3分〕小明乘车从南充到成都,行车的平均速度y (km/h)和行车时间x (h)之间的函数图像是〔〕 ABCD5.〔2017浙江台州,9,4分〕如图,反比例函数xm y =的图象与一次函数b kx y -=的图象交于点M ,N ,已点M 的坐标为〔1,3〕,点N 的纵坐标为-1,根据图象信息可得关于x 的方程xm =b kx -的解为〔〕A.-3,1B.-3,3C.-1,1D.3,-16.〔2017河北,12,3分〕根据图5—1所示的程序,得到了y 与x 的函数图象,过点M 作PQ ∥x 轴交图象于点P,Q ,连接OP,OQ.那么以下结论 ①x <0时,x2y =,②△OPQ 的面积为定值, ③x >0时,y 随x 的增大而增大④MQ=2PM ⑤∠POQ 可以等于90°图5—2图5—1PQM其中正确的结论是〔〕A 、①②④B 、②④⑤C 、③④⑤D 、②③⑤7〔2017湖北宜昌,15,3分〕如图,直线y=x +2与双曲线y=xm 3-在第二象限有两个交点,那么m 的取值范围在数轴上表示为〔〕【二】填空题8.〔2017浙江金华,16,4分〕如图,将一块直角三角板OAB 放在平面直角坐标系中,B 〔2,0〕,∠AOC =60°,点A 在第一象限,过点A 的双曲线为y =kx ,在x 轴上取一点P ,过点P作直线OA 的垂线l ,以直线l 为对称轴,线段OB 经轴对称变换后的像是O ′B ′. 〔1〕当点O ′与点A 重合时,点P 的坐标是 .〔2〕设P 〔t ,0〕当O ′B ′与双曲线有交点时,t 的取值范围是.〔第8题图〕9.〔2017宁波市,18,3分〕如图,正方形A 1B 1P 1P 2的顶点P 1、P 2在反比例函数y =2x 〔x >0〕的图像上,顶点A 1、B 1分别在x 轴和y 轴的正半轴上,再在其右侧作正方形P 2P 3A 2B 2,顶点P 3在反比例函数y =2x 〔x >0〕的图象上,顶点A 3在x 轴的正半轴上,那么点P 3的坐标为10.〔2017浙江衢州,5,4分〕在直角坐标系中,有如下图的t ,R ABO AB x ∆⊥轴于点B ,斜边3105AO AOB =∠=,sin ,反比例函数(0)ky x x=>的图像经过AO 的中点C ,且与AB 交于点D ,那么点D 的坐标为.11、〔2017江苏苏州,18,3分〕如图,点A 的坐标为〔3,3〕,AB ⊥x 轴,垂足为 B ,连接OA ,反比例函数y=xk 〔k>0〕的图象与线段OA 、AB 分别交于点C 、D.假设AB=3BD ,以点C 为圆心,CA 的45倍的长为半径作圆,那么该圆与x 轴的位置关系是___________〔填“相离”、“相切”或“相交”〕12.〔2017四川成都,25,4分〕在平面直角坐标系xOy 中,反比例函数2(0)ky k x=≠满足:当0x <时,y 随x 的增大而减小、假设该反比例函数的图象与直线y x =-都经过点P ,且OP =,那么实数k=_________.13.〔2017安徽芜湖,15,5分〕如图,在平面直角坐标系中有一正方形AOBC ,反比例函数k y x=经过正方形AOBC 对角线的交点,半径为〔4-ABC ,那么k 的值为、14.〔2017湖北武汉市,16,3分〕如图,□ABCD 的顶点A ,B 的坐标分别是A 〔-1,0〕,B 〔0,-2〕,顶点C ,D 在双曲线y=xk 上,边AD 交y 轴于点E ,且四边形BCDE 的面积是△ABE面积的5倍,那么k =_____、15.〔2017湖北黄石,15,3分〕假设一次函数y=kx +1的图象与反比例函数y =x1的图象没有公共点,那么实数k 的取值范围是16〔2017内蒙古乌兰察布,17,4分〕函数1(0)y x x =≥,xy 92=(0)x >的图象如下图,那么结论:①两函数图象的交点A 的坐标为〔3,3)②当3x >时,21y y >③当1x =时,BC=8④当x 逐渐增大时,1y 随着x 的增大而增大,2y 随着x 的增大而减小、其中正确结论的序号是_.17〔2017湖北荆州,16,4分〕如图,双曲线)0(2x xy =经过四边形OABC 的顶点A 、C ,yy 1=x y 2=9xx第17题图∠ABC =90°,OC 平分OA 与x 轴正半轴的夹角,AB ∥x 轴,将△ABC 沿AC 翻折后得到△AB 'C ,B '点落在OA 上,那么四边形OABC 的面积是.【三】解答题18.〔2017广东广州市,23,12分〕Rt △ABC 的斜边AB 在平面直角坐标系的x 轴上,点C 〔1,3〕在反比例函数y =kx 的图象上,且sin ∠BAC =35、〔1〕求k 的值和边AC 的长; 〔2〕求点B 的坐标、19.〔2017山东泰安,26,10分〕如图,一次函数y=k 1x+b 的图象经过A 〔0,-2〕,B 〔1,0〕两点,与反比例函数y=12x 的图象在第一象限内的交点为M ,假设△OBM 的面积为2。
2019年下学期九年级数学培优讲义2:一次函数综合

初三培优讲义2:一次函数综合一、选择题1.若直线经过第一、二、四象限,则直线的图象大致是( )A. B. C. D.2.已知直线不经过第一象限,则m的取值范围是( )A. B. C. D.3.已知一次函数的图象与x轴的正半轴相交,且函数值y随自变量x的增大而增大,则k,b的取值情况为( )A. ,B. ,C. ,D. ,4.如图,是等腰直角三角形,,,点P是边上一动点,沿的路径移动,过点P作于点D,设,的面积为y,则下列能大致反映y与x函数关系的图象是( )A. B.C. D.5.小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,看作一个容器然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部,则下面可以近似地刻画出容器最高水位h与注水时间t之间的变化情况的是( )A. B.C. D.二、填空题6.如图,直线与直线交于点,则关于x的不等式的解集是______.7.如果直线与两坐标轴所围成的三角形面积是9,则b的值为______.8.如图,直线与x轴、y轴分别交于点A和点B,x轴上有一点,点P为直线一动点,当值最小时点P的坐标为______.9.在平面直角坐标系中,直线l:与x轴交于点,如图所示依次作正方形、正方形、、正方形,使得点、、、在直线l上,点、、、在y轴正半轴上,则点的坐标是______.10.如图1,点P从的顶点B出发,沿匀速运动到点A,图2是点P运动时,线段BP的长度y随时间x变化的关系图象,其中M为曲线部分的最低点,则的面积是______.11.如图,一次函数的图象与x轴的交点坐标为,则下列说法:随x的增大而减小;;关于x的方程的解为;不等式的解集是.其中说法正确的有__ ____把你认为说法正确的序号都填上.12.已知一次函数的图象经过第二、三、四象限,与x轴的交点为,则不等式的解集是___ ___.13.已知一次函数的图象过点和点,若,则x的取值范围是______.三、解答题14.如图,函数与的图象交于.求出m、n的值;直接写出不等式的解集;求出的面积.15.如图,直线分别与x轴、y轴相交于点A、点B.求点A和点B的坐标;若点P是y轴上的一点,设、的面积分别为与,且,求点P的坐标.16.如图,点A、B的坐标分别为,,直线与坐标轴交于C、D两点.求直线AB:与CD交点E的坐标;直接写出不等式的解集;求四边形OBEC的面积;利用勾股定理证明:.17.如图,已知直线与坐标轴分别交于点、,动点C从原点O出发沿OA方向以每秒1个单位长度向点A运动,动点D从点B出发沿BO方向以每秒1个单位长度向点O运动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动,设运动时间为t秒.直接写出直线的解析式:__ ____ ;若E点的坐标为,当的面积为5时.求t的值;探索:在y轴上是否存在点P,使的面积等于的面积?若存在,请求出P点的坐标;若不存在,请说明理由.18.在平面直角坐标系xOy中,直线与x轴,y轴分别交于点A,B,抛物线经过点A,将点B向右平移5个单位长度,得到点C.求点C的坐标;求抛物线的对称轴;若抛物线与线段BC恰有一个公共点,结合函数图象,求a的取值范围.19.。
2019年中考数学培优练习一次函数.doc.docx

2019 年中考数学培优练习一次函数一、选择题1- 121、下列函数( 1)y=πx (2)y=2x-1 (3) y=x(4) y=2-3x (5) y=x- 1 中,是一次函数的有()A、4个B、3 个C、2个D、1 个2、函数yx2的自变量的取值范围是()x3A.>1 B.>1且≠3C.≥1D.≥1且≠33、若直线 y=﹣ 2x﹣ 4 与直线 y=4x+b 的交点在第三象限,则 b 的取值范围是()A.﹣ 4<b< 8B.﹣ 4< b< 0C. b<﹣ 4 或 b> 8D.﹣ 4≤b≤84、下列图形中,表示一次函数y=mx+n 与正比例y=mnx( m, n 是常数,且 mn≠0)图象的是()A. B. C. D.5、如图,一次函数1y x 2的图象上有两点A、 B, A点的横坐标为20<2, B 点的横坐标为a(a<4且 a≠2),过点 A、B 分别作 x 轴的垂线,垂足为 C、D,△ AOC、△ BOD 的面积分别为S1、S2, S1与S2的大小关系是()A.S1>S2B. S1= S2C.S1<S2D.无法确定6.如果在一次函数中 , 当自变量x的取值范围是- 1<x< 3 时,函数 y 的取值范围是- 2<y< 6,那么此函数解析式为 ( )A. y 2xB. y2x 4C. y 2x或y2x 4D. y2x 或 y2x47、点1(1, 1),点2(2,2)是一次函数y =- 4x+ 3 图象上的两个点,且x1<2,则y1 与P x y P x y x y2的大小关系是()A、y1>y2B、y1> y2>0C、y1<y2D、 y1= y28、若函数y=2x+3与y=3x-2b 的图象交x 轴于同一点,则 b 的值为()A.- 3B.-3C. 9D.-9 249、如图所示,函数y1x141,1),( 2, 2)两点.当 y1> y2时, x 和 y2x3的图象相交于(﹣3的取值范围是()A. x<﹣ 1B.﹣ 1< x< 2C. x> 2D. x<﹣ 1 或 x> 210、如图,在平面直角坐标系中,直线y=x﹣与矩形ABCO的边OC、BC分别交于点E、F,已知OA=3,OC=4,则△ CEF 的面积是()A. 6B.3C. 12D.二.填空题1 .若一次函数的图象经过点(2,-1),且与直线y=2x+1平行, 则其表达式为.2、已知点P(a, b)在一次函数y=4x+3 的图象上,则代数式4a﹣ b﹣ 2 的值等于_________.3、直线y2x 向上平移3个单位,再向左平移 2 个单位后的解析式为________.4、在平面直角坐标系xOy 中,已知点A( 0, 1), B( 1, 2),点P 在x 轴上运动,当点P到 A、B两点距离之差的绝对值最大时,点P 的坐标是_________.5、在平面直角坐标系中,点O是坐标原点,过点A(1,2)的直线y=kx+b与x轴交于点B,且 S△AOB=4,则 k 的值是 _________ .6.如图,一次函数y=kx+b ( k< 0)的图象经过点A.当 y< 3 时, x 的取值范围是_________.7.一次函数y=kx+b (k为常数且k≠0)的图象如图所示,则使y>0 成立的x 取值范围为_________.8.如,直 1:点 C的坐_________与.x 、 y 分相交于点A、B,△ AOB与△ ACB 关于直l称,9.直 y=2x+6 与直 y= -2x 1 的像与x 成的三角形面是_____.与 y 成的三角形面是_____10、如,一系列“黑色梯形”是由x 、直y=x 和 x 上的正奇数1、3、 5、 7、9、⋯所的点且与y 平行的直成的.从左到右,将其面依次S1、S2、 S3、⋯、 S n、⋯.S1=_________, S n=_________.11、在直角坐系中,正方形A1B1C1O1、A2B2C2C1、⋯、A n B n C n C n﹣1按如所示的方式放置,其中点A1、A2、A3、⋯、 A n均在一次函数y=kx+b的象上,点C1、 C2、 C3、⋯、 C n均在 x 上.若点B1的坐(的坐_________.1, 1),点B2的坐(3, 2),点A n三、解答1、已知与成正比例,且(1)求与之的函数关系式;(2)当.,求的.2、如图,直线分别交x轴、y轴于A、B两点,线段AB 的垂直平分线分别交x 轴、 y 轴于 C、 D两点.( 1)求点 C 的坐标;( 2)求△ BCD的面积.3、某商场筹集资金12.8 万元,一次性购进空调、彩电共30 台.根据市场需要,这些空调、彩电可以全部销售,全部销售后利润不少于 1.5 万元,其中空调、彩电的进价和售价见表格.空调彩电进价(元 / 台)54003500售价(元 / 台)61003900设商场计划购进空调x 台,空调和彩电全部销售后商场获得的利润为y 元.(1)试写出 y 与 x 的函数关系式;(2)商场有哪几种进货方案可供选择?(3)选择哪种进货方案,商场获利最大?最大利润是多少元?4、如图,直线OC、BC的函数关系式分别为y=x 和 y=-2x+6 ,动点 P(x ,0) 在 OB上移动 (0<x<3) ,过点 P作直线l与 x 轴垂直。
2019年中考数学知识点过关培优训练卷:垂直平分线的性质应用(附解析)
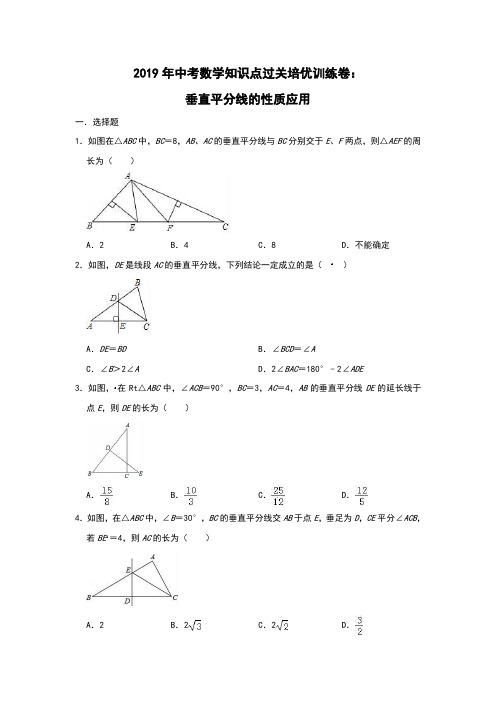
2019年中考数学知识点过关培优训练卷:垂直平分线的性质应用一.选择题1.如图在△ABC中,BC=8,AB、AC的垂直平分线与BC分别交于E、F两点,则△AEF的周长为()A.2 B.4 C.8 D.不能确定2.如图,DE是线段AC的垂直平分线,下列结论一定成立的是()A.DE=BD B.∠BCD=∠AC.∠B>2∠A D.2∠BAC=180°﹣2∠ADE3.如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AB的垂直平分线DE的延长线于点E,则DE的长为()A.B.C.D.4.如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠ACB,若BE=4,则AC的长为()A.2 B.2C.2D.5.如图,以C为圆心,以大于点C到AB距离为半径作弧交AB于点D、E,再以D、E为圆心,以大于为半径作弧,两弧交于点F,作射线CF,则()A.CF平分∠ACB B.CF⊥ABC.CF平分AB D.CF垂直平分AB6.如图,△ABC,AB>AC>BC,边AB上存在一点P,使得PA+PC=AB.下列描述正确的是()A.P是AC的垂直平分线与AB的交点B.P是BC的垂直平分线与AB的交点C.P是∠ACB的平分线与AB的交点D.P是以点B为圆心,AC长为半径的弧与边AB的交点7.如图,在△ABC中,BD平分∠ABC,BC的垂直平分线交BC于点E,交BD于点F,连接CF,若∠A=60°,∠ABD=24°,则∠ACF的度数为()A.24°B.30 C.36°D.48°8.如图,在△ABC中,∠C=90°,AB的垂直平分线交AB于D,交BC于E,连接AE,若CE =5,AC=12,且△ACE的周长为30,则BE的长是()A.5 B.10 C.12 D.139.如图,DE是△ABC中AC边的垂直平分线,若BC=6cm,AB=8cm,则△EBC的周长为()A.14cm B.18cm C.20cm D.22cm10.如图,在△ABC中,∠ABC=50°,∠BAC=20°,D为线段AB的垂直平分线与直线BC 的交点,连结AD,则∠CAD=()A.40°B.30°C.20°D.10°二.填空题11.如图,在△ABC中,DE是AC的垂直平分线且分别交BC,AC于点D和E,∠B=60°,∠C=25°,则∠BAD的度数为.12.已知点P在线段AB的垂直平分线上,PA=4cm,则PB=cm.13.如图△ABC中,AC=12,DE为AB的垂直平分线,△BCE的周长为20,则BC的长为.14.如图,在四边形ABCD中,E为AB的中点,DE⊥AB于点E,∠A=66°,∠ABC=90°,BC=AD,则∠C的大小为.15.如图,△ABC中,AC的垂直平分线DE分别交BC于点E,交AC于点D,连接BD,AB=AD,∠CED=45°+∠BAC,△ABD的面积为54,则线段BD的长为.16.如图,已知在锐角△ABC中,AB、AC的中垂线交于点O,则∠ABO+∠ACB=.17.如图,在Rt△ABC中,∠ACB=90°,BC=6,AB的垂直平分线交AB于D,交AC于E,若CD=5,则AE=.18.如图,在△ABC中,∠B=40°,∠C=45°,AB的垂直平分线交BC于点D,AC的垂直平分线交BC于点E,则∠DAE=.19.如图,分别以线段BC的两个端点为圆心,以大于BC长为半径画弧,两弧分别相交于D、E两点,直线DE交BC于点F,点A是直线DE上的一点,连接AB、AC,若AB=12cm,∠C=60°,则CF=cm.20.如图,在平面直角坐标系中,平行于x轴的线段AB上所有点的纵坐标都是﹣1,横坐标x的取值范围是1≤x≤5,则线段A B上任意一点的坐标可以用“(x,﹣1)(1≤x≤5)”表示.若射线CD垂直平分AB于点C,那么按照类似这样的规定,射线CD上任意一点的坐标可以表示为.三.解答题21.如图,△ABC中,AB,AC边的垂直平分线分别交BC于点D,E,垂足分别为点F,G,△ADE的周长为6cm.(1)求△ABC中BC边的长度;(2)若∠BAC=116°,求∠DAE的度数.22.如图,在△ABC中,∠C=90°,边AB的垂直平分线DE交AC于D.(1)若CA=16cm,BC=8cm,求DC的长度;(2)若△BDC的周长是n+2,AB=n,求△ABC的面积.(用含n的代数式表示).23.在△ABC中,DE垂直平分AB,分别交AB、BC于点D、E,MN垂直平分AC,分别交AC、BC于点M、N,连接AE,AN.(1)如图1,若∠BAC=100°,求∠EAN的度数;(2)如图2,若∠BAC=70°,求∠EAN的度数;(3)若∠BAC=α(α≠90°),请直接写出∠EAN的度数.(用含α的代数式表示)24.如图,在四边形ABC D中,M,N分别是CD,BC的中点,且AM⊥CD,AN⊥BC.(1)求证:∠BAD=2∠MAN;(2)连接BD,若∠MAN=70°,∠DBC=40°,求∠ADC.26.如图,C,D是AB的垂直平分线上两点,延长AC,DB交于点E,AF∥BC交DE于点F.求证:(1)AB是∠CAF的角平分线;(2)∠FAD=∠E.27.已知:如图,AF平分∠BAC,BC垂直平分AD,垂足为E,CF上一点P,连结PB交线段AF相交于点M.(1)求证:AB∥CD;(2)若∠DAC=∠MPC,请你判断∠F与∠MCD的数量关系,并说明理由.28.下面是小东设计的“作△ABC中BC边上的高线”的尺规作图过程.已知:△ABC.求作:△ABC中BC边上的高线AD.作法:如图,①以点B为圆心,BA的长为半径作弧,以点C为圆心,CA的长为半径作弧,两弧在BC下方交于点E;②连接AE交BC于点D.所以线段AD是△ABC中BC边上的高线.根据小东设计的尺规作图过程,(1)使用直尺和圆规,补全图形;(保留作图痕迹)(2)完成下面的证明.证明:∵=BA,=CA,∴点B,C分别在线段AE的垂直平分线上()(填推理的依据).∴BC垂直平分线段AE.∴线段AD是△ABC中BC边上的高线.参考答案一.选择题1.解:∵AB的中垂线交BC于E,AC的中垂线交BC于F,∴EA=EB,FA=FC,则△AEF的周长=AE+EF+AF=BE+EF+FC=BC=8,故选:C.2.解:∵DE是线段AC的垂直平分线,∴∠BA C=∠DCA,∴2∠BAC=180°﹣2∠ADE,D正确,故选:D.3.解:设CE=x,连接AE.∵DE是线段AB的垂直平分线,∴AE=BE=BC+CE=3+x,∴在Rt△ACE中,AE2=AC2+CE2,即(3+x)2=42+x2,解得x=.在Rt△ABC中,AB==5,∴BD=AD=,在Rt△BDE中,DE==,故选:B.4.解:∵DE是BC的垂直平分线,∴EB=EC,∴∠ECB=∠B=30°,∴DE=BE=2,由勾股定理得,BD==2,∴BC=2BD=4,∵CE平分∠ACB,∴∠ECB=∠ACE=30°,∴∠A=90°,又∠B=30°,∴AC=BC=2,故选:B.5.解:由作图可知:直线CF⊥AB,故选:B.6.解:∵PA+PC=BC,∴PA=PC,∴点P在BC的垂直平分线上,即点P为BC的垂直平分线与AB的交点.故选:B.7.解:∵BD平分∠ABC,∴∠DBC=∠ABD=24°,∵∠A=60°,∴∠ACB=180°﹣60°﹣24°×2=72°,∵BC的中垂线交BC于点E,∴BF=CF,∴∠FCB=24°,∴∠ACF=72°﹣24°=48°,故选:D.8.解:∵CE=5,AC=12,且△ACE的周长为30,∴AE=13.∵AB的垂直平分线交AB于D,交BC于E,∴BE=AE=13,故选:D.9.解:∵DE是△ABC中AC边的垂直平分线,∴AE=CE,∴CE+BE=AB=8cm.∵BC=6cm,∴△EBC的周长=BC+CE+BE=BC+AB=6+8=14(cm).故选:A.10.解:∵D为线段AB的垂直平分线与直线BC的交点,∴DA=DB,∴∠DAB=∠ABC=50°,∴∠CAD=∠DAB﹣∠BAC=50°﹣20°=30°.故选:B.二.填空题11.解:∵DE是AC的垂直平分线且分别交BC,AC于点D和E,∴AD=CD,∴∠C=∠DAC,∵∠C=25°,∴∠DAC=25°,∵在△ABC中,∠B=60°,∠C=25°,∴∠BAC=180°﹣∠B﹣∠C=95°,∴∠BAD=∠BAC﹣∠DAC=95°﹣25°=70°,故答案为:70°.12.解:∵点P在线段AB的垂直平分线上,∴PB=PA,∵PA=4cm,∴PB=4cm.故答案为4cm.13.解:∵DE为AB的垂直平分线,∴AE=BE,∵△BCE的周长为20,∴BC+BE+CE=BC+AE+CE=BC+AC=20cm,∵AC=12,∴BC=8.故答案为:814.解:如图,连接BD.∵AE=EB,DE⊥AB,∴DA=DB,∴∠A=∠DBA=66°,∵∠ABC=90°,∴∠DBC=24°,∵BC=AD,∴BD=BC,∴∠C=∠BDC=(180°﹣24°)=78°,故答案为78°.15.解:如图,作AH⊥BD于H交BC于M,作AK⊥CB交CB的延长线于K,作MP⊥AC于P.∵AB=AD,AH⊥BD,∴∠DAH=∠ABC,设∠DAH=α,则∠CED=45°+α,∵ED⊥AC,∴∠EDC=90°,∴∠C=45°﹣α,∴∠AMB=∠MAC+∠C=45°,∵A M垂直平分线段BD,∴MB=MD,∵MH⊥BD,∴∠BMH=∠DMH=45°,∴BH=MH=DH,设BH=MH=DH=a,∵AK⊥CK,∴∠K=90°,∵∠KMA=∠KAM=45°,∴AK=KM,∵∠DMC=∠K=90°,∴DM∥AK,∵AD=DC,∴KM=CM,设AK=KM=CM=m,则AC=m,∵△CPM∽△CKA,∴==,∴==,∴PM=m,PC=m,∴PA=,∴tan∠PAM===,∵DH=a,∴AH=3a,=•BD•AH=×2a×3a=54,∵S△ABD∴a=3或﹣3(舍弃)∴BD=2a=6.故答案为16.解:∵BE是AC的垂直平分线,∴BA=BC,BE⊥AC,∴∠ACB=∠A,∵∠ABO+∠A=90°,∴∠ABO+∠ACB=90°,故答案为:90°.17.解:如图,连接BE,∵AB的垂直平分线交AB于D,交AC于E,∴AE=BE,∵Rt△ABC中,∠ACB=90°,D是AB的中点,∴AB=2CD=10,又∵BC=6,∴AC=8,设AE=BE=x,则CE=8﹣x,∵∠BCE=90°,∴Rt△BCE中,CE2+BC2=BE2,即(8﹣x)2+62=x2,解得x=,∴AE=,故答案为:.18.解:∵点D、E分别是AB、AC边的垂直平分线与BC的交点,∴AD=BD,AE=CE,∴∠B=∠BAD,∠C=∠CAE,∵∠B=40°,∠C=45°,∴∠B+∠C=85°,∠BAC=95°,∴∠BAD+∠CAE=85°,∴∠DAE=∠BAC﹣(∠BAD+∠CAE)=95°﹣85°=10°,故答案为:10°19.解:由作图可知:AE垂直平分线段BC,∴AB=AC,BF=CF,∴∠B=∠C=60°,∵AB=12cm,∠AFB=90°,∴BF=AB=6(cm)故答案为:6.20.解:∵点A的坐标为(1,﹣1),点B的坐标为(5,﹣1),C是AB的中点,∴点C的坐标为(3,﹣1),∴线CD上任意一点的坐标可以表示为:(3,y)(y≥﹣1),故答案为:(3,y)(y≥﹣1).三.解答题21.解:(1)∵AB的中垂线交BC于D,AC的中垂线交BC于E,∴DA=DB,EA=EC,则△ADE的周长=AD+DE+AE=BD+DE+EC=BC=6(cm),∴BC=6cm,(2)∵∠BAC=116°,∴∠B+∠C=180°﹣116°=64°,∵DA=DB,EA=EC,∴∠B=∠DAB,∠C=∠EAC,∵∠ADE=∠B+∠DAB,∠AED=∠C+∠EAC,∴∠ADE+∠AED=128°,∴∠DAE=180°﹣128°=52°.22.解:(1)∵DE垂直平分线段AB,∴DA=DB,设CD=x,则AD=BD=(16﹣x)cm,在Rt△BDC中,∵BD2=CD2+BC2,∴(16﹣x)2=x2+82,∴x=6,∴CD=6cm.(2)∵△BDC的周长=n+2,∴BD+CD+BC=n+2,∵AD=DB,∴AD+DC+BC=n+2,设BC=x,AC=y,则有:,①2﹣②得到:2xy=4n+4,∴xy=2n+2,=xy=n+1.∴S△ABC23.解:(1)∵DE垂直平分AB,∴AE=BE,∴∠BAE=∠B,同理可得:∠CAN=∠C,∴∠EAN=∠BAC﹣∠BAE﹣∠CAN,=∠BAC﹣(∠B+∠C),在△ABC中,∠B+∠C=180°﹣∠BAC=80°,∴∠EAN=∠BAC﹣(∠BAE+∠CAN)=100°﹣80°=20°;(2)∵DE垂直平分AB,∴AE=BE,∴∠BAE=∠B,同理可得:∠CAN=∠C,∴∠EAN=∠BAE+∠CAN﹣∠BAC,=(∠B+∠C)﹣∠BAC,在△ABC中,∠B+∠C=180°﹣∠BAC=110°,∴∠EAN=∠BAE+∠CAN﹣∠BAC=110°﹣70°=40°;(3)当0°<α<90°时,∠EAN=180°﹣2α;当180°>α>90°时,∠EAN=2α﹣180°.24.(1)证明:连接AC,∵M是CD的中点,AM⊥CD,∴AM是线段CD的垂直平分线,∴AC=AD,又AM⊥CD,∴∠3=∠4,同理,∠1=∠2,∴∠2+∠3=∠BAD,即BAD=2∠MAN;(2)∵AM⊥CD,AN⊥BC.∠MAN=70°,∴∠BCD=360°﹣90°﹣90°﹣70°=110°,∴∠BDC=180°﹣∠DBC﹣∠BCD=30°,∠BAD=2∠MAN=140°,∵AB=AC,AD=AC,∴AB=AD,∴∠ADB=∠ABD=20°,∴∠ADC=∠ADB+∠BDC=50°.25.解:(1)∵DE垂直平分AB,∴AE=BE,∴∠BAE=∠B,同理可得∠CAN=∠C,∴∠EAN=∠BAC﹣∠BAE﹣∠CAN=∠BAC﹣(∠B+∠C),在△ABC中,∠B+∠C=180°﹣∠BAC=70°,∴∠EAN=110°﹣70°=40°.(2)∵DE垂直平分AB,∴AE=BE,∴∠BAE=∠B,同理可得∠CAN=∠C,∴∠EAN=∠BAE+∠CAN﹣∠BAC=(∠B+∠C)﹣∠BAC,在△ABC中,∠B+∠C=180°﹣∠BAC=100°,∴∠EAN=100°﹣80°=20°.(3)当0°<α<90°时,∠EAN=180°﹣2α;当90°<α<180°时,∠EAN=2α﹣180°.26.证明:(1)∵点C是AB的垂直平分线上的点,∴CB=CA,∴∠CB A=∠CAB,∵AF∥BC交DE于点F,∴∠BAF=∠CBA,∴∠BAF=∠CAB.即AB是∠CAF的角平分线.(2)∵点D是AB的垂直平分线上的点,∴DB=DA,∴∠DBA=∠DAB,∵∠DBA=∠E+∠CAB,∠DAB=∠FAD+∠BAF,∠CAB=∠BAF,∴∠E=∠FAD.27.解:(1)∵BC垂直平分AD,∴AC=CD,∠CAD=∠CDA,∵AF平分∠BAC,∴∠CAD=∠BAD,∴∠CDA=∠BAD,∴AB∥C D;(2)结论:∠F=∠MCD,理由:∵∠DAC=∠CDA,∠DAC=∠MPC,∴∠CDA=∠MPC,又∵∠CDA+∠CDM=180°,∠MPC+∠MPF=180°,∴∠CDM=∠MPF;又∵AF平分∠BAC,AE⊥BC,AE=AE.∴△ACE≌△ABE(ASA),∴AC=AB.又∵AF平分∠BAC,AM=AM,∴△ACM≌△ABM(SAS),∴∠AMC=∠AMB,又∵∠AMB=∠PMF.∴∠AMC=∠PMF.又∵∠AMC+∠MCD+∠CDM=180°,∠PMF+∠MPF+∠F=180°,∴∠F=∠MCD.28.解:(1)图形如图所示:(2)理由:连接BE,EC.∵AB=BE,EC=CA,∴点B,点C分别在线段AE的垂直平分线上(到线段两个端点距离相等的点在线段的垂直平分线上),∴直线BC垂直平分线段AE,∴线段AD是△ABC中BC边上的高线.故答案为:BE,EC,到线段两个端点距离相等的点在线段的垂直平分线上.。
2019年中考数学知识点过关培优训练卷:等腰三角形的性质与判定(附解析)

2019年中考数学知识点过关培优训练卷:等腰三角形的性质与判定一.选择题1.如图,在△ABC中,AB=AC,点D在AC上,DE∥AB,若∠CDE=160°,则∠B的度数为()A.80°B.75 C.65°D.60°2.如图,在△ABC中,CE平分∠ACB,点D在BC的延长线上,CF平分∠ACD,且EF∥BC交AC于M,若CM=5,则CE2+CF2等于()A.75 B.100 C.120 D.1253.如图,在△ABC中,AB=6,AC=4,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC 分别交AB、AC于M、N,则△AMN的周长为()A.12 B.10C.8 D.不确定4.如图,△ABC的面积为9cm2,BP平分∠ABC,AP⊥BP于P,连接PC,则△PBC的面积为()A.3cm2B.4cm2C.4.5cm2D.5cm25.在等腰三角形△ABC(AB=AC,∠BAC=120°)所在平面上有一点P,使得△PAB,△PBC,△PAC都是等腰三角形,则满足此条件的点P有()A.1个B.2个C.3个D.4个6.如图,△ABC的面积为10cm2,BP是∠ABC的平分线,AP⊥BP于P,则△PBC的面积为()A.4cm2B.5cm2C.6 cm2D.7 cm27.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过O点作EF∥BC交AB于点E,交AC于点F,过点O作OD⊥AC于D,下列四个结论.①EF=BE+CF②∠BOC=90°+∠A③点O到△ABC各边的距离相等④设OD=m,AE+AF=mn,正确的结论有()个.=n,则S△AEFA.1个B.2个C.3个D.4个8.如图,△ABC中,BO平分∠ABC,CO平分△ABC的外角∠ACD,MN经过点O,与AB,AC 相交于点M,N,且MN∥BC,则BM,CN之间的关系是()A.BM+CN=MN B.BM﹣CN=MN C.CN﹣BM=MN D.BM﹣CN=2MN 9.如图,△ABC中,AC=DC=3,BD垂直∠BAC的角平分线于D,E为AC的中点,则图中两个阴影部分面积之差的最大值为()A.1.5 B.3 C.4.5 D.910.已知点P是△ABC内一点,且它到三角形的三个顶点距离之和最小,则P点叫△ABC的费马点(Fermatpoint).已经证明:在三个内角均小于120°的△ABC中,当∠APB=∠APC=∠BPC=120°时,P就是△ABC的费马点.若点P是腰长为的等腰直角三角形DEF 的费马点,则PD+PE+PF=()A.2B.1+C.6 D.3二.填空题11.如图,在△ABC中,CD是∠ACB的平分线,DE∥BC交AC于点E,若DE=6cm,AE=5cm,则AC=cm.12.如图,△ABC中,BO平分∠ABC,CO平分∠ACB,MN经过点O,与AB,AC相交于点M,N,且MN∥BC.若AB=7,AC=6,那么△AMN的周长是.13.如图,在Rt△ABC中,∠C=90°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点在△ABC的其他边上,则可以画出的不同的等腰三角形的个数最多为.14.如图,在Rt△ABC中,∠C=90°,D为AB上的点,BD=CD=5,则AD=.15.在一次夏令营活动中,小明同学从营地A出发,要到A地的北偏东 60°方向的C处,他先沿正东方向走了200m到达B地,再沿北偏东30°方向走,恰能到达目的地C(如图),那么,由此可知,B、C两地相距m.16.如图,已知BD⊥AG,CE⊥AF,BD、CE分别是∠ABC和∠ACB的角平分线,若BF=3,ED =2,GC=5,则△ABC的周长为.17.如图,在△ABC中,AB=AC,点E在CA延长线上,EP⊥BC于点P,交AB于点F,若AF =2,BF=3,则CE的长度为.18.如图,△ABC中,∠B=90°.∠BAC的平分线交BC于点E,CD⊥AE于点D,若AC=13,AD=12,则AB=.19.如图,△ABC中,AD是∠BAC的平分线,DE∥AB交AC于点E,若DE=7,CE=6,则AC 的长为.20.如图,在△ABC中,BC=8cm,∠BPC=118°,BP、CP分别是∠ABC和∠ACB的平分线,且PD∥AB,PE∥AC,则△PDE的周长是cm,∠DPE=°.三.解答题21.如图,△ABC是等腰三角形,AB=AC,点D是AB上一点,过点D作DE⊥BC交BC于点E,交CA延长线于点F.(1)证明:△ADF是等腰三角形;(2)若∠B=60°,BD=4,AD=2,求EC的长,22.已知:在△ABC中,∠ACB=90°,点P是线段AC上一点,过点A作AB的垂线,交BP 的延长线于点M,MN⊥AC于点N,PQ⊥AB于点Q,AQ=MN.求证:(1)△APM是等腰三角形;(2)PC=AN.23.如图,已知在四边形ABCD中,AB=10cm,∠A=∠C=90°,点E、点F分别在边AB、CD上,且EF∥BC,∠DEF=∠FBC.(1)求证:∠AED=∠EBF;(2)当∠EBF=∠FBC时,EF=cm.24.如图,在等腰△ABC中,AB=AC,D为底边BC延长线上任意一点,过点D作DE∥AB,与AC延长线交于点E.(1)则△CDE的形状是;(2)若在AC上截取AF=CE,连接FB、FD,判断FB、FD的数量关系,并给出证明.25.如图,在Rt△ABC中,CM平分∠ACB交AB于点M,过点M作MN∥BC交AC于点N,且MN平分∠AMC,若AN=1.(1)求∠B的度数;(2)求CN的长.26.如图1,在四边形ABCD中,DC∥AB,BD平分∠ABC,CD=4.(1)求BC的长;(2)如图2,若∠ABC=60°,过点D作DE⊥AB,过点C作CF⊥BD,垂足分别为E、F,连接EF.请判断△DEF的形状并证明你的结论.27.如图,在△ABC中,AB=AC,∠BAC=36°,BD是∠ABC的平分线,交AC于点D,E是AB的中点,连接ED并延长,交BC的延长线于点F,连接AF,求证:(1)EF⊥AB;(2)△ACF为等腰三角形.28.如图,在△ABC中,BA=BC,D在边CB上,且DB=DA=AC.(1)如图1,填空∠B=°,∠C=°;(2)若M为线段BC上的点,过M作直线MH⊥AD于H,分别交直线AB、AC与点N、E,如图2①求证:△ANE是等腰三角形;②试写出线段BN、CE、CD之间的数量关系,并加以证明.29.如图,已知BD平分∠ABC,AD∥BC,且AC=AD.(1)求证:△ABD为等腰三角形;(2)判断∠C与∠D的数量关系,并说明理由.30.如图,在四边形ABCD中,∠B=90°,DE∥AB交BC于E,交AC于F,∠CDE=∠ACB=30°.(1)求证:△FCD是等腰三角形;(2)若BC=DE,求∠CAD的度数.31.如图1,在等腰Rt△ABC中,∠C=90°,O是AB的中点,AC=6,∠MON=90°,将∠MON绕点O旋转,OM、ON分别交边AC于点D,交边BC于点E(D、E不与A、B、C重合)(1)判断△ODE的形状,并说明理由;(2)在旋转过程中,四边形CDOE的面积是否发生变化?若不改变,直接写出这个值,若改变,请说明理由;(3)如图2,DE的中点为G,CG的延长线交AB于F,请直接写出四边形CDFE的面积S 的取值范围.参考答案一.选择题1.解:∵∠CDE=160°,∴∠ADE=20°,∵DE∥AB,∴∠A=∠ADE=20°,∴∠B=(180°﹣∠A)=(180°﹣20°)=80°.故选:A.2.解:∵CE平分∠ACB,CF平分∠ACD,∴∠ACE=∠ACB,∠ACF=∠ACD,即∠ECF=(∠ACB+∠ACD)=90°,∴△EFC为直角三角形,又∵EF∥BC,CE平分∠ACB,CF平分∠ACD,∴∠ECB=∠MEC=∠ECM,∠DCF=∠CFM=∠MCF,∴CM=EM=MF=5,EF=10,由勾股定理可知CE2+CF2=EF2=100.故选:B.3.解:∵∠ABC和∠ACB的平分线交于点E,∴∠ABE=∠CBE,∠ACE=∠BCE,∵MN∥BC,∴∠CBE=∠BEM,∠BCE=∠CEN,∴∠ABE=∠BEM,∠ACE=∠CEN,∴BM=ME,CN=NE,∴△AMN的周长=AM+ME+AN+NE=AB+AC,∵AB=AC=4,∴△AMN的周长=6+4=10.故选:B.4.解:延长AP交BC于E,∵BP平分∠ABC,∴∠ABP=∠EBP,∵AP⊥BP,∴∠APB=∠EPB=90°,在△ABP和△EBP中,,∴△ABP≌△EBP(ASA),∴AP=PE,∴S△ABP =S△EBP,S△ACP=S△ECP,∴S△PBC =S△ABC=×9cm2=4.5cm2,故选:C.5.解:如图,满足条件的所有点P的个数为2,故选:B.6.解:延长AP交BC于E,∵BP平分∠ABC,∴∠ABP=∠EBP,∵AP⊥BP,∴∠APB=∠EPB=90°,在△ABP 和△EBP 中,,∴△ABP ≌△EBP (ASA ),∴AP =PE ,∴S △ABP =S △EBP ,S △ACP =S △ECP ,∴S △PBC =S △ABC =×10=5(cm 2),故选:B .7.解:∵在△ABC 中,∠ABC 和∠ACB 的平分线相交于点O ,∴∠OBC =∠ABC ,∠OCB =∠ACB ,∠A +∠ABC +∠ACB =180°,∴∠OBC +∠OCB =90°﹣∠A ,∴∠BOC =180°﹣(∠OBC +∠OCB )=90°+∠A ;故②正确;∵在△ABC 中,∠ABC 和∠ACB 的平分线相交于点O ,∴∠OBC =∠OBE ,∠OCB =∠OCF ,∵EF ∥BC ,∴∠OBC =∠EOB ,∠OCB =∠F OC ,∴∠EOB =∠OBE ,∠FOC =∠OCF ,∴BE =OE ,CF =OF ,∴EF =OE +OF =BE +CF ,故①正确;过点O 作OM ⊥AB 于M ,作ON ⊥BC 于N ,连接OA ,∵在△ABC 中,∠ABC 和∠ACB 的平分线相交于点O ,∴ON =OD =OM =m ,∴S △AEF =S △AOE +S △AOF =AE •OM +AF •OD =OD •(AE +AF )=mn ;故④正确;∵在△ABC 中,∠ABC 和∠ACB 的平分线相交于点O ,∴点O到△ABC各边的距离相等,故③正确.故选:D.8.证明:∵ON∥BC,∴∠MO C=∠OCD∵CO平分∠ACD,∴∠ACO=∠DCO,∴∠NOC=∠OCN,∴CN=ON,∵ON∥BC,∴∠MOB=∠OBD∵BO平分∠ABC,∴∠MBO=∠CBO,∴∠MBO=∠MOB,∴OM=BM∵OM=ON+MN,OM=BM,ON=CN,∴BM=CN+MN,∴MN=BM﹣CN.故选:B.9.解:延长BD交AC于点H.设AD交BE于点O.∵AD⊥BH,∴∠ADB=∠ADH=90°,∴∠ABD+∠BAD=90°,∠H+∠HAD=90°,∵∠BAD=∠HAD,∴∠ABD=∠H,∴AB =AH ,∵AD ⊥B H ,∴BD =DH ,∵DC =CA ,∴∠CDA =∠CAD ,∵∠CAD +∠H =90°,∠CDA +∠CDH =90°,∴∠CDH =∠H ,∴CD =CH =AC ,∵AE =EC ,∴S △ABE =S △ABH ,S △CDH =S △ABH ,∵S △OBD ﹣S △AOE =S △ADB ﹣S △ABE =S △ADH ﹣S △CDH =S △ACD ,∵AC =CD =3,∴当DC ⊥AC 时,△ACD 的面积最大,最大面积为×3×3=.故选:C .10.解:如图:过点D 作DM ⊥EF 于点M ,在△BDE 内部过E 、F 分别作∠MEP =∠MFP =30°,则∠EPF =∠FPD =∠EPD =120°,点P 就是费马点,在等腰Rt △DEF 中,DE =DF =,DM ⊥EF ,∴EF =DE =2∴EM =DM =1,故cos30°=,解得:PE =,则PM =,故DP =1﹣,同法可得PF =则PD +PE +PF =2×+1﹣=+1. 故选:B .二.填空题(共10小题)11.解:∵CD平分∠ACB交AB于D,∴∠ACD=∠DCB,∵DE∥BC,∴∠EDC=∠DCB,∴∠EDC=∠ECD,∴DE=EC=4cm,∵AE=5cm,∴AC=AE+EC=5+6=11(cm).故答案为:11.12.解:∵BO平分∠ABC,CO平分∠ACB,∴∠MBO=∠OBC,∠OCN=∠OCB,∵MN∥BC,∴∠MOB=∠OBC,∠NOC=∠OCB,∴∠MBO=∠MOB,∠NOC=∠NCO,∴MO=MB,NO=NC,∵AB=7,AC=6,∴△AMN的周长=AM+MN+AN=AB+AC=6+7=13.故答案为:13.13.解:如图:可以画出7个等腰三角形;故答案为7.14.解:在Rt△ABC中,∠C=90°,∵BD=DC,∴∠B=∠DCB,∵∠B+∠A=90°,∠DCB+∠DCA=90°,∴∠A=∠DCA,∴AD=DC=5,故答案为5.15.解:∵B在A的正东方,C在A地的北偏东 60°方向,∴∠BAC=90°﹣60°=30°,∵C在B地的北偏东30°方向,∴∠ABC=90°+30°=120°,∴∠C=180°﹣∠BAC﹣∠ABC=180°﹣30°﹣120°=30°,∴∠BAC=∠C,∴BC=AB=200m.故答案为:200.16.解:∵AG⊥BD,AF⊥CE,BD,CE分别是∠ABC和∠ACB的角平分线,∴AB=BG,AC=FC.∴AE=EF,AD=GD∴ED是△AFG中位线,∴FG=2ED=4;∴BG=AB=BF+FG=7,CF=AC=CG+FG=9,=3+7+9+9=28.∴C△ABC17.证明:在△ABC中,∵AB=AC,∴∠B=∠C,∵EP⊥BC,∴∠C+∠E=90°,∠B+∠BFP=90°,∴∠E=∠BFP,又∵∠BFP=∠AFE,∴∠E=∠AFE,∴AF=AE,∴△AEF是等腰三角形.又∵AF=2,BF=3,∴CA=AB=5,AE=2,∴CE=7.18.解:∵∠BAC的平分线交BC于点E,∴∠BAE=∠CAD,∵CD⊥AE,∴∠D=∠B=90°,∵AC=13,AD=12,∴CD=5,∵∠AEB=∠CED,∴∠BAE=∠DCE,∴∠DCE=∠DAC,∵∠D=∠D,∴△CDE∽△ADC,∴=,∴=,∴DE=,∴AE=,∵∠BAE=∠DAC,∠B=∠D,∴△ABE∽△ADC,∴,∴=,∴AB=,故答案为:.19.解:∵△ABC中,AD是∠BAC的平分线,∴∠BAD=∠CAD,∵DE∥AB,DE=7,CE=6,∴∠CAD=∠ADE,∴AE=DE=7,∴AC=AE+CE=7+6=13.故答案为:13.20.解:(1)∵BP、CP分别是∠ABC和∠ACB的角平分线,∴∠ABP=∠PBD,∠ACP=∠PCE,∵PD∥AB,PE∥AC,∴∠ABP=∠BPD,∠ACP=∠CPE,∴∠PBD=∠BPD,∠PCE=∠CPE,∴BD=PD,CE=PE,∴△PDE的周长=PD+DE+PE=BD+DE+EC=BC=8cm.故答案为8(2)∵∠PBD=∠BPD,∠PCE=∠CPE,∠BPC=118°,∴∠DPE=118°﹣∠PBC﹣∠PCB∵∠BPC+∠PBC+∠PCB=180°,∴∠PBC+∠PCB=180°﹣118°,∴∠DPE=118°﹣(∠PBC+∠PCB)=118°﹣180°+118°=56°.故答案为56.三.解答题(共11小题)21.解:(1)∵AB=AC,∴∠B=∠C,∵FE⊥BC,∴∠F+∠C=90°,∠BDE+∠B=90°,∴∠F=∠BDE,而∠BDE=∠FDA,∴∠F=∠FDA,∴AF=AD,∴△ADF是等腰三角形;(2)∵DE⊥BC,∴∠DEB=90°,∵∠B=60°,BD=4,∴BE=BD=2,∵AB=AC,∴△ABC是等边三角形,∴BC=AB=AD+BD=6,∴EC=BC﹣BE=4.22.证明:(1)∵BA⊥AM,MN⊥AC,∴∠BAM=∠ANM=90°,∴∠PAQ+∠MAN=∠MAN+∠AMN=90°,∴∠PAQ=∠AMN,∵PQ⊥AB MN⊥AC,∴∠PQA=∠ANM=90°,∴在△PQA与△ANM中,,∴△PQA≌△ANM(ASA)∴AP=AM,∴△APM是等腰三角形;(2)由(1)知,△PQA≌△ANM,∴AN=PQ AM=AP,∴∠AMB=∠APM∵∠APM=∠BPC,∠BPC+∠PBC=90°,∠AMB+∠ABM=90°∴∠ABM=∠PBC∵PQ⊥AB,PC⊥BC∴PQ=PC(角平分线的性质),∴PC=AN.23.解:(1)∵EF∥BC,∴∠EFB=∠FBC,∵∠DEF=∠FBC,∴∠DEF=∠EFB,∴ED∥BF,∴∠AED=∠EBF;(2)∵EF∥BC,∠A=∠C=90°,∴∠DFE=∠C=∠A=90°,∵DE∥BF,∴∠DEF=∠EFB,∵∠DEF=∠FBC,∴∠EFB=∠FBC,∵∠AED=∠FBC,∴∠AED=∠DEF,在△AED与△FED中,,∴△AED≌△FED(AAS),∴AE=EF,∵∠EBF=∠FBC,∴∠EFB=∠EBF,∴BE=EF,∴AE=BE=AB=5,∴EF=5.故答案为:5.24.解:(1)△CDE是等腰三角形,理由:∵AB=AC,∴∠ABC=∠ACB,∵DE∥AB,∴∠ABC=∠CDE,∴∠DCE=∠CDE,∴△CDE是等腰三角形;故答案为:等腰三角形;(2)BF=DF,理由:∵AB∥DE,∴∠A=∠E,∵AF=CE,∴AF=DE,AF+CF=CE+CF,即EF=AC=AB,在△AFB与△EDF中,∴△ABF≌△EDF(SAS),∴BF=DF.25.解:(1)∵CM平分∠ACB,MN平分∠AMC,∴∠ACM=∠BCM,∠AMN=∠CMN,又∵MN∥BC,∴∠AMN=∠B,∠CMN=∠BCM,∴∠B=∠BCM=∠ACM,∵∠A=90°,∴∠B=×90°=30°;(2)由(1)得,∠AMN=∠B=30°,∠MCN=∠CMN,∠A=90°,∴MN=2AN=2,MN=CN,∴CN=2.26.解:(1)∵DC∥AB,∴∠CDB=∠ABD,∵∠ABD=∠CBD,∴BC=CD=4;(2)△DEF是等边三角形,理由:∵BC=CD,CF⊥BD,∴BF=DF,又∵DE⊥AB,∴EF=BD=DF,∵∠BDE=90°﹣∠EBD=90°﹣×60°=60°,∴△DEF是等边三角形.27.证明:(1)∵AB=AC,∠BAC=36°,∴∠ABC=72°,又∵BD是∠ABC的平分线,∴∠ABD=36°,∴∠BAD=∠ABD,∴AD=BD,又∵E是AB的中点,∴DE⊥AB,即FE⊥AB;(2)∵FE⊥AB,AE=BE,∴FE垂直平分AB,∴AF=BF,∴∠BAF=∠ABF,又∵∠ABD=∠BAD,∴∠FAD=∠FBD=36°,又∵∠ACB=72°,∴∠AFC=∠ACB﹣∠CAF=36°,∴∠CAF=∠AFC=36°,∴AC=CF,即△ACF为等腰三角形.28.解:(1)∵BA=BC,∴∠BCA=∠BAC,∵DA=DB,∴∠BAD=∠B,∵AD=AC,∴∠ADC=∠C=∠BAC=2∠B,∴∠DAC=∠B,∵∠DAC+∠ADC+∠C=180°,∴2∠B+2∠B+∠B=180°,∴∠B=36°,∠C=2∠B=72°,故答案为:36;72;(2)①在△ADB中,∵DB=DA,∠B=36°,∴∠BAD=36°,在△ACD中,∵AD=AC,∴∠ACD=∠ADC=72°,∴∠CAD=36°,∴∠BAD=∠CAD=36°,∵MH⊥AD,∴∠AHN=∠AHE=90°,∴∠AEN=∠ANE=54°,即△ANE是等腰三角形;②CD=BN+CE.证明:由①知AN=AE,又∵BA=BC,DB=AC,∴BN=AB﹣AN=BC﹣AE,CE=AE﹣AC=AE﹣BD,∴BN+CE=BC﹣BD=CD,即CD=BN+CE.29.(1)证明:∵BD平分∠ABC,∴∠ABD=∠DBC,∵AD∥BC,∴∠D=∠BDC,∴∠ABD=∠D,∴△ABD为等腰三角形;(2)∠C=2∠D,理由:∵△ABD为等腰三角形;∴AB=AD,∵AD=AC,∴AB=AC,∴∠ABC=∠C,∴∠C=2∠D.30.(1)证明:∵∠B=90°,∠ACB=30°,∴∠BAC=60°∵AB∥DE,∴∠EFC=∠BAC=60°,∵∠CDE=30°,∴∠FCD=∠EFC﹣∠CDE=60°﹣30°=30°,∴∠FCD=∠FDC,∴FD=FC,即△FCD为等腰三角形;(2)解:∵DE∥AB,∴∠DEC=∠B,在△DCE和△CAB中,,∴△DCE≌△CAB,(ASA),∴CA=CD,∴∠CAD=∠ADC==75°.31.解:(1)△ODE是等腰直角三角形,理由:连接OC,在等腰Rt△ABC中,∵O是AB的中点,∴OC⊥AB,OC平分∠ACB,∴∠OCE=45°,OC=OA=OB,∠COA=90°,∵∠DOE=90°,∴∠AOD=∠COE,在△AOD与△COE中,,∴△AOD≌△COE,(ASA),∴OD=OE,∴△ODE是等腰直角三角形;(2)在旋转过程中,四边形CDOE的面积不发生变化,∵△AOD≌△COE,∴四边形CDOE的面积=△AOC的面积,∵AC=6,∴AB=6,∴AO=OC=AB=3,∴四边形CDOE的面积=△AOC的面积=×3×3=9;(3)当四边形CDFE是正方形时,其面积最大,四边形CDFE面积的最大值=9,故四边形CDFE的面积S的取值范围为:0<S≤9.。
备考2019年中考数学压轴题专项培优训练:四边形(附解析)

备考2019年中考数学压轴题专项培优训练:四边形1.把Rt△ABC和Rt△DEF按如图①摆放(点C与E重合),点B、C(E)、F在同一条直线上.已知:∠ACB=∠EDF=90°,∠DEF=45°,AC=8,BC=6,EF =10.如图②,△DEF从图①的位置出发,以每秒1个单位的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点A出发,以每秒1个单位的速度沿AB向点B匀速移动;当点P移动到点B时,点P停止移动,△DEF也随之停止移动.DE与AC交于点Q,连接PQ,设移动时间为t(s).(1)△DEF在平移的过程中,AP=CE=(用含t的代数式表示);当点D落在Rt△ABC的边AC上时,求t的值.(2)在移动过程中,当0<t≤5时,连接PE,①设四边形APEQ的面积为y,求y与t之间的函数关系式并试探究y的最大值;②是否存在△PQE为直角三角形?若存在,请直接写出t的值;若不存在,请说明理由.2.如图1,在正方形ABCD中,E,F分别为BC,CD的中点,连接AE,BF,交点为G.若正方形的边长为4(1)求证:AE⊥BF;(2)将△BCF沿BF对折,得到△BPF(如图2),延长FP交BA的延长线于点Q,求AQ的长;(3)将△ABE绕点A逆时针方向旋转,使边AB正好落在AE上,得到△AHM (如图3),若AM和BF相交于点N,求四边形MNGH的面积.3.如图1,已知三角形纸片△AB C和△DEF重合在一起,AB=AC,DE=DF,△ABC ≌△DEF.数学实验课上,张老师让同学们用这两张纸片进行如下操作:【操作探究1】保持△ABC不动,将△DEF沿射线BC方向平移至图2所示位置,通过度量发现BE:CE=1:2,则S△CGE:S△CAB=;【操作探究2】保持△ABC不动,将△DEF通过一次全等变换(平移、旋转或翻折后和△ABC拼成以BC为一条对角线的菱形,请用语言描述你的全等变换过程.(友情提醒:描述过程要完整)【操作探究3】将两个三角形按图3所示放置:点C与点F重合,AB∥DE.保持△ABC不动,将△DEF沿射线DA方向平移.若AB=13,BC=10,设△DEF 平移的距离为m.①当m=0时,连接AD、BE,判断四边形ABED的形状并说明理由;②在平移的过程中,四边形ABED能否成为正方形?若能,请求出m的值;若不能,请说明理由.4.如图,已知正方形ABCD的边长为4、点P是AB边上的一个动点,连接CP,过点P作PC的垂线交AD于点E,以PE为边作正方形PEFG、顶点G在线段PC 上,对角线EG、PF相交于点O.(1)若AP=1,则AE=;(2)①点O与△APE的位置关系是,并说明理由;②当点P从点A运动到点B时,点O也随之运动,求点O经过的路径长;(3)在点P从点A到点B的运动过程中,线段AE的大小也在改变,当AP =,AE达到最大值,最大值是.5.问题背景:在综合与实践课上,老师让同学们以“矩形纸片的剪拼”为主题开展数学活动.如图1:将矩形纸片ABCD沿对角线AC剪开,得到△ABC和△ACD.并且量AB=4cm,AC=8cm,问题解决:(1)将图1中的△ACD以点为A旋转中心,按逆时针方向能转∠α,使∠α=∠BAC,得到如图2所示的△AC'D,过点C作AC'的平行线,与DC'的延长线交于点E,则四边形ACEC'的形状是.(2)缜密小组将图1中的△ACD以点A为旋转中心,按逆时针方向旋转,使B、A、D三点在同一条直线上,得到如图3所示的△AC'D,连接CC',取CC'的中点F,连接AF并延长到点G,使FG=AF,连接CG、C'G,得到四边形ACGC',发现它是正方形,请你证明这个结论.实践探究:(3)创新小组在缜密小组发现结论的基础上,进行如下操作:将△ABC沿着BD方向平移,使点B与点A重合,此时A点平移至A'点,A'C与BC'相交于点H,如图4所示,连接CC',试求tan∠C'CH的值.6.在矩形ABCD中,AC、BD交于点O,点P、E分别是直线BD、BC上的动点,且PE=PC,过点E作EF∥AC交直线BD于点F(1)如图1,当∠COD=90°时,△BEF的形状是(2)如图2,当点P在线段BO上时,求证:OP=BF(3)当∠COD=60°、CD=3时,请直接写出当△PEF成为直角三角形时的面积.7.在正方形ABCD中,对角线AC、BD交于点O,点P在线段BC上(不含点B),∠BPE=∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.(1)当点P与点C重合时(如图①):①求证:△BOG≌△POE;②猜想:=;(2)当点P与点C不重合时,如图②,的值会改变吗?试说明理由.8.在矩形ABCD中,E为射线BC上一点,DF⊥AE于F,连接DE.(1)如图1,若E在线段BC上,且CE=EF,求证:AD=AE;(2)若AB=6,AD=10,在点E的运动过程中,连接BF.①当△ABF是以AB为底的等腰三角形时,求BE的长;②当BF∥DE时,若S△ADF=m,S△DCE=n,探究m﹣n的值并简要说明理由.9.如图,在平面直角坐标系xOy中,把矩形COAB绕点C顺时针旋转α角,得到矩形CFED.设FC与AB交于点H,且A(0,4),C(8,0).(1)当α=60°时,△CBD的形状是;(2)设AH=m①连接HD,当△CHD的面积等于10时,求m的值;②当0°<α<90°旋转过程中,连接OH,当△OHC为等腰三角形时,请直接写出m的值.10.如图,在等边△ABC中,BC=8cm,射线AG∥BC,点E从点A出发沿射线AG 以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF;(2)①当t为时,以A、F、C、E为顶点的四边形是平行四边形(直接写出结果);②当t为时,S△ACE=2S△FCE.(直接写出结果)11.如图,四边形AOBC中,点C到直线OA,OB的距离相等为m,∠AOB=90°,OC平分∠AOB,OB长为n,且m=++4,四边形AOBC的面积为6.(1)求线段OA的长;(2)P为AB延长线上一点,PQ∥OC,交CB延长线于Q,探究∠OAP、∠ABQ、∠Q的数量关系并说明理由;(3)作AD平行CB交CO延长线于D,BE平分∠CBH,BE反向延长线交CO延长线于F,若设∠ADO=α,∠F=β,试求α+2β的值.12.(1)问题发现:如图1,在Rt△ABC中,AB=AC,D为BC边上一点(不与点B、C重合)将线段AD绕点A逆时针旋转90°得到AE,连接EC,则线段BD与CE的数量关系是,位置关系是;(2)探究证明:如图2,在Rt△ABC与Rt△ADE中,AB=AC,AD=AE,将△ADE绕点A旋转,使点D落在BC的延长线上时,连接EC,写出此时线段AD,BD,CD之间的等量关系,并证明;(3)拓展延仲:如图3,在四边形ABCF中,∠ABC=∠ACB=∠AFC=45°.若BF=13,CF=5,请直接写出AF的长.13.如图(1),已知△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点.作正方形DEFG,使点A、C分别在DG和DE上,连接AE、BG.(1)试猜想线段BG和AE的关系(位置关系及数量关系),请直接写出你得到的结论;(2)将正方形DEFG绕点D逆时针方向旋转一角度α后(0°<α<90°),如图(2),通过观察或测量等方法判断(1)中的结论是否仍然成立?如果成立,请予以证明;如果不成立,请说明理由;(3)若BC=DE=2,正方形DEFG绕点D逆时针方向旋转角度α(0°<α<360°)过程中,当BG为最小值时,求AF的值.14.综合与实践:问题情境:(1)如图1,点E是正方形ABCD边CD上的一点,连接BD、BE,将∠DBE绕点B顺针旋转90°,旋转后角的两边分别与射线DA交于点F和点G.①线段BE和BF的数量关系是;②写出线段DE、DF和BD之间的数量关系,并说明理由;操作探究:(2)在菱形ABCD中,∠ADC=60°,点E是菱形ABCD边CD所在直线上的一点,连接BD、BE,将∠DBE绕点B顺时针旋转120°,旋转后角的两边分别与射线DA交于点F和点G.①如图2,点E在线段DC上时,请探究线段DE、DF和BD之间的数量关系,写出结论并给出证明.②如图3,点E在线段CD的延长线上时,BE交射线DA于点M,若DE=DC=2a,直接写出线段FM和AG的长度.15.如图O为坐标原点,四边形ABCD是菱形,A(﹣8,8),B点在第一象限,AB=10,AB与y轴交于点F,对角线AC交y轴于点E(1)直接写出B、C点的坐标;(2)动点P从C点出发以每秒2个单位的速度沿折线段C﹣D﹣A运动,设运动时间为t秒,请用含t的代数式表示△EDP的面积;(3)在(2)的条件下,是否存在一点P,使△APE沿其一边翻折构成的四边形是菱形?若存在,请直接写出当t为多少秒时存在符合条件的点P;若不存在,请说明理由.16.如图,在平面直角坐标系中,长方形ABCD的顶点A(a,0),B(b,0)在坐标轴上,C的纵坐标是2,且a,b满足式子:(1)求出点A、B、C的坐标.(2)连接AC,在y轴上是否存在点M,使△COM的面积等于△ABC的面积,若存在请求出点M的坐标,若不存在请说明理由.(3)若点P是边CD上一动点,点Q是CD与y轴的交点,连接OP,OE平分∠AOP交直线CD于点E,OF⊥OE交直线CD于点F,当点P运动时,探究∠OPD 和∠EOQ之间的数量关系,并证明.参考答案1.解:(1)如图1,△DEF在平移的过程中,AP=CE=t;当D在AC上时,如图2,∵DE=DF,∴EC=CF=EF=5,∴t=5.故答案为:t;(2)①如图3,过点P作PM⊥BC于M,∴∠BMP=∠ACB=90°,∴△ABC∽△PBM,∴,∴,∴PM=8﹣t,又∵∠EDF=90°,∠DEF=45°,∴∠EQC=∠DEF=45°,∴CE=CQ=t,∴y=S△ACB﹣S△ECQ﹣S△PBE=AC•BC﹣EC•CQ﹣BE•PM,=×8×6﹣×t×t﹣(6﹣t)(8﹣t),=﹣t(0<t≤5),∵a=﹣<0,∴当x=﹣=﹣=时,y最大值=﹣×+×=,②存在.i)当∠PQE=90°时,如图4,过点P作PH⊥BE于H,过点P作PW⊥AC于W,∴△ABC∽△APW,∴,即,∴PW=t,AW=t,∴QW=8﹣t﹣t=8﹣t,EH=t﹣t=t,由①可得:CE=CQ=t,PH=8﹣t∴PQ2=PW2+QW2=(t)2+(8﹣t)2=t2﹣t+64,PE2=PH2+EH2=(8﹣t)2+(t)2=t2﹣t+64,EQ2=CE2+CQ2=t2+t2=2t2∵∠PQE=90°,在Rt△PEQ中,PQ2+EQ2=PE2,即:(t2﹣t+64)+(2t2)=t2﹣t+64解得:t1=0(舍去)t2=;当∠PEQ=90°,PE2+EQ2=PQ2即:(t2﹣t+64)+(2t2)=t2﹣t+64解得:t1=0(舍去)t2=20(舍去)∴此时不存在;当∠EPQ=90°时PQ2+PE2=EQ2,即:(t2﹣t+64)+(t2﹣t+64)=2t2,t1=(舍去)t2=4,综合上述:当t=或t=4时,△PQE是直角三角形.2.解:(1)证明:如图1,∵E,F分别是正方形ABCD边BC,CD的中点,∴CF=BE,在Rt△ABE和Rt△BCF中,∵,∴Rt△ABE≌Rt△BCF(SAS),∠BAE=∠CBF,又∵∠BAE+∠BEA=90°,∴∠CBF+∠BEA=90°,∴∠BGE=90°,∴AE⊥BF;(2)如图2,根据题意得,FP=FC,∠PFB=∠BFC,∠FPB=90°,∵CD∥AB,∴∠CFB=∠ABF,∴∠ABF=∠PFB,∴QF=QB,∵PF=FC=2,PB=BC=4,在Rt△BPQ中,设QB=x,∴x2=(x﹣2)2+42,∴x=5,∴AQ=BQ﹣AB=5﹣4=1;(3)∵正方形边长为4,∵∠BAE=∠EAM,AE⊥BF,∴AN=AB=4,∵∠AHM=90°,∴GN∥HM,…(8分)∴△AGN∽△AHM∴=()2,∴=()2,∴S△AGN=,∴S四边形GHMN=S△AHM﹣S△AGN=4﹣=,∴四边形GHMN的面积是.3.解:(1)如图2,由题意知DE∥AB,∴△CGE∽△CAB,∴=()2,∵=,∴=,则=()2=,故答案为:4:9;(2)将△DEF沿EF翻折或绕BC中点旋转180°;(3)①∵AB∥DE且AB=BC=DC=DE,∴四边形ABED是平行四边形,∵∠DEC+∠CEB+∠CBE+∠ABC=180°,且∠DEC=∠ABC,∠CEB=∠CBE,∴∠DEC+∠CEB=90°,即∠BED=90°,∴四边形ABED是矩形;②能,如图,过点A作AG⊥BC,过点C作CH⊥BE,CM⊥AB,∴BG=BC=5,∴AG==12,∵S△ABC=AB•CM=BC•AG,∴CM==,则BH=CM=,BE=2BH=,∵四边形ABED是正方形,∴平移后BE=AB,则m=+13=或m=﹣13=.4.解:(1)∵四边形ABCD、四边形PEFG是正方形,∴∠A=∠B=∠EPG=90°,PF⊥EG,AB=BC=4,∠OEP=45°,∴∠AEP+∠APE=90°,∠BPC+∠APE=90°,∴∠AEP=∠BPC,∴△APE∽△BCP,∴,即,解得:AE=;故答案为:;(2)①点O在△APE的外接圆上,理由是:证明:如图1,取PE的中点Q,连接A Q,OQ,∵∠POE=90°,∴OQ=PE,∵△APE是直角三角形,∴点Q是Rt△APE外接圆的圆心,∴AQ=PE,∴OQ=AQ=EQ=PQ,∴O在以Q为圆心,以OQ为半径的圆上,即点O在△APE的外接圆上;(到圆心的距离等于半径的点必在此圆上),故答案为:点O在△APE的外接圆上;②连接OA、AC,如图2所示,∵四边形ABCD是正方形,∴∠B=90°,∠BAC=45°,∴AC==4,∵A、P、O、E四点共圆,∴∠OAP=∠OEP=45°,∴点O在AC上,当P运动到点B时,O为AC的中点,OA=AC=2,即点O经过的路径长为2;(3)设AP=x,则BP=4﹣x,由(1)得:△APE∽△BCP,∴,∴,∴AE=(x﹣2)2+1,∴x=2时,AE的最大值为1,即当AP=2时,AE的最大值为1.故答案为:2,1.5.解:(1)在如图1中,∵AC是矩形ABCD的对角线,∴∠B=∠D=90°,AB∥CD,∴∠ACD=∠BAC,在如图2中,由旋转知,AC'=AC,∠AC'D=∠ACD,∴∠BAC=∠AC'D,∵∠CAC'=∠BAC,∴∠CAC'=∠AC'D,∴AC∥C'E,∵AC'∥CE,∴四边形ACEC'是平行四边形,∵AC=AC',∴▱ACEC'是菱形,故答案为:菱形;(2)在图1中,∵四边形ABCD是矩形,∴AB∥CD,∴∠CAD=∠ACB,∠B=90°,∴∠BAC+∠ACB=90°在图3中,由旋转知,∠DAC'=∠DAC,∴∠ACB=∠DAC',∴∠BAC+∠DAC'=90°,∵点D,A,B在同一条直线上,∴∠CAC'=90°,由旋转知,AC =AC ',∵点F 是CC '的中点,∴AG ⊥CC ',CF =C 'F ,∵AF =FG ,∴四边形ACGC '是平行四边形,∵AG ⊥CC ',∴▱ACGC '是菱形,∵∠CAC '=90°,∴菱形ACGC '是正方形;(3)在Rt △ABC 中,AB =4,AC =8,∴AC '=AC =8,AD =BC =4,sin ∠ACB ==,∴∠ACB =30°,由(2)结合平移知,∠CHC '=90°,在Rt △BCH 中,∠ACB =30°,∴BH =BC •sin30°=2,∴C 'H =BC '﹣BH =8﹣2,在Rt △ABH 中,AH =AB =2,∴CH =AC ﹣AH =8﹣2=6,在Rt △CHC '中,tan ∠C ′CH ==.6.解:(1)△BEF 是等腰直角三角形,理由是:如图1,∵∠COD =90°,∴AC ⊥BD ,∴矩形ABCD 是正方形,∴∠ACB =45°,∵EF ∥AC ,∴∠FEB =∠ACB =45°,∠F =∠BOC =90°,∴△BEF 是等腰直角三角形,故答案为:等腰直角三角形;(2)如图2,∵四边形ABCD是矩形,∴AC=BD,OB=BD,OC=AC,∴OB=OC,∴∠OBC=∠OCB=∠FBE,∵∠FBE=∠BEP+∠EPB,∠OCB=∠PCB+∠OCP,∵PE=PC,∴∠BEP=∠PCB,∴∠EPB=∠OCP,∵EF∥AC,∴∠COP=∠BFE,∴△PEF≌△CPO(AAS),∴OC=PF=OB,∴OB﹣PB=PF﹣PB,即OP=BF;(3)∵四边形ABCD是矩形,∴AC=BD,OD=BD,OC=AC,∴OD=OC,∵∠COD=60°,∴△COD是等边三角形,∴OC=CD=3,如图3,当∠PEF=90°时,∵EF∥AC,∴∠POC=∠OFE=60°,∴∠BFE=120°,∴OB =OC , ∴∠OBC =∠OCB =∠FEB =30°,∵∠FEP =90°,∴∠PEC =60°,∵PE =PC ,∴△PEC 是等边三角形,∴∠PCB =60°,∴∠PCO =60°﹣30°=30°=∠FPE ,∴△PFE ≌△COP (ASA ),∴PF =OC =3,Rt △PFE 中,EF =,PE =,∴S △PEF ===;∴当△PEF 成为直角三角形时的面积是.7.(1)①证明:∵四边形ABCD 是正方形,P 与C 重合,∴OB =OP ,∠BOC =∠BOG =90°,∵PF ⊥BG ,∠PFB =90°,∴∠GBO =90°﹣∠BGO ,∠EPO =90°﹣∠BGO ,∴∠GBO =∠EPO ,在△BOG 和△POE 中,∵,∴△BOG ≌△POE (ASA );②由①知,△BOG ≌△POE ,∴BG =PE ,∵∠BPE =∠ACB ,∠BPF +∠GPF =∠ACB ,∴∠BPF =∠GPF ,∵BF⊥PE,∴BF=BG,∴=,故答案为:;(2)解:猜想.证明:如图2,过P作PM∥AC交BG于M,交BO于N,∴∠PNE=∠BOC=90°,∠BPN=∠OCB.∵∠OBC=∠OCB=45°,∴∠NBP=∠NPB.∴NB=NP.∵∠MBN=90°﹣∠BMN,∠NPE=90°﹣∠BMN,∴∠MBN=∠NPE,在△BMN和△PEN中,∵,∴△BMN≌△PEN(ASA),∴BM=PE.∵∠BPE=∠ACB,∠BPN=∠ACB,∴∠BPF=∠MPF.∵PF⊥BM,∴∠BFP=∠MFP=90°.在△BPF和△MPF中,,∴△BPF≌△MPF(ASA).∴BF=MF.即BF=BM.∴BF=PE.即.8.(1)证明:在矩形ABCD中,∠DCE=90°,AD∥BC,∴∠ADE=∠DEC,∠DCE=∠DFE=90°,∵CE=EF,DE=DE,∴△CED≌△FED(HL),∴∠CED=∠FED,∴∠ADE=∠AED,∴AD=AE;(2)①分两种情况:当点E在线段BC上时,AF=BF,如图 1 所示:∴∠ABF=∠BAF,∵∠ABF+∠EBF=90°,∠BAF+∠BEF=90°,∴∠EBF=∠BEF,∴EF=BF,∴AF=EF,∵DF⊥AE,∴DE=AD=10,在矩形ABCD中,CD=AB=6,∠DCE=90°,∴CE=8,∴BE=10﹣8=2;当点E在BC延长线上时,AF=BF,如图 2 所示:同理可证AF=EF,∵DF⊥AE,∴DE=AD=10,在矩形ABCD中,CD=AB=6,∠DCE=90°,∴CE=8,∴BE=10+8=18,综上,BE的长是2或8;②m﹣n=0,理由如下:当BF∥DE时,延长BF交AD于G.如图3:在矩形ABCD中,AD∥BC,AD=BC,AB=CD,∠BAG=∠DCE=90°,∵BF∥DE,∴四边形BEDG是平行四边形,∴BE=DG,∴S△DEF=,AG=CE,▱BEDGS △BEF +S △DFG =S ▱BEDG ,∵△ABG ≌△CDE ,∴S △ABG =S △CDE ,∵S △ABE =S ▱BEDG ,∴S △ABE =S △BEF +S △DFG ,∴S △ABF =S △DFG ,∴S △ABF +S △AFG =S △DFG +S △AFG ,即S △ABG =S △ADF ,∴S △CDE =S △ADF ,即m ﹣n =0.9.解:(1)∵矩形COAB 绕点C 顺时针旋转60度的角,得到矩形CFED , ∴∠BCD =60°,CB =CD ,∴△CBD 为等边三角形;故答案为:等边三角形;(2)①∵四边形CFED 是矩形,∴∠DCH =90°,∵△CHD 的面积等于10,∴CD •CH =10,∵CD =4,∴,CH =5,Rt △BCH 中,由勾股定理得:BH ===3, ∴AH =8﹣3=5,即m =5;②当△OHC 为等腰三角形时,分三种情况:i )当OH =CH 时,如图2,∵OA=BC,∴Rt△AOH≌Rt△BCH(HL),∴AH=BH=4,即m=4;ii)当OH=OC=8时,如图3,∵OA=4,由勾股定理得:AH===4,即m=4;iii)当OC=CH=8时,如图4,此时F与H重合,则BH=4,∴m=8﹣4,综上,m的值是4或4或8﹣4.10.(1)证明:∵AG∥BC,∴∠EAD=∠DCF,∠AED=∠DFC,∵D为AC的中点,∴AD=CD,∵在△ADE和△CDF中,,∴△ADE≌△CDF(AAS);(2)解:①当点F在C的左侧时,根据题意得:AE=tcm,BF=2tcm,则CF=BC﹣BF=6﹣2t(cm),∵AG∥BC,∴当AE=CF时,四边形AECF是平行四边形,即t=8﹣2t,解得:t=;当点F在C的右侧时,根据题意得:AE=tcm,BF=2tcm,则CF=BF﹣BC=2t﹣8(cm),∵AG∥BC,∴当AE=CF时,四边形AEFC是平行四边形,即t=2t﹣8,解得:t=8;综上可得:当t=或8s时,以A、C、E、F为顶点四边形是平行四边形.故答案为或8s.②∵AG∥BC,∴当AE=2CF时, S△AEC=S△EFC,∴t=2(8﹣2t)或t=2(2t﹣8),解得t=或,故答案为:或.11.解:分别以OB、OA所在的直线为x、y轴建立平面直角坐标系.(1)由题意,解得n=2,∴m=4,∴B(2,0),C(4,4).如图1中,∵S四边形AOBC=S△OBC+S△AOC,∴×2×4+×OA×4=6,∴OA=1.(2)如图2中,结论:∠ABQ+∠OAB﹣∠Q=135°.理由如下:∵OC∥PQ,∴∠Q=∠OCB,∵∠ABQ=∠1+∠OCB=∠1+∠Q,∠1=180°﹣∠OAB﹣∠AOC=180°﹣∠OAB ﹣45°=135°﹣∠OAB,∴∠ABQ=∠Q+135°﹣∠OAB,∴∠ABQ+∠OAB﹣∠Q=135°.(3)如图3中,∵AD∥BC,∴∠ADC=∠DCB=α,∵BE平分∠CBx,∴∠CBE=∠EBx,∵∠CBE=∠F+∠OCB=α+β,∴∠OBF=∠EBx=α+β,∵C(4,4),∴OC平分∠AOB,∴∠COB=45°=∠F+∠OBF=α+(α+β),∴α+2β=45°.12.解:(1)在Rt△ABC中,AB=AC,∴∠B=∠ACB=90°,∵∠BAC=∠DAE=90°,∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,在△BAD和△CAE中,,∴△BAD≌△CAE(SAS),∴BD=CE,∠B=∠ACE=45°,∵∠ACB=45°,∴∠BCE=45°+45°=90°,故答案为:BD=CE,BD⊥CE;(2)2AD2=BD2+CD2,理由是:如图2,∵∠BAC=∠DAE=90°,∴∠BAD=∠CAE,在△ABD和△ACE中,∵,∵△BAD≌△CAE(SAS),∴BD=CE,∠B=∠ACE=45°,∴∠BCE=∠ACB+∠ACE=45°+45°=90°,∴DE2=CE2+CD2,∵AD=AE,∠DAE=90°,∴DE=AD,∴2AD2=BD2+CD2;(3)如图3,将AF绕点A逆时针旋转90°至AG,连接CG、FG,则△FAG是等腰直角三角形,∴∠AFG=45°,∵∠AFC=45°,∴∠GFC=90°,同理得:△BAF≌△CAG,∴CG=BF=13,Rt△CGF中,∵CF=5,∴FG=12,∵△FAG是等腰直角三角形,∴AF==6.13.解:(1)结论:BG=AE.理由:如图1,∵△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点,∴AD⊥BC,BD=CD,∴∠ADB=∠ADC=90°.∵四边形DEFG是正方形,∴DE=DG.在△BDG和△ADE中,,∴△ADE≌△BDG(SAS),∴BG=AE.(2)①成立BG=AE.理由:如图2,连接AD,∵在Rt△BAC中,D为斜边BC中点,∴AD=BD,AD⊥BC,∴∠ADG+∠GDB=90°.∵四边形EFGD为正方形,∴DE=DG,且∠GDE=90°,∴∠ADG+∠ADE=90°,∴∠BDG=∠ADE.在△BDG和△ADE中,,∴△BDG≌△ADE(SAS),∴BG=AE;②如图③中,连接AF.如图②中,在△BDG中,∵BD=1,DG=2,∴2﹣1≤BG≤1+2,∴GB的最小值为1,此时如图③中,G,B,D共线,在Rt△AEF中,AF===.14.解:(1)①∵∠DBE绕点B顺针旋转90°,如图(1)由旋转可知,∠DBE=∠GBF,∵四边形ABCD是正方形,∴∠BDC=∠ADB=45°,∵∠DBG=90°,∴∠G=45°,∴∠G=∠BDG,∴GB=BD,∴△GBF≌△DBE(SAS),∴BE=BF;故答案为:BE=BF②DF+DE=BD,理由如下:由旋转可知,∠DBE=∠GBF,∵四边形ABCD是正方形,∴∠BDC=∠ADB=45°,∵∠DBG=90°,∴∠G=45°,∴∠G=∠BDG,∴GB=BD,∴△GBF≌△DBE(SAS),∴DE=GF,∴DF+DE=DG,∵DG=BD,即DE+DF=BD;(2)①DF+DE=BD,理由如下:在菱形ABCD中,∠ADB=∠CDB=∠ADC=,由旋转120°得∠EBF=∠DBG=120°,∠EBD=∠FBG,在△DBG中,∠G=180°﹣120°﹣30°=30°,∴∠BDG=∠G=30°,∴BD=BG,∴△EBD≌△FBG(ASA),∴DE=FG,∴DE+DF=DF+FG=DG,过点B作BM⊥DG于点M,如图(2)∵BD=BG,∴DG=2DM,在Rt△BMD中,∠BDM=30°,∴BD=2BM.设BM=a,则BD=2a,DM=,∴DG=2a,∴,∴DF+DE=BD,②过点B作BM⊥DG,BN⊥DC,如图(3)∵DE=DC=2a,由①中同理可得:FM=7a,AG=4a.15.解:(1)如图1中,作AH⊥CD于H.∵四边形ABCD是菱形,∴CD=AB=BC=10,CD∥AB,∵A(﹣8,8),∴AH=OH=8,DH==6,∴OD=2,OC=8,∴B(2,8),C(8,0).(2)如图2,连接DE,作EK⊥AD于K.设直线AC的解析式为y=kx+b,∵A(﹣8,8),C(8,0),∴,∴,∴直线AC地方解析式为y=﹣x+4,∴E(0,4),∴EF=OE=4,∵四边形ABCD是菱形,∴∠EAF=∠EAK,∵AE=AE,∠AFE=∠AKE=90°,∴△AEF≌△AEK(AAS),∴EF=EK=4,当0≤t<5时,S=×4(10﹣t)=﹣2t+20.当5<t≤10时,S=×4(t﹣10)=2t﹣20.(3)①如图3中当点P在AD上,AP=AE时,沿PE翻折,可得四边形PAEA′为菱形,在Rt△AEF中,AE===4,∴AP=AE=4,∴t=20﹣4②如图4中,当点P在AD上,PA=PE时,沿AE翻折,可得四边形PAP′E是菱形,设PA=PE=EP′=AP′=x,在RtEFP′中,则有x2=(8﹣x)2+42,∴x=5,∴PA=5,∴t=20﹣5=15,综上所述,满足条件的t的值为20﹣4或15s.16.解:(1)∵又∵≥0,|b﹣4|≥0,∴a+b﹣2=0,b﹣4=0,∴a=﹣2,b=4,∴A(﹣2,0).B(4,0),∵四边形ABCD是矩形,点C的纵坐标为2,∴C(4,2).(2)设M(,t),∵S△ABC=×(4+2)×2=6,△COM的面积=△ABC的面积,∴•|t|•4=6,解得t=±3,∴M点坐标为(0,3)或(0,﹣3);(3)结论:∠OPD=2∠EOQ.∵OE平分∠AOP,∴∠AOE=∠POE=∠1+∠2,∵OF⊥OE,∴∠1+∠2+∠3=90°,∠4+∠AOE=90°,∴∠3=∠4,∵CD⊥y轴,∴CD∥AB,∴∠OPD=∠POB=2∠3,∵∠1+∠2+∠3=90°,∠2+∠3+∠4=90°,∴∠1+∠2+∠3=∠2+2∠3,∴∠1=∠3,∴∠OPD=2∠EOQ.。
【中考专题】2019年中考数学二轮 二次函数 专项培优(含答案)
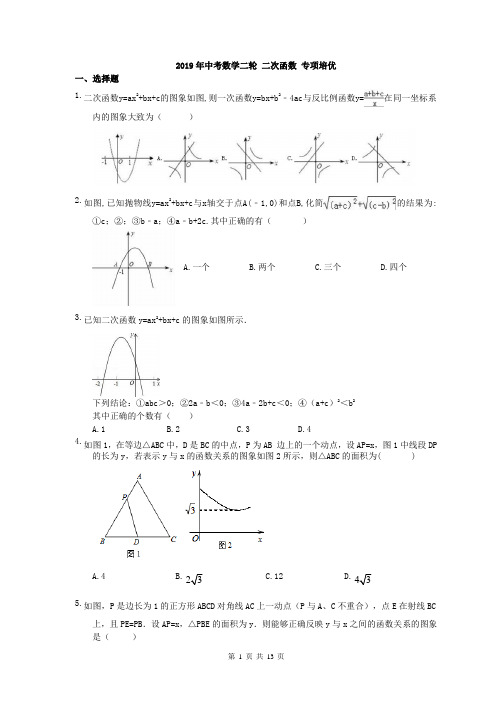
2019年中考数学二轮二次函数专项培优一、选择题1.二次函数y=ax2+bx+c的图象如图,则一次函数y=bx+b2﹣4ac与反比例函数y=在同一坐标系内的图象大致为()2.如图,已知抛物线y=ax2+bx+c与x轴交于点A(﹣1,0)和点B,化简的结果为:①c;②;③b﹣a;④a﹣b+2c.其中正确的有()A.一个B.两个C.三个D.四个3.已知二次函数y=ax2+bx+c的图象如图所示.下列结论:①abc>0;②2a﹣b<0;③4a﹣2b+c<0;④(a+c)2<b2其中正确的个数有()A.1B.2C.3D.44.如图1,在等边△ABC中,D是BC的中点,P为AB 边上的一个动点,设AP=x,图1中线段DP的长为y,若表示y与x的函数关系的图象如图2所示,则△ABC的面积为( )C.12D.A.4B.5.如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在射线BC上,且PE=PB.设AP=x,△PBE的面积为y.则能够正确反映y与x之间的函数关系的图象是()6.如图,二次函数y=ax2+bx+c的图象与x轴的交点的横坐标分别为﹣1,3,则下列结论正确的个数有()①ac<0;②2a+b=0;③4a+2b+c>0;④对于任意x均有ax2+bx≥a+b.A.1B.2C.3D.47.如图,直线y=0.5x+2与y轴交于点A,与直线y=﹣0.5x交于点B,以AB为边向右作菱形ABCD,点C恰与原点O重合,抛物线y=(x﹣h)2+k的顶点在直线y=-0.5x上移动.若抛物线与菱形的边AB、BC都有公共点,则h的取值范围是()A.﹣2≤h≤0.5B.﹣2≤h≤1C.﹣1≤h≤1.5D.﹣1≤h≤0.58.已知a≥2,m2﹣2am+2=0,n2﹣2an+2=0,则(m﹣1)2+(n﹣1)2的最小值是()A.6B.3C.﹣3D.09.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b>m(am+b)(m≠1的实数).其中正确的结论有( )A.2个 B.3个 C.4个 D.5个10.如图,在平面直角坐标系中,四边形OABC是矩形,点A(4,0),C(0,3).直线y=0.5x由原点开始向上平移,所得的直线y=-0.5x+b与矩形两边分别交于M、N两点,设△OMN面积为S,那么能表示S与b函数关系的图象大致是()A. B. C. D.11.如图,某校的围墙由一段相同的凹曲拱组成,其拱状图形为抛物线的一部分,栅栏的跨径AB以相同间隔0.2米用5根立柱加固,拱高OC为0.36米,则立柱EF的长为()A.0.4米B.0.16米C.0.2米D.0.24米12.如图,正方形ABCD中,AB=8 cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以1 cm/s的速度沿BC,CD运动,到点C,D时停止运动,设运动时间为t(s),△OEF的面积S(cm2),则S(cm2)与t(s)的函数关系可用图象表示为( B )二、填空题13.如图,抛物线C是二次函数y=x2﹣10x在第四象限的一段图象,它与x轴的交点是O、A1;将C1绕1点A1旋转180°后得抛物线C2;它与x轴的另一交点为A2;再将抛物线C2绕A2点旋转180°后得抛物线C3,交x轴于点A3;如此反复进行下去…,若某段抛物线上有一点P,则a= .14.如图,抛物线与交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:①无论x取何值,的值总是正数;②;③当x=0时,;④AB+AC=10;⑤.其中正确结论的个数是:.15.如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴的交点A、B的横坐标分别为﹣1,3,与y轴负半轴交点C.在下面五个结论中:①bc>0;②a+b+c<0;③c=﹣3a;④当﹣1<x<3时,y>0;⑤如果△ABC为直角三角形,那么仅a=一种情况.其中正确的结论是.(只填序号)16.如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴正半轴相交于A、B两点,与y轴相交于点C,对称轴为直线x=2,且OA=OC,则下列结论:①abc>0;②9a+3b+c<0;③c>﹣1;④关于x的方程ax2+bx+c=0(a≠0)有一个根为 -a-1.其中正确的结论个数有(填序号)17.体育公园的圆形喷水池的水柱(如图1)如果曲线APB表示落点B离点O最远的一条水流(如图2),其上的水珠的高度)y(米)关于水平距离x(米)的函数解析式为y=﹣x2+4x+2.25,那么圆形水池的半径至少为米时,才能使喷出的水流不落在水池外.18.定义符号min{a,b}的含义为:当a≥b时,min{a,b}=b.当a<b时,min{a,b}=a.若当-2≤x≤3,min{x2-2x-15,m(x+1)}=x2-2x-15,则实数m的取值范围是________三、解答题19.已知二次函数y=a(x-m)2-a(x-m)(a、m为常数,且a≠0).(1)求证:不论a与m为何值,该函数的图象与x轴总有两个公共点;(2)设该函数的图象的顶点为C,与x轴交于A、B两点,与y轴交于点D.①当△ABC的面积等于1时,求a的值;②当△ABC的面积与△ABD的面积相等时,求m的值.20.如图,在平面直角坐标系中,抛物线y=-x2+bx+c经过点A(3,0)和B(2,3).过点A的直线与y轴的负半轴相交于点C,且tan∠ACO=3.(1)求这条抛物线的表达式及对称轴;(2)连接AB、BC,求∠ABC的正切值;(3)若点D在x轴下方的对称轴上,当S△ABC=S△ADC时,求点D的坐标.21.在坐标系中,已知抛物线y=x2﹣2x+n﹣1与y轴交于点A,其对称轴与x轴交于点B.(1)当△OAB是等腰直角三角形时,求n的值;(2)点C的坐标为(3,0),若该抛物线与线段OC有且只有一个公共点,结合函数的图象求n的取值范围.22.某商店经销一种学生用双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(个)与销售单价x(元)有如下关系:y=﹣x+60(30≤x≤60).设这种双肩包每天的销售利润为w元.(1)求w与x之间的函数关系式;(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?(3)如果物价部门规定这种双肩包的销售单价不高于42元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?23.某公司销售一种进价为20元/个的计算器,其销售量y(万个)与销售价格x(元/个)的变化如下表:同时,销售过程中的其他开支(不含进价)总计40万元.(1)观察并分析表中的y与x之间的对应关系,用所学过的一次函数,反比例函数或二次函数的有关知识写出y(万个)与x(元/个)的函数解析式.(2)求出该公司销售这种计算器的净得利润z(万元)与销售价格x(元/个)的函数解析式,销售价格定为多少元时净得利润最大,最大值是多少?(3)该公司要求净得利润不能低于40万元,请写出销售价格x(元/个)的取值范围,若还需考虑销售量尽可能大,销售价格应定为多少元?24.如图,在平面直角坐标系中,圆D与y轴相切于点C(0,4),与x轴相交于A、B两点,且AB=6.(1)则D点的坐标是(,),圆的半径为;(2)sin∠ACB= ;经过C、A、B三点的抛物线的解析式;(3)设抛物线的顶点为F,证明直线FA与圆D相切;(4)在x轴下方的抛物线上,是否存在一点N,使△CBN面积最大,最大值是多少,并求出N点坐标.25.如图,已知抛物线y=ax2﹣5ax+2(a≠0)与y轴交于点C,与x轴交于点A(1,0)和点B.(1)求抛物线的解析式;(2)求直线BC的解析式;(3)若点N是抛物线上的动点,过点N作NH⊥x轴,垂足为H,以B,N,H为顶点的三角形是否能够与△OBC相似?若能,请求出所有符合条件的点N的坐标;若不能,请说明理由.答案1.D2.C3.D.4.D5.A.6.C7.A8.A9.A10.B11.C12.B13.答案为24.14.答案为:①②④⑤;15.答案为①②③⑤16.答案为:①③④;17.答案为:4.5.18.答案为:-3≤m≤7.19.20.21.解:(1)二次函数的对称轴是x=﹣1,则B的坐标是(1,0),当△OAB是等腰直角三角形时,OA=OB=1,则A的坐标是(0,1)或(0,﹣1).抛物线y=x2﹣2x+n﹣1与y轴交于点A的坐标是(0,n﹣1).则n﹣1=1或n﹣1=﹣1,解得n=2或n=0;(2)①当抛物线的顶点在x轴上时,△=(﹣2)2﹣4(n﹣1)=0,解得:n=2;②当抛物线的顶点在x轴下方时,如图,由图可知当x=0时,y<0;当x=3时,y≥0,即,解得:﹣2≤n<1,综上,﹣2≤n<1或n=2.22.23.解:(1)根据表格中数据可得出:y与x是一次函数关系,设解析式为:y=ax+b,则,解得:,故函数解析式为:y=﹣0.1x+8;(2)根据题意得出:z=(x﹣20)y﹣40=(x﹣20)(﹣0.1x+8)﹣40=﹣0.1x2+10x﹣200,=﹣0.1(x2﹣100x)﹣200=﹣0.1 [(x﹣50)2﹣2500]﹣200=﹣0.1(x﹣50)2+50,故销售价格定为50元/个时净得利润最大,最大值是50万元.(3)当公司要求净得利润为40万元时,即﹣0.1(x﹣50)2+50=40,解得:x1=40,x2=60.如上图,通过观察函数y=﹣0.1(x﹣50)2+50的图象,可知按照公司要求使净得利润不低于40万元,则销售价格的取值范围为:40≤x≤60.而y与x的函数关系式为:y=﹣0.1x+8,y随x的增大而减少,因此,若还需考虑销售量尽可能大,销售价格应定为40元/个.24.25.解:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一对一教学过程一、选择题:1、若方程()2519x -=的两根为a 和b ,且a b >,则下列结论中正确的是( ) A .a 是19的算术平方根 B .b 是19的平方根 C.5a -是19的算术平方根 D .5b +是19的平方根 2、过三点A (2,2),B (6,2),C (4,5)的圆的圆心坐标为( ) A .(4,176) B .(4,3) C.(5,176) D .(5,3) 3、如图,⊙O 是ABC ∆的外接圆,2=BC ,030=∠BAC ,则劣弧BC 的长等于( )A 、32π B .3πC. 332π D .33π4、如图,一艘海轮位于灯塔P 的南偏东045方向,距离灯塔nmile 60的A 处,它沿正北方向航行一段时间后, 到达位于灯塔P 的北偏东030方向上的B 处,这时,B 处与灯塔P 的距离为( ) A .nmile 360 B .nmile 260 C. nmile 330 D .nmile 2305、一艘轮船在静水中的最大航速为h km /35,它以最大航速沿江顺流航行120km 所用时间,与以做大航速逆流 航行90km 所用时间相等,设江水的流速为h vkm /,则可列方程为( )A .359035120-=+v vB .v v +=-359035120C. 359035120+=-v v D .v v -=+359035120 6、若321x x -=-( )11x +-,则( )中的数是( )A .1-B .2-C .3-D .任意实数7、如图,垂直于x 轴的直线AB 分别与抛物线1C :2x y =(0≥x )和抛物线2C :42x y =(0≥x )交于B A ,两点,过点A 作x CD //轴分别与y 轴和抛物线1C 交于点F E ,,则EADOFES S ∆∆的值为( ) A .62 B .42 C. 41 D .618、已知正方形MNOK 和正六边形ABCDEF 边长均为1,把正方形放在正六边形中,使OK 边与AB 边重合, 如图所示.按下列步骤操作:将正方形在正六边形中绕点B 顺时针旋转,使KM 边与BC 边重合,完成第 一次旋转;再绕点C 顺时针旋转,使MN 边与CD 边重合,完成第二次旋转;……在这样连续6次旋转的过程中,点B ,M 间的距离可能是( ) A .1.4B .1.1C .0.8D .0.59、如图是边长为10cm 的正方形铁片,过两个顶点剪掉一个三角形,以下四种剪法中,裁剪线长度所标的数据 (单位:cm )不正确的( )10、下列命题是假命题的是( )A .不在同一直线上的三点确定一个圆B .角平分线上的点到角两边的距离相等 C.正六边形的内角和是720 D .角的边越长,角就越大 11、菱形的两条对角线分别是12和16,则此菱形的边长是( ) A .10 B .8 C.6 D .512、如图是国际数学日当天淇淇和嘉嘉的微信对话,根据对话内容,下列选项错误的是( )A 、4446+-=B .004446++=C .34446++=D .14446-÷+=13、如图,已知圆柱的底面直径6BC π=,高3AB =,小虫在圆柱表面爬行,从C 点爬到A 点,然后再沿另一面爬回C 点,则小虫爬行的最短路程为( ) A .32B .35C .65D .6214、如图,10个不同的正偶数按下图排列,箭头上方的每个数都等于其下方两数的和,如123a a a ,表示123a a a =+,则1a 的最小值为( ) A .32B .36C .38D .4015、甲、乙两组各有12名学生,组长绘制了本组5月份家庭用水量的统计图表,如图,比较5月份两组家庭用 水量的中位数,下列说法正确的是( )A 、甲组比乙组大B .甲、乙两组相同C .乙组比甲组大D .无法判断16、如图,若抛物线23y x =-+与x 轴围成封闭区域(边界除外)内整点(点的横、纵坐标都是整数)的个数 为k ,则反比例函数ky x=(0x >)的图象是( )17、如图,直线36y x =-分别交x 轴,y 轴于A ,B ,M 是反比例函数ky x=(0x >)的图象上位于直 线上方的一点,//MC x 轴交AB 于C ,MD MC ⊥交AB 于D ,43AC BD ⋅=,则k 的值为( ) A .3-B .4-C .5-D .6-18、如图,已知点A 、B 分别在反比例函数1y x =(0x >),4y x=-(0x >)的图像上,且OA ⊥OB , 则OBOA的值为( ) A 2.23.4 19、二次函数y=x 2+bx+c ,若b+c=0,则它的图象一定过点( )20、如题9图,四边形ABCD 内接于⊙O ,DA=DC ,∠CBE=50°,则∠DAC 的大小为( )A.130°B.100°C.65°D.50°A . (﹣1,﹣1)B . (1,﹣1)C . (﹣1,1)D . (1,1)21、如题10图,已知正方形ABCD ,点E 是BC 边的中点,DE 与AC 相交于点F ,连接BF ,下列结论:①ABF ADF S S =△△; ②4CDF CBF S S =△△;③2ADF CEF S S =△△;④2ADF CDF S S =△△,其中正确的是( ) A.①③ B.②③ C.①④ D.②④22、如图,边长为1的正方形ABCD 中,点E 在CB 延长线上,连接ED 交AB 于点F ,AF=x (0.2≤x ≤0.8),EC=y . 则在下面函数图象中,大致能反映y 与x 之闻函数关系的是( )二、填空题:1、已知函数()21y x =--图像上两点()12,y A ,()2,a y B ,其中2a >,则1y 与2y 的大小关系是1y2y(填“<”、“>”或“=”).2、正方形111C A B O ,2221C C A B ,3332C C A B ,⋅⋅⋅按如图的方式放置,点1A ,2A ,3A ,⋅⋅⋅和点1C ,2C , 3C ,⋅⋅⋅分别在直线1y x =+和x 轴上,则点2018B 的纵坐标是 .A .B .C .D .3、如图,四边形ABCD 是菱形,⊙O 经过点,,A C D ,与BC 相交于点E ,连接,AC AE ,若78D ∠=︒,则 EAC ∠= .4、已知431a b ÷=,则整式863a b ÷-的值为 .5、如题16图(1),矩形纸片ABCD 中,AB=5,BC=3,先按题16图(2)操作,将矩形纸片ABCD 沿过点A 的直线 折叠,使点D 落在边AB 上的点E 处,折痕为AF ;再按题16图(3)操作:沿过点F 的直线折叠,使点C 落 在EF 上的点H 处,折痕为FG,则A 、H 两点间的距离为 .6、函数1y x =与24y x=的图像如图所示,下列关于函数12y y y =+的结论:①函数的图像关于原点中心对称; ②当2x <时,随的增大而减小;③当0x >时,函数的图像最低点的坐标是(2,4),其中所有正确结论的 序号是 .7、如图,菱形ABCD 的对角线相交于点O ,2=AC ,32=BD ,将菱形按如图方式折叠,使点B 与点O 重 合,折痕为EF ,则五边形AEFCD 的周长为 .8、如图,把正方形铁片OABC 置于平面直角坐标系中,顶点A 的坐标为)0,3(,点)2,1(P 在正方形铁片上,将 正方形铁片绕其右下角的顶点按顺时针方向依次旋转90,第一次旋转至图①位置,第二次旋转至图②位 置……,则正方形铁片连续旋转2017次后,点P 的坐标为 . 9、对于函数xy 2=,当函数值1-<y 时,自变量x 的取值范围是 .10、如图,四边形ABCD 是菱形,O 是两条对角线的交点,过O 点的三条直线将菱形分成阴影和空白部分.当菱形的两条对角线的长分别为6和8时,则阴影部分的面积为 .11、观察下列各式:13=12 13+23=32 13+23+33=62 13+23+33+43=102…猜想13+23+33+…+103= . 12、如图,ABC ∆内接于O ,90ACB ∠=︒,ACB ∠的角平分线交O 于D ,若6AC =,52BD =,则BC 的长为 .13、如图,直线y kx =和4y ax =+交于(1,)A k ,则不等式64kx ax kx -<+<的解集为 . 14、如图,正方形ABCD 中,BE EF FC ==,2CG GD =,BG 分别交AE ,AF 于M ,N .下列结论: ①AF BG ⊥;②43BN NF =;③38BM MG =;④12CGNF ANGD S S =.其中正确的结论的序号是 . 三、解答题:1、张老师计划到超市购买甲种文具100个,他到超市后发现还有乙种文具可供选择.如果调整文具的购买品种, 每减少购买1个甲种文具,需增加购买2个乙种文具.设购买x 个甲种文具时,需购买y 个乙种文具. (1)①当减少购买一个甲种文具时,x = ,y = ; ②求y 与x 之间的函数表达式.(2)已知甲种文具每个5元,乙种文具每个3元,张老师购买这两种文具共用去540元.甲,乙两种文具各 购买了多少个?2、如图,,PA PB 是⊙O 的切线,,A B 为切点.连接AO 并延长,交PB 的延长线于点C ,连接PO ,交⊙O 于 点D .(1)求证:PO 平分APC ∠.(2)连结DB ,若30C ∠=︒,求证//DB AC .3、如图,港口B 位于港口A 的南偏东37︒方向,灯塔C 恰好在AB 的中点处,一艘海轮位于港口A 的正南方 向,港口B 的正西方向的D 处,它沿正北方向航行5km ,到达E 处,测得灯塔C 在北偏东45︒方向上.这 时,E 处距离港口A 有多远?(参考数据:sin370.60,cos370.80,tan370.75︒≈︒≈︒≈)4、已知函数()21y x m x m =-+-+(m 为常数) (1)该函数的图像与x 轴公共点的个数是( )A.0B.1C.2D.1或2(2)求证:不论m 为何值,该函数的图像的顶点都在函数()21y x =+的图像上. (3)当23m -≤≤时,求该函数的图像的顶点纵坐标的取值范围.5、如图,AB 是⊙O 的直径,弦AB CD ⊥,垂足为H ,连结AC ,过弧BD 上一点E 作AC EG //交CD 的 延长线于点G ,连结AE 交CD 于点F ,且FG EG =,连结CE . (1)求证:ECF ∆∽GCE ∆; (2)求证:EG 是⊙O 的切线;(3)延长AB 交GE 的延长线于点M ,若43tan =G ,33=AH ,求EM 的值.6、如图,已知抛物线a ax ax y 9322--=与坐标轴交于C B A ,,三点,其中)3,0(C ,BAC ∠的平分线AE 交y 轴于点D ,交BC 于点E ,过点D 的直线l 与射线AB AC ,分别交于点N M ,. (1)直接写出a 的值、点A 的坐标及抛物线的对称轴;(2)点P 为抛物线的对称轴上一动点,若PAD ∆为等腰三角形,求出点P 的坐标; (3)证明:当直线l 绕点D 转动时,ANAM 11+均为定值,并求出该定值.7、如图,16AB =,O 为AB 中点,点C 在线段OB 上(不与点O ,B 重合),将OC 绕点O 逆时针旋转270︒ 后得到扇形COD ,AP ,BQ 分别切优弧CD 于点P ,Q ,且点P ,Q 在AB 异侧,连接OP . (1)求证:AP BQ =;(2)当43BQ =时,求QD 的长(结果保留π);(3)若APO ∆的外心在扇形COD 的内部,求OC 的取值范围.。
