算法基本语句知识点及典型例题
常用算法举例

常用算法举例一、求面积、体积、方程的根,将公式的表达式用变量或常量表示出来,输出即可;二、累加、累乘(包括偶数和奇数的变换运算)三、典型算法举例:1、求两个数或三个数或多个数的最大值、最小值思路:用表判断的if语句就可完成,也可使用函数的调用;若是多个数,则采取从键盘上输入第一个数,并假定它是最大值存放在变量max中,以后每输入一个数便与max比较,若输入的数较大,则最大值是新的数值,存放到max中,数据输入完,最大值也就确定了。
main( ){int a,b,c,d;scanf(“%d,%d,%d”.&a,&b,&c);d=max(a,b,c);printf(“max=%d”,d);}int max(x,y,z)int x,y,z;{int p;p=x;if (p<y) p=y;if (p<z) p=z;return(p);}求10个数的最大值main( ){int I,k,max;scanf(“%d”,&max);for (I=2;I<11;I++){scanf(“%d”,&k);if (max<k) mzk=k;}printf(“max=%d\n”,max);}2、判断是否为闰年思路:闰年应满足条件之一:(a)能被4整除,但不能被100整除;(b)能被4整除又能被400整除main( ){int year,leap;scanf("%d",&year);if (year%4==0 ){ if (year%100==0){if (year%400==0)leap=1;else leap=0;}elseleap=1;}elseleap=0;if (leap)printf(“%d is “,year);elseprintf(“%d is not”,year);printf(“a leap year/n”);}此程序还可以简化用 (year%4==0 &&year%100!=0 || year%400==0)直接进行判断也可;此题还可求某范围内的闰年。
算法基本语句知识点及典型例题

基本算法语句一、输入、输出语句和赋值语句 (1)输入语句 ①输入语句的一般格式②输入语句的作用是实现算法的输入信息功能;③“提示内容”提示用户输入什么样的信息,变量是指程序在运行时其值是可以变化的量;④输入语句要求输入的值只能是具体的常数,不能是函数、变量或表达式; ⑤提示内容与变量之间用分号“;”隔开,若输入多个变量,变量与变量之间用逗号“,”隔开。
(2)输出语句 ①输出语句的一般格式②输出语句的作用是实现算法的输出结果功能;③ “提示内容”提示用户输入什么样的信息,表达式是指程序要输出的数据;④输出语句可以输出常量、变量或表达式的值以及字符。
(3)赋值语句 ①赋值语句的一般格式②赋值语句的作用是将表达式所代表的值赋给变量;③赋值语句中的“=”称作赋值号,与数学中的等号的意义是不同的。
赋值号的左右两边不能对换,它将赋值号右边的表达式的值赋给赋值号左边的变量; ④赋值语句左边只能是变量名字,而不是表达式,右边表达式可以是一个数据、常量或算式;⑤对于一个变量可以多次赋值。
注意:①赋值号左边只能是变量名字,而不能是表达式。
如:2=X 是错误的。
②赋值号左右不能对换。
如“A=B ”“B=A ”的含义运行结果是不同的。
③不能利用赋值语句进行代数式的演算。
(如化简、因式分解、解方程等) ④赋值号“=”与数学中的等号意义不同。
5:条件语句(1)条件语句的一般格式有两种:①IF—THEN—ELSE语句;②IF—THEN语句。
①IF—THEN—ELSE语句IF—THEN—ELSE语句的一般格式为图1,对应的程序框图为图2。
图1②IF—THEN语句IF—THEN语句的一般格式为图36:循环语句循环结构是由循环语句来实现的。
对应于程序框图中的两种循环结构,一般程序设计语言中也有当型(WHILE型)和直到型(UNTIL型)两种语句结构。
即WHILE语句和UNTIL语句。
(1)WHILE语句①WHILE语句的一般格式是②当计算机遇到WHILE语句时,先判断条件的真假,如果条件符合,就执行WHILE与WEND之间的循环体;然后再检查上述条件,如果条件仍符合,再次执行循环体,这个过程反复进行,直到某一次条件不符合为止。
专题50:算法初步知识点及典型例题(原卷版)

专题50:算法初步知识点及典型例题(原卷版)【知识梳理】知识点一、算法1.算法的概念(1)古代定义:指的是用阿拉伯数字进行算术运算的过程。
(2)现代定义:算法通常是指按照一定规则解决某一类问题的明确和有限的步骤。
(3)应用:算法通常可以编成计算机程序,让计算机执行并解决问题。
2.算法的特征:①指向性:能解决某一个或某一类问题;②精确性:每一步操作的内容和顺序必须是明确的;算法的每一步都应当做到准确无误,从开始的“第一步”直到“最后一步”之间做到环环相扣,分工明确.“前一步”是“后一步”的前提,“后一步”是“前一步”的继续.③有限性:必须在有限步内结束并返回一个结果;算法要有明确的开始和结束,当到达终止步骤时所要解决的问题必须有明确的结果,也就是说必须在有限步内完成任务,不能无限制的持续进行.④构造性:一个问题可以构造多个算法,算法有优劣之分。
3.算法的表示方法:(1) 用自然语言表示算法: 优点是使用日常用语, 通俗易懂;缺点是文字冗长, 容易出现歧义;(2) 用程序框图表示算法:用图框表示各种操作,优点是直观形象, 易于理解。
注:泛泛地谈算法是没有意义的,算法一定以问题为载体。
例1.下面给出一个问题的算法:S1输入x;S2若x≤2,则执行S3;否则,执行S4;S3输出-2x-1;S4输出x2-6x+3.问题:(1)这个算法解决的是什么问题?(2)当输入的x值为多大时,输出的数值最小?知识点二:流程图1. 流程图的概念:流程图,是由一些图框和流程线组成的,其中图框表示各种操作的类型,图框中的文字和符合表示操作的内容,流程线表示操作的先后次序。
2.流程图常用符号:图形符号名称含义开始/结束框用于表示算法的开始与结束输入/输出框用于表示数据的输入或结果的输出处理框描述基本的操作功能,如“赋值”操作、数学运算等判断框判断某一条件是否成立,成立时在出口处标明“是”或“Y”;不成立时标明“否”或“N”流程线表示流程的路径和方向连接点用于连接另一页或另一部分的框图注释框框中内容是对某部分流程图做的解释说明3.画流程图的规则:(1)使用标准的框图的符号;(2)框图一般按从上到下、从左到右的方向画;(3)除判断框图外,大多数框图符号只有一个进入点和一个退出点。
基本算法语句与算法案例教案练习含答案

基本算法语句与算法案例教案练习含答案第一章:算法概述1.1 算法的定义与特性定义:算法是解决问题的一系列清晰、有序的步骤。
特性:可行性、确定性、有穷性、足够性。
1.2 算法的表示方法伪代码:使用简化的语言描述算法。
流程图:使用图形符号表示算法步骤。
第二章:基本算法语句2.1 输入输出语句输入:从用户或文件获取数据。
输出:向用户或文件输出数据。
2.2 赋值语句赋值:将一个值或表达式赋给变量。
2.3 条件语句如果:根据条件执行相应的操作。
否则:当条件不满足时执行的操作。
2.4 循环语句循环:重复执行一段代码直到条件不满足。
第三章:算法案例3.1 冒泡排序算法目的:对一组数据进行从小到大的排序。
步骤:比较相邻元素,交换不符合顺序的元素。
3.2 查找算法线性查找:从数组的一端开始,逐个比较元素。
二分查找:在有序数组中,通过比较中间元素确定位置。
3.3 插入排序算法目的:对一组数据进行从小到大的排序。
步骤:将未排序的元素插入到已排序的序列中。
第四章:算法分析4.1 时间复杂度分析定义:算法执行时间与输入规模的关系。
常见时间复杂度:O(1)、O(n)、O(n^2)、O(log n)。
4.2 空间复杂度分析定义:算法执行过程中所需内存与输入规模的关系。
常见空间复杂度:O(1)、O(n)。
第五章:算法设计与优化5.1 贪心算法特点:局部最优解构成全局最优解。
应用:最小树、最短路径等。
5.2 分治算法特点:将问题分解为子问题,递归解决。
应用:归并排序、快速傅里叶变换等。
5.3 动态规划算法特点:利用多阶段决策过程的最优解。
应用:背包问题、最长公共子序列等。
第六章:递归算法6.1 递归的基本概念定义:一个函数直接或间接地调用自身。
特点:自顶向下、分而治之。
6.2 递归算法的实现直接递归:函数直接调用自身。
间接递归:函数通过其他函数间接调用自身。
6.3 递归算法的应用计算阶乘、斐波那契数列等。
第七章:图算法7.1 图的基本概念顶点、边、无向图、有向图、权重等。
算法、程序框图与基本语句知识点及联系—精品文档
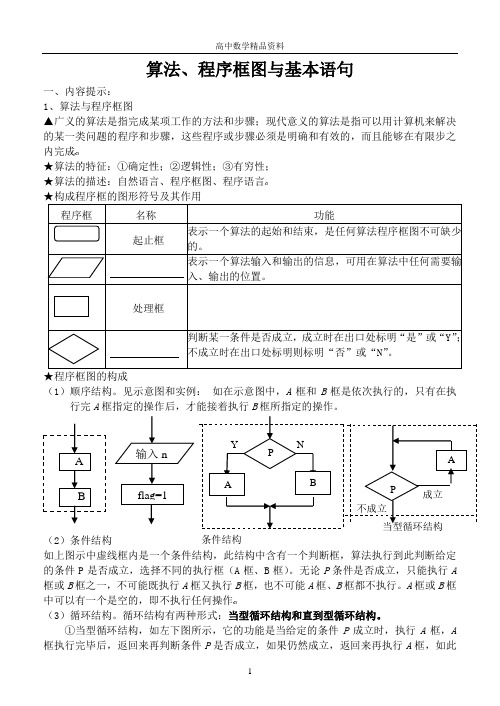
算法、程序框图与基本语句一、内容提示: 1、算法与程序框图▲广义的算法是指完成某项工作的方法和步骤;现代意义的算法是指可以用计算机来解决的某一类问题的程序和步骤,这些程序或步骤必须是明确和有效的,而且能够在有限步之内完成★算法的特征:①确定性;②逻辑性;③有穷性; ★算法的描述:自然语言、程序框图、程序语言 ★构成程序框的图形符号及其作用程序框名称功能起止框表示一个算法的起始和结束,是任何算法程序框图不可缺少的。
表示一个算法输入和输出的信息,可用在算法中任何需要输入、输出的位置。
处理框判断某一条件是否成立,成立时在出口处标明“是”或“Y ”;不成立时在出口处标明则标明“否”或“N ”。
★程序框图的构成(1)顺序结构。
见示意图和实例: 如在示意图中,A 框和B 框是依次执行的,只有在执行完A 框指定的操作后,才能接着执行B 框所指定的操作。
(2)条件结构如上图示中虚线框内是一个条件结构,此结构中含有一个判断框,算法执行到此判断给定的条件P 是否成立,选择不同的执行框(A 框、B 框)。
无论P 条件是否成立,只能执行A 框或B 框之一,不可能既执行A 框又执行B 框,也不可能A 框、B 框都不执行。
A 框或B 框中可以有一个是空的,即不执行任何操作(3)循环结构。
循环结构有两种形式:当型循环结构和直到型循环结构。
①当型循环结构,如左下图所示,它的功能是当给定的条件P 成立时,执行A 框,A 框执行完毕后,返回来再判断条件P 是否成立,如果仍然成立,返回来再执行A 框,如此A B输入n flag=1 P A B YN A 成立 不成立 P 当型循环结构条件结构反复执行A 框,直到某一次返回来判断条件P 不成立时为止,此时不再执行A 框,离开循环结构。
继续执行下面的框图。
②直到型循环结构,如右下图所示,它的功能是先执行重复执行的A 框,然后判断给定的条件P 是否成立,如果P 仍然不成立,则返回来继续执行A 框,再判断条件P 是否成立。
基本算法语句(上课用)

【变式练习】
下列给出的赋值语句正确的是 ④ . ①3=B ②x+y=0 ③A=B=-2 ④T=T﹡T 【解析】根据赋值语句的格式可知,赋值号左侧为单 个变量,右侧为表达式(赋值语句有运算功能),故填 ④. 答案:④
1.了解算法的程序设计语言与算法的自然语言、程序框 图的差异. 2.正确理解输入语句、输出语句、赋值语句的结构. (重点) 3.能够准确应用输入、输出语句和赋值语句将程序框图 转化为算法语句.(难点)
微课1 例1.用描点法作函数y=x3+3x2-24x+30的图象时,需要 求出自变量和函数的一组对应值.编写程序,分别计算 当x= -5,-4,-3,-2,-1,0,1,2,3,4,5时的函数值.
INPUT “a,b,c=”;a,b,c
转化
在这个程序中,第3行中的PRINT语句称为输出 语句,其一般格式是:
PRINT “提示内容”;表达式
其中,“提示内容”一般是提示用户输出什么 样的信息,它通常是常量或变量的值;表达式一 般是表示输出信息所对应的字母或代数式.PRINT 语句可以在计算机的屏幕上输出运算结果和系统 信息.
多个变量,中间用 表达式之间用“,”隔 2.一个语句只能有
“,”隔开.
开.
一个“=”,并且
明
3.无计算功能,不能 输入表达式.
3.表达式可以是变量, 也可以是计算公式.
只能给一个变量赋 值.
4.输入多个数据时用 4.有计算功能,能直
“,”分隔
接输出计算公式的值
3.有计算功能,可 以把表达式的值赋 给一个变量
算法分析: 根据题意,对于每一个输入的自变量的值,都要
例谈基本算法语句
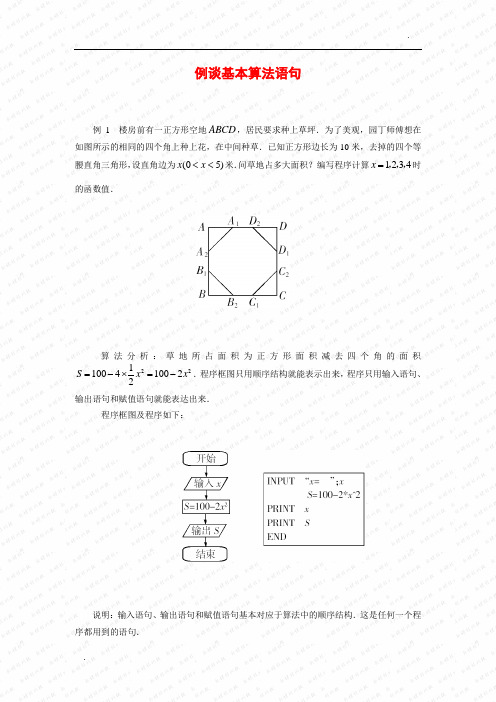
例谈基本算法语句例1楼房前有一正方形空地ABCD,居民要求种上草坪.为了美观,园丁师傅想在如图所示的相同的四个角上种上花,在中间种草.已知正方形边长为10米,去掉的四个等腰直角三角形,设直角边为(05)x x<<米.问草地占多大面积?编写程序计算1234x=,,,时的函数值.算法分析:草地所占面积为正方形面积减去四个角的面积221100410022S x x=-⨯=-.程序框图只用顺序结构就能表示出来,程序只用输入语句、输出语句和赋值语句就能表达出来.程序框图及程序如下:说明:输入语句、输出语句和赋值语句基本对应于算法中的顺序结构.这是任何一个程序都用到的语句.例2 邮局寄信不超过20克付邮资80分,超过20克不超过40克付邮资90分,超过40克不超过60克付邮资100分,现有一封信重x 克(060x <≤),问应付邮资多少分?算法分析:这是一个分段函数,80(020)()90(2040)100(4060)x f x x x ⎧<⎪=<⎨⎪<⎩≤ ≤ ≤,根据条件不同,结果不同,程序结构中需要用到条件结构,程序中用到条件语句.程序框图:说明:条件语句是表达算法中的条件结构,因为算法的流程根据条件是否成立有不同的流向,就需要对条件作出判断,所以程序中用到条件语句.例3 设计求2+4+6+…+2n 的值的算法,画出程序框图,编写程序.算法分析:只需一个累加变量和一个计数变量,将累加变量初始值设为0,计数变量是2~2n 之间的偶数.程序框图【当型(WHILE 型)】及程序如下:程序框图【直到型(UNTIL型)】及程序如下:说明:循环语句是用来实现循环结构的,对应程序框图中的两种循环结构,程序设计语言中也有当型和直到型两种语句,对于同一个题目可以分别用这两种语句表达.WHILE语句,先判断条件真假,如果条件符合就执行WHILE与WEND之间的循环体;然后检查上述条件反复进行,直到某一次条件不符合为止.因此,当型循环也称为“前测试型”循环,而直到型循环称为“后测试型”循环.。
基本算法语句与算法案例教案练习(含答案)

基本算法语句与算法案例教案练习(含答案)第一章:算法概述1.1 算法的定义介绍算法的概念和特点强调算法在解决问题中的重要性1.2 算法的特性讨论算法的输入、输出、有穷性和确定性举例说明算法的基本特性1.3 算法描述介绍算法描述的方法,如伪代码和流程图练习编写简单的算法描述第二章:基本算法语句2.1 输入输出语句学习输入输出语句的语法和使用方法练习编写输入输出语句2.2 赋值语句了解赋值语句的作用和格式练习使用赋值语句进行变量赋值2.3 条件语句掌握条件语句的语法和执行过程练习编写条件语句解决问题2.4 循环语句学习循环语句的种类和特点练习使用循环语句编写算法第三章:算法案例分析3.1 排序算法学习冒泡排序和选择排序的基本思想编写冒泡排序和选择排序的算法实现3.2 搜索算法了解二分查找和深度优先搜索的基本原理编写二分查找和深度优先搜索的算法实现3.3 递归算法理解递归算法的概念和应用编写递归算法的实例,如计算阶乘和Fibonacci 数列3.4 图算法学习图的基本概念和算法,如DFS 和BFS编写图算法的实例,如拓扑排序和最短路径第四章:算法设计与分析4.1 算法设计策略学习贪心算法、动态规划和分治算法的设计思想练习使用不同的算法设计策略解决问题4.2 算法分析方法了解时间复杂度和空间复杂度的概念分析常见算法的复杂度,并比较其优劣4.3 算法优化技巧学习常用的算法优化技巧,如缓存、预处理和分治练习使用算法优化技巧提高算法效率第五章:算法实践与测试5.1 算法编程基础学习编程语言的基本语法和数据结构练习使用编程语言实现算法5.2 算法测试与调试学习测试算法的方法和技巧练习使用调试工具和技巧解决算法问题5.3 算法竞赛与挑战了解算法竞赛和在线编程挑战的平台和规则参与算法竞赛和挑战,提高算法能力第六章:算法与数据结构6.1 数据结构基础介绍数据结构的概念和重要性学习线性表、栈、队列、链表等基本数据结构6.2 算法与数据结构的关联讨论算法和数据结构之间的关系学习如何选择合适的数据结构来优化算法6.3 常见数据结构算法掌握数组、链表、树、图等数据结构的操作算法练习使用不同数据结构解决实际问题第七章:算法伦理与算法文化7.1 算法伦理探讨算法伦理的重要性学习算法公平性、透明性和可解释性的概念7.2 算法在现实世界中的应用分析算法在各个领域中的应用和影响讨论算法如何影响社会和个人7.3 算法文化与历史了解算法的发展历程学习著名算法家和他们的贡献第八章:算法高级主题8.1 并行算法介绍并行算法的基本概念和原理学习并行算法的设计和分析方法8.2 分布式算法探讨分布式系统中的算法设计学习分布式算法的一致性和容错性8.3 量子算法简介量子计算和量子算法的基本原理了解量子算法与经典算法的关系和差异第九章:算法面试与职业发展9.1 算法面试准备学习算法面试的常见题型和准备策略练习解决算法面试中的典型问题9.2 算法面试技巧掌握算法面试的沟通和表达技巧学习如何在面试中展示自己的算法能力9.3 算法工程师的职业发展探讨算法工程师的职业路径和发展前景学习如何提升自己的算法技能和职业竞争力第十章:算法案例集锦10.1 经典算法案例收集和分析经典算法案例学习这些案例背后的算法思想和技巧10.2 创新算法案例探索新兴领域的算法应用学习创新算法如何解决现实问题10.3 算法案例解析分析算法案例的优缺点和适用场景学习如何从案例中汲取经验,提高自己的算法能力重点和难点解析重点一:算法的定义和特性算法的定义是计算机科学中的核心概念,理解算法的特性对于掌握算法至关重要。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基本算法语句一、输入、输出语句和赋值语句 (1)输入语句 ①输入语句的一般格式②输入语句的作用是实现算法的输入信息功能;③“提示内容”提示用户输入什么样的信息,变量是指程序在运行时其值是可以变化的量;④输入语句要求输入的值只能是具体的常数,不能是函数、变量或表达式; ⑤提示内容与变量之间用分号“;”隔开,若输入多个变量,变量与变量之间用逗号“,”隔开。
(2)输出语句 ①输出语句的一般格式②输出语句的作用是实现算法的输出结果功能;③ “提示内容”提示用户输入什么样的信息,表达式是指程序要输出的数据;④输出语句可以输出常量、变量或表达式的值以及字符。
(3)赋值语句 ①赋值语句的一般格式②赋值语句的作用是将表达式所代表的值赋给变量;③赋值语句中的“=”称作赋值号,与数学中的等号的意义是不同的。
赋值号的左右两边不能对换,它将赋值号右边的表达式的值赋给赋值号左边的变量; ④赋值语句左边只能是变量名字,而不是表达式,右边表达式可以是一个数据、常量或算式;⑤对于一个变量可以多次赋值。
注意:①赋值号左边只能是变量名字,而不能是表达式。
如:2=X 是错误的。
②赋值号左右不能对换。
如“A=B ”“B=A ”的含义运行结果是不同的。
③不能利用赋值语句进行代数式的演算。
(如化简、因式分解、解方程等) ④赋值号“=”与数学中的等号意义不同。
5:条件语句(1)条件语句的一般格式有两种:①IF—THEN—ELSE语句;②IF—THEN语句。
①IF—THEN—ELSE语句IF—THEN—ELSE语句的一般格式为图1,对应的程序框图为图2。
图1②IF—THEN语句IF—THEN语句的一般格式为图36:循环语句循环结构是由循环语句来实现的。
对应于程序框图中的两种循环结构,一般程序设计语言中也有当型(WHILE型)和直到型(UNTIL型)两种语句结构。
即WHILE语句和UNTIL语句。
(1)WHILE语句①WHILE语句的一般格式是②当计算机遇到WHILE语句时,先判断条件的真假,如果条件符合,就执行WHILE与WEND之间的循环体;然后再检查上述条件,如果条件仍符合,再次执行循环体,这个过程反复进行,直到某一次条件不符合为止。
这时,计算机将不执行循环体,直接跳到WEND语句后,接着执行WEND之后的语句。
因此,当型循环有时也称为“前测试型”循环。
(2)UNTIL语句①UNTIL语句的一般格式是对应的程序框图是②直到型循环又称为“后测试型”循环,从UNTIL 型循环结构分析,计算机执行该语句时,先执行一次循环体,然后进行条件的判断,如果条件不满足,继续返回执行循环体,然后再进行条件的判断,这个过程反复进行,直到某一次条件满足时,不再执行循环体,跳到LOOP UNTIL 语句后执行其他语句,是先执行循环体后进行条件判断的循环语句。
分析:当型循环与直到型循环的区别:(1)当型循环先判断后执行,直到型循环先执行后判断; (2)在WHILE 语句中,是当条件满足时执行循环体,在UNTIL 语句中,是当条件不满足时执行循环. 7:辗转相除法与更相减损术(1)辗转相除法。
也叫欧几里德算法,用辗转相除法求最大公约数的步骤如下:①用较大的数m 除以较小的数n 得到一个商0S 和一个余数R ;②若R =0,则n 为m ,n 的最大公约数;若0R ≠0,则用除数n 除以余数R 得到一个商1S 和一个余数1R ;③若1R =0,则1R 为m ,n 的最大公约数;若1R ≠0,则用除数R 除以余数1R 得到一个商2S 和一个余数2R ;……依次计算直至n R =0,此时所得到的1n R 即为所求的最大公约数。
(2)更相减损术①任意给出两个正数;判断它们是否都是偶数。
若是,用2约简;若不是,执行第二步。
②以较大的数减去较小的数,接着把较小的数与所得的差比较,并以大数减小数。
继续这个操作,直到所得的数相等为止,则这个数(等数)就是所求的最大公约数。
(3)辗转相除法与更相减损术的区别:①都是求最大公约数的方法,计算上辗转相除法以除法为主,更相减损术以减法为主,计算次数上辗转相除法计算次数相对较少,特别当两个数字大小区别较大时计算次数的区别较明显。
②从结果体现形式来看,辗转相除法体现结果是以相除余数为0则得到,而更相减损术则以减数与差相等而得到8:秦九韶算法与排序(1)秦九韶算法概念:f(x)=a n x n+a n-1x n-1+….+a1x+a0求值问题f(x)=a n x n+a n-1x n-1+….+a1x+a0=(a n x n-1+a n-1x n-2+….+a1)x+a0=(( a n x n-2+a n-1x n-3+….+a2)x+a1)x+a0 =......=(...( a n x+a n-1)x+a n-2)x+...+a1)x+a0求多项式的值时,首先计算最内层括号内依次多项式的值,即v1=a n x+a n-1然后由内向外逐层计算一次多项式的值,即v2=v1x+a n-2 v3=v2x+a n-3 ...... v n=v n-1x+a0这样,把n次多项式的求值问题转化成求n个一次多项式的值的问题。
(2)两种排序方法:直接插入排序和冒泡排序①直接插入排序基本思想:插入排序的思想就是读一个,排一个。
将第1个数放入数组的第1个元素中,以后读入的数与已存入数组的数进行比较,确定它在从大到小的排列中应处的位置.将该位置以及以后的元素向后推移一个位置,将读入的新数填入空出的位置中.(由于算法简单,可以举例说明)②冒泡排序基本思想:依次比较相邻的两个数,把大的放前面,小的放后面.即首先比较第1个数和第2个数,大数放前,小数放后.然后比较第2个数和第3个数......直到比较最后两个数.第一趟结束,最小的一定沉到最后.重复上过程,仍从第1个数开始,到最后第2个数...... 由于在排序过程中总是大数往前,小数往后,相当气泡上升,所以叫冒泡排序.9:进位制(1)概念:进位制是一种记数方式,用有限的数字在不同的位置表示不同的数值。
可使用数字符号的个数称为基数,基数为n,即可称n进位制,简称n 进制。
现在最常用的是十进制,通常使用10个阿拉伯数字0-9进行记数。
对于任何一个数,我们可以用不同的进位制来表示。
比如:十进数57,可以用二进制表示为111001,也可以用八进制表示为71、用十六进制表示为39,它们所代表的数值都是一样的。
一般地,若k 是一个大于一的整数,那么以k 为基数的k 进制可以表示为:110()110...(0,0,...,,)n n k n n a a a a a k a a a k --<<≤<,而表示各种进位制数一般在数字右下脚加注来表示,如111001(2)表示二进制数,34(5)表 典型例题例1.判断下列给出的输入语句、输出语句和赋值语句是否正确?为什么?(1)输入语句 INPUT a ;b ;c (2)输出语句 A =4 (3)赋值语句 3=B(4)赋值语句 A =B =-2解析:(1)错,变量之间应用“,”号隔开; (2)错,PRINT 语句不能用赋值号“=”; (3)错,赋值语句中“=”号左右不能互换; (4)错,一个赋值语句只能给一个变量赋值。
例2.请写出下面运算输出的结果。
(1) dd PRINT c c d b a c b a ;""2/)(35=*=+=== (2)cb ac b a PRINT bc a b b a c b a ,,;",,"21===-+=+===(3)cb ac b a PRINT ac c b b a c b a ,,;",,"302010=========解析:(1)16;语句2/)(b a c +=是将a ,b 和的一半赋值给变量c ,语句c c d *=是将c 的平方赋值给d ,最后输出d 的值。
(2)1,2,3;语句b a c +=是将a ,b 的和赋值给c ,语句b c a b -+=是将b c a -+的值赋值给了b 。
(3)20,30,20;经过语句b a =后a ,b ,c 的值是20,20,30。
经过语句c b =后a ,b ,c 的值是20,30,30。
经过语句a c =后a ,b ,c 的值是20,30,20。
练习:1.已知变量a ,b 已被赋值,要交换a 、b 的值,采用的算法是( )A .a =b ,b =aB .a =c ,b =a ,c =bC .a =c ,b =a ,c =aD .c =a ,a =b ,b =c 2.下列给出的赋值语句中正确的是( )A 4M =B M M =-C 3B A ==D 0x y +=例3.写出求三个数a ,b ,c 的方差的程序。
解析:方差是在初中统计内容中学习过的知识,计算所有数的方差首先计算所有数的平均数x ,通过公式nx x x x x x s n 222212)(........)()(-++-+-=来计算。
算法步骤:第一步:计算平均数3cb a x ++=; 第二步:计算方差3)()()(2222a x a x a x s -+-+-=;第三步:得到的结果即为所求。
程序如下: INPUT a ,b ,c y=(a+b+c)/3S=((a -y)2+ (b -y)2+ (c -y)2)/3 PRINT S END例4.编写一个程序,要求输入的两个正数a 和b 的值,输出a b 和b a 的值。
程序1:INPUT “a,b :”;a ,b A=a^b B=b^aPRINT “a b =”;A ,“b a =”;B END例5.编写程序,输出两个不相等的实数a 、b 的最大值。
解:算法:第一步:输入a , b 的数值;第二步:判断a ,b 的大小关系,若a >b ,则输出a 的值,否则输出b 的值。
程序如下:(“IF—THEN —ELSE”语句) IN PUT“a ,b”;a ,b IF a >b THEN PRINT a ELSEPRINT b END IF END例6.高等数学中经常用到符号函数,符号函数的定义为⎪⎩⎪⎨⎧<-=>=0,10,00,1x x x y ,试编写程序输入x 的值,输出y程序一:(嵌套结构) 程序框图:(右图) 程序语言: INPUT x IF x >0 THEN y =1 ELSEIF x =0 THEN y =0 ELSE y =-1 END IF END IF PRINT y END例7.设计一个计算1×3×5×7×…×99的算法,编写算法程序。
解析: 算法如下: 第一步:s =1; 第二步:i =3; 第三步:s =s×i; 第四步:i =i +2;第五步:如果i≤99,那么转到第三步; 第六步:输出s ; 程序如下:(“WHILE 型”循环语句) s =1 i =3WHILE i <=99 s =s*i i =i +2 WENDPRINT s END例8. 求三个数72,120,168的最大公约数. 解法1:用辗转相除法先求120,168的最大公约数,因为168120148,12048224,48242=⨯+=⨯+=⨯ 所以120,168的最大公约数是24. 再求72,24的最大公约数,因为72243=⨯,所以72,24的最大公约数为24, 即72,120,168的最大公约数为24.解法2:用更相减损术先求120,168的最大公约数,168-120=48,120-48=72,72-48=24,48-24=24 所以120,168的最大公约数为24. 再求72,24的最大公约数, 72-24=48,48-24=2472,24的最大公约数为24,即72,120,168的最大公约数为24.例9.用秦九韶算法求多项式5432()23456f x x x x x x =+++++在2x =时的值. 分析:先改写多项式,再由内向外计算.5432:()23456((((2)3)4)5)6f x x x x x x x x x x x =+++++=+++++解010*********,243114265576120v v v x v v x v v x v v x v v x ==+==+==+==+==+= 本题也可简写为下式:12345622822521144112657120例10.完成下列进制的转化(3)(10)(10)__________(8)(1)10202____(2)101==解: 420(3)(10)(1)10202132323101=⨯+⨯+⨯=(2)用8反复去除101,直到商为0止,所得的余数(从末位读起)就是十进制数101的8进制表示8101812581401余数 所以(10)(8)101145=一、选择题1 当2=x 时,下面的程序输出的结果是 ( )A 3B 7C 15D 17 2下边程序运行后输出的结果为( )A 50B 5C 25D 0二、填空题15()51a j WHILE j a a j MOD j j WENDPRINT aEND ==<==+=+10411i s WHILE i s s x i i WEND PRINT I s U xE T N NP D==<==*+=+1.下面程序运行后输出的结果为_______________解析: 22,-222 三个数324,243,135的最大公约数是_________________解析:324243181,13581154,8154127,54272=⨯+=⨯+=⨯+=⨯.填27 三、解答题用秦九韶算法求多项式5432()34157678f x x x x x x =+-+++在2x =-时的值.543201021324354:()34157678((((34)15)76)7)83,421511769871898386f x x x x x x x x x x x v v v x v v x v v x v v x v v x =+-+++=+-+++==+=-=-=-=+==+=-=+=9.解520033,x y IF x THEN x y ELSE y y END IF PRINT x y y xEND==-<=-=+--。
