基于最大特征值估计的C3算法及应用
核主元分析在故障诊断中的研究与应用

核主元分析在故障诊断中的研究与应用摘要化工在工业生产中占有举足轻重的地位,它几乎涉及到人们生活的各个方面,近年来,随着科学技术,尤其是计算机技术的飞速发展,化工过程生产装置的规模越来越大,工艺越来越复杂,自动化水平越来越高,因此化工过程的安全性和可靠性就显得特别重要。
采用故障诊断技术来提高化工过程的安全性和可靠性是一种有效而重要的方法,因此对化工过程进行故障诊断研究具有极其重要的价值。
本文介绍了主元分析法和核主元分析法在故障诊断的研究应用,并在化工过程中进行了仿真应用研究,针对主元分析法(PCA)应用于复杂非线性的化工过程故障检测时存在性能差的问题。
我们提出利用核主元分析法(KPCA)来进行故障检测的思想,从而将输入空间中复杂的非线性问题转化为特征空间中的线性问题,在特征空间中采用T2和SPE 的贡献率检测出系统的故障。
TE过程的研究应用验证了算法的可行性,达到了预期的效果。
关键词:故障检测主元分析核主元分析TE过程Ikernel principal component analysis in failure diagnosis research andapplicationAbstractChemical industry plays a very important role in industrial production, it involves almost all aspects of people,s lives. In recent years, along with the development of scienee and technology, especially computer technology, production units of chemieal industry become bigger and bigger. Technological processes beeome more complex, automatic level becomes higher and higher. Therefore, the security and reliability of chemieal proeess is more important. There is are many methods to improve system’s, fault diagnosis technology is avery effeetive and important method to improve the security and reliability of chemical proeess. So research on fault diagnosis has vitally important value for chemical industry process.The thesis introduces the methods of principal component analysis and kernel principal component analysis are analyzed for fault diagnosis, and simulations are applied to Tennessee Eastman chemical proeess. For complex and nonlinear chemical industry processes, the performance of fault detection is very poor when principal component analysis (PCA) is used. Thus the concept of using kernel principal component analysis (KPCA) to conduct fault detection is proposed, which will make the complex nonlinear problem in input space convert into linear problem in feature space, according to calculate the contribution of each original variable for Hotelling T2 and SPE to research on fault detection. The application study of Tennessee Eastman chemical process proves the feasibility of the proposed methods, and achieves the expected results.Key Words:fault detection; principal component analysis; kernel principal component; Tennessee Eastman processII目录摘要 (I)Abstract (II)第一章绪论 (1)1.1课题背景 (1)1.2 故障诊断方法 (1)1.2.1 依赖于模型的故障诊断方法 (1)1.2.2 不依赖于模型的故障诊断方法 (2)1.3 仿真技术 (3)1.4 动态系统仿真工具Matlab/Simulink简介 (3)1.5 本论文主要研究工作 (3)第二章基于特征样本核主元分析的过程故障检测方法 (4)2.1 主元分析方法介绍 (4)2.2 应用PCA的前提条件 (4)2.3 PCA基本原理及PCA算法 (4)2.4 主元分析故障检测的基本方法 (5)2.5 核主元分析研究背景 (6)2.6 核主元分析 (6)2.6.1 核主元算法 (6)2.6.2 特征样本提取 (8)2.7 核主元在线故障监测方法 (9)2.7.1 基于T2和SPE的在线故障检测方法 (9)2.7.2 核主元的故障监测步骤 (10)2.8 主元分析法和核主元分析法的比较 (11)第三章TE过程描述 (13)3.1 TE模型实验系统的概述 (13)3.2 数据的生成 (15)3.3 TE仿真模型 (15)第四章仿真过程的建立与结果 (18)4.1 数据来源 (18)4.2 故障检测分析 (19)III第五章总结 (27)参考文献 (28)致谢 (30)附录 (I)IV南京工业大学本科毕业设计(论文)第一章绪论1.1课题背景目前,故障诊断技术已成为一个十分活跃的研究领域。
利用相干属性剖面特征进行层位解释

利用相干属性剖面特征进行层位解释李雪峰;阎建国;赵州;姚爽【摘要】利用相干属性的平面特征进行断层识别及沉积特征识别,已得到了较为广泛的应用,而相干属性的剖面特征却常常受到忽略.我们的研究表明,除平面特征外,相干属性的剖面特征往往能提供关于地质构造和沉积特征的更加精细的信息,特别是可以直接利用相干属性剖面进行层位追踪解释.而且在利用相干属性剖面特征进行层位解释时,具有层位追踪准确,分辨率高等优点.这里提出利用相干体属性的剖面特征进行层位追踪解释的方法,并通过对比利用振幅剖面特征进行层位解释的方法步骤,探讨总结了利用相干剖面进行层位追踪解释的优缺点,以及利用相干属性剖面进行层位追踪解释的方法步骤和工作流程,为层位的追踪解释提供了另一种可选择的方法,这种方法在实际应用中也取得了良好的效果.【期刊名称】《物探化探计算技术》【年(卷),期】2011(033)002【总页数】6页(P134-139)【关键词】相干属性剖面;振幅剖面;层位追踪解释【作者】李雪峰;阎建国;赵州;姚爽【作者单位】成都理工大学,信息工程学院,四川,成都,610059;成都理工大学,地球探测与信息技术教育部重点实验室,四川,成都,610059;成都理工大学,信息工程学院,四川,成都,610059;成都理工大学,信息工程学院,四川,成都,610059【正文语种】中文【中图分类】TE122.3+22目前,国内、外主要应用相干分析技术进行断层裂缝识别和河道砂体空间展布特征等的分析,而且也主要是应用相干体的时间切片或沿层切片等平面特征来进行平面分析。
程谦等人[1]对高分辨相干剖面上的沉积特征(如,上超、前积等)和礁体特征(如,边界、内幕等)的识别进行了研究。
作为相干剖面特征及其应用的系列研究的一部份,我们认为相干剖面除了可以识别沉积特征和礁体特征外,还可以用来进行层位追踪解释。
相干体是一种用定量化计算出波形相似性的方法,它通过在时空中定义“全局化的”孔径计算来实现。
第7章矩阵特征值和特征向量的数值解

3 2.689 319 6.737 850 6.747 559 0.398 562 0.998 561 1.000 000
4 1.595 686 2.379 870 2.381 309 0.670 088 0.999 396 1.000 000
5 2.680 956 6.772 616 6.723 220 0.398 761 0.999 910 1.000 000
的常用方法是迭代每一步对向量 u (k ) 规范化。引入函数 max( u (k ) ),它表示取
向 量 u (k ) 中 按模 最大 的分 量,例 如, u (k ) =(2,-5,4)T,则 max( u (k ) )=-5,这 样
u(k) ma x(u
(k
)
)
的最大分量为
1,即完成了规范化。
7.1 幂法
(6) if mk m0 或 mk m0 (1 mk ) then 输
出 mk , vi (i 1,2,, n), 停止计算; (7) m0 mk ; k k 1; 返回第 3 步。
例 7.1.1 试用幂法求矩阵
7 3 - 2
A
3
4
-
1
- 2 -1 3
按模最大的特征值和相应的特征向量 ( 105 ) 。
k
u(k)
v(k)
0
0.4
0.5
0.6
0.666 667 0.833 33 1.000 00
1 2.833 335 7.000 06 7.166 673 0.395 349 0.976 744 1.000 00
2 1.604 652 2.372 096 2.395 352 0.669 902 0.990 291 1.000 000
相干和方差数据体的算法研究及应用

相干和方差数据体的算法研究及应用陈凤云;杭远;康建林【摘要】研究了相干数据体的C3算法以及方差数据体算法,编制开发了利用相干和方差数据体技术进行地震资料处理的数据处理系统,利用相干和方差数据体的时间切片和顺层切片来分析相邻道地震信号的相似性,进而探测小断层和分析地质构造.通过对实际资料的分析解释可以看出,相干和方差数据体技术对断层解释是非常有效的,可以提高解释精度,缩短勘探周期.【期刊名称】《物探与化探》【年(卷),期】2006(030)003【总页数】5页(P250-253,257)【关键词】地震数据处理;相干和方差算法;时间切片;顺层切片;断层识别【作者】陈凤云;杭远;康建林【作者单位】中国矿业大学,资源学院,江苏,徐州,221008;中国矿业大学,资源学院,江苏,徐州,221008;中国矿业大学,资源学院,江苏,徐州,221008【正文语种】中文【中图分类】P631.4相干和方差数据体技术是近几年发展起来的地震资料解释新技术,能够对三维地震地质信息自动拾取,在识别断层以及了解与储集层特征密切相关的砂体展布等方面非常有效,能够准确识别断层及地层不连续变化,甚至能够更加准确地给出断裂带的产状及延展方向,直至探明更小的地质异常体。
应用三维相干和方差数据体时间切片和顺层切片进行构造解释和岩性解释,可以帮助解释人员迅速认识构造及岩性的整体空间展布特征,从而达到加快解释速度、提高解释精度及缩短勘探周期的目的。
相干和方差数据体算法是不同的算法模型,可以单独使用任何一种方法进行处理解释,也可以联合使用,互相验证,进而提高解释精度。
进行数据处理解释时,需要根据具体的地质构造特征、地震资料质量、地质任务等来选择不同的算法模型。
因这2种算法原理相似,为方便理解,对其一并叙述。
1 方法原理相干体技术是利用相邻道地震信号之间的相似性来描述地层、岩性等的横向非均匀性,进而探测小断层、地质构造异常及岩性的整体空间展布特征。
GeoEast属性提取及分析子系统主要模块介绍—LQH按分类_20130401

antiform
kneg = 0
plane
kneg > 0
dome 26
曲率---振幅曲率
构造曲率与振幅曲率
构造曲率:倾角反映时间对x,y方向上的二阶导数;输入数据为倾角扫描结果。 振幅曲率:倾角反映振幅对x,y方向上的二阶导数;输入数据为相干能量梯度。
两 种 滤 波 方 法
带通滤波(按距离关系):通过参数给
功能和特色
用于构造解释及识别特殊岩性体 储层预测 用于油气检测
1. 多窗口地层倾角扫描 2. 构造导向滤波 3. 相干体 4. 边缘检测 5. 属性体比例融合
出空间滤波面元大小 Dis1 距离1(4*dx<=距离1<=nline*dx Dis2 距离2(<=距离1) Dis3 距离3(>=距离4) Dis4 距离4(=2*dx) 分数导数滤波:参数取值范围 0.25~2。一 般取值为0.25、0.5、0.75.其值越小,尺度
越大。
Lamda Min 一般为2*dx; Reference Velo 参考速度与倾角扫描时 参数一致; operator_dip 滤波算子振幅截断比例,最 大振幅乘以截距的门槛值,大于其输出, 小于其充零。
20
相干-实际效果
基于特征值算法的相干时间切片 (t=1660ms)
21
功能和特色
用于构造解释及识别特殊岩性体 储层预测 用于油气检测
1. 多窗口地层倾角扫描 2. 构造导向滤波 3. 相干体 4. 边缘检测 5. 属性体比例融合
6. 方差体(1)
7. 体曲率类(22) 8. 边缘保护平滑滤波
11. 相干和能量梯度类(10)
多窗口倾角扫描-概述
在三维地震资料解释中,解释的地震反射层位的倾角 和方位角是非常重要的, 由于在通常情况下,不能得到一个精确的时深转换关 系,所以倾角和方位角体只是体现了倾角和方位角的 相对变化关系。通常,利用垂直窗口进行倾角和方位 角估算比在拾取的层位进行估算能提供更为稳定的估 算结果。倾角和方位角体是体曲率、相干、能量梯度 和构造导向滤波的基础。
传统经典断层识别实战——相干、曲率
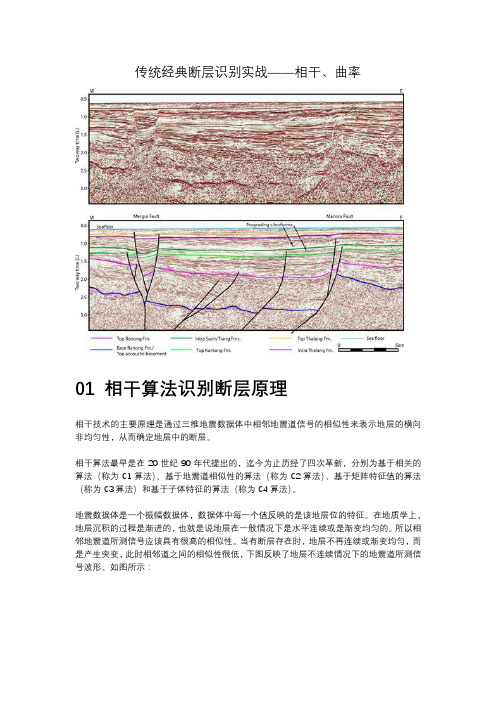
传统经典断层识别实战——相干、曲率01 相干算法识别断层原理相干技术的主要原理是通过三维地震数据体中相邻地震道信号的相似性来表示地层的横向非均匀性,从而确定地层中的断层。
相干算法最早是在20世纪90年代提出的,迄今为止历经了四次革新,分别为基于相关的算法(称为C1算法)、基于地震道相似性的算法(称为C2算法)、基于矩阵特征值的算法(称为C3算法)和基于子体特征的算法(称为C4算法)。
地震数据体是一个振幅数据体,数据体中每一个值反映的是该地层位的特征。
在地质学上,地层沉积的过程是渐进的,也就是说地层在一般情况下是水平连续或是渐变均匀的。
所以相邻地震道所测信号应该具有很高的相似性。
当有断层存在时,地层不再连续或渐变均匀,而是产生突变,此时相邻道之间的相似性很低,下图反映了地层不连续情况下的地震道所测信号波形。
如图所示:通过计算横向和纵向相邻道之间的相关值得到三维相干值数据体,从而将三维地震振幅数据体转换成相干数据体。
相干切片是相干数据体的水平切片,体现某一时间深度不同相干值的点构成的平面。
断层线是该平面上相干值小的点连成的线,通常是断层的所在位置。
用三维相干算法计算地震相干数据体突出了不相干的数据,其相干体水平切片表现了断层线所在位置,为油气储层评价提供了理论依据。
02 曲率识别断层原理曲率用来反映几何体的弯曲程度,描述的是曲线上任意一点的弯曲程度,表明曲线偏离直线的程度。
曲率越大,表示曲线的弯曲程度越大。
地震曲率断层检测技术由A.Roberts首先提出的,在构造解释中,我们可以根据层位的解释数据计算其曲率,从而可以定量描述其构造特征。
图给出了背单斜、向斜和断层曲率描述,其中背斜的曲率为正,向斜的曲率为负,而且褶皱越厉害,曲率值越大,平层和单斜层的曲率为零,断层在平滑后可近似认为其曲率由正到负或由负到正的变化。
显然,上述曲率对于单斜和水平地层的区分是无能为力的,对于平行断层,水平面上或沿层面上有方向变化的复杂构造,也是无能为力的,必须要借助于以二维曲面分析为基础的曲率属性。
c3算法——精选推荐
④-->⑥ 是,异常。类定义失败。
表头: 列表的第一个元素 (列表:ABC,那么表头就是A,B和C就是表尾)
表尾: 列表中表头以外的元素集合(可以为空)
merge 简单的说即寻找合法表头(也就是不在表尾中的表头),如果所有表中都未找到合法表头则异常。
#C3定义引用结束
例如:
L(D) = L(D(O))
= A + B + D + C + E + F + merge(O,O)#O是合法表头
=A+B+D+C+E+F+O
= [A,B,D,C,E,F,O]
获取C3的数组列表,可以梳理清楚子类执行过程中向上执行的顺序
= D + merge(L(O)L(B) = L(B(D,E))
= B + merge(L(D) , L(E))
= B + merge(DO , EO) # 第一个列表DO的表头D,其他列表比如EO的表尾都不含有D,所以可以将D提出来,即D是合法表头
= B + D + merge(O , EO) #从第一个开始表头是O,但是后面的列表EO的表尾中含有O所以O是不合法的,所以跳到下一个列表EO
= B + D + E + merge(O , O)
= [B,D,E,O]
同理:
L(C) = [C,E,F,O]
L(A(B,C)) = A + merge(L(B),L(C),BC)
= A + merge(BDEO,CEFO,BC)#B是合法表头
= A + B + merge(DEO,CEFO,C)#D是合法表头
几种属性原理分析
在计算过零点强相干同向轴的相似性时,上式给出的相似 估算对一些小相干值的地震同向轴来讲是不稳定的,为了 避免这个问题,采用与相似性速度分析相同的技巧,求垂 向上2k+1个样点的平均值,即:
八 几种典型属性原理及应用
4
基于复地震道的相干计算
在计算零值附近同相轴的相干体仍然会造成 一些假象,通常假设有一个背景级别的不相 干噪音,一旦地震信号的噪音低于背景噪音, 相干算法将识别为地震不相干,将产生地相 干的假象。应用复地震道技术就可以解决这 个问题。
八 几种典型属性原理及应用
相干计算可以在相干较弱或被噪声干扰的情况下,提供出 数据相似性的定量值。通过对地震数据体相干属性的量化 处理,针对波形进行相干运算,生成新的不同于常规地震 振幅数据体的相干属性体。这种数据体可以用于较为复杂 的断层及隐蔽地层岩性的解释,而这些复杂的地质特征在 常规地震数据中往往无法识别和解释。 相干体技术的特殊之处就在于突出那些横向不连续、不相 干的地震地质特征,如断层、三角洲、河道等,能够更加 客观真实地反映地下多种地质情况,帮助研究人员从整体 概念上分析和认识问题,提高解释工作的效率和精度。
解释的断层平面分布和相干分析叠合图
a
b
(a) 常规的时间~振幅切片与(b) 相干体等时切片的比较
八 几种典型属性原理及应用
目前,生成三维地震相干属性数据体的算法 很多,主要都是基于水平方向来实现。根据 资料的信噪比及算法的稳定性,主要包括C1、 C2、 C3三种相干算法。
八 几种典型属性原理及应用
将两条曲线的线性相关系数定义为:
r越接近于1,两条曲线对比段的关系就越密切;r接近 于0(或小于0),两条曲线对比段就越无关系。
求最大特征值和权重向量_概述说明以及解释
求最大特征值和权重向量概述说明以及解释1. 引言1.1 概述本文旨在介绍和解释求最大特征值和权重向量的概念、方法以及其在实际应用中的重要性。
最大特征值和权重向量是一种常见的数学工具,被广泛应用于许多领域,如经济学、市场营销和生态系统保护等。
通过该方法,可以量化不同因素对整体结果的贡献程度,并帮助做出决策。
1.2 文章结构本文将按照如下结构进行讲解:首先,我们将对最大特征值和权重向量进行定义和解释;接着,介绍了一些常用的求解方法,并阐述了它们所蕴含的意义;然后,我们将详细介绍几种求取最大特征值和权重向量的具体方法;随后,在实际应用与案例分析部分,我们将探讨这些方法在经济领域、市场营销和生态系统保护等领域中的具体应用案例;最后,我们将总结本文内容并展望未来最新研究动态以及潜在应用领域。
1.3 目的本文旨在提供对于求最大特征值和权重向量的全面概述,包括定义、解释、求解方法以及实际应用案例。
通过阅读本文,读者将有助于理解并掌握最大特征值和权重向量的概念、意义和求解技巧,以在实际问题中运用相关知识做出准确决策。
同时,本文也旨在为研究人员提供一个全面了解该领域最新动态并探索未来潜在应用领域的参考资料。
以上就是“1. 引言”部分的内容,接下来将继续撰写接下来各个部分的详细内容。
2. 最大特征值和权重向量2.1 定义与解释在数学和统计学中,最大特征值和权重向量是矩阵理论和特征值问题的关键概念。
在矩阵中,特征值表示线性变换后新向量方向不发生改变的尺度因子,而权重向量则代表着每个特征对于整体模式的贡献程度。
具体来说,对于一个矩阵A,它的最大特征值λ_max是该矩阵所包含的所有特征值中绝对值最大的一个。
而对应于λ_max的特征向量即为权重向量。
2.2 求解方法求解最大特征值和权重向量有多种方法,常用的包括幂法、反幂法以及特征投影法。
- 幂法(Power Method)是一种迭代算法,通过将初始随机向量经过A的连续乘积进行归一化操作来逼近最大特征值和相应的特征向量。
基于最大特征值估计的C3算法及应用
基于最大特征值估计的C3算法及应用隋京坤;郑晓东;李艳东【摘要】The third⁃generation coherence algorithm,C3,is robust to suppress noise and posseses high resolution.However,the process of computing eigenvalues of the covariance matrix in C3 istime⁃consuming.To avoid computing all eigenvalues,this paper proposes a fast convergence algorithm based an eigenvalue estimation of real symmetric matrices to calculate the dominant eigenvalue.To control the precision of the algorithm,this paper presents an error evaluation formula.By adding traces along the boundary of the seismic datavol⁃ume,we avoid judging whether the spatial window oversteps the boundary when recursion strategy is applied in a horizontal direction. The application to real data shows that the efficiency of C3 is improved by approxinately 3 times.%第三代相干体算法( C3算法)具有分辨率高、压制噪声能力强的优点,但是该算法需要计算协方差矩阵的特征值,所以耗时较多。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
æλn-m ö 2k
ç÷
+
…
+
æλ1 ö 2k
ç÷
≥1
。
è λn ø
èλn ø
可得 F(k)≥λn,故 F(k)是收敛函数。 又因为
lim
æ
ç
λ
i
ö
÷
k
=
0
,
(i
=
1,…,n
-
m)
k➝+∞ èλn ø
lim 2k m = 1 。
k➝ +∞
于是进一步有
lim
k➝ +∞
T 2k k
= λn。
(8)
显然,A2k 比 Ak 的收敛速度要快,而 A2k = A2k-1 ×
dTn( x,y,t) = [ dn1,dn2,…,dnJ ] ,n = - N,…,N 则可将数据体内的地震道表示为矩阵
D( x,y,t) = [ d -N,d -N+1,…,dN] T,
(1)
相关矩阵 C(x,y,t)的计算方法
N
∑ C( x,y,t) = DTD = dndTn = n = -N
第 38 卷第 6 期 2014 年 12 月
物 探 与 化 探
GEOPHYSICAL & GEOCHEMICAL EXPLORATION
Vol.38,No.6 Dec.,2014
doi:10.11720 / wtyht.2014.6.36 隋京坤,郑晓东,李艳东.基于最大特征值估计的 C3 算法及应用[ J] .物探与化探,2014,38( 6) :1293- 1297.http: / / doi.org / 10.11720 / wtyht.2014. 6.36 Sui J K,Zheng X D,Li Y D.A fast algorithm to estimate the dominant eigenvalue of Real Symmetric Matrices and its application to C3 algorithm[ J] .Geo⁃ physical and Geochemical Exploration,2014,38(6) :1293-1297.http: / / doi.org / 10.11720 / wtyht.2014.6.36
(7)
根据式(3),易知补道后的矩阵特征值仅多出 J -L
个 0 特征值,对 Ec 值无影响。 2.2 实对称矩阵特征值估计的快速收敛算法
王其申[13] 给出了任意实对称矩阵最大与最小
特征值可以逐步收敛的一种包含关系,但这种关系
的收敛速度较慢,为了高效地求取特征值,在前者的
基础上提出了改进的快速收敛算法,并给出了控制
其特征值求解方程为 CL - λE = 0 。
则补道之后的相关矩阵
éêCL … 0 ùú
C = ê︙ ⋱ ︙ú ,
(6)
ëêê 0 … 0 ûúú
式(6)中省略号处的值均为 0,矩阵 C 特征值求解方
6期
隋京坤等:基于最大特征值估计的 C3 算法及应用
·1295·
程为
C - λE = λJ-L(CL - λE) = 0 。
基于最大特征值估计的 C3 算法及应用
隋京坤,郑晓东,李艳东
( 中国石油勘探开发研究院,北京 100083)
摘 要: 第三代相干体算法( C3 算法) 具有分辨率高、压制噪声能力强的优点,但是该算法需要计算协方差矩阵的特 征值,所以耗时较多。 为提高大矩阵特征值分解的运算速度,提出了一种估计最大特征值的快速收敛算法,通过运 用 A2k 矩阵的迹来构造一种收敛速度更快的特征值估计方法,并给出了这种方法的误差估计表达式,实现计算精度 的有效控制。 文中还讨论了地震数据体边缘补地震道方法,解决了将递推算法应用到平面方向时空间窗越过边界 的问题。 实例表明,本算法的计算效率明显高于常规的 C3 算法。 关键词:第三代相关算法;特征值估计;相关矩阵优化;补边;快速收敛算法 中图分类号: P631.4 文献标识码: A 文章编号: 1000-8918(2014)06-1293-05
在 C3 算法实现过程中,主要有数据读取、相关 矩阵求取、特征值求取及相干值求取四个主要步骤, 而其中第二与第三步耗时最多。 为了实现 C3 算法 的高效计算,前人针对这两步提出了多种优化算法。 针对第二步,叶增炉等[6] 于 2006 年提出了递推算 法。 而为了对算法中耗时最多的特征值求取过程进 行优化,前人则进行了更加广泛的探索,提出了许多 解决方法。 其中一类方法是降低相关矩阵的维数: Cohen 等[7] 通过计算数据体的四个子数据体的相关
性来构造相关矩阵,减少了相关矩阵的维数,李艳东 等[8] 通过引入超道技术将相关矩阵转化为四维矩 阵,它们的计算结果相对于 C3 算法都有不同程度 的改变。 另一类方法是不进行特征值分解,而是引 入特征值估计算法。 这方面的研究成果,最著名的 要数 Gersgorian 圆盘定理[9] 和 Collatz 定理[10] ;前者 断言 n 阶矩阵的特征值必被包含在复平面上的 n 个 圆盘的并集内,后者则是针对实对称矩阵的特征值, 其内容是:设 A 为 n 阶实对称矩阵,X = [x1,…,xn ] T 是一任意 n 维向量,记 Y = AX,则至少有 A 的一个 特征值 λ 满足:min( yi / xi ) ≤λ ≤max( yi / xi ) ,但是 它们都不能保证估计值的收敛,计算精度较低。 孙 夕平等[11] 将乘幂法引入到 C3 算法中,估算出相关 矩阵的最大 特 征 值, 提 高 了 估 计 算 法 的 计 算 精 度。 王晓凯等[12] 综合了使用了乘幂法及递推法,并根据 地震数据的特点,通过计算相关矩阵最大特征值对 应的特征向量,并将它作为下一采样点的初始迭代 向量,提高了乘幂法在地震数据中的计算效率。 但 由于乘幂法推导过程中有多次使用近似算式,故未 能通过算法本身实现对计算值与实际值误差的控 制。
1 C3 算法原理[3]
C3 算法是一种基于特征结构分析的相干体算
法,算法中 相 干 值 的 计 算 可 以 使 用 多 道 地 震 记 录。
在计算采样点( x,y,t) 处的相干值时,首先定义一个
包含该点的数据体( 由二维的空间窗及一维的时间
窗控制),假设时间窗内包含 J 道地震记录,时间窗
内采样点数为 2N+1,令
y,t+1)的计算量,其中乘法计算由 J ×( J + 1) ( 2N +
1) / 2 次,降为 J×(J+1)次。
式( 4) 是在 时 间 轴 方 向 递 推 算 法 的 应 用, 在 空
间内仍然 可 以 使 用 递 推 算 法[10] , 利 用 相 关 矩 阵 C
(x,y,t),只要更新其中部分元素就可以得到 C( x+
相干体技术是不连续性检测的一项重要技术, 它可以揭示断裂、地层层序等地质现象。 第一代相 干体是基于互相关的算法,由 Bahorich 和 Farmer 于 1995 年提出[1] 。 第二代相干体是基于相关性的算 法[2] ,这种算法使用多道地震记录,增强了压制噪 声的能力,但分辨率不高。 第三代相干体是基于特 征值结构分析的算法[3] ,这种算法可以显著提高压 制噪声的能力和分辨率,但计算效率不高。 张军华 等[4] 提出利用递推算法提高相干体计算效率。 赵 汝敏等[5] 针对复杂断块的断裂地震特征,利用超道 构建技术,并与基于小波变换的相干技术集成,再进 行相干计算。
ö - 1÷÷ × tr( C) ≥ ε ,
ø
(9)
其中:ε 为算法的精度,即计算值与实际值允许的最
N
∑ dn1 dn2
n = -N
…
∑ n
N =-
d
N
n1
d
nL
ùú ú
êN
∑ CL
=
ê ên
=
dn2
-N
dn1
ê ê
︙
N
∑ d2n2
n = -N
︙
N
ú
∑ …
n
=
-
d
N
n2
d
nL
ú ú
,
(5)
⋱
︙
ú ú
êN
N
∑ ∑ ëêên=-dNnL
d
n1
dnL dn2
n = -N
…
N
ú
∑d
2 nL
n = -N
ûúú
n = -N
ûúú
定义点(x,y,t)处相干值 Ec(x,y,t)为
Ec(x,y,t) =
λ max
J
=
λ max
J
,
(3)
∑ ∑ Cjj
λj
j=1
j=1
其中:λmax 是 λj 中的最大值。
由式(2)易知相关矩阵 C(x,y,t)为正定或半正
定矩阵,故 Ec 取值在 1 / J ~ 1 之间。 当数据体不同 道的波形都相同时,Ec = 1,当波形不同时 Ec 小于 1, 且波形间差异越大,Ec 越小。 波形间的差异能反映 地质体的变化,故 Ec 能够刻画地质体的不连续性。
∑ éê
ê
N
d2n1
n = -N
N
∑ dn1 dn2
n = -N
…
∑ n
N
dn1
= -N
dnJ
ùú ú
êN
∑ ê
ên
=
dn2
-N
dn1
ê ê
︙
N
∑d
2 n2
n = -N
︙
N
ú
∑ …
n
=
dn2
-N
dnJ
ú ú
, (2)
⋱
︙
ú ú
êN
N
∑ ∑ ëêê
n
=
-
d
