工程制图5(平面的投影及平面上的点)
合集下载
工程制图_05平面立体的投影与曲面立体的投影(含截交线和螺旋面)

截平面定位尺寸 60°
应标注立体的原形尺寸
和切口截平面的定位尺
寸,不注切口截交线的
Ø
定形尺寸。
JK系列
切 口 立 体 尺 寸 注 法
截平面定位尺 寸
截平面定位尺寸 SR
平面立体的截交线
截平面:截切立体的平面称为截平面。
JK系列
平 面 立 体 的 截 交 线
截交线:截平面与立体表面的交线称为截交线。
圆球的三个投影均为等径圆,并且是圆球上平行于相应 投影面的最大轮廓圆。H面投影的轮廓圆是上、下两半球的可 见性分界线,V面投影的轮廓圆是前、后两半球的可见性分界 线,W面投影的轮廓圆是左、右两半球的可见性分界线.
JK系列
圆球面上取点
A点在右前上方 B、C点在球面
的球面上
的赤道圆上
VW
a
(a")
a
( a)"
面 的 圆
dc
d"(c")
D
C
例 1 0
R2
a"(b")
B
ab
A
JK系列
[例11] 补绘四分之一圆球被切割后的H、W投影。
例
1
1
圆球的截交线
都是圆
JK系列
圆柱螺旋线 形成:一动点沿一直线等速移动,而该直线同时绕 螺旋面
螺 线旋
与它平行的一轴线等速旋转时动点的轨迹。
投影:H面投影为圆周,V面投影为正曲线。注意后半圆柱的 螺旋线不可见,
圆
截平面与柱轴平行 截平面与柱轴斜交
矩形
椭圆
投 影 图 与 立 体 图
截平面
截平面
截平面
[例1] 带凸截口圆柱的画法.
工程制图第3章 点、直线和平面的投影

W X
β
SH
O
α
Y
H
YH
V
a
A
a
b c
B
b
H
水平面
a
b a W c
C
a
c
b c
b c
b a c
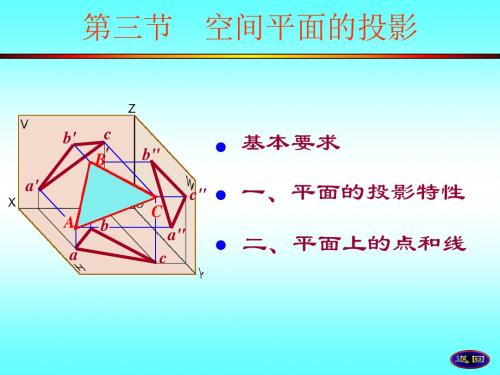
投影特性: 1. abc、 abc积聚为一条线积聚为一直条线,具有积聚性 2. 水平投影abc反映 ABC实形
V b
正平面
b
b
a
B
b
c
W
a
a
A a
2.投影面垂直线
垂直于某一投影面的直线
(1) 铅垂线 (2) 正垂线 (3) 侧垂线
3.一般位置直线
与三个投影面都倾斜的直线
水平线 — 平行于水平投影面的直线 z
Z
a b
a
b
a
b
A
a
X
O
YW
X
B O
b
a
a
b
Y
投影特性:1. ab OX ; ab OYW 3. 反映、 角的真实大小
α
H
V SB
A
b
b
侧垂面
SbW
c β c
a
W
α a
c
C
a
b c
H
a
投影特性: 1、 侧面投影abc积聚为一条直线 2 、 水平投影abc、正面投影 abc为 ABC的类似形
3 、 abc与OZ、 OY的夹角反映α、β角的真实大小
V S
侧垂面的迹线表示 Z
SH
b
QV
a
A
c
C
正垂面
b
β
SH
O
α
Y
H
YH
V
a
A
a
b c
B
b
H
水平面
a
b a W c
C
a
c
b c
b c
b a c
投影特性: 1. abc、 abc积聚为一条线积聚为一直条线,具有积聚性 2. 水平投影abc反映 ABC实形
V b
正平面
b
b
a
B
b
c
W
a
a
A a
2.投影面垂直线
垂直于某一投影面的直线
(1) 铅垂线 (2) 正垂线 (3) 侧垂线
3.一般位置直线
与三个投影面都倾斜的直线
水平线 — 平行于水平投影面的直线 z
Z
a b
a
b
a
b
A
a
X
O
YW
X
B O
b
a
a
b
Y
投影特性:1. ab OX ; ab OYW 3. 反映、 角的真实大小
α
H
V SB
A
b
b
侧垂面
SbW
c β c
a
W
α a
c
C
a
b c
H
a
投影特性: 1、 侧面投影abc积聚为一条直线 2 、 水平投影abc、正面投影 abc为 ABC的类似形
3 、 abc与OZ、 OY的夹角反映α、β角的真实大小
V S
侧垂面的迹线表示 Z
SH
b
QV
a
A
c
C
正垂面
b
工程制图 (5)

4.平面的迹线表示法
从前述可知,特殊位置面的积聚性投影即可确定平面的空间 位置,而平面投影的目的主要是表达平面的空间位置,因此对于 特殊位置面,我们完全可以只用平面有积聚性的一面投影来表达 。此时用有积聚性的平面迹线表示特殊位置平面就相当简单。
PV
X
SV
X
铅垂面T
X
TH
正垂面P
水平面S
为了表明该积聚直线表达的是平面而不是直线,我们规定用一个 大写字母加上投影面字母作为角标表示所表达的平面。
正平面 水平面 侧平面 正垂面 铅垂面 侧垂面
3.各类平面的投影特征
有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)
规定:平面与H、V、W投影面的夹角α、β、γ
3.各类平面的投影特征
正平面
位置特点 平行于V面,垂直于H、W面
投影特征
正面投影反映平面实形,水平投影 、侧面投影都积聚为Y轴的垂直线, 即正平面上所有点的Y坐标都相等。
迹线在投影图上 应加上迹线符号
正面迹线
侧面迹线
水平迹线
平面P与H面的交线称为平面P的水平迹线(H面迹线),用PH表示 平面P与V面的交线称为平面P的正面迹线(V面迹线),用PV表示 平面P与W面的交线称为平面P的侧面迹线(W面迹线),用PW表示
有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)
各类平面的投影特征
《工程制图》
目录
1.平面的几何表示法 2.平面的分类 3.各类平面的投影特征 4.平面的极限表示法
1.平面几何表示法
2.平面的分类
根据平面在三投影面体系中的位置不同,将平面分为三类
倾斜面 ∠H、V、W
投影面平行面
工程制图 平面的投影-线面相对位置解读
(2) p'与x、z轴的夹角反映α、 角的真实大小 (3) p、 p为平面P的类似形
(一)投影面的垂直面
2.铅垂面:只垂直于H面,倾斜于V面和W面的平面
z p' p' p" O
P
p"
x
yW
p
p
yH
投影特性 :(1) H面投影积聚为一条线p
(2) p与x、 y轴的夹角反映β、角的真实大小 (3) p'、 p为平面P的类似形
b'
b' c'
z b"
c'
b" a' c" x O a"
c" yW
B
a'
A
a 投影特性:
C
b
c
b
a" a c yH
(1) 一般平面的三面投影既不反映实形也没有积聚性。 (2) 其三面投影均为空间平面的类似形,且面积缩小。
平面投影特性判断
正平面
铅垂面
侧平面
正平面
正垂面
侧平面
侧垂面
一般位置平面
二、平面上的点和线
C
D A B
A C F a
D
D A B a C K E B F b c(f) d(e)
K
F
E
d(e) a b
E
c(f)
c(f)
k
d(e)
k
b
一
二
三
一、平行问题
1.直线与平面平行
直线与平面平行具有下列几何关系: 若直线与平面平行<- ->该直线必平行于平面上的一条直线; 当平面垂直于投影面时<- ->该直线的投影必然与平面具有积聚性 的投影平行。
(一)投影面的垂直面
2.铅垂面:只垂直于H面,倾斜于V面和W面的平面
z p' p' p" O
P
p"
x
yW
p
p
yH
投影特性 :(1) H面投影积聚为一条线p
(2) p与x、 y轴的夹角反映β、角的真实大小 (3) p'、 p为平面P的类似形
b'
b' c'
z b"
c'
b" a' c" x O a"
c" yW
B
a'
A
a 投影特性:
C
b
c
b
a" a c yH
(1) 一般平面的三面投影既不反映实形也没有积聚性。 (2) 其三面投影均为空间平面的类似形,且面积缩小。
平面投影特性判断
正平面
铅垂面
侧平面
正平面
正垂面
侧平面
侧垂面
一般位置平面
二、平面上的点和线
C
D A B
A C F a
D
D A B a C K E B F b c(f) d(e)
K
F
E
d(e) a b
E
c(f)
c(f)
k
d(e)
k
b
一
二
三
一、平行问题
1.直线与平面平行
直线与平面平行具有下列几何关系: 若直线与平面平行<- ->该直线必平行于平面上的一条直线; 当平面垂直于投影面时<- ->该直线的投影必然与平面具有积聚性 的投影平行。
土木工程制图第三章点-直线和平面的投影PPT课件

① 铅垂线与H面垂直同时与V面、W面平行。 ② 正垂线与V面垂直同时与H面、W面平行。 ③ 侧垂线与W面垂直同时与H面、V面平行。
(3)投影面垂直线的投影特点为:在它所垂直的投 影面上的投影积聚为一点,另外两个投影垂直 于相应的投影轴,如图3.15所示。
可编辑课件PPT
24
投影面垂直线
土木工程制图
ax
a●
解法二: 用圆规直接量 取aaz=aax
a● ax
a●
az
a
●
可编辑课件PPT
7
例2:已知点的两面投影,求第三 投影,如下图所示。
土木工程制图
(a) 已知
(b) 作图
分析:因为根据点的任意可编两辑面课件投PPT影可以求出第三投影。 8
四、特殊位置的点
土木工程制图
注意:A点的侧面投影a"应在OYW轴上,C点的水平投影
(b) 正平线
21
(c) 侧平线
投影面平行线投影特性
土木工程制图
水平线
a b Z a
Xa β γ b YH
实长
实长
b b α
YW X
b
正平线
a Z a
γ
b
侧平线
a
Z a
β
b
α
YW X a
a
b
YH
YH
与H面的夹角:α
实长
b
YW
与V面的夹角:β
投影特性
与W面的夹角:γ
1)在其平行的那个投影面上的投影反映实长, 并反映直线与另两投影面的真实倾角。
O b
a AB实长
△Z
△Z
A0 a′
OX
B0
a
YH
(3)投影面垂直线的投影特点为:在它所垂直的投 影面上的投影积聚为一点,另外两个投影垂直 于相应的投影轴,如图3.15所示。
可编辑课件PPT
24
投影面垂直线
土木工程制图
ax
a●
解法二: 用圆规直接量 取aaz=aax
a● ax
a●
az
a
●
可编辑课件PPT
7
例2:已知点的两面投影,求第三 投影,如下图所示。
土木工程制图
(a) 已知
(b) 作图
分析:因为根据点的任意可编两辑面课件投PPT影可以求出第三投影。 8
四、特殊位置的点
土木工程制图
注意:A点的侧面投影a"应在OYW轴上,C点的水平投影
(b) 正平线
21
(c) 侧平线
投影面平行线投影特性
土木工程制图
水平线
a b Z a
Xa β γ b YH
实长
实长
b b α
YW X
b
正平线
a Z a
γ
b
侧平线
a
Z a
β
b
α
YW X a
a
b
YH
YH
与H面的夹角:α
实长
b
YW
与V面的夹角:β
投影特性
与W面的夹角:γ
1)在其平行的那个投影面上的投影反映实长, 并反映直线与另两投影面的真实倾角。
O b
a AB实长
△Z
△Z
A0 a′
OX
B0
a
YH
绘制平面的投影

单元五 绘制平面的投影
• (4)一般直线与一般位置平面相交 由于一般直线与一般位置平面 没有积聚性,不能在投影图上直接定出其交点,如图5-20所示,求 交点时,可采用辅助平面进行作图。 ①包含直线EF作辅助平面垂直于H面; ②求平面ABC与辅助平面的交线MN; ③求交线MN与直线EF的交点K,即为所求直线与平面的交点; ④利用重影点,判别其投影重合部分的可见性。
单元五 绘制平面的投影
图5-3平面的迹线表示法 (a)迹线表示的一般位置平面;(b)迹线表示的垂直平面
单元五 绘制平面的投影
投影面垂直面可分为以下三类: ①垂直于H面,简称铅垂面;②垂直于V面,简称正垂面; ③垂直于W面,简称侧垂面,如图5-4所示。
图5-4投影面的垂直面(a)铅垂面;(b)正垂面;(c)侧垂
投影面平行面的共性:平面在所平行的投影面上的投影反映实形,其他 两投影都积聚为与相应投影轴平行的直线,如图5-8所示。
图5-8投影面平行面的性质
单元五 绘制平面的投影
➢ 3、一般位置平面 与三个投影面既不垂直也不平行的平面为一般位置 平面,其各个投影都没有积聚性,都小于实形。如图5-1所示。
➢ 学习任务三:分析如图5-9所示工程构造物翼墙有几个面,并分析各平 面与投影面的相对位置。
的两点[图5-12(a)]。②直线通过平面上的一点,且平行于该平面 上的一直线[图5-12(b)]。
单元五 绘制平面的投影
• (2)点在平面上的几何条件是:点在平面内的某一直线上,如图5-13所示。
图5-13平面上的点
单元五 绘制平面的投影
➢ 学习任务六:已知如图5-14(a)中五边形ABCDE上A、D、E 三点的两 投影及另两点B、C的正面投影,要求补全五边形的水平投影。
机械工程制图点的投影课件

程
学
A
院
B
被挡住的投
a(b)
c d
影加( )
空间两点在某一投影面上的投影重合为一点时, 则称此两点为该投影面的重影点。
•18
•2024/4/30
点在空间的a上 下、前后、 a
程
a
学
左右位置关系。
院
b
b
A
a X
X
B
O
b
b
O
YW
b
b
a
Y
a
判断方法: ▲x 坐标大的在左 ▲y 坐标大的在前 ▲z 坐•1标5 大的在上
YH
•2024/4/30
例3 判断两点的相对位置
机
械
工 程 学
a●
Z ●a
院
b ●
● b
X
o
YW
a●
●
b
YH
B点在A点之前、
之右、之下。
一.点在二面投影体系中的投影
机 械
5.点的二面投影特性
工 程
aa´ox
a´
学
院 特性1:点的投影连线垂直于 X
o
相应的投影轴
A(a,a) x= oax
a
Z
y=aax =Aa´
V a
●
A(x, y,z)
z= axa´=Aa
z X ax
A
●x
特性2:点到投影面的距离等
y
O
于它在相邻投影面的投影到投
a●
•水平投影用相应的小写字母表示,如a、b、c等;
•正面投影用相应的小写字母加撇表示,如a′、b′、c′;
•侧面投影用相应的小写字母加两撇表示,如a″、b″、c″。
工程制图 第五章 平面形体的投影

6
7(8)
8 3
● ● ●
6
7
●
1
2(3) 4(5) 3 1 8
(5) 1 (4)
●
2
5 7
6
4
2
第三节
直线与平面立体贯穿
直线与立体表面的交点称为贯穿点 求贯穿点的实质是求直线与平面交点的问题。 利用积聚投影 方法: 辅助平面法
例1: 求直线AB与三棱柱的贯穿点
一、长方体组合
二、斜面体组合
b P a(c) c P a b c P
b
a B P C A
例1:已知长方体的三面投影,某一平面被切割后,求其 它两面投影。
例2:已知长方体被切割后的两面投影,求第三面投影。
b a a
b
a b
投影图分析:
底面:水平面 顶面:水平面 侧面: 后面:正平面 左、右后面:铅垂面 左、右前面:铅垂面
正棱柱图例:
五棱柱
五棱柱
六棱柱 六棱柱
三棱柱 三棱柱
四棱柱 四棱柱 (长方体 ) (长方体 )
已知棱柱表面上两点M、N的V面投影,确定其他两面投影。 棱柱表面定点:
m
(n)
k
m
(n)
中途返回请按“ESC” 键
改变例1: 求直线AB 与三棱柱的贯穿点
例2
求直线AB 与三棱锥的贯穿点
改变例2 求直线AB与三棱锥的贯穿点
第四节
两平面立体相贯
例3 画出三棱锥与三棱柱全贯的投影图
例4 画出三棱锥与三棱柱互贯的投影图
第五节 平面基本体的组合
图1 房屋形体的分析 图2 水塔形体分析
第五章 平面形体的投影
7(8)
8 3
● ● ●
6
7
●
1
2(3) 4(5) 3 1 8
(5) 1 (4)
●
2
5 7
6
4
2
第三节
直线与平面立体贯穿
直线与立体表面的交点称为贯穿点 求贯穿点的实质是求直线与平面交点的问题。 利用积聚投影 方法: 辅助平面法
例1: 求直线AB与三棱柱的贯穿点
一、长方体组合
二、斜面体组合
b P a(c) c P a b c P
b
a B P C A
例1:已知长方体的三面投影,某一平面被切割后,求其 它两面投影。
例2:已知长方体被切割后的两面投影,求第三面投影。
b a a
b
a b
投影图分析:
底面:水平面 顶面:水平面 侧面: 后面:正平面 左、右后面:铅垂面 左、右前面:铅垂面
正棱柱图例:
五棱柱
五棱柱
六棱柱 六棱柱
三棱柱 三棱柱
四棱柱 四棱柱 (长方体 ) (长方体 )
已知棱柱表面上两点M、N的V面投影,确定其他两面投影。 棱柱表面定点:
m
(n)
k
m
(n)
中途返回请按“ESC” 键
改变例1: 求直线AB 与三棱柱的贯穿点
例2
求直线AB 与三棱锥的贯穿点
改变例2 求直线AB与三棱锥的贯穿点
第四节
两平面立体相贯
例3 画出三棱锥与三棱柱全贯的投影图
例4 画出三棱锥与三棱柱互贯的投影图
第五节 平面基本体的组合
图1 房屋形体的分析 图2 水塔形体分析
第五章 平面形体的投影
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B. 水平面投影r和正面投影r’ 都积聚为直线, 分别∥OYH轴和OZ轴。
侧平面的迹线表示法
V
Rv
Rv
R
X
x
R
(b)
H
H
侧平面R可只用(a它) 的正面迹线Rv或RH表示 。
投影面平行面的投影特性:
(1)在所平行的投影面上的投影反映实形。 (2)在另外两个投影面上的投影都积聚为直线, 平行于相应的投影轴。
作法1: 在平面内的两 已知边上各取一点连成 直线。
作法2: 在平面内的一 已知边上取一点,再过 点作平面内另一直线的 平行线。
b’
1’
a’ X
a
2’ c’
c 2
1
b
直线ⅠⅡ即为所求。
2.平面上取点
点在平面上的几何条件: 点在该平面的一已知直线上。
B
P
∵直线L在P面上, A
M
∴M点在平面P上。
L
C
正垂面的迹线表示法
QV有积聚性,它与X轴的夹角即α;QH⊥X轴。
Z
V
PZ
QV
QV
QW W
x
α
PX
X
O
QH H
QH
PY
Y
正垂面P可只用它的正面迹线Qv表示
侧垂面--仅⊥W面的平面 Z
r’ r’’
R
r
r’
X
r” β
α
O
YW
p rγ
YH
A.侧面投影r’’ 积聚为一倾斜线段,并反映α、 β角。 B.水平投影r 和正面投影r’ 都是小于原平面的类似形。
γ
(2)铅垂圆的投影
铅垂直径CD
水平直径AB
长轴:铅垂直(a径) CD铅的垂投面影上圆c’的d投’=影D
(b)
短轴:水平直径AB的投影a’b’=Dcosβ
铅垂圆的投影作图
c’
c”
D D
a’
O' b’
O”
a”
b”
X a
d’
β
c’(d’) Oγ
b
d”
长轴:铅垂直径CD的投影 c’d’=c”d”=D
短轴:水平直径AB的投影 a’b’=Dcosβa”b”=Dcosγ
3
1
2
a
b
yH
可按已知点的两个投影求第三投影的方法作出△abc。
例10 已知一平面ABCD。(1)判别点K是否在平面上;
(2)已知平面上点E的正面投影,求作其水平投影。
b’
f’ a’
k’
g’
c’ e’
X
d’
f bk a
c
dg
e
∵ K点不在直线FC上,∴ K点不在平面上。
1.平面上取直线
直线在平面上的几何条件:
(1) 通过平面上的两已知点。
B
P
M
A
N
C
直线MN在平面上
(2) 通过平面上的一点并平行于平面上的另一 直线。
E
M
D
F
N
P
直线MN在平面P上
结论 -- 要在平面上取直线,应先在平面上的已知 直线上取点,再过点作直线。
例5 在△ABC给定的平面上作一任意直线。
铅垂面--仅⊥H面的平面
铅垂面的迹线表示法
PH有积聚性,它与X轴 的夹角即β;Pv⊥X轴。
V
p
pv
pv
x
β
PH
(b)
X
X
β
PH
H
PH
(c)
(a)
铅垂面P可只用它的水平迹线PH表示。
正垂面--仅⊥V面的平面 Z
q’ Q
q’ γ
p”q”
α
X
O
YW
q’’
p qγ
q YH
A. 正面投影p’积聚为一倾斜线段,并反映α、γ角。 B. 水平投影p和侧面投影p”都是小于原平面的类似形。
二、各种位置平面的投影特性
1. 投影面垂直面 垂直于一个投影面而对另外两个投影 面倾斜的平面。
铅垂面--仅⊥H面的平面 正垂面--仅⊥V面的平面 侧垂面--仅⊥W面的平面
铅垂面--仅⊥H面的平面
Z
p’
p”
X
O
YW
β
pγ
YH
A. 水平投影p积聚为一倾斜线段,并反映β、γ角。 B. 正面投影p’和侧面投影p”都是小于原平面的类似形。
在平面上取点的一般方法:含该点在平面上作 辅助直线,然后在所作直线上取点。
例6 已知点D在△ABC所决定的平面上,求作
其正面投影d’。
A
a’
1’
d’
c’
Ⅰ
b’
D
C
c
B
空间分析
b
d1
a 作法1
D点一定在该平面的一条直线上。
例7 已知点D在△ABC所决定的平面内,求 作其正面投影d’。
a’
A
d’
2’
垂直面上圆的投影特性:
(1)在与圆平面垂直的投影面上,圆的投影是直线 段,长度等于圆的直径。 (2)在与圆平面倾斜的投影面上的投影是椭圆,长 轴是圆平面上平行于这个投影面的直径的投影,短 轴是圆平面上与上述直径相垂直的直径的投影。
三、平面上的点和直线
1.平面上取直线 2.平面上取点 3.平面上的特殊直线 4. 换面法
水平面--// H面的平面
p’
Z p”
X
O
YW
p
YH
A. 水平投影p反映平面P的实形; B. 正面投影p’和侧面投影p”都积聚为直线,
分别∥OX轴和OYW轴。
水平面的迹线表示法
V
Pv
Pv
P
X
x
(b)
H
水平面P可只用(a)它的正面迹线Pv表示。
正平面--// V面的平面
Z
q’ Q
q’
X
O
q’’
q”
侧垂面的迹线表示法
z
V X
RV R
RZ
O RW W x
H
RH
RY Y
RV
RZ
RW
o
RY
yw
W
RYH
RH
YH
侧垂面R可只用它的侧面迹线RW表示 。
投影面垂直面的投影特性:
(1)在所垂直的投影面上的投影积聚为直线, 它与投影轴的夹角反映平面对另外两个投影面的 倾角。 (2)在另外两个投影面上的投影是小于原平面 的类似形。
面的投影积聚为倾斜于投影轴的
直线,长度等于圆的直径。另外
O'
两个投影为椭圆。
X
O
圆平面为正垂面
(3)当圆倾斜于投影面时,它的投影为圆的类似 形-- 椭圆。
圆的投影的作图方法
1)当圆∥投影面时
反映圆的实形
O'
X
O
长度=圆的直径 圆平面为正平面
2)当圆⊥投影面时(1)正垂圆的投影
正垂直径AB
正平直径DE 长轴和短轴
c’
b’
D
c
Ⅱ
C
b
B
2d
空间分析
a 作法2
例8 试完成平面四边形ABCD的水平投影。
c’
分析: 平面ABCD的 b’
k’
对角线一定相交。
d’
a’
X
a
d
b
k
C点一定在该平面的一条直线上。
c
例9 完成侧垂面△ABC的水平投影。
c’
3’
1’
2’
a’ X
c
z c”
3”
b’ O
1”(2”)
a”(b”) yw
例1 含直线AB (ab, a’b’) 作铅垂面 (用平面图形表示)。
分析:铅垂面的水平投影
a’
为斜交于X轴的直线,有积
聚性。
X
本题铅垂面用三角形表示。
a
b’
c’ b
c
2. 投影面平行面
平行于某一投影面的平面。
• // H面的平面--水平面 • // V面的平面--正平面 •// W面的平面– 侧平面
PW X
O
PX
O
PYW
YW
H PH
(a)
PY
Y
PH
(b)
PYH
YH
②迹线是平面上的直线。因此,平面可用它的两 条迹线表示。
Z
PZ
PV
PV
PW
PX
X
PH
平面对一个投影面的投影特性
△ABC倾斜于P面
投影为小于原平面的 类似形
△abc<△ABC
△ABC⊥P面 投影积聚为一直线
abc
△ABC∥P面
投影反映实形 △abc≌△ABC
YW
q
q YH
A. 正面投影q’反映平面P的实形;
B. 水平投影q和侧面投影q”都积聚为直线, 分别∥OX轴和OZ轴。
正平面的迹线表示法
a’
X
QH
a
正平面Q可只用它的水平迹线QH表示。
侧平面--// W面的平面
V r‘ R
r’
W
X r’‘
Z
r”
O
YW
r
r YH
A. 侧面投影r’’反映平面R的实形;
平面的投影可以由其中一组几何元素的投影 来表示。
不
在 同
a’
一
直
线x
上
的
三a
点
a’
平
行
两x
直
线
a
b’ c’
c b
b’ c’
c b
一
直 线
a’
和
直
侧平面的迹线表示法
V
Rv
Rv
R
X
x
R
(b)
H
H
侧平面R可只用(a它) 的正面迹线Rv或RH表示 。
投影面平行面的投影特性:
(1)在所平行的投影面上的投影反映实形。 (2)在另外两个投影面上的投影都积聚为直线, 平行于相应的投影轴。
作法1: 在平面内的两 已知边上各取一点连成 直线。
作法2: 在平面内的一 已知边上取一点,再过 点作平面内另一直线的 平行线。
b’
1’
a’ X
a
2’ c’
c 2
1
b
直线ⅠⅡ即为所求。
2.平面上取点
点在平面上的几何条件: 点在该平面的一已知直线上。
B
P
∵直线L在P面上, A
M
∴M点在平面P上。
L
C
正垂面的迹线表示法
QV有积聚性,它与X轴的夹角即α;QH⊥X轴。
Z
V
PZ
QV
QV
QW W
x
α
PX
X
O
QH H
QH
PY
Y
正垂面P可只用它的正面迹线Qv表示
侧垂面--仅⊥W面的平面 Z
r’ r’’
R
r
r’
X
r” β
α
O
YW
p rγ
YH
A.侧面投影r’’ 积聚为一倾斜线段,并反映α、 β角。 B.水平投影r 和正面投影r’ 都是小于原平面的类似形。
γ
(2)铅垂圆的投影
铅垂直径CD
水平直径AB
长轴:铅垂直(a径) CD铅的垂投面影上圆c’的d投’=影D
(b)
短轴:水平直径AB的投影a’b’=Dcosβ
铅垂圆的投影作图
c’
c”
D D
a’
O' b’
O”
a”
b”
X a
d’
β
c’(d’) Oγ
b
d”
长轴:铅垂直径CD的投影 c’d’=c”d”=D
短轴:水平直径AB的投影 a’b’=Dcosβa”b”=Dcosγ
3
1
2
a
b
yH
可按已知点的两个投影求第三投影的方法作出△abc。
例10 已知一平面ABCD。(1)判别点K是否在平面上;
(2)已知平面上点E的正面投影,求作其水平投影。
b’
f’ a’
k’
g’
c’ e’
X
d’
f bk a
c
dg
e
∵ K点不在直线FC上,∴ K点不在平面上。
1.平面上取直线
直线在平面上的几何条件:
(1) 通过平面上的两已知点。
B
P
M
A
N
C
直线MN在平面上
(2) 通过平面上的一点并平行于平面上的另一 直线。
E
M
D
F
N
P
直线MN在平面P上
结论 -- 要在平面上取直线,应先在平面上的已知 直线上取点,再过点作直线。
例5 在△ABC给定的平面上作一任意直线。
铅垂面--仅⊥H面的平面
铅垂面的迹线表示法
PH有积聚性,它与X轴 的夹角即β;Pv⊥X轴。
V
p
pv
pv
x
β
PH
(b)
X
X
β
PH
H
PH
(c)
(a)
铅垂面P可只用它的水平迹线PH表示。
正垂面--仅⊥V面的平面 Z
q’ Q
q’ γ
p”q”
α
X
O
YW
q’’
p qγ
q YH
A. 正面投影p’积聚为一倾斜线段,并反映α、γ角。 B. 水平投影p和侧面投影p”都是小于原平面的类似形。
二、各种位置平面的投影特性
1. 投影面垂直面 垂直于一个投影面而对另外两个投影 面倾斜的平面。
铅垂面--仅⊥H面的平面 正垂面--仅⊥V面的平面 侧垂面--仅⊥W面的平面
铅垂面--仅⊥H面的平面
Z
p’
p”
X
O
YW
β
pγ
YH
A. 水平投影p积聚为一倾斜线段,并反映β、γ角。 B. 正面投影p’和侧面投影p”都是小于原平面的类似形。
在平面上取点的一般方法:含该点在平面上作 辅助直线,然后在所作直线上取点。
例6 已知点D在△ABC所决定的平面上,求作
其正面投影d’。
A
a’
1’
d’
c’
Ⅰ
b’
D
C
c
B
空间分析
b
d1
a 作法1
D点一定在该平面的一条直线上。
例7 已知点D在△ABC所决定的平面内,求 作其正面投影d’。
a’
A
d’
2’
垂直面上圆的投影特性:
(1)在与圆平面垂直的投影面上,圆的投影是直线 段,长度等于圆的直径。 (2)在与圆平面倾斜的投影面上的投影是椭圆,长 轴是圆平面上平行于这个投影面的直径的投影,短 轴是圆平面上与上述直径相垂直的直径的投影。
三、平面上的点和直线
1.平面上取直线 2.平面上取点 3.平面上的特殊直线 4. 换面法
水平面--// H面的平面
p’
Z p”
X
O
YW
p
YH
A. 水平投影p反映平面P的实形; B. 正面投影p’和侧面投影p”都积聚为直线,
分别∥OX轴和OYW轴。
水平面的迹线表示法
V
Pv
Pv
P
X
x
(b)
H
水平面P可只用(a)它的正面迹线Pv表示。
正平面--// V面的平面
Z
q’ Q
q’
X
O
q’’
q”
侧垂面的迹线表示法
z
V X
RV R
RZ
O RW W x
H
RH
RY Y
RV
RZ
RW
o
RY
yw
W
RYH
RH
YH
侧垂面R可只用它的侧面迹线RW表示 。
投影面垂直面的投影特性:
(1)在所垂直的投影面上的投影积聚为直线, 它与投影轴的夹角反映平面对另外两个投影面的 倾角。 (2)在另外两个投影面上的投影是小于原平面 的类似形。
面的投影积聚为倾斜于投影轴的
直线,长度等于圆的直径。另外
O'
两个投影为椭圆。
X
O
圆平面为正垂面
(3)当圆倾斜于投影面时,它的投影为圆的类似 形-- 椭圆。
圆的投影的作图方法
1)当圆∥投影面时
反映圆的实形
O'
X
O
长度=圆的直径 圆平面为正平面
2)当圆⊥投影面时(1)正垂圆的投影
正垂直径AB
正平直径DE 长轴和短轴
c’
b’
D
c
Ⅱ
C
b
B
2d
空间分析
a 作法2
例8 试完成平面四边形ABCD的水平投影。
c’
分析: 平面ABCD的 b’
k’
对角线一定相交。
d’
a’
X
a
d
b
k
C点一定在该平面的一条直线上。
c
例9 完成侧垂面△ABC的水平投影。
c’
3’
1’
2’
a’ X
c
z c”
3”
b’ O
1”(2”)
a”(b”) yw
例1 含直线AB (ab, a’b’) 作铅垂面 (用平面图形表示)。
分析:铅垂面的水平投影
a’
为斜交于X轴的直线,有积
聚性。
X
本题铅垂面用三角形表示。
a
b’
c’ b
c
2. 投影面平行面
平行于某一投影面的平面。
• // H面的平面--水平面 • // V面的平面--正平面 •// W面的平面– 侧平面
PW X
O
PX
O
PYW
YW
H PH
(a)
PY
Y
PH
(b)
PYH
YH
②迹线是平面上的直线。因此,平面可用它的两 条迹线表示。
Z
PZ
PV
PV
PW
PX
X
PH
平面对一个投影面的投影特性
△ABC倾斜于P面
投影为小于原平面的 类似形
△abc<△ABC
△ABC⊥P面 投影积聚为一直线
abc
△ABC∥P面
投影反映实形 △abc≌△ABC
YW
q
q YH
A. 正面投影q’反映平面P的实形;
B. 水平投影q和侧面投影q”都积聚为直线, 分别∥OX轴和OZ轴。
正平面的迹线表示法
a’
X
QH
a
正平面Q可只用它的水平迹线QH表示。
侧平面--// W面的平面
V r‘ R
r’
W
X r’‘
Z
r”
O
YW
r
r YH
A. 侧面投影r’’反映平面R的实形;
平面的投影可以由其中一组几何元素的投影 来表示。
不
在 同
a’
一
直
线x
上
的
三a
点
a’
平
行
两x
直
线
a
b’ c’
c b
b’ c’
c b
一
直 线
a’
和
直
