钢筋混凝土偏心受力构件承载力计算精品
合集下载
偏心受压构件承载力计算例题

=1375mm2
13
6.验算垂直于弯矩作用平面的承载力
l0/b=2500/300=8.33>8
1
1 0.002 (l0 / b 8)2
1
1 0.002(8.33 8)2
=0.999 Nu =0.9[(As+As′)fy′+Afc]
=0.9×0.999[(1375+1375) ×300+300×500×11.9]
40)
198
为大偏心受压。
4
(4)求As=Asˊ
e
ei
h 2
as
(1.024 59
400 2
40)mm
771mm
x
=90.3mm
>2a
' s
=80mm,
则有
Asˊ=As=
Ne
1
f cbx h0
x 2
f
y
h0
as
260 103
460
0.55
(0.8 0.55)(460 40)
=0.652
12
x h0
=0.652×460=299.9mm
5.求纵筋截面面积As、As′
As=As′=
Ne 1 fcbx(h x / 2)
f
' y
(h0
as'
)
1600 103 342.5 1.0 11.9 300 299.9(500 299.9 / 2) 300 (460 40)
=2346651N>N=1600kN
13
6.验算垂直于弯矩作用平面的承载力
l0/b=2500/300=8.33>8
1
1 0.002 (l0 / b 8)2
1
1 0.002(8.33 8)2
=0.999 Nu =0.9[(As+As′)fy′+Afc]
=0.9×0.999[(1375+1375) ×300+300×500×11.9]
40)
198
为大偏心受压。
4
(4)求As=Asˊ
e
ei
h 2
as
(1.024 59
400 2
40)mm
771mm
x
=90.3mm
>2a
' s
=80mm,
则有
Asˊ=As=
Ne
1
f cbx h0
x 2
f
y
h0
as
260 103
460
0.55
(0.8 0.55)(460 40)
=0.652
12
x h0
=0.652×460=299.9mm
5.求纵筋截面面积As、As′
As=As′=
Ne 1 fcbx(h x / 2)
f
' y
(h0
as'
)
1600 103 342.5 1.0 11.9 300 299.9(500 299.9 / 2) 300 (460 40)
=2346651N>N=1600kN
钢筋混凝土受压构件和受拉构件—偏心受压柱计算
① 当同一主轴方向的杆端弯矩比: M1 0.9
M2
② 轴压比:
N 0.9
fc A
③ 构件的长细比满足要求: l0 34 12( M1 )
i
M2
M1、M2:分别为已考虑侧移影响的偏心受压构件两端截面按结构弹性
分析确定的对同一主轴的组合弯矩设计值,绝对值较大端为M2,绝对值较小 端为 M1;当构件按单曲率弯曲时, M1/M2取正值,否则取负值。
α1fc
α1fcbx x=ξh0
f 'yA's A's
b
h0用平面的受压承载力计算
可能垂直弯矩作用平面先破坏,按非偏心方向的轴心受 压承载力计算
N Nu 0.9 ( fc A f yAs )
2.对称配筋矩形截面小偏压构件的截面设计
对称配筋,即As=As',fy = fy',as = as ' 截面设计:已知:截面尺寸、内力设计值M及N、材料强度等级、构件计算长度,
Ne f y As (h0 as ')
e
ei
h 2
as
e ei
N e’
fyAs As
α1fcbx x
α1fc
f 'yA's A's
b
as
h0
a's
h
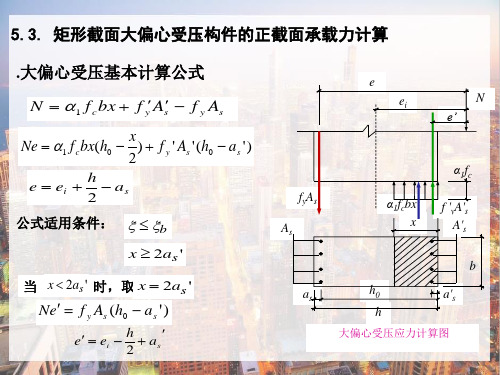
大偏心受压应力计算图
2.对称配筋矩形截面大偏压构件的截面设计
对称配筋,即As=As',fy = fy',as = as ' 截面设计:已知:截面尺寸、内力设计值M及N、材料强度等级、构件计算长度,
5.3. 矩形截面大偏心受压构件的正截面承载力计算
.大偏心受压基本计算公式
N 1 f cbx f y As f y As
偏心受压构件承载力计算例题

【解】fc=11.9N/mm2,fy=
1 =1.0, 1 =0.8
1.求初始偏心距ei
f
= 300N/mm2,
y
b=0.55,
M e0= N
180103 112.5 1600
ea=(20,
h 30
)= max (20, 500
30
)=20mm
ei=e0+ea=112.5+20=132.5mm
3 0 0 (4 6 0 4 0 ) =1375mm2
6.验算垂直于弯矩作用平面的承载力
l0/b=2500/300=8.33>8
1
10.00(l20/b8)2源自10.002(18.338)2
=0.999 Nu =0.9[(As+As′)fy′+Afc]
=0.9×0.999[(1375+1375) ×300+300×500×11.9]
=1235mm2
(5)验算配筋率
As=Asˊ=1235mm2> 0.2%bh=02% ×300×400=240mm2, 故配筋满足要求。
(6)验算垂直弯矩作用平面的承载力
lo/ b=3000/300=10>8
1
10.00(l20/b8)2
10.0021(108)2
=0.992
Nu =0.9φ[fc A + fyˊ(As +Asˊ)] =0.9×0.992[9.6×300×400+300(1235+1235)]
eo=M/N=150×106/260×103=577mm ea=max(20,h/30)= max(20,400/30)=20mm ei=eo+ea = 577+20=597mm
精编第七章 钢筋溷凝土偏心受力构件承载力计算资料

第7章 钢筋混凝土偏心受力构件承载力计算
本章的重点是: 了解偏心受压构件的受力特性,熟悉两种不同的受压
破坏特性及两类受压构件 掌握其判别方法; 熟悉偏心受压构件的二阶效应及计算方法; 掌握偏心受压构件的受力特性及正截面承载力计算方
法; 掌握偏心受压构件斜截面受剪承载力计算方法。
§7.1 概述
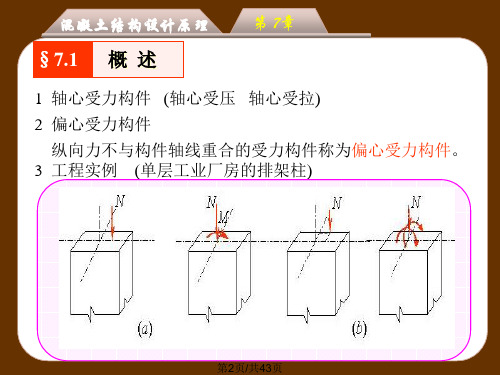
结构构件的截面上受到轴力和弯矩的共同作用或受 到偏心力的作用时,该结构构件称为偏心受压构件。
xn
cu
h0 xnb
cu
h0
3. 矩形截面偏心受压构件不对称配筋计算
(1)构件大小偏心的判别
理论判别式:当
时,为大偏心受压构件;
b
当 b时,为小偏心受压构件。
经验判别式:
当偏心距ηei≤0.3h0 时,按小偏心受压计算;
当偏心距ηei>0.3h0时,先按大偏心受压计算.
1 1 1400 ei
fyAs
f'yA's
◆ 截面受拉侧混凝土较早出现裂缝,As的应力随荷载增加发展
较快,首先达到屈服。
◆ 裂缝迅速开展,受压区高度减小。
◆ 最后受压侧钢筋A's 受压屈服,压区混凝土压碎而达到破坏。
◆ 这种破坏具有明显预兆,变形能力较大,破坏特征与配有受 压钢筋的适筋梁相似,承载力主要取决于受拉侧钢筋。
D3
D2
D1
ÓÐ ²à ÒÆ ¿ò ¼Ü ½á ¹ µÄ ¶þ ½×Ч¦Ó
(1)无侧移钢筋混凝土柱:η-l0法
对于无侧移钢筋混凝土柱在偏心压力作用下将产生挠曲
变形,即侧向挠度 。侧向挠度引起附加弯矩N 。当柱的长
细比较大时,挠曲的影响不容忽视,计算中须考虑侧向挠度 引起的附加弯矩对构件承载力的影响。
本章的重点是: 了解偏心受压构件的受力特性,熟悉两种不同的受压
破坏特性及两类受压构件 掌握其判别方法; 熟悉偏心受压构件的二阶效应及计算方法; 掌握偏心受压构件的受力特性及正截面承载力计算方
法; 掌握偏心受压构件斜截面受剪承载力计算方法。
§7.1 概述
结构构件的截面上受到轴力和弯矩的共同作用或受 到偏心力的作用时,该结构构件称为偏心受压构件。
xn
cu
h0 xnb
cu
h0
3. 矩形截面偏心受压构件不对称配筋计算
(1)构件大小偏心的判别
理论判别式:当
时,为大偏心受压构件;
b
当 b时,为小偏心受压构件。
经验判别式:
当偏心距ηei≤0.3h0 时,按小偏心受压计算;
当偏心距ηei>0.3h0时,先按大偏心受压计算.
1 1 1400 ei
fyAs
f'yA's
◆ 截面受拉侧混凝土较早出现裂缝,As的应力随荷载增加发展
较快,首先达到屈服。
◆ 裂缝迅速开展,受压区高度减小。
◆ 最后受压侧钢筋A's 受压屈服,压区混凝土压碎而达到破坏。
◆ 这种破坏具有明显预兆,变形能力较大,破坏特征与配有受 压钢筋的适筋梁相似,承载力主要取决于受拉侧钢筋。
D3
D2
D1
ÓÐ ²à ÒÆ ¿ò ¼Ü ½á ¹ µÄ ¶þ ½×Ч¦Ó
(1)无侧移钢筋混凝土柱:η-l0法
对于无侧移钢筋混凝土柱在偏心压力作用下将产生挠曲
变形,即侧向挠度 。侧向挠度引起附加弯矩N 。当柱的长
细比较大时,挠曲的影响不容忽视,计算中须考虑侧向挠度 引起的附加弯矩对构件承载力的影响。
《大偏心受拉构件承载力计算》微课课件.

水工混凝土结构
2.大偏拉计算简图
α1f cbh0
f y'A 's
as‘
e'
h0-as'
e0 f yA s e as
N
大偏心受拉构件
水工混凝土结构
3.大偏拉计算公式
KN
' ' f A f bx f ≤ y s c y As
KNe ≤ fcbx(h0 0.5x) f y' As' (h0 as' )
水工混凝土结构
钢筋混凝土柱设计
2014.09
钢筋混凝土柱设计
微课 大偏心受拉构件承载力计算
水工混凝土结构
1.偏心受拉构件的破坏特征
1)大偏心受拉破坏 当轴力处于纵向钢筋之外时发生此种破坏。破坏时距纵向拉力 近的一侧混凝土开裂,混凝土开裂后不会形成贯通整个截面的裂 缝,最后,与大偏心受压情况类似,钢筋屈服,而离轴力较远一 侧的混凝土被压碎 。 2)小偏心受拉破坏 当轴力处于纵向钢筋之间时发生此种破坏。全截面均受拉应 力,但As一侧拉应力较大,As一侧拉应力较小。随着拉力增加, As一侧首先开裂,但裂缝很快贯通整个截面,破坏时混凝 ①截面设计:对称配筋时必有 x 2 s 按不对称配筋 x 2 s 时的情形处理。
②截面校核:类似于不对称配筋。
水工混凝土结构
式中 e—轴向力作用点至受拉钢筋As合力点之间的距离;
e e0 0.5h a
水工混凝土结构
2)适用条件 同大偏心受压构件。 3)不对称配筋计算方法
①截面设计;类似于大偏心受压构件。
②截面校核,一般已知构件尺寸、配筋、材料强度。 若再已知N可求出x和e0或再已知e0则可求出x和N。 4)对称配筋计算方法
钢筋混凝土偏心受力构件承载力计算.pptx
Nu A(N0,0)
B(Nb,Mb)
⑸如截面尺寸和材料强度保持
不变,Nu-Mu相关曲线随配 筋率的增加而向外侧增大。
C(0,M0) Mu
第16页/共43页
混凝土结构设计原理
第 7章
§7.4 偏心受压构件的破坏特征
N M=N e0
e0 N
As
As? = As
As?
压弯构件
偏心受压构
件 偏心距e0=0时,轴心受压构件
…7-2
ei e0 ea
…7-3
第4页/共43页
混凝土结构设计原理
第 7章
3 偏心距增大系数
二阶效应——轴力在结构变形和位移时产生的附加内力。
无侧移
有侧移
第5页/共43页
混凝土结构设计原理
第 7章
y px y f ?sin le
f
ei N
le
xN ei
◆ 由于侧向挠曲变形,轴向力将 N ei 产生二阶效应,引起附加弯矩。
h / 2)
f
' y
As
(h0'
as )
…7-23
As
Ne'
1 fcbh(h0 0.5h)
f
' y
(h0'
as
)
式中:
e' h / 2 as' ei
ei e0 ea
此时不考虑,ei中扣除ea。
…7-24
第29页/共43页
混凝土结构设计原理
第 7章
❖矩形截面 对称 配筋偏心受压构件正截面承载力
N
◆在未达到截面承载力极限状态 之前,侧向挠度 f 已呈不稳定
N0
发展 即柱的轴向荷载最大值发生在
钢筋砼偏心受力构件承载力计算

Nu(kN)
1000 800 600 400 200
0
受压破坏
B
A
界限破坏
受拉破坏
10 20 30 40
利用M-N相关曲线寻找最不利内力:
• 作用在结构上的荷载往往有很多种,在结构设 计时应进行荷载组合;
• 在受压构件同一截面上可能会产生多组M、N 内力他们当中存在一组对该截面起控制作用;
• 这一组内力不容易凭直观多组M、N中挑选出 来,但利用N-M相关曲线的规律,可比较容易 地找到最不利内力组合
As先屈服,然后受压混凝土达到c,max,
As f y。
受拉破坏 (大偏心受
压破坏)
N
cmax1
cmax2
cu
ei N
ei N
sAs
f yAs
sAs
f yAs
(a) N
(b)
(c)
N的偏心较小一些或N的e0大,
然而As较多。 截面大部分受压
受
而少部分受拉,荷载增大沿构 件受拉边一定间隔将出现垂直
ei+ f = ei(1+ f / ei) = ei
=1 +f / ei
…7-6
––– 偏心距增大系数
ei N
af ei
f
N
图7-9
l
2 0
10
1
f
cu y
h0
规范采用了的界限状态为 依据,然后再加以修正
1 1
1 4 0 0 ei
(
l0 h
)2
1
2
h0
…7-7
式中: ei = e0+ ea
短柱 中长柱 细长柱
––– 材料破坏 ––– 失稳破坏
7.偏心受压构件的截面承载力计算20191120精品文档

梁。
s As
f y'As'
◆受压破坏特征:破坏是由于混凝土被压碎而引起的,破坏时
靠近纵向力一侧钢筋达到屈服强度,远侧钢筋可能受拉也可
能受压,受拉时未屈服,受压时可能屈服也可能未屈服。
◆ 承载力主要取决于压区混凝土和受压侧钢筋,破坏具有脆性 性质。
ÊÜ À Æ »µ ÊÜ Ñ¹ Æ »µ
偏心受压构件的破坏形态展开图
ns11219ei /7h0×(lhc)2近似取 ns11310ei /0h0×(lhc)2
ei e0ea M N2 ea
n
s1130(M N 021ea)/h0
×(lc)2 h
对于“受压破坏”的小偏心受压构件上式显然不适用
在计算破坏曲率时,需引进一个修正系数c,对截面曲率进行修
P—Δ效应
最大一阶和二阶弯矩在柱端且符号相同。 当二阶弯矩不可忽略时,应考虑结构侧移的影响。
N F
N
M0max Mmax
Mmax =Mmax +M0max
7.2.2 矩形截面偏心受压构 件承载力计算公式
一、 区分大小偏心受压破坏的 界限破坏
≤b属于大偏心破坏形态 > b属于小偏心破坏形态
N ( ei+ f )
图示典型偏心受压柱,跨中侧
向挠度为f。因此,对跨中截面, 轴力N的偏心距为ei + f ,即跨 中截面的弯矩为M =N ( ei + f )。
xN ei
(一) P-δ效应
y y f × sin px
le f
ei N
le
在截面和初始偏心距相同的情
N ei
况下,柱的长细比l0/h不同,侧
7.2偏心受压构件正截面承载力计算
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
规范规定,采用把初始偏心距乘以一个偏心距 增大系数η的方法解决纵向弯曲的影响问题,即:
ei
f
f (1 ei )ei
ei
根据偏心受压构件试验挠曲线的实验结果和理
论分析,规范给出了偏心距增大系数的如下计算公
式:
1 1 1400 ei
(
l0 h
)
2
1
2
h0
式中ξ1和ξ2
ξ1=0.5fcA/N
ξ1=0.2+2.7ei/h0 当计算的ξ1>1时,取ξ1=1 当l0/h>15时,ξ2=1.15-0.01l0/h 当l0/h≤15时,取ξ2=1。
对称配筋时,As′=As,fy′=fy,并要求配筋率ρ和 ρ′同时大于0.2%
As=As′≥0.002bh 由式(6.6)
x=N/(α1fcb) 如果2as′≤x≤ξbh0,则由式(6.7)
如果2as′≤x≤ξbh0,则由式(6.7)
As
As
Ne
1 febx(h0
f y (h0 as )
x) 2
b
1
1
fy
Es cu
大、小偏心的判别式为:
当ξ≤ξb时,或x≤ξbh0 当ξ>ξb时,或x>ξbh0时为小偏心受压。
6.1.2 偏心距增大系数η
6.1.2.1 附加偏心距ea
规范规定附加偏心距ea:取20mm和偏心方向截 面最大尺寸的1/30
ei=e0+ea
6.1.2.2 偏心距增大系数η
钢筋混凝土偏心受压构件,在承受偏心压力后, 会产生纵向弯曲变形,然后纵向力又将加剧纵向弯 曲变形,这种现象随柱的长细比和初始偏心距的增 大而增大,见图6.4。
ea=20mm(>h/30=350mm/30=11.7mm)
ei=e0+ea=(574+20)mm=594mm l0/h=11.4>5
ξ1=0.5fcA/N=1.82>1.0,取ξ1=1.0 l0/h=11.4<15,取ξ2=1.0 η=1.049
Hale Waihona Puke (3) 求As及As′。 e=ηei+h/2-as=763.1mm As=As′=1358mm2
小偏心受压破坏无明显预兆,混凝土强度越高, 破坏越突然。图6.3为小偏心受压破坏形态。
大、小偏心受压之间的根本区别是:截面破坏 时受拉钢筋是否屈服。
图6.3 小偏心受压破坏形态
6.1.1.3 大、小偏心的界限
大、小偏心受压破坏之间存在一种极限状态, 称为“界限破坏”。
根据界限破坏特征和平截面假定,不难推算出 界限破坏时截面相对受压区高度公式为:
如果x<2as′,则由式(6.11)可得:
As
As
Ne f y (h0 as )
【例6.1】已知设计荷载作用下的轴向压力设计值 N=230kN,弯矩设计值M=132kN·m(沿长边作用),柱截 面尺寸b=250mm,h=350mm,as=as′=35mm,柱计算高度 l0=4m,混凝土强度等级为C20,钢筋采用HRB335级钢筋。
这种破坏始于受拉钢筋先达到屈服强度,最后 由混凝土(受压区)被压碎而引起的。图6.2为大偏 心受压破坏。
图6.2 大偏心受压破坏形态
6.1.1.2 小偏心受压破坏
当偏心距较小,或者虽然偏心距较大但受拉纵 向钢筋配置得太多时,构件的破坏始于靠近纵向力 一侧。在破坏时,靠近纵向力一侧的钢筋首先屈服, 该侧混凝土也达到极限压应变;而另一侧的钢筋和 混凝土应力均较小,且可能受拉,也可能受压。这 种破坏称为小偏心受压破坏。
工程中的排架柱、多高层房屋的柱等都是偏心 受压构件;矩形截面水池的池壁等则属于偏心受拉 构件。
规范规定:偏心受力构件应进行正截面承载力 计算;当同时作用有剪力V时还应进行斜截面承载力 计算。
图6.1 偏心受力构件的受力状态类型
本章内容
6.1 偏心受压构件承载力计算 6.2 偏心受压构件的构造要求
6.1 偏心受压构件承载力计算
6.1.1 试验研究分析
偏心受压构件的正截面受力性能可视为轴心受 压构件(M=0)和受弯构件(N=0
试验结果表明:截面的平均应变符合平截面假 定;构件的最终破坏是由于受压区混凝土被压碎所 造成的。由于引起混凝土被压碎的原因不同,偏心 受压构件的破坏形态可分为两类。
6.1.1.1 大偏心受压破坏
当偏心距较大且受拉区钢筋配置得不太多时, 在荷载作用下,柱截面靠近纵向力一侧受压,另一 侧受拉。随着荷载的增加,首先在受拉边产生横向 裂缝。随着荷载不断增加,受拉区的裂缝不断发展 和加宽,受拉区的纵向钢筋首先屈服,裂缝开展比 较明显,受压区不断减小,受压边缘混凝土达到极 限压应变εcu而被压碎,构件宣告破坏。
当轴向力N偏离截面形心或构件同时承受轴向力 和弯矩时,则成为偏心受力构件。轴向力为压力时 称为偏心受压构件;轴向力为拉力时称为偏心受拉 构件(图6.1)。
偏心受力构件又分为单向偏心和双向偏心两类: 当轴向力的作用线仅与构件截面的一个方向的形心 线不重合时,称为单向偏心(图6.1 (a)、(b)、(d)、 (e));两个方向都不重合时,称为双向偏心(图6.1 (c)、(f)
图6.4 纵向弯曲变形
6.1.3 矩形截面对称配筋大偏心受压时的 基本公式和适用条件、设计实例
6.1.3.1 大偏心受压时的基本公式和适用条件
当ξ≤ξb时为大偏心受压,其正截面承载力计算的 基本假定与受弯构件相同,计算应力图形如图6.5所示。
∑Y=0 N≤α1fcbx+fy′As′-fyAs ∑M=0 Ne≤α1fcbx(h0-x/2)+fy′As′(h0-as′)
【解】已知fc=9.6N/mm2,fy=fy′=300N/mm2, α1=1.0, ξb=0.55, h0=(350-35) mm=315mm。
(1) 求x。 x=N/(α1fcb)= 95.8mm<ξbh0=173.3mm 且>2as′=2×35mm=70mm
(2) 求ei及η。 e0=M/N=574mm
ξ≤ξb 或 x≤ξbh0
与双筋受弯构件相似,为保证截面破坏时受压钢
x≥2as′ 当x<2as′时,可偏安全地取η=h0-as′,并对受压钢
Ne′≤fyAs(h0-as′)
图6.5 大偏心受压构件的截面计算
6.1.3.2 对称配筋时的计算方法
偏心受压构件的配筋有两种情况:非对称配筋 和对称配筋。所谓非对称配筋即As′≠As,而对称配筋 为As′=As,钢筋种类亦对称。
ei
f
f (1 ei )ei
ei
根据偏心受压构件试验挠曲线的实验结果和理
论分析,规范给出了偏心距增大系数的如下计算公
式:
1 1 1400 ei
(
l0 h
)
2
1
2
h0
式中ξ1和ξ2
ξ1=0.5fcA/N
ξ1=0.2+2.7ei/h0 当计算的ξ1>1时,取ξ1=1 当l0/h>15时,ξ2=1.15-0.01l0/h 当l0/h≤15时,取ξ2=1。
对称配筋时,As′=As,fy′=fy,并要求配筋率ρ和 ρ′同时大于0.2%
As=As′≥0.002bh 由式(6.6)
x=N/(α1fcb) 如果2as′≤x≤ξbh0,则由式(6.7)
如果2as′≤x≤ξbh0,则由式(6.7)
As
As
Ne
1 febx(h0
f y (h0 as )
x) 2
b
1
1
fy
Es cu
大、小偏心的判别式为:
当ξ≤ξb时,或x≤ξbh0 当ξ>ξb时,或x>ξbh0时为小偏心受压。
6.1.2 偏心距增大系数η
6.1.2.1 附加偏心距ea
规范规定附加偏心距ea:取20mm和偏心方向截 面最大尺寸的1/30
ei=e0+ea
6.1.2.2 偏心距增大系数η
钢筋混凝土偏心受压构件,在承受偏心压力后, 会产生纵向弯曲变形,然后纵向力又将加剧纵向弯 曲变形,这种现象随柱的长细比和初始偏心距的增 大而增大,见图6.4。
ea=20mm(>h/30=350mm/30=11.7mm)
ei=e0+ea=(574+20)mm=594mm l0/h=11.4>5
ξ1=0.5fcA/N=1.82>1.0,取ξ1=1.0 l0/h=11.4<15,取ξ2=1.0 η=1.049
Hale Waihona Puke (3) 求As及As′。 e=ηei+h/2-as=763.1mm As=As′=1358mm2
小偏心受压破坏无明显预兆,混凝土强度越高, 破坏越突然。图6.3为小偏心受压破坏形态。
大、小偏心受压之间的根本区别是:截面破坏 时受拉钢筋是否屈服。
图6.3 小偏心受压破坏形态
6.1.1.3 大、小偏心的界限
大、小偏心受压破坏之间存在一种极限状态, 称为“界限破坏”。
根据界限破坏特征和平截面假定,不难推算出 界限破坏时截面相对受压区高度公式为:
如果x<2as′,则由式(6.11)可得:
As
As
Ne f y (h0 as )
【例6.1】已知设计荷载作用下的轴向压力设计值 N=230kN,弯矩设计值M=132kN·m(沿长边作用),柱截 面尺寸b=250mm,h=350mm,as=as′=35mm,柱计算高度 l0=4m,混凝土强度等级为C20,钢筋采用HRB335级钢筋。
这种破坏始于受拉钢筋先达到屈服强度,最后 由混凝土(受压区)被压碎而引起的。图6.2为大偏 心受压破坏。
图6.2 大偏心受压破坏形态
6.1.1.2 小偏心受压破坏
当偏心距较小,或者虽然偏心距较大但受拉纵 向钢筋配置得太多时,构件的破坏始于靠近纵向力 一侧。在破坏时,靠近纵向力一侧的钢筋首先屈服, 该侧混凝土也达到极限压应变;而另一侧的钢筋和 混凝土应力均较小,且可能受拉,也可能受压。这 种破坏称为小偏心受压破坏。
工程中的排架柱、多高层房屋的柱等都是偏心 受压构件;矩形截面水池的池壁等则属于偏心受拉 构件。
规范规定:偏心受力构件应进行正截面承载力 计算;当同时作用有剪力V时还应进行斜截面承载力 计算。
图6.1 偏心受力构件的受力状态类型
本章内容
6.1 偏心受压构件承载力计算 6.2 偏心受压构件的构造要求
6.1 偏心受压构件承载力计算
6.1.1 试验研究分析
偏心受压构件的正截面受力性能可视为轴心受 压构件(M=0)和受弯构件(N=0
试验结果表明:截面的平均应变符合平截面假 定;构件的最终破坏是由于受压区混凝土被压碎所 造成的。由于引起混凝土被压碎的原因不同,偏心 受压构件的破坏形态可分为两类。
6.1.1.1 大偏心受压破坏
当偏心距较大且受拉区钢筋配置得不太多时, 在荷载作用下,柱截面靠近纵向力一侧受压,另一 侧受拉。随着荷载的增加,首先在受拉边产生横向 裂缝。随着荷载不断增加,受拉区的裂缝不断发展 和加宽,受拉区的纵向钢筋首先屈服,裂缝开展比 较明显,受压区不断减小,受压边缘混凝土达到极 限压应变εcu而被压碎,构件宣告破坏。
当轴向力N偏离截面形心或构件同时承受轴向力 和弯矩时,则成为偏心受力构件。轴向力为压力时 称为偏心受压构件;轴向力为拉力时称为偏心受拉 构件(图6.1)。
偏心受力构件又分为单向偏心和双向偏心两类: 当轴向力的作用线仅与构件截面的一个方向的形心 线不重合时,称为单向偏心(图6.1 (a)、(b)、(d)、 (e));两个方向都不重合时,称为双向偏心(图6.1 (c)、(f)
图6.4 纵向弯曲变形
6.1.3 矩形截面对称配筋大偏心受压时的 基本公式和适用条件、设计实例
6.1.3.1 大偏心受压时的基本公式和适用条件
当ξ≤ξb时为大偏心受压,其正截面承载力计算的 基本假定与受弯构件相同,计算应力图形如图6.5所示。
∑Y=0 N≤α1fcbx+fy′As′-fyAs ∑M=0 Ne≤α1fcbx(h0-x/2)+fy′As′(h0-as′)
【解】已知fc=9.6N/mm2,fy=fy′=300N/mm2, α1=1.0, ξb=0.55, h0=(350-35) mm=315mm。
(1) 求x。 x=N/(α1fcb)= 95.8mm<ξbh0=173.3mm 且>2as′=2×35mm=70mm
(2) 求ei及η。 e0=M/N=574mm
ξ≤ξb 或 x≤ξbh0
与双筋受弯构件相似,为保证截面破坏时受压钢
x≥2as′ 当x<2as′时,可偏安全地取η=h0-as′,并对受压钢
Ne′≤fyAs(h0-as′)
图6.5 大偏心受压构件的截面计算
6.1.3.2 对称配筋时的计算方法
偏心受压构件的配筋有两种情况:非对称配筋 和对称配筋。所谓非对称配筋即As′≠As,而对称配筋 为As′=As,钢筋种类亦对称。
