受扭构件的截面承载力计算
受扭构件截面抵抗矩计算

Asv ft ρ sv = ≥ ρ sv ,min = 0.28 bs f yv
抗扭纵筋最小配筋率为
ρ stl ,min =
Astl ,min bh
T ft = 0.6 Vb f y
(3)简化计算的条件 ) 1)不进行抗剪计算的条件: )不进行抗剪计算的条件 ①一般构件
V ≤ 0.35 f t bh0
2)T形或工字形截面 ) 形或工字形截面 对于T形或工字形截面构件,《规范》将其划分为若 干个矩形截面,然后按矩形截面分别进行配筋计算。矩 形截面划分的原则是首先保证腹板截面的完整性,然后 再划分受压和受拉翼缘,如图所示。划分的矩形截面所 承担的扭矩,按其受扭抵抗矩与截面总受扭抵抗矩的比 值进行分配。 对腹板、受压和受拉翼缘部分的矩形截面抗扭塑性 抵抗矩Wtw、Wtf′和Wtf分别按下列公式计算
(3)矩形截面纯扭构件的抗裂扭矩 ) 混凝土材料既非完全弹性,也不是理想弹塑性,而 是介于两者之间的弹塑性材料。 矩形截面纯扭构件的抗裂扭矩Tcr按下式计算
Tcr = 0.7 f tWt
式中 0.7——考虑到混凝土非完全塑性材料的强度降低 系数; f t——混凝土抗拉强度设计值; Wt——截面抗扭抵抗矩,按下式计算
(2)截面尺寸限制及最小配筋率 ) 1)截面尺寸限制条件 ) 为了避免超筋破坏,构件截面尺寸应满足下式要求
V T + ≤ 0.25βc f c bh0 Wt
2)构造配筋问题 ) ①构造配筋的界限:当满足下式要求时,箍筋和抗扭 纵筋可采用构造配筋。
V T + ≤ 0 .7 f t bh 0 W t
②最小配筋率:配箍率必须满足以下最小配箍率要求
0.875 V ≤ f t bh0 λ +1
受扭构件承载力计算

(1)腹板
(6-8)
(2)受压翼缘
(6-9)
(3)受拉翼缘
(6-10)
上一页 下一页 返回
第一节纯扭构件承载力计算
四、箱形截面纯扭构件承载力计算
箱形截面纯扭构件承载力按下式计算:
(6-11) (6-12)
(6-13)
上一页 返回
第二节弯剪扭构件承载力计算
一、弯剪扭构件截面限制条件 (1)在弯矩、剪力和扭矩共同作用下,对hw/b毛6的矩形、T形、I形截面和 hw/tw ≤ 6的箱形截面构件(图6-2 ),其截面应符合下列条件: (6-14) (6-15)
试验表明,对于钢筋混凝土矩形截面受扭构件,其破坏形态与配置 钢筋的数量多少有关,可以分为三类: (1)少筋破坏。 (2)适筋破坏。 (3)超筋破坏。
上一页 下一页 返回
第一节纯扭构件承载力计算
二、矩形截面纯扭构件承载力计算
矩形截面纯扭构件承载力按下式计算:
(6-2) (6-3)
三、T形和I形截面纯扭构件承载力计算
(3)在轴向压力、弯矩、剪力和扭矩共同作用下的钢筋混凝土矩形截面框架 柱,其纵向钢筋截面面积应分别按偏心受压构件的正截面受压承载力和 剪扭构件的受扭承载力计算确定,并应配置在相应的位置;箍筋截面面积 应分别按剪扭构件的受剪承载力和受扭承载力计算确定,并应配置在相 应的位置。
上一页 下一页 返回
第二节弯剪扭构件承载力计算
上一页 返回
图6-1工程中常见的受扭构件
返回
图6-2受扭构件截面
返回
图6-2受扭构件截面
返回
表6-2受扭构件纵筋的构浩要求
返回
(6-4) (6-5) (6-6)
上一页 下一页 返回
第一节纯扭构件承载力计算
钢筋混凝土受扭构件承载力计算_习题讲解

第六章 钢筋混凝土受扭构件承载力计算_习题讲解1、钢筋混凝土矩形截面构件,截面尺寸mm h b 450250⨯=⨯扭矩设莡值m kN T ⋅=10,旷凝土强嚦等皧为C30(2/3.14mm N f c =,),纵向钢筋和箍筋均采用HPB235级钢筋(2/210mm N f f y yv ==),试计算其配筋。
(类似习题6-1)解:(1)验算构件截面尺寸26221046.11)2504503(6250)3(61mm b h b W t ⨯=-⨯⨯=-= (6-5)c c t f mm N W T β25.0/87.01046.111010266<=⨯⨯= 2/58.33.140.125.0mm N =⨯⨯=满足c c t f W T β25.0<是规范对构件截面尺寸的限定性要求,本题满足这一要求。
(2)抗扭钢筋计算t t f mm N W T 7.0/87.01046.111010266<=⨯⨯= 按构造配筋即可。
2.已知矩形截面梁,截面尺寸300×400mm ,混凝土强度等级2/6.9(20mm N f C c =,2/1.1mm N f t =),箍筋HPB235(2/210mm N f yv =),纵筋HRB335(2/300mm N f y =)。
经计算,梁弯矩设计值,剪力设计值kN V 16=,扭矩设计值m kN T ⋅=8.3,试确定梁的配筋。
(类似习题6-2) 解:(1)按h w /b ≤4情况,验算梁截面尺寸是否符合要求 252210135)3004003(6300)3(mm b h b W t ⨯=-⨯=-=截面尺寸满足要求。
(2)受弯承载力%2.0%165.03001.14545min 〈=⨯==y t f f ρ;取0.2%A s =ρmin ×bh=0.2%×300×400=240mm 2(3)验算是否直接按构造配筋由公式(6-36)01600038000000.4280.70.7 1.10.7730036513500000t t V T f bh W +=+=<=⨯=⨯ 直接按构造配筋。
第八部分受扭构件的截面承载力计算

Ast1 ucor fyv
试验表明,当0.5≤z ≤2.0范围时,受扭破坏时纵筋和箍筋基本
上都能达到屈服强度。但由于配筋量的差别,屈服的次序是有 先后的。
《规范》建议取0.6≤z ≤1.7,设计中通常取z =1.0~1.3。
三、破坏形式
按照配筋率的不同,受扭构件的破坏形态也可分为适筋破坏、 少筋破坏、部分超筋破坏和超筋破坏。
受弯纵筋As和A's
抗扭纵筋:Astl z
Ast1 s
fyv fy
ucor
A's
Astl /3
抗扭箍筋: A st 1 s
抗剪箍筋: nA sv 1 s
A's + Astl /3
+
As 4 Asv1 s
+
=
Astl /3
Astl /3 Ast1 s
=
Astl /3
As+ Astl /3 2 Asv1 s
无腹筋
有腹筋
8.4.2 《规范》弯剪扭构件的配筋计算 由于在弯矩、剪力和扭矩的共同作用下,各项承载力是相互
关联的,其相互影响十分复杂。为了简化,《规范》偏于安全 地将受弯所需的纵筋与受扭所需纵筋分别计算后进行叠加,而 对剪扭作用为避免混凝土部分的抗力被重复利用,考虑混凝土 项的相关作用,箍筋的贡献则采用简单叠加方法。
对于在轴向压力、弯矩、剪力和扭矩共同作用下的钢筋混凝 土矩形截面框架柱,其配筋计算方法与弯剪扭构件相同,即 ◆ 按轴压力和弯矩进行正截面承载力计算确定纵筋As和A's; ◆ 按剪扭承载力按下式计算确定配筋,然后再将钢筋叠加。
V uv(1 .7 1ft5 b0 h 0 .0N ) 7 1 .0 fyn vs s1 v A h 0
七章钢筋混凝土受扭构件承载力计算
翼缘 —— 纯扭;
腹板—— 剪扭;
全截面——弯剪扭分别配筋再叠加。
(五)箱形截面剪扭构件承载力计算
1、一般剪扭构件 抗扭承载力下式计算:
T 0.35ht ftWt 1.2
f yv
Ast1 Acor s
2、集中力作用下的独立剪扭构件
(7-14)
(六)箱形截面弯剪扭构件承载力计算
(3)按照叠加原则计算剪扭的箍筋用量和纵筋用量。
(二)矩形截面弯扭构件承载力计算
图7-11 弯扭构件的钢筋叠加
(三)矩形截面弯剪扭构件承载力计算
﹡《规范》规定,其纵筋截面面积由受弯承载力和受扭 承载力所需的钢筋截面面积相叠加,箍筋截面面积则由 受剪承载力和受扭承载力所需的箍筋截面面积相叠加, 其具体计算方法如下:
(3)当箍筋或纵筋过多时,为部分超配筋破坏。
(4)当箍筋和纵筋过多时,为完全超配筋破坏。
因此,在实际工程中,尽量把构件设计成(2)、(3), 避免出现(1)、(4)。
(二)抗扭钢筋配筋率对受扭构件受力性能的影响
《规范》采用纵向钢筋与箍筋的配筋强度比值 进行控制, (0.6≤ ≤1.7)
f y Astl s
﹡像矩形、T形和I形截面一样,箱形截面弯剪扭 构件承载力计算中,弯矩按纯弯构件计算剪力和 扭矩按剪扭构件计算。
三、受扭构件计算公式的适用条件及构造要求
(一)截面尺寸限制条件
当 hw b 4
时,
V bh0
T 0.8Wt
0.25c
fc
(7-15)
当
hw
b6
时,
V bh0
T 0.8Wt
0.2c
fc
——混凝土抗拉强度设计值;
第8章-受扭构件承载力的计算-自学笔记汇总
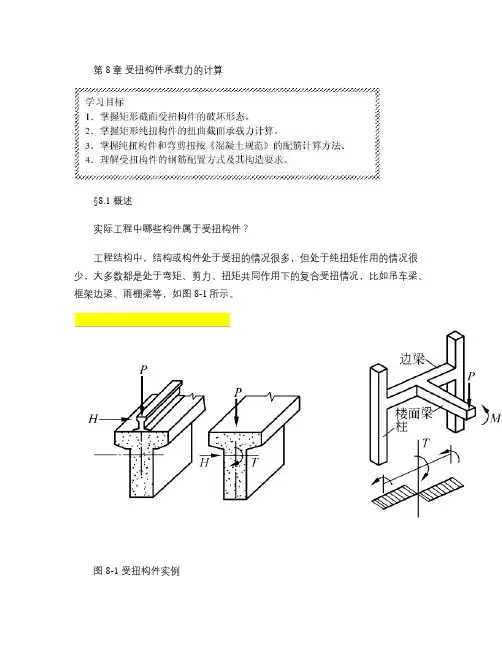
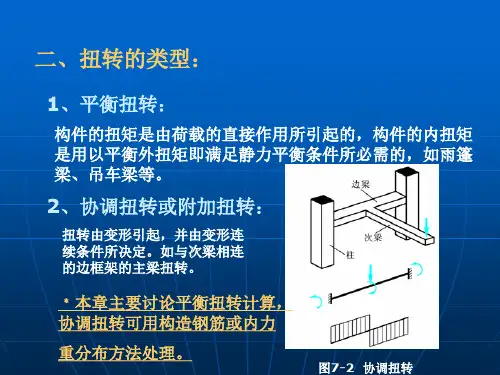
第8章受扭构件承载力的计算§8.1 概述实际工程中哪些构件属于受扭构件?工程结构中,结构或构件处于受扭的情况很多,但处于纯扭矩作用的情况很少,大多数都是处于弯矩、剪力、扭矩共同作用下的复合受扭情况,比如吊车梁、框架边梁、雨棚梁等,如图8-1所示。
图8-1 受扭构件实例受扭的两种情况:平衡扭转和协调扭转。
静定的受扭构件,由荷载产生的扭矩是由构件的静力平衡条件确定的,与受扭构件的扭转刚度无关,此时称为平衡扭转。
如图8-1(a )所示的吊车梁,在竖向轮压和吊车横向刹车力的共同作用下,对吊车梁截面产生扭矩T 的情形即为平衡扭转问题。
对于超静定结构体系,构件上产生的扭矩除了静力平衡条件以外,还必须由相邻构件的变形协调条件才能确定,此时称为协调扭转。
如图8-1(b )所示的框架楼面梁体系,框架的边梁和楼面梁的刚度比对边梁的扭转影响显著,当边梁刚度较大时,对楼面梁的约束就大,则楼面梁的支座弯矩就大,此支座弯矩作用在边梁上即是其承受的扭矩,该扭矩由楼面梁支承点处的转角与该处框架边梁扭转角的变形协调条件所决定,所以这种受扭情况为协调扭转。
§8.2 纯扭构件的试验研究8.2.1 破坏形态钢筋混凝土纯扭构件的最终破坏形态为:三面螺旋形受拉裂缝和一面(截面长边)的斜压破坏面,如图8-3所示。
试验研究表明,钢筋混凝土构件截面的极限扭矩比相应的素混凝土构件增大很多,但开裂扭矩增大不多。
图8-2 未开裂混凝土构件受扭图8-3 开裂混凝土构件的受力状态 8.2.2 纵筋和箍筋配置对纯扭构件破坏性态的影响受扭构件的四种破坏形态受扭构件的破坏形态与受扭纵筋和受扭箍筋配筋率的大小有关,大致可分为适筋破坏、部分超筋破坏、完全超筋破坏和少筋破坏四类。
对于正常配筋条件下的钢筋混凝土构件,在扭矩作用下,纵筋和箍筋先到达屈服强度,然后混凝土被压碎而破坏。
这种破坏与受弯构件适筋梁类似,属延性破坏。
此类受扭构件称为适筋受扭构件。
受扭构件截面抵抗矩计算ppt课件
(2)截面破坏的几种形态
1)少筋破坏
当纵筋和箍筋中只要有一种配置不足时便会出 现此种破坏。斜裂缝一旦出现,其中配置不足的钢筋便 会因混凝土卸载很快屈服,使构件突然破坏。破坏属于 脆性破坏,类似于粱正截面承载能力时的少筋破坏。设 计中通过规定抗扭纵筋和箍筋的最小配筋率来防止少筋 破坏;
2)适筋破坏
如前所述,当构件纵筋和箍筋都配置适中时出现此种 破坏。从斜裂缝出现到构件破坏要经历较长的阶段,有较 明显的破坏预兆,因而破坏具有一定的延性。
V
0.875
1
f t bh0
2)不进行抗扭计算的条件:
T 0.175 ftWt
(4)截面设计的主要步骤
① 验算截面尺寸; ② 验算构造配筋条件; ③ 确定计算方法,即是否可简化计算;
④ 根据M值计算受弯纵筋; ⑤ 根据V和T计算箍筋和抗扭纵筋;
⑥ 验算最小配筋率并使各种配筋符合《规范》构造要求。
(3)矩形截面纯扭构件的抗裂扭矩 混凝土材料既非完全弹性,也不是理想弹塑性,
而是介于两者之间的弹塑性材料。
矩形截面纯扭构件的抗裂扭矩Tcr按下式计算
Tcr 0.7 ftWt
式中 0.7——考虑到混凝土非完全塑性材料的强度
降低
系数;
f t——混凝土抗拉强度设计值; Wt——截面抗扭抵抗矩,按下式计算
3)剪扭型破坏
当剪力和扭矩都较大时,由于剪力与扭矩所产生的 剪应力的相互迭加,首先在其中一个侧面出现裂缝,然 后向顶面和底面扩展,使该侧面、顶面和底面形成扭曲 破坏面,与之相交的纵筋与箍筋都达到其抗拉屈服强度, 最后使另一侧面被压碎而破坏。
T Tu 0.35t ftWt 1.2
f yv
修--受扭构件承载力计算(有打印)
受扭构件承载力计算一、(纯扭) 某矩形截面纯扭构件,承受扭矩设计值为m KN T .18=,截面尺寸mm 500250⨯,C25混凝土,箍筋为HRB335级钢筋,纵筋为HRB400级钢筋。
混凝土净保护层厚度为c=30mm 。
环境类别为二类,试计算截面的配筋数量。
(注:2/9.11mm N f c =,2/27.1mm N f t =,2/360mm N f y =,2/300mm N f yv =)解题思路:本题属矩形截面纯扭构件的计算,先验算截面尺寸,再验算是否需要按计算配置受扭筋;若不需按计算配置抗扭钢筋,则按构造要求配筋;若需要按计算配置抗扭钢筋,可先假定ς值,然后按矩形截面钢筋混凝土纯扭构件的抗扭承载力计算公式即可求得,按步骤进行计算。
【解】2/9.11mm N f c =,2/27.1mm N f t =,2/360mm N f y =,2/300mm N f yv =,混凝土保护层为mm 301、验算截面尺寸是否满足要求362210021.13)2505003(6250)3(6mm b h b W t ⨯=-⨯⨯=-= 975.29.110.125.025.0728.110021.138.010188.066=⨯⨯==⨯⨯⨯=c c t f W T β 故截面尺寸满足要求2、验算是否按计算配置抗扭钢筋m KN T m KNN W f t t .18.58.1110021.1327.17.07.06==⨯⨯⨯=故需按计算配置受扭钢筋3、抗扭箍筋的计算mm b cor 190230250=⨯-=,mm h cor 440230500=⨯-=(1)假定1.1=ζ(2)由t t W f T 35.0≤+s f A A yv st cor 12.1ζ得387.04401903001.12.110021.1327.135.010182.135.0661=⨯⨯⨯⨯⨯⨯-⨯=-=cor yv t t st A f W f T s A ς(3)箍筋直径及间距的确定选用8Φ箍筋(213.50mm A sv =),双肢箍,2=n则mm A s st 130387.03.50387.01=== 取mm s 120=<mm s 200max = (满足构造要求)即所配箍筋为120@8Φ(4)验算抗扭箍的配筋率%12.030027.128.028.0%34.01202503.5022min ,1===≥=⨯⨯==yv t sv st sv f f bs A ρρ 满足要求4、抗扭纵筋的计算(1)按cor st yv stl y st yv corstly A f s A f s A f A f μμζ11/==得 214841203.503604401903001.1mm s A f u f A st y cor yv stl =⋅⨯⨯⨯=⋅=ς (2)验算抗扭纵筋配筋率%30.036027.185.085.0%387.0500250484min ,=⨯==≥=⨯==y t tl stl tl f f bh A ρρ 满足要求(3)选筋:选用(2678mm A s =)弯、剪、扭构件计算三、 某雨篷梁,承受弯矩、剪力、扭矩设计值为m KN M .25=, KN V 40=,m KN T .6=,截面尺寸mm 240240⨯,C25混凝土,箍筋为HRB335级钢筋,纵筋为HRB400级钢筋。
第五章-受扭构件承载力计算
第五章 受扭构件承载力计算
基础 知识
➢ 材料特性 ➢ 设计方法
构件 设计
学习内容
➢ 受弯构件 ➢ 受剪构件 ➢ 受扭构件 ➢ 偏压、偏拉构件 ➢轴拉构件 ➢轴压构件 ➢变形、裂缝 ➢预应力混凝土结构
结构设计, 后续课程
➢ 桥梁工程
弯梁桥的截面上除有弯矩M剪力V外,还存在扭矩T。由
开裂后的箱形截面受扭构件的受力可比拟成空间桁架:
纵筋为受拉弦杆, 箍筋为受拉腹杆, 斜裂缝间的混凝土为受压腹杆。
裂缝 箍筋
纵筋
T T
F4+F4=Ast4st
F1+F1=Ast1st
s F3+F3=Ast3st
F2+F2=Ast2st
箱形截面的剪应力分布,可采用薄壁管理论
T
rqds
2q
1 2
rds
纵筋的拉力
对隔离体ABCD
F1 F2 qhcorctg
相应其它三个面的隔离体
F1' F4 ' qbcorctg F4 F3 qhcorctg F3' F2 ' qbcorctg
裂缝 箍筋
纵筋
T T
F4+F4=Ast4fy
C
D
F1+F1=Ast1fy
B
F3+F3=Ast3fy
As
F2+F2=Ast2fy
纯扭构件在工程中几乎是没有的。工程中构件往往要同时 承受轴力、弯矩、剪力和扭矩。对于钢筋混凝土弯扭构件, 轴力对配筋的影响很小,可以忽略不计。为简化计算,设计 中可分别计算在弯扭和剪扭共同作用下的配筋,然后再进行 叠加。
5受扭构件承载力计算-1
= 1 f tW t 2
A st1 f yv s
A cor
1 = 0.35
2 = 1.2
避免少筋
公式的适用条件: 避免完全超筋
5.2 在弯、剪、扭共同作用下的矩形构件承载力的计算 5.2.1 剪扭构件承载力的计算
外部荷载 条件
扭弯比ψ =T/M
扭剪比χ =T/Vb 构件截面形状、尺寸、 配筋和材料强度
0
(2)剪扭构件抗扭承载力计算公式
V T 0.35 f W 1.2
0 d u t td t
fA A
sv sv 1
cor
S
v
2)抗剪扭配筋的上下限 (1)抗剪扭配筋的上限 v T 0 . 51 10 bh W (2)抗剪扭配筋的下限
0 d 0 d 0 t
3
箱形截面具有抗扭刚度大、能承担异号弯矩 且平整美观。
国内抗扭研究时间短,成果少; 美国砼学会(ACI)的实验研究表明,箱形梁的
抗扭承载力与实心矩形梁相近。
5.5 构造要求
u cor A st1 f yv s
符号规定见教材
实验表明: 当0.5 2 一般两者可以发挥作用 《规范》规定: 0.6 1.7
当 = 1~1.2, 纵筋和箍筋的用量比最佳
5.1.3 纯扭构件的承载力计算理论 以变角空间桁架模型为理论基础,确定有关基 本变量,根据大量实测数据回归分折的经验公式:
W t W tw W tf W tf
Ⅰ型截面总的受扭塑性抵抗矩为:
'
W t W tw W tf W tf
W tw
W tf
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2021/3/1
1
6.1 概述
平衡扭转:由荷载直接作用。
平衡扭转
2021/3/1
2
协调扭转:由于变形协调关系所产生的受扭。
约束扭转
2021/3/1
3
6.2 试验研究
一、纯扭构件的破坏特征
1. 素混凝土矩形截面
三面开裂,一面受压,空间扭曲斜裂面;脆性破坏,抗扭 承载力很低。
(一)剪-扭相关关系
◆ 计算中的简化处理
部分相关:混凝土部分相关, 钢筋部分不相关
2021/3/1
13
AB段,bv ≤0.5,bt = 1.0; 忽略剪力 CD段,bt ≤0.5,bc = 1.0;忽略扭矩
BC段直线为,
t
1.5
V 1
Tc0
T Vc0
A
令
t
Tc Tc0
,
v
Vc Vc0
2
2
B
VC VCO
15
(二)剪扭构件的计算 Tu Tc Ts tTc0 Ts
1. 计算公式
受扭承载力公式
Vu Vc Vs vVc0 Vs
T Tu 0.35t ftWt 1.2
f yv
Ast1 s
Acor
受剪承载力公式
V
Vu
0.7(1.5
t ) ftbh0
1.25 f yv
Asv s
h0
或
V
hf 2 2
(bf
b)
Wtf
h
2 f
2
(b f
b)
h
Wt Wtw Wtf Wtf
bf'
hf'
b
hw
hf
bf
有效翼缘宽度应满足bf' ≤b+6hf' 及bf ≤b+6hf的条件,且 hw/b≤6。
2021/3/1
11
3、扭矩分配
腹板: 受压翼缘: 受拉翼缘:
2021/3/1
12
二、弯剪扭构件承载力计算
2021/3/1
4
2. 钢筋混凝土矩形截面
螺旋形裂缝 三面开裂,一面受压,螺旋形主 裂缝,破裂面为一空间曲面。
2021/3/1
5
3、受扭构件的配筋方式
横向箍筋和纵筋承担扭矩 。
箍筋:封闭。 纵筋:沿截面周边均匀对称布置,尤其对角必须布置受扭纵筋。
2021/3/1
6
二、钢筋混凝土纯扭构件的破坏形态
Vu
1.75
1
(1.5
t
)
ftbh0
1.0
f yv
Asv s
h0
2021/3/1
16
2. 截面尺寸限制及最小配筋率
1)截面尺寸限制条件
hw/b≤4
V bh0
T 0.8Wt
0.25c
fc
hw/b=6
V bh0
T 0.8Wt
0.2c
fc
若不满足应加大截面尺寸和提高混凝土等级
2)构造配筋
2021/3/1
22
2. 简化计算
( 1 )不进行抗剪计算的条件:
V 0.35 ftbh0
或
V
0.875
1
f t bh0
为弯扭构件
受弯构件正截面 纯扭的受扭承载力
2021/3/1
23
(2)不进行抗扭计算的条件:
T 0.175 ftWt
受弯构件正截面
为弯剪构件
和斜截面
2021/3/1
24
3、计算步骤:
① 验算截面尺寸; ② 验算构造配筋条件; ③ 确定计算方法,即是否可简化计算; ④ 根据M值计算受弯纵筋; ⑤ 根据V和T计算箍筋和抗扭纵筋; ⑥ 验算最小配筋率并使各种配筋符合《规范》构造要求。
2021/3/1
25
三、T型截面的配筋计算
腹板:同时承受V和Tw作用,按剪扭相关公式计算; 翼缘:仅承受Tf’及Tf作用 ,按纯扭公式计算;
2021/3/1
26
【6-1】一钢筋混凝土连续梁受均布荷载作用,截面尺寸 为b×h =300mm×600mm,as=as'=35mm,混凝土保护 层厚度为25mm;在支座处承受的内力: M=90kN·m ,V =103.8kN,T=28.3kN·m。采用的混凝土强度等级为C25, 纵向钢筋为HRB335,箍筋为热轧HPB235级钢筋。 试确定该截面配筋。
传统机械按键结构层图:
按
PCBA
键
开关 键
传统机械按键设计要点: 1.合理的选择按键的类型, 尽量选择平头类的按键,以 防按键下陷。 2.开关按键和塑胶按键设计 间隙建议留0.05~0.1mm,以 防按键死键。 3.要考虑成型工艺,合理计 算累积公差,以防按键手感 不良。
(三)弯剪扭构件计算方法 1、简化处理
TC TCO
1
TC VC 1.5 TCO VCO
C
D
2021/3/1
14
剪扭构件混凝土受扭承载力降低系数βt
(1)一般剪扭构件的βt
t
1.5
1 0.5 V
Wt
T bh0
0.5 t 1.0
(2)集中荷载作用下矩形截面剪扭构件的βt
t
1
1.5
0.2( 1) V
Wt
T bh0
2021/3/1
V bh0
T Wt
0.7 ft
17
3)最小配筋率
sv
Ast bs
sv,min
0.28
ft f yv
,若
,取
4)构造要求:抗扭纵筋的间距不大于200mm,且不大于b
2021/3/1
18
1.什么是传统机械按键设计?
传统的机械按键设计是需要手动按压按键触动PCBA上的 开关按键来实现功能的一种设计方式。
规范规定:
Tcr 0.7 ftWt
T f W T f W cr弹 2021/3/1
t te cr塑
tt
Wt
b2 6
(3h b)
8
2、抗扭承载力计算
T Tu 0.35 ftWt 1.2
f yv Ast1 s
Acor
配筋强度比ζ——受扭纵筋与封闭箍筋的体积比和强 度比的乘积
(a)截面核心 (b)纵筋与箍筋对应的体积
1. 适筋破坏
纵筋和箍筋都配置适中,延性破坏。
2.少筋破坏
纵筋和箍筋中配置过少 ,脆性破坏。
3. 超筋破坏
纵筋和箍筋都配置过多,脆性破坏。
4. 部分超筋破坏
箍筋和纵筋比例不合适, 破坏过程有一定的延性。
2021/3/1
7
6.3 建筑工程中受扭构件承载力计算
一、纯扭构件承载力计算:
(一)矩形截面:
1. 开裂扭矩Tcr:
◆将受弯与受扭所需纵筋分别计算后进行叠加 ◆对剪扭作用考虑混凝土项的相关作用 ◆受扭箍筋和受剪箍筋采用简单叠加方法
2021/3/1
20
(1)纵筋配置方法
受弯纵筋As和A's 剪扭共同作用,抗扭纵筋(均匀对称布置)
叠加(相应位置)
2021/3/1
21
(2)箍筋的配置方法
抗剪箍筋 抗扭箍筋
叠加
2021/3/1
《规20范21/3》/1 规定0.6≤ζ≤1.7. 设计时常取ζ=1.0~1.2。
9
(二)T形或工字形截面纯扭构件
1、截面划分的原则
将T形划分为若干矩形截面,分为腹板、受拉、受压翼缘。
bf'
hf'
h
b
hw
hf
bf
2021/3/1
10
2、划分的各矩形截面受扭塑性抵抗矩
Wtw
b2 6
(3h
b)
Wtf
