河工大高等数学试卷
2018-2019湖工大高等数学-2

收敛,其中
常数 0 .
3
(D) f (0,1) f (1, 0)
8.曲面 x 1 sin y z 1在点 (1, 1, 0) 处的法线方程为(
);
(A) x 1 y 1 z 1 1 1
(B) x 1 y 1 z 1 1 1
(C) x 1 y 1 z 1 1 1
(D) x 1 y 1 z 1 1 1
9. 已知曲线 L 为抛物线 y x2 的一部分( 0 x 1),则对弧长的曲线积分
注意
四三二一
、 试
、考意、姓:
、 密
卷生名封
印在、线
刷答准内 不题考不 清前证准
18.计算曲面积分 I (2x z)dydz zdxdy 其中 为有向曲面
楚应号答 。先不题
z x2 y2 (0 z 1) ,其法向量与 z 轴正向的夹角为锐角;
可将许。
举姓涂
手名改
向、, 监学否
封
考号则
;
(x, y)(0,0)
3.函数 z ln1 xy 在点 (0,1) 处的全微分 dz =
;
4.空间曲面 : x2 y2 z 2 1,则 (x3 z2 )dS =
;
5.
( 1)n1
n 1
n 2n
=
.
二、选择题(本题共 5 小题,每小题 3 分,共 15 分)
6.已知向量 b 与 a 共线,方向相反,且 | b | 5 | a | ,则 a+b 由 a 表示为(
教、试
师年卷
询级无
问和效
。 班。
级
填
写
在
指
定
的
方
框
内
。
19.将函数 f (x) 1 展开成 (x 2) 的幂级数,并指出其收敛域. 3 x
河南农业大学2015-2016学年第二学期《高等数学》(工科)期末考试试卷(A)

1河南农业大学2015-2016学年第二学期《高等数学》(工科)期末考试试卷(A )一、判断题(每小题2分,共计20分)( R )1、两个单位向量的数量积一定等于1.( W )2、设有向量,,a b c ,则()()a b c a b c ⋅=⋅.(R )4、沿梯度方向时,方向导数取得最大值.( R )5、若σ为D 的面积,则D dxdy σ=⎰⎰. ( W )6、设平面闭区}{(,),Dx y a x a x y a =-≤≤≤≤,}{1(,)0,D x y x a x y a =≤≤≤≤,则14DD xydxdy xydxdy =⎰⎰⎰⎰. ( R )7、设L 是任意一条分段光滑的曲线,则220L xydx x dy +=⎰. ( W )8、若级数1n n u∞=∑收敛,1n n v ∞=∑发散,则级数()1n n n u v ∞=+∑可能发散,也可能收敛. ( R )9、对级数1n n u∞=∑,lim 0n n u →∞=是该级数收敛的必要非充分条件.( R )10、若级数1n n n a x ∞=∑在2x =-处收敛,该级数的收敛半径一定大于等于2.二、填空题(每空2分,共计20分).1、已知两点(4,0,5),(7,1,3)A B ,则与向量AB 方向一致的单位向量为______________. 2、曲面222231xy z +-=在点(1,1,1)处的法线方程为________________________. 3、向量(2,1,1),(2,3,)a k β==-,且a β⊥,则k =______________. 4、交换积分次序1220o I dy x y dx ==⎰____________________________.5、设2x z y ⎛⎫= ⎪⎝⎭,则z x∂=∂_______________________. 6、级数11(2)n n x n∞=-∑的收敛区间为______________. 7、设L 为圆周221x y +=,则22()Lx y ds +=⎰__________________. 8、设cos ,cos ,cos αβγ是有向曲面∑在点(,,)x y z 处的法向量的单位余弦,则两类曲面积分间关系是 Pdydz Qdzdx Rdxdy ∑++⎰⎰=_____________________.2 9、设∑为球面2222x y z R ++=的外侧,则32222()xdydz ydxdz zdxdy x y z ∑++=++⎰⎰_________.10、设()f x 是以4为周期的周期函数,在[]2,2-定义为120()02x f x xx -≤≤⎧=⎨<<⎩,则傅立叶级数在2x =收敛于________________. 三、计算题(每题10分,共计60分)1、计算二重积分D ,其中D 是由直线,1,0y x y x ===所围成的平面区域.2、设函数()f u 在(0,)+∞内具有二阶导数,且z f =满足22220z z x y ∂∂+=∂∂.证明:()()0f u f u u '''+=.3、将函数2()2x f x x x =+-展成x 的幂级数.4、计算曲面积分:xyzdS ∑⎰⎰,其中∑是球面2221x y z ++=外侧在0,0x y ≥≥的部分.5、利用格林公式计算:3222(2cos )(12sin 3)L xy y x dx y x x y dy -+-+⎰,其中L 为抛物线22x y π=上由点(0,0)到(,1)2π的一段弧.6、设一平面经过原点及点(6,3,2)-,且与平面428x y z -+=垂直,求此平面方程.。
高一数学河大版试卷

高一数学河大版试卷考试范围:xxx;考试时间:xxx分钟;出题人:xxx姓名:___________班级:___________考号:___________1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上一、选择题1.已知函数的图象恒过定点A,若点A也在函数的图象上,则=()A.0 B.1 C.2 D.32.符合下列条件的三角形有且只有一个的是()A.B.C.D.3.下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为14,18,则输出的a=()A.0 B.2 C.4 D.144.等差数列满足,公差,若,则()A. B. C. D.5.下列说法中,错误的是()A.B.若的逆否命题为真命题C.命题D.若6.若对一切实数恒成立,则实数的取值范围是()A. B. C. D.7.线性回归方程=bx+a必过A.(0,0)点 B.(,0)点 C.(0,)点 D.(,)点8.设f(x)是定义在R上的偶函数,切f(x)在[0,+∞)上为增函数,则f(-2)、f(-π)、f(3)的大小关系是()A.f(-π)>f(-2)>f(3)B.f(-π)>f(3)>f(-2)C.f(-π)<f(3)<f(-2)D.f(-π)<f(-2)<f(3)9.已知集合,,则等于( )A. B. C. D.10.下列几何体各自的三视图中,有且仅有两个视图相同的是A.①② B.②④ C.①③ D.①④11.下列函数中,在区间(0,1)上是增函数的是A. B. C.12.已知函数是定义在上的奇函数,当时,,若,都有,则实数的取值范围为()A. B. C. D.13.(2011春•天心区校级期末)下列四个说法:(1)函数f(x)>0在x>0时是增函数,x<0也是增函数,所以f(x)是增函数;(2)若函数f(x)=ax2+bx+2与x轴没有交点,则b2﹣8a<0且a>0;(3)y=x2﹣2|x|﹣3的递增区间为[1,+∞);(4)y=1+x和表示相等函数.其中说法正确的个数是()A.0 B.1 C.2 D.314.已知是奇函数,且.若,则().A. B. C. D.15.下列四个函数:①;②;③;④其中定义域与值域相同的函数有A.1个B.2个C.3个D.4个16.设函数是R上的奇函数,且当时,,则等于()A. B. C.1 D.17.(2009•锦州一模)一个几何体的三视图如图所示,则该几何体的表面积是()A.6+8 B.12+8 C.12+7 D.18+218.一空间几何体的三视图如图所示,则该几何体的体积为A.B.C.D .19.若是周期为的奇函数,则可以是( )A .B .C .D .20. 过正方形的顶点,引⊥平面,若,则平面ABCD 和平面所成的二面角的大小是 A .B .C .D .评卷人 得 分二、填空题21.已知数列{a n }的通项公式为a n = (-1)n n ,则a 4=_____. 22.已知且满足,则的最小值为 . 23.若均为正实数,则的最大值是 _____ .24.(本题满分9分)某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比。
华北水利水电大学大一下学期高数期末考试

华北水利水电大学大一下学期高数期末考试一、选择题(在下列各题的四个备选答案中,只有一个是符合题意的,请将正确答案前的字母写在答题纸上;本题共32分,每小题4分)1、已知⊙O的直径为3cm,点P到圆心O的距离OP=2cm,则点P()A、在⊙O外B、在⊙O上C、在⊙O内D、不能确定2、已知△ABC中,∠C=90°,AC=6,BC=8,则cose的值是()A、0.6B、0.75C、0.8D、0.853、△ABC中,点M、N分别在两边AB、AC上,MN∥BC,则下列比例式中,不正确的是()A、1B、2C、3D、44、既是中心对称图形又是轴对称图形的是()A、1B、-1C、2D、-25、已知⊙O1、⊙O2的半径分别是1cm、4cm,O1O2=cm,则⊙O1和⊙O2的位置关系是()A、外离B、外切C、内切D、相交6、某二次函数y=ax2+bx+c的图像,则下列结论正确的是()A、ao,b0,c0B、a0,b0,c;0C、a0,b0,c0D、a0,b0,c07、下列命题中,正确的是()A、平面上三个点确定一个圆B、等弧所对的圆周角相等C、平分弦的直径垂直于这条弦D、与某圆一条半径垂直的直线是该圆的切线8、把抛物线y=-x2+4x-3先向左平移3个单位,再向下平移2个单位,则变换后的抛物线解析式是()A、y=-(x+3)2-2B、y=-(x+1)2-1C、y=-x2+x-5D、前三个答案都不正确二、填空题(本题共16分,每小题4分)9、已知两个相似三角形面积的比是2∶1,则它们周长的比_____。
10、在反比例函数y=中,当x0时,y随x的增大而增大,则k的取值范围是_________。
11、水平相当的甲乙两人进行羽毛球比赛,规定三局两胜,则甲队战胜乙队的概率是_________;甲队以2∶0战胜乙队的概率是________。
12、已知⊙O的直径AB为6cm,弦CD与AB相交,夹角为30°,交点M恰好为AB的一个三等分点,则CD的长为_________cm。
高二数学河大版试卷

高二数学河大版试卷考试范围:xxx;考试时间:xxx分钟;出题人:xxx姓名:___________班级:___________考号:___________1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上一、选择题1.下列求导运算正确的是()A.B.C.D.2.已知与之间的一组数据(表一):则对的线性回归方程为必过点()A. B. C. D.3.计算定积分=()A. B. C. D.4.如图在长方形ABCD中,AB=,BC=1,E为线段DC上一动点,现将AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为 ( )A. B. C. D.5.设,则 ( )A. B. C. D.6.已知等比数列的公比,则的值为().A. B. C. D.7.下列四个命题中,真命题的个数为()(1)若两平面有三个公共点,则这两个平面重合;(2)两条直线可以确定一个平面;(3)若;(4)空间中,相交于同一点的三条直线在同一平面内。
A.1 B.2 C.3 D.48.如图,在空间直角坐标系中有直三棱柱,,则直线与直线夹角的余弦值为()A. B. C. D.9.设a,b∈R,则“a>b”是“a|a|>b|b|”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件10.双曲线的渐近线方程是()A. B. C. D.11.某程序框图如图所示,若输出的,则判断框内为()A. B. C. D.12.在同一坐标系中,将曲线变为曲线的伸缩变换是()A. B. C. D.13.设函数为奇函数,,则()A. B. C. D.514.已知函数有唯一的零点,则其零点所在区间为()A.(0 ,1) B.(1 ,2) C.(2 ,3) D.(3 ,4)15..设有一个回归方程y=3-5x则变量x增加一个单位时A.y平均减少5个单位B.y平均增加3个单位.C.y平均减少3个单位D.y平均增加5个单位.16.在△ABC中,若则△ABC的形状是A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定17.下表是降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨)标准煤的几组对应数据,根据表中提供的数据,求出y关于x的线性回归方程,那么表中m的值为( )A. 4B. 3.5C. 4.5D. 318.下表是某厂1-4月份用水量(单位:百吨)的一组数据:月份14用水量由散点图可知,用水量与月份之间有较好的线性相关关系,其线性回归方程为,则()A.10.5 B.5.15 C.5.2 D.5.2519.已知抛物线焦点为,点为其准线与轴的交点,过点的直线与抛物线相交于两点,则△DAB的面积的取值范围为A.B.C.D.20.函数在区间上的最大值为()A. B. C. D.二、填空题21.复数,,则等于_________________。
合肥工业大学大一上学期高数期末考试题

高数期末考试一、填空题(本大题有4小题,每小题4分,共16分) 1.=+→xx x sin 2)31(lim .2. ,)(cos 的一个原函数是已知x f x x =⋅⎰x x x x f d cos )(则 .3.lim(cos cos cos )→∞-+++=22221n n nnnn ππππ .4. =-+⎰21212211arcsin -dx xx x .二、单项选择题 (本大题有4小题, 每小题4分, 共16分)5. )时( ,则当,设133)(11)(3→-=+-=x x x x xx βα.(A )()()x x αβ与是同阶无穷小,但不是等价无穷小; (B )()()x x αβ与是等价无穷小;(C )()x α是比()x β高阶的无穷小; (D )()x β是比()x α高阶的无穷小.6.)(0),sin (cos )( 处有则在设=+=x x x x x f .(A )(0)2f '= (B )(0)1f '=(C )(0)0f '= (D )()f x 不可导.7. 若()()()02xF x t x f t dt=-⎰,其中()f x 在区间上(1,1)-二阶可导且'>()0f x ,则( ).(A )函数()F x 必在0x =处取得极大值; (B )函数()F x 必在0x =处取得极小值;(C )函数()F x 在0x =处没有极值,但点(0,(0))F 为曲线()y F x =的拐点; (D )函数()F x 在0x =处没有极值,点(0,(0))F 也不是曲线()y F x =的拐点。
(A )22x (B )222x +(C )1x - (D )2x +.三、解答题(本大题有5小题,每小题8分,共40分)8. 设函数=()y y x 由方程sin()1x ye xy ++=确定,求'()y x 以及'(0)y . 9.设函数)(x f 连续,=⎰1()()g x f xt dt,且→=0()limx f x A x ,A 为常数. 求'()g x 并讨论'()g x 在=0x 处的连续性. 10. 求微分方程2ln xy y x x '+=满足=-1(1)9y 的解.四、 解答题(本大题10分)11. 已知上半平面内一曲线)0()(≥=x x y y ,过点(,)01,且曲线上任一点M x y (,)00处切线斜率数值上等于此曲线与x 轴、y 轴、直线x x =0所围成面积的2倍与该点纵坐标之和,求此曲线方程. 五、解答题(本大题10分)12. 过坐标原点作曲线x y ln =的切线,该切线与曲线x y ln =及x 轴围成平面图形D.(1) 求D 的面积A ;(2) 求D 绕直线x = e 旋转一周所得旋转体的体积V . 六、证明题(本大题有2小题,每小题4分,共8分)13. 设函数)(x f 在[]0,1上连续且单调递减,证明对任意的[,]∈01q ,1()()≥⎰⎰qf x d x q f x dx.14. 设函数)(x f 在[]π,0上连续,且)(0=⎰πx d x f ,cos )(0=⎰πdx x x f .证明:在()π,0内至少存在两个不同的点21,ξξ,使.0)()(21==ξξf f (提示:设⎰=xdxx f x F 0)()()解答一、单项选择题(本大题有4小题, 每小题4分, 共16分) 1、D 2、A 3、C 4、C二、填空题(本大题有4小题,每小题4分,共16分)5. 6e . 6.c x x +2)cos (21 .7. 2π. 8.3π.三、解答题(本大题有5小题,每小题8分,共40分) 9. 解:方程两边求导0,0x y ==,(0)1y '=-10. 解:767u x x dx du == 11. 解:101233()2xf x dx xe dx x x dx---=+-⎰⎰⎰12. 解:由(0)0f =,知(0)0g =。
河南工业大学高等数学试卷A
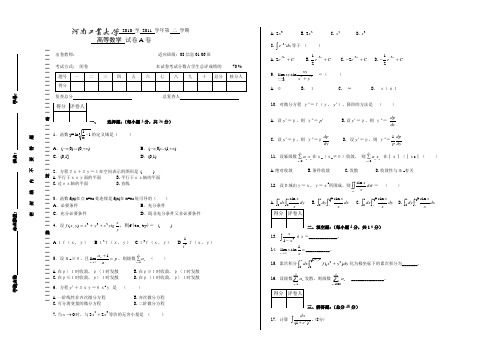
2010 至 2011 学年第 二 学期高等数学 试卷A 卷出卷教师: 适应班级:08信息01-06班考试方式: 闭卷 本试卷考试分数占学生总评成绩的 70 % 复查总分 总复查人一、选择题:(每小题3分,共36分)1.函数y=31x1ln -的定义域是( ) A .),0()0,(+∞⋃-∞ B .),1()0,(+∞⋃-∞ C .(0,1]D .(0,1)2.方程2x+3y=1在空间表示的图形是 ( )A.平行于xoy面的平面B.平行于oz轴的平面C.过oz轴的平面D.直线3.函数f(x)在点x=x 0处连续是f(x)在x=x 0处可导的( ) A .必要条件B .充分条件C .充分必要条件D .既非充分条件又非必要条件4.设332(,)xf x y x y x ytg y=++,则f(tx,ty)= ( )A.tf(x,y)B.t2f(x,y)C.t3f(x,y) D.21tf(x,y)5.设an ≥0,且1limn n a p a→∞+=,则级数1n n a ∞=∑ ( ) A.在p〉1时收敛,p〈1时发散 B.在p≥1时收敛,p〈1时发散 C.在p≤1时收敛,p〉1时发散 D.在p〈1时收敛,p〉1时发散 6.方程y '+3xy=6x2y 是 ( )A.一阶线性非齐次微分方程B.齐次微分方程C.可分离变量的微分方程D.二阶微分方程 7.当0x →时,与2332x x +等价的无穷小量是 ( )A.32xB.23xC.2xD.3x8.2xe dx -⎰等于 ( )A.22xeC -+ B.212x e C -+ C.22x e C --+ D.212x e C --+9.22lim sinx y xyxy x y→→+ = ( ) A. 0 B. 1 C. ∞ D. sin110.对微分方程 y"=f(y,y '),降阶的方法是 ( ) A. 设y '=p,则 y"=p ' B.设y '=p,则 y"=dp dyC. 设y '=p,则 y"=pdp dy D. 设y '=p,则 y"=1dp p dy11.设幂级数0n n n a x ∞=∑在xo (xo ≠0)收敛, 则0n n n a x ∞=∑ 在│x│〈│xo │ ( )A.绝对收敛B.条件收敛C.发散D.收敛性与an 有关 12.设D域由y=x,y=x2所围成,则sin Dxd x σ⎰⎰= ( ) A.1100sin xdx dy ⎰⎰B.10y x dy dx x ⎰C.10x x dx dy x ⎰D.10x x dy dx x ⎰二、填空题:(每小题4分,共16分)13.41xx -⎰dx=_____________。
高等数学期末试卷2020河南大学

高等数学期末试卷2020河南大学一、填空题(每小题2分,共20分)1、函数)12ln(2+-=x y z 的定义域为 .2、设3745y xy x z +-=,则=∂∂∂yx z 2 . 3、设)1ln(22y x z ++=,则=)2,1(dz.4、=+-→22)1,0(),(1limyx xyy x . 5、设平面区域D 由y y x 222=+围成,则=⎰⎰Dd σ .6、交换积分次序=⎰⎰xe dy y xf dx ln 01),( .7、化二次积分为极坐标形式的二次积分=+⎰⎰-220220)(y a adx y x dy .8、部分和数列{}n S 有界是正项级数∑∞=1n nu收敛的 条件.9、级数)0(11>∑∞=p nn p 当 时收敛.10、若级数∑∞=1n n u 条件收敛,则级数∑∞=1n nu必定 .二 、选择题(每小题3分,共15分)1、设)ln(2y x z +=,则=∂∂∂yx z2( ) A 22)(1y x +-B 22)(1y x +C 22)(2y x y +-D 21yx +- 2、设yx ez 2=,则=dz ( )A dy x xydx 22+ B xydy dx x 22+C )2(22dy x xydx eyx + D )2(22dx x xydy eyx +3、交换二次积分次序=⎰⎰--2101),(ydx y x f dy ( )A⎰⎰-0121),(y dx y x f dy B ⎰⎰-0121),(x dy y x f dxC⎰⎰--2101),(xdy y x f dx D ⎰⎰--011),(dy y x f dx4、由曲线x e y =,x e y -=与1=x 围成的图形的面积为( )A 21-+-ee B 21---e e C 21++-e e D 21-+--e e5、级数)0(0≠∑∞=a aqn n当( )时收敛.A 11≤≤-qB 11≤<-qC 11<≤-qD 11<<-q三、计算题(每小题10分,共50分)第1页 共4页第2页 共4页1、设),(22y x xy f z =,求xz∂∂,y z ∂∂,22x z ∂∂.2、求函数333y xy x z+-=的极值点及极值.3、求二重积分⎰⎰Dxdxdy ,其中D 是以)0,0(O ,)2,1(A 和)1,2(B 为顶点的三角形闭区域.4、求幂级数∑∞=----112112)1(n n n x n 的收敛域及和函数.5、将函数x a x f =)(展开成x 的幂级数.四、应用题(15分)从斜边之长为2的一切直角三角形中,求有最大周长的直角三角形.第3页 共4页 第4页 共4页。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
河工大高等数学试卷 This manuscript was revised by the office on December 10, 2020.
河北工业大学函授生考试试卷 课程 高等数学 教师 王英新 2012 /2013 学年 第 2 学期 班级 2013级 姓名____________ 成 绩_______
一、 填空题(20分)
1
、函数22ln(3)z x y =+-的定义域是322≤+y x .
2、函数22(,)4()f x y x y x y =---的驻点为(-2,2)
3、设2(,)e x f x y xy =+,则()1,2x f =24e +
4、在直角坐标系下,二重积分中的面积元素d σ= dxdy
5、级数123n +++++是__发散__(收敛或发散)
6、微分方程''5'60y y y ++=的特征根是(-3,-2))
7、D
dxdy ⎰⎰=_π2__(D 为单位圆)
8、当p 时,级数1
11(1)n p n n
∞-=-∑时绝对收敛 9、设L 是立方抛物线3x y =上从原点)0,0(到点)1,1(一段弧,则曲线积分22d d L xy x x y +=⎰ 1
10、函数1()12f x x
=
-的麦克劳林展开式的收敛域为 二、计算题(50分) 1.求2sin 2z x y =的两个一阶偏导数
2.计算函数e xy z =在(2,1)处的全微分
θ
3.计算二重积分D
xydxdy ⎰⎰,其中D 是有抛物线2y x =及直线2y x =-所围成的闭区域
4.求椭圆cos ,sin x a y b θθ==所围成图形的面积。
5.求微分方程''2'30y y y --=的通解
三、在区间(1,1)-内求幂级数01n
n x n ∞
=+∑的和函数。
(10分)
四、将函数()ln(1)
=+展开成的x幂级数。
(10分)
f x x
五、某厂要用铁板做成一个体积为23
m的有盖长方形水箱,问当长宽高各取怎样的尺寸时,才能用料最省。
(10分)。
