控制图讲稿
合集下载
质量管理手法系列培训-控制图ppt课件
类 别
控制图符号
控制图名称
控制界限
类别 控制图符号
控制图名称
控制界限
UCLX=X+A2R
CLX=X
X-R
均值-极差控制图
UCLX=X-A2R UCLR=D4R
CLR=R
LCLR=D3R
UCLX=X+A3s
CLX=X
X-s
均值-标准差控制图
UCLX=X-A3s UCLs=B3s
计
CLs=s
计
量 控
LCLs=B3s
➢ 概述 ➢ ●定义：控制图是对过程质量加以丈量、记录并进展控
制
➢ 管理的一种用统计方法设计的图。
样
控制图
本
统
计
数
值
UCL-上控制界限
CL-中心 线
LCL-下控制界限
时间或样本号
控制图由正态分布演化而来。正态分布可用两个参数
即均值μ和规范差σ来决议。正态分布有一个结论对质量管 理很有用，即无论均值μ和规范差σ取何值，产质量量特性 值落在μ±3σ之间的概率为99.73%，落在μ±3σ之外的概 率为100%-99.73%= 0.27%，而超越一侧，即大于μ+3σ 或小于μ-3σ的概率为0.27%/2=0.%≈1‰,休哈特就根据这 一现实提出了控制图。 由于上下的数值大小不合常规，
A
B
XC
×
C
B
A
LCL
延续5点中有4点落在同一侧的C区以 外
UC L
A
B
XC
×
C
B
A
LCL
延续15点落在中心线两侧的C区内
延续8点落在中心线两侧且无一再C 区内
在点随机陈列的情况下，判别过程稳态，既没有异常波 动的准那么：
控制图使用培训讲义全
3.统计与概率论简介
Z值表
4.均值极差图（ Xbar-R图）
生产过程中用控制图对过程质量特性进行测定、记录、评 估，从而监察过程是否处于控制状态，对过程异常提前进行 预警。
控制图种类有多种，而使用最多的是均值极差控制图 （Xbar-R图)。
4.均值极差图（ Xbar-R图）
控制图类别
数值 分布
M：规范中心（规格中心） M = USL LSL
2
T:规范宽度（规格公差），T=USL-LSL ,T描述的是客户要求的宽与严。
T/2：半公差
ε：偏移量（或偏移系数），反应数据中心偏离规格中心的大小 ε=|M - μ|
K:相对偏移量（或修正系数） ，反应数据中心偏离规格中心的程度，也有用Ca。
K= ε T/2
4.均值极差图（ Xbar-R图）
术语（控制图中的线）： USL:规范上限 ，也有用TU来表示的
LSL:规范下限，也有用TL来表示的 CL:控制限（或控制中心线） UCL:上控制限， UCL=μ+3σ LCL:下控制限， LCL=μ-3σ A区的边界 UWL:上警告限， UWL=μ+2σ LWL:下警告限， LWL=μ-2σ B区的边界
σˆ 同理：后面 是s 的估计值
总体
μ
=
X1 X 2 .... X N N
=
1 N
N i =1
Xi
3.统计与概率论简介
总体均值 总体标准差
样本均值 样本标准差
N
m
=
xi
i =1
=
x1 x2 ...xN
N
N
s=
N
( xi m )2
i =1
N
质量管理学控制图课件.ppt
• 计算统计量的中心值和控制界限。
x 图：
中心值CL＝
＝ ＝x29.86（g）
UCL＝ ＝x＋ A2 R ≈ 45.69（g）
LCL＝
＝ x—
A2
R
≈
14.03（g）
注：A2为随着样本容量n而变化的系数，可由控制图系数选用表中选取。
第13页，共35页。
R 图：
中心值 CL＝ R＝27.44（g） UCL＝ D4 R≈ 58.04（g）
• 在质量改进方面，可以用来确认某过程是否得到了改进。
第5页，共35页。
二、应用控制图的步骤
应用步骤如下：
选择控制图拟控制的质量特性，如重量、不合格品数等；
选用合适的控制图种类； 确定样本容量和抽样间隔；
收集并记录至少20～ 25个样本的数据，或使用以前所记录的数据； 计算各个样本的统计量，如样本平均值、样本极差、样本标准差等；
• 在不对该过程做任何调整的同时，继续用同样的方法对 多装量抽样、观察和打点。如果在继续观察时，控制图 显示出存在异常原因，则应进一步分析具体原因，并采 取措施对过程进行调整。
第16页，共35页。
四、控制图的观察与分析
点子没有超出控制线（在控制线上的点子按出超出处理），
控制界限内的点子排列无缺陷，反映工序处于控制状态，生 产过程稳定，不必采取措施。 控制图上的点子出现下列情形之一时，即判断生产过程异常：
34.2
25
24
28
27
22
32
54
163
32.6
32
25
42
34
15
29
21
141
23.2
27
累计
746.6
控制图ppt课件
过程控制图Байду номын сангаас述
生产运营部
1
主要内容
• 一、引言 • 二、什么是控制图？ • 三、控制图的分类 • 四、控制图的判稳、判异 • 五、控制图的应用 • 六、控制图的制作示例
2
一、引言
• 背景：
药品质量源于设计，是生产出来的，不是 检验出来的。
法规提出需求，6sigma精益生产管理提出
方法。 生产过程控 制
时需保持原有状态。 ③确认：确认某一过程的改进效果，是
否得到改进，是否需要改进。
9
二、什么是控制图？
• 2.5控制图的作用
控制图主要是以预防为主，把影响产品质量的诸因素消灭 在萌芽状态，以保证质量、降低成本、提高生产效率、提 高经济效益的目的。具体作用如下：
能及时发现生产过程中的一场现象和缓慢变异，能预防不合格品 发生，从而降低生产费用和提高生产效率； 能有效分析和判断生产过程工序质量的稳定性； 可查明设备和工艺手段的实际精度，以便做出正确的技术决定； 为真正的制定工序目标和规格界限，特别是对配合零部件的最优 化确立了可靠的基础；
• 5.2如何选择控制图？
28
五、控制图的应用
• 5.3控制图制作步骤一般为： ①按规定的抽样间隔和样本大小抽取样
本,收集数据； ②测量样本的质量特性值，计算其统计
量数值； ③在控制图上描点； ④控制图修正； ⑤判断生产过程。
29
五、控制图的应用
使工序的成本和质量成为可预测的。
10
三、控制图的分类
• Content
s
01 按数值质量特性分类
02
按控制图用途分 类
11
三、控制图的分类
• 3.1按数值质量特性分类： • 计量型控制图： 指产品需实际量测而取得的连续性实际值,并 对其做数理分析,以说明该产品在此量测特性 的品质状况的方法。 • 计数值控制图： 它是以计件产品的不良件数或点数的表示方 法,数据在理论上有不连续的特性,故称为离型 变量。
生产运营部
1
主要内容
• 一、引言 • 二、什么是控制图？ • 三、控制图的分类 • 四、控制图的判稳、判异 • 五、控制图的应用 • 六、控制图的制作示例
2
一、引言
• 背景：
药品质量源于设计，是生产出来的，不是 检验出来的。
法规提出需求，6sigma精益生产管理提出
方法。 生产过程控 制
时需保持原有状态。 ③确认：确认某一过程的改进效果，是
否得到改进，是否需要改进。
9
二、什么是控制图？
• 2.5控制图的作用
控制图主要是以预防为主，把影响产品质量的诸因素消灭 在萌芽状态，以保证质量、降低成本、提高生产效率、提 高经济效益的目的。具体作用如下：
能及时发现生产过程中的一场现象和缓慢变异，能预防不合格品 发生，从而降低生产费用和提高生产效率； 能有效分析和判断生产过程工序质量的稳定性； 可查明设备和工艺手段的实际精度，以便做出正确的技术决定； 为真正的制定工序目标和规格界限，特别是对配合零部件的最优 化确立了可靠的基础；
• 5.2如何选择控制图？
28
五、控制图的应用
• 5.3控制图制作步骤一般为： ①按规定的抽样间隔和样本大小抽取样
本,收集数据； ②测量样本的质量特性值，计算其统计
量数值； ③在控制图上描点； ④控制图修正； ⑤判断生产过程。
29
五、控制图的应用
使工序的成本和质量成为可预测的。
10
三、控制图的分类
• Content
s
01 按数值质量特性分类
02
按控制图用途分 类
11
三、控制图的分类
• 3.1按数值质量特性分类： • 计量型控制图： 指产品需实际量测而取得的连续性实际值,并 对其做数理分析,以说明该产品在此量测特性 的品质状况的方法。 • 计数值控制图： 它是以计件产品的不良件数或点数的表示方 法,数据在理论上有不连续的特性,故称为离型 变量。
控制图讲稿1
控制图的控制限分别位于中心线的两侧3σ距离处。3σ控制限表明，若过程处于统计控制状态，则大约有99.7%的子组值将落在控制界限之内。换句话说，当过程受控时，大约有0.3%的风险，或每点绘1000次中，平均有3次，描绘点会落在上控制限或下控制线之外。 许多场合，在控制图上另外加上2σ控制限是有益的。这样，任何落在2σ界限外的子组值都可以作为失控状态即将来临的一个警示信号，因此，2σ控制限有时也称作“警戒限”。在对控制图进行判断的是否，会用到1 σ，2 σ，3 σ限，这在后面会讲到。
X-s图制作范例
s控制限的计算: UCLs=B4*s CLs=s LCLs＝B3*s B3,B4为常数，通过查表可得。
X图控制限的计算： UCLX=X+A3*s CLX=X LCLX=X-A3*s A3为常数，通过查表可得。
（3）Me－R控制图 Me－R控制图与X－R图也很相似，只是用中位数（Me)代替均值（X）。由于中位数的计算比均值简单，所以多用于现场需要把测定数据直接记入控制图进行控制的场合，这是，为了简便，自然规定为奇数个数据。现在多用电脑进行绘图，计算平均值已经不成问题，故Me－R图的应用逐渐减少。
P控制图
不合格品数控制图
np控制图
计点值
泊松分布
单位不合格数控制图
U控制图
不合格数控制图
C控制图
控制图中常用符号的解析： n 子组大小，单个子组中子组观测值的个数 k 子组数 X 质量特性的观测值 X 子组的平均值 Me 子组中位数。对于一组升序或降序排列的n个子组观测值X1,X2…..，当n为奇数时，中位数等于该组数中间的那个数；当n为偶数时，中位数等于该组数中间两个数的平均值。 R 子组极差。子组观测值中极大值与极小值之差。 注：在单值图的情况下，R代表移动极差，即两个相邻观测值的差值的绝对值。 S 子组标准偏差 s＝
控制图讲义统计过程控制(SPC)
spc
统计过程分析
控制界限的构成
11
Edited by Mr. jose lee
spc
统计过程分析
普 通 原 因(偶因) 与 特 殊 原 因(异因) 之变异
随机变异: 过程中变异因素是始终存在,且不易识别的原因造成的, 并假定为过程所固有。
普通原因
偶然原因(偶因) 一般 原因
结果为: 在统计的控制状态下， 其产品之特性有固定(典型)的分配(布)。
24
Edited by Mr. jose lee
spc
统计过程分析
X R 绘图步骤
4.求控制界限 (1) 控制X 图 CL＝ X ＝ 50.16
UCL＝ X＋A2 R＝ 50.16＋(0.58) (4.8)＝ 52.93 LCL＝ X－A2R ＝ 50.16－(0.58) (4.8)＝ 47.39
CL = R
2.实例：
UCL = D4 R LCL = D3 R
某工厂制造一批紫铜管，应用 X-R控制图来控制其内径，尺寸
单位为m/m，利用下页数据表之资料，求得其控制界限并绘图。
（n = 5）
22
Edited by Mr. jose lee
spc
统计过程分析
X－R控制图用数据表
产品名称：紫铜管
机械号码：XXX
1. 柏拉图（决定控制重点） 2. 统计检定 3. 控制图 4. 抽样计划 5. 变异数分析／回归分析
6
Edited by Mr. jose lee
spc
统计过程分析
过程控制系统
过程中对策 绩 效 报 告 成 品 改 善
过程中对策 人员 设备 材料 成 方法 环境
7
品
SPC控制图2篇
SPC控制图第一篇：SPC控制图1. 介绍SPC控制图（Statistical Process Control）是一种质量管理工具，用于监控和管理过程中的变异性。
它基于统计原理，通过收集和分析过程数据，可以帮助我们实时判断过程是否处于控制状态，并及时采取措施进行调整和修正，以保证产品或服务的稳定性和可靠性。
2. SPC控制图的基本原理SPC控制图有两个基本原则：稳定性和可预测性。
稳定性是指过程在一个可控制的范围内运行，没有特殊原因的变异性；可预测性是指过程的性能可以通过数据进行预测和估计，而不需要依赖特殊原因的出现。
3. SPC控制图的类型常用的SPC控制图有以下几种类型：（1）X-Bar和R控制图：用于监控连续性数据的平均值和范围。
（2）X-Bar和S控制图：与X-Bar和R控制图类似，但用标准差代替范围。
（3）P控制图：用于监控离散型数据的不良率或缺陷率。
（4）C控制图：用于监控离散型数据的计数。
4. SPC控制图的使用步骤（1）收集数据：根据所监控的过程特性，选择合适的采样方法和样本大小，收集数据。
（2）构建控制图：根据采集到的数据，计算样本平均值、范围、标准差、不良率等统计指标，绘制控制图。
（3）判断过程状态：分析控制图上的数据点和规则，判断过程是否处于控制状态。
（4）监控过程：定期收集和更新数据，绘制新的控制图，进行持续监控和分析。
5. SPC控制图的应用范围SPC控制图可以应用于各行各业的生产过程和服务过程中，如制造业的生产线、医疗行业的手术过程、金融行业的交易过程等。
通过使用SPC控制图，可以及时发现潜在问题，并采取纠正措施，提升过程的稳定性和可靠性。
6. SPC控制图的优势与挑战（1）优势：- 实时监控：SPC控制图可以提供实时的过程数据，帮助管理者及时判断过程状态。
- 判断能力：通过分析控制图上的数据点和规则，可以判断过程是正常变异还是有特殊原因的变异。
- 效益显著：SPC控制图可以帮助企业降低不良率、提高产品质量，并节约成本。
控制图的原理及应用教案
控制图的原理及应用教案一、控制图的概述•控制图是用来监测和分析过程稳定性的工具。
它能够帮助我们判断过程是否受到了特殊因素的影响，从而帮助我们定位问题和改进过程。
•控制图包括过程监控图、变动图、普通图等，每种图形都有其特定的使用场景和目的。
二、控制图的基本原理•均值控制图的原理：通过收集和分析过程数据，确定过程的中心线和控制上下限，根据数据的离散程度来判断过程的稳定性。
•范围控制图的原理：通过跟踪样本范围的变化，来评估过程的稳定性和一致性。
•动态测量控制图的原理：通过在过程控制中，采样循环中检测结果的变化，来判断过程的稳定性。
•经济控制图的原理：通过分析与经济因素相关的数据，来优化过程并减少资源的浪费。
三、控制图的应用场景1.生产过程监控：通过定期采样和测量关键参数，将数据绘制在控制图上，及时发现过程异常和问题并采取相应的纠正措施。
2.产品质量控制：通过控制图来监测产品参数的变化和偏离，确保产品质量在可接受范围内，并及时发现潜在问题。
3.供应链管理：通过掌握供应链中各个环节的数据，绘制控制图来分析供应链的稳定性和可靠性，及时处理延迟和异常情况。
4.服务质量监控：对于服务行业，可以使用控制图来衡量并监控关键指标，及时发现异常情况并采取相应的改进措施。
5.实验过程控制：在实验过程中，采用控制图能够帮助我们评估实验结果的稳定性和一致性，从而提高实验的可靠性。
四、控制图的应用步骤1.收集数据：需要收集与需要监控的过程相关的数据。
2.绘制控制图：选择适当的控制图类型并将数据绘制在控制图上。
3.判断过程稳定性：通过分析控制图数据的模式和规律，判断过程的稳定性。
4.分析过程问题：如果控制图中存在异常点或趋势，说明过程可能存在问题，需要进一步分析和排查。
5.纠正和改进：根据分析结果采取纠正措施，并对过程进行改进以提高稳定性和一致性。
6.持续监控：持续收集数据并绘制控制图，监控过程的稳定性和持续改进。
五、控制图的优势和局限性优势•提供直观的数据展示和分析方式，便于快速理解和判断过程稳定性。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
X图控制限的计算： UCLX=X+A2*R CLX=X LCLX=X-A2*R A2为常数，通过查表可得。 n A2 2 1.880 3 1.023 4 0.729 5 0.577 6 0.483 7 0.419 8 0.373
根据计算结果进行绘图，可以在电子表格中进行，也 可以在MINITABEL软件中进行。
2 3
1.67>CPK ≥1.33 1.33>CPK ≥1,00
合格 警告
4
1.00>CPK ≥0.67
不足
5
0.67>CPK
非常不足
CPK计算示例
Z=
p 1− p / n
(
p− p
)
这样，中心线和控制限如下所示改为常数，而与子组的大小无关： UCL=3 CL=0 LCL=-3
同样，u图可以用同样的方法进行转换：
Z =
u−u u/n
P图制作示例
那怎样的子组频数和子组大小是合适的呢？
关于子组频数和子组大小，无法制定通用的规则，可根据实际 情况考虑。通常，子组大小取4或5，而பைடு நூலகம்样频数，一般在初期时高 ，一旦达到统计控制状态后就低。通常认为，抽取大小为4或5的20 ～25个子组就足够了。
三、控制图的判断 当我们把控制图做好后，我们如何判断这个控制是否正常呢？
将控制图分为6个区，每个区宽1σ。这6个区标号分别为A,B,C,C,B,A,两个A区 ，两个B区及C区都关于中心线的对称。 以下为控制图是否正常的8个检验模式。
四、CPK值的计算 CPK为制程能力指数，反应制程满足实际尺寸要求的能力，CPK数值越大，制 程越能保证实际尺寸的加工要求，评估制程满足实际尺寸要求的能力，并以此统 计分析结果确定生产能力是否满足大批量生产的要求
X 子组的平均值 Me 子组中位数。对于一组升序或降序排列的n个子组观测值X1,X2…..，当n为奇 数时，中位数等于该组数中间的那个数；当n为偶数时，中位数等于该组数中间 两个数的平均值。 R 子组极差。子组观测值中极大值与极小值之差。 注：在单值图的情况下，R代表移动极差，即两个相邻观测值的差值的绝对值。 S 子组标准偏差
单值－移动极差控制图 X-Rs控制图 Rs控制图 计件值 二项分布 不合格品率控制图 不合格品数控制图 计点值 泊松分布 单位不合格数控制图 不合格数控制图 P控制图 np控制图 np控制图 U控制图 C控制图
控制图中常用符号的解析： n k X 子组大小，单个子组中子组观测值的个数 子组数 质量特性的观测值
X-S图的制作与前面讲到的X-R图是一样的。
s控制限的计算: UCLs=B4*s CLs=s LCLs＝B3*s B3,B4为常数，通过查表可得。 X图控制限的计算： UCLX=X+A3*s CLX=X LCLX=X-A3*s A3为常数，通过查表可得。
X-s图制作范例
（3）Me－R控制图 Me－R控制图与X－R图也很相似，只是用中位数（Me)代替均值（X）。由于中位 数的计算比均值简单，所以多用于现场需要把测定数据直接记入控制图进行控制的 场合，这是，为了简便，自然规定为奇数个数据。现在多用电脑进行绘图，计算平 均值已经不成问题，故Me－R图的应用逐渐减少。 以下给出Me－R图控制限的计算公式： Me图控制限的计算： UCLMe=Me+A4*s CLMe=Me LCLMe=Me-A4*s A3为常数，通过查表可得。
s＝
∑ ( Xi − X )
n −1
2
P
子组不合格品率
P＝子组的不合格品数/子组大小 np U C 子组的不合格品数 子组单位产品不合格数 子组不合格数
常规控制图的性质 常规控制图要求从过程中以近似等间隔抽取的数据。此间隔 可以用时间来定义（例如：每小时）或者用数量来定义（例如: 每批）。通常，每个子组由具有相同可测量单位和相同子组大 小的同一产品或服务所组成。从每一个子组得到一个或多个子 组特征值，如子组平均值X，子组极差R或标准差S。 常规控制图就是给定的子组特性值与子组号对应的一种图形 ，它包含一条中心线(CL)，作为所点绘特性的基准值。在评定 过程是否处于统计控制状态时，此基准值通常作为所考察数据 的平均值。对于过程控制，此基准值通常为产品规范中所规定 特性的长期值，或者是基于过程以往经验所点绘特性的标称值 ，或者是产品或服务的隐含目标值。控制图还包含由统计方法 确定两条控制线，位于中心线的各一侧，称为上控制限（ UCL),和下控制限（LCL)
统计量 P
中心线
3σ控制限
p
np
p ± 3× p 1− p / n
(
)
np
n p ± 3 n p 1− p
(
)
C u
c u
c±3 c
u ±3 u/n
这些控制图的计算是类似的，但子组大小发生变化时情况将有所不同。当子组大 小为常数，同一组控制限可以用于每一个子组；当子组大小发生变化时，则每一 子组都需要计算各自的控制限。因此，np图和c图可以用于子组大小为常数的情 况，而p图和u图则可以用于上述两种情形。 如果子组大小变化不大时，则可采用单一的基于平均子组大小的一组控制限。当 子组变化较大时，可采用另一种利用标准化变量的方法。例如：不点绘p值，而 改为点绘标准化值Z。公式如下：
R控制限的计算: UCLR=D4*R CLR=R LCLR＝D3*R D3,D4为常数，通过查表可得。
Me－R控制图在这里不进行示例讲解，大家可以根据以上两种图的做法进行 练习。
（4）X－Rs图 X－Rs图多用于下列场合：对每一个产品都进行检验，采用自动化检查和测量场合 ；取样费时、昂贵的场合；以及如化工与液体流程式的过程，产品均匀，多抽样也 无太大的意义的场合。由于它不像前三中控制图哪样取得较多的信息，所以它判断 过程的灵敏度也要差一些。 在单值控制图情形下，由于没有合理的子组来提供批内变异的估计，故控制限就基 于两个观测值的移动极差所提供的变差来计算。移动极差就是在一个序列中相邻两 个观测值质检的绝对差。 以下给出X－Rs图控制限的计算公式： Rs控制限的计算: UCLRs=D4*Rs CLRs=Rs LCLRs＝D3*Rs D3,D4为常数，通过查表可得。 X图控制限的计算： UCLX=X+E2*Rs CLX=X LCLX=X-E2*Rs E2为常数，通过查表可得。
我们如何制作X－R控制图呢？通过以下示例讲解 根据统计学原理导出的R，X的计算公式： R控制限的计算: UCLR=D4*R CLR=R LCLR＝D3*R D3,D4为常数，通过查表可得。
系数D3、D4的数值表 n D3 D4 2 0 3.267 3 0 2.574 4 0 2.282 5 0 2.114 6 0 2.004 7 0.076 1.924 8 0.136 1.864
Ca（准确度）＝
样本平均值－规格中心 样本平均值－规格中心 规格公差 / 2 规格公差 / 2
Cp（精确度）＝
规格公差 6σ
CPK（综合指标）＝（1-Ca）×Cp
序号 1
CPK CPK≥1.67 CPK≥1.67
制程能力判断 处置 太佳 制程了能力太好，可酌情 缩小规格，或考虑管理成 本的降低 理想状态，继续保持 使制程保持管制的状态， 否则产品随时有发生不良 品的危险，需注意 产品有不良品产生，需全 检，制程要妥善管理及改 善 应采取紧急措施，改善品 质并追究原因。
X-Rs图制作范例
（五）、计数型控制图 计数数据表示通过记录所考察的子组中每个个体是否具有某种特性（或特征 ），计算具有该特性的个体的数量，或记录一个单位产品。〕、一组产品、 或一定面积内此中事件发生的次数所获得的观测值。 在前面讲到计量控制图情形下，按通常惯例采用一对控制图，其中一张用于 控制平均值，另一张用于控制离散，因为计量控制图基于正态分布，而正态 分布取决于上下两个参数。在计数控制图情形下则不同，所假定的分布只有 一个独立的参数，即平均水平，故用一张控制图就足够了。P图和NP图基于 二项分布，而c图和u图则基于泊松分布。 控制图控制限的公式如下表：
X-R图制作范例
（2）X－S图 X-S图与X-R图相似，只是用标准差（s）代替极差（R）图而已。极差计算 简便，故R图得到广泛的应用，但当样本量n>10时，应用极差估计总体标 准偏差σ的效率减低，需要应用s图来代替R图。现在由于微机的应用基本普 及，s图的计算已经不成问题，故X-S图的应用也将越来越广泛。
许多场合，在控制图上另外加上2σ控制限是有益的。这样，任何落在2σ界 限外的子组值都可以作为失控状态即将来临的一个警示信号，因此，2σ控制 限有时也称作“警戒限”。在对控制图进行判断的是否，会用到1 σ，2 σ，3 σ限，这在后面会讲到。
二、控制图的应用和绘制 （1）X－R图控制图 对于计量数据而言，这是最常用最基本的控制图。它用于控制对象为长度，重量 ，强度，纯度，时间和生产量等计量值的场合。 X控制图主要用于观察正态分布的均值的变化，R图用于观察正态分布的分散或 变异的变化，而X-R图则将二者联合运用，用于观察正态分布的变化。
控制图的基本知识及应用
质量管理部 闻静
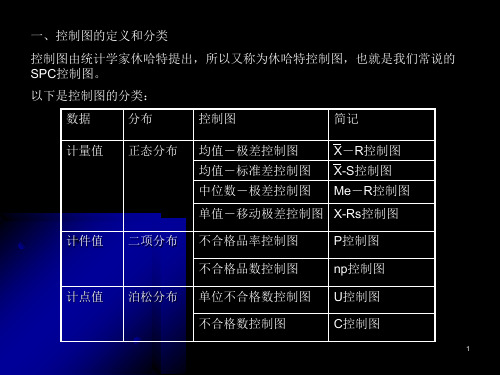
一、控制图的定义和分类 控制图由统计学家休哈特提出，所以又称为休哈特控制图，也就是我们常说的 SPC控制图。 以下是控制图的分类： 数据 计量值 分布 正态分布 控制图 均值－极差控制图 均值－标准差控制图 中位数－极差控制图 简记 X－R控制图 X-S控制图 Me－R控制图 Me－
3#铸轧线Fe含量标准偏差管控图 0.020 0.015 0.010 0.005 0.000 1 2 3 4 5 6 7 8 9 10 11
控制图的控制限分别位于中心线的两侧3σ距离处。3σ控制限表明，若过 程处于统计控制状态，则大约有99.7%的子组值将落在控制界限之内。换句话 说，当过程受控时，大约有0.3%的风险，或每点绘1000次中，平均有3次，描 绘点会落在上控制限或下控制线之外。