柱锥台球表面积
柱锥台球的体积与表面积

2 锥体的体积
V = 1/3πr²h
如何计算柱锥台球的体积
1
Step 1
测量柱体的半径(r)和高度(h)
Step 2
2
使用柱体的体积公式计算柱体的体积(Vc)
3
Step 3
测量锥体的半径(r)和高度(h)
Step 4
4
使用锥体的体积公式计算锥体的体积(Vc)
5
Step 5
将柱体的体积和锥体的体积相加得到柱锥台 球的总体积(V)
4
使用锥体的表面积公式计算锥体的表面积
(A c)
5
Step 5
将柱体的表面积和锥体的表面积相加得到柱 锥台球的总表面积(A)
柱锥台球的尺寸影响体积和表 面积吗?
柱锥台球的尺寸,如半径和高度,会直接影响它的体积和表面积。增加柱锥 台球的尺寸会增加其体积和表面积。
柱锥台球的体积和表面积之间 的关系
柱锥台球的体积和表面积之间是相互关联的。当柱锥台球的体积增加时,它 的表面积也会增加。
柱锥台球的表面积公式
1 柱体的表面积
A = 2πrh + 2πr²
2 锥体的表面积
A = πr(l + r)
如何计算柱锥台球的表面积径(r)和高度(h)
Step 2
2
使用柱体的表面积公式计算柱体的表面积
(A c)
3
Step 3
测量锥体的半径(r)和斜高(l)
Step 4
柱锥台球的体积与表面积
柱锥台球是一种特殊形状的台球,它由柱体和锥体两部分组成。在本演示中, 我们将讨论柱锥台球的体积和表面积,以及与数学和物理学的关系。
柱锥台球的形状
柱锥台球由一个底部较大的柱体和一个顶部较小的锥体组成。这种特殊形状 让它成为一个有趣的几何体。
1.3 柱、锥、台和球体的表面积和体积1
D A
1.设六正棱锥的底面边长为1,侧棱长 .设六正棱锥的底面边长为 , 那么它的体积为( 为 5 ,那么它的体积为( )
2.正棱锥的高和底面边长都缩小原来 .
1 则它的体积是原来的( 的 ,则它的体积是原来的( 2
)
5.已知圆锥的母线长为8,底面周长为 .已知圆锥的母线长为 , 6π,则它的体积是 , .
7. 若球的大圆面积扩大为原来的 倍,则 若球的大圆面积扩大为原来的3倍 它的体积扩大为原来的( 它的体积扩大为原来的( )倍?
8一个正方体的所有顶点都在球面上,若这 一个正方体的所有顶点都在球面上, 一个正方体的所有顶点都在球面上 个球的体积是V, 个球的体积是 ,则这个正方体的体积 是 .
D O A B E
C
已知正四棱锥底面正方形长为4cm, 例2. 已知正四棱锥底面正方形长为 , 高与斜高的夹角为30° 高与斜高的夹角为 °,求正四棱锥的侧 面积及全面积.(单位: 精确到0.01 ) 面积及全面积 (单位:cm2,精确到
棱柱、棱锥、 棱柱、棱锥、棱台 和球的体积
取一摞纸张放在桌面上(如图所示 取一摞纸张放在桌面上 如图所示) , 如图所示 并改变它们的放置方法, 并改变它们的放置方法,观察改变前后 的体积是否发生变化? 的体积是否发生变化?
2. 2.V圆台=π(r2+Rr+R2)h,其 )h,其 分别为圆台的上、 中r、R分别为圆台的上、 、 分别为圆台的上 下底面的半径,高为 下底面的半径,高为h.
A O B S C A' S' O' B' h D D' C'
五. 球的体积 4 V球= π R 3,其中 为球的半径 其中R为球的半径 为球的半径.
柱体、椎体、台体的表面积

S 2 r (r
【计算公式】
圆台表面积
S (r r r l rl )
2 2
棱柱、棱锥表面积 各面积之和,由于各面均为三角形,四边形,五 边形等等,所以在这里就不以公式形式列出.
柱体、椎体、台体的表面积
2r)×4=24π(cm2)
柱体、椎体、台体的表面积
【变形训练】 圆锥的底面半径为5 cm,高为12 cm,当它的 内接圆柱的底面半径为何值时,圆锥的内接圆 柱全面积有最大值?最大值是多少? 解:如图SAB是圆锥的轴截面,
其中SO=12,OB=5.设圆锥内
接圆柱底面半径为O1C=x,由
△SO1C∽△SOB,
知识点柱体椎体台体的表面积柱体椎体台体的表面积计算公式圆柱圆锥表面积2srrlsrrl柱体椎体台体的表面积计算公式圆台表面积22srrrlrl棱柱棱锥表面积各面积之和由于各面均为三角形四边形五边形等等所以在这里就不以公式形式列出
柱体、椎体、台体 的表面积
知识点——
柱体、椎体、台体的表面积
【计算公式】 圆柱,圆锥表面积
SO1 SO SO 12 , SO1 O1C x, 则 O1C OB OB 5
柱体、椎体、台体的表面积
【变形训练】
12 x ,则圆柱的 ∴OO1=SO-SO1=12- 5 12 x ) x+ 全面积S=S侧+2S底=2π(12- 5 7
2πx2=2π(12x-
5 30 360 cm2. 当x= cm时,S取到最大值 7 7 x ).
【典型例题】
3、已知圆台的母线长为4 cm,母线与轴的夹角 1 为30°,上底面半径是下底面半径的 ,求这 2 个圆台的侧面积. 解:如图是将圆台还原为圆锥 后的轴截面, 由题意知AC=4 cm, ∠ASO=30°, 1 O1C= OA,
高中数学 立体几何的柱,锥,台,球的公式
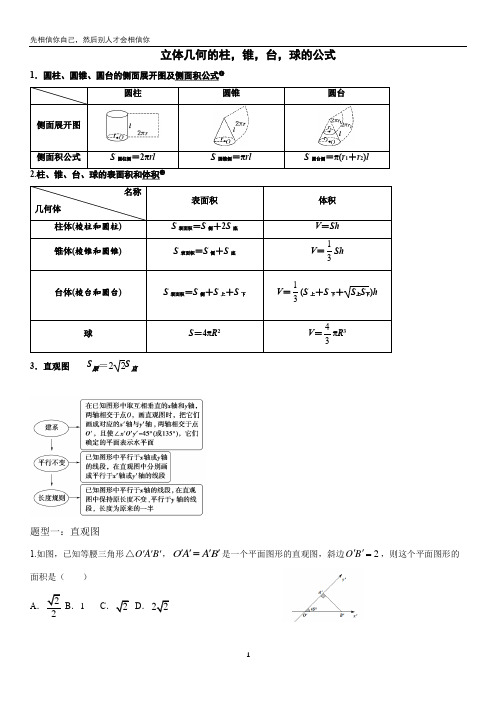
立体几何的柱,锥,台,球的公式1.圆柱、圆锥、圆台的侧面展开图及侧面积公式❶圆柱圆锥圆台侧面展开图侧面积公式S 圆柱侧=2πrlS 圆锥侧=πrlS 圆台侧=π(r 1+r 2)l2.柱、锥、台、球的表面积和体积❷名称几何体表面积 体积 柱体(棱柱和圆柱) S 表面积=S 侧+2S 底 V =Sh 锥体(棱锥和圆锥)S 表面积=S 侧+S 底V =13Sh 台体(棱台和圆台) S 表面积=S 侧+S 上+S 下 V =13(S 上+S 下+S 上S 下)h 球S =4πR 2V =43πR 3 3.直观图 S 原=22S 直题型一:直观图1.如图,已知等腰三角形O A B '''△,OA AB ''''=是一个平面图形的直观图,斜边2O B ''=,则这个平面图形的面积是( ) A .22B .1C .2D .222.一个梯形的直观图是一个如图所示的等腰梯形,且1A B ''=,3O C ''=,2O A ''=,则原梯形的面积为( )A .22B .42C .8D .43.如图所示为水平放置的正方形ABCO ,在平面直角坐标系xOy 中点B 的坐标为(2,2),用斜二测画法画出它的直观图A ′B ′C ′O ′,则四边形A ′B ′C ′O ′的面积为___________.4.如图所示,是三角形ABC 的直观图,则三角形ABC 的面积S △ABC =_______;(请用数字填写)5.如图,正方形O ′A ′B ′C ′的边长为1,它是一个水平放置的平面图形的直观图,则原图形的周长为( ) A .4 B .6C .8D .222+6.正三角形ABC 的边长为2 cm ,如图,△A’B’C’为其水平放置的直观图,则△A’B’C’的周长为( ) A .8 cmB .6 cmC .(2 +√6)cmD .(2 + 2√3)cm7.用斜二测画法画出水平放置的△ABC 的直观图如图所示,已知A’C’ = 3,B’C’ = 2,则△ABC 中AB 边上的中线长为_________.8.(多空题)在如图所示的直观图中,四边形O ′A ′B ′C ′为菱形且边长为2 cm ,则在平面直角坐标系中原四边形OABC 为________(填具体形状),其面积为________ cm 2.9.已知用斜二测画法得到的某水平放置的平面图形的直观图是如图所示的等腰直角△O B C ''',其中1O B ''=,则原平面图形中最大边长为( ) A .2B .22C .3D .2310.如图,△A ′B ′C ′表示水平放置的△ABC 根据斜二测画法得到的直观图,A B ''在x '轴上,B ′C ′与x '轴垂直,且2B C ''=,则△ABC 的边AB 上的高为( )A .2B .22C .4D .4211.如图所示,△A ′B ′C ′表示水平放置的△ABC 在斜二测画法下的直观图,A ′B ′在x ′轴上,B ′C ′与x ′轴垂直,且B ′C ′=3,则△ABC 的边AB 上的高为( ) A .6√2 B .3√3 C .3√2 D .3题型二棱柱、棱锥、棱台的表面积和体积1.正三棱锥的所有棱长均为a ,则该三棱锥的表面积为( ) A .33a 2B .23a 2C .3a 2D .4a 22.已知正四棱锥的底面边长是2,侧棱长是5,则该正四棱锥的表面积为( ) A .3B .12C .8D .433.已知高为3的棱柱ABC -A 1B 1C 1的底面是边长为1的正三角形,如图,则三棱锥B -AB 1C 的体积为( ) A .41 B .21 C .63 D .43 4.将一个棱长为a 的正方体,切成27个全等的小正方体,则表面积增加了( ) A .26aB .212aC .218aD.224a5.将一个正方体截去四个角后得到一个正四面体,这个正四面体的体积是正方体体积的( )A .21 B .31 C .61 D .41 6.如图所示,在三棱台ABC - A 1B 1C 1中,A 1B 1:AB = 1:2,则三棱锥B - A 1B 1C 1与三棱锥A 1 - ABC 的体积比为( ) A .1:2 B .1:3 C .1:2D .1:47.在底面半径为1的圆锥中,若该圆锥侧面展开图的面积是2π,则该圆锥的体积为( )A .B .C .D .8.已知球A 与球B 的体积之比为8:27,则球A 与球B 的半径之比为( ) A .:B .4:9C .2:3D .3:29.球的一个截面面积为49πcm 2,球心到球截面距离为24cm ,则球的表面积是 . 10.用一个平面截半径为25cm 的球,截面面积是49πcm 2,则球心到截面的距离是 . 11.已知一个长方体的三个面的面积分别是2,3,6,则这个长方体的体积为_________。
圆锥圆柱圆台球的表面积和体积公式

圆锥圆柱圆台球的表面积和体积公式圆锥、圆柱和圆台球是几何学中常见的三个立体图形,它们都具有特定的表面积和体积公式。
在本篇文章中,我将为您介绍这三个图形的定义、特点以及如何计算它们的表面积和体积。
一、圆锥圆锥是由一个圆和与圆上每一点相连的一条线段组成的立体图形。
圆锥有一个顶点和一个底面,底面是一个圆,而顶点则位于底面的正上方。
圆锥的表面积公式为:S = πr² + πrl其中,S表示圆锥的表面积,r表示底面圆的半径,l表示圆锥的斜高。
圆锥的体积公式为:V = (1/3)πr²h其中,V表示圆锥的体积,r表示底面圆的半径,h表示圆锥的高。
二、圆柱圆柱是由两个平行圆面和连接两个圆面的侧面组成的立体图形。
圆柱的底面是一个圆,而圆柱的高则是连接两个底面中心的线段。
圆柱的表面积公式为:S = 2πr² + 2πrh其中,S表示圆柱的表面积,r表示底面圆的半径,h表示圆柱的高。
圆柱的体积公式为:V = πr²h其中,V表示圆柱的体积,r表示底面圆的半径,h表示圆柱的高。
三、圆台球圆台球是由两个平行圆面和连接两个圆面的侧面组成的立体图形,其中一个圆面的半径较大,另一个圆面的半径较小。
圆台球的底面是一个圆,而圆台球的高则是连接两个底面中心的线段。
圆台球的表面积公式为:S = π(R+r)l + πR² + πr²其中,S表示圆台球的表面积,R表示底面较大圆的半径,r表示底面较小圆的半径,l表示圆台球的斜高。
圆台球的体积公式为:V = (1/3)πh(R²+r²+Rr)其中,V表示圆台球的体积,R表示底面较大圆的半径,r表示底面较小圆的半径,h表示圆台球的高。
通过以上公式,我们可以方便地计算出圆锥、圆柱和圆台球的表面积和体积。
这些公式的应用范围广泛,例如在建筑设计、工程测量以及日常生活中都有重要的应用。
在实际问题中,我们可以根据给定的数据,将公式中的参数代入,计算出具体的数值。
柱体、锥体和台体的表面积的计算

台体的表面积
定义和特点
台体是由两个平行的圆形底 面和它们之间的侧面组成的 立体。
表面积计算公式
台体的表面积 = π(R + r)l + πR² + πr²,其中 R 是上底圆 的半径,r 是下底圆的半径, l 是台体的斜高。
示例
如果台体的上底圆半径为 4 米,下底圆半径为 3 米,斜 高为 6 米,则表面积为 191.03 平方米。
使用公式计算表面积的注意事项
1 单位一致
确保所有的尺寸都使用同 一种单位(如米、厘米) 进行计算和输入。
2 精确度
在计算过程中保持足够的 精确度,以避免计算结果 的误差。
3 要素考虑
根据不同几何体的表面积 计算公式,确保将所有必 要的参数(如底面半径、 高度、斜高)全部考虑进 去。
表面积计算应用举例
柱体、锥体和台体的表面 积的计算
欢迎来到本次演讲,我们将深入探讨柱体、锥体和台体的表面积计算方法以 及它们的定义和特点。
柱体的表面积
1 定义和特点
柱体是一个横截面为圆形的立体,表面由两个圆和一个侧面组成。
2 表面积计算公式
柱体的表面积 = 2πr² + 2πrh,其中 r 是底面圆的半径,h 是柱体的高度。
3 示例
如果柱体的半径为 3 米,高度为 5 米,则表面积为 94.25 平方米。
锥体的表面积
定义和特点
锥体是一个横截面为圆形且垂直 于底面的立体,表面由一个底面 圆和一个侧面组成。
表面积计算公式
锥体的表面积 = πr² + πrl,其中 r 是底面圆的半径,l 是锥体的斜 高。
示例
如果锥体的底面半径为 4 米,斜 高为 5 米,则表面积为 94.97 平 方米。
柱、锥、台、球的表面积与体积精例

表面积与体积
X
一. 棱柱的侧面积、表面积与体积 1. 直棱柱的侧面积、表面积与体积
S侧=C•h
S表= S侧+2S底 S表= S侧+2S底
V棱柱= S•h
2. 斜棱柱的侧面积、表面积与体积
S侧=C’•L
二. 棱锥的侧面积、表面积与体积
S侧= S△1+S △2 +S △3 +… S表= S侧+S底
2
它的体积是
2cm
俯视图
4_________. 2 cm
4 3
3
例2
已知长方体ABCD-A1B1C1D1的长、宽、高分别 为3,2,1,求沿其表面从点A到点C1的最短距离。 D1 C1 B1 A1 1 C E D
2 2 3
A
B 1
例2
已知长方体ABCD-A1B1D1的长、宽、高分别为3, 2,1,求沿其表面从点A到点C1的最短距离。 D1 C1 B1 F A
A
5 4 B 4
3 C B 4 C
12 5
5
5
A
A
3
C
3
思考:
1.用棱长为1的正方体的体积作为单位体积,下图 长方体的体积的数值为24.假如将体积单位改用棱 长为2的正方体的体积,这个长方体的体积变为多 少?
2.一个正方体和一个圆柱等高,并且侧面积相等。 比较它们的体积哪个大?为什么? P 3.求证:经过长方体相对两个面 的中心的任意平面,把长方体分 成体积相等的两个柱体。 Q
1
D
2
1 C 2
1
A
3Ba来自 例2已知长方体ABCDD1 A1B1C1D1的长、宽、高分 别为3,2,1,求沿其表面 A1 从点A到点C1的最短距离。 D
柱锥台球表面积和体积获奖解析PPT课件

S侧面积
=
1 2
c2(l+x)-
1 2
Cc1’Xx
=
1 2
c2 l +
1 2
c2x
-
1 2
c1x
=
1 2
+ 12(c2 - c1)X
S
又∵
c1 c2
=
X X+l
∴
x
=
c1 l c2- c1
c1 c2
=
1 2
+
12(c2
-
c1)cc21-
l
c1
l
O 1 rr1 M
l
=
1 2
+
1 2
c1l
r R2
O2
N
例3.已知正四棱台上底面边长为4 cm,侧棱和下底面边
长都是8 cm,求它的侧面积.
[解] 法一:在 Rt△B1FB 中, B1F=h′, BF=12(8-4)=2,B1B=8, ∴B1F= 82-22=2 15, ∴h′=B1F=2 15. ∴S 正棱台侧=4×12×(4+8)×2 15 =48 15(cm2).
三.台体的表面积(一)
1
S侧正棱台= 2 (c+c’)·h’
a' h h'
a
台体的表面积(二)
如图,上底周长是 c’=2πr1、c=πr2,侧面母线长 是l
S侧面积 = (12 c 1+c2)l=∏(r 1+r2)l
S
c1 c2
O 1 rr1 M
l
l
r R2
O2
N
证明: 将圆台补成圆锥.作其侧面展开图,设SM=x
人教版高中数学必修二(B版)第一章 P25-32
