(完整版)理论力学课后习题答案第11章达朗贝尔原理及其应用
《理论力学(Ⅰ)》PPT 第11章
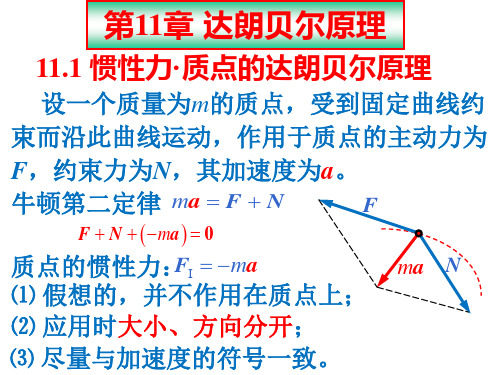
11.1 惯性力·质点的达朗贝尔原理
设一个质量为m的质点,受到固定曲线约
束而沿此曲线运动,作用于质点的主动力为
F,约束力为N,其加速度为a。
牛顿第二定律 ma F N
F
F N ma 0
质点的惯性力:FI ma
ma N
⑴ 假想的,并不作用在质点上;
⑵ 应用时大小、方向分开;
FAy
l aC1 2 α1
ml FIC1 maC1 2 α1
M IC1
ml 2 12 α1
A
FIC1
FAx αM1
IC1
l aC2 lα1 2 α2
ml 2 M IC2 12 α2
FIC2
maC2
mlα1
ml 2
α2
Fmg C1aC1
B α FIC2
2
M IC2
mg C2aC2
Fix 0
ωα O aC ain
MO
MO JOα
Fi M O Fit α miri2 M
负号表示矩的转向与α相反
IO
x
C
FIO FIit
y
ait FIin
结论:⑴ 定轴转动刚体惯性力系向轴心简
化,结果为通过轴心的一个惯性力和一个惯
性力偶。 FIO MaC,M IO JOα ⑵ 定轴转动刚体惯性力系向质心简化,结
ae P
FIAe
ar
P sin 2φ
aB ae 2 Q P sin2 φ
B Q FIB
φ
N
例11-6 长为l、质量为m的两均质细杆AB和 BD,用光滑铰链B相连接,并自由地挂在铅 直位置。今以水平力F作用于AB杆的中点, 求此瞬时两杆的角加速度及A点的约束力。
理论力学11

Mo (Fi ) Mo (FNi ) Mo (FIi ) 0
由此可得: 作用在质点系中所有的主动力、约束力和
惯性力在形式上构成平衡力系。这就是质点系 的达朗贝尔原理(形式2)。
由于质点系的内力总是成对存在,且等值、反 向、共线,因此上式中将不包含内力。
例 2 已知一飞轮,质量为m ,质量可认为分
内任一质点的质量为mi,到 转轴的距离为ri, 则刚体内任 一质点的惯性力为FIi=-miai。
在转轴上任选一点O为简化 中心, 建立直角坐标系如图, 质点的坐标为xi, yi, zi, 现分 x 别计算惯性力系对三个坐标 轴的矩MIx, MIy, MIz。
z
ai ri mi
k Oj
zi FIi
y
i yi xi
gl
sin q
xd
x
dFI
B x
dFI d m an
Pw2 sinq x d x
gl
于是整个杆的惯性力的 合力的大小为
y C
w
A
q
an
dFI
B x
RI
l Pw2 sinq x d x P lw2 sinq
0 gl
2g
设RI的作用点到点A的距离为d, 由合力矩定理有
l
RI (d cosq ) 0 (x cosq ) d FIi
11.2.2 刚体绕定轴转动
现在讨论以下三种特殊情况:
MIO
1. 当转轴通过质心C时, aC
=0, FIR=0, MIO=-JCa。
此时惯性力系简化为一惯
O
w a
理论力学第十一章 达朗贝尔原理(动静法)

讨论:1)脱离角α与滚筒的角速度和滚筒半径有关,而与钢球质量无关。
2)
筒壁。此时转筒
的转速称为临界转速,对球磨机而言,要求n小于nL,否则球磨机就不能工作。
§11-2 刚体惯性力系的简化
刚体平移时惯性力系的简化
当刚体平移时,任一瞬时体内各点的加速度相等。若记某瞬 时刚体质心加速度为aC,则该瞬时体内任一质量为m的质点 的加速度ai=aC,虚加在该点上的惯性力Fgi=-miai=-miaC 。 刚体内每一点都加上相应的惯性力,由静力学知,该空间平 行力系可简化为过质心的合力,即
式中,Fgτ=-maτ,称为切向惯性力 Fgn=-man称为法向惯性力(也称离心力)
负号表示它们分别与切向加速度和法向加速度的方向相反。
§11-1 惯性力与质点的达朗贝尔原理
质点系的动静法
对由n个质点组成的非自由质点系,设其中任一质点的质量 为mi,某瞬时加速度为ai,作用其上的主动力F,约束反力 Fni,假想在该质点上加上惯性力Fgi=-mai,由质点达朗贝 尔原理,则
=- maC
该力偶的力偶矩等于惯性力系对刚体惯性力系的简化
结论 当刚体有质量对称面,且绕垂直于质量对称面的定轴 转动时,惯性力系可以简化为对称面内的一个力和一个力偶。 该力等于刚体的质量与质心加速度的乘积,方向与质心加速 度方向相反,且力的作用线通过转轴;
该力偶的力偶矩等于刚体对转轴的转动惯量与角加速度的乘 积,其转向与角加速度转向相反。惯性力系向点O简化的结 果如图b)所示。
Fg=-m a
质点的达朗伯原理:质点在运动的每一瞬时,作用 于质点上的主动力、约束反力与假想地在质点上 的惯性力,在形式上构成一平衡力系。
§11-1 惯性力与质点的达朗贝尔原理
理论力学-达朗贝尔原理及其应用

t aC
FIR =-m a C
a
n C
C
n FR
t n 2、定轴转动 FIR =-m aC =-m( aC aC )
FR
3、平面运动 FIR =-m a C
C
O
FR
Ft R
aC
12.3 刚体惯性力系的简化
惯性力系的主矩与刚体的运动形式有关!
理论力学 第三篇 动力学
第三篇 动力学
第12章 达朗贝尔原理
第12章 达朗贝尔原理
12.1 质点惯性力与达朗贝尔原理 12.2 质点系的达朗贝尔原理 12.3 刚体惯性力系的简化
第12章 达朗贝尔原理
12.1 质点惯性力与达朗贝尔原理
12.1 质点惯性力与达朗贝尔原理
z m A
FI2 a1
m C FIi m2 a2
mi
FR FIi mi ai maC
主矢
ai
FIR maC
主矢与刚体的运动形式无关。
主矩
12.3 刚体惯性力系的简化
刚体平移时,惯性力系向质心简化 ● 主矢
1.刚体作平移
m1
FIR maC
FI2
m2 FI1
a2 maC FIR an m FIn n
12.2 质点系的达朗贝尔原理
例题3
FnIi FtIi F at an
Ny
r
a
FI1
A
mg
解: 对象:系统 受力:如图 运动:略 方程: FNx 惯性力 F I1 n FI 2 a F dm a
B m2g
B 理论力学-第11章 达朗贝尔原理及其应用-2解析

本课程有部分内容与《大学物理》重复,如点的运动、刚体 简单运动、质点运动微分方程、质点的动量、动量矩和动能 定理等,对这些内容,本课程只作适当的复习或让学生自学。
第11章 达朗贝尔原理及其应用
引入惯性力的概念,应用达朗贝尔原理,将静力学中求解 平衡问题的方法用于分析和解决动力学问题。这种方法称为 “动静法”。“动”代表研究对象是动力学问题;“静”代表 研究问题所用的方法是静力学方法。 达朗贝尔原理是在18世纪随着机器动力学问题的发展而提 出的,它提供了有别于动力学普遍定理的新方法,尤其适用于 受约束质点系统求解动约束力和动应力等问题。因此在工程技 术中有着广泛应用,并且为“分析力学”奠定了理论基础。 达朗贝尔原理虽然与动力学普遍定理具有不同的思路, 但却获得了与动量定理、动量矩定理形式上等价的动力学方程, 并在某些应用领域也是等价的。
刚体作定轴转动时惯性力系的简化结果
这里仅讨论刚体有质量对称 面且转轴与质量对称面垂直的
情形。这种情形下,可以先将
惯性力系的主矢与刚体的运动形式无关;惯性力系的主矩 与刚体的运动形式有关。
刚体平移时惯性力系的简化结果
刚体平移时,由于同一瞬时刚体内各质点的加速度都相同, 惯性力系为平行力系,所以,惯性力系简化结果为通过质心C 的合力,用FIR表示:
FIR m a C
其中m为刚体的质量;aC为刚体的质心加速度。
e i Ii e O i
O ( FIi ) 0
这两个矢量式可以写出六个投影方程。 根据达朗贝尔原理,只要在质点系上施加惯性力,就 可以应用上述方程求解动力学问题,这就是质点系的动静法。
11.2 惯性力系的简化
惯性力系的主矢与主矩 刚体平移时惯性力系的简化结果
刚体作定轴转动时惯性力系的简化结果 刚体作平面运动时惯性力系的简化结果
理力11(动力学-李卓球)-达朗贝尔原理
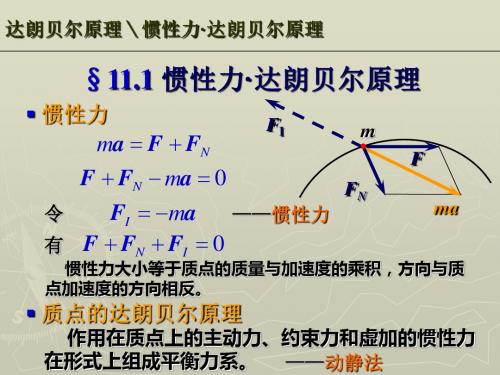
(e) (i ) M ( F ) M ( F ) M ( F ) 0 O i O i O Ii (e) F i FIi 0 (e) M O (Fi ) M O (FIi ) 0
小。
3
例题
第11章 达朗贝尔原理
例 题 11-1
4
例题
第11章 达朗贝尔原理
例 题 11-1
解: 以小球为研究的质点。质点作匀速圆周
运动,只有法向加速度,在质点上除作用有
O θ
重力mg和绳拉力F外,再加上法向惯性力FI,
如图所示。
l
v2 FI man m l sin
F eb en mg
作用在质点上的主动力、约束力和虚加的惯性力 在形式上组成平衡力系。 ——动静法
..\惯性力· 达朗贝尔原理\质点的达朗贝尔原理
质点达朗贝尔原理的投影形式
Fx FNx FIx Fx 0 Fy FNy FIy Fy 0 Fz FNz FIz Fz 0
i i i
应用达朗贝尔原理求解质点动力学问题的步骤
1、分析质点所受的主动力和约束力; 2、分析质点的运动,确定加速度; 3、在质点上施加与加速度方向相反的惯性力。 4、应用达朗贝尔原理建立平衡方程求解
2
例题
第11章 达朗贝尔原理
例 题 11-1
如图所示一圆锥摆。质
O θ l
量m = 0.1 kg的小球系于长l = 0.3 m 的绳上,绳的一端 系在固定点 O ,并与铅直线 成θ =60º 角。如小球在水平 面内作匀速圆周运动,求小 球的速度v与绳的张力F的大
理论力学——达郎贝尔原理

(e) FIR - Fi -ma c
M IO M Iz -J z
讨论 ①刚体作匀速转动,转轴不通过质点C 。
求解步骤 ①选取研究对象。原则与静力学相同。 ②受力分析。画出全部主动力和外约束反力。
③运动分析。主要是刚体质心加速度,刚体角加速
度,标出方向。 ④虚加惯性力。在受力图上画上惯性力和惯性力偶, 一定要 在 正确进行运动分析的基础
上。熟记刚体惯 性力系的简化结果。
⑤列动静方程。选取适当的矩心和投影轴。 ⑦求解求知量。
M
y
解得
1 M y FRxOB M Ix M IxOB FAx AB
1 M x FRyOB M Ix FIyOB FAy AB
1 M y FRxOA M Ix FIxOA FBx AB
1 M x FRyOA M Ix FIyOA FBy AB
min
求:轴承A,B的约束力
解:
0.1 12000π 1 an e m 158 m 2 s s 1000 30
2
2
F man 3160N
n I
FNA FNB
1 20 9.8 3160N 1680N 2
内容
§13-1
惯性力〃质点的达朗贝尔原理
Force of Inertia ·D’Alembert’s Principle of a Particle
§13-2 质点系的达朗贝尔原理
理论力学11—达朗贝尔原理2
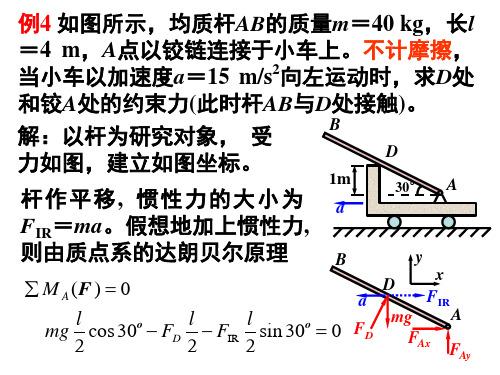
静平衡与动平衡的概念
静平衡:
动平衡:转轴为中心惯性主轴时, 转动时不产生附加动反力。 动平衡的刚体,一定是静平衡的; 反过来,静平衡的刚体,不一定是动平 衡的。
[例8] 质量不计的转轴以角速度 匀速转动, 其上固结着两个质量均为m的小球A和B。指出 在图示各种情况下,哪些是静平衡的?哪些是 动平衡的?
z B
FB
由式 (1) 和 (2) 解得
b e FA (1 )P ab g
2
FIO
A
FA
O C
e
a e FB (1 )P ab g
2
aP
(b)
b
两轴承所受的力分别和 FA 、FB 的大小相等而 方向相反。
E 例10 均质杆的质量为m, 长为2l, A 一端放在光滑地面上, 并用两软 a C 绳支持 , 如图所示。求当 BD 绳 aB t 30o 切断的瞬时, B点的加速度、AE aCB B 绳的拉力及地面的约束力。 D aB 解: 以杆AB为研究对象,杆AB y FT 作平面运动。 以点 B为基点, A E 则点C 的加速度为
sin j r l r 4
2 2
MA
y FAy
C
B
x
cos j
l
2 l 2 r2 4
将已知数值代入以上三式,解之得
FAx mra
l FAy mg ma 2
1 1 2 M A W,B端与重G、半径为 r的均质圆轮铰接。在圆轮上作用一矩为M的力 偶,借助于细绳提升重为P的重物C。试求固定 l 端A的约束力。 解:先以轮和重物为研究对象 , A B 受力如图。假想地加上惯性力 M
M A (F ) 0
C
a
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第 11 章 达朗贝尔原理及其应用11-1 均质圆盘作定轴转动,此中图( a ),图( c )的转动角速度为常数,而图( b ),图( d )的角速度不为常量。
试对图示四种情况进行惯性力的简化。
≠≠(a )(b )(c )(d )习题 11-1 图F I F I nOO F I tM I OO O≠M IO≠(a )(b )(c )( d )习题 11-1 解图解:设圆盘的质量为m ,半径为 r ,则如习题 11-1 解图:(a ) F I mr 2 , M I O 0( b ) F I nmr 2 , F I tmr ,M IOJ O3 mr 22( c ) F I 0,M IO 0( d ) F I0,M IOJ O1 mr 2211- 2 矩形均质平板尺寸如图,质量 27kg ,由两个销子AA 、B 悬挂。
若忽然撤去销子 B ,求在撤去的刹时平板的角加速度和销子A 的拘束力。
C解:如图( a ):设平板的质量为 m ,长和宽分别为 a 、 b 。
F I mM I AJ A[ 1m( a 2 b 2 ) m AC 2] 习题 11-2 图122F AyM A (F ) 0;M IA 0 ; 47.04 rad/s F IF Ax AF x0 ; F I sinF Ax0 ;此中: sin3M IA 5CF Ax95.26 NF y0 ; F I cosF Aymg0 ; sin4aC mg5Bm5 1 .Bm51.F Ay 27 9.8 3.375 47.04 0.8 137.6 N11- 3 在均质直角构件 ABC 中, AB 、 BC 两部分的质量各为 AE 保持在图示地点。
若忽然剪断绳索,求此刹时连杆 AD 、 BE已知 l = 1.0m , φ= 30o 。
3.0kg ,用连杆 AD 、 DE 以及绳索所受的力。
连杆的质量忽视不计,C解:如图( a ):设 AB 、 BC 两部分的质量各为 m = 3.0kg 。
l直角构件 ABC 作平移,其加快度为a = a A ,质心在 O 处。
lF I2maABM O (F)0 ;φφl3llF B cos F A cos (F A F B ) sin 0( 1)DE4 44FAD0 ;习题 11-3 图F A F B 2mg cos( 2)C联立式( 1)和式( 2),得: F B mg 3F A3l/4F I1F A( 3 1)mg5.38 N ;3l/4 O4ABaA F AF Bmg 345.5 NF B φ 2mg φ(a )11- 4 两种情况的定滑轮质量均为 m,半径均为 r 。
图 a 中的绳所受拉力为 W ;图 b 中块重力为 W 。
试剖析两种情况下定滑轮的角加快度、绳中拉力和定滑轮轴承处的拘束反力能否同样。
解: 1、图( a ):① J O a Wr1mr 2Wr2aa 2W(1)mr②绳中拉力为 W(2)③F x 0 , F Ox(3)F y0 , F OyW(4)2、图( b ):① M IO1 mr2 b (5)2F I W W(6)a r bg gM O 0, M IOF I r Wr 0(5)、( 6)代入,得b2Wg(7)r (mg 2W )②绳中拉力(图c ):F y 0 , T bF I WT b W W a mg W(8)gmg 2W③轴承反力:F x0 , F Ox 0(9)F y0 , F Oy F I WF OymgW(10)mg 2WbF OyF OyF OxF OxM I OaF Ia W习题 11-4 图T bF IaW(a)因而可知,定滑轮的角加快度 a 、 b ,绳中拉力,轴承反力均不同样。
11- 5 图示调速器由两个质量各为m1的圆柱状的盘子所构成,两圆盘被偏爱地是悬于与调速器转动轴相距 a 的十字形框架上,而此调速器则以等角速度绕铅垂直轴转动。
圆盘的中心到悬挂点的距离为l,调速器的外壳质量为m2,放在这两个圆盘上并可沿铅垂轴上下滑动。
如不计摩擦,试求调速器的角速度与圆盘偏离铅垂线的角度之间的关系。
解:取调速器外壳为研究对象,由对称可知壳与圆盘接触地方受之拘束反力为 m2 g / 2 。
取左圆盘为研究对象,受力如图(a),惯性力F I m1( a l sin)2由动静法m2 g ym2g)l sin2FAy习题 11-5 图M A0 ,( m1g F I l cos02OFAx x将 F I值代入,解出F I A22m1m2g t an2m1 (a l sin)m1 g(a)11- 6 图示双重物经过无重滑轮用绳连结,滑轮又铰接在无重支架上。
已知物G1、G2的质量分别为 m1 = 50kg , m2 = 70kg ,杆 AB 长 l1 = 120cm , A、C 间的距离 l2= 80cm ,夹角θ= 30 ?。
试求杆CD 所受的力。
F B FAyBAB F Ax AθC F I1 F I2BθG1C D G1G2a F CD F B′G2m1gm2 g习题 11-6 图( a)( b)解:取滑轮和物 G1、G2如图( a)所示,设物 G1、G2的加快度为 a,则其惯性力分别为:F I 1 m1a ; F I 2 m2aM B(F ) 0;(F I1FI 2m1 g m2 g)r 0 ; a m2m1g20 g gm2m11206F y 0 ;F B F I 1F I 2m1g m2 g0;F B10g120g350 g取杆 AB 为研究对象,受力如图(b)所示,33M A(F)0; F CD sin l2F B l1 0 ; F CD 2l1350g3430 N 3.43 kN l2311- 7 直径为、重 890N的匀质圆柱以图示方式装置在卡车的箱板上,为防备运输时圆柱前后转动,在其底部垫上高10.2cm 的小木块,试求圆柱不致产生转动,卡车最大的加快度?F I O amg0.102mA解:图( c )中F I maM AF I 0 .102)2( 0.61 0.102)2mamg22a maxa 6.51 m/s 2议论 :若 a a max ,则惯性力惹起的对 A 点的力矩会大于重力 mg 对 A 点的矩,使圆柱向后转动。
原文求a min 不合理。
11- 8两匀质杆焊成图示形状,绕水平轴 A 在铅垂平面内作等角速转动。
在图示地点时,角速度0.3 rad/s 。
设杆的单位长度重力的大小为100N/m 。
试求轴承 A的拘束反力。
解:( 1)求 A 处拘束力重力: P 100 30 N质量: m 100 3.061 kg质心 O 点地点: r 0.1333 mF Inmr2F I τ 0 ( 0 )习题 11-8图轴承 A 的拘束反力F Ax0.122 N ( F x0 )FAy30 N (F y0 )FAy(2)求 B 截面弯矩Cr考虑 BD 段受力,只有惯性力d F I ,在 yFInAFAxB方向重量对 B 截面弯矩有贡献。
OP微段质量:100 N/m Dd md xg(a)yAd F Id m x 222x 22d xd F I y d F I coshxdF IyR0.3100x22d xdxx 22dF I0.2 1006Dd x d x0 .05M Axd F I y6x d x 61 0 .052(b)2=0.000765N m=0·.765N ·mm11- 9 图示均质圆轮铰接在支架上。
已知轮半径、重力的大小 Q = 20kN ,重物 G 重 力的大小 P = 100N ,支架尺寸l = 0.3m ,不计支架质量,轮上作用一常力偶,其矩 M = 32kN ·m 。
试求( 1 )重物 G 上涨的加快度; ( 2)支座 B 的拘束力。
l lF OF A llF BM IOABOM ABCDQCDF IO MG aOG习题 11-9 图PF O ′(a )(b )解:取滑轮和物 G 1、G 2 如图( a )所示,设物 G 1、G 2 的加快度为 a ,则其惯性力分别为:F I 1 m 1a ; F I 2 m 2aM B (F ) 0; (F I1F I 2m 1 g m 2 g)r 0 ; a m 2m1 g 20 g gm 2 m 1 120 6 F y 0 ; F B F I 1 F I 2m 1gm 2 g 0 ;F B10g120g350 g 取杆 AB 为研究对象,受力如图( b )所示,33M A (F ) 0 ; F CD sin l 2F B l 1 0; F CD2l 1 350 g 3430 N 3.43 kNl 2 311- 10 图示系统位于铅直面内,由鼓轮 C 与重物半径 R = 2 r ,对过 C 且垂直于鼓轮平面的轴的展转半径轮中心 C 的加快度; ( 2) AB 段绳与 DE 段绳的张力。
A 构成。
已知鼓轮质量为m ,小半径为 r ,大 ρ= 1.5 r ,重物 A 质量为 2m 。
试求( 1)鼓F DE解:设鼓轮的角加快度为 ,在系统上加惯性力如图( a )所示,则其惯性力分别为:FI C mr ; F IA 2m rMI CJ Cm22mr M D (F)0 ;(mg F I C F I A 2mg) rM a Cr3g4 g221EEF AB F ICM ICF IACD BCD BA a A2F IAAmgA2mgI C 0( a )2mg( b )习题 11- 10 图F y 0;F DEF IC F I A mg 2mg0; F DE3mg mr59 mg取重物 A 为研究对象,受力如图(b )所示,21F y0;F ABF I A 2mg 0; F AB2mg 2mr2(14)mg34 mg212111- 11 凸轮导板机构中,偏爱轮的偏爱距 OAe。
偏爱轮绕 O轴以匀角速度 转动。
当导板 CD在最低地点时弹簧的压缩为 b 。
导板质量为 m 。
为使导板在运动过程中一直不走开偏爱轮,试求弹簧刚度系数 的最小值。
解:此题结果与 转向没关,因议论加快度。
1、图( a ),导板上点 B 的运动代表导板运动y B esin t ray B e 2 sint当 πt时, a 取极值2y习题 11-11 图F Ia e2,方向向下。
2、导板受力:πF Imgamax时,导板上受惯性力k2B2,方向向上。
CDF Imer此力力争使导板与凸轮脱开,AFF 与板重 为使不脱开,应使弹簧力O exOπ 力 mg 之和大于 F I :2xmg FF Img k(2e b) mekm(e 2g )2e b议论 :1、当 e 2g 时,表示可不加弹簧。
3、板至最低地点时, a 也取极植,但此时惯性力是向下的,不存在离开凸轮的问题。
