组合图形的面积练习题
小学五年级数学《组合图形的面积》试题及答案

五年级数学(上册):《组合图形的面积》试题1、求图形的面积(单位:厘米)梯形面积:三角形面积:(8+12)×8.5÷2 12×3÷2= 20×8.5÷2 = 36÷2= 170÷2 = 18(cm2)= 85(cm2)图形面积= 梯形面积–三角形面积:85-18=67(cm2)2、校园里有两块花圃(如图),你能计算出它们的面积吗?(单位:m)图形面积=长方形面积6×(5-2)+ 正方形面积(2×2)图形面积=长方形面积 - 梯形面积6×(5-2)+ 2×2 10×6 –[(3+6)×2÷2 ]= 6×3 + 4 = 60 -[ 9×2÷2 ]= 18 + 4 = 60 - 9= 22(m2)= 51(m2)3、下图直角梯形的面积是49平方分米,求阴影部分的面积。
直角梯形的高=直角三角形的高(阴影部分面积)直角梯形的高= 49÷(6+8)×2 直角三角形面积= 6×7÷2= 49÷14× 2 = 42÷2= 3.5× 2 = 21(dm²)= 7(dm²)4、图中梯形中空白部分是直角三角形,它的面积是45平方厘米,求阴影部分面积。
直角梯形的高=直角三角形的高梯形面积=(5+12)×7.5÷2= 45÷12×2= 17×7.5÷2= 3.75×2 = 127.5÷2= 7.5(cm2)= 63.75(cm2)阴影部分面积=梯形面积–空白部分面积:63.75 - 45 = 18.75(cm2)5、阴影部分面积是40平方米,求空白部分面积。
(单位:米)梯形的高=三角形的高(阴影部分三角形)梯形面积=(6+10)×8÷2= 40÷10× 2 = 16×8÷2= 4× 2 = 128÷2= 8(m2)= 64(m2)空白部分面积=梯形面积–阴影部分面积:64–40 = 24(m2)6、如图,平行四边形面积240平方厘米,求阴影部分面积。
五年级组合图形的面积精选32题
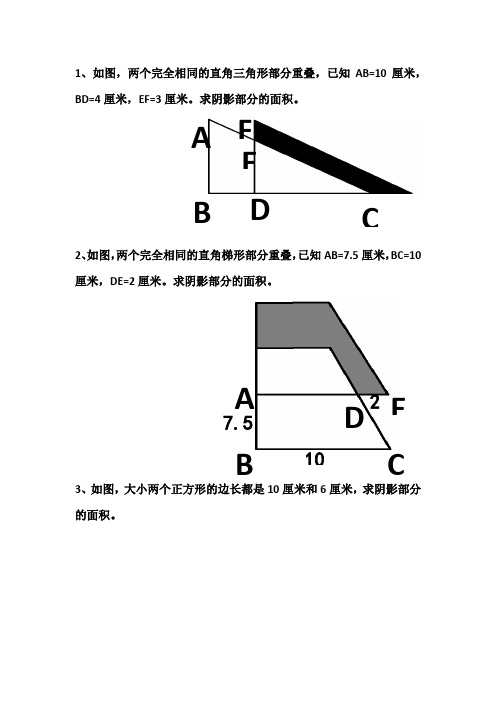
1、如图,两个完全相同的直角三角形部分重叠,已知AB=10厘米,BD=4厘米,EF=3厘米。
求阴影部分的面积。
2、如图,两个完全相同的直角梯形部分重叠,已知AB=7.5厘米,BC=10厘米,DE=2厘米。
求阴影部分的面积。
3、如图,大小两个正方形的边长都是10厘米和6厘米,求阴影部分的面积。
ABCDEFADEBC107.524、如图,大小两个正方形的边长都是10厘米和6厘米,求阴影部分的面积。
5、如图,由长方形ABCD 和直角梯形BEFC 组成,其中阴影部分的面积是36.5平方厘米,CD 是5厘米。
求长方形ABCD 的面积。
6、如图,平行四边形ABCD 的底BC 长12厘米,线段EF 长8.3厘米,求图中阴影部分的面积总和是多少平方厘米?ABCDEFABCDFEG7、如图,梯形上底长5.4厘米,下底长8.6厘米,高长4厘米,求三角形甲的面积比三角形乙的面积小多少平方厘米?8、如图,ABCD 是长方形,AB=8厘米,BC=6厘米,三角形ABF 的面积比三角形DEF 的面积大12平方厘米,求DE 长多少厘米?9、如图,平行四边形ABCD 的底BC 长10厘米,直角三角形FBC 的直角边FC 长8厘米。
已知阴影部分的总面积比三角形EFG 的面积大10平方厘米。
求EF 的长度。
甲乙ABCDEF8681010、如图,△ABC 和△DCB 都是直角三角形,已知AB=3.4厘米,BC=7.2厘米,且甲比乙的面积大3.6平方厘米,求CD 的长。
11、如图,CA=AB=4厘米,三角形ABE 的面积比三角形CDE 的面积小2平方厘米,求CD 的长。
12、如图,甲的面积比乙的面积大36平方厘米,已知AB 长8厘米,BC 长12厘米,CD 长6厘米,求DE 的长。
ABCD甲乙7.23.4ABCDE4ABCDE 甲乙812613、如图,D 是AC 的中点,E 、F 是BC 边上的三等分点,已知阴影部分的面积为20平方厘米,求三角形ABC 的面积。
北师大版数学五年级上册 第六单元《组合图形的面积》测试卷(含答案)
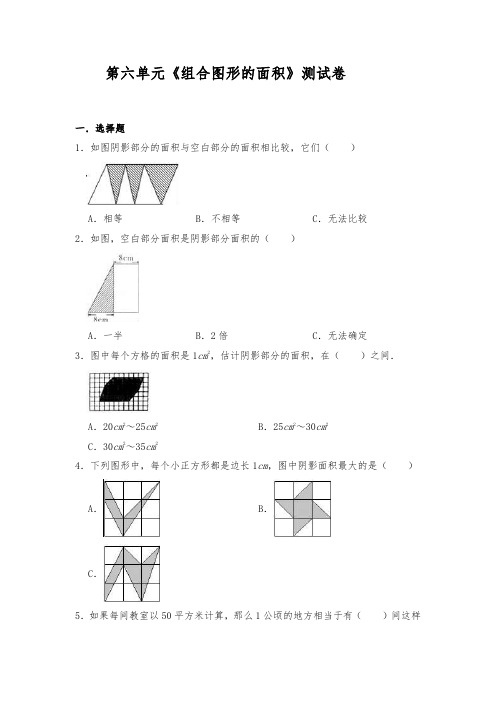
第六单元《组合图形的面积》测试卷一.选择题1.如图阴影部分的面积与空白部分的面积相比较,它们()A.相等B.不相等C.无法比较2.如图,空白部分面积是阴影部分面积的()A.一半B.2倍C.无法确定3.图中每个方格的面积是1cm2,估计阴影部分的面积,在()之间.A.20cm2~25cm2B.25cm2~30cm2C.30cm2~35cm24.下列图形中,每个小正方形都是边长1cm,图中阴影面积最大的是()A.B.C.5.如果每间教室以50平方米计算,那么1公顷的地方相当于有()间这样A.20 B.200 C.2000 D.506.北京故宫的占地面积是720000平方米,合()公顷。
A.72 B.720 C.72007.平方千米和公顷之间的进率是()A.10 B.100 C.1000 D.100008.乐乐在计算如图中树叶的面积时作了一些标记。
如果每个方格的面积是1平方厘米,这片树叶的面积大约是()平方厘米。
A.22 B.40 C.70二.填空题9.如图中阴影部分的面积大约是cm2(每个小格是1cm2).10.把两个完全一样的正方体拼成一个长方体,拼成的长方体的表面积是原来两个正方体表面积和的.11.如图,大小两个正方形拼在一起,阴影部分面积为28平方厘米,小正方形边长为4厘米,则图中空白部分的面积是平方厘米.12.2公顷= 平方米 90000平方米= 公顷17平方千米= 公顷 400公顷= 平方千米13.一个风景区的占地面积是4平方千米50公顷,合起来是公顷,也就是平方米。
14.如图,AB=BC=CD=4厘米,DF=3厘米,则阴影部分的面积是平方15.用方格纸估计一个不规则图形的面积时,数出这个图形一共包含58个整格和26个不满整格.如果每个小方格表示1平方分米,这个图形的实际面积比平方分米大一些,比平方分米小一些.16.一个零件的横截面如图(单位:厘米),它的面积是.三.判断题17.一间教室的面积约为50平方米,那么200间这样的教室总面积约为1公顷.()18.3滴水有1升.()19.小学生的一步大约长50厘米.()20.是一个仓库侧面墙的示意图.要给这面墙粉刷涂料,粉刷的面积可以用长方形的面积加上梯形的面积.()21.计算的面积,只能把它分成一个正方形和一个三角形来计算.()四.计算题22.算出图形的面积。
人教版五年级上册数学《组合图形的面积》计算专项练习

人教版五年级数学上册《组合图形的面积》计算专项练习1.计算下面的图形中阴影部分的面积。
(单位:cm)2.求下面图形的面积。
(单位:cm)3.求下列组合图形的面积。
(1)(2)4.求阴影部分的面积。
(单位:厘米)5.求下面组合图形的面积。
6.计算下面图形阴影部分的面积。
7.先画出辅助线,再计算组合图形的面积。
(单位:厘米)8.计算下面各组合图形的面积。
(单位:厘米)(1)(2)9.计算下面图形阴影部分的面积。
(单位:厘米)(1)(2)10.计算下面图形的面积。
11.计算下面组合图形的面积。
(单位:厘米)12.已知平行四边形的面积是48平方分米,求阴影部分的面积。
13.计算下面组合图形的面积。
(单位:cm)14.下面的梯形中涂色部分的面积是多少?15.如图,三角形ABC的面积是24cm2,AC长6cm,AE长2.5cm,求阴影部分的面积。
16.求组合图形的面积。
17.下图是两个完全相同的直角梯形重叠在一起,求阴影部分的面积。
(单位:cm)18.计算下列图形的面积。
(单位:cm)(1)(2)19.求下面组合图形的面积。
(单位:分米)20.求下面组合图形的面积。
(单位:cm)21.求出如图中涂色部分的面积.22.计算图形的面积。
先把你的想法在图中画一画,再计算。
(单位:dm)23.计算涂色梯形的面积。
参考答案1.【答案】(3.5+2.4)×2.4÷2=7.08(cm2)2.【答案】(8.5+15)×13÷2−8.5×3÷2=140(cm2)3.【答案】(1)24×8÷2+(24+14)×8÷2=248(cm2)(2)12×8−(12−5−5+7)×4÷2=78(cm2)【解析】(1)本题考查了组合图形的面积,观察图形可知组合图形的面积=三角形面积+梯形面积,然后根据三角形面积和梯形面积公式代入数据计算。
五年级组合图形练习题

五年级组合图形练习题练习题一:组合图形的面积计算1. 问题描述下图中的图形由若干个矩形组成,每个矩形的长和宽分别如下:•矩形A:长5cm,宽4cm•矩形B:长8cm,宽3cm•矩形C:长6cm,宽2cm•矩形D:长3cm,宽5cm请计算以下问题:1.整个图形的面积是多少平方厘米?2.图形中矩形A所占比例是多少?2. 解题思路问题1中要求求出整个图形的面积,而这个图形由四个矩形组成。
我们可以分别计算每个矩形的面积,然后将它们相加得到整个图形的面积。
问题2中要求求出矩形A在整个图形中所占的比例。
我们可以先计算出整个图形的面积,再计算矩形A的面积,最后用矩形A的面积除以整个图形的面积即可得到所占比例。
我们可以使用以下公式来计算矩形的面积:$$ \\text{面积} = \\text{长} \\times \\text{宽} $$3. 解题步骤3.1 计算每个矩形的面积根据给定的长和宽,我们可以得到每个矩形的面积:•矩形A的面积为 $5 \\text{ cm} \\times 4 \\text{ cm} = 20 \\text{ cm}^2$•矩形B的面积为 $8 \\text{ cm} \\times 3 \\text{ cm} = 24 \\text{ cm}^2$•矩形C的面积为 $6 \\text{ cm} \\times 2 \\text{ cm} = 12 \\text{ cm}^2$•矩形D的面积为 $3 \\text{ cm} \\times 5 \\text{ cm} = 15 \\text{ cm}^2$3.2 计算整个图形的面积将每个矩形的面积相加即可得到整个图形的面积:$$ \\text{整个图形的面积} = 20 \\text{ cm}^2 + 24\\text{ cm}^2 + 12 \\text{ cm}^2 + 15 \\text{ cm}^2 = 71\\text{ cm}^2 $$3.3 计算矩形A所占比例将矩形A的面积除以整个图形的面积即可得到所占比例:$$ \\text{矩形A所占比例} = \\frac{20 \\text{ cm}^2}{71 \\text{ cm}^2} $$通过计算得知,矩形A所占比例约为 0.2817,即约为28.17%。
(完整版)五年级组合图形的面积典型例题

五年级上册组合图形面积计算题1:一个等腰直角三角形,最长的边是10 厘米,这个三角形的面积是多少平方厘米?【巩固练习1】:如图正方形中套着一个长方形,正方形的边长是12 厘米,长方形的四个角的顶点把正方形的四条边各分成两段,其中长的一段是短的 2 倍。
求中间长方形的面积。
2:求右面平行四边形的周长。
5412巩固练习2】:求右面三角形的AB上的高典型例题3:求右图等腰直角三角形中阴影部分的面积。
单位:厘米)10巩固练习3】:求四边形ABCD的面积。
(单位:厘米)典型例题4:有一种将正方形内接于等腰直角三角形。
已知等腰直角三角形的面积是72 平方厘米,正方形的面积分别是多少?巩固练习4】:有一种将正方形内接于等腰直角三角形。
已知等腰直角三角形的面积是72 平方厘米,正方形的面积分别是多少?典型例题5:图中两个正方形的边长分别是10厘米和 6 厘米,求阴影部分的面积。
【巩固练习5】:图中两个正方形的边长分别是阴影部分的面积。
巩固练习6】求右图等腰直角三角形中阴影部分的面积。
(单位:厘米)典型例题7:在一个直角三角形铁皮上剪下一块正方形,剩三角形,已知AD=3cm,DB=4cm,两个三角形面积和是多少?2、已知正方形ABCD的边长是7 厘米,求正方形EFGH的面积A下两个3、求下图长方形ABCD的面积(单位:厘米)4、如图,用48m长的篱笆靠墙围了一个梯形养鸡场,求养鸡场的面积?5、在一个直角三角形铁皮上剪下一块正方形,剩下两个三角形,已知AD=4cm,DB=6cm,两个三角形面积和是多少?A【练一练】如果用铁丝围成如下图一样的平行四边形,需要用多少厘米铁丝?(单位:厘米)例2 】下图中甲和乙都是正方形,求阴影部分的面积。
单位:厘米)【练一练】平行四边形ABCD 的边长BC=10厘米,直角三角形BCE 的直角边EC 长8厘米,已知阴影部分的面积比三角形EFG 的面积大10 平方厘米。
求CF 的长。
【例4】两条对角线把梯形ABCD 分割成四个三角形。
组合图形的面积练习题5道
组合图形的面积练习题5道2、求下面图形的面积。
你能想出几种方法。
、求下面图形的面积。
2、计算下面图形中阴影部分的面积。
30dm25dmm七、求下列阴影部分的面积。
③已知:阴影部分的面积为24平方厘米,求梯形的面积。
8dm16cm8dm②已知S平=48dm2,求S阴。
④求S阴。
312cm三、“实践操作”显身手:10分16cm2、求下面图形的面积。
组合图形面积计算练习姓名:1、计算下列组合图形的面积2、求下列阴影部分的面积。
③已知:阴影部分的面积为24平方厘米,求梯形的面积。
12cm②已知S平=48dm2,求S阴。
dm ④求S阴。
dm组合图形面积计算练习姓名:1、求下面各图形的面积。
3、求下面图形的面积。
16cm4、已知右面的两个正方形边长分别为6分米和4分米,求图中阴影部分的面积。
5、计算右边图形的面积。
发展题:如图,ABCD是一个长12厘米,宽5厘米的长方形,求阴影部分三角形ACE的面积。
组合图形的面积如图,ABCD是直角梯形,求阴影部分的面积和。
下图1的长方形是一块草坪,中间有两条宽1米的走道,求植草的面积。
下图2中,边长为10和15的两个正方体并放在一起,求三角形ABC的面积。
下图3中,三角形ABC的面积是36平方厘米,三角形ABE与三角形AEC的面积相等,如果AB=9厘米,FB=FE,求三角形AFE的面积。
下图1中两个正方形的边长分别是10厘米和6厘米,求阴影部分的面积。
下图2中三角形ABC面积是36平方厘米,AC长8厘米,DE长3厘米,求阴影的面积。
下图3中BC=10厘米,EC=8厘米,且阴影部分面积比三角形EFG的面积大10平方厘米。
求平行四边形的面积。
下图1求四边形ABCD的面积。
下图2已知正方形ABCD的边长是7厘米,求正方形EFGH的面积。
下图3图中两个正方形的边长分别是6厘米和4厘米,求阴影部分的面积。
下图4中两个完全一样的三角形重叠在一起,求阴影部分的面积。
下图1中,甲三角形的面积比乙三角形的面积大多少平方厘米?下图2中正方形的边长为8厘米,CE为20厘米,梯形BCDF的面积是多少平方厘米?如下图3,正方形ABCD 中,AB=4厘米,EC=10厘米,求阴影部分的面积。
五年级数学上册《组合图形的面积》测试卷及答案-北师大版
五年级数学上册《组合图形的面积》测试卷及答案-北师大版一.选择题(共8小题)1.如图,边长相等的两个正方形中,画了甲、乙两个三角形(用阴影表示),它们的面积相比()A.甲的面积大B.乙的面积大C.相等2.点A是长方形内任意一点,阴影部分的总面积与空白部分总面积比较,哪个的面积较大?A.阴影部分面积大B.空白部分面积大C.一样大D.无法确定3.图中每个小方格的面积是1cm2.请你估计一下,这个脚印的面积约是()A.45B.35C.254.下面图形中涂色部分面积与其它不同的一个是()5.中心广场的占地面积约为5公顷,()个中心广场的面积约为1平方千米.A.2 B.20 C.2006.丫丫家的面积有110平方分米.她家所在的小区有300平方千米.丫丫最喜欢楼下的游乐场了,它有10公顷那么大呢.这段话里有()处错误.A.1 B.2 C.37.“6平方千米〇601公顷”,比较大小,在〇里应填的符号是()A.>B.<C.=D.×8.如图:树叶的面积约是()(每个小方格的面积是1cm2)A.15cm2~25cm2B.35cm2~45cm2C.55cm2~65cm2二.填空题(共8小题)9.如图是一个不规则的土地,估测一下,它的面积大约是平方米.10.如图,平行四边形中,阴影部分的面积是36.5dm2,平行四边形的面积是平方分米.11.右图平行四边形的面积是25平方厘米,阴影部分的面积是平方厘米.12.如果1平方米能站9人,那么1公顷能站人,1平方千米能站人.13.260000000平方米=公顷=平方千米800平方千米=公顷=平方米14.如下图所示,平行四边形的面积是28cm2,阴影部分的面积是cm2.15.如图中这片树叶的面积约是cm2.16.如图是一个平行四边形被分成了三个三角形,涂色图形的面积是40cm2,没涂色的三角形的面积是cm2.三.判断题(共5小题)17.200个50平方米的教室面积是1公顷.(判断对错)18.100个1角的硬币大约重1千克.(判断对错)19.一张床的周长估计是2米.(判断对错)20.计算的面积,只能把它分成一个正方形和一个三角形来计算.(判断对错)21.如图中阴影部分的面积是14平方厘米.(判断对错)四.计算题(共2小题)22.求下面组合图形的面积.(单位:dm)23.如图,阴影部分是两个正方形,周长分别为12厘米和32厘米.求空白部分的总面积是多少平方厘米?五.操作题(共2小题)24.先估计下面图形的面积,再用1平方厘米的正方形学具量一量,填在括号里.25.分割组合图形(不计算):你有哪几种分割方法便于计算其面积,请画出分割示意图.六.应用题(共6小题)26.某街心广场有一块地(如图所示),李叔叔要在这块地上铺满草坪.(1)他需要购买多少平方米草皮?(2)如果每平方米草皮需要68元,请你估计一下,李叔叔要带多少元钱才能一次性把草皮买够?请写出你的估计过程.27.王大伯从平行四边形菜地中划出一块三角形地种西红柿,其余地方种黄瓜(如图),这块黄瓜地的面积是多少平方米?28.一个果园形状如图,一棵果树占地5m2,这个果园一共可以种多少棵树?29.李阿姨家有一块菜地,(如图)这块菜地的面积有多少平方米?30.王村有一块梯形果园,村里进行道路规划时,有一条公路穿过了这个果园.这个果园的实际面积是多少平方米?31.下面三个大正方形的边长都是32厘米,先计算每个正方形中一个小方格的面积,再估计出荷叶的面积.你觉得哪幅图估计得最接近实际面积?参考答案一.选择题(共8小题)1.解:两个阴影三角形的底等于正方形的边长,三角形的高也等于正方形的边长,因此两个三角形等底等高,所以面积相等;故选:C.2.解:阴影部分两个三角形的高等于长方形宽,底等于长方形的长,空白部分两个三角形的高等于长方形的长,底等于长方形的宽,所以阴影部分的面积与空白部分的面积相等。
(完整版)《组合图形的面积》练习题(含答案)
(完整版)《组合图形的面积》练习题(含答
案)
-CAL-FENGHAI.-(YICAI)-Company One1
组合图形的面积
测试题
1、下面的图形是由两个三角形组成的,请画出这两个三角形。
A
B D
C
2、已知平行四边形的面积是48平方分米,求阴影部分的面积。
3dm
8dm
3、求下面个图形的面积、(单位:分米)
(1)(2) 14
8
6 6
12
3 6
12
(3)(4) 8
2.5
5.4 4 1.5
4.2 6
3
4、如图所示,梯形的周长是52厘米,求阴影部分的面积。
16
5、校园里有一块花圃,(如图所示),算出它的面积。
(单位:米)
6 2
2
5
6、大小正方形如图放置,阴影部分为重叠部分,求空白部分面积。
(单位:厘米)
7
7
22
7、有一块土地如图所示,你能用几种方法求出它的面积(
单位:米)
12
15
8
22
7、如图所示,一个平行四边形背分成A、B两被封,A的面积比B的面积打40平方米,A的上底是多少?
B
A
8米
【参考答案】。
数学五年级上册《组合图形的面积》练习题(含答案)
【同步专练A 】6.4 组合图形的面积(基础应用篇)一、单选题(共8题)1.如图,长方形A B C D 的周长是14C m,在它的每条边上各画一个以该边为边长的正方形,已知这四个正方形的面积是50C m2,那么长方形A B C D 面积是()平方厘米.A . 12B . 6C . 10D . 492.一个正方形边长是6真米,如果把它的边长增加2厘米,则它的面积增加().A . 4B . 12C . 283.两个()的梯形可以拼成一个平行四边形.A . 形状相同B . 等底等高C . 完全一样D . 大小相等4.在如图梯形中,两个阴影部分的面积相比( )A . 甲大于乙B . 乙大于甲C . 甲等于乙D . 无法比较5.如图A 、B 分别是长方形长和宽的中点,阴影部分面积是长方形的()A .B .C .D .6.下图中每个大三角形的大小、形状完全相同,都是正三角形,从第二排选出合适的图形,把这一个图形的序号填在()里.A .B .C .D .7.下图中阴影甲、阴影乙是梯形中的两个三角形,它俩的面积().A . 相等B . 甲大C . 乙大8.2个边长3厘米的正方形拼成一个长方形,拼成的长方形的周长比原来2个正方形周长和减少了()厘米.A . 9B . 6C . 4D . 2二、判断题(共8题)9.任何一个梯形都可以分成两个等高的三角形. ()10.梯形的上底下底越长,面积越大. ()11.两个完全一样的梯形可以拼成一个平行四边形. ()12.用8个1立方厘米的小方块拼成一个正方体.如果拿去一个小方块,它的表面积不变.()13.面积相等的图形,形状一定相同.()14.平行四边形的面积大于梯形面积. ()15.把一个长方形框架拉成平行四边形,它的面积不变.()16.用4个边长1C m的小正方形拼成两个不同的图形,这两个图形的周长不同,面积也不同. ()三、填空题(共8题)17.下图中每个方格的边长是1厘米,整个图形的周长是________厘米,面积是________平方厘米.18.如图中A B =3厘米,C D =12厘米,ED =8厘米,A F=7厘米.四边形A B D E的面积是________平方厘米.19.右图中三角形的面积是长方形面积的________,这个梯形的面积是________C m2.20.李伯伯家有一块菜地(如图),今年准备种白菜,每平方米种25棵.要求这块地一共可以种多少棵白菜,请列出综合算式:________.21.一个直角三角形,三条边分别是5厘米、4厘米、3厘米,它的面积是________平方厘米,用两个这样的三角形拼成的长方形面积是________平方厘米.22.在长8分米,宽6分米的铁皮上,剪掉一个最大的圆,剩下的铁皮的面积是________23.3米长的绳子平均分成5段,每段是全长的________,每段长________.24.如图,阴影部分的面积和空白部分的面积比是5:7,正方形的边长是8厘米,D E的长是________厘米.四、计算题(共6题)25.以B D 为边时,高20C m,以C D 为边时,高14C m,▱A B C D 周长为102厘米,求面积?26.看图计算它们的面积.(单位:米)27.求出如图中涂色部分的面积.28.求下面组合图形的面积(单位:C m)(1)(2)29.求阴影部分的面积.30.计算下面图形的面积.(单位:厘米)五、解决问题(共6题)31.22万张16开草稿纸大约重1吨,1吨木材约有3.44立方米,可生产0.69吨草稿纸. (1)生产1吨草稿纸大约需木材多少立方米?(保留一位小数)(2)回收1千克废纸可生产0.8千克再生纸,我市有中、小学生共17.5万人,每人每学年回收2千克废纸,全市的中、小学生一学年回收的废纸可生产多少千克再生纸?相当于节省木材多少立方米?32.如下图,在一块梯形的地中间有一个长方形的游泳池,其余的地方是草地,草地的面积是多少平方米?33.李叔叔家有一块菜地(如下图),这块菜地的面积有多少平方米?34.求下列各图形的面积.(单位:厘米)(1)(2)(3)35.求阴影部分面积.36.我们都知道,三角形面积的计算公式是“底×高÷2”.那么,为什么要“÷2”呢?请写一写或画一画的方式,把你的想法表达出来.参考答案一、单选题1. A2. C3. C4. C5. A6. D7. A8. B二、判断题9. 正确10. 错误11. 正确12. 正确13. 错误14. 错误15. 错误16. 错误三、填空题17. 12;618. 4619. 一半;1220. (12×5+12×4÷2)×2521. 6;1222. 19.74平方分米23. ;米24.四、计算题25. 解:C D 边上的高与B D 边上的高的比是:14:20= ;平行四边形的底C D 为:102÷(1 )÷2=102=102×=30(厘米);平行四边形的面积为:30×14=420(平方厘米);答:平行四边形的面积是420平方厘米26. 解:①2×2+ ×(0.3+2+0.5)×1.8=4+ ×2.8×1.8=4+2.52=6.52(平方米)答:面积是6.52平方米②20×16﹣×(3+9)×5=320﹣×12×5=320﹣30=290(平方米)答:面积是290平方米③×52×22+ ×(20+31)×48=572+ ×51×48=572+1224=1796(平方米)答:面积是1796平方米27. 解:(60+80)×30÷2﹣60×20÷2 =140×30÷2﹣1200÷2=2100﹣600=1500(C m2).答:涂色部分的面积为1500C m228.解:(1)(18+36)×18÷2—18×8÷2=486-72=414(平方厘米)(2)23×12÷2+(23+46)×15÷2=138+517.5=655.5(平方厘米)29. 解:①×5×6×2=30(D m2);②×(4+6)×4= ×10×4=20(D m2);故答案为:30D m2, 20D m2.30.解:(5+10)×8÷2-5×3÷2=15×8÷2-15÷2=60-7.5=52.5(平方厘米)答:图形的面积是52.5平方厘米.五、解决问题31.(1)解:3.44÷0.69=5.0(m2)答:生产1吨草稿纸大约需木材5.0立方米. (2)解:17.5万人=175000人2×175000×0.8=280000(千克)280000÷1000×5=1400(m2)答:相当于节省木材1400立方米.32. 解:(40+70)×30÷2=110×30÷2=3300÷2=1650(平方米)30×15=450(平方米)1650-450=1200(平方米)答:草地的面积是1200平方米.33. 解:23×12+17×12=480(平方米)答:这块菜地的面积有480平方米.34.(1)25×18=450(平方厘米)答:这个平行四边形的面积是450平方厘米.(2)30×10÷2=150(平方厘米)答:这个三角形的面积是150平方厘米.(3)(24+54)×30÷2=1170(平方厘米)答:这个梯形的面积是1170平方厘米.35.解:24×11÷2 =264÷2=132(平方厘米)答:阴影部分的面积是132平方厘米.36.解:用两个完全相同的三角形拼成一个平行四边形,因为平行四边形的面积=底×高,而平行四边形的一半为三角形,所以要“÷2”11。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
组合图形的面积练习题姓名:
一、填空
(1)两个完全一样的梯形可以拼成一个()形。
(2)一个梯形上底和下底的和是15厘米,高是8.8厘米,面积是()平方厘米。
(3)平行四边形的底是2分米5厘米,高是底的1.2倍,它的面积是()平方厘米。
(4)有一堆圆木堆成梯形,最上面一层有3根,最下面一层有7根,一共堆了5层,这堆圆木共有()根。
二、判断题
(1)平行四边形的面积大于梯形面积。
()
(2)梯形的上底下底越长,面积越大。
()
(3)任何一个梯形都可以分成两个等高的三角形。
()
(4)两个形状相同的三角形可以拼成一个平行四边形。
()
三、测量并计算下列图形的面积
四、计算下列组合图形的面积
图
形面积计
算专项练
习
1、填表。
图形名称 面积公式(文字) 面积公式(字母) 长方形 正方形
平行四边形 三角形 梯形
2、求下面图形的面积(单位:m )。
你能想出几种方法。
1、求下面图形的面积。
(单位:cm )
15 2 30dm
12dm 5m
25dm 5m
15
30 40
3m
20
10
6
4
3
4
8
2 10
32
20
12
七、求下列阴影部分的面积。
① ②已知S 平=48dm 2,求S 阴。
③已知:阴影部分的面积为24平方厘米,求梯形的面积。
3、求下面各图形的面积。
(单位:分米)
13cm
16cm
3dm
12cm
7cm
4dm
8dm
三、“实践操作”显身手:10分
16cm
12cm
14cm 24m
10m
8m
1、求下面图形中阴影部分的面积。
2、求下面图形的面积。
