第九节 各种积分间的关系3
4.3、定积分与不定积分的关系

解
cot xdx
2 2 2 4 4
csc x 1 dx cot x 1 . 4 2 4 4
从性质 4.13 的结论可知, 变上限函数 p(x)是闭区间上连续函数 f ( x) 的一 个原函数,由此得到函数可积的一个条件: 若函数 f ( x) 在 a, b 上连续,则 f ( x) 在 a, b上可积。
第4章 积分及其应用
d 1 2 t sin t dt 求 dx x
例5
(图(b)) (3)当
f xdx 表示由曲线
b a
b
a
f x dx 表示几部分的代数和:
f x 在 a, b 上既有负值又有正值时,定积分
f x 0 时,取面积的正值, f x 0 时,取面积的负值(图(c))
第4章 积分及其应用
第4章 积分及其应用
例 3 利用定积分的几何意义,求下面定积分的值。
0 sin 2tdt
0
x2
lim
x 0
x sin 2tdt' sin 2 x 0 1. lim 2 x ' 2x x 0
第4章 积分及其应用
“ x ” ,即
在性质 4.13 中,如果将变上限函数的上限“ x ”换成函数
p x a
y y=f(x)
f(ξi )
0
a x0 x1
x2 xi 1ξ xi i
xn 1 x b n
x
第4章 积分及其应用
(3)求和:将一个个小矩形的面积加起来
将一个个的小矩形的面积相加,就是曲边梯形的面积的一个近似值, 即
高等数学中五类积分之间的关联

(通联:郑州科技学院基础部)
26 2019 第 3 期 下 (总 第 295 期 )
Z HONG GUO NONG CUN JIAO YU
高等数学中五类积分之间的关联
王 涛 席祥祥
本文针对高等数学教学过程中的定积 分概念,利用密度函数与求不同几何物体的 质量,引入五类不同类型的积分定义与概 念,力求学生易于理解和掌握定积分概念。
一、引言 定积分是高等数学在最重要的基本内 容,但冗长的定义和难以理解的内涵往往 使学生望而生畏。本通过求不同几何物体 的质量,对高等数学中的五类积分的概念 进行分析和阐述,以期使学生易于理解和 掌握五类积分的基本概念和内涵。 二、五类抽象的积分 在高等数学教材中,分别有定积分、重 积分、线积分和面积分。我们通过对不同几 何形状和不同维数的物体求质量的问题, 引入如下问题: 问题 1:设有一直线型构件 ,其 放 在平 面 直 角坐 标 系 的 轴 上 所 占 区 间 为 [a,b],且 其 线 密 度 ρ(x)在 [a,b]上 连 续 ,问 该 构 件 的 质量为多少? 问题 2:(平 面 型构 件 的 质量 )已 知 某平 面型构件在 xoy 面所占区域为 D,且 面 密 度 ρ(x,y)在 D 上连续,问如何求该构件的质量? 问题 3:(空 间 型构 件 的 质量 )已 知 某物 体 在 o-xyz 直 角 坐 标 系 中 所 占 空 间 区 域 为 Ω,且体 密 度 ρ(x,y,z)在 Ω 上 连 续,问 如 何 求该物体的质量? 问题 4:(曲 线 型构 件 的 质量 )已 知 某曲 线型构件在空间直角坐标系中所占空间曲 线为 Γ,且 线 密度 ρ(x,y,z)在 Γ 上 连 续 ,问 如何求该构件的质量? 问题 5: (曲 面 型构 件 的 质量 )已 知 某 曲面型构件在空间直角坐标系中所占空间 曲面为 Σ,且 面 密度 ρ(x,y,z)在 Σ 上 连续 , 问如何求该构件的质量? 分析上述五个问题会发现它们有一个 共同点,均为求物体质量的问题,不同点只 在于物体的形态以及涉及到的密度形式不 同,但质量计算的思想都是一样的(以下三 种形式之一): 质量 = 线密度×长度;质量 = 面密 度×面积;质量 = 体密度×体积。 关于问题 1,学生已知的物理知识是密 度恒定来求质量,如:已知线密度 ρ,则质量 m= ρx(其中代表长度),引导学生如何 用已 知的思想来解决未知的事物。于是提出如 下的四部曲: ① 分 割 [a,b]:a=x0 <x1 <···xn=b,记 Δxi=xi-xi-1 ②近似:(由于 ρ(x)在[a,b]上连续,当 小区间[xi-1,xi]充分小的时候,ρ(x)在该区间
数学分析简明教程22 各种积分间的联系与场论初步

页脚内容1第二十二章 各种积分间的联系与场论初步§1 各种积分间的联系1.应用格林公式计算下列积分:(1)ydx x dy xy L ⎰-22,其中L 为椭圆22a x +22by =1取正向;(2),)()(⎰-++Ldy y x dx y x L 同(1);(3)dy y x dx y x L)()(222+-+⎰, L 是顶点为)5,2(),2,3(),1,1(C B A 的三角形的边界,取正向;(4),1,)()(223333=+--+⎰y x L dy y x dx y x L为取正向;(5),sin sin ydy e xdx e x Ly -+⎰ L 为矩形d y c b x a ≤≤≤≤, 的边界,取正向;(6)],))cos(sin ())cos(sin [(dy y x xy x dx y x xy y e Lxy +++++⎰其中L 是任意逐段光滑闭曲线.解(1)原式 =()()d xdy y x dxdy x y DD⎰⎰⎰⎰+=--2222)(=ab()r dr r b r a d ⎰⎰+122222220sin cos θθθπ(广义极坐标变换)=())(3sin cos 3122202222b a ab d b a ab +=+⎰πθθθπ.(2)⎰-++Ldy y x dx y x )()(=⎰⎰=-Ddxdy 0)11(.(3)原式 ⎰⎰+-=Ddxdy y x x ))(22(页脚内容2⎪⎪⎭⎫ ⎝⎛+-=-=⎰⎰⎰⎰⎰⎰-+-+215231143124322yy y y D dx ydy dx ydy ydxdy 9143))5(127)(47(2252221-=-+--=⎰⎰dy y y dy y y . (4)原式π23)(3)33(2222-=+-=--=⎰⎰⎰⎰DD dxdy y x dxdy y x .(5)原式 dxdy x e y e Dy x ⎰⎰--=-)cos sin ()cos sin (⎰⎰⎰⎰+-=-b ad cdcydy b ax e dx x ydy dx e)sin )(sin ()cos )(cos 11(a b e e c d ee cd b a --+--=. (6))]cos(sin [),(y x xy ye y x P xy ++=,)]cos(sin [),(y x xy x e y x Q xy ++=,)]sin(cos [sin )]cos(sin [y x xy xy xy e y x xy x ye xQxy xy --++++=∂∂ )]sin()cos(sin )cos (sin [y x y x y xy xy xy xy e xy --+++=,)]sin(cos [sin )]cos(sin [y x xy xy xy e y x xy y xe yPxy xy +-++++=∂∂ )]sin(cos sin )cos (sin [y x xy x xy xy xy xy e xy +-+++=,)cos()(y x x y e yPx Q xy +-=∂∂-∂∂, 所以,原式⎰⎰+-=Dxy dxdy y x x y e ,)cos()( 其中D 为L 包围的平面区域.页脚内容32.利用格林公式计算下列曲线所围成的面积: (1)双纽线θ2cos 22a r =;(2)笛卡尔叶形线)0(333>=+a axy y x ;(3)t t a x sin )cos 1(2+=,t t a y cos sin 2⋅=,π≤≤20t .解(1)⎰⎰⎰⎰==12||D Ddxdy dxdy D ⎰-⨯=L ydx xdy 212 ⎰=--=44)]sin (sin cos cos [ππθθθθθd r r r r 24424422cos a d a d r ===⎰⎰--ππππθθθ,其中1D 由θ=2cos 22a r ,44π≤θ≤π-所围成. (2)作代换,tx y =则得曲线的参数方程为313tatx +=,3213t at y +=.所以, dt t t a dx 233)1()21(3+-=,dt t t at dy 233)1()2(3+-=, 从而,dt t t a ydx xdy 2322)1(9+=-,于是,面积为 D =⎰C x y y x d -d 21=dt t t a ⎰∞++02322)1(29=223a . (3)D =⎰-cydx xdy 21=页脚内容4{}⎰-++⋅--⋅+π2022322]sin )sin (cos 2cos )cos 1[(cos sin )sin cos sin 2(sin )cos1(21dt t t t t t a t t a t t t a t t a{}⎰π-++⋅--⋅+2022322]sin )sin (cos 2cos )cos 1[(cos sin )sin cos sin 2(sin )cos1(21dt t t t t t a t t a t t t a t t a=21tdt t t a 2cos )cos 1(sin 22022+⎰π=24a π 3.利用高斯公式求下列积分: (1)y x z x z y z y x sd d d d d d 222++⎰⎰.其中(a )S 为立方体a z y x ≤≤,,0的边界曲面外侧;(b )S 为锥面)0(222h z z y x ≤≤=+,下侧. 解:(a )y x z x z y z y x sd d d d d d 222++⎰⎰=2⎰⎰++vdxdydz z y x )(=2⎰⎰⎰++aa a dz z y x dy dx 0)(=43a(b)补充平面1S :h z h y x =≤+,222的上侧后,1S S +成为闭曲面的外侧, 而⎰⎰++1222S dxdy z dzdx y dydz x =⎰⎰xyD dxdy h 2=22h h π⋅= π4h 所以 :⎰⎰++Sdxdy z dzdx y dydz x 222+π4h页脚内容5=⎰⎰+++1222S S dxdy z dzdx y dydz x=2z y x z y x V⎰⎰⎰++d d )d (=2⎰⎰xyD dxdy⎰+++h y x z z y x 22)d (=⎰⎰++xyD y x y x y x y x h y x h d )]d (- )+2(-+)+([222222=⎰⎰π-θ+θ-+θ+θθ20222])sin (cos 2)sin (cos 2[hrdr r r h hr d=1214h θ+θ+θ⎰πd 20)3sin 2cos 2(=2π4h 所以⎰⎰++Sdxdy z dzdx y dydz x 222=442h h π-π=42h π- (2)⎰⎰++Sdxdy z dzdx y dydz x 333, 其中S 是单位球面的外侧;解:⎰⎰++Sdxdy z dzdx y dydz x 333=3⎰⎰⎰++Vz y x z y x d d )d (=3⎰⎰⎰ππρρϕϕθ2014sin d d d=512π (3)设S 是上半球面222y x a z --=的上侧,求 (a )⎰⎰++Sy x z x z y z y x d d d d d d(b)⎰⎰++-+Sy x z y xy x z z y x z y xzd )d (2d )d (d d 2222页脚内容6解:补充平面1S :222,0a y x z ≤+=,下侧后,1S S +成为闭曲面的外侧,而 (a )⎰⎰=++10S zdxdy ydzdx xdydz所以⎰⎰=++Szdxdy ydzdx xdydz ⎰⎰+=++1S S zdxdy ydzdx xdydz 3⎰⎰⎰Vdxdydz=213433⋅π⋅a =2π3a(b)⎰⎰++-+1d )d (2d )d (d d 2222S y x z y xy x z z y x z y xz =⎰⎰xyD xydxdy 2=2⎰π20d θr r a⎰θθ03d cos sin =0所以 ⎰⎰++-+Sy x z y xy x z z y x z y xzd )d (2d )d (d d 2222=⎰⎰+++-+1d )d (2d )d (d d 2222S S y x z y xy x z z y x z y xz =⎰⎰⎰++Vdxdydz z y x )(222=⎰π20d θ⎰20πsin ϕd ϕ⎰a4 d ρρ=554a π(4)⎰⎰+-++-++-Sy x y x z x z x z y z y y x d )d (d )d (d )d z (222222,S 是 2222)()()(R c z b y a x =-+-+- 的外侧.解:⎰⎰+-++-++-Sy x y x z x z x z y z y y x d )d (d )d (d )d z (222222,=3⎰⎰⎰V dxdydz =V 3=3343R π⋅=4π3R4.用斯托克斯公式计算下列积分:页脚内容7(1)⎰++Lzdz dy dx y x 32, 其中(a )L 为圆周0,222==+z a y x ,方向是逆时针;(b )L 为y x z y ==+,122 所交的椭圆,沿x 轴正向看去,按逆时针方向; 解: (a )取平面0=z 上由交线围成的平面块为S ,上侧,由Stokes 公式⎰++Lzdz dy dx y x 32=⎰⎰Szy x z y x dxdydzdxdydz1///32∂∂∂∂∂∂ =⎰⎰-Sdxdy y x 223=⎰⎰----ax a xa dy y dx x 02222223=dx x a x a3222)(2⎰--=616a π-(b )取平面y x =上由交线围成的平面块为S ,上侧,由由Stokes 公式⎰++Lzdz dy dx y x32=⎰⎰∂∂∂∂∂∂Szy x z y x dxdy dzdx dydz 132=⎰⎰-Sdxdy y x 223=⎰⎰-xyD dxdy y x 223=616a π-页脚内容8(2)dz y x dy x z dx z y L)()()(-+-+-⎰,L 是从)0,0,(a 经)0,,0(a 至),0,0(a 回到)0,0,(a 的三角形;解: 三角形所在的平面为a z y x =++,取平面a z y x =++上由以上三角形围成的平面块为S ,取上侧,由stokes 公式dz y x dy x z dx z y L)()()(-+-+-⎰=⎰⎰---∂∂∂∂∂∂Syx x z z y z y x dxdy dzdx dydz=⎰⎰++-S dxdy dzdx dydz 2 =2-(⎰⎰Sdydz +⎰⎰Sdzdx +⎰⎰Sdxdy )=2-(⎰⎰yzD dydz +⎰⎰zx D dzdx +⎰⎰xyD dxdy )=23a -(3)dz y x dy y x dx z y L)()()(222222+++++⎰,其中(a )L 为1=++z y x 与三坐标轴的交线,其方向与所围平面区域上侧构成右手法则;(b )L 是曲线Rx z y x 2222=++, rx y x 222=+ (0,0><<z R r ),它的方向与所围曲面的上侧构成右手法则;解:(a )中取平面1=++z y x 上与三坐标面交线所围平面块为S ,上侧;(b )中取曲面Rx z y x 2222=++上由L 所围曲面块为S ,上侧, 则由stokes 公式,得页脚内容9dz y x dy y x dx z y L)()()(222222+++++⎰=⎰⎰+++∂∂∂∂∂∂Sy x x z z y z y x dxdy dzdx dydz 222222 ⎰⎰-+-+-=Sdxdy y x dzdx x z dydz z y )()()(2=2))()()((dxdy y x dzdx x z dydz z y SSS⎰⎰⎰⎰⎰⎰-+-+-则(a )⎰+++++Ldz y x dy z x dx z y )()()(222222= dS y x x z z y S⎰⎰γ-+β-+α-]cos )(cos )(cos )[(2=0 (因为cos α=cos β=cos γ=31)(b ) 注意到球面的法线的方向余弦为: R R x -=αcos , R y =βcos ,Rz=γcos ,所以 dz y x dy z x dx z y L)()()(222222+++++⎰=2⎰⎰-+-+-SdS y x x z z y ]cos )(cos )(cos )[(γβα =2⎰⎰-SdS y z )(由于曲面S 关于oxz 平面对称,故⎰⎰=SydS .0 又⎰⎰⎰⎰π⋅=γ=SSrR dS R zdS 2cos页脚内容10于是dz y x dy z x dx z y L)()()(222222+++++⎰=22r R π(4)xdz zdy dx y L++⎰,L 是2222a z y x =++,0=++z y x ,从x 轴正向看去圆周是逆时针方向.解:平面0=++z y x 的法线的方向余弦为 cos 31cos cos ===γβα,于是,dS xz y z y x xdz zdy ydx L S⎰⎰⎰∂∂∂∂∂∂γβα=++cos cos cos =⎰⎰++-SdS )cos cos (cos γβα=332a π-=23a π-5. 设L 为平面上封闭曲线L ,l 为平面的任意方向,证明:⎰=Lds l n 0),cos(,其中n 是L 的外法线方向。
03积分学知识点总结

03积分学知识点总结积分学是微积分的重要组成部分,也是数学中的基础知识。
下面是关于积分学的一些主要知识点的总结。
1. 不定积分:不定积分是求函数的原函数的过程,也被称为反导函数。
对于给定的函数f(x),不定积分记作∫f(x)dx。
2. 定积分:定积分是在给定的区间上求函数的面积的过程。
对于给定的函数f(x),在[a, b]区间上的定积分记作∫f(x)dx,表示x从a到b的面积。
4. 积分的基本性质:积分具有线性性质,即对于任意常数a和函数f(x)、g(x),有∫(a*f(x)+b*g(x))dx=a*∫f(x)dx+b*∫g(x)dx。
此外,积分具有可加性,即∫(a to c) f(x)dx=∫(a to b) f(x)dx+∫(b to c) f(x)dx。
5. 分部积分法:分部积分法是求不定积分的一种方法,它利用了导数与积分之间的关系。
对于两个可导的函数u(x)和v(x),应用分部积分法,可以得到∫u(x)v'(x)dx=u(x)v(x)-∫v(x)u'(x)dx。
这种方法可以将一个积分转化为另一个更容易求解的积分。
6. 曲线的弧长:曲线的弧长是指曲线在一定区间上的长度。
对于给定的曲线y=f(x),在[a, b]区间上的弧长可以通过积分来计算,即∫(ato b) sqrt(1+(dy/dx)^2)dx。
其中,dy/dx是曲线y=f(x)的导数。
7. 旋转体的体积:旋转体的体积是指通过将曲线或曲面绕轴或直线旋转一周所形成的体积。
对于给定的曲线y=f(x),在[a, b]区间上绕x轴旋转一周所形成的旋转体的体积可以通过积分来计算,即V=∫(a to b) πy^2dx。
8.定积分的应用:定积分在物理学、经济学、几何学等领域都有重要应用。
例如,它可以用来计算曲线下的面积、求解变速运动的位移和速度、计算平均值等。
9.微元法:微元法是在对函数进行积分时,将函数分割为许多无穷小的微元,然后通过求和的方式逼近整体。
数学分析简明教程22 各种积分间的联系与场论初步

第二十二章 各种积分间的联系与场论初步§1 各种积分间的联系1.应用格林公式计算下列积分:(1)ydx x dy xy L ⎰-22,其中L 为椭圆22a x +22by =1取正向;(2),)()(⎰-++Ldy y x dx y x L 同(1);(3)dy y x dx y x L)()(222+-+⎰, L 是顶点为)5,2(),2,3(),1,1(C B A 的三角形的边界,取正向;(4),1,)()(223333=+--+⎰y x L dy y x dx y x L为取正向;(5),sin sin ydy exdx e xLy-+⎰L 为矩形d y c b x a ≤≤≤≤, 的边界,取正向;(6)],))cos(sin ())cos(sin [(dy y x xy x dx y x xy y e L xy+++++⎰其中L 是任意逐段光滑闭曲线.解(1)原式 =()()d xdy y x dxdy x yDD⎰⎰⎰⎰+=--2222)(=ab()r dr r b r a d ⎰⎰+1022222220sin cos θθθπ(广义极坐标变换)=())(3sin cos 3122202222b a ab d b aab+=+⎰πθθθπ.(2)⎰-++Ldy y x dx y x )()(=⎰⎰=-Ddxdy 0)11(.(3)原式 ⎰⎰+-=Ddxdy y x x ))(22(⎪⎪⎭⎫ ⎝⎛+-=-=⎰⎰⎰⎰⎰⎰-+-+215231143124322yy y y D dx ydy dx ydy ydxdy9143))5(127)(47(2252221-=-+--=⎰⎰dy y y dy y y .(4)原式π23)(3)33(2222-=+-=--=⎰⎰⎰⎰DD dxdy y x dxdy y x . (5)原式 dxdy x e y eDy x⎰⎰--=-)cos sin ()cos sin (⎰⎰⎰⎰+-=-b adcdcydy bax e dx x ydy dx e)sin )(sin ()cos )(cos 11(a b e e c d ee cd b a --+--=. (6))]cos(sin [),(y x xy ye y x P xy++=,)]cos(sin [),(y x xy x e y x Q xy++=,)]sin(cos [sin )]cos(sin [y x xy xy xy e y x xy x ye xQxy xy --++++=∂∂ )]sin()cos(sin )cos (sin [y x y x y xy xy xy xy e xy --+++=,)]sin(cos [sin )]cos(sin [y x xy xy xy e y x xy y xe yPxy xy +-++++=∂∂ )]sin(cos sin )cos (sin [y x xy x xy xy xy xy e xy +-+++=,)cos()(y x x y e yPx Q xy +-=∂∂-∂∂, 所以,原式⎰⎰+-=Dxy dxdy y x x y e ,)cos()( 其中D 为L 包围的平面区域. 2.利用格林公式计算下列曲线所围成的面积: (1)双纽线θ2cos 22a r =;(2)笛卡尔叶形线)0(333>=+a axy y x ;(3)t t a x sin )cos 1(2+=,t t a y cos sin 2⋅=,π≤≤20t . 解(1)⎰⎰⎰⎰==12||D Ddxdy dxdy D ⎰-⨯=L ydx xdy 212 ⎰=--=44)]sin (sin cos cos [ππθθθθθd r r r r 24424422cos a d a d r ===⎰⎰--ππππθθθ,其中1D 由θ=2cos 22a r ,44π≤θ≤π-所围成. (2)作代换,tx y =则得曲线的参数方程为313t at x +=,3213t at y +=.所以,dt t t a dx 233)1()21(3+-=,dt t t at dy 233)1()2(3+-=,从而,dt t t a ydx xdy 2322)1(9+=-,于是,面积为 D =⎰C x y y x d -d 21=dt t t a ⎰∞++02322)1(29=223a . (3)D =⎰-cydx xdy 21={}⎰-++⋅--⋅+π2022322]sin )sin (cos 2cos )cos 1[(cos sin )sin cos sin 2(sin )cos1(21dtt t t t t a t t a t t t a t t a{}⎰π-++⋅--⋅+2022322]sin )sin (cos 2cos )cos 1[(cos sin )sin cos sin 2(sin )cos1(21dt t t t t t a t t a t t t a t t a=21tdt t t a 2cos )cos 1(sin 22022+⎰π=24a π 3.利用高斯公式求下列积分:(1)y x z x z y z y x sd d d d d d 222++⎰⎰。
各种积分间的联系

一、格林 (Green) 公式 首先,引进一个重要概念,即单连通区域的概念. 一个平面区域 D ,如果全落在此区域内的任何一条封闭 曲线都可以不经过 D 以外的点而连续地收缩为一点,则 称此区域 D 为单连通的,否则称为复连通的.可见,单连 通区域也就是不含有”洞”甚至不含有”点洞”的区 域. D 单连通区域 上的二重积分和沿其边界的曲线积 分之间有如下的关系: 定理(格林公式) y x 平面单连通区域,函数 和 在 续并具有对 ∫∫ ( ∂Q −的连续偏导数,则有 和 ∂P )dxdy = ∫ Pdx + Qdy.
当区域 V 不是二维单连通是,则高斯公式仍旧成立. 此时边界曲面的法方向仍取法线方向. 例3 计算
∫∫ xdydz + ydzdx + zdxdy,
S
S 为球面 x 2 + y 2 + z 2 = R 2 的外侧.
三、斯托克斯 (stokes) 公式 我们要把格林公式由平面推广到曲面,使在具有光 滑边界曲面的光滑曲面上的积分和其边界上的积分联 系起来,得到下面的关系: 定理(斯托克斯公式) 若光滑曲面 S 的边界为光 滑曲线 L ,函数 P( x, y, z ), Q( x, y, z ), R( x, y, z ) 在曲面 S 及曲 线 L上具有对 x, y, z 的连续偏导数,则成立以下的公式
∫ Pdx + Qdy + Rdz
L
∂R ∂Q ∂P ∂R = ∫∫[( − ) cos(n, x) + ( − ) cos(n, y ) + ∂y ∂z ∂z ∂x S ∂Q ∂P ( − ) cos(n, z )]dS ∂x ∂y ∂R ∂Q ∂P ∂R ∂Q ∂P = ∫∫ ( − )dydz + ( − )dzdx + ( − )dxdy, ∂y ∂z ∂z ∂x ∂x ∂y S
数学分析简明教程22 各种积分间的联系与场论初步

数学分析简明教程22各种积分间的联系与场论初步第二十二章 各种积分间的联系与场论初步§1 各种积分间的联系1.应用格林公式计算下列积分:(1)ydx x dy xy L ⎰-22,其中L 为椭圆22a x +22by =1取正向;(2),)()(⎰-++Ldy y x dx y x L 同(1);(3)dy y x dx y x L)()(222+-+⎰, L 是顶点为)5,2(),2,3(),1,1(C B A 的三角形的边界,取正向;(4),1,)()(223333=+--+⎰y x L dy y x dx y x L为取正向;(5),sin sin ydy e xdx e x Ly -+⎰ L 为矩形d y c b x a ≤≤≤≤, 的边界,取正向;(6)],))cos(sin ())cos(sin [(dy y x xy x dx y x xy y e Lxy +++++⎰其中L 是任意逐段光滑闭曲线.解(1)原式 =()()d xdy y x dxdy x y DD⎰⎰⎰⎰+=--2222)(=ab()r dr r b r a d ⎰⎰+122222220sin cos θθθπ(广义极坐标变换)=())(3sin cos 3122202222b a ab d b a ab +=+⎰πθθθπ.(2)⎰-++Ldy y x dx y x )()(=⎰⎰=-Ddxdy 0)11(.(3)原式 ⎰⎰+-=Ddxdy y x x ))(22(⎪⎪⎭⎫ ⎝⎛+-=-=⎰⎰⎰⎰⎰⎰-+-+215231143124322yy y y D dx ydy dx ydy ydxdy 9143))5(127)(47(2252221-=-+--=⎰⎰dy y y dy y y .(4)原式π23)(3)33(2222-=+-=--=⎰⎰⎰⎰DD dxdy y x dxdy y x .(5)原式 dxdy x e y e Dy x ⎰⎰--=-)cos sin ()cos sin (⎰⎰⎰⎰+-=-b ad cdcydy b ax e dx x ydy dx e)sin )(sin ()cos )(cos 11(a b e e c d ee c d b a --+--=. (6))]cos(sin [),(y x xy y e y x P xy ++=,)]cos(sin [),(y x xy x e y x Q xy ++=,)]sin(cos [sin )]cos(sin [y x xy xy xy e y x xy x ye xQxy xy --++++=∂∂ )]sin()cos(sin )cos (sin [y x y x y xy xy xy xy e xy --+++=,)]sin(cos [sin )]cos(sin [y x xy xy xy e y x xy y xe yPxy xy +-++++=∂∂ )]sin(cos sin )cos (sin [y x xy x xy xy xy xy e xy +-+++=,)cos()(y x x y e yPx Q xy +-=∂∂-∂∂, 所以,原式⎰⎰+-=Dxy dxdy y x x y e ,)cos()( 其中D 为L 包围的平面区域.2.利用格林公式计算下列曲线所围成的面积: (1)双纽线θ2cos 22a r =;(2)笛卡尔叶形线)0(333>=+a axy y x ;(3)t t a x sin )cos 1(2+=,t t a y cos sin 2⋅=,π≤≤20t . 解(1)⎰⎰⎰⎰==12||D Ddxdy dxdy D ⎰-⨯=L ydx xdy 212 ⎰=--=44)]sin (sin cos cos [ππθθθθθd r r r r 24424422cos a d a d r ===⎰⎰--ππππθθθ,其中1D 由θ=2cos 22a r ,44π≤θ≤π-所围成. (2)作代换,tx y =则得曲线的参数方程为313tatx +=,3213t at y +=.所以, dt t t a dx 233)1()21(3+-=,dt t t at dy 233)1()2(3+-=,从而,dt t t a ydx xdy 2322)1(9+=-,于是,面积为D =⎰C x y y x d -d 21=dt t t a ⎰∞++02322)1(29=223a . (3)D =⎰-cydx xdy 21= {}⎰-++⋅--⋅+π2022322]sin )sin (cos 2cos )cos 1[(cos sin )sin cos sin 2(sin )cos1(21dtt t t t t a t t a t t t a t t a{}⎰π-++⋅--⋅+2022322]sin )sin (cos 2cos )cos 1[(cos sin )sin cos sin 2(sin )cos1(21dt t t t t t a t t a t t t a t t a=21tdt t t a 2cos )cos 1(sin 22022+⎰π=24a π 3.利用高斯公式求下列积分: (1)y x z x z y z y x sd d d d d d 222++⎰⎰.其中(a )S 为立方体a z y x ≤≤,,0的边界曲面外侧; (b )S 为锥面)0(222h z z y x ≤≤=+,下侧. 解:(a )y x z x z y z y x sd d d d d d 222++⎰⎰=2⎰⎰++vdxdydz z y x )(=2⎰⎰⎰++aa a dz z y x dy dx 0)(=43a(b)补充平面1S :h z h y x =≤+,222的上侧后,1S S +成为闭曲面的外侧, 而 ⎰⎰++1222S dxdy z dzdx y dydz x =⎰⎰xyD dxdy h 2=22h h π⋅= π4h所以 : ⎰⎰++Sdxdy z dzdx y dydz x 222+π4h=⎰⎰+++1222S S dxdy z dzdx y dydz x=2z y x z y x V⎰⎰⎰++d d )d (=2⎰⎰xyD dxdy⎰+++h y x z z y x 22)d (=⎰⎰++xyD y x y x y x y x h y x h d )]d (- )+2(-+)+([222222=⎰⎰π-θ+θ-+θ+θθ20222])sin (cos 2)sin (cos 2[hrdr r r h hr d=1214h θ+θ+θ⎰πd 20)3sin 2cos 2(=2π4h 所以 ⎰⎰++Sdxdy z dzdx y dydz x 222=442h h π-π=42h π-(2)⎰⎰++Sdxdy z dzdx y dydz x 333, 其中S 是单位球面的外侧;解:⎰⎰++Sdxdy z dzdx y dydz x 333=3⎰⎰⎰++Vz y x z y x d d )d (=3⎰⎰⎰ππρρϕϕθ2014sin d d d=512 π (3)设S 是上半球面222y x a z --=的上侧,求(a )⎰⎰++Sy x z x z y z y x d d d d d d(b) ⎰⎰++-+Sy x z y xy x z z y x z y xz d )d (2d )d (d d 2222解:补充平面1S :222,0a y x z ≤+=,下侧后,1S S +成为闭曲面的外侧,而 (a ) ⎰⎰=++10S zdxdy ydzdx xdydz所以 ⎰⎰=++Szdxdy ydzdx xdydz ⎰⎰+=++1S S zdxdy ydzdx xdydz 3⎰⎰⎰Vdxdydz=213433⋅π⋅a =2π3a(b) ⎰⎰++-+1d )d (2d )d (d d 2222S y x z y xy x z z y x z y xz=⎰⎰xyD xydxdy 2=2⎰π20d θr r a⎰θθ03d cos sin =0所以 ⎰⎰++-+Sy x z y xy x z z y x z y xz d )d (2d )d (d d 2222=⎰⎰+++-+1d )d (2d )d (d d 2222S S y x z y xy x z z y x z y xz =⎰⎰⎰++Vdxdydz z y x )(222 =⎰π20d θ⎰20πsin ϕd ϕ⎰a4 d ρρ=554a π(4)⎰⎰+-++-++-Sy x y x z x z x z y z y y x d )d (d )d (d )d z (222222,S 是 2222)()()(R c z b y a x =-+-+- 的外侧.解:⎰⎰+-++-++-Sy x y x z x z x z y z y y x d )d (d )d (d )d z (222222,=3⎰⎰⎰Vdxdydz =V 3=3343R π⋅=4π3R4.用斯托克斯公式计算下列积分: (1)⎰++Lzdz dy dx y x 32, 其中(a )L 为圆周0,222==+z a y x ,方向是逆时针;(b )L 为y x z y ==+,122 所交的椭圆,沿x 轴正向看去,按逆时针方向; 解: (a )取平面0=z 上由交线围成的平面块为S ,上侧,由Stokes 公式⎰++Lzdz dy dx y x 32=⎰⎰Szy x z y x dxdydzdxdydz1///32∂∂∂∂∂∂ =⎰⎰-Sdxdy y x 223=⎰⎰----ax a xa dy y dx x 02222223=dx x a x a3222)(2⎰--=616a π-(b )取平面y x =上由交线围成的平面块为S ,上侧,由由Stokes 公式⎰++Lzdz dy dx y x 32=⎰⎰∂∂∂∂∂∂Szy x z y x dxdy dzdx dydz 132=⎰⎰-Sdxdy y x 223=⎰⎰-xyD dxdy y x 223=616a π-(2)dz y x dy x z dx z y L)()()(-+-+-⎰,L 是从)0,0,(a 经)0,,0(a 至),0,0(a 回到)0,0,(a 的三角形;解: 三角形所在的平面为a z y x =++,取平面a z y x =++上由以上三角形围成的平面块为S ,取上侧,由stokes 公式dz y x dy x z dx z y L)()()(-+-+-⎰=⎰⎰---∂∂∂∂∂∂Syx x z z y z y x dxdy dzdx dydz =⎰⎰++-S dxdy dzdx dydz 2 =2-(⎰⎰Sdydz +⎰⎰Sdzdx +⎰⎰Sdxdy )=2-(⎰⎰yzD dydz +⎰⎰zx D dzdx +⎰⎰xyD dxdy )=23a -(3)dz y x dy y x dx z y L)()()(222222+++++⎰,其中(a )L 为1=++z y x 与三坐标轴的交线,其方向与所围平面区域上侧构成右手法则;(b )L 是曲线Rx z y x 2222=++, rx y x 222=+ (0,0><<z R r ),它的方向与所围曲面的上侧构成右手法则;解:(a )中取平面1=++z y x 上与三坐标面交线所围平面块为S ,上侧;(b )中取曲面Rx z y x 2222=++上由L 所围曲面块为S ,上侧, 则由stokes 公式,得 dz y x dy y x dx z y L)()()(222222+++++⎰=⎰⎰+++∂∂∂∂∂∂Sy x x z z y z y x dxdy dzdx dydz 222222⎰⎰-+-+-=Sdxdy y x dzdx x z dydz z y )()()(2=2))()()((dxdy y x dzdx x z dydz z y SSS⎰⎰⎰⎰⎰⎰-+-+-则(a ) ⎰+++++Ldz y x dy z x dx z y )()()(222222= dS y x x z z y S⎰⎰γ-+β-+α-]cos )(cos )(cos )[(2=0 (因为cos α=cos β=cos γ=31)(b ) 注意到球面的法线的方向余弦为: R R x -=αcos , R y =βcos ,Rz=γcos ,所以dz y x dy z x dx z y L)()()(222222+++++⎰=2⎰⎰-+-+-SdS y x x z z y ]cos )(cos )(cos )[(γβα=2⎰⎰-SdS y z )(由于曲面S 关于oxz 平面对称,故⎰⎰=SydS .0 又⎰⎰⎰⎰π⋅=γ=SSrR dS R zdS 2cos于是dz y x dy z x dx z y L)()()(222222+++++⎰=22r R π(4)xdz zdy dx y L++⎰,L 是2222a z y x =++,0=++z y x ,从x 轴正向看去圆周是逆时针方向.解:平面0=++z y x 的法线的方向余弦为 cos 31cos cos ===γβα,于是,dS xz y z y x xdz zdy ydx L S⎰⎰⎰∂∂∂∂∂∂γβα=++cos cos cos =⎰⎰++-SdS )cos cos (cos γβα=332a π-=23a π-5. 设L 为平面上封闭曲线L ,l 为平面的任意方向,证明:⎰=Lds l n 0),cos(,其中n是L 的外法线方向。
各类积分之间的联系与计算(朱静)
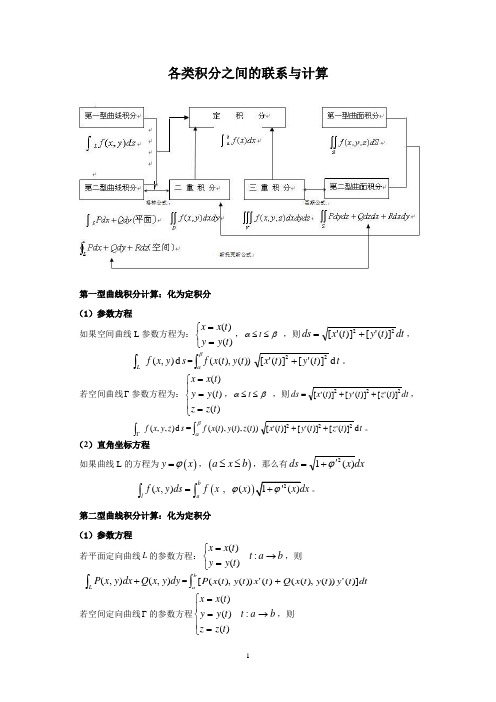
各类积分之间的联系与计算第一型曲线积分计算:化为定积分 (1)参数方程如果空间曲线L 参数方程为:⎩⎨⎧==)()(t y y t x x ,βα≤≤t ,则dt t y t x ds 22)]('[)]('[+=,s y x f Ld ),(⎰=⎰βα))(),((t y t x f t t y t x d )]('[)]('[22+。
若空间曲线Γ参数方程为:⎪⎩⎪⎨⎧===)()()(t z z t y y t x x ,βα≤≤t ,则dt t z t y t x ds 222)]('[)]('[)]('[++=,s z y x f d ),,(⎰Γ=⎰βα))(),(),((t z t y t x f t t z t y t x d )]('[)]('[)]('[222++。
(2)直角坐标方程如果曲线L 的方程为()y x ϕ=,()a x b ≤≤,那么有dx x ds )(12ϕ'+=((,) , ()blaf x y ds f x x ϕ=⎰⎰。
第二型曲线积分计算:化为定积分(1)参数方程若平面定向曲线L 的参数方程:b a t t y y t x x →⎩⎨⎧==:)()(,则⎰+L dy y x Q dx y x P ),(),(=⎰+badt t y t y t x Q t x t y t x P )]('))(),(()('))(),(([若空间定向曲线Γ的参数方程b a t t z z t y y t x x →⎪⎩⎪⎨⎧===:)()()(,则⎰Γ++dzz y x R dy z y x Q dx z y x P ),,(),,(),,(=⎰++b adt t z t z t y t x R t y t z t y t x Q t x t z t y t x P )]('))(),(),(()('))(),(),(()('))(),(),(([(2)直角坐标方程若曲线L 的方程为()y x ϕ=,b a x →: 则[]dx x y x y x Q x y x P dy y x Q dx y x P bal⎰⎰'+=+)()(,())(,(),(),(二重积分的计算:化为二次积分(1)直角坐标系若),(y x f 在x 型区域}),()(|),{(21b x a x y y x y y x D ≤≤≤≤=上连续 则σd y x f D⎰⎰),(=11()()(,)by x ay x dx f x y dy ⎰⎰.若),(y x f 在y 型区域}),()(|),{(21d y c y x x y x y x D ≤≤≤≤=上连续,则σd y x f D⎰⎰),(=⎰⎰)()(21),(y x y x dcdx y x f dy .(2)极坐标变换极坐标变换:⎩⎨⎧==θθsin cos r y r x , πθ20,0,≤≤+∞<≤r⎰⎰⎰⎰=DDrdrd r r f dxdy y x f θθθ)sin ,cos (),(情形1 原点D O ∉1)∆为θ型区域,即}),()(|),{(21βθαθθθ≤≤≤≤=∆r r r r ,此时.)sin ,cos (),()()(21dr r r r f d dxdy y x f r r D⎰⎰⎰⎰=θθβαθθθ2)∆为r 型区域,即}),()(|),{(2121r r r r r r ≤≤≤≤=∆θθθθ,此时.)sin ,cos (),()()(2121θθθθθd r r f rdr dxdy y x f r r r r D⎰⎰⎰⎰=情形2 原点O 是积分区域D 的内点,D 的边界极坐标方程为)(θr r =,则变换后的区域}20),(0|),{(πθθθ≤≤≤≤=∆r r r ,此时.)sin ,cos (),()(020dr r r r f d dxdy y x f r D⎰⎰⎰⎰=θπθθθ情形3 原点O 在积分区域的边界曲线)(θr r =上,}),(0|),{(βθαθθ≤≤≤≤=∆r r r ,此时有.)sin ,cos (),()(0dr r r r f d dxdy y x f r D⎰⎰⎰⎰=θβαθθθ广义极坐标变换:⎩⎨⎧==θθsin cos br y ar x πθ20,0,≤≤+∞<≤r⎰⎰⎰⎰=DDabrdrd br ar f dxdy y x f θθθ)sin ,cos (),(三重积分的计算:化为三次积分 (1)直角坐标系投影法(以投影到xy 平面为例)我们先在z 轴上做积分,暂时将y x ,看成是常数.把函数()z y x f ,,看作是z 的函数,将它在区间()()],,,[21y x z y x z 上积分得到“线”的质量()()()⎰y x z y x z dz z y x f ,,21,,.显然这个结果是y x ,的函数,再把这个结果在平面区域xy D 上做二重积分“体”的质量()()()d x d y dz z y x f y x z y x z D xy⎪⎭⎫ ⎝⎛⎰⎰⎰,,21,,,即 ⎰⎰⎰⎰⎰⎰=),(),(V21),,(V ),,(y x z y x z D dz z y x f dxdy d z y x f xy若}),()(),,(),(|),,{(2121b x a x y y x y y x z z y x z z y x V ≤≤≤≤≤≤=,⎰⎰⎰⎰⎰⎰=),(),()()(V2121),,(d V ),,(y x z y x z x y x y badz z y x f y dx d z y x f ;若}),()(),,(),(|),,{(2121d y c y x x y x y x z z y x z z y x V ≤≤≤≤≤≤=,⎰⎰⎰⎰⎰⎰=),(),()()(V2121),,(d V ),,(y x z y x z y x y x dcdz z y x f x dy d z y x f ;截面法(以截面平行于xy 平面为例)确定V 位于平面21c z c z ==与之间,即],[21c c z ∈,过z 作平行于xoy 面的平面截V ,得截面z D ,不难得到: “面”的质量(),,zD f x y z dxdy ⎰⎰,“体”的质量 dzdv z y x f Vc c ⎰⎰⎰⎰=21),,(⎰⎰zD dxdy z y x f ),,((2)柱面坐标变换,,20,0,,sin ,cos :+∞<<-∞≤≤+∞<≤===z r z z r y r x T πθθθdz rdrd dV θ=⎰⎰⎰Vdxdydz z y x f ),,(=.),sin ,cos (⎰⎰⎰'V dz rdrd z r r f θθθ{}212121/),()(),,(),(),,(θθθθθθθθ≤≤≤≤≤=r r r z z r z z r V⎰⎰⎰Vdxdydz z y x f ),,(=rdz z r r f dr d r z r z r r ),sin ,cos (),(),()()(212121⎰⎰⎰θθθθθθθθθ(3)球坐标变换,0,20,0,rcos ,sin sin ,cos sin :πϕπθϕθϕθϕ≤≤≤≤+∞<≤===r z r y r x T θϕϕd drd r dV sin 2=⎰⎰⎰Vdxdydz z y x f ),,(.sin )cos ,sin sin ,cos sin (2⎰⎰⎰'=V d drd rr r r f θϕϕϕθϕθϕ{}212121/),()(),,(),(),,(θθθθϕθϕθϕθϕθϕ≤≤≤≤≤=r r r r V⎰⎰⎰Vdxdydz z y x f ),,(=dr r r r f d d r r ϕϕθϕθϕϕθθϕθϕθϕθϕθθsin )rcos ,sin sin ,cos sin (2),(),()()(212121⎰⎰⎰广义球坐标变换,0,20,0,rcos ,sin sin ,cos sin :πϕπθϕθϕθϕ≤≤≤≤+∞<≤===r c z br y ar x T⎰⎰⎰Vdxdydz z y x f ),,(.sin )cos ,sin sin ,cos sin (2⎰⎰⎰'=V d drd abcr cr br ar f θϕϕϕθϕθϕ第一型曲面积分:化为二重积分(1)直角坐标方程若光滑曲面S :()y x z z ,=,()D y x ∈,, ),,(z y x f 为定义在S 上的连续函数,则()⎰⎰SdS z y x f ,,=()⎰⎰++Dy x dxdy z z y x z y x f 221),(,,(2)参数方程第二型曲面积分:化为二重积分 (1)直角坐标方程设函数),,(z y x R 在有向光滑曲面∑:),(y x z z =,xy D y x ∈),(上连续,则有⎰⎰⎰⎰±=∧∑xyD dxdy y x z y x R dy dx z y x R )),(,,(),,((上侧取正,下侧取负)若曲面为∑:),(z y x x =,则有⎰⎰⎰⎰±=∧∑yzD dydz z y z y x P dz dy z y x P ),),,((),,( (前侧取正,后侧取负)若曲面为∑:),(z x y y =,则有⎰⎰⎰⎰±=∧∑xzD dxdz z z x y x Q dz dx z y x Q )),,(,(),,((右侧取正,左侧取负)注:如果S 的法线方向与相应坐标轴的正向成钝角的那一侧为正侧,则相应的公式右端要加“-”号(2)参数方程格林公式: 若函数),(),,(y x Q y x P 在闭区域D 上连续,且有连续的一阶偏导数,则有,)(⎰⎰⎰+=∂∂-∂∂L DQdy Pdx d yPx Q σL 为区域D 的边界曲线,并取正方向.设区域D 的边界L 由一条光滑曲线或几条光滑曲线组成,规定边界曲线的正方向为:当人沿边界行走时,区域D 总在他的左边;与上述方向相反的方向称为负方向,记为L -.为便于记忆,格林公式可写成下述形式=∂∂∂∂⎰⎰σd QP x Dy ⎰+LQdy Pdx .格林公式沟通了平面区域上的二重积分与其边界曲线上的曲线积分之间的联系.高斯公式:设空间闭区域Ω是由分片光滑的闭曲面2所围成,P (x,y,z ),Q(x,y,z),R(x,y,z)在Ω上具有一阶连续偏导数,则有公式:⎰⎰⎰⎰⎰Ω∑++=∂∂+∂∂+∂∂Rdxdy Qdzdx Pdydz dxdydz z R y Q x P )(这里∑是由Ω的整个边界曲面的外侧构成。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
j
y
= rot A
P
Q R
高斯公式与斯托克斯公式可写成: 高斯公式与斯托克斯公式可写成:
同理可证 故有
d u = P d x + Qd y + Rd z
u = P, x u = Q, y u =R z
(3) (4) 若(3)成立, 则必有 (3)成立, 成立
一阶偏导数连续, 因P, Q, R 一阶偏导数连续, 故有
P 2u Q = = y xy x
Q R R P = , = x z z y
dI lim I 1 = lim = S → M ∫ Aτ ds S S → M S Γ dS
n
M
Γ
S
在点M处绕方向 表达了向量场 A 在点 处绕方向 n 旋转趋势 的大小,称为 在点M处绕方向 环流密度. 的大小 称为 A 在点 处绕方向n 环流密度 环流密度也是一种变化率. 环流密度也是一种变化率
第九节 各种积分间的关系
三、斯托克斯公式 环流量与旋度
1. 斯托克斯公式 封闭曲线可以张成曲面, 封闭曲线可以张成曲面,该曲线也可看作 曲面的边界. 曲面的边界 斯托克斯公式揭示空间曲面片边界曲线 上的曲线积分与曲面片上的曲面积分之间 的曲线积分与曲面片上的曲面积分之间 的关系. 关系.
定理4 斯托克斯公式) 定理4 (斯托克斯公式) 设空间光滑曲面片 的边界曲线是光滑(或分段光滑) Σ 的边界曲线是光滑(或分段光滑)闭曲线Γ , 函数 P( x, y, z), Q( x, y, z), R( x, y, z) 在包含Σ 在内的一个空间区域内有一阶连续偏导数, 在内的一个空间区域内有一阶连续偏导数, 则有 R Q P R Q P ∫∫ ( y z )dydz + ( z x )dzdx + ( x y )dxdy Σ = ∫ Pdx + Qdy + Rdz 的方向符合右手规则. 证明从略. 其中 Γ 和 Σ 的方向符合右手规则. 证明从略.
Γ
(1)公式的行列式形式表示 公式的行列式形式表示: 注: 公式的行列式形式表示
∫∫
Σ
dydz dzdx dxdy y x z P Q R
=
∫ Pdx + Qdy + Rdz
Γ
(2)公式的另一形式 公式的另一形式 cos α cos β cos γ
∫∫
Σ
x P
y Q
dS = z R
∫
Γ
d u = P d x + Qd y + Rd z
(4) 在G内处处有 内处处有
P y
=
Q x
,
Q z
= ,
R y
R x
=
P z
证: (4) (1) 由斯托克斯公式可知结论成立; 由斯托克斯公式可知结论成立; (1) (2) (自证) 自证) (2) (3) 设函数 ( x, y,z ) u( x, y, z) = ∫ P d x + Qd y + Rd z
在点M处绕不同方向可能有不同 向量场 A在点 处绕不同方向可能有不同 的环流密度. 的环流密度. 旋度的定义 中一点M处存在这样一个 若在向量场 A 中一点 处存在这样一个 向量, 在点M的环流密度取得 向量,其方向是使 A在点 的环流密度取得 最大值的方向, 其模等于该点处环流密度的 最大值的方向, 最大值, 最大值,则称此向量为场 A 在点 的旋度, 在点M的旋度, 记作 rot A.
围成的区域 另解:利用对称性, 另解:利用对称性,得
3 = 2
Dxy : x + y = 1, x = 0, y = 0
1
Σ
z
1
Dxy
o
Σ
1 y
3 I = ∫∫ dydz + dzdx + dxdy = 3 ∫∫ dxdy = 2 Dxy Σ
x
Dx y
与平面 y = z 的 例2. Γ 为柱面 . 交线,从 轴正向看为顺时针, 交线 从 z 轴正向看为顺时针 计算 解 设∑为平面 z = y 上被 Γ 所围椭圆域 , 且取下侧, 由斯托克斯公式,得 且取下侧, 由斯托克斯公式,
Σ
o
1
Σ
1 y
x
dydz = ( z x ) dxdy , dxdz = z y dxdy ,
(
)
∵ Σ : z = 1 x y , z x = 1, z y = 1 ∴ I = ∫∫ dydz + dzdx + dxdy = ∫∫ 3dxdy = ∫∫ 3dxdy
Σ
将以上三个积分化为对 曲面积分, 将以上三个积分化为对 x,y 的曲面积分,
I = ∫∫ zdzdx ydxdy = ∫∫ [( 1) z + y ]dxdy = 0
Σ Σ
z
Γ
Σ
y
o x
2
为下侧, 另解: 另解:∑:z = y 为下侧,法向量 n = (0,1, 1) 其方向余弦 利用斯托克斯公式得 cosα cos β cosγ
I = ∫∫
∑
x
y
z
dS
y
2
Γ
其中 Γ 为平面 x + y + z = 1 被三个坐标面截得的三角形的整个边界, 被三个坐标面截得的三角形的整个边界, 它的正向与三角形上侧符合右手规则. 它的正向与三角形上侧符合右手规则. 解 记三角形所在平面部分上侧为 Σ 由斯托克斯公式得到
z
1
I = ∫∫ dydz + dzdx + dxdy
旋度的计算公式
rot A= =
R Q P R Q P ( ),( ),( ) = y z z x x y
i
x
j
y
k
z
P
Q
R
于是得斯托克斯公式的向量形式 :
或
∫∫ rot A nd S = ∫ Aτ ds ∫∫Σ(rot A)n d S = ∫ Γ Aτ ds
Σ Γ
旋度的力学意义: 旋度的力学意义: 转动, 设某刚体绕定轴 l 转动, 为刚体上任一点 为刚体上任一 角速度为ω , M为刚体上任一点, 建立坐标系如图, 建立坐标系如图, 则
y
+∫ x d y +∫ ( x + y) d z
0
z
= xy + ( x + y)z = xy + yz + zx
0
z
(x, y, z)
o
x
(x,0,0)
y
(x, y,0)
3.环流量与旋度 环流量与旋度 斯托克斯公式 R Q P R Q P ∫∫ ( y z )dydz + ( z x )dzdx + ( x y )dxdy Σ
u =
2
u x
i+
2u x2
u y
j+
2u y2
u z
k = gradu
2u z2
u = u = gradu
=
+
+
= u
(2) A = P( x, y, z) i + Q( x, y, z) j + R( x, y, z) k,
则 A =
× A =
P x
+
Q y
+
k
z
R z
= div A
i
同理
证毕
例3 验证曲线积分
∫ ( y + z)d x + (z + x)d y + ( x + y)dz
Γ
与路径无关, 并求函数 与路径无关
u( x, y, z) = ∫
( x, y,z ) (0,0,0)
( y + z)d x + (z + x)d y + ( x + y)d z
解 令
P = y+ z , Q= z+ x , R= x+ y
空间曲线积分的四个等价条件: 空间曲线积分的四个等价条件: (1) 对G内任一分段光滑闭曲线 Γ, 有 内任一分段光滑闭曲线 ∫ P d x + Qd y + Rd z = 0
Γ
(2) 对G内任一分段光滑曲线 Γ, 内任一分段光滑曲线
∫
Γ
P d x + Qd y + Rd z 与路径无关
(3) 在G内存在某一函数 u, 使 内存在某一函数
P Q Q P R R 关. ∴ 积分与路径无关
u( x, y, z) = ∫
( x, y,z )
(0,0,0)
( y + z)d x + (z + x)d y + ( x + y)d z
积分与路径无关, 积分与路径无关, 因此
Pdx + Qdy + Rdz
(3) 如果Σ是 xoy 面上的一块平面区域, 如果Σ 面上的一块平面区域, 则斯托克斯公式就是格林公式, 则斯托克斯公式就是格林公式, 公式就是格林公式 故格林公式 是斯托克斯公式的特例. 是斯托克斯公式的特例. 特例
Q P ∫∫ ( x y )dxdy = D
∫
qx r
3
qy qz r3 r3
这说明, 在除点电荷所在原点外, 这说明, 在除点电荷所在原点外, 整个电场无旋 无旋. 整个电场无旋.
例5. 设 . 的外法向量, n 为Σ 的外法向量, 计算 I = ∫∫ Σrot A ndS .
i j
y
k
z
解 rot A =
x
= (0, 0,1)
2y
3x z2
z
o x
l
M r
