随机环境中随机指标分枝过程矩的渐近性
合集下载
raven渐进式矩阵概

raven渐进式矩阵概
Raven渐进式矩阵概是一种矩阵分解算法,它可以将矩阵分解成两个低维度的矩阵,这样可以减少计算量,并加速矩阵乘法的运算速度。
它的原理是通过随机分块和处理矩阵来实现高效的矩阵分解。
以下是Raven渐进式矩阵概的分步骤阐述:
1. 随机分块
Raven渐进式矩阵概先将矩阵随机分成数个块。
这些块可以有不同的大小,并不需要完全相等。
随机分块可以将矩阵分解成子问题,这样可以有效地减少计算量。
2. 处理矩阵
接下来,Raven渐进式矩阵概需要通过处理块来减少矩阵的维度。
处理矩阵的方法很多,其中最常用的就是奇异值分解(SVD)。
SVD可以将一个矩阵分解成三个低维度矩阵:左奇异矩阵U,右奇异矩阵V和奇异值对角矩阵S。
这个分解可以让我们跟踪矩阵的最大特征值,从而有效地减少计算量。
3. 重复拆分
通过随机分块和处理矩阵,我们已经将矩阵分解成低维度的子矩阵。
我们可以继续对这些子矩阵进行重复拆分,这样我们就可以得到更小的矩阵。
这个操作可以反复进行,直到我们得到的子矩阵足够小,可以直接进行矩阵乘法计算。
4. 合并子矩阵
最后,我们需要将这些小子矩阵合并成一个完整的矩阵。
这个操作可以通过矩阵乘法来实现。
最终,我们将得到原始矩阵的分解版本。
总体来说,Raven渐进式矩阵概可以让我们将矩阵分解成低维度的子矩阵,从而减少计算量,并提高矩阵乘法的运算速度。
这个算法在大规模数据分析和机器学习中应用广泛,是许多高效算法背后的核心原理。
随机环境中的两性Galton-Watson分枝过程

Ab t a t A ie u l l n Wa s n b a c ig p o e si g n r l d t o eg n r l r c i g mo e,t a ,t e sr c b s x a t - to r n h n r c s e e a ̄e am r e e a a hn d l h t s h Ga o s o bn i b s x a l n W as n b a c i gp o e si n o e vr n n s n t i mo e,t eo s r g p o a i t itiu in ie u l Gat — to r n h n r c s r d m n i me t.I s o na o h d l h f p n r b blyds b t i i r o i n t . d b t o t l d b tt n r r o i n io me t r c s .S mec traf rc r i x i c in a d f r o — s o i . u n r l y asai ay eg d ce v r n n o e s o r e o e t n e t t n n i. c oe o p i i a n o o n c r i x i ci n a eo t i e r e r c s . e t ne t t r b n df o e s a n o a o t p h Ke r s b s x a Ga tn Wa s nb a c i g p o e s s b a c ig p o e s s n r n o e vr n n s s t n r y wo d ie u l l — to rn h n r c s e ; r n h n r c s e d m n i me t ; t i a o i a o a o y eg d cs q e c ; e t ci np o a i te r o i e u n e xi t rb blis n o i
一类临界可交换随机环境中分枝过程的灭绝概率

p r o c e s s e s i n e x c h a n g e a b l e r a n d o m e n v i r o n me n t s a n d t h e n s t u d y t h e p r o p e r t i e s o f t h e e x t i n c t i o n p r o b bi a l i t y o f t h e l a t t e r
关 键 词 可 交换 环 境
Th e Ex t i n c t i o n Pr o b a b i l i t i e s o f Cr i t i c a l Br a n c h i n g Pr o c e s s e s i n Ex c h a n g e a b l e Ra n d o m En v i r o n me n t s
收稿 日期 : 2 0 1 3年 1 月1 5 t 3 程的灭绝概率
5 l
间, ={ , n∈了 1 } 是概率空间 ( 力, J , P ) 上的一个随机环境. 记P ( ・I )=P f ( ・ ) , 对应地 ,
有 记号 ( 。 ) .
第3 3卷
第 1 期
数 学 理 论 与应 用
MATHEMAT【 C AL THE0RY AND AP P UC A nONS
V0 1 . 3 3 No . 1 M8 r .2 0 1 3
2 0 1 3年 3月
一
类 临 界 可 交 换 随 机 环 境 中分 枝 过 程 的 灭 绝 概 率
, …, l , …, k ∈ E
m
i i i )V m ∈N, k∈ T , 1 , …
( = J n , 1 ≤i ≤m , 0 ≤n ≤| j } )=n nP f ( = J ’ n i ) , a . s . ,
关 键 词 可 交换 环 境
Th e Ex t i n c t i o n Pr o b a b i l i t i e s o f Cr i t i c a l Br a n c h i n g Pr o c e s s e s i n Ex c h a n g e a b l e Ra n d o m En v i r o n me n t s
收稿 日期 : 2 0 1 3年 1 月1 5 t 3 程的灭绝概率
5 l
间, ={ , n∈了 1 } 是概率空间 ( 力, J , P ) 上的一个随机环境. 记P ( ・I )=P f ( ・ ) , 对应地 ,
有 记号 ( 。 ) .
第3 3卷
第 1 期
数 学 理 论 与应 用
MATHEMAT【 C AL THE0RY AND AP P UC A nONS
V0 1 . 3 3 No . 1 M8 r .2 0 1 3
2 0 1 3年 3月
一
类 临 界 可 交 换 随 机 环 境 中分 枝 过 程 的 灭 绝 概 率
, …, l , …, k ∈ E
m
i i i )V m ∈N, k∈ T , 1 , …
( = J n , 1 ≤i ≤m , 0 ≤n ≤| j } )=n nP f ( = J ’ n i ) , a . s . ,
随机环境中具有迁入的分枝过程的时序估计量的性质

记
一 ) ( +
一
一 )
: .
CO "
() 5
卢c =∑ e () ,
其中 ] i+ I i I ̄i l l -lL E: N> 3 )i N
Oi i  ̄/1 i
, =
( 6 )
. i c } 易证 Ⅳ >
L 。
置一 峨
和 O j: 关于 . 可测,  ̄< I ) 于是有 是
第 2 卷第 4 5 期 2008年 12月
经
济
数
学
v0. 5 No. j2 4
De . 2 0 e O8
MA HE TI N 日C 0 ̄ S T MA CS I ( ⅡC
随机环 境 中具有 迁
胡杨利 , 志 , 申 汪和松
:
E ( 一 ] ( E∑ )s . [ c m =∞) ( { )
式() .4得证 . 11 : 置 ≥c . 2 }由于
~
对 固定的 > , o 0 令 2=懈 { , 一 lN :i { ≥ +1 ∑ 0 n> , - n 。 ,c n n f :
,
} { } , 和 独立 则称 ={ } 。 是具有迁入 的随机环境中的分枝过程 . 本文恒设 独立同分布 , = X , { o‰ , 1 n i 1, . , }1 =∑J。 i m = 4 , X l = , =
,
,
则m= ( = ( , + 磁 ( + ( = ( + () = 1 哦 1 m= 1 磁 1 1 1令 ) ) ) ) ) .
,
兰
=f l c , in : } 誊 n { =
—
, ∑ ic 由 X 于 一 -
0 . 7
一 ) ( +
一
一 )
: .
CO "
() 5
卢c =∑ e () ,
其中 ] i+ I i I ̄i l l -lL E: N> 3 )i N
Oi i  ̄/1 i
, =
( 6 )
. i c } 易证 Ⅳ >
L 。
置一 峨
和 O j: 关于 . 可测,  ̄< I ) 于是有 是
第 2 卷第 4 5 期 2008年 12月
经
济
数
学
v0. 5 No. j2 4
De . 2 0 e O8
MA HE TI N 日C 0 ̄ S T MA CS I ( ⅡC
随机环 境 中具有 迁
胡杨利 , 志 , 申 汪和松
:
E ( 一 ] ( E∑ )s . [ c m =∞) ( { )
式() .4得证 . 11 : 置 ≥c . 2 }由于
~
对 固定的 > , o 0 令 2=懈 { , 一 lN :i { ≥ +1 ∑ 0 n> , - n 。 ,c n n f :
,
} { } , 和 独立 则称 ={ } 。 是具有迁入 的随机环境中的分枝过程 . 本文恒设 独立同分布 , = X , { o‰ , 1 n i 1, . , }1 =∑J。 i m = 4 , X l = , =
,
,
则m= ( = ( , + 磁 ( + ( = ( + () = 1 哦 1 m= 1 磁 1 1 1令 ) ) ) ) ) .
,
兰
=f l c , in : } 誊 n { =
—
, ∑ ic 由 X 于 一 -
0 . 7
【国家自然科学基金】_遍历定理_基金支持热词逐年推荐_【万方软件创新助手】_20140803
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
科研热词 推荐指数 鞅收敛定理 1 非线性算子半群 1 随机环境中随机游动 1 随机环境中的随机徘徊 1 随机环境中的分枝链 1 遍历定理 1 遍历 1 转移矩阵 1 计算机应用 1 算法理论 1 稳定婚姻匹配 1 相关 1 状态频率 1 渐近殆非扩张曲线 1 森林 1 枚举 1 暂留性 1 强大数定律 1 常返性 1 容量 1 右可逆半群 1 先序遍历 1 信道 1 依时随机环境中的马尔可夫链 1 依时随机环境中的马尔可夫过程 1 依时依空的随机环境中的马尔可夫链 1 三重循环马氏链 1 mimo 1
推荐指数 3 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2014年 序号 1 2 3 4 5 6 7 8 9
2014年 科研热词 推荐指数 遍历性 2 生成元 2 cesàro遍历 2 迭代函数系统:markov-feller算子1 局部凸拓扑 1 双连续余弦函数 1 双连续c半群 1 双连续c余弦函数 1 不变概率测度 1
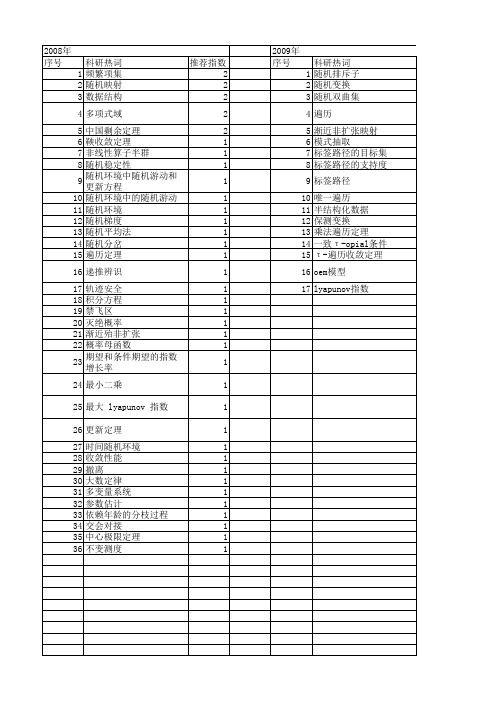
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
科研热词 随机抽取 标签路径的目标集 标签路径的支持度 标签路径 唯一遍历 半结构化数据 保测变换 乘法遍历定理 一致τ -opial条件 τ -遍历收敛定理 oem模型 lyapunov指数
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
一类随机环境中的随机游动

粉 ∑
一
( 2)
这里 由过程的定义可知 当 z a时 , 辛 ( ) 0P () l当 z三 b , j z : l P z 一 , ・ z 一 ; 三 时 P = () ,
P t z) = 0 ]( .
l
返性准 则和 一些 极 限性 质 .
关键词 随 机 环境 ;随机 蝣 动 ;常 返性 ;首 中 时
中图分 类号
O 2 1 6 1.2
文 献 标识 码
A
X■
一
t
随 机 环 境 中 的 随 机 过 程 是 概 率 论 的 一 个 新 的 分 枝 , 机 环 境 中 的 随 机 游 动 ( 记 为 随 简
维普资讯
第 3 期
柳 向 东 等 : 类 随 机 环 境 中 的 随 机 游 动 一
・9 2 9・
( 若∑ 。 一 . 。且∑ ,… i ) ( 。 ) 一。, … 一 <。, i… X 一。 a . 。 。 则l a r . c . e () i 若∑二 ( … ) 一o, j . . 。 且∑二 一。, 一o 一l n—X < l 一 … 。则 。 i f ,. i m{I n
与 S l n一致 的 结果 . oo mo
定义 l 设 { , ,. , ∈ z) 为 概 率 空 间 ( , ( 。 )) , , 0, P) 卜的 一 列 随机 向 量 , 中 ( , 其 /) }
独 立 同分 布 , e一 { , ,. , ∈ z)定 义 在 z上 的 . 足 r 记 ( 。 )) , 满 列条 件 为 R I W RE:
(i i)如果 Eo a> 0 则 l … 。一 一 ∞ Ⅱ e i lg , i a r ..
随机环境中具有随机控制函数的两性分枝过程

+ 1 和 + 1 分 别表示 第 佗代 所有配 对 生成 的雌 性和雄 性 总数 .
定义 2 随机环境中两性分枝过程 { ) ≥ 0 称为上可加的,如果其配对 函数是上可加
( ∑( , m ) ) ∑ ( , m  ̄ n , i ) .
定义 3 如果 对任 意 的 X , n∈肌 ,有
具有 随机控制 函数 的两性分枝过程 ,在独立 同分布 的环 境下 ,此过程是 随机环 境 中的 马氏链 ,同时给 出了概率母 函数之 间的关系表达式 .当过程 的控制 函数 是上可加时 , 本文推 导 出了配对 单元平均增长率 的极限性质 ,从而推广 了经典两性分枝过程 的相关
理论 .
.
列 ,对任意给定的 0∈e, P t . ( 0 ) 是概率分布律.
定义 1 若 { Z n } ≥ 0 满足
z + 1 = ( + 1 , + 1 ) ,
收稿 日 期: 2 0 1 2 — 0 9 — 0 7 . 作者简介:宋 明珠 ( 1 9 7 9 年1 1 月生) ,女,硕士,讲师. 研 究方向:随机环境 中的马 氏链 基金项 目: 教育 部人 文社科青年基金 ( 1 2 YJ CZ H 2 1 7 ) 高校省级 自然科学研 究项 目( k j 2 0 1 3 z 3 3 1 ) ;铜陵学院 自 然 科学研究项 目( 2 0 1 2 t l x y 1 2 ) .
第3 0 卷 第 6 期
2 0 1 3 年1 2 月
工
程
数
学
学
报
V o 1 . 3 0 N 。 . 6
De c .2 0 1 3
CHI NES E J OURNAL OF ENGI NEERI NG M ATHEM ATI CS
定义 2 随机环境中两性分枝过程 { ) ≥ 0 称为上可加的,如果其配对 函数是上可加
( ∑( , m ) ) ∑ ( , m  ̄ n , i ) .
定义 3 如果 对任 意 的 X , n∈肌 ,有
具有 随机控制 函数 的两性分枝过程 ,在独立 同分布 的环 境下 ,此过程是 随机环 境 中的 马氏链 ,同时给 出了概率母 函数之 间的关系表达式 .当过程 的控制 函数 是上可加时 , 本文推 导 出了配对 单元平均增长率 的极限性质 ,从而推广 了经典两性分枝过程 的相关
理论 .
.
列 ,对任意给定的 0∈e, P t . ( 0 ) 是概率分布律.
定义 1 若 { Z n } ≥ 0 满足
z + 1 = ( + 1 , + 1 ) ,
收稿 日 期: 2 0 1 2 — 0 9 — 0 7 . 作者简介:宋 明珠 ( 1 9 7 9 年1 1 月生) ,女,硕士,讲师. 研 究方向:随机环境 中的马 氏链 基金项 目: 教育 部人 文社科青年基金 ( 1 2 YJ CZ H 2 1 7 ) 高校省级 自然科学研 究项 目( k j 2 0 1 3 z 3 3 1 ) ;铜陵学院 自 然 科学研究项 目( 2 0 1 2 t l x y 1 2 ) .
第3 0 卷 第 6 期
2 0 1 3 年1 2 月
工
程
数
学
学
报
V o 1 . 3 0 N 。 . 6
De c .2 0 1 3
CHI NES E J OURNAL OF ENGI NEERI NG M ATHEM ATI CS
随机环境分枝过程中的极限定理与大偏差定理新解

are limited,the new explanation of limit theorem and large deviation theorem for environment first⁃arrival is put forward.
Keywords:limit theorem;large deviation theorem;random environment;environment first⁃arrival
教学有效性的研究与实践(GH14662)
0
j
1
j=0
任意一个 θ∈Θ,其概率母函数如下:
f θ ( s) = p 0 + p1 s + p 2 s2 + ⋯ + p n s + ⋯
n
若 m θ = f ′θ (1),σ 2θ = f θ″ (1) + f ′θ (1) - [ f ′θ (1)] ,m θ 为 环 境
mnini源自n=0 i=1ni |
j ni∈x
式中:ξ 为随机环境;Z 是其分枝过程。按照该过程,
Copyright©博看网 . All Rights Reserved.
第1期
,θ∈Θ,可 以 简 单 记 为
若 Z 0 = 1,对 于 任 意 的 θ∈Θ
(
)
P θ·
| = θ ,P θ ·
( ) = P θ·ξ
( ) = P ·ξ
( | 0 = θ ),对 应 的 期 望 值 为
对 任 意 的 t > 0 来 说 ,W n → W,EW t < ∞,在 此 情 况
下,针对 Q, a.s.θ,有:
ì
1 log P æ log Z n x ö = ï0,
Keywords:limit theorem;large deviation theorem;random environment;environment first⁃arrival
教学有效性的研究与实践(GH14662)
0
j
1
j=0
任意一个 θ∈Θ,其概率母函数如下:
f θ ( s) = p 0 + p1 s + p 2 s2 + ⋯ + p n s + ⋯
n
若 m θ = f ′θ (1),σ 2θ = f θ″ (1) + f ′θ (1) - [ f ′θ (1)] ,m θ 为 环 境
mnini源自n=0 i=1ni |
j ni∈x
式中:ξ 为随机环境;Z 是其分枝过程。按照该过程,
Copyright©博看网 . All Rights Reserved.
第1期
,θ∈Θ,可 以 简 单 记 为
若 Z 0 = 1,对 于 任 意 的 θ∈Θ
(
)
P θ·
| = θ ,P θ ·
( ) = P θ·ξ
( ) = P ·ξ
( | 0 = θ ),对 应 的 期 望 值 为
对 任 意 的 t > 0 来 说 ,W n → W,EW t < ∞,在 此 情 况
下,针对 Q, a.s.θ,有:
ì
1 log P æ log Z n x ö = ï0,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
i r n o en i n e t n a d m vr m ns. o
Ke wo d Ra d m y i d x d y rs no l n e e
R n o e vr n n Mo n s a d m n i me t o me t
1 问题 的提 出
19 9 6年 E p 提 出指标 服从 泊松 过程 的随机指 标分 枝 过程 , ps 文献 [ ] 明 了随机 指 标下 的 1证 临界 分枝 过程矩 的渐近 性 。本文 提 出随 机环境 中 随机指 标分 枝 过 程 , 考 虑它 的条 件 矩 和矩 并
一
设 J={i ≥1 为正的独立同分布随机变量序列, J, i } 且具有分布函数 F ( ):P , ≤ 。 ( ) 假定 _ , 与 , z相互独立。
对应的 过 更新 程为:o oS =∑ : ≥1 任意的t , ( = u{≥0 S: , J凡 , o 对 ≥o令Ⅳ f s : ) p
的一些 性 质ห้องสมุดไป่ตู้。
设 ( 5 P 为概率空 间, = { ,,…} ,, ) E 0 12 为状态集 , E 为状态空间, , 是一个 ( ,) ( ) 可测空 间, = { ; 凡≥0 为定义在 ( 弓 P 上取值于 ( , } 力,, ) )的随机环境序列 。记 ( ) ‘
第3 0卷 第 1期 21 0 0年 3月
数 学理论与应用
MATHEMATCAL HEORY AND P CAT1 I r AP U 0NS
V0 . 0 No 1 】3 . M8 .2 O r O1
随机 环 境 中随机 指标 分 枝 过 程 矩 的渐 近性
刘贵兰 胡杨 利 尹 悦
=P 。I) ( )=E ・I)rr ‘ ( , ‘ ( , e )=vt I) a( a( o
Z = { r≥0 为定义于 ( 5 P 且取值于 ( , ) z; t } , , ) E 占 的随机环境 中的分枝过程 :
Z
Z = , 川 =∑ 。 。 1z
国家 自 然科 学基 金 ( o 17 12 ;0 7 02 、 N :0 7 0 1 14 1 1 ) 湖南 省 自然 科学 基 金项 目( 8J 0 ) 湖南 省教 育 科 学规 划 课题 0J 07 、 3 ( J 0 BG 0 ) X K 6 J 0 8 及湖南省高等学校科研基金项 目( 7 0 3 0 C 5 ; C 1 ;8 10 0 C 7 ) 0 A 0 ;9 0 9 0 13 0 C 2 ; 7 0 8 资助 9 李 应求 教授推荐
=
:
在式 ( ) 1 中令 =0有
P(( = )= (0 =∑P( 0。 f £ 0 t) y) ; )() £
‘ 0
进 一步 , 假设 如下 条件成 立 :
( )生成后代数对应的概率母 函数满足 1
厶
()=s e 1一 ) s +b ( s . +D ( ( 1一s ) s , ) , 1 t
C agh , 1 14 h nsa 40 1 )
Ab t a t I i p p r e p o e t e a y tt o mu a o emo n so a d ml d x d b a c ig p o e s s sr c n t s a e ,w r v s mp oi f r l sf rt me t f n o y i e e r n h n rc s e h h c h r n
Ra d m v r n e t n o En i o m n s
Li u Gui n l H u Ya g i a nl Yi e n Yu
( ol eo ah ma c n o p t gS i c ,C a gh n es y o S in ea d T c n l y C l g f te t sa d C m u n c n e h n sa U i r t f ce c n eh o g , e M i i e v i o
S ≤ t, l()为计数 过程 。 }则 V t
记 E ( :∑ k )=∑ F ( , , 日f, l 更 数, ( )= Nt ) 。 ( P 。“ £ 则{( £ ) ≥0 ) ≥o 为 新函
其 中 P ()=P{ ()=k , ¨() , ^ Nt }F 为 ( )的 k 重卷积。 令 Yt ()=Z t , 州 ≥0 则称 { () t } Y t,≥0 为随机环境中随机指标分枝过程 。显然有 Y 0 ()
( 长沙理工大学数 学与计算科学学院, 长沙,114 40 1 )
摘 要 引入 了随机 环境 中随机指标分枝过程模 型, 证明 了该模型矩 的渐近性 。
随机 指标 随机环境 分枝过程 矩
关键 词
Ra d m l n e e a c n o e s s i n o y I d x d Br n hi g Pr c s e n
=
1。
‘
令 (;)=E ( ) 由于 N()与 , s es 。 t Z 独立 , 全概 率公式计 算 有 用
(; £ )=∑s t1£ ) s " (( P ,)=n
:
∑s ( 1= ( ) ) ∑ ( ( ) £ ) ∑P( ( 。 tt )
收稿 日期 :09年 8月 l 20 71 3
数学理论与应用
第n 代单个粒子产生的后代数 对应的条件概率母 函数为
妒( = ex fs E(! ) s )=∑ )。 (
第 代粒子总数 z 对应的条件概率母 函数为
() =E ( ) : f( 。 … () ) s es 0 f( 厶 5 …) 。
Ke wo d Ra d m y i d x d y rs no l n e e
R n o e vr n n Mo n s a d m n i me t o me t
1 问题 的提 出
19 9 6年 E p 提 出指标 服从 泊松 过程 的随机指 标分 枝 过程 , ps 文献 [ ] 明 了随机 指 标下 的 1证 临界 分枝 过程矩 的渐近 性 。本文 提 出随 机环境 中 随机指 标分 枝 过 程 , 考 虑它 的条 件 矩 和矩 并
一
设 J={i ≥1 为正的独立同分布随机变量序列, J, i } 且具有分布函数 F ( ):P , ≤ 。 ( ) 假定 _ , 与 , z相互独立。
对应的 过 更新 程为:o oS =∑ : ≥1 任意的t , ( = u{≥0 S: , J凡 , o 对 ≥o令Ⅳ f s : ) p
的一些 性 质ห้องสมุดไป่ตู้。
设 ( 5 P 为概率空 间, = { ,,…} ,, ) E 0 12 为状态集 , E 为状态空间, , 是一个 ( ,) ( ) 可测空 间, = { ; 凡≥0 为定义在 ( 弓 P 上取值于 ( , } 力,, ) )的随机环境序列 。记 ( ) ‘
第3 0卷 第 1期 21 0 0年 3月
数 学理论与应用
MATHEMATCAL HEORY AND P CAT1 I r AP U 0NS
V0 . 0 No 1 】3 . M8 .2 O r O1
随机 环 境 中随机 指标 分 枝 过 程 矩 的渐 近性
刘贵兰 胡杨 利 尹 悦
=P 。I) ( )=E ・I)rr ‘ ( , ‘ ( , e )=vt I) a( a( o
Z = { r≥0 为定义于 ( 5 P 且取值于 ( , ) z; t } , , ) E 占 的随机环境 中的分枝过程 :
Z
Z = , 川 =∑ 。 。 1z
国家 自 然科 学基 金 ( o 17 12 ;0 7 02 、 N :0 7 0 1 14 1 1 ) 湖南 省 自然 科学 基 金项 目( 8J 0 ) 湖南 省教 育 科 学规 划 课题 0J 07 、 3 ( J 0 BG 0 ) X K 6 J 0 8 及湖南省高等学校科研基金项 目( 7 0 3 0 C 5 ; C 1 ;8 10 0 C 7 ) 0 A 0 ;9 0 9 0 13 0 C 2 ; 7 0 8 资助 9 李 应求 教授推荐
=
:
在式 ( ) 1 中令 =0有
P(( = )= (0 =∑P( 0。 f £ 0 t) y) ; )() £
‘ 0
进 一步 , 假设 如下 条件成 立 :
( )生成后代数对应的概率母 函数满足 1
厶
()=s e 1一 ) s +b ( s . +D ( ( 1一s ) s , ) , 1 t
C agh , 1 14 h nsa 40 1 )
Ab t a t I i p p r e p o e t e a y tt o mu a o emo n so a d ml d x d b a c ig p o e s s sr c n t s a e ,w r v s mp oi f r l sf rt me t f n o y i e e r n h n rc s e h h c h r n
Ra d m v r n e t n o En i o m n s
Li u Gui n l H u Ya g i a nl Yi e n Yu
( ol eo ah ma c n o p t gS i c ,C a gh n es y o S in ea d T c n l y C l g f te t sa d C m u n c n e h n sa U i r t f ce c n eh o g , e M i i e v i o
S ≤ t, l()为计数 过程 。 }则 V t
记 E ( :∑ k )=∑ F ( , , 日f, l 更 数, ( )= Nt ) 。 ( P 。“ £ 则{( £ ) ≥0 ) ≥o 为 新函
其 中 P ()=P{ ()=k , ¨() , ^ Nt }F 为 ( )的 k 重卷积。 令 Yt ()=Z t , 州 ≥0 则称 { () t } Y t,≥0 为随机环境中随机指标分枝过程 。显然有 Y 0 ()
( 长沙理工大学数 学与计算科学学院, 长沙,114 40 1 )
摘 要 引入 了随机 环境 中随机指标分枝过程模 型, 证明 了该模型矩 的渐近性 。
随机 指标 随机环境 分枝过程 矩
关键 词
Ra d m l n e e a c n o e s s i n o y I d x d Br n hi g Pr c s e n
=
1。
‘
令 (;)=E ( ) 由于 N()与 , s es 。 t Z 独立 , 全概 率公式计 算 有 用
(; £ )=∑s t1£ ) s " (( P ,)=n
:
∑s ( 1= ( ) ) ∑ ( ( ) £ ) ∑P( ( 。 tt )
收稿 日期 :09年 8月 l 20 71 3
数学理论与应用
第n 代单个粒子产生的后代数 对应的条件概率母 函数为
妒( = ex fs E(! ) s )=∑ )。 (
第 代粒子总数 z 对应的条件概率母 函数为
() =E ( ) : f( 。 … () ) s es 0 f( 厶 5 …) 。
