15.5几何体的体积(2)
15.5几何体的体积(2)--椎体、球

2. 柱体(棱柱、圆柱)体积 结论 柱体的体积等于它的底面 积s 和高h的积。 V柱体= sh
锥体的体积(1)
结论1:等底等高的两个三棱锥的体积相等.
将三棱锥以△ABC为底面、 AA1为侧棱补成一个三棱柱. 联结B’C,再把该三棱柱
A’
A’ B’
C’
分割成三个三棱锥.
C’
3
B’
2
A
C
1
A C B
到一个正三棱锥A-BCD,求它的体积是正方体体
积Байду номын сангаас几分之几?
A B D 问题 、如果改为求 问题 12 、你能有几种 棱长为 a的正四面 解法?
体A-BCD的体积。 解一、补形,将三棱 你能有几种解法? 解二、利用体积公式 锥补成一个正方体。
解三、将四面体分割为 三棱锥C-ABE和三棱
1 V四面体= 3 S△BCD· h
例6. 已知正四棱锥相邻两个侧面所成二面
角为120o, 底面边长a, 求它的高、体积. S E D C O
A
B
解:连结AC、BD交于O,连结SO,
则SO为正四棱锥的高.
过B作BE⊥SC, E为垂足.连结DE,
则∠DEB为二面角D-SC-EB的平面角,
S
所以DEB=120o.
E D
C
O
A
B
连结OE,
P D
1 Sh 3
例1 已知正四棱锥P-ABCD 的棱长都 为a,求其体积和表面积.
C B
A
O
1 2 2 3 2 V aa a 3 2 6 3 2 S全 4 a a 2 ( 3 1)a 2 4
练习:P.41 练习15.5(2) P.42 练习15.5(3)
几何体的体积 PPT
祖氏父子的成就
祖暅是南北朝时代杰出的数学家祖冲之的儿子,字 景烁。受家庭的影响,尤其是父亲的影响,他从小 就热爱科学,对数学具有特别浓厚的兴趣,祖冲之 除了在计算圆周率方面的成就,还与他的儿子祖暅 一起,用巧妙的方法解决了球体体积的计算。他们 当时采用的原理,在西方被称为“卡瓦列利” (Cavalieri)原理,但这是在祖氏父子以后一千多 年才由意大利数学家卡瓦列利发现的。为了纪念祖 氏父子发现这一原理的重大贡献,数学上也称这一 原理为“祖暅(geng)原理”。
V柱体= sh
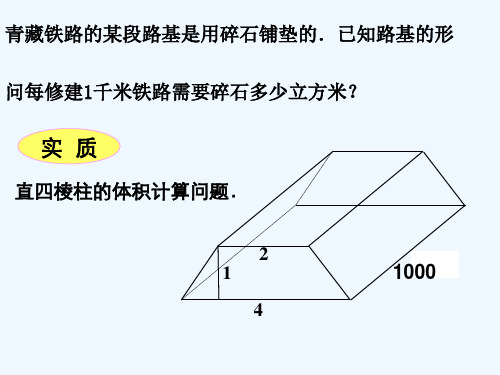
青藏铁路的某段路基是用碎石铺垫的.已知路基的形 状尺寸如图所示(单位:米), 问每修建1千米铁路需要碎石多少立方米?
实质
直四棱柱的体积计算问题.
2 1
4
10100000
例题分析
例2.已知三棱柱的角底三面角 A是 B形 , 直 C 两直角 A C 、B C 的长分3厘 别米 为4厘 和米,棱柱 B的 1B的侧 长为 10厘米,求满足的下三列棱条柱件 V的 . 体积
青藏铁路的某段路基是用碎石铺垫的.已知路基的形 问每修建1千米铁路需要碎石多少立方米?
实质
直四棱柱的体积计算问题.
2 1
4
10100000
问题1 长方体的体积?
回顾
V长方体=abh =sh (a-长,b-宽,h-高,s-底面积)
问题2 体积的概念?
体积——几何体占有空间部分的大小 面积——图形占有平面部分的大小
三个条件缺一不可,否则不能得出两个几何体的体积一定相等.
大家应该也有点累了,稍作休息 大家有疑问的,可以询
10
祖暅原理的功能?
功能一:证明几何体的体积相等.(面积相等 推出体积相等)
底面积和高都相等的平行六面体和三棱锥的
常见体积计算公式

常见体积计算公式在几何学中,常见的体积计算公式主要包括立方体、正方体、圆柱体、圆锥体、球体等几种常见的几何形体。
下面将逐个介绍这些几何形体的体积计算公式。
1.立方体立方体是一种边长相等的六个面构成的立体,其中相邻的六个面两两平行并相等。
立方体的体积计算公式为:V=a^3,其中V表示体积,a表示边长。
2.正方体正方体是一种特殊的立方体,它的边长相等,并且所有的面都是正方形。
正方体的体积计算公式与立方体相同,即V=a^3,其中V表示体积,a表示边长。
3.圆柱体圆柱体是由两个平行圆面围成的立体,其中底面的圆心与顶面的圆心相连成的直线垂直于底面,并且底面与顶面之间的距离(高度)保持不变。
圆柱体的体积计算公式为:V=πr^2h,其中V表示体积,π取近似值3.14,r表示底面半径,h表示高度。
4.圆锥体圆锥体是由一个圆锥面和一个圆锥顶面围成的立体,其中圆锥面的边缘是一个圆,并且与圆锥顶面的圆心相连成的直线垂直于圆锥面的圆心。
圆锥体的体积计算公式为:V=(1/3)πr^2h,其中V表示体积,π取近似值3.14,r表示圆锥底面半径,h表示高度。
5.球体球体是由所有与一些点的距离小于或等于一个给定值的点组成的立体。
球体的体积计算公式为:V=(4/3)πr^3,其中V表示体积,π取近似值3.14,r表示半径。
除了上述几种几何形体外,还有一些其他特殊的几何形体的体积计算公式,如圆环的体积计算公式为:V=π(R^2-r^2)h,其中V表示体积,π取近似值3.14,R表示外圆半径,r表示内圆半径,h表示高度。
需要注意的是,这些体积计算公式只适用于特定的形体,并且在实际计算时,需要根据具体的形态和尺寸进行适当的调整和计算。
几何体的体积计算

几何体的体积计算几何体是指在三维空间中具有一定形状和尺寸的立体物体。
几何体的体积是指该物体所占空间的大小,计算几何体的体积是数学中的一个重要问题。
本文将介绍几种常见几何体的体积计算方法。
一、立方体的体积计算方法立方体是最简单的几何体,它的六个面都是正方形。
立方体的体积计算公式如下:体积 = 边长 x 边长 x 边长其中,边长指的是立方体的边长。
二、长方体的体积计算方法长方体也是一种常见的几何体,它有六个面,其中相邻两个面是相等的长方形。
长方体的体积计算公式如下:体积 = 长 x 宽 x 高其中,长、宽、高分别指的是长方体的长、宽、高。
三、圆柱体的体积计算方法圆柱体由一个平行于底面的圆和与底面相切的侧面组成。
圆柱体的体积计算公式如下:体积= π x 半径 x 半径 x 高其中,π取近似值3.14,半径指的是圆柱体底面圆的半径,高指的是圆柱体的高度。
四、球体的体积计算方法球体是由所有与球心距离相等的点所组成的几何体。
球体的体积计算公式如下:体积= (4/3) x π x 半径 x 半径 x 半径其中,π取近似值3.14,半径指的是球体的半径。
五、锥体的体积计算方法锥体由一个圆锥和与圆锥底面相切的侧面组成。
锥体的体积计算公式如下:体积= (1/3) x π x 半径 x 半径 x 高其中,π取近似值3.14,半径指的是锥体底面圆的半径,高指的是锥体的高度。
六、棱柱的体积计算方法棱柱由底面和连接底面顶点与底面对应点的侧面组成。
棱柱的体积计算公式如下:体积 = 底面积 x 高其中,底面积指的是棱柱底面的面积,高指的是棱柱的高度。
七、棱锥的体积计算方法棱锥由底面和连接底面顶点与底面对应点的侧面组成。
棱锥的体积计算公式如下:体积 = (1/3) x 底面积 x 高其中,底面积指的是棱锥底面的面积,高指的是棱锥的高度。
以上是常见几何体的体积计算方法。
通过应用这些公式,我们可以准确计算各种形状的几何体的体积,从而更好地理解和利用几何概念。
几何体的体积计算不同几何体的体积

几何体的体积计算不同几何体的体积几何体的体积计算几何体的体积是指在三维空间中占据的容积大小,是几何学中一个重要的概念。
在实际生活中,我们经常需要计算不同几何体的体积,以便进行建筑设计、容器容量规划或物体重量计算等。
本文将介绍几种常见几何体的体积计算方法。
一、立方体的体积计算立方体是三维空间中最常见的几何体之一。
它的所有边长相等,每个面都是正方形。
计算立方体的体积十分简单,只需要将边长进行立方运算即可。
假设立方体的边长为a,则它的体积V为:V = a³二、长方体的体积计算长方体也是常见的几何体,它的长度、宽度和高度可以是不相等的。
计算长方体的体积需要将它的长度、宽度和高度相乘。
假设长方体的长度为L,宽度为W,高度为H,则它的体积V为:V = L × W × H三、球体的体积计算球体是自然界中常见的几何体,它具有无限个相同大小的曲面。
计算球体的体积需要知道它的半径。
假设球体的半径为r,则它的体积V为:V = (4/3) × π × r³四、圆柱体的体积计算圆柱体是由一个圆面和一个平行于圆底的矩形面组成的几何体。
计算圆柱体的体积需要知道它的底面积和高度。
假设圆柱体的底面积为A,高度为H,则它的体积V为:V = A × H其中,圆柱体的底面积A可以通过底面半径r和圆周率π计算得到:A = π × r²五、金字塔的体积计算金字塔是由底面为多边形的一个顶点和多个侧面三角形组成的几何体。
计算金字塔的体积需要知道它的底面积和高度。
假设金字塔的底面积为A,高度为H,则它的体积V为:V = (1/3) × A × H六、锥体的体积计算锥体是由侧面为三角形的一个顶点和一个圆锥底面组成的几何体。
计算锥体的体积需要知道它的底面积和高度。
假设锥体的底面积为A,高度为H,则它的体积V为:V = (1/3) × A × H综上所述,计算几何体的体积需要根据几何体的形状及相关的参数进行相应的计算公式,其中立方体、长方体、球体、圆柱体、金字塔和锥体是常见几何体的体积计算方法。
常用几何体体积公式

常用几何体体积公式一、正方体体积公式。
1. 公式。
- 设正方体的棱长为a,其体积V = a^3。
2. 推导。
- 正方体是特殊的长方体,它的长、宽、高都相等,长方体体积V =长×宽×高,对于正方体来说,长、宽、高都是a,所以V=a× a× a=a^3。
3. 示例。
- 若正方体棱长a = 3cm,则其体积V=3^3=27cm^3。
二、长方体体积公式。
1. 公式。
- 设长方体的长、宽、高分别为a、b、c,则体积V = abc。
2. 推导。
- 可以把长方体看作是由许多个单位小正方体堆积而成的。
长a表示沿x轴方向小正方体的个数,宽b表示沿y轴方向小正方体的个数,高c表示沿z轴方向小正方体的个数,那么总的小正方体个数(即体积)就是abc。
3. 示例。
- 长方体长a = 4cm,宽b = 3cm,高c = 2cm,则体积V = 4×3×2 = 24cm^3。
三、圆柱体积公式。
1. 公式。
- 设圆柱底面半径为r,高为h,则体积V=π r^2h。
2. 推导。
- 把圆柱底面分成许多相等的扇形,然后把圆柱切开,可以拼成一个近似的长方体。
这个长方体的底面积等于圆柱的底面积π r^2,高等于圆柱的高h,根据长方体体积公式V = 底面积×高,所以圆柱体积V=π r^2h。
3. 示例。
- 圆柱底面半径r = 2cm,高h = 5cm,则体积V=π×2^2×5 = 20π cm^3≈62.8cm^3(π取3.14)。
四、圆锥体积公式。
1. 公式。
- 设圆锥底面半径为r,高为h,则体积V=(1)/(3)π r^2h。
2. 推导。
- 通过实验发现,等底等高的圆柱和圆锥,圆锥的体积是圆柱体积的(1)/(3)。
因为圆柱体积V=π r^2h,所以圆锥体积V=(1)/(3)π r^2h。
3. 示例。
- 圆锥底面半径r = 3cm,高h = 4cm,则体积V=(1)/(3)π×3^2×4 = 12π cm^3≈37.68cm^3(π取3.14)。
几何体积知识点总结
几何体积知识点总结一、立体几何体积概念几何体积是一个几何体能够容纳的三维空间的度量。
在三维空间中,立体几何体的大小可以用体积来表示。
几何体的体积是指其中所包含的三维空间的大小,通常被表示为立方单位的数量。
几何体的体积是由它的几何形状以及尺寸决定的。
二、几何体积的计算公式1. 立方体的体积计算公式立方体是一种所有的边都相等,所有的角都是直角的几何体。
它的体积可以用公式V =a^3来计算,其中a表示立方体的边长。
2. 长方体的体积计算公式长方体是一种所有的边都相等,所有的角都是直角的几何体。
长方体的体积可以用公式V = lwh来计算,其中l表示长方体的长度,w表示宽度,h表示高度。
3. 圆柱体的体积计算公式圆柱体是一种上下底面积相等且平行的圆柱体。
它的体积可以用公式V = πr^2h来计算,其中r表示底面圆的半径,h表示圆柱体的高。
4. 圆锥体的体积计算公式圆锥体是一种圆锥形的几何体,它的底面是一个圆,与它的底面平行的面叫做锥面。
圆锥体的体积可以用公式V = (1/3)πr^2h来计算,其中r表示底面圆的半径,h表示圆锥体的高。
5. 球体的体积计算公式球体是一种所有的点到球心的距离都相等的几何体。
它的体积可以用公式V = (4/3)πr^3来计算,其中r表示球体的半径。
6. 正四面体的体积计算公式正四面体是一个底面为正三角形的四面体。
它的体积可以用公式V = (1/3)Ah来计算,其中A表示底面正三角形的面积,h表示正四面体的高。
7. 正六面体的体积计算公式正六面体是一个底面和侧面都是正方形的六面体。
它的体积可以用公式V = a^3来计算,其中a表示正六面体的边长。
8. 锥体的体积计算公式锥体是一种具有一个顶点和一个底面的几何体。
它的体积可以用公式V = (1/3)πr^2h来计算,其中r表示底面的半径,h表示锥体的高。
以上是一些常见立体几何体的体积计算公式,可以通过这些公式计算不同几何体的体积。
三、几何体积的单位几何体积的单位通常使用立方单位。
空间几何体体积(第二节)
S′=0
V锥体=
1 3
Sh 这里S是底面积,h是高
五. 例题 例: 如图:已知圆台的上底面半径为1下底面半径为2,母 线长为2,求该圆台的体积
练习 如图:已知棱台的上底面是长为1 A’ 正方形,下底面是长为2 D ’ 正方形,侧棱长为2 A 求该棱台的体积
B’ C’ B
C
D
例 体积为52cm2的圆台,一个底面面积是另一个底 面面积的9倍,那么,截得这个圆台的圆锥体积 为 54cm2 。
所以,三棱锥D-ABC的体积是正方体的三分之一。
四. 台体的体积公式
锥体的性质 如果锥体被平行于底面的平面所截,那么所得的截面 与底面相似,截面面积与底面面积的比等于顶点到截 2 S h 面距离与锥体高的平方比 1 1 A
S
h
2
P
S O
h
O’
h
C’ C
A’
D’
B’ B D
S
A
问题:你能由锥体的体积公式得到台 体的体积公式吗?
一. 柱体的体积公式
直棱柱 (长方体) 斜棱柱
h S V=sh
该斜棱柱的体积是什么?
祖暅原理:
两等高的几何体若在所有等高处的水平截面的 面积相等,则这两个几何体的体积相等.
一. 柱体的体积公式 问题:底面积相等、高也相等的棱柱与圆柱,它们的 体积有何关系如何?
h
h
h
S
S
S
由祖暅原理可得:
V柱体 Sh
几何体占有空间大小的部分叫做几何体的体积
复习
1.正方体的体积公式 V正方体=a3(这里a为棱长) 2.长方体的体积公式 V长方体=abc(这里a,b,c分别为长方体长、宽、高)
高三数学15.5几何体的体积教案2沪教版高三上学期
15.5 几何体的体积(2)【教学目标】1、学生通过具体实验感知三棱锥体积公式,通过严谨证明确认三棱锥体积公式,通过对新知识的应用推广得到n 棱锥的体积公式,通过具体实例初步应用锥体体积公式.2、能应用割补法求体积以及体积法求点到面的距离,在这个过程中,提高分析、综合、抽象、概括等逻辑推理能力.【教学重点与难点】三棱锥体积公式及其探求.【教学过程】一、棱锥的体积1.等底等高的三棱锥的体积相等.例:已知三棱锥O ABC -和P DEF -的底面积都是S ,高都是h .求证:三棱锥O ABC -和P DEF -的体积相等.证明:把两个三棱锥的底面都放在平面α上,任意作平面//βα,设平面β截三棱锥O ABC -所得的截线为三角形'''A B C ∆,其面积为1S ;平面β截三棱锥P DEF -所得的截线为三角形'''D E F ∆,其面积为2S .如果三棱锥的顶点O 和P 与平面β的距离为1h ,那么推得:1'''h OA OB OC OA OB OC h ===和1''''''h A B B C C A AB BC CA h===,于是得'''A B C ABC ∆∆,相似比是1h h ,同理可得'''D E F DEF ∆∆,相似比也是1h h .由相似形的性质得211()S h S h =, 222()S h S h =.即2112()h S S S h==. 因为任意平行于底面的平面截两个三棱锥时,所得的截面面积相等,所以由祖暅原理得三棱锥O ABC -和P DEF -的体积相等,即等底等高的三棱锥的体积相等.2.观察三棱锥O ABC -,正好含在三棱柱OPQ ABC -中,于是我们通过连接,OB OC ,把三棱柱OPQ ABC -中的三棱锥O ABC -找出来,发现三棱柱OPQ ABC -是由三棱锥O ABC -和四棱锥O BCQP -组成的.进一步的,连接BQ ,那么此时比较明显的有: OPQ ABC O ABC O BPQ O BCQ V V V V ----=++ 由于等底等高的三棱锥的体积相等,故有:13O ABC O BPQ O BCQ OPQ ABC V V V V ----=== 三棱锥的体积公式:13V Sh = 重要结论:(1)一个三棱锥可以分解成一个三棱锥与一个四棱锥,其中四棱锥的体积是三棱锥体积的两倍;(2)一个三棱锥可以分解成三个体积相等的棱锥.平面几何中求面积时,我们经常会用到割补法.同样的,立体几何求体积也会用到此法.上述的证明方法,本质上就是把一个三棱锥补成三棱柱后,再加以证明,是求体积的“补”法.3.四棱锥的体积三棱锥体积的证明中用到了一个三棱锥非常个性化的特征:可以以任何一个顶点作为三棱锥的顶点.这是其它任何棱锥所不具备的特征.那么,我们已经知道,并且证明了三棱锥的体积,四棱锥中有没有三棱锥呢?通过连接AC ,可得: P ABCD P ABC P ADC V V V ---=+()1133ABC ADC ABCD S S h S h =+= 其中h 是P 到底面ABCD 的距离,即四棱锥的高. 4.n 棱锥的体积 基本上可由学生自行完成.课本P39也讲述的非常清楚.5.圆锥的体积*课堂巩固练习*1、已知:正三棱锥的底面边长为1,且它的侧棱与底面所成角为3π,求这个三棱锥的体积和表面积。
几何体的体积
计算过程: V=5^3=125cm^3
结论:立方体的体积等于其 边长的立方
长方体的体积公式:V=abc 实例:长方体的长、宽、高分别为5cm、4cm、3cm,计算其体积 计算过程:V=5cm*4cm*3cm=60cm³ 结论:长方体的体积可以通过长、宽、高的乘积得到
实例:已知圆柱体的半径为 3cm,高为5cm,求其体积
设计制造:计算零件体积,优化设 计
装配调试:计算装配体积,提高效 率
添加标题
添加标题
添加标题
添加标题
质量控制:测量零件体积,确保质 量
成本控制:计算材料体积,降低成 本
土壤测量:计算土壤体积, 了解土壤质量
灌溉系统设计:计算灌溉用 水量,优化灌溉方案
肥料施用:计算肥料用量, 提高肥料利用率
农业机械设计:计算机械体 积,优化机械结构
建筑设计:计算建筑物的体积,确定材料用量 工业设计:计算产品体积,优化产品设计 物流运输:计算货物体积,合理安排运输空间 环保领域:计算垃圾体积,制定垃圾处理方案
圆柱体体积公式: V=πr^2h
计算过程: V=π(3^2)5=45πcm^3
结论:圆柱体的体积为 45πcm^3
圆锥体体积公式: V=1/3*π*r^2*h
圆锥体底面半径: r
圆锥体高度:h
圆锥体体积计算: V=1/3*π*r^2*h
建筑设计:计算建筑物的体积,确定建筑材料的用量 建筑施工:计算建筑物的体积,确定施工进度和成本 建筑改造:计算建筑物的体积,确定改造方案和成本 建筑维护:计算建筑物的体积,确定维护方案和成本
棱锥体:所有面都是三 角形的立体图形
椭圆体:所有面都是椭 圆形的立体图形
立方体的体积计算公式为:V=a^3,其中a为立方体的边长 立方体的体积计算公式也可以表示为:V=s^3,其中s为立方体的表面积 立方体的体积计算公式还可以表示为:V=2^3,其中2为立方体的对角线长度 立方体的体积计算公式还可以表示为:V=h^3,其中h为立方体的高
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
补 割
割 补
+
先补后割与先割后补是处理几何问题常用 的方法(即割补法)。能否将上述思维方 法迁移到求三棱锥的体积上来?
公式推导
显然此三棱柱的底 面积为 S ,高为 h . ∴V三棱柱 = S h
S B C
A′
C′
B′
h A
公式推导
显然此三棱柱的底 面积为 S ,高为 h . ∴V三棱柱 = S h
A B C
A′
C′
B′
公式推导
显然此三棱柱的底 面积为 S ,高为 h . ∴V三棱柱 = S h
A B C
A′
C′
B′
公式推导
A′ A′ A′ B′ B′ B′ B′ C C A B C C′ C′ 显然此三棱柱的底 C′
面积为 S ,高为 h . ∴V三棱柱 = S h
A′
′
C
公式推导
A′ B′ A′ C′
A′
A′ B′
B′A′
C B′ B′
A B
C
C C C B B
B
公式推导
A′ B′ A′ C′
A′
A′ B′
B′A′
C B′ B′
A B
C
C C C B B
B
公式推导
A′ A′ A′ A′ B′ B′ C′ B′ C′ C′ C′
B′
C C A B C
C
公式推导
分析.∵ S △ A’AB (面1) = S △ A’B’B (面2) (底 ) C点到面 A’AB (面1)的距离等于C点 到面 A’B’B(面2)的距离(高) ∴ V三棱锥C - A’ AB= V三棱锥C -A’B’B 即 V1= V2 4 同理可证 V2= V3 ( 怎证 ? ) (用 S△B B’ C (面4) = S△ C’ B’ C (面3) 可证 ) ∴ V1= V2= V3 因此 V1= V2= V3 = 即 V三棱锥A’-- ABC =
1 3
A′ B′
C′
h
A
S
B
C
V三 棱柱 =
1 3
1 3
Sh
棱锥 V三棱锥=
Sh (底面积为S ,高为 h)
三棱锥的体积问题已经解决了, 那么一般棱锥的体积如何呢?
由等底面积等高的两个锥体的体积 相等,得
课堂小结
知识 方面 本节课学习了利用祖暅原理、 割补法获得了棱锥的体积公式, 并初步体会棱锥体积公式的应 用; 体会到联想、类比、猜想、证 明等合情推理及逻辑推理的方 法在探索新知识方面的重要作 用。
思维 能力 方面
公式推导
推导1 等底面积等高的任意两个锥体的体积相等
β
h1
S1 h
h1
S2 h
s
α 只要证明S1= S2 即可
s
公式推导
β h1 S1 h1 S2
h
h
s
α
h1 h
S
2
s
2
∵截面与底面相似,它们的面积比等于相对应的高的平方比
即
∴
S1 S
= =
S
2
2
=
h1 h
S
2
S1 S
2
S
S1 S2
公式推导
推导1
等底面积等高的两个锥体的体积相等
(定理)
祖暅原理
推导2
+
S1 S2
但锥体的体积如何求出?
锥体的代表 ?
三棱锥
“简单”的锥体作代表 因为锥体体积只和底面积、高有关,而与形状无关。 故我们选用最简单的三棱锥作为突破口。
公式推导
推导3
那么怎样研究三棱锥的体积呢?
回忆直角三角形面 积公式探求过程:
复习
1.祖暅原理
夹在两个平行平面间的两个几 何体,被平行于这两个平面的任意 平面所截,如果截得的两个截面的 面积总相等,那么这两个几何体的 体积相等.
2.棱柱体积 定理 棱柱的体积等于它的底面 积s 和高h的积。V棱柱= sh
问题
棱锥体积公式及其探索思路?
棱锥的体积公式V棱锥=?
等底面积等高的任意两个 锥体的体积 是否相等?
