山西授阳中学2017_2018学年高二数学上学期第二次月考试题文

合集下载

山西省康杰中学2017_2018学年高二数学上学期第二次月考试题文

1康杰中学2017—2018学年度第一学期第二次月考高二数学（文）试题2018.1一、选择题（本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，选择一个符合题目要求的选项.）1. 命题“若x 2>y 2,则x >y ”的逆否命题是 A ．“若x <y ,则x 2<y 2” B ．“若x >y ,则x 2>y 2” C ．“若x ≤y ,则x 2≤y 2”D ．“若x ≥y ,则x 2≥y 2”2. 抛物线x 2＝y 的准线方程是A ．4x +1=0B ．4y +1=0C ．2x +1=0D ．2y +1=0 3. 已知p ：1<m <3，q ：m 满足方程+＝1表示椭圆，那么p 是q 的 x 2m －1y 23-mA ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件4. 在平面直角坐标系xOy 中，已知点F 1(－5，0)，F 2(5，0)，动点P 满足|PF 1|-|PF 2|=8，则动点P 的轨迹方程是A ．＋＝1B ．－＝1 x 216y 29x 216y 29C ．－＝1(x <0)D ．－＝1(x >0) x 216y 29x 216y 295. 已知命题p ：“∀x ∈[0,1]，a ≥e x ”，命题q ：“∃x ∈R，x 2＋4x ＋a ＝0”，若命题“p ∧q ”是真命题，则实数a 的取值范围是 A ．[e,4]B ．[1,4]C ．(4,＋∞)D ．(－∞,1]6. 已知双曲线C ：－＝1(a >0，b >0)的离心率为，则C 的渐近线方程为x 2a 2y 2b 252 A ． B ． C ． D ． x y 41±=x y 31±=x y 21±=x y ±=7. 抛物线上一点P 到直线的距离与到点的距离之差的最大值为24y x =1x =-()2,2Q2A ． BC ．D358. 过点M (1，1)作斜率为－的直线与椭圆E ：＋＝1(a ＞b ＞0)相交于A ，B 两点，若12x 2a 2y 2b2M 是线段AB 的中点，则椭圆E 的离心率等于A ．B ．C ．D ．122232339. 过抛物线的焦点且倾斜角为的直线l 与抛物线在第一、四象限)0(22>=p px y F 60分别交于两点,则的值等于B A ,BFAF A ． B ．4C ．3D ．2510. 已知F 为抛物线C ：y 2＝4x 的焦点，过F 作两条互相垂直的直线l 1，l 2，直线l 1与C 交于A ，B 两点，直线l 2与C 交于D ，E 两点，则|AB |+|DE |的最小值为 A ．16 B ．14C ．12D ．1011. 设A ，B 是椭圆C ：＋＝1长轴的两个端点，若C 上存在点M 满足∠AMB =120°，则x 23y 2mm 的取值范围是A ．(0，1]∪[9，+∞)B ．(0，]∪[9，+∞) 3C ．(0，1]∪[4，+∞)D ．(0，]∪[4，+∞)312. 已知双曲线，A 1，A 2是实轴的顶点，F 是右焦点，B (0,b )是)0,0(12222>>=-b a by a x 虚轴的一个顶点，若在线段BF 上（不含端点）存在不同的两点P i （i =1，2），使得△P iA 1 A 2（i =1，2）构成以A 1 A 2为斜边的直角三角形，则双曲线的离心率e 的取值范围是A ．B ．C ．D ． ⎪⎪⎭⎫ ⎝⎛+235,2()2,1⎪⎪⎭⎫ ⎝⎛+∞+,215⎪⎪⎭⎫⎝⎛+215,2二、填空题（本大题共4小题，每小题5分，共20分.把答案填在题中横线上.）313. 已知命题p ：，则¬ p 为_________. 1)1(,0>+>∀xe x x 14. 右图是抛物线形拱桥，当水面在l 时，拱顶离水面2 m ，水面宽4 m ，当水面下降1 m 后，水面宽________m. 15. 已知正方形ABCD ，则以A ，B 为焦点，且过C ，D 两点的椭圆的离心率为_________.16. 在平面直角坐标系xOy 中，双曲线的右支与焦点为F 的抛)0,0(12222>>=-b a by a x 物线x 2=2py （p >0）交于A ，B 两点，若|AF |+|BF |=4|OF |，则该双曲线的渐近线方程为____________________.三、解答题（解答应写出文字说明，证明过程或演算步骤.）17. （本小题满分10分）已知p ：，q ：，若 2131≤--x )0(01222>≤-+-m m x x ¬ p 是¬ q 的必要不充分条件，求实数m 的取值范围.18. （本小题满分12分）已知命题p ：，不等式恒成]1,1[-∈∀m 8322+≥--m a a 立；命题q ：关于x 的一元二次方程：x 2-4ax +2a +6=0无负根，若“”为假，q p ∧“”为真，求实数a 的取值范围 q p ∨19. （本小题满分12分）已知动点P 到定点F (1，0)的距离与到定直线l ：x =－1的距离相等，设动点P 的轨迹为曲线C . （1）求曲线C 的方程；（2）过点F 且倾斜角为135°的直线交曲线C 于A ，B 两点，求|AB |.20. （本小题满分12分）已知椭圆E ：的左、右焦点分别是F 1、F 2，)0(12222>>=+b a by a x4椭圆E 上的点到点F 1距离的最大值是+，短轴一个顶点到F 2的距离为. 323（1）求椭圆E 的方程；（2）设过点F 1且斜率为1的直线l 与椭圆E 交与A ，B 两点，求△ABF 2的面积21. （本小题满分12分）设A ，B 为曲线C ：上两点，A 与B 的横坐标之和为442x y =（1）求直线AB 的斜率.（2）设M 为曲线C 上一点，C 在M 处的切线与直线AB 平行，且AM ⊥BM ，求直线AB 的方程.22. （本小题满分12分）已知椭圆C ：过点，且离心率e )0(12222>>=+b a by a x 3(1,)2A 为 12（1）求椭圆C 的方程；（2）E 、F 是椭圆上的两个动点，如果直线AE 的斜率与AF 的斜率互为相反数，证明直线EF 的斜率为定值，并求出这个定值.高二数学（文）答案一、选择题 1. C 2. B 3. B 4. D 5. A 6. C 7. D8. B 9. C 10. A11. A 12. D 二、填空题13. ，（或）0x ∃≤(1)1xx e +≤0000,(1)1x x x e∃≤+≤14.16.1-y x =三、解答题517. 解析：由得1:123x p --≤2010-≤≤ 由得22:210q x x m -+-≤22(1)x m -≤∵∴ …………………………4分0m >11m x m -≤≤+∵是的必要不充分条件 p ⌝q ⌝∴ 且 q p ⌝⇒⌝p q ⌝⇒⌝∴且p q ⇒q p ⇒即是的充分不必要条件……………………………………7分p q ∴（等号不能同时成立）12110m m -≤-⎧⎨+≥⎩∴………………………………………10分9m ≥18. 解析： ∵[]1,1m ∈-⎡⎤⎣⎦∵，不等式[]1,1m ∀∈-23a a --≥∴得或233a a --≥2a ≤-3a ≥∴命题为真命题时，或……………………3分p 2a ≤-3a ≥命题：关于的一元二次方程：无负根 q x 24260x ax a -++=①方程无实根： 2164(26)0a a ∆=-+<得 312a -<<②方程有实根且均为非负根∴ 得 ………………7分 2164(26)040260a a a a ⎧∆=-+≥⎪≥⎨⎪+≥⎩32a ≥∴命题为真命题时，……………………8分q 1a >-∵“”为假，“”为真 ∴一真一假p q ∧p q ∨,p q6∴真假时：设p q231a a a ≤-≥⎧⎨≤-⎩2a ≤-假真时：设………………11分p q 231a a -<<⎧⎨>-⎩13a -<<综上：实数的取值范围是：或 …………12分a 2a ≤-13a -<<19. 解析：（1）设点(,)P x y 由题曲线C 是以为焦点，直线为准线的抛物线 (1,0)F 1x =-∴曲线C 的方程是：…………………………4分24y x =（2）直线AB 的方程为： …………………………5分 1y x =-+设11(,)A x y 22(,)B x y 则………………7分1212112AB AF BF x x x x =+=+++=++由设214y x y x =-+⎧⎨=⎩2610x x -+=∴……………………10分 126x x +=∴……………………12分12||28AB x x =++=20. 解析：（1）由题222a c a a b c ⎧+=⎪⎪=⎨⎪=+⎪⎩解得…………………………6分1,a b c ===设11(,)A x y 22(,)B x y 由得2213y x x y ⎧=+⎪⎨+=⎪⎩2430x ++=或7∴……………………9分 12x x +=1234x x ⋅=∴的面积 2ABF ∆121212S F F y y =⨯⨯-121||2x x =⨯-=……………………12分==或：弦长AB ===点到直线AB 的距离 2F2d ==∴的面积2ABF ∆12S AB d =⨯⨯=21. 解：（1）设1122(,),(,)A x y B x y由题，12x x ≠22121212,,444x x y y x x ==+=2221212121214414ABx x y y x x k x x x x --+====--∴直线AB 的斜率为1…………………………4分（2）由题设曲线C 在点M 处的切线方程为y x m =+由得24y x mx y =+⎧⎪⎨=⎪⎩2440x x m --=∴ ∴ 16160m ∆=+=1m =-∴点M(2, 1) ………………………………6分设直线AB 的方程：y x t =+8由得24y x t x y =+⎧⎪⎨=⎪⎩2440x x t --= 设16160t ∆=+>1t >-…………………………8分12124,4x x x x t +=⋅=-1212(2)(2)(1)(1)MA MB x x y y ⋅=--+--1212122()4(1)(1)x x x x x t x t =-++++-+- 212122(3)()4(1)x x t x x t =+-+++-284(3)4(1)0t t t =-+-++-=解得或（舍去）…………………………11分 7t =1t =-∴直线AB 的方程为 …………………………12分7y x =+文22. 解析：（1）由题：解得22222914112a bc e a a b c ⎧⎪+=⎪⎪⎪==⎨⎪⎪=+⎪⎪⎩2,1a b c ===∴椭圆C 的方程为：……………………4分22143x y +=（2）法一：设直线AE 的方程为： 3(1)2y k x -=-由得223(1)2143y k x x y ⎧-=-⎪⎪⎨⎪+=⎪⎩222(34)4(23)41230k x k k x k k +--+--=∴ ………………9分2222412312129,342(34)k k k k E k k ⎛⎫+---+ ⎪++⎝⎭9由题直线AF 的方程为 3(1)2y k x -=--∴ ………………9分2222412312129,342(34)k k k k F kk ⎛⎫+---+ ⎪++⎝⎭∴ …………11分 2222222212129121291212(34)2(34)412341232423434EFk k k k k k k k k k k k k k k -++--+-++===+----++∴直线EF 的斜率为定值，且这个定值为………………12分12法二：设直线EF 的方程为1122,(,)(,)y kx m E x y F x y =+由得22143y kx m x y =+⎧⎪⎨+=⎪⎩222(34)84120k x kmx m +++-= ……………………6分122834kmx x k +=-+212241234m x x k-⋅=+∴ 12122112123333()(1)()(1)2222011(1)(1)AE AF y y kx m x kx m x k k x x x x --+--++--+=+==----…………………………7分∴122133(+)(1)()(1)22kx m x kx m x --++--121232()()232kx x m k x x m =+--+-+222412382()2334234m km k m k m k k -=⋅---⋅-+++ 22212241263(21)(232)03434k k km m k k m k k-+---+===++得或 ……………………10分 12k =322km -=时过定点,舍去 …………11分322k m -=33(1)22y kx k k x =+-=-+3(1,2A10∴直线EF 的斜率为定值，且这个定值为 ……………………12分12。

山西授阳中学2018_2019学年高二数学上学期期中试题理2-含答案师生通用

山西省汾阳中学2018-2019学年高二数学上学期期中试题理一、单选题（每题5分）1．直线的倾斜角是（）．A ．B ．C ．D ． 2．已知m ,n 是不同的直线,是不同的平面,有下列命题: ①若,则; ②若,则; ③若,则且.上述说法正确的个数是A.0B.1C.2D.33．经过点M （2，2）且在两坐标轴上截距相等的直线是（）A ． x+y=4B ． x+y=2或x=yC ． x=2或y=2D ． x+y=4或x=y4．圆心在y 轴上，半径为1，且过点（1，2）的圆的方程为（）A ． ()2221x y +-=B ． ()2221x y ++= C ． ()()22131x y -+-=D ． ()2231x y +-= 5．已知直线l 经过()()()22,1,1,A B m m R ∈两点，则直线l 的斜率的取值范围是（）A ． [)1,+∞ B ． (),-∞+∞ C ． (),1-∞ D ． (],1-∞6．一圆锥底面半径为2，母线长为6，有一球在该圆锥内部且与它的侧面和底面都相切，则这个球的半径为（）A ．1 C D ．7．一个三棱锥的三视图是三个直角三角形，如图所示，则该三棱锥的外接球表面积为（）A ．29πB ．30πC ．292π D ．216π 8如图在一个60︒的二面角的棱上有两个点A B 、，线段AC 、BD 分别在这个二面角的两个面内，并且都垂直于棱AB ，且1,2AB AC BD ===，则CD 的长为( )A ． 2B ．．． 19．直线l 与两直线y =1和x-y-7=0分别交于A ,B 两点,若线段AB 的中点为M (1,-1),则直线l 的斜率为?? A. B. C.- D.-10．直线y =x+b 与曲线x =有且仅有一个公共点,则b 的取值范围是 A.|b|= B.-1<b ≤1或b =-C.-1≤b ≤1D.以上结论均不对11．如图,点E 为正方形ABCD 边CD 上异于点C ,D 的动点,将△ADE 沿AE 翻折成△SAE ,使得平面SAE ⊥平面ABCE ,给出下列三个说法:①存在点E 使得直线SA ⊥平面SBC ;②平面SBC 内存在直线与SA 平行;③平面ABCE 内存在直线与平面SAE 平行.其中正确说法的个数是??A.0B.1C.2D.312如果圆()()228x a y a -+-=a 的取值范围是（）A ．(][)3,11,3--B ．()3,3-C ．[]1,1-D ．()()3,11,3--二、填空题（每空5分）13．圆226290x y x y +--+=与圆22280x y y +--=的位置关系是 .14．若直线l ： 1y kx =+被圆C ： 22230x y x +--=截得的弦最短，则k= .15．正四棱锥的侧棱长与底面边长都是2，则侧棱与底面所成角的大小为 . 16．ABC ∆为正三角形，P 是ABC ∆所在平面外一点，PA PB PC ==且:2:3APB ABC S S ∆∆=，则二面角P AB C --的大小___________；三、解答题（17题10分，其他各12分）17．已知圆同时满足下列三个条件：①与轴相切；②半径为；③圆心在直线上.求圆的方程. 18．如图,已知点P 是平行四边形ABCD 所在平面外一点,M 、N 分别是AB 、PC 的中点.(1)求证:MN ∥平面PAD;(2)在PB 上确定一个点Q,使平面MNQ ∥平面PAD.19如图，在四棱锥P -ABCD 中，底面ABCD 是边长为a 的正方形，E 、F 分别为PC 、BD 的中点，侧面⊥PAD 底面ABCD ，且AD PD PA 22==。

山西省汾阳中学2017-2018学年高二上学期第二次月考数

高二文科数学月考试卷时间:120分钟满分:150分一、选择题(每小题5分,共12小题60分)1、集合，集合，则与的关系是 ( )2对于任意实数）A.C.3、已知、则与的夹角是( )A. B. C. D.4）5( )A.B.C.D.6、下列选项中，说法正确的是（）A.B.C.D.7围是（）8( )9、的右焦点，关于直线也在椭圆上，则该椭圆的离心率是（）10的距离为，则半径的取值范围（）11、引直线与曲线交于，两点，为坐标原点，最大值时，直线的斜率等于（）12、如图，已知椭圆的中心为原点,为的左焦点，为上一点，满足，则椭圆的方程为( )二、填空题(每小题5分,共4小题20分)13，过的周长为__________14、以、为焦点的椭圆1P切值为2，则此椭圆离心率e的大小为__________15、已知双曲线C的一条渐近线与直线：线的一个焦点到的距离为2，则的标准方程为__________16.为椭圆上任一点，点的坐标为__________.三、解答题(第17题10分,第18题12分,第19题12分,第20题12分,第21题12分,第22题12分,共6小题70分)17的方程．18).（I（II若是真命题，求的取值范围.19，为的中点，是.（1（2）求点到平面20（1（2上有实数根，求的取值范围.21（1）求角的大小；（2）,项和.22，点在底面上的射.（I（II边上是否存在点，使得理由.高二文科数学月考试卷答案解析第1题答案C第1题解析第2题答案C第2题解析第3题答案B第3题解析①②∴∴与的夹角为..．第4题答案C第4题解析∴应选C.第5题答案D第5题解析根据面面平行的判定定理和性质定理及线面平行的判定定理和性质定理A，B选项不正确，因为平行于同一条直线的直线与平面的位置关系可是平行的或者是线在面内；‎C选项不正确因为两条直线平行于同一个平面两条直线的位置关系可能是相交、平行、异面三种情况之一；‎D 选项正确，由题设中的条件可以证得面面平行的判定定理所需要的条件，故命题正确．‎故选D第6题答案C第6题解析存在量词否定后为全称量词，故A题都真.故B C等，也可能互补或终边相同.故D错.第7题答案C第7题解析第8题答案D第8题解析设球的半径为，则D．第9题答案B第9题解析设点的坐标为，因为关于直线，所以所以点的在椭圆上，所以B．第10题答案A第10题解析由故选A．第11题答案B第11题解析设直线的斜率为，若直线与曲线有两个交点，且直线不与轴重合则∴直线的方程为：法一：圆心到直线的距离直线被半圆所截得的弦长为有最大值为，再注意到，故选．有最大值为，此时圆心到直线的距离第12题答案B第12题解析焦距为，右焦点为，连接为的左焦点..由勾股定理，得第13题答案12第13题解析.第14题答案第14题解析解答：P为椭圆与y2，e 第15题答案第15题解析的一个焦点到的距离为的标准方程为第16题答案第16题解析如图所示，当且仅当点是圆在x轴下方的交点时等号成立)的最大值为.第17题答案第17题解析斜率为，又中点第18题答案（I（II第18题解析（I（II）则,，因为是真命题，则，因为是真命题，则第19题答案（1）详见解析；（2第19题解析（1的中点，连接∵为（2，知点和点到面到平面为，∴点到平面第20题答案（1（2第20题解析（1），（2k.第21题答案（1（2第21题解析（1（2的公差为，由已知得∴第22题答案（I）证明略；（II）证明略第22题解析（I是（II的中点，的中点，连结∵是的中点，是过作于，连结。

山西省应县2017-2018学年高二9月月考数学试卷(文)含答案

应县高二年级月考一数学试题（文） 2017.9时间：120分钟满分：150分命题人：荣印一、选择题：(本大题共12小题，每小题5分，共60分，每小题给出的四个选项，只有一项是符合题目要求的).1、直线x ＝的倾斜角是( ) 4πA. 90° B. 60° C. 45° D. 不存在2、若m n ，是两条不同的直线，αβγ，，是三个不同的平面，则下列为真命题的是（）A ．若m βαβ⊂⊥，，则m α⊥B ．若α∩γ＝m ，m n ∥，则αβ∥C ．若m β⊥，m α∥，则αβ⊥D ．若αγ⊥，αβ⊥，则βγ⊥3、已知两条直线y=ax﹣2和y=（a+2）x+1互相垂直，则a 等于（）A ．2B ．1C ．0D ．﹣14、直线：，：，若，则的值为（）A. -3B. 2C. -3或2D. 3或-25、四面体ABCD 中，E 、F 分别是AC 、BD 的中点，若CD=2AB ，EF ⊥AB ，则EF 与CD 所成的角等于（）A ．30°B ．45°C ．60°D ．90°6、点(1,2)--关于直线1x y +=对称的点坐标是（）A ．()3,2B ．()3,2--C ．()1,2--D ．()2,37、如图是一个空间几何体的三视图,其中正视图和侧视图都是半径为2的半圆,俯视图是半径为2的圆,则该几何体的体积等于（）正视图侧视图俯视图A ．43π B ．83π C ．163π D ．323π8、已知点(),M a b 在直线34200x y +-=的最小值为（）A. 3B. 4C. 5D. 69．一空间几何体的三视图如图所示，则该几何体的体积为( ) A ．2π＋2 B ．4π＋2 C ．2π＋D ．4π＋33233 3310、已知点，若直线与线段相交，则实数k 的取值范围是（） A. B. 或 C. D. 或11、将直线3y x =绕原点逆时针旋转90°，再向右平移1个单位，所得到的直线为（）A ．113y x =+ B ．113y x =-+ C ．33y x =- D ．1133y x =-+ 12、平面四边形ABCD 中，1===CD AD AB ，CD BD BD ⊥=,2，将其沿对角线BD 折成四面体BCD A -'，使平面⊥BD A '平面BCD ，若四面体BCD A -'顶点在同一个球面上，则该球的体积为( )A. π23 B. π3 C. π32 D. π2 二、填空题(共4小题，每小题5分，共20分)13、两个半径为1的铁球，熔化后铸成一个大球，这个大球的半径为．14、如图， '''O A B ∆是水平放置的ABC ∆的直观图，则ABC ∆的周长为 ______.15、已知直线()()20a x y a a R -+-=∈在两坐标轴上的截距互为相反数，则实数a =16．如图2－8，在棱长为2的正方体ABCD －A 1B 1C 1D 1中，E 为BC 的中点，点P 在线段D 1E 上，点P 到直线CC 1的距离的最小值为______．三、解答题（共6小题，共70分，要求在答题卡上写出详细的解答过程。

山西大学附属中学20172018学年高二上学期10月月考试题数学Word版含答案

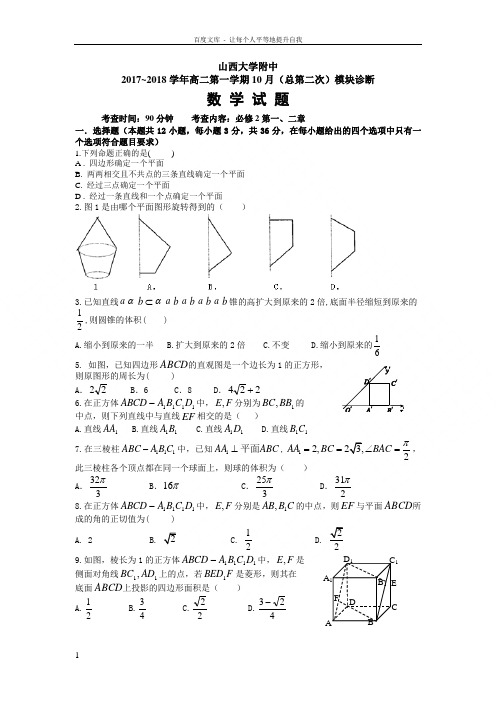
ABC DA 1B 1C 1D 1 F E山西大学附中2017~2018学年高二第一学期10月（总第二次）模块诊断数学试题考查时间：90分钟考查内容：必修2第一、二章一．选择题（本题共12小题，每小题3分，共36分，在每小题给出的四个选项中只有一个选项符合题目要求）1.下列命题正确的是( ) A . 四边形确定一个平面B. 两两相交且不共点的三条直线确定一个平面C. 经过三点确定一个平面D . 经过一条直线和一个点确定一个平面2.图1是由哪个平面图形旋转得到的（）3.已知直线a αb ⊂αa b a b a b a b 锥的高扩大到原来的2倍,底面半径缩短到原来的21,则圆锥的体积( ) A .缩小到原来的一半 B .扩大到原来的2倍 C .不变 D .缩小到原来的61 5. 如图，已知四边形ABCD 的直观图是一个边长为1的正方形，则原图形的周长为( )A ．22B ．6C ．8D ．224+6.在正方体1111D C B A ABCD -中，F E ,分别为1,BB BC 的中点，则下列直线中与直线EF 相交的是（）A.直线1AAB.直线11B AC.直线11D AD.直线11C B7.在三棱柱111ABC A B C -中，已知1AA ABC ⊥平面,12,23,2AA BC BAC π==∠=，此三棱柱各个顶点都在同一个球面上，则球的体积为（）A ．323πB ．16πC ．253π D ．312π8.在正方体1111D C B A ABCD -中，F E ,分别是C B AB 1,的中点，则EF 与平面ABCD 所成的角的正切值为( )2 C. 1229.如图，棱长为1的正方体1111D C B A ABCD -中，F E ,是侧面对角线11,AD BC 上的点，若F BED 1是菱形，则其在底面ABCD 上投影的四边形面积是（）A.21B.43C.22D.423-10.如图，已知三棱柱111ABC A B C -的侧棱与底面边长都相等，1A 在底面ABC 上的射影为BC 的中点，则异面直线AB 与1CC 所成的角的余弦值为（）A.3 B.5 C.7 D.3411.如图，四面体ABCD 中，截面PQMN 是正方形，则在下列结论中，下列说法错误的是（） A ．AC BD ⊥ B ．AC BD = C.//AC 截面PQMN D ．异面直线PM 与BD 所成的角为45 12．如图，矩形ABCD 中，AD AB 2=，E 为边AB 的中点，将ADE ∆沿直线DE 翻转成DE A 1∆（∉1A 平面ABCD ）．若O M ,分别为线段C A 1,DE 的中点，则在ADE ∆ 翻转过程中，下列说法错误的是（）A. 与平面DE A 1垂直的直线必与直线BM 垂直B. 异面直线BM 与E A 1所成角是定值C. 一定存在某个位置，使MO DE ⊥D. 三棱锥ADE A -1外接球半径与棱AD 的长之比为定值二．填空题（本大题共4小题，每小题4分，共16分） 13.若一个正四面体的棱长为a ，则它的表面积为_________. 14.如图,是一个无盖器皿的三视图，正视图、侧视图和俯视图中的正方形边长为2，正视图、侧视图中的虚线都是半圆，则该器皿的表面积是___________.15.设甲、乙两个圆柱的底面积分别为21S S ，，体积分别为21V V ，，若它们的侧面积相等，且4921=S S ，则21V V的值是________． 16. 如图，PA ⊥⊙O 所在的平面，AB 是⊙O 的直径，C 是⊙O 上的一点，E 、F 分别是点A 在PB 、PC 上的射影．给出下列结论：①AF⊥PB ；②EF ⊥PB ； ③AF ⊥BC ； ④AE ⊥平面PBC ．其中正确命题的序号是（把正确的序号都填上）三．解答题（本题共5大题，共48分）（解答题不能用空间向量）17．如图，在四边形ABCD 中，AD DC ⊥，//AD BC ，3AD =，2CD =，22AB =45DAB ∠=，四边形绕着直线AD 旋转一周.(1)求所形成的封闭几何体的表面积； (2)求所形成的封闭几何体的体积.NMA BDCO18.如图，在三棱锥P ABC -中，H G,F,,E 分别是BC PC,AC,AB,的中点，且BC AC PB,PA ==(1)证明：PC AB ⊥； (2)证明：平面PA B FGH ABEF 2,//==BE AF EF AB 24=EF 22=AB ABCD AD ABEFM Q ,EF AC ,P BM //PQ BCE AM BCM20.如图，在四棱锥O ABCD -中，底面ABCD 是边长为1的菱形，4ABC π∠=, OA ABCD ⊥底面, 2OA =,M 为OA 的中点，N 为BC 的中点（1）证明：直线MN OCD平面‖；（2）求异面直线AB 与MD 所成角的大小；21.如图，在四棱锥P ABCD -中，底面ABCD 是平行四边形，45ADC ∠=︒，1AD AC ==，O 为AC 的中点，PO ⊥平面ABCD ，2PO =，M 为PD 的中点．（1）证明：AD ⊥平面PAC ；（2）求直线AM 与平面ABCD 所成角的正切值．山西大学附中2016~2017学年高二第一学期10月（总第二次）模块诊断数学试题考查时间：90分钟考查内容：必修2第一、二章一．选择题（本题共12小题，每小题3分，共36分，在每小题给出的四个选项中只有一个选项符合题目要求）1-6 BADACD 7-12 ADBDBC二．填空题（本大题共4小题，每小题4分，共16分） 13. 23a 14. π+24 15.2316. ①②③ 三．解答题（本题共5大题，共48分） 17．解：过点B 作BE AD ⊥于点E ，因为22AB =45DAB ∠=，所以2BE =，所以1DE = 所以四边形ABCD 绕着直线AD 旋转一周所形成的封闭几何体为一个底面半径为2，母线为1的圆柱及一个底面半径为2，高为2的圆锥的组合体. 2分（1）所以几何体的表面积为(22221222842S ππππ=⨯+⨯⨯+⨯⨯=+, 5分（2）体积为22120212233V πππ=⨯⨯+⨯⨯⨯=. 8分 18. 试题解析：（Ⅰ）证明：连接EC ，AB EC ⊥有 2分又,PB PA =PE AB ⊥∴ 2分PEC PC PEC AB 面面⊂⊥∴,PC AB ⊥∴ 5分（Ⅱ）连结FH ，交于EC 于O ，连接GO ，则FH ,//.PEC GO PE ∆中AB E =FH O =解：（1）因为AB ∥EM ，且AB ＝EM ，所以四边形ABEM 为平行四边形．连接AE ，则AE 过点P ，且P 为AE 中点，又Q 为AC 中点，所以PQ 是△ACE 的中位线，于是PQ ∥CE ． 4分 ∵CE ⊂平面BCE ，PQ ⊄平面BCE ，∴PQ ∥平面BCE ． 5分（2）AD ⊥平面ABEF ⇒BC ⊥平面ABEF ⇒BC ⊥AM ． 7分在等腰梯形ABEF 中，由AF ＝BE ＝2，EF ＝24，AB ＝22，可得∠BEF ＝45°，BM ＝AM ＝2，∴AB 2＝AM 2＋BM 2，∴AM ⊥BM ． 9分又BC∩BM＝B ，∴AM ⊥平面BCM ． 10分20．方法一（1）取OB 中点E ，连接ME ，NEME CD ME CD ∴，‖AB,AB ‖‖，又,NE OC MNE OCD ∴平面平面‖‖，MN OCD ∴平面‖,方法二取OD的中点F ，因为MF AD AD NF 21=NC AD AD NC 21=MFCN MN FC MN OCD ∴平面‖CD ‖AB,MDC ∠∴AB MD ,AP CD P ⊥于MP ⊥⊥平面A BC D ，∵OA ∴CD MP 2,42ADP π∠=∵∴DP =222MD MA AD =+=AB MD 3π（1）证明：∵45ADC ∠=︒，且1AD AC ==，∴90DAC ∠=︒，即AD AC ⊥。

山西省应县2017-2018学年高二9月月考数学试卷(文)有答案

应县高二年级月考一数学试题（文） 2017.9时间：120分钟满分：150分命题人：荣印一、选择题：(本大题共12小题，每小题5分，共60分，每小题给出的四个选项，只有一项是符合题目要求的).1、直线x ＝4π的倾斜角是( )A. 90°B. 60°C. 45°D. 不存在2、若m n ，是两条不同的直线，αβγ，，是三个不同的平面，则下列为真命题的是（） A ．若m βαβ⊂⊥，，则m α⊥ B ．若α∩γ＝m ，m n ∥，则αβ∥ C ．若m β⊥，m α∥，则αβ⊥ D ．若αγ⊥，αβ⊥，则βγ⊥3、已知两条直线y=ax ﹣2和y=（a+2）x+1互相垂直，则a 等于（） A ．2 B ．1 C ．0 D ．﹣14、直线：，：，若，则的值为（） A. -3 B. 2 C. -3或2 D. 3或-25、四面体ABCD 中，E 、F 分别是AC 、BD 的中点，若CD=2AB ，EF ⊥AB ，则EF 与CD 所成的角等于（）A ．30°B ．45°C ．60°D ．90° 6、点(1,2)--关于直线1x y +=对称的点坐标是（）A ．()3,2B ．()3,2--C ．()1,2--D ．()2,37、如图是一个空间几何体的三视图,其中正视图和侧视图都是半径为2的半圆,俯视图是半径为2的圆,则该几何体的体积等于（）A ．43π B ．83π C ．163π D ．323π8、已知点(),M a b 在直线34200x y +-=）A. 3B. 4C. 5D. 6 9．一空间几何体的三视图如图所示，则该几何体的体积为( )正视图侧视图俯视图A ．2π＋2 3B ．4π＋2 3C ．2π＋233D ．4π＋233 10、已知点，若直线与线段相交，则实数k 的取值范围是（）A. B. 或 C. D. 或11、将直线3y x =绕原点逆时针旋转90°，再向右平移1个单位，所得到的直线为（）A ．113y x =+ B ．113y x =-+ C ．33y x =- D ．1133y x =-+12、平面四边形ABCD 中，1===CD AD AB ，CD BD BD ⊥=,2，将其沿对角线BD 折成四面体BCD A -'，使平面⊥BD A '平面BCD ，若四面体BCD A -'顶点在同一个球面上，则该球的体积为( )A.π23B. π3C. π32D. π2 二、填空题(共4小题，每小题5分，共20分)13、两个半径为1的铁球，熔化后铸成一个大球，这个大球的半径为．14、如图， '''O A B ∆是水平放置的ABC ∆的直观图，则ABC ∆的周长为 ______.15、已知直线()()20a x y a a R -+-=∈在两坐标轴上的截距互为相反数，则实数a = 16．如图2－8，在棱长为2的正方体ABCD －A 1B 1C 1D 1中，E 为BC 的中点，点P 在线段D 1E 上，点P 到直线CC1的距离的最小值为______．三、解答题（共6小题，共70分，要求在答题卡上写出详细的解答过程。

山西省实验中学2017-2018学年高二上学期10月月考数学(理)试题

山西省实验中学2020-2021学年高二上学期10月月考数学（理）试题学校:___________姓名：___________班级：___________考号：___________一、单选题1．下列说法正确的是（）A ．有一个面是多边形，其余各面都是三角形，由这些面围成的几何体是棱锥B ．有两个面平行且相似，其余各面都是梯形的多面体是棱台C ．如果一个棱锥的各个侧面都是等边三角形，那么这个棱锥可能为六棱锥D ．有两个相邻侧面是矩形的棱柱是直棱柱2．下列命题中错误的是（）A ．如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面βB ．如果平面α⊥平面γ，平面β⊥平面γ，l αβ=，那么l ⊥平面γC ．不存在四个角都是直角的空间四边形D ．空间图形经过中心投影后，直线还是直线，但平行直线可能变成相交的直线 3．一个空间几何体的三视图如图所示，则该几何体的体积为（）A ．403B ．803C ．40D ．804．如图，已知四边形ABCD 的直观图是一个边长为 1 的正方形，则原图形的周长为（）A ．B ．6C ．8D ．2+5．如图，棱长为1的正方体1111ABCD A B C D -中， E F ，是侧面对角线1BC ， 1AD上一点，若1BED F 是菱形，则其在底面ABCD 上投影的四边形面积（）A ．12B ．34C D 6．如图,在正方体1111ABCD A B C D -中,棱长为1,E F 、分别为11C D 与AB 的中点,1B 到平面1A FCE 的距离为A ．5B ．5C ．2D ．37．直四棱柱1111ABCD A B C D -的半球SO ，四边形ABCD 为正方形，则该四棱柱的体积最大时，AB 的长是（）A ．1BCD ．28．如图,在直三棱柱111ABC A B C -中， 1,2,AB AC AB AA AC ⊥===过BC 的中点D 作平面1ACB 的垂线，交平面11ACC A 于E ，则BE 与平面11ABB A 所成角的正切值为（）A ．5B ．10C ．10D ．5二、填空题9．如图，在正方体1111ABCD A B C D -中，M 、N 分别是CD 、1CC 的中点，则异面直线1A M 与DN 所成角的大小是____________．10．若一条直线与一个正四棱柱各个面所成的角都为,则cos α=_____．11．平面α内的60MON ∠=,PO 是α的斜线，345PO POM PON =∠=∠=，，那么点P 到平面α的距离为__________．12．如图，正方体1111ABCD A B C D -的棱长为1，P 为BC 的中点，Q 为线段1CC 上的动点，过点A ,P ,Q 的平面截该正方体所得的截面记为S .则下列命题正确的是_________（写出所有正确命题的编号）. ①当102CQ时，S 为四边形；②当12CQ 时，S 为等腰梯形；③当34CQ 时，S 与11C D 的交点R 满足1113C R =；④当314CQ 时，S 为六边形；⑤当1CQ =时，S 的面积为2.13．如图，在三棱锥P ABC -中，1AC BC CP ===，且AC BC ⊥，PC ⊥平面ABC ，过P 作截面分别交,AC BC 于,E F ，且二面角P EF C --的大小为60，则截面PEF 面积的最小值为 .14．Rt ABC ∆中CA CB ==,M 为AB 的中点，将ABC ∆沿CM 折叠，使AB 、之间的距离为1，则三棱锥M ABC -外接球的体积为__________．15．在棱长为1的正方体1111ABCD A B C D -中，M 为AB 的中点，N 为1BB 的中点，O 为平面11BCC B 的中心，过O 作一直线与AN 交于P ，与CM 交于Q ，则PQ 的长为__________．16．如图，在棱长为1的正方体1111D ABC A B C D -中，点,E F 分别是棱1,BC CC 的中点,P 是侧面11BCC B 内一点，若1A P 平行于平面AEF ,则线段1A P 长度的取值范围是_________.三、解答题17．（本小题共12分）如图，在直三棱柱111ABC A B C -中，AC BC =，点D 是AB 的中点，（1）求证：CD ⊥平面11A ABB ；（2）求证：1//AC 平面1CDBAB 1A 1C1BDC18．如图，在四棱锥P ﹣ABCD 中，PA ⊥面ABCD ，AB=BC=2，AD=CD=，PA=，∠ABC=120°，G 为线段PC 上的点．（Ⅰ）证明：BD ⊥平面PAC ；（Ⅱ）若G 是PC 的中点，求DG 与PAC 所成的角的正切值；（Ⅲ）若G 满足PC ⊥面BGD ，求的值．19．已知四棱锥P ABCD -的底面为直角梯形，//,90AB CD DAB ∠=︒，PA ⊥底面ABCD ，且112PA AD DC AB ====，M 是PB 的中点.（1）证明：平面PAD ⊥平面PCD ；（2）求二面角A CM B --的余弦值.参考答案1．D【解析】选项A,棱锥的定义是如果一个多面体的一个面是多边形,其余各面是有一个公共顶点的三角形,那么这个多面体叫做棱锥,即其余各面的三角形必须有公共的顶点,选项错误;选项B,棱台是由棱锥被平行于地面的平面所截而得, 而有两个面平行且相似，其余各面都是梯形的多面体也有可能不是棱台,如图所示,选项错误;选项C,棱锥的各个侧面都是等边三角形，顶角都是60度,360660︒=︒,即这个棱锥不可能为六棱锥,选项错误;选项D, 若棱柱有两个相邻侧面是矩形，则侧棱与底面两条相交的两边垂直，则侧棱与底面垂直，此时棱柱一定是直棱柱，选项正确;故选D.2．D【解析】选项A, 假若平面α内存在直线垂直于平面β，根据面面垂直的判定定理可知两平面垂直．故此命题成立；选项B, 由面面垂直的性质可以分别在α、β内作异于l 的直线垂直于交线，再由线面垂直的性质定理可知所作的垂线平行，进而得到线面平行再由线面平行的性质可知所作的直线与l 平行，又∵两条平行线中的一条垂直于平面那么另一条也垂直于平面，故命题成立；选项C,假设存在四个角都是直角的空间四边形A-BCD,则,,AD AB AD CD ⊥⊥AD 为AB,CD 的公垂线, ,,BC AB BC CD ⊥⊥BC 为AB,CD 的公垂线,这与公垂线的性质矛盾,故命题正确;选项D, 空间图形经过中心投影后，直线是直线或者点，平行直线投影后可能是平行直线，重合直线，或者是两个点，不可能相交,命题错误;故选D.3．A【解析】该几何体为四棱锥,如图所示,其中SA ⊥平面ABCD,SA=4,底面ABCD 是直角梯形,4,1,4,AD BC AB ===该几何体的体积为1144044323V +=⨯⨯⨯=,故选A.点睛：思考三视图还原空间几何体首先应深刻理解三视图之间的关系，遵循“长对正，高平齐，宽相等”的基本原则，其内涵为正视图的高是几何体的高，长是几何体的长；俯视图的长是几何体的长，宽是几何体的宽；侧视图的高是几何体的高，宽是几何体的宽.由三视图画出直观图的步骤和思考方法：1、首先看俯视图，根据俯视图画出几何体地面的直观图；2、观察正视图和侧视图找到几何体前、后、左、右的高度；3、画出整体，然后再根据三视图进行调整.4．C【解析】试题分析：因为四边形ABCD 的直观图是一个边长为1的正方形，所以原图形为平行四边形，一组对边为1，另一组对边长为3=，所以圆图形的周长为()2138+=，故选C.考点：平面图形的直观图.5．B【解析】试题分析：在棱长为1的正方体1111D ABC A B C D -中， 11BC AD ==AF x =，x =解得x =，即菱形1BED F =，则1BED F 在底面ABCD 上的投影四边形是底边为34，高为1的平行四边形，其面积为34，故选B.考点：平面图形的投影及其作法.6．D【解析】设点1B 到平面1A FCE 的距离为h ．∵正方体棱长为1，∴1122A F FC A C EF ====， ∴11112611311222A CF AB FS S =⨯⨯==⨯⨯=，又1111B A CF C A B F V V --=，∴1111332=⨯⨯，解得h =即点1B 到平面1A FCE ．选D ．点睛：在空间中求点到面的距离时可利用空间向量进行求解，即将距离问题转化为向量的运算问题处理．另外也可利用等积法求解，解题时可将所求的距离看作是一个三棱锥的高，求出其体积后；将此三棱锥的底面和对应的高改换，再次求出其体积．然后利用同一个三棱锥的体积相等建立关于所求高为未知数的等式，解方程求出未知数即可得到所求的高．7．D【解析】设四棱柱底面边长为a,高为b (0b <<,则2222a b ⎛⎫+= ⎪ ⎪⎝⎭,即2262a b =-,四棱柱的体积为()23262,61V a b b b V b '==-=-,令0V '=,解得b=1,则函数在()0,1上单调递增,在(上单调递减,所以b=1,a=AB=2时体积最大,故选D.点睛：空间几何体与球接、切问题的求解方法：(1)求解球与棱柱、棱锥的接、切问题时，一般过球心及接、切点作截面，把空间问题转化为平面图形与圆的接、切问题，再利用平面几何知识寻找几何中元素间的关系求解．(2)若球面上四点构成的三条线段两两互相垂直，一般把有关元素“补形”成为一个球内接长方体求解．8．C【解析】试题分析：连接及交点为，连接，由图形易知面，，故面，故与点重合，取中点,连接和，有几何关系易判断为BE 与平面11ABB A 所成角，，，故，故选项为C.考点：直线与平面所成的角.9．2π 【详解】试题分析：分别以1,,DA DC DD 所在直线为,,x y z 轴，建立空间直角坐标系，设2DA =，则()()()112,0,2,0,1,0,2,1,2A M A M =--， ()()()()1112,1,20,2,10,2,1,0,2,1cos ,0A M DNN DN AM DN A M DN AM DN --⋅=∴〈〉===1AM DN ⊥，即异面直线A 1M 与DN所成角的大小是2π 考点：异面直线所成的角10．60°【解析】略11【解析】由最小角定理可得:cos cos ?cos ,,cos 2POM POH MOH POH POH ∠=∠∠=∠∠=,sin ?sin 3POH PH PO POH ∠=∴=∠==点P 到平面α故12．①②③⑤【详解】②当CQ =12时，即Q 为CC 中点，此时可得PQ ∥AD ，AP =QD = = ，故可得截面APQD 为等腰梯形，S 等腰梯形，故②正确；①由如图当点Q 向C 移动时，满足102CQ ，只需在DD 上取点M 满足AM ∥PQ ，即可得截面为四边形APQM ，如图所示，S 是四边形，故①正确；③当CQ =34时，如图，延长DD 至N ，使DN =12，连接AN 交AD 于S ，连接NQ 交CD 于R ，连接SR ，可证AN ∥PQ ，由△NRD ∽△QRC ，可得CR ：DR =CQ ：DN =1：2，故可得CR =13，故③正确；④由③可知当34＜CQ ＜1时，只需点Q 上移即可，此时的截面形状仍然如图所示的APQRS ，如图S 是五边形，故④不正确；⑤当CQ =1时，Q 与C 重合，取AD 的中点F ，连接AF ，可证PC ∥AF ，且PC =AF ，可知截面为APCF 为菱形，故其面积为12AC •PF =122= ，如图S 是菱形，面积为22=，故⑤正确，故答案为①②③⑤．考点：正方体的性质.13．23【解析】试题分析：过P 做PG ⊥EF ，垂足为G ，连接CG 则由三垂线定理可得EF ⊥CG ，∴∠PGC 即为二面角角P-EF-C 的平面角，∴∠PGC=60°，PC=1，∴在三角形PEF 斜边EF 边上的高为，，设CE=a ，CF=b ，则，在三角形CEF 中，ab=3≥∴ab≥3，∴23ab ≥,∴三角形PEF 的面积为12233ab ⨯=≥,故截面PEF 面积的最小值为23考点：本题考查了二面角的应用．点评：解决此类问题的关键是利用三垂线定理作出二面角，然后利用基本不等式求出最值即可14．54【解析】Rt ABC ∆中, 2CA CB AB ==∴=,又M 为AB 的中点，1MA MB MC ∴===,故对折后三棱锥M-ABC 的底面为边长为1的等边三角形,如图所示, 其外接球可化为以MAB 为底面,以MC 为高的正三棱柱的外接球,设三棱锥M-ABC 外接球的球心为O,则球心到MAB的距离1122d MC ==,平面MAB 的外接球半径r =,故三棱锥M-ABC 外接球的半径R ===则体积为334433V R ππ=== 54,故填54.15．3【解析】连接ON ，由ON∥AD 知，AD 与ON 确定一个平面α．又O 、C 、M 三点确定一个平面β（如图所示）．∵三个平面α，β和ABCD 两两相交，有三条交线OP 、CM 、DA ，其中交线DA 与交线CM 不平行且共面．∴DA 与CM 必相交，记交点为Q ，∴OQ 是α与β的交线．连接OQ 与AN 交于P ，与CM 交于Q ，故直线OPQ 即为所求作的直线．在Rt APQ ∆中, 1AQ =,又APQ OPN ∆~∆,2,AP AQ AN AP PQ PN NO ∴===∴=∴==.16．42⎡⎢⎣⎦，【详解】试题分析：如下图所示，分别取棱111,BB B C 的中点,M N ，连接MN ，连接1BC ，因为,,,M N E F 为所在棱的中点，所以11//,//MN BC EF BC ，所以//MN EF ，又MN ⊄平面,AEF EF ⊂平面AEF ，所以//MN 平面AEF ；因为11//,AA NE AA NE =，所以四边形1AENA 为平行四边形，所以1//A N AE ，又1A N ⊄平面AEF ，AE ⊂平面AEF ，所以1//A N 平面AEF ，又1A N MN N =，所以1//A MN 平面AEF ，因为P 是侧面11BCC B 内一点，且1//A P 平面AEF ，则P 必在线段MN 上，在直角11A B M ∆中，12A M ===，同理，在直角11A B N ∆中，求得1A N =所以AMN ∆为等腰三角形，当P 在MN 中点O 时，1A P MN ⊥，此时1A P 最短，P 位于,M N 处时1A P 最长，14AO ===，112A M A N ==，所以线段1A P 长度的取值范围是42⎡⎢⎣⎦，.考点：点、线、面的距离问题.【方法点晴】本题主要考查了点、线、面的距离问题，其中解答中涉及到直线与平面平行的判定与性质，三角形的判定以及直角三角形的勾股定理等知识点的综合考查，着重考查了学生分析问题和解答问题的能力，以及推理与运算能力，同时考查了学生空间想象能力的训练，试题有一定的难度，属于中档试题.17．(1)见解析；（2）见解析。

2017_2018学年高二数学上学期第二次月考试题文(1)

山西省汾阳中学2017-2018学年高二数学上学期第二次月考试题文时间:120分钟满分:150分一、选择题(每小题5分,共12小题60分)1、集合，集合，则与的关系是( )B. D.2）A. B.C.3、已知、是非零向量且满足则与的夹角是( )A. B. C. D.4）5( )A.B.C.D.6、下列选项中，说法正确的是（）A.B.C.D.7取值范围是（）D.8( )9率是（）C.10）11交于，两点积取最大值时，直线的斜率等于（）C.如图，已知椭圆的中心为原点,为( )A. B. C. D.二、填空题(每小题5分,共4小题20分)13__________141P正切值为2，则此椭圆离心率e的大小为__________15、已知双曲线C为2，则的标准方程为__________16.__________.三、解答题(第17题10分,第18题12分,第19题12分,第20题12分,第21题12分,第22题12分,共6小题70分)17的方程．18（I（II）.19.（1（220（1（2.21.（1）求角的大小；（2）,求的前项和.22、如图，.（I（II理由.高二文科数学月考试卷答案解析第1题答案C第1题解析第2题答案C第2题解析,,第3题答案B第3题解析∵∴即①∵∴即②由①②知∴∴与的夹角为..．第4题答案C第4题解析∴应选C.第5题答案D第5题解析根据面面平行的判定定理和性质定理及线面平行的判定定理和性质定理A，B选项不正确，为平行于同一条直线的直线与平面的关系是平行的或是线在面；‎C选项不正确为两条直线平行于同一个平面两条直线的关系能是相交、平行、异面三种情一；‎D选项正确，由题设中的条件以证得面面平行的判定定理所需要的条件，故命题正确．‎故选D第6题答案C第6题解析存在量词否定后为全称量词，故A要求两个命题都真.故B错；故C是假命题；则能相等，也能互补或终边相同.故D错.第7题答案C第7题解析所以，数形结合得直线的斜第8题答案D第8题解析D．第9题答案B第9题解析。

山西省太原市2017_2018学年高二数学10月月考试题理

山西省太原市2017-2018学年高二数学10月月考试题理一、选择题（每小题4分,共40分,每小题只有一个正确答案）1. 若一个圆锥的轴截面是等边三角形，其面积为3，则这个圆锥的全面积为 A . 3π B. 33π C . 6π D. 9π2.已知,m n 是两条不同直线，,,αβγ是三个不同平面，下列命题中正确的是 A. 若αα⊥⊥n m ,，则n m // B. 若γβγα⊥⊥,，则βα//C. 若βα//,//m m ，则βα//D. 若αα//,//n m ，则n m //3. 如图，网格纸上小正方形的边长为1，用粗实线画出某几何体的三视图，则该几何体的体积为A．12π+．124π+ C ．48π+ D ．843π+4. 设,,,A B C D 是空间四个不同的点，在下列命题中，不正确．．．的是 A ．若AC 与BD 共面,则AD 与BC 共面B ．若AC 与BD 是异面直线,则AD 与BC 是异面直线 C ．若AB AC =,DB DC =,则AD BC ⊥ D ．若AB AC =,DB DC =,则AD BC =5. 正四棱锥的体积为12，底面对角线的长为则侧面与底面所成的二面角的正切值等于 A6. 《九章算术》是我国古代数学名著，它在几何学中的研究比西方早一千多年.例如堑堵指底面为直角三角形，且侧棱垂直于底面的三棱柱；阳马指底面为矩形，一侧棱垂直于底面的四棱锥.如图，在堑堵ABC-A 1B 1C 1中，AC ⊥BC ，若A 1A=AB=2 ，当阳马B-A 1ACC 1体积最大时，则堑堵ABC-A 1B 1C 1的体积为A.23D. 7. 已知某几何体的三视图如右图所示，则该几何体的外接球表面积为 A.8πB. 32πC. 8πD. 9. “牟合方盖”是我国古代数学家刘徽在研究球的体积的过程中构造的一个和谐优美的几何体．它由完全相同的四个曲面构成，相对的两个曲面在同一个圆柱的侧面上，好似两个扣合（牟合）在一起的方形伞（方盖）．其直观图如下左图，图中四边形是为体现其直观性所作的辅助线．其实际直观图中四边形不存在．当其正视图和侧视图完全相同时，它的正视图和俯视图分别可能是A ．,a bB ．,a cC ．,c bD ．,b d10．已知正方体ABCD A 1B 1C 1D 1的棱长为1，E ，F 分别为棱AA 1与CC 1的中点，过直线EF的平面分别与BB 1，DD 1相交于点M ，N.设BM ＝x ，x ∈[0，1]，有以下四个结论，其中不．正确．．的结论是 A. 平面MENF⊥平面BDD 1B 1B. 当x ＝12时，四边形MENF 的面积最小C. 四边形MENF 的周长L ＝f (x )，x ∈[0，1]是单调函数D. 四棱锥C 1MENF 的体积V ＝g (x )为常函数二、填空题（每小题4分，共16分）11. 已知一个圆台的下底面半径为r ，高为h ，当圆台的上底半径r′变化时，圆台体积的变化范围是________．12. 设甲，乙两个圆柱的底面面积分别为12,S S ，体积为12,V V ，若它们的侧面积相等,且1294S S =，则12V V 的值是 . 13. 如图，四棱台ABCD A'B'C'D'-的底面为菱形，P 、Q 分别为B'C'，C'D '的中点.若AA '∥平面BPQD ，则此棱台上下底面边长的比值为 .14. 如图，在直三棱柱ABC A'B'C'-中，底面为直角三角形，∠ACB＝90︒，AC ＝6，BC ＝CC'P 是BC'上一动点，则CP ＋PA '的最小值是___________. 三、解答题（共44分）15. （本小题满分10分）如图所示，已知四棱锥P ABCD 的侧棱PD ⊥底面ABCD ，且底面ABCD 是直角梯形，AD⊥CD，AB∥CD，AB ＝AD ＝12CD ＝2，点M 在侧棱PC 上．（1）求证：BC⊥平面BDP ；（2）若侧棱PC 与底面ABCD 所成角的正切值为12，点M为侧棱PC 的中点，求异面直线BM 与PA 所成角的余弦值．16. （本小题满分10分）如图，C 、D 是以AB 为直径的圆上两点，==AD AB 232，BC AC =，F 是AB 上一点，且AB AF 31=，将圆沿直径AB 折起，使点C 在平面ABD 的射影E 在BD 上，已知2=CE .（1）求证：AD⊥BC；（2）求三棱锥CFD A -的体积．17.（本小题满分12分）如图所示，在多面体111A B D DCBA 中，四边形11AA B B ，11,ADD A ABCD 均为正方形，E 为11B D 的中点，过1,,A D E 的平面交1CD 于F（1）证明：1//EF B C ；（2）求二面角11E A D B --余弦值.18. （本小题满分12分）如图所示,长方体1111D C B A ABCD -中，2111==B A AA ，2=BC ,E 为线段1CC 中点.（1）求证：平面BE A 1⊥平面CD B 1；（2）若点P 为侧面11ABB A （包含边界）内的一个动点，且//1P C平面BEA 1,求线段P C 1长度的最小值.太原五中2017-2018学年度第一学期月考A高二数学(理科)答案一、选择题（每小题4分,共40分,每小题只有一个正确答案）二、填空题（每小题4分，共16分）11.⎝ ⎛⎭⎪⎫13πr 2h ，πr 2h ；12.32；13.23；14. 三、解答题（共44分）15．解：(1)证明：由已知可得BD ＝BC ＝2 2，∴BD 2＋BC 2＝16＝DC 2，故BD⊥BC. 又PD⊥平面ABCD ，BC ⊂平面ABCD ，故PD⊥BC，又BD∩PD＝D ，∴BC⊥平面BDP.(2)如图，取PD 的中点N ，并连接AN ，MN ， BM∥AN，则∠PAN 即为异面直线BM 与PA 所成的角．又PD⊥底面ABCD ，∴∠PCD 即为PC 与底面ABCD 所成的角，即tan ∠PCD＝12，∴PD＝12CD ＝2，即PN ＝12PD ＝1，AN ＝5，PA ＝2 2，则在△PAN 中，cos ∠PAN＝AP 2＋AN 2－PN 22AP·AN ＝3 1010，即异面直线BM 与PA 所成角的余弦值为3 1010.16. （1）证明：依题⊥AD BD ， ⊥CE 平面ABD ∴⊥CE ADBD E CE = ∴⊥AD 平面BCE ∴AD⊥BC ……5分（2）解： F 到AD 的距离等于13BD ∴231321=⋅⋅=∆FAD S ．⊥CE 平面ABD∴662233131=⋅⋅=⋅⋅==∆--CE S V V FAD AFD C CFD A ． 17.解：（1）因为111//,AD BC A D ⊂平面1A DE ,1B C ⊄平面1ADE ，所以1//B C 平面1A D E ,又1B C ⊂平面11B CD ，平面1A DE ⋂平面11B CD =EF ，所以EF//1B C .(2)将几何体补成正方体知，BD 1⊥平面1A DE ，所以BD 1⊥A 1DAD 1⊥平面11A B CD ，所以AD 1⊥A 1D ，所以交线A 1D⊥平面ABD 1.二面角11E A D B --的平面角与∠AD 1B =18. 解：（Ⅰ）在长方体1111D C B A ABCD -中，CD ⊥平面11B BCC ∴BE CD ⊥又∵E 为线段1CC 的中点，由已知易得BC B Rt 1∆∽BCE Rt ∆∴C BB EBC 1∠=∠，∴01190=∠+∠C BB EBB ,故C B BE 1⊥，且C CD C B = 1，∴BE ⊥平面CD B 1 又⊂BE 平面BE A 1，∴平面BE A 1⊥平面CD B 1（2）取线段A 1B 1的中点M ，线段BB 1的中点N ，连接C 1M ，C 1N ，MN ，则 C 1N ∥BE ，MN ∥A 1B.又∵MN ∩C 1N=N ，BA 1∩BE=B ， ∴平面C 1MN ∥平面A 1BE.要使得线段C 1P 长度最小，则C 1P⊥MN,在⊿C 1MN 中，C 1M=C 1N=3MN=2，则C 1P=210。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

山西省汾阳中学2017-2018学年高二数学上学期第二次月考试题文时间:120分钟满分:150分
一、选择题(每小题5分,共12小题60分)
1、集合，集合，则与的关系
是()
A. B. C. D.
2、函数对于任意实数满足条件，若，则（）
A. B.
C. D.
3、已知、是非零向量且满足则与的夹角是()
A. B. C. D.
4、若为圆的弦的中点，则直线的方程是（）
A. B. C. D.
5、设为两条直线，为两个平面，则下列四个命题中，正确的命题是()
A.若且，则
B.若，，则
C.若，则
D.若是两条异面直线，且，，则
6、下列选项中，说法正确的是（）
A.命题“，”的否定是“，”
B.命题“为真”是命题“为真”的充分不必要条件
C.命题“若，则”是假命题
D.命题“若，则”的逆否命题为真命题
7、已知点，直线与线段相交，则实数的取值范围是（）
A.
B. C.或 D.
8、已知正方体的外接球的体积是，则这个正方体的棱长是()
A.
B.
C.
D.
9、已知点是椭圆的右焦点，关于直线的对称点也在椭圆上，则该椭圆的离心率是（）
D.
A. B.
C.
10、若圆上有且只有两个点到直线的距离为，则半径的取值范围（）
A. B. C. D.
11、过点引直线与曲线交于，两点，为坐标原点，当
的面积取最大值时，直线的斜率等于（）
D.
A. B. C.
12、
如图，已知椭圆的中心为原点,为的左焦点，为上一点，满足，且，则椭圆的方程为()
A. B. C. D.
二、填空题(每小题5分,共4小题20分)
13、短轴长为，离心率的椭圆两焦点为，过作直线交椭圆于两点，则的周长为__________
14、以、为焦点的椭圆＝1（）上一动点P，当最大时
的正切值为2，则此椭圆离心率e的大小为__________
15、已知双曲线C：的一条渐近线与直线：垂直，且双曲线的一个焦点到的距离为2，则的标准方程为__________
16、设分别是椭圆的左、右焦点.为椭圆上任一点，点的坐标为，
则的最大值为__________.
三、解答题(第17题10分,第18题12分,第19题12分,第20题12分,第21题12分,第22题12分,共6小题70分)
17、已知一直线与椭圆相交于两点，弦的中点坐标为，求直线的方程．
18、已知函数(其中)..
（I）若命题“”是假命题，求的取值范围；
（II）设命题或；命题，.若是真命题，求的取值范围.
19、如图，在四棱锥中，平面，四边形为正方形，
，为的中点，是的中点.
（1）求证：平面；
（2）求点到平面的距离．
20、已知向量，，设函数
,.
（1）求函数的最小正周期和单调递减区间；
（2）若方程在区间上有实数根，求的取值范围.
21、在中，角的对应边分别是，满足.
（1）求角的大小；
（2）已知等差数列的公差不为零，若，且成等比数列,求的前项和.
22、如图，四棱锥的底面为矩形，，点在底面
上的射影在上，分别是的中点.
（I）证明：平面；
（II）在边上是否存在点，使得平面？若存在，求出的值；若不
存在，请说明理由.
高二文科数学月考试卷答案解析
第1题答案
C
第1题解析
两个集合的代表元素不同
第2题答案
C
第2题解析
,
,
,
第3题答案
B
第3题解析
∵∴即①
∵∴即②由①②知
∴
∴与的夹角为..．
第4题答案
C
第4题解析
由知圆心为.
据，
∴.
∴的方程为，即.
∴应选C.
第5题答案
D
第5题解析
根据面面平行的判定定理和性质定理及线面平行的判定定理和性质定理A，B选项不正确，
因为平行于同一条直线的直线与平面的位置关系可是平行的或者是线在面内；C选项不正确
因为两条直线平行于同一个平面两条直线的位置关系可能是相交、平行、异面三种情况之一；D选项正确，
由题设中的条件可以证得面面平行的判定定理所需要的条件，故命题正确．
故选D
第6题答案
C
第6题解析
存在量词否定后为全称量词，故A错；为真，只要有一个真即可，为真，要求两个命题都真.故B错；当，也成立，故C是假命题；若，则可能相等，也可能互补或终边相同.故D错.
第7题答案
C
第7题解析
∵直线可化为过定点，所
以，数形结合可得直线的斜率的取值范围是或，即或，得的取值范围是或
D
第8题解析
设球的半径为，则，∴．再设正方体的棱长为，则其体
对角线长为，由正方体外接球的性质有，从而解得．故选D．
第9题答案
B
第9题解析
设点的坐标为，因为关于直线的对称点，所以
，即，解得：，所以点
的坐标是，因为点在椭圆上，所以，即
，整理得：，解得：或
（舍去），所以该椭圆的离心率是
，故选B．
第10题答案
A
第10题解析
由题目可知圆心到直线的距离等于
，由得,故选A．
第11题答案
B
由，得
∴曲线表示单位圆在轴上方的部分（含与轴的交点）由题知，直线斜率存在，
设直线的斜率为，若直线与曲线有两个交点，且直线不与轴重合则，
∴直线的方程为：，即，
法一：圆心到直线的距离，
直线被半圆所截得的弦长为
，
，
令，则，
所以当，即，亦即时，
有最大值为，再注意到，
所以，故选．
法二：设，，则
，
当，即为等要直角三角形时，有最大值为，
此时圆心到直线的距离（），解得.
第12题答案
B
第12题解析
设椭圆标准方程为,焦距为，右焦点为，连接，
因为为的左焦点.所以.
由知，，所以
.
由
知..即.
在中.由勾股定理，得
，
由椭圆定义，得，从而.
得，于是，
所以椭圆的方程为.
第13题答案
12
第13题解析
经题意分析得则，的周长
.
第14题答案
第14题解析
解答：当最大时P为椭圆与y轴的交点，的正切值为2，即
，∵，则椭圆离心率e为。

第15题答案
第15题解析
由题意得：，而的一个焦点到的距离为，所以
，的标准方程为
第16题答案
第16题解析
如图所示，
连接，由椭圆的定义可知
(当且仅当点是
与椭圆在x轴下方的交点时等号成立)，故的最大值为.
第17题答案
第17题解析
设,由点差法有，，两式相减得，，
∴直线斜率为，又中点在椭圆内，∴直线方程为
.
第18题答案
（I）；
（II）.
第18题解析
（I）若命题“”是假命题，则即
，解得；（II）因为是真命题，
则,都为真命题，当时，，因为是真命题，则，
所以，即；当时，
，因为是真命题，则，使，所以
，即，综上所述：.
第19题答案
（1）详见解析；
（2）.
第19题解析
（1）证明：取的中点，连接，.
∵为的中点，∴且.
又且，
∴且，四边形是平行四边形，
∴.
又平面，平面，
∴平面.
（2）由平面，知点和点到面的距离相等，设点到平面
的距离为，
∵，∴.
又，，
∴，
∴
∴点到平面的距离为．
第20题答案
（1），单调递减区间为；
（2）.
第20题解析
（1）
，
则函数的最小正周期，
由，得，
即单调递减区间为.
（2）由，得，故k在的值域内取值即可.
，
则，即.
第21题答案
（1）；
（2）
第21题解析
（1）∵，
∴，∴，
又，∴.
（2）设的公差为，由已知得，且，
∴且不为零，即，
∴，∴，
∴
.
第22题答案
（I）证明略；
（II）证明略
第22题解析
（I）在矩形中，，且是的中点，
∴∠=∠,
∴∠=∠,
∵∠∠,∴∠∠,即⊥.
由题可知面面，且交线为，∴面.
（II）取的中点，的中点，连结、.
∵，且∴四边形为平行四边形，∴
∵是的中点，是的中点，∴，∴.
过作交于，连结，
∵,，∴平面平面，∴平面.
由可知：∴。