【全国百强校】天津一中人教版高中数学必修1《23幂函数》导学案(无答案)
【全国百强校】天津一中人教版高中数学必修1《2.1.1指数与指数幂的运算(1)》导学案(无答案) - 副本

第二章 基本初等函数2.1指数函数考纲要求:(1)掌握根式的概念和性质,并能熟练应用于相关计算中(2)理解分数指数幂的概念,掌握有理指数幂的运算性质,会对根式、分数指数幂进行互化.(3)理解指数函数的概念,并能正确作出其图象,掌握指数函数的性质.(4)掌握指数形式的函数定义域、值域,判断其单调性.第一课时 2.1.1指数与指数幂的运算(1)学习目标1、理解指数幂指数取值范围的扩充,能够进行分数指数幂与根式的互化2、掌握有理数指数幂的运算性质,灵活地运用运算公式进行有理数指数幂的运算和化简,会进行根式与有理数指数幂的相互转化。
重点、难点 掌握有理数指数幂的运算性质,灵活地运用运算公式进行有理数指数幂的运算和化简,会进行根式与有理数指数幂的相互转化。
【课前导学】1、 根式:(1) n 次方根的定义 _____________________________________(2)a 的n 次方根的取值规律:① 当n 为奇数时0a >,a 的 n 次方根为一个正数;0a <,a 的n 次方根为一个负数;0a = ,a 的n 次方根为零.② 当 n 为偶数时0a >,a 的n 次方根为两个互为相反数的数;0a <,a 的n 次方根不存在;0a =,a 的n 次方根为零.(3) a 的n 次方根的符号表示___________________________(4)根式运算的依据2、 分数指数幂(1).分数指数幂正数的分数指数幂的意义,规定:*______(0,,,1)m n a a m n N n =>∈>,*___________(0,,,1)mn a a m n N n -==>∈>0的正分数指数幂等于0,0的负分数指数幂没有意义(2).实数指数幂的运算性质(1)______r s a a ⋅=),,0(R s r a ∈>(2)()______r s a =),,0(R s r a ∈>(3)()______r ab =),,0(R s r a ∈>【预习自测】1、化简①55)31(-. ② 66)31(-.③224349b ab a +-.(a <6b )2、求下列各式的值:(1)432981⨯; (2)63125.132⨯⨯;(3)1075325555⋅⋅【典型例题】例1.求值:。
【新导学案】高中数学人教版必修一:23《幂函数》.doc

2.3《幕函数》导学案【学习目标】:通过具体实例了解幕函数的图象和性质,体会幕函数的变化规律及蕴含其屮的对称性并能进行简单的应用.【重点难点】重点:从五个具体幕函数中认识幕函数的一些性质.难点:画五个卷函数的图象并由图象概括其性质.【知识链接】(1)边长为d的正方形面积S = a2,这里S是。
的函数;丄(2).面积为S的正方形边长a = S—这里。
是S的函数;(3)边长为a的立方体体积V=a\这里V是a的函数;观察上述三个函数,有什么共同特征?(指数定,底变)【学习过程】鬲函数的图象与性质①给出定义:一般地,形如= («G /?)的函数称为幕函数,其中G为常数.丄②作出下列函数的图彖:(1) y = x ;(2) y = x2;(3) y = x2;(4) y = x_l;(5)y = x3.观察图象,举例学习这类函数的一些性质.归纳概括幕函数的的性质及图象变化规律:.(1)所有的幕函数在(0, +OO)都有定义,并且图象都过点(1, 1);(II)&>0吋,幕函数的图彖通过原点,并且在区间[0,+oo)上是增函数.特别地,当a>l吋, 幕函数的图象下凸;当0vac 1时,幕函数的图象上凸;(Ill) QVO时,幕函数的图象在区间(0,+oo)上是减函数.在第一象限内,当无从右边趋向原点时,图象在y轴右方无限地逼近y轴正半轴,当兀趋于+ 8时,图象在兀轴上方无限地逼近兀轴止半轴. 【例题分析】例1、利用幕函数的性质,比较下列各题屮两个幕的值的大小:3 3 6 6 _3 _3 _1 _丄(1) 23, 2.4\ (2) 0.3P, 0.35匚(3) (QN (馆戸;(4) 1.1刁,0.9王例2证明幕函数/(兀)=頁在[0,+00]上是增函数【基础达标】2.如图所示,曲线是幕函数?=屮在笫一象限内的图象,已知a分别取一1,1,丄,2四个值,贝q相2应图象依次为:______________ .X 2.在同一坐标系内,作岀下列函数的图象的草图,你能发现什么规律?2(1)y = x~3和y = x3.;5 4MB(2)y = x4 f\\y = x5・3.比较大小:2 2 _丨_ 丄3 3 6 6 _3①(2 + /门与2刁;②1.1刁与0.9刁;③23与2.44;④0.3P与0・35和⑤(VI)石与3(V3)_i.【学习反思】(1)我们今天学习了哪一类基本函数,它们定义是怎样描述的?(2)你能根据函数图象说出有关幕函数的性质吗?赠:我的写字心得体会从小开始练习写字,几年来我认认真真地按老师的要求去练习写字。
高一数学人教版必修1导学案设计 :2.3幂函数(无答案)

第二章 基本初等函数(Ⅰ)2.3 幂函数【学习目标】1.了解幂函数的概念,会画五个幂函数的图象,并能结合图像了解幂函数图像的变化情况和性质2.了解五个常见的幂函数的性质,并能进行初步的应用3.利用计算机等工具,了解幂函数和指数函数的本质差别,使学生充分认识到现代技术在人们认识世界的过程中的作用,从而激发学生的学习欲望4.进一步渗透数形结合与类比的思想方法【预习提纲】1.幂函数概念:一般地,我们把形如 的函数称为幂函数,其中x 是自变量,α是常数。
2.幂函数的图象在同一平面直角坐标系中作出幂函数1223,,,,,y x y x y x y x y x --===== 12y x =的图象。
3.幂函数的性质(1)所有的幂函数在 都有定义,并且图象都过定点(2)0α>,幂函数的图象都通过原点,并且在[0,+∞]上是特别地,当1α>时,(0,1)x y x α∈=的图象都在y =x 图象的下方,α越大,下凸的程度越大。
当01α<<时,(0,1),x y x α∈=的图象都在y =x 图象的上方,α越小,上凸的程度越大。
(3)0α<,幂函数的图象在区间(0,+∞]上是 ,并且以x 轴正半轴与y 轴正半轴为幂函数的渐近浅。
(4)当α为奇数时,幂函数为 ;当α为偶数时,幂函数为 。
(奇、偶函数)【例题精讲】例1、证明幂函数()f x =[)0,+∞上是增函数。
例2.利用函数的性质 ,判断下列两个值的大小(1)11662,3 (2)3322(1),(0)x x x +> (3)22244(4),4a --+例3 讨论函数32x y =的定义域、奇偶性,作出它的图象,并根据图象说明函数的单调性.【归纳点拨】1. 幂函数在第四象限无图像,在其他象限的图象可由定义域和奇偶性确定;2. 幂函数的性质的讨论主要在第一象限,其变化规律十分明显,结合图形可掌握的更牢。
【课堂反馈】1.求下列幂函数的定义域、奇偶性(1)23y x -= (2)32y x -= (3)34y x -= (4)3y x =2.比较下列各组数中两个值的大小(1)1.52.5,0.32.5(2)0.50.50.7,0.8-3.已知函数21m y x+=在区间(0,)+∞上是单调性增函数,求实数m 的取值范围。
2020学年人教版高中数学必修一2.3幂函数word导学案

2.3 幂函数班级:__________姓名:__________设计人__________日期__________课前预习· 预习案【温馨寄语】你是花季的蓓蕾,你是展翅的雄鹰,明天是你们的世界,一切因你们而光辉【学习目标】1.能熟练利用幂函数的图象和性质解决相关的综合问题.2.结合函数,,,,的图象,了解它们的变化情况. 3.通过实例了解幂函数的概念.【学习重点】幂函数的图像和性质【学习难点】幂函数的图像和性质【自主学习】1.幂函数的概念(1)解析式为: (其中为常数).(2)自变量是: .2.常见的五种幂函数的图象与性质幂函数图象定义域__________ __________ __________ __________ __________值域__________ __________ __________ __________ __________奇偶性__________ __________ __________ __________ __________单调性__________ __________ __________ __________ __________过定点____________________________【预习评价】1.下列函数中不是幂函数的是A. B. C.D.2.幂函数是二次函数,则A.1B.4C.2D.33.已知,,则 .4.幂函数的定义域为,其奇偶性是 .5.幂函数在(0,+∞)上是减函数,则的取值范围是 .知识拓展· 探究案【合作探究】1.幂函数的解析式根据幂函数的解析式,完成下列填空,并明确其具有的三个结构特征:(1)特征1:自变量在位置,且只能是而不能为关于的代数式.(2)特征2:指数位置为,不含变量.(3)特征3:的系数是 .2.幂函数的图象和性质根据幂函数为常数)的解析式及当到不同范围内值时在第一象限的图象的特征,思考下列问题:(1)观察上面的图象,①当时图象都经过定点, .②当时,图象经过定点 .(2)观察上面的幂函数图象,分析幂函数在区间(0,+∞)上为增函数时,满足的条件是什么?在区间(0,+∞)上为减函数时,满足的条件是什么?3.幂函数的图象和性质幂函数中,令(其中,).讨论,的取值是如何影响函数的奇偶性的?【教师点拨】1.对幂函数解析式的说明(1)定义中所说的形如为常数)的形式一般来说是不可改变的,否则就不是幂函数.(2)解析式中的指数是常数.2.对幂函数图象与性质的三点说明(1)定点:所有幂函数的图象均过定点(1,1).(2)单调性:当时,在区间(0,+∞)上是增函数;当时,在区间(0,+∞)上是减函数.(3)图象特征:当时在区间(0,+∞)上增加得越来越快;当时在区间(0,+∞)上增加得比较缓慢.【交流展示】1.在,,,四个函数中,幂函数有A.1个B.2个C.3个D.4个2.已知是幂函数,求,的值.3.如图所示的曲线是幂函数的第一象限的图象,已知,相应于曲线,,,的值依次为A. B.C. D.4.已知幂函数的图象过点,试求出该函数的定义域、单调区间、奇偶性.5.若,则的取值范围是A. B. C. D.6.把,,,,按从小到大的顺序排列 .【学习小结】1.幂函数的判断方法(1)看形式:判断一个函数是否是幂函数,关键看解析式是否符合为常数)这一结构形式.(2)明特征:幂函数的解析式具有三个特征,只要有一个特征不具备,则不是幂函数. 2.求幂函数解析式的依据及常用方法(1)依据:若一个函数为幂函数,则该函数应具备幂函数解析式所具备的特征,这是解决与幂函数有关问题的隐含条件.(2)常用方法:设幂函数解析式为,根据条件求出.3.幂函数图象的画法(1)确定幂函数在第一象限内的图象:先根据的取值,确定幂函数在第一象限内的图象.(2)确定幂函数在其他象限内的图象:根据幂函数的定义域及奇偶性确定幂函数在其他象限内的图象.4.求幂函数中含参数问题的三个步骤【当堂检测】1.已知函数为幂函数,求其解析式. 2.比较下列各组数中两个数的大小:(1)与.(2) 与.(3) 与.答案课前预习· 预习案【自主学习】1.(1)y=x a(2)x2.R R R [0,+∞)(-∞,0)∪(0,+∞)R [0,+∞)R [0,+∞){y|y∈R且y≠0}奇偶奇非奇非偶奇增x∈[0,+∞)增,x∈(-∞,0)减增增x∈(0,+∞)减,x∈R(-∞,0)减(1,1)【预习评价】1.D2.B3.-14.(0,+∞)非奇非偶函数5.a>2知识拓展· 探究案【合作探究】1.(1)底数(2)常数α(3)12.(1)①(0,0) (1,1) ②(1,1)(2)当α>0时,y=x a在(0,+∞)上为增函数.当α<0时,y=x a在(0,+∞)上为减函数.3.当p,q都为奇数时,幂函数y=x a(α为常数)为奇函数;当p为奇数,q为偶数时,幂函数y=x a(α为常数)为偶函数.【交流展示】1.B2.由题意得解得所以m=-3,.3.B4.因为,所以,即,所以.由,得x≠0,所以f(x)的定义域为(-∞,0)∪(0,+∞).又因为,所以f(x)是偶函数.因为,f(x)在(0,+∞)上是减函数,又f(x)为偶函数,所以f(x)在(-∞,0)上是增函数.故f(x)的单调减区间为(0,+∞),增区间务(-∞,0). 5.C6.【当堂检测】1.因为为幂函数,所以m2-3m+3=1,解得m=1或m=2.当m=1时,幂函数解析式为;当m=2时,幂函数解析式为.2.(1)因为幂函数y=x0.5在(0,+∞)上是单调递增的,又,所以.(2)因为幂函数y=x-1在(-∞,0)上是单调递减的,又,所以.(3)因为函数力为减函数,又,所以,又因为函数在(0,+∞)上是增函数,且,所以,所以.。
高中数学 23幂函数导学案(无答案)新人教A版必修1 学案

湖北省监利县第一中学高中数学 2.3幂函数导学案(无答案)新人教A 版必修1学习目标:1.了解幂函数的概念2.会画出几个常见的幂函数的图象,幂指数的变化对函数图像的影响3.了解几个常见的幂函数的性质,并能简单应用 预习案1.阅读教材第77-78页,完成下列学习 2、幂函数的概念一般地,函数___________________叫做幂函数,其中________是自变量,________是常数. 3、幂函数的图象与性质幂函数的性质总结:(1)所有幂函数在 上都有意义,而且图像都通过点 ,幂函数的图像不过第 象限.(2)当0>α时,幂函数的图象都通过点 , ;而且在 上都是增函数.当0<α时,幂函数的图象都过 点;在 上都是减函数探究案1、幂函数)(x f 的图象过点(4,2),则)81(f 等于_____________ 2、函数53)(-=xx f 的奇偶性为 ______________.3、函数()()23-+=x x f 的定义域为__________, 单调减区间为__________单调增区间为__________4 在固定的压力差(压力差为常数)下,当气体通过圆形管道时,其流量速率V 与管道半径R( 单位:cm )的4次方成正比,1,写出气流流量速率V 关于管道半径R 的函数解析式2,假设气体在半径为3 cm 的管道中,流量速率为400 cm 3/s.求该气体通过半径为R cm 的管道时,其流量速率V 的表达式;3已知(2)中的气体通过的管道半径为5 cm ,计算该气体的流量速率.4、求下列函数的定义域和值域: (1)32-=x y ; (2)43-=xy (3)212)2(--=x x y幂函数x y =2x y = 3x y =21x y =1-=x y图象,定义域 值域 奇偶性 单调性 定点3若3131)23()1(---<+a a ,试求a 的取值范围.4已知幂函)(x f 的图象过点(2,22),试求出此函数的解析式,并作出图象,判断奇偶性,单调性学习小结:1、 幂函数的概念及其指数函数表达式的区别2、 常见幂函数的图象和幂函数的性质3、 数形结合。
高中-数学-人教A版-高中数学必修一第二章2.3《幂函数》 导学案(无答案)
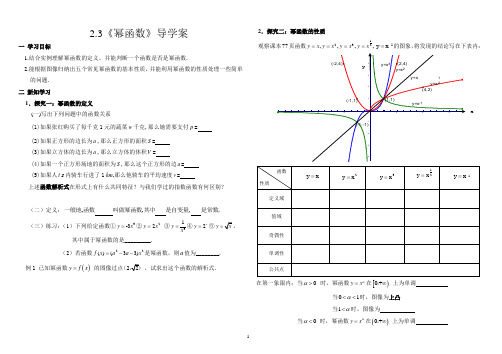
2.3《幂函数》导学案一 学习目标1.结合实例理解幂函数的定义,并能判断一个函数是否是幂函数.2.能根据图像归纳出五个常见幂函数的基本性质,并能利用幂函数的性质处理一些简单的问题.二 新知学习1.探究一:幂函数的定义 (一)写出下列问题中的函数关系(1)如果张红购买了每千克1元的蔬菜w 千克,那么她需要支付p = (2)如果正方形的边长为a ,那么正方形的面积S =(3)如果立方体的边长为a ,那么立方体的体积V =(4)如果一个正方形场地的面积为S ,那么这个正方形的边a = (5)如果人t s 内骑车行进了1 km ,那么他骑车的平均速度v =上述函数解析式在形式上有什么共同特征?与我们学过的指数函数有何区别?(二)定义:,,,一般地函数叫做幂函数其中是自变量是常数.(三)练习:(1)下列给定函数①3-3y x =②22y x = ③31y x=④2x y =⑤y = 其中属于幂函数的是_________.(2)若函数22)33()(x a a x f --=是幂函数,则a 值为________.例1 已知幂函数()y f x =的图像过点(2 ,试求出这个函数的解析式.2.探究二:幂函数的性质观察课本77页函数,,,,2132x y x y x y x y ====x y =-1的图象,将发现的结论写在下表内:.在第一象限内:当0α> 时,幂函数y x α=在[)0+∞, 上为单调 当01α<<时,图像为上凸 当1α<时,图像为当0α< 时,幂函数y x α=在()0+∞, 上为单调3.幂函数性质的简单应用例2 证明幂函数()f x x = 在[)0+∞, 上是增函数.三 练习反馈1.下列函数中不是幂函数的是 ( )A. 3y x =B.y x =C.2y x =D.1y x -=2.如图所示,曲线是幂函数y x α=在第一象限内的图象,已知α分别取1-1,122,,四个值,则相应图象依次为:_______________.3.若幂函数()y f x =的图像经过点()93,,则()25f =______________. 4.比较下列各组数的大小:(1)11220.750.76 (2)()22-3.14π5. 幂函数()21m y m m x =--在区间()0+∞,上是减函数,则m 的值为_____. 四 小结1.幂函数的定义; 2.幂函数的基本性质. 五 作业A 组课本82页第10题;B 组资料课时作业142页12题和13题.。
高中数学 第二章 2.3 幂函数导学案(无答案)新人教A版必修1(2021年最新整理)

高中数学第二章2.3 幂函数导学案(无答案)新人教A版必修1编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(高中数学第二章2.3 幂函数导学案(无答案)新人教A版必修1)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为高中数学第二章2.3 幂函数导学案(无答案)新人教A版必修1的全部内容。
2.3 幂函数2。
3 幂函数学习目标1.通过具体实例了解幂函数的概念;2.会画幂函数y x=,2y x=,3y x=,1y x-=,12y x=的图象,并通过其图象了解幂函数的图象和性质;重点难点会用常见的幂函数的性质解决比较大小等问题.类比研究一般函数、指数函数、对数函数的方法【幂函数的概念】(1)如果张红购买了每千克1元的蔬菜w千克,那么她需要支付p元,这里是的函数.(2)如果正方形的边长为a,那么正方形的面积S,这里是的函数.(3)如果立方体的边长为a,那么立方体的体积V,这里是的函数.(4)如果一个正方形场地的面积为S,那么这个正方形的边长a=,这里是的函数.(5)如果某人t s内骑车行进了1 km,那么他骑车的平均速度v=km/s,这里是的函数.问题1 上面5个问题中函数的对应法则分别是什么?问题2 上面5个问题中的5个函数有什么共同特征?上面5个问题中涉及到的函数,都是形如:y=xα,其中是自变量,是常数.【幂函数定义】一般地,函数y=xα叫做幂函数,其中x是自变量,α是常数.【注意】只有满足函数解析式右边的系数为1,底数为自变量x,指数为常数这三个条件,才是幂函数.如:y =3x 2,y =(2x )3,y =42x ⎛⎫⎪⎝⎭ (填“是"或“不是”)幂函数.问题4 观察下列两组函数,说出它们的共同点与不同点:(1)y =x 2,y =x 3,12y x =,y =x -1;(2)y =2x ,y =3x ,y =(错误!)x ,y =0.3x .共同点:均是幂的形式.不同点:第一组: 是自变量,第二组: 是自变量.例1 写出下列函数的定义域,并分别指出它们的奇偶性:(1) 3y x =;(2)12y x = ;(32y x -=.训练1 已知221(22)23m y m m x n -=+-+-是定义域为R 的幂函数,求m ,n 的值.求幂函数的定义域时,通常要对幂的指数做变形,把负指数变成正指数,把分数指数变成根式的形式,这样易于看出自变量的受限程度.【幂函数的图象和性质】如下图在同一坐标系内作出函数y x =; 2y x =; 3y x =; 12y x =; 1y x -=的图象,思考下列问题:-6-6661122334455-1-1-2-2-3-3-4-4-5-5x y o-6-6661122334455-1-1-2-2-3-3-4-4-5-5xyo训练2 证明幂函数f (x )=x 3在定义域上是增函数.例3 比较大小:(1) 215.1,217.1;(2)(-1.2)3,(-1。
高中数学 2.3 幂函数导学案 新人教A版必修1

《2.3 幂函数》导学案【学习目标】其中2、3是重点和难点1.通过具体实例了解幂函数的图象和性质,体会幂函数的变化规律及蕴含其中的对称性。
2.画五个幂函数的图象并由图象概括其性质。
3.从五个具体幂函数中认识幂函数的一些性质,能利用性质解决数学问题。
【课前导学】预习教材第77-78页,找出疑惑之处,完成新知学习。
1.幂函数的概念:形如 的函数称为幂函数,其中 是自变量, 是常数。
2.幂函数的性质:(1)幂函数的图象都过点 ; (2)当0α>时,幂函数在[0,)+∞上 ;当0α<时,幂函数在(0,)+∞上 ; (3)当2,2α=-时,幂函数是 ;当11,1,3,3α=-时,幂函数是 。
【预习自测】首先完成教材上P79第1、2题,然后做自测题。
1、幂函数()f x的图象过点,则()f x 的解析式是 __ 。
2、下列所给出的函数中,是幂函数的是( )A .3x y -=B .3-=x yC .32x y =D .13-=x y 3、如图所示,幂函数αx y =在第一象限的图象, 比较1,,,,,04321αααα的大小( ) A .102431<<<<<αααα B .104321<<<<<αααα C .134210αααα<<<<< D .142310αααα<<<<< 4、函数2-=x y 在区间]2,21[上的最大值是 ( )A .41 B .1-C .4D .4-【课中导学】首先独立思考探究,然后合作交流展示。
探究一:看教材P77页5个具体的问题,这些函数的解析式结构有何共同特点?其一般形式如何?定义:幂函数的概念。
注意:幂函数与指数函数的区别。
探究二:在同一平面直角坐标系内作出函数12312,,,,y x y x y x y x y x -=====的图象,它们的定义域、值域、奇偶性、单调性、公共点分别如何? 归纳:幂函数的性质。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十一课时 2.3幂函数
学习目标
1.了解幂函数的概念
2.会画出几个常见的幂函数的图象
3.了解几个常见的幂函数的性质,并能简单应用 重、难点
了解几个常见的幂函数的性质,并能简单应用
【课前导学】阅读教材第77-78页,完成下列学习
1、幂函数的概念
一般地,函数___________________叫做幂函数,其中________是自变量,________是常数.
2、幂函数的图象与性质
幂函数的性质总结:
(1)所有幂函数在 上都有意义,而且图像都通过点 ,幂函数的图像不过第 象限.
(2)当0>α时,幂函数的图象都通过点 , ;而且在 上都是增函数.
当0<α时,幂函数的图象都过 点;在 上都是减函数 (3)在第一象限内,直线1=x 侧,逆时针方向,α逐渐增大 【预习自测】首先完成教材上79页习题
1、幂函数)(x f 的图象过点(4,2),则)8
1(f 等于_____________ 5
3
)(-=x
x f
3、函数()()
2
3-+=x x f 的定义域为__________,单调增区间为__________,单点调区间为
__________
4、求下列函数的定义域和值域: (1)3
2-=x y ; (2)4
3-
=x
y (3)2
12
)
2(-
-=x x y
【典型例题】
例1 比较下列各组数的大小:
(1) 25
3-
2
51.3-
(2)32)3
2(-
- 32
)6(--π
(3)8
78-- 8
791⎪⎭
⎫ ⎝⎛- (4) 521.4,32
8.3-,()539.1-
例2 当∈x (0,+∞)时,幂函数3
222
)1(--⋅--=m m x m m y 为减函数,求实数m 的值.
例3 若3
13
1)
23()1(-
--<+a a ,试求a 的取值范围.
例4 当∈x (0,+∞)时,幂函数3
22
)1(-+⋅--=m m x m m y 为增函数,求函数的解析式.
课后反思。
