Abaqus梁结构经典计算
abaqus梁结构分析
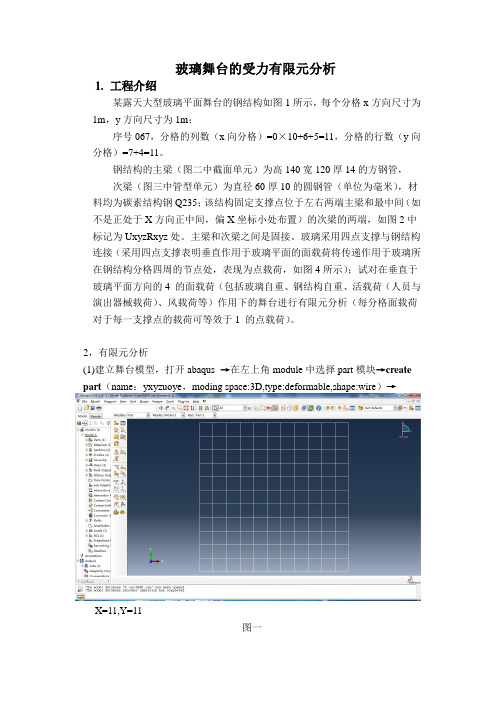
玻璃舞台的受力有限元分析1.工程介绍某露天大型玻璃平面舞台的钢结构如图1所示，每个分格x方向尺寸为1m，y方向尺寸为1m；序号067，分格的列数（x向分格）=0×10+6+5=11，分格的行数（y向分格）=7+4=11。
钢结构的主梁（图二中截面单元）为高140宽120厚14的方钢管，次梁（图三中管型单元）为直径60厚10的圆钢管（单位为毫米），材料均为碳素结构钢Q235；该结构固定支撑点位于左右两端主梁和最中间（如不是正处于X方向正中间，偏X坐标小处布置）的次梁的两端，如图2中标记为UxyzRxyz处。
主梁和次梁之间是固接。
玻璃采用四点支撑与钢结构连接（采用四点支撑表明垂直作用于玻璃平面的面载荷将传递作用于玻璃所在钢结构分格四周的节点处，表现为点载荷，如图4所示）；试对在垂直于玻璃平面方向的4 的面载荷（包括玻璃自重、钢结构自重、活载荷（人员与演出器械载荷）、风载荷等）作用下的舞台进行有限元分析（每分格面载荷对于每一支撑点的载荷可等效于1 的点载荷）。
2，有限元分析(1)建立舞台模型，打开abaqus→在左上角module中选择part模块→create part（name：yxyzuoye，moding space:3D,type:deformable,shape:wire）→X=11,Y=11图一(2)定义材料属性和截面形状，在module中选择property模块→create material(Y=206Gpa,E=0.3)→create section主梁截面形状及尺寸如图二图二次梁截面形状及尺寸如图三图三→赋予截面属性assign section→assign beam orientation→done(3)装配：进入assembly模块→create instance→点击ok完成装配。
(4)进入step模块设置步：进入step模块→create step(initial，static，general) →点击continue→点击ok完成。
abaqus应用梁单元PPT教学课件
截面点： 当应用在ABAQUS横截面库的建立梁轮廓的方式来定义梁横截面，并要 求在分析过程中计算横截面的工程性质时，在通过分布于梁横截面上的一 组截面点上，ABAQUS计算梁单元的响应。 对于矩形横截面，所有的截面点如图所示。对于该横截面，在点1、5、21 和25上提供了默认的输出。在图中所示的梁单元中总共使用了50个截面点 （两个积分点，每个积分点上有25个截面点）来计算刚度。
第12页/共19页
实心横截面 在扭转作用下，非圆型的实心横截面不再保持平面，而是发生翘曲。 应用St.Venant翘曲理论在横截面上每一个截面点处计算由翘曲引起的剪切 应变的分量。 实心横截面的翘曲被认为是无约束的，所产生的轴向应力可以忽略不计 。 实心横截面梁的扭转刚度取决于材料的剪切模量G和梁截面的扭转常数J。 扭转常数取决于梁横截面的形状和翘曲特征。 对于在横截面上产生较大非弹性变形的扭转载荷，应用这种方法不能够 得到精确的模拟。
对于二维梁单元，n1的方向总是（0.0, 0.0, -1.0）。 对于三维梁单元，给定一个近似的n1方向，ABAQUS定义梁的n2方向为t×v。 在n2确定后，ABAQUS定义实际的n1方向为n2×t。上述过程确保了局部切线与局部 梁截面轴构成了一个正交系。
第5页/共19页
梁单元曲率 梁单元的曲率是基于梁的n2方向相对于梁轴的取向。如果n2方向不与
当要求在分析前计算梁截面的性质时，ABAQUS就不在截面点上计算梁 的响应，而是应用截面的工程性质确定截面的响应。
第4页/共19页
横截面方向 ： 用户必须在整体笛卡儿空间中定义梁横截面的方向。从单元的第一节点
到下一个节点的矢量被定义为沿着梁单元的局部切线t，梁的横截面垂直于这 个局部切线矢量。矢量n1和n2代表了局部（1-2）梁截面轴。这三个矢量t、 n1、n2构成了局部、右手法则的坐标系。
abaqus梁单元最大主应变
abaqus梁单元最大主应变在Abaqus中，梁单元的最大主应变可以通过查看模型的应力应变结果来获得。
具体步骤如下：1.在后处理模块中，选择"Stress"或"Strain"选项卡。
2.选择相应的应力或应变分量。
3.确保模型已经完全运行，并且已经得到了收敛的结果。
4.在结果窗口中，找到"Stress"或"Strain"的表格，并查看最大主应变值。
需要注意的是，Abaqus中的梁单元是一种一维单元，主要用于模拟细长的结构，如桥梁、建筑物的梁等。
因此，梁单元的最大主应变可能会受到模型的具体尺寸、边界条件、载荷等因素的影响。
同时，还需要注意Abaqus中默认的应变单位是工程应变，即真实应变减去1。
在Abaqus中，梁单元的最大主应变（E1）可以通过以下公式计算：E1=(F/A)-(1-v)(ε1+ε2)其中：F是梁单元的力（N）A是梁单元的面积（m²）v是泊松比ε1和ε2是梁单元在x和y方向上的应变分量需要注意的是，这个公式适用于线弹性材料，并且假设梁单元是均匀的。
对于非均匀或非线性的材料，可能需要使用更复杂的公式来计算最大主应变。
弹性应变率是一个物理量，用于描述物体在受到外力作用时发生的形变速度。
它是应力和应变之间的导数关系，表示单位时间内应变的变化量。
弹性应变率可以用来描述材料的弹性和动态行为，特别是在冲击、振动等动态加载条件下。
弹性应变率可以通过材料的弹性模量和应变率之间的关系计算得出。
具体来说，弹性应变率（E）可以表示为：E=dσ/dt/(1-v^2)其中，dσ/dt是应力的时间导数，v是泊松比，E是弹性模量。
弹性应变率在材料科学、地震工程、生物医学等领域有广泛应用，可以帮助人们更好地理解材料的动态行为和力学性能。
在Abaqus中设置梁单元的最大主应变需要注意以下几点：1.确保模型正确建立：在设置最大主应变之前，需要先建立正确的模型，包括正确的梁单元类型、尺寸、材料属性等。
ABAQUS计算矩形截面梁详解版
矩形截面梁有限元分析对下面矩形截面简支梁进行线弹性分析，截面尺寸b ×h ：200×500mm ，跨度L=6m ，跨中受集中荷载F=10kN ，考虑体力，单位体积重量γ=7.85t/m ³，弹性模量E=206×103N/mm 2，泊松比ν=0.3，分别利用8节点6面体块单元和梁/杆单元进行计算分析，并对跨中截面进行解析计算结果和有限元结果作对比。
通过结构力学知识求解 集中荷载F=10kN 作用下两端支座反力为F/2=5kN ，取一半结构对支座求弯矩∑M=0，可求得跨中弯矩大小为FL/4=15kN ．m 。
自重作用下q=γ×b ×h=785kg/m=7.7 kN/m 。
两端支座反力为qL/2=23.1kN ，取一半结构对支座求弯矩∑M=0，可求得跨中弯矩大小为qL 2/8=34.65kN ．m 。
叠加得M max =49.62kN截面上的最大正应力zMyI σ=其中，对于矩形截面2h y =312bh I =得b(mm)h(mm)I(mm 4)M(kN.m)σmax (MPa)200500208333333349.62 5.9544200mm500mm3单位:建议采用国际单位制采用m、kg、N、s国际单位制时，重力加速度9.8m/s2，质量为kg，密度为7850 kg/m3，E=206×109Pa，泊松比ν=0.3，ABAQUS操作打开ABAQUS界面开始→所有程序→ABAQUS6.10-1→ABAQUS CAE，依次出现创建Part创建Part，重新命名liang23，选择三维（3D）可变形体（Deformable）实体（Solid）单元，建模方式选择拉伸（Extrusion），截面的大致尺寸（Approximate site）便于建模，默认即可。
continue继续点击，以坐标的格式创建模型。
依次在中输入（0,0）回车，（-3,0）回车，（-3，-0.5）回车，（0,-0.5）回车，（0,0）回车，点击下图中的或点击一次鼠标中键，继续点击下图中的或点击一次鼠标中键，（注：点击一次鼠标中键等价于）出现如下对话框Depth表示拉伸（Extrusion）距离，取值为0.1，继续，出现下图（此模型为1/4半梁，之所以不一次建好，是为了后续工作中跨中施加一个集中力）点击保存一下（注：ABAQUS不自动保存）文件名（File）取（liang23）继续回到Property（特性）二、进入Module（模块）列表中选择Property（特性）功能模块，出现如下点击，创建材料，出现Name随便命名比如默认的（Material-1），点击，选择下拉菜单Density（密度）取为7850，（注：统一成国际单位7.85t/m3=7850 kg/m3）继续点击（力学特性）选择下拉菜单Elasticity（弹性）→Elastic（弹性）出现在（杨氏模量，即弹性模量）写入206e9，（注：E=206×103N/mm2=206×109Pa），在（泊松比）写入0.3，（注：ν=0.3，）继续创建截面属性，点击，出现（可重命名，也可默认）继续出现继续。
在Abaqus中使用梁单元进行计算
在Abaqus中使用梁单元进行计算在Abaqus中使用梁单元进行计算(2012-03-26 11:28:00)转载▼标签：分类：ABAQUSabaqus梁杂谈xiaozity 助理工程师:在练习老庄的Crane例题时，欲提取梁元的截面应力。
反复折腾后，小小体会，总结如下：（1）书中讲到：“线性梁元B21、B31及二次梁元B22、B32是考虑剪切变形的Timoshenko 梁单元；而三次梁元B23、B33不能模拟剪切变形，属Euler梁单元”。
（2）众所周知，当要考虑剪切变形时，例如深梁，采用Timoshenko梁单元比较合适。
三次梁元由于可模拟轴线方向的三阶变量，因而对static问题，一个构件常常用一个三次单元就足够，特别对于分布载荷的梁，三次梁元的精度相当高。
（3）Abaqus 会默认在积分点处的若干截面点输入应力值；但用户可自定义应力输出的截面点位置，这通过property-section-manage-edit-output points 来定义输出应力值的截面点；（4）特别要指出的是，无论B22还是B33还是其它梁元，其输出的应力分量只有S11，如图所示；那么，现在的问题是：1：S11代表什么应力，根据经验，大家会认为11是1方向的正应力或主应力等等2：为什么没有S22、S33、S12......下面分别说明：1：S11表达的是梁元的弯曲应力，即局部坐标系下截面上的正应力2：只输出S11，而无其它应力，这是因为梁元之所以成为梁元，有一基本前提就是用梁元来模拟的构件，其正应力是最主要的，而剪应力是可忽略的；一个基本的佐证就是：众所周知，在建立梁的总势能方程时，总是讲剪切应变能是小量，因而它总是被忽略掉的；忽略剪应力的一个结果是：mises应力将与S11在数值上完全相同，不仅Abaqus如此，Ansys 也是如此，这也难怪有人讲：“Timoshenko梁单元是骗人的，它根本没有考虑剪应力”；对这件事情，我想作如下评价：（A）不仅Timoshenko梁单元，其它梁元（不考虑剪切变形）确实在应力的层面没有考虑剪应力的影响，这可从mises应力与S11的比较看出来；而为什么这样处理，理由如上所述，剪应力是高阶量，可忽略，否则就认为不能用梁元来模拟。
abaqus经典例题集
abaqus经典例题集下面是一些abaqus的经典例题，以帮助大家更好地理解和掌握这款强大的有限元分析软件。
1.线性弹性问题例题1：在一个长方形平板上施加均匀分布的载荷，求解板的应力和应变。
解题步骤：-创建模型，定义几何参数和材料属性；-划分网格；-应用边界条件；-施加载荷；-求解；- 后处理，查看结果。
2.非线性问题例题2：一个简支梁在受力过程中，梁的横截面半径发生变化。
求解梁的挠度和应力。
解题步骤：-创建模型，定义几何参数、材料属性和边界条件；-划分网格；-应用材料的本构关系；-施加载荷；-求解；- 后处理，查看结果。
3.热力学问题例题3：一个平板在均匀温度差的作用下，求解热应力和温度分布。
解题步骤：-创建模型，定义几何参数、材料属性、边界条件和温度差；-划分网格；-应用热力学本构关系；-施加温度边界条件；-求解；- 后处理，查看结果。
4.耦合问题例题4：一个悬臂梁在受到弯曲应力和剪切应力的同时，还受到温度的变化。
求解梁的应力和温度分布。
解题步骤：-创建模型，定义几何参数、材料属性、边界条件、载荷和温度变化；-划分网格；-应用耦合场本构关系；-施加边界条件、载荷和温度边界条件；-求解；- 后处理，查看结果。
5.接触问题例题5：两个物体相互挤压，求解接触面上的应力和接触力。
解题步骤：-创建模型，定义几何参数、材料属性、边界条件和接触属性；-划分网格；-应用接触算法；-施加边界条件和接触力；-求解；- 后处理，查看结果。
通过以上五个经典例题的讲解，相信大家对abaqus的应用有了更深入的了解。
在实际应用中，我们应根据具体问题选择合适的分析类型，并灵活运用所学知识。
希望大家能在实践中不断提高，成为优秀的有限元分析工程师。
(完整)基于规范和ABAQUS的组合梁承载力计算
基于规范和ABAQUS 的组合梁承载力计算摘 要:分别应用钢结构设计规范公式和有限元软件对完全抗剪连接组合梁的正弯矩区段进行塑性设计,计算其正截面抗弯承载力设计值.通过有限元软件绘出弯矩-跨中位移曲线。
对两种方法的计算结果进行对比,分析误差原因.关键字：组合梁;塑形设计；规范；有限元1 概述本文以一道例题来对比理论计算方法和有限元软件得到正截面抗弯承载力设计值，并分析造成误差的原因,例题如下：某办公楼内一完全抗剪连接组合梁，翼缘板计算宽度e b 为1630mm,板厚c h 为110mm ，混凝土强度等级为C30，轴心抗压强度设计值c f =14.3N/mm 2;钢梁为I32a ，Q235钢，截面面积A 为73.52cm 2。
应用塑性设计法计算组合梁正弯矩截面抗弯承载力设计值u M .如果翼缘板计算宽度e b 为1230mm ，板厚c h 为100mm,混凝土强度等级为C20，计算此时的截面抗弯承载力设计值u M .采用有限元软件对该组合梁进行有限元模拟，要求:（1)采用三等分加载，为保证得出纯弯段的极限承载力，可根据需要自行对剪弯段进行加强；(2）由于是完全抗剪连接,有限元软件计算中可不考虑栓钉作用；（3）通过有限元软件绘出弯矩-跨中位移曲线；（4）有限元混凝土应力—应变关系按《砼规》，钢材应力—应变关系取为理想弹塑性）；（5）有限元分析计算得到的承载力与规范公式计算结果进行对比,分析其差异原因。
2 应用钢结构规范公式对组合梁进行正截面抗弯承载力计算因题中采用的I32a 钢梁不方便计算，现改为以下截面，如图1所示,其面积s A 为73.8cm 2。
图1 组合梁钢梁截面图（1）be =1630mm ，c h =110mm ，混凝土强度等级为C30时： 材料强度设计值混凝土轴心抗压强度设计值c f =14。
3N/mm 2,Q235钢抗拉、抗压强度设计值y f =210N/mm 2。
判断塑性中和轴位置 s 738021015498001549.8y A f N kN =⨯== 163011014.325639902563.99e c c b h f N kN =⨯⨯==s y e c c A f b h f < ,因此中和轴在混凝土受压翼缘板内，如图2所示。
abaqus悬臂梁例题
abaqus悬臂梁例题
ABAQUS是一种常用的有限元分析软件，用于模拟和分析工程结构的行为。
下面是一个简单的ABAQUS悬臂梁的例题，以便说明如何进行有限元分析：
问题描述：
考虑一个简单的悬臂梁，长度为L，截面为矩形，要分析该梁的挠度和应力分布。
步骤：
1.建立模型：首先，在ABAQUS中建立一个新模型。
定义悬臂梁的几何参数，如长度L 和梁截面的宽度和高度。
2.创建网格：划分悬臂梁的几何形状，创建有限元网格。
可以选择合适的单元类型，如梁单元或壳单元，以模拟结构行为。
3.应用边界条件：定义悬臂梁的支持条件，通常悬臂梁的一端是固定支持，另一端是自由端。
在ABAQUS中，你可以定义这些支持条件。
4.施加载荷：定义悬臂梁所受的载荷，如集中力、分布载荷等。
5.设置材料属性：指定悬臂梁所用的材料属性，如弹性模量、泊松比等。
6.运行分析：运行有限元分析，ABAQUS将计算悬臂梁的挠度和应力分布。
7.分析结果：分析完成后，你可以查看和可视化分析结果，包括挠度云图、应力云图等，以了解悬臂梁的行为。
这只是一个简单的悬臂梁分析示例，ABAQUS提供了广泛的功能来进行复杂结构的有限元分析。
具体的模型参数和步骤可能会因实际情况而有所不同。
你可以根据你的具体问题和需求来调整和扩展这个示例。
需要在软件中具体设置和模拟这个问题，以获得详细的分析结果。
ABAQUS计算钢筋混凝土竖向荷载受压
学习abaqus已经有两个月的时间了，对于cae建模也有了一定基础，下面是cae建的钢筋混凝土在竖向荷载下受弯的一个例子和大家分享下。
尺寸图如下：Abaqus计算过程：1 创建部件（part）1.1创建混凝土部件(1)点击左侧的create part，弹出的对话框中，填写如图1-1所示；分别选择三维，实体，拉伸，大约尺寸为3000，点击continue，进去二维绘图区。
(2)点击做左侧的create lines，输入4个坐标，依次为（-1250,0），（-1250,300），（1250,300），（1250,0），完成如1-2所示尺寸的长方体。
(3)生成三维实体，在绘图区点击鼠标中键，弹出对话框中，将Depth设为150，点击ok，即形成尺寸为2500（长）×150（宽）×300（高）的立方体。
如图1-3所示。
图1-1如1-2所示二维长方体如1-3所示三维长方体1.2创建垫块部件（1）画出二维实体图，create part设置同上，选择create lines，依次输坐标（0,0），（0,60），（200,60），（200,0），（0，0），具体尺寸如图1-4。
(2)生成三维实体，在绘图区点击鼠标中键，弹出对话框中，将Depth设为150，点击ok，即形成尺寸为2500（长）×150（宽）×60（高）的立方体。
如图1-5所示。
如1-4所示垫块二维如1-5所示垫块三维实体1.3 创建plate2方法同前，几何坐标为（0,0），（0,60），（100,60），（100,0），如图1-6，三维模型如图1-7。
如1-6所示plate2的二维如1-7所示plate2的三维实体1.4 创建箍筋（1）点击左侧的create part，弹出的对话框中，填写如图1-8所示，注意shape形式为wire （2）输入几何坐标（0,35），（0,265），（80,265），（80,35），（0,35），二维如图1-9图1-8所示箍筋part图1-9所示箍筋二维1.5 创建受压筋注意shape形式为wire，输入坐标（-1225，265），（1225,265）三维图1-10图1-10所示受压筋三维1.6 创建受拉筋方法同前，输入坐标（-1225，35），（1225,35）三维图1-11图1-10所示受拉筋三维2 创建材料和截面属性（proprety）2.1混凝土本构点击左侧的create material，name为concrete，点击mechanical，elastic，填写杨氏模量为29500mpa，泊松比为0.3，如图2-1。
abaqus梁单元后处理截面积
abaqus梁单元后处理截面积梁单元在有限元分析中是一种常用的元素类型，用于模拟梁在结构中的力学行为。
在abaqus中，梁单元可以用来分析结构中的梁、悬臂梁和桁架等构件。
在进行有限元分析后处理时，截面积是一个重要的参数，可以用来评估梁的承载能力和受力情况。
本文将对abaqus梁单元后处理截面积进行详细介绍，包括截面积的计算方法、影响因素以及在实际工程中的应用。
一、梁单元及其截面积的计算方法1.梁单元的基本原理梁单元是结构分析中常用的一种有限元元素，用于模拟梁在结构中的受力情况。
在有限元分析中，梁单元通常由两个节点和一组单元材料构成，可以模拟梁在结构中的变形和受力行为。
梁单元的理论基础源于梁理论和有限元方法，通过对梁单元的受力、变形和材料性质等进行建模，可以对梁的力学行为进行分析和计算。
2.截面积的计算方法在abaqus中，梁单元的截面积可以通过以下公式进行计算：A = b * h其中，A表示截面积，b表示梁的宽度，h表示梁的高度。
在实际应用中，梁的截面通常是矩形、圆形或其他形状，可以根据具体的结构形式和设计要求来确定梁的截面积。
二、影响梁截面积的因素1.结构形式梁的截面积受到结构形式的影响，不同的结构形式需要具有不同截面积的梁来承受相应的荷载。
例如，在悬臂梁和桁架中，梁的截面积通常需要更大，以满足其承载能力和刚度的要求。
2.荷载情况梁的截面积还受到荷载情况的影响，不同的荷载情况需要不同截面积的梁来承受。
例如，在承受较大弯矩和剪力的情况下，梁的截面积需要更大，以确保结构的安全性和稳定性。
3.材料性质梁的材料性质对其截面积也有影响，不同材料的梁在相同受力情况下需要不同截面积来保证其承载能力。
例如，在使用高强钢材料时，梁的截面积可以相对较小，而在使用低强度材料时，梁的截面积需要更大。
三、梁单元截面积在实际工程中的应用1.结构设计与优化梁单元截面积的计算是结构设计与优化的重要环节，通过合理确定梁的截面积可以满足结构的强度、刚度和稳定性要求，从而提高结构的安全性和经济性。
ABAQUS模拟塑性铰
工程概况
超静定梁结构见图1，梁长L=10m，横截面为矩形，尺寸为 0.1m×0.2m；材料为理想弹塑性，结构右端约束竖直方向， 左端为固支边界条件；跨中受集中力荷载作用。
FP
l/2 l/2
图1 梁结构布置图
理论分析
bh2 0.1 0.2 2 Mu s 200 200kN m 4 4
Fpu 6 6 M u 200 120 kN l 10
理论极限荷载为120kN
有限元分析
材料参数
E 200GGPa
0.3
Y 200MPa
F=100kN
出现塑性区域
F=112.5kN
固定端出现塑性铰
F=120kN
梁中部出现塑性铰
F=122kN
达到极限荷载
中性轴应力分布图
中性轴塑性应变分布图
方法对比
有限元方法
极限荷载 122
理论方法120相对误差 Nhomakorabea1.7%
（kN）
有限元方法与理论方法相差较小，故有限元方法 可以较为精确地求解塑性铰问题。
ABAQUS简支梁分析(梁单元和实体单元)
基于ABAQUS简支梁受力和弯矩的相关分析（梁单元和实体单元）对于简支梁，基于 ABAQUS2016，首先用梁单元分析了梁受力作用下的应力，变形，剪力和力矩；对同一模型，并用实体单元进行了相应的分析。
另外，还分析了梁结构受力和弯矩作用下的剪力及力矩分析。
对于CAE仿真分析具体细节操作并没有给出详细的操作，不过在后面上传了对应的cae，odb，inp文件。
不过要注意的是本文采用的是ABAQUS2016进行计算，低版本可能打不开，可以自己提交inp文件自己计算即可。
可以到小木虫搜索：“基于ABAQUS简支梁受力和弯矩的相关分析”进行相应文件下载。
对于一简支梁，其结构简图如下所示，梁的一段受固支，一段受简支，在梁的两端受集中载荷，梁的大直径D=180mm，小直径d=150mm，a=200mm，b=300mm，l=1600mm，F=300000N。
现通过梁单元和实体单元分析简支梁的受力情况，变形情况，以及分析其剪力和弯矩等。
材料采用45#钢，弹性模量E=2.1e6MPa，泊松比v=0.28。
图1 简支梁结构简图1.梁单元分析ABAQUS2016中对应的文件为beam-shaft.cae ，beam-shaft.odb，beam-shaft.inp。
在建立梁part的时候，采用三维线性实体，按照图1所示尺寸建立，然后在台阶及支撑梁处进行分割，结果如图2所示。
图2 建立part并分割接下来为梁结构分配材料，创建材料，定义弹性模量和泊松比，创建梁截面形状，如图3，非别定义两个圆，圆的直接分别为180和150mm。
然后创建两个截面，截面选择梁截面，再选择图2中的所有梁，定义梁的方向矢量为（0，0，-1）（点击图3中的n2，n1，t那个图标即可创建梁的方向矢量），最后把创建好的梁赋给梁结构。
图3 创建梁截面形状接下来装配实体，再创建分析步，在创建分析步的时候，点击主菜单栏的Output，编辑Edit Field Output Request，在SF前面打钩，这样就可以在结果后处理中输出截面剪力和力矩，如图4所示。
abaqus梁单元后处理截面积
abaqus梁单元后处理截面积Abaqus梁单元是有限元分析软件Abaqus/Explicit和Abaqus/Standard中的一种元素类型。
它可以用来对梁结构进行静力和动力分析，常见的应用包括钢结构、混凝土结构、木质结构等。
梁单元在实际工程中的应用十分广泛，是工程结构分析中不可或缺的一部分。
梁单元后处理中的截面积是很重要的一个参数，它可以用来计算梁的承载能力、挠度、应力等重要性能指标。
本文将结合Abaqus梁单元的相关理论知识，详细介绍梁单元后处理截面积的计算方法，并探讨其在工程实践中的应用。
一、Abaqus梁单元的理论基础Abaqus梁单元是基于梁理论的有限元素，它考虑了梁的几何非线性、材料非线性和大变形效应。
在Abaqus中，梁单元可以分为三种类型：轴对称梁单元、平面梁单元和空间梁单元，它们分别适用于不同的工程分析场景。
梁单元的基本假设是梁的截面保持平面，横截面内的应力和应变保持线性分布。
根据梁单元的基本理论，可以得到梁的截面积在后处理中的重要性质，包括截面面积、截面惯性矩、截面模量等参数。
二、梁单元后处理截面积的计算方法在Abaqus中，可以通过使用相关后处理命令来获取梁单元的截面积。
以Abaqus/CAE为例，可以通过菜单栏中的“Visualization”->“Internal Forces”->“Section Forces”来获取梁单元的截面应力、截面力和截面应变等参数。
在上述步骤中，首先需要选择要进行截面分析的梁单元，然后选择所需的后处理参数，并进行计算。
通过这些步骤，可以获取梁单元的截面积及其相关参数，用于后续的工程分析和设计。
三、梁单元后处理截面积的工程应用梁单元后处理截面积的工程应用非常广泛，它可以用来评估梁的承载能力、疲劳寿命、挠度、应力分布等重要性能指标。
在实际工程中，工程师可以通过对梁单元的截面积进行分析和计算，来评估梁的受力性能，并进行必要的结构优化和改进。
ABAQUS混凝土框架有限元计算分析
ABAQUS混凝土框架有限元计算分析混凝土框架是指由多个混凝土构件组成的结构，如梁、柱、板等。
ABAQUS可以对这些构件进行建模，并进行结构强度、刚度和变形等的分析。
以下是一些常见的ABAQUS混凝土框架有限元计算分析的应用：1.强度分析：ABAQUS可以对混凝土框架进行强度分析，包括承载能力和极限状态的评估。
通过施加荷载，可以模拟结构发生破坏的情况，并计算结构在不同荷载水平下的承载能力。
这对于评估结构的安全性和合理设计具有重要意义。
2.变形分析：ABAQUS可以模拟混凝土框架在加载过程中的变形情况。
通过施加荷载，可以计算结构在不同荷载水平下的变形和位移。
这对于评估结构的稳定性、变形控制和结构设计具有重要意义。
3.动力响应分析：ABAQUS可以对混凝土框架进行动力响应分析，包括模拟结构在地震、风载等外部激励下的振动和响应。
这可以帮助工程师评估结构的抗震能力、动态特性和响应特性。
4.疲劳分析：ABAQUS可以模拟混凝土框架在反复加载条件下的疲劳行为。
通过施加循环荷载，可以计算结构在不同循环次数下的疲劳寿命和疲劳破坏情况。
这对于评估结构的耐久性和疲劳寿命具有重要意义。
5.温度分析：ABAQUS可以模拟混凝土框架在温度变化下的热应力和变形。
通过施加不同温度梯度，可以计算结构在不同温度变化下的热应力和热变形。
这对于评估结构的热稳定性、温度控制和材料性能具有重要意义。
ABAQUS混凝土框架有限元计算分析需要进行合适的建模和网格划分。
首先，工程师需要确定需要模拟的混凝土结构的几何形状和尺寸。
然后，可以使用ABAQUS提供的建模工具，如宏命令语言（Python）、预处理器和后处理器，进行建模和后续分析。
在建模过程中，需要注意选择合适的单元类型和材料模型。
对于混凝土结构，常用的单元类型包括网格单元、梁单元、细胞单元等。
材料模型可以根据需要选择弹性、塑性、损伤等模型。
此外，还需要设置适当的边界条件和加载条件，以模拟实际工况。
ABAQUS简支梁分析（梁单元和实体单元）
ABAQUS简⽀梁分析（梁单元和实体单元）基于ABAQUS简⽀梁受⼒和弯矩的相关分析（梁单元和实体单元）对于简⽀梁，基于 ABAQUS2016，⾸先⽤梁单元分析了梁受⼒作⽤下的应⼒，变形，剪⼒和⼒矩；对同⼀模型，并⽤实体单元进⾏了相应的分析。
另外，还分析了梁结构受⼒和弯矩作⽤下的剪⼒及⼒矩分析。
对于CAE仿真分析具体细节操作并没有给出详细的操作，不过在后⾯上传了对应的cae，odb，inp⽂件。
不过要注意的是本⽂采⽤的是ABAQUS2016进⾏计算，低版本可能打不开，可以⾃⼰提交inp⽂件⾃⼰计算即可。
可以到⼩⽊⾍搜索：“基于ABAQUS简⽀梁受⼒和弯矩的相关分析”进⾏相应⽂件下载。
对于⼀简⽀梁，其结构简图如下所⽰，梁的⼀段受固⽀，⼀段受简⽀，在梁的两端受集中载荷，梁的⼤直径D=180mm，⼩直径d=150mm，a=200mm，b=300mm，l=1600mm，F=300000N。
现通过梁单元和实体单元分析简⽀梁的受⼒情况，变形情况，以及分析其剪⼒和弯矩等。
材料采⽤45#钢，弹性模量E=2.1e6MPa，泊松⽐v=0.28。
图1 简⽀梁结构简图1.梁单元分析ABAQUS2016中对应的⽂件为beam-shaft.cae ，beam-shaft.odb，beam-shaft.inp。
在建⽴梁part的时候，采⽤三维线性实体，按照图1所⽰尺⼨建⽴，然后在台阶及⽀撑梁处进⾏分割，结果如图2所⽰。
图2 建⽴part并分割接下来为梁结构分配材料，创建材料，定义弹性模量和泊松⽐，创建梁截⾯形状，如图3，⾮别定义两个圆，圆的直接分别为180和150mm。
然后创建两个截⾯，截⾯选择梁截⾯，再选择图2中的所有梁，定义梁的⽅向⽮量为（0，0，-1）（点击图3中的n2，n1，t那个图标即可创建梁的⽅向⽮量），最后把创建好的梁赋给梁结构。
图3 创建梁截⾯形状接下来装配实体，再创建分析步，在创建分析步的时候，点击主菜单栏的Output，编辑Edit Field Output Request，在SF前⾯打钩，这样就可以在结果后处理中输出截⾯剪⼒和⼒矩，如图4所⽰。
ABAQUS应用梁单元计算简支梁
ABAQUS应用梁单元计算简支梁梁是一种常用的结构元素，广泛应用于建筑、桥梁、机械等领域中。
在工程实践中，经常需要对梁进行计算分析，以确定其受力状态和变形情况。
ABAQUS是一种常用的有限元分析软件，可以用于求解梁结构的力学问题。
本文将介绍如何使用ABAQUS进行简支梁的计算分析。
首先，我们需要将梁模型导入ABAQUS软件中。
梁的几何形状可以使用线、点或者直接输入坐标点的方式进行定义。
梁的截面信息（如截面类型、尺寸等）也需要进行定义。
在ABAQUS中，可以选择多种截面类型，例如矩形、圆形等。
根据实际情况选择合适的截面类型，并根据设计要求输入相应的尺寸。
在模型定义完成后，需要定义边界条件。
对于简支梁而言，端点处的位移应设定为零。
在ABAQUS中，可以通过选择固定边界条件或者施加等效约束条件来实现。
选择固定边界条件需要定义节点的自由度受限情况，而施加等效约束条件则可以直接将节点的位移限制为零。
在定义了几何形状、截面信息和边界条件后，需要定义材料参数。
梁的弹性模量、泊松比和密度等参数需要根据实际材料性质进行设定。
在ABAQUS中，可以选择多种材料模型，例如线弹性模型、双线性弹塑性模型等。
根据实际需求选择合适的材料模型，并输入相应的参数。
模型导入并定义完毕后，需要进行网格划分。
在ABAQUS中，可以选择多种网格划分算法，例如四边形单元、六面体单元等。
根据实际需求选择合适的网格划分算法，并根据划分精度设定网格尺寸。
在进行网格划分时，需要注意保证梁模型的几何形状和截面信息的精确性，避免过度简化导致计算结果的不准确。
完成网格划分后，可以进行加载条件的定义。
在ABAQUS中，可以定义多种加载条件，例如集中力、均布载荷等。
根据实际需求选择合适的加载条件，并输入相应的加载参数。
完成加载条件的定义后，可以进行求解运算。
在ABAQUS中，可以选择静力分析或者动力分析方法进行求解。
根据实际需求选择合适的求解方法，并进行计算。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Abaqus梁结构经典计算
一榀轻钢结构库房框架，结构钢方管构件，材质E=210GPa，μ=，
ρ=7850kg/m3（在不计重力的静力学分
析中可以不要）。
F=1000N，此题要计入重力。
计算水平梁中点下降位移。
文件与路径
顶部下拉菜单File, Save As ExpAbq02。
一部件
创建部件，命名为Prat-1。
3D，可变形模型，线，图形大约范围20(m)。
选用折线绘出整个图示屋架。
退出Done。
二性质
1 创建截面几何形状：Module，Property，Create Profile，
将截面(1)命名为Profile-1，选Box型截面，按图输入数据，关闭。
直至完成截面(3)。
2 定义各段梁的方向：
选中所有立杆，输入截面主惯性轴1方向单位矢量(1,0,0)，选中横梁和斜杆，输入截面主轴1方向单位矢量(0,1,0)，关闭。
还有好办法，请大家自己捉摸。
3 定义截面力学性质：
将截面(1) Profile-1命名为Section-1，梁，梁，截面几何形状选
Profile-1，输入E=210GPa，G=，ν=，ρ=7850，关闭。
直至完成截面(3) Section-3。
4 将截面的几何、力学性质附加到部件上：
选中左右立柱和横梁，将各Section-1~3信息注入Part-1的各个杆件上，要对号入座。
5 保存模型：
将本题的CAE模型保存为。
三组装
创建计算实体，以Prat-1为原形，用Independent方式或Dependent生成实体。
四分析步
创建分析步，命名为Step-1，静态Static，通用General。
注释：无，时间：不变，非线性开关：关。
五载荷
1 施加位移边界条件：
命名为BC-1，在分析步Step-1中，性质：力学，针对位移和转角。
选中立柱两脚，约束全部自由度。
2 创建载荷：
命名为Load-1，在分析步Step-1中，性质：力学，选择集中力。
选中顶点，施加Fy=F2=-1000(N)。
六网格
对部件Prat-1进行。
1 撒种子：
针对部件，全局种子大约间距。
2 划网格：
针对部件，OK。
3 保存你的模型：
将本题的CAE模型保存为。
七建立项目
命名为ExpAbq02，选择完整分析，其余不变，OK。
八观察结果
1 看图：
打开结果文件，看位移图。
2 看数据：
显示某节点结果数据，例如水平梁中点垂直位移。
3 保存你的模型：
将本题的CAE模型保存为。