第1课时 位似图形.ppt
合集下载
27.3+第1课时+位似图形的概念及画法 课件+-2023--2024学年人教版数学九年级下册
OA
练习1:如何判断一组图形是位似图形呢?下面各组图 形是位似图形吗?
答:都是位似图形 总结:同时满足这两个条件的图形叫做位似图 形.两个条件缺一不可。 一是:两个相似图形 二是:对应顶点的连线相交
于一点.
练习2:画出下列图形的位似中心.
P O
知识点 2 位似图形的性质
合作探究
活动1:位似图形和相似图形有怎样的区别与联系呢?
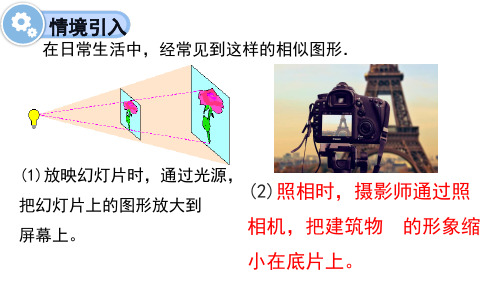
情境引入
在日常生活中,经常见到这样的相似图形.
(1)放映幻灯片时,通过光源,
(2)照相时,摄影师通过照
把幻灯片上的图形放大到
屏幕上。
相机,把建筑物 的形象缩
小在底片上。
第二十七章 相 似
27.3 位 似
第1课时 位似图形的概念及画法
学习目标
1.理解位似图形的概念及相似比.
图 形 2.能够按照要求利用位似图形进行放大或缩小.
A
A'
C
C'
O
B
B'
练习:如图,四边形木框 ABCD 在灯泡 O 发出的光照
射下形成影子四边形 A′B′C′D′,若 OB∶OB′=1∶2,
则四边形 ABCD 与四边形 A′B′C′D′ 的面积比为 ( D )
A.4∶1
B. 2∶1 C.1∶ 2 D.1∶4
A'
A
灯泡 O
B B'
D
C
D'
C'
知识点 3 位似图形的画法
A' D'
D
A'B'C'D' 就是所要求的图O 形. B'
B
C'
C
(2)对于上面的问题,还有其他方法吗?如果在四边
练习1:如何判断一组图形是位似图形呢?下面各组图 形是位似图形吗?
答:都是位似图形 总结:同时满足这两个条件的图形叫做位似图 形.两个条件缺一不可。 一是:两个相似图形 二是:对应顶点的连线相交
于一点.
练习2:画出下列图形的位似中心.
P O
知识点 2 位似图形的性质
合作探究
活动1:位似图形和相似图形有怎样的区别与联系呢?
情境引入
在日常生活中,经常见到这样的相似图形.
(1)放映幻灯片时,通过光源,
(2)照相时,摄影师通过照
把幻灯片上的图形放大到
屏幕上。
相机,把建筑物 的形象缩
小在底片上。
第二十七章 相 似
27.3 位 似
第1课时 位似图形的概念及画法
学习目标
1.理解位似图形的概念及相似比.
图 形 2.能够按照要求利用位似图形进行放大或缩小.
A
A'
C
C'
O
B
B'
练习:如图,四边形木框 ABCD 在灯泡 O 发出的光照
射下形成影子四边形 A′B′C′D′,若 OB∶OB′=1∶2,
则四边形 ABCD 与四边形 A′B′C′D′ 的面积比为 ( D )
A.4∶1
B. 2∶1 C.1∶ 2 D.1∶4
A'
A
灯泡 O
B B'
D
C
D'
C'
知识点 3 位似图形的画法
A' D'
D
A'B'C'D' 就是所要求的图O 形. B'
B
C'
C
(2)对于上面的问题,还有其他方法吗?如果在四边
【人教版九年级数学下册】第二十七章27.3 第1课时 位似图形的概念及画法 精品课件

6. 如图,F 在 BD 上,BC、AD 相交于点 E,且 AB∥CD∥EF, (1) 图中有哪几对位似三角形? 选其中一对加 以证明; 答案:△DFE 与 △DBA,△BFE 与 △BDC, △AEB 与 △DEC 都是位似图形;证明略.
(2) 若 AB=2,CD=3,求 EF 的长. 解:∵ △BFE ∽△BDC,△AEB ∽△DEC, AB=2,CD=3, BE EF 2 AB BE 2 , ,∴ ∴ BC DC 5 DC EC 3
3. 下列说法: ①位似图形一定是相似图形;②相似图形一定是位 似图形;③两个位似图形若全等,则位似中心在两 个图形之间;④若五边形ABCDE与五边形 A′B′C′D′E′位似,则其中 △ABC 与 △A′B′C′ 也是位 似的,且位似比相等. 其中正确的有 . ①④
4. 如图,△ABC与△DEF是位似图形,位似比为 2 : 3,已知 AB=4,则 DE 的长为_____ 6 .
O
三 画位似图形
例1 把四边形 ABCD 缩小到原来的 1/2. (2) OA 、 OB 、 OC 、 B'B' (3) 顺次连接点 A' 、 B' 、 C' D'OD ,所得四边形 A' (1) 分别在线段 在四边形外任选一点 O (、 如图 ) ;上取点 A' 、 OA' OB' OC' OD' 1 、 C' D' 就是所要求的图形. OA OB OC OD 2 C' 、D' ,使得 ; 利用位似,可 A 以将一个图形 D 放大或缩小 B A' B' D' C C' O
一 位似图形的概念
第1课时 位似图形课件北师大版数学九年级上册

相似比叙述正确的是( C )
A. 位似中心是点 B ,相似比是2∶1
B. 位似中心是点 D ,相似比是2∶1
C. 位似中心在点 G , H 之间,相似比为2∶1
D. 位似中心在点 G , H 之间,相似比为1∶2
第2题图
1 2 3 4 5 6 7 8 9 10 11 12 13
第1课时 位似图形
基础通关 能力突破 素养达标
第1课时 位似图形
(3)求 AP 的长; (3)解:△ ADP 与△ BCP 不是位似图形, ∵直线 AB 与直线 DC 的交点不是点 P .
基础通关 能力突破 素养达标
1 2 3 4 5 6 7 8 9 10 11 12 13
第1课时 位似图形
基础通关 能力突破 素养达标
12.
视力表用来测量一个人的视力情况,如图是视力表的一部
1 2 3 4 5 6 7 8 9 10 11 12 13
第1课时 位似图形
基础通关 能力突破 素养达标
【解析】如图,连接 BO 并延长,延长线经过点 M , Q , 且 MO =2 BO , ∴以点 O 为位似中心,把△ ABC 放大为原来的2倍, 点 B 的对应点为点 M .
1 2 3 4 5 6 7 8 9 10 11 12 13
(1)证明:∵∠ DAP =∠ CBP ,∠ DPA =∠ CPB , ∴△ ADP ∽△ BCP .
1 2 3 4 5 6 7 8 9 10 11 12 13
第1课时 位似图形
基础通关 能力突破 素养达标
(2)△ ADP 与△ BCP 是不是位似图形?为什么?
1 2 3 4 5 6 7 8 9 10 11 12 13
第6题图
1 2 3 4 5 6 7 8 9 10 11 12 13
《27.3 第1课时 位似图形的概念及画法》课件(三套)

作法一:(1)在四边形ABCD外任取一点O; (2)过点O分别作射线OA,OB,OC,OD; (3)分别在射线OA,OB,OC,OD上取点 A′、B′、C′、D′, 使得 OA OB OC OD 1
OA OB OC OD 2
(4)顺次连结A′B′、B′C′、C′D′、D′A′,得到所要画 的四边形A′B′C′D′,如图2.
把右图中的五边形ABCDE扩大到原来的2倍。
练 A
一B
E
练 C
●
O D
D` ●
`E ●
`●
A
●
C`
●
B`
四、归纳小结
1、如果两个图形不仅是相似图形,而且是每组对 应点连线相交于 一点 ,对应边互相 平行 ,那么 这样的两个图形叫做__位__似__图_形__.这个点叫 做 位似中心 .
2、利用位似进行作图的关键是确定_位__似_中__心 _和 _关__键__点____.
第二十七章 相似 27.3 位似
第1课时 位似图形的概念及画法
一、新课引入 1、我们学过的图形变换形式有哪些?
平移、旋转、对称
2、什么叫相似?相似与全等有什么区别与联系? 相似:形状相同。 全等:大小、形状相同,能够重合 区别:相似不一定全等,但全等一定相似。 联系:形状相同
二、学习目标
1 了解位似图形及其有关概念,了解 位似与相似的联系和区别,掌握位 似图形的性质;
解析:由题意得,五边形ABCDE与五边形A′B′C′D′E′ 是位似图形,所以五边形ABCDE与五边形A′B′C′D′E′ 相似,所以它们的周长的比等于对应边的比,即等于
OA 10 1 . OA 20 2
答案:1
2
通过这节课的学习,你有哪些收获? 1.如果两个相似图形的每组对应点所在的直线都交于一点, 对应边平行,那么这样的两个图形叫做位似图形, 这个交 点叫做位似中心, 这时两个相似图形的相似比又叫做它们 的位似比. 2.位似图形的对应点和位似中心在同一条直线上,它们到 位似中心的距离之比等于位似比.
初中数学《图形的位似》_PPT完整版【北师大版】1

初中数学《图形的位似》教学分析北 师大版1 -精品 课件ppt (实用 版)
初中数学《图形的位似》教学分析北 师大版1 -精品 课件ppt (实用 版)
课堂小结 ❖ 位似图形的概念:
如果两个图形不仅形状相同,而且所在的 直线都经过同一个点,那么这样的两个图形叫 做位似图形,这个点叫做位似中心,这时的相 似比又称为位似比. ❖ 位似图形的性质: 1.位似图形是相似图形,具备相似图形的所 有性质 2.位似图形上的任意一对对应点到位似中心 的距离之比等于位似比
似多边形,点O叫做位似中心.其中k为相似多边形的相似比.
下面两组也位似多边形.
初中数学《图形的位似》教学分析北 师大版1 -精品 课件ppt (实用 版)
初中数学《图形的位似》教学分析北 师大版1 -精品 课件ppt (实用 版)
例1:如图,已知△ABC,以点O为位似中心画△DEF,使其与△ABC
初中数学《图形的位似》教学分析北 师大版1 -精品 课件ppt (实用 版)
初中数学《图形的位似》教学分析北 师大版1 -精品 课件ppt (实用 版) 初中数学《图形的位似》教学分析北 师大版1 -精品 课件ppt (实用 版)
将黄色五角星缩 小为原来的一半
。
。
。。
。
。
。
。
。
O
。
。
初中数学《图形的位似》教学分析北 师大版1 -精品 课件ppt (实用 版)
• 1.若△ABC与△A’B’C’的相似比为:
1:2,则OA:OA’=( 1:2 A’ )。
A
B
B’
O
C
C’
性质:位似图形上任意一对对应点到位似中心的距离 之比等于相似比.
初中数学《图形的位似》教学分析北 师大版1 -精品 课件ppt (实用 版)
第1课时 位似图形及其画法(教材配套课件)

所以 S 四边形 = BCDE 25 S 四边形 = B′C′D′E′ 25 ×18=50.
9
9
·数学
1.下列各组图形中,不是位似图形的是( B )
2.已知△ABC,以点A为位似中心,作出△ADE,使△ADE是△ABC放大2倍的图形,这 样的图形可以作出( B ) (A)1个 (B)2个 (C)4个 (D)无数个
AB
AC AB
同理可得, AE = AD = AC = AB =k,
AE AD AC AB
又因为四边形 BCDE 与四边形 B′C′D′E′的对应顶点相交于一点 A, 所以四边形 BCDE 与四边形 B′C′D′E′是位似图形.
·数学
(2)若 AB = 3 ,S 四边形 B′C′D′E′=18,求 S 四边形 BCDE.
或一边上,也可
能在两个图形的 一侧 或中间.
(2)位似图形上任意一对对应点到位似中心的距离之比等于 相似比 .
(3)每组对应点的连线都经过 位似中心
.
·数学
探究点一:位似图形的画法 【例 1】如图,已知▱ABCD 及一点 O,以点 O 为位似中心,将▱ABCD 缩小为原来的 1 .
2
·数学
【导学探究】 1.▱ABCD 的位似图形与▱ABCD 分别在点 O 的 同
BB 2 【导学探究】 2.四边形BCDE与四边形B′C′D′E′的相似比为 为 25∶9 .
5∶3
,面积比
解:(2)因为 AB = 3 ,所以 AB = 3 ,所以四边形 BCDE 与四边形 B′C′D′E′
BB 2
AB 5
的相似比为 5∶3,面积比为 25∶9,因为 S 四边形 B′C′D′E′=18,
·数学
九年级数学上册3.6位似第1课时位似图形的概念及画法教学课件(新版)湘教版
A.'
A
O.
B
C
B’
C’
OA:OA’ =OB:OB’ =OC:OC’= 1:2
第十五页,共19页。
思考:还有没其他(qítā)作法?
C’
B’
A
. O
B
C
A'
如果(rúguǒ)位似中心跑到三角形内部呢?
你会了吗?
第十六页,共19页。
课堂小结
回味无穷 (huí wèi
• 位似图形的概念:
wú qióng)
来的2倍?
E
B
O
C
F
D
A
D
B
O
C
F
A
E
对应点连线(lián xiàn位)都似交中于心____________
对应(duìyìng)平线行段或__在___一__条__直__线__上__________________
第十四页,共19页。
练习与拓展
1.如图,已知△ABC和点O.以O为位似中心,求作△ABC 的位似图形(túxíng),并把△ABC的边长扩大到原来的两倍.
3.6 位 似 第1课时(kèshí) 位似图形的概念
及画法
第一页,共19页。
新课导入
这种相似有什 么(shén me)特
征?
相似(xiānɡ sì)图形
第二页,共19页。
相似(xiānɡ sì)图 形
这种相似有什 么(shén me)特
征?
第三页,共19页。
相似(xiānɡ sì) 图形
照相机把人物的影像 (yǐnɡ xiànɡ)缩小到底片
上
这种相似 (xiānɡ sì)有什
么特征?
第四页,共19页。
A
O.
B
C
B’
C’
OA:OA’ =OB:OB’ =OC:OC’= 1:2
第十五页,共19页。
思考:还有没其他(qítā)作法?
C’
B’
A
. O
B
C
A'
如果(rúguǒ)位似中心跑到三角形内部呢?
你会了吗?
第十六页,共19页。
课堂小结
回味无穷 (huí wèi
• 位似图形的概念:
wú qióng)
来的2倍?
E
B
O
C
F
D
A
D
B
O
C
F
A
E
对应点连线(lián xiàn位)都似交中于心____________
对应(duìyìng)平线行段或__在___一__条__直__线__上__________________
第十四页,共19页。
练习与拓展
1.如图,已知△ABC和点O.以O为位似中心,求作△ABC 的位似图形(túxíng),并把△ABC的边长扩大到原来的两倍.
3.6 位 似 第1课时(kèshí) 位似图形的概念
及画法
第一页,共19页。
新课导入
这种相似有什 么(shén me)特
征?
相似(xiānɡ sì)图形
第二页,共19页。
相似(xiānɡ sì)图 形
这种相似有什 么(shén me)特
征?
第三页,共19页。
相似(xiānɡ sì) 图形
照相机把人物的影像 (yǐnɡ xiànɡ)缩小到底片
上
这种相似 (xiānɡ sì)有什
么特征?
第四页,共19页。
人教版第二学期数学九年级下 27.3 位似第1课时 位似图形的概念及画法课件(共20张PPT)
E′
D′
D
E
O
A
A′
B
C′
A
C
B′
C′
O
B
C
B′
A′
归纳:
1. 位似图形的对应角相等,对应边成比例,周长比
等于相似比,面积比等于相似比的平方;
2. 位似图形的对应点的连线相交于一点,即经过位似中心;
3. 位似图形的对应边互相平行或在同一条直线上;
4. 位似图形上任意一对对应点到位似中心的距离之比等
于相似比.
例2 如图所示,四边形ABCD 和四边形A′ B′ C′ D′位似,相似比1 = 2,四边
形A′ B′ C′D′和四边形A″ B″ C″D″位似,相似比2 = 1. 则四边形A″ B″ C″ D″
和四边形ABCD 是位似图形吗?如果是,请说明理由并求出相似比.
解:∵ 四边形ABCD 和四边形A′ B′ C′ D′位似,
E
OD;在射线OA、OB、OC、
H
A
OD上分别取点D、E、F,使
D
O
B
C
OE = 2OA , OF = 2OB , OG =
2OC , OH = 2OD;顺次连结E、
F、G、H,使正方形ABCD与
F
G
5.如图所示,四边形ABCD的一个位似图形是四边形A′ B′ C′ D′ ,
且A,B,C,D的对应点分别是A′ ,B′ ,C′ ,D′. 图中给出了AB的对应
似中心的位似图形,且
′
=
=
′
′
=
′
;五边形ABCDE 与五
边形A′ B′ C′ D′ E′是以点O 为位似中心的位似图形,且′ = ′ =
人教版九年级下册 27.3 第1课时 位似图形的概念及画法26张PPT
第二十七章
相
似
27.3 位 似
第1课时 位似图形的概念及画法
学习目标
1. 掌握位似图形的概念、性质和画法. (重点)
2. 掌握位似与相似的联系与区别. (难点)
检查预习
1.位似图形的定义
2.相似图形与位似图形有什么相同点与不同点? 3.位似图形有什么性质? 4.如何画位似图形?
导入新课
图片引入 如图,是幻灯机放映图片的示意图,在幻灯机 放映图片的过程中,这些图片之间有什么关系? 连接图片上对应的点,你有什么发现?
A
A. 2 DE = 3 MN C. 3∠A = 2∠F
B. 3 DE = 2 MN D. 2∠A = 3∠F
3. 下列说法: ①位似图形一定是相似图形;②相似图形一定是位 似图形;③两个位似图形若全等,则位似中心在两 个图形之间;④若五边形ABCDE与五边形A′B′C′D′E′ 位似,则其中 △ABC 与 △A′B′C′ 也是位似的,且位 似比相等. 其中正确的有 ①④ .
练一练1:判断下列各对图形哪些是位似图形,哪些不是. (3)正五边形ABCDE与正五边形A′B′C′D′E′;五边 形ABCDE与五边形A′B′C′D′E′;
(2)在平行四边形ABCD中,△ABO与△CDO
2.判断下面的正方形是不是位似图形?
A D
不是
E (1) B C F G
显然,位似图形是相似图形的特殊情形.相似图形不 一定是位似图形,可位似图形一定是相似图形
想一想
• 3.你能作出下列位似图形的位似中心吗?:
O
O
二Hale Waihona Puke 位似图形的性质思考 如图,D,E分别是△ABC的边AB,AC上的点, (1)如果DE ∥ BC则△ADE与△ABC是位似图形吗?
相
似
27.3 位 似
第1课时 位似图形的概念及画法
学习目标
1. 掌握位似图形的概念、性质和画法. (重点)
2. 掌握位似与相似的联系与区别. (难点)
检查预习
1.位似图形的定义
2.相似图形与位似图形有什么相同点与不同点? 3.位似图形有什么性质? 4.如何画位似图形?
导入新课
图片引入 如图,是幻灯机放映图片的示意图,在幻灯机 放映图片的过程中,这些图片之间有什么关系? 连接图片上对应的点,你有什么发现?
A
A. 2 DE = 3 MN C. 3∠A = 2∠F
B. 3 DE = 2 MN D. 2∠A = 3∠F
3. 下列说法: ①位似图形一定是相似图形;②相似图形一定是位 似图形;③两个位似图形若全等,则位似中心在两 个图形之间;④若五边形ABCDE与五边形A′B′C′D′E′ 位似,则其中 △ABC 与 △A′B′C′ 也是位似的,且位 似比相等. 其中正确的有 ①④ .
练一练1:判断下列各对图形哪些是位似图形,哪些不是. (3)正五边形ABCDE与正五边形A′B′C′D′E′;五边 形ABCDE与五边形A′B′C′D′E′;
(2)在平行四边形ABCD中,△ABO与△CDO
2.判断下面的正方形是不是位似图形?
A D
不是
E (1) B C F G
显然,位似图形是相似图形的特殊情形.相似图形不 一定是位似图形,可位似图形一定是相似图形
想一想
• 3.你能作出下列位似图形的位似中心吗?:
O
O
二Hale Waihona Puke 位似图形的性质思考 如图,D,E分别是△ABC的边AB,AC上的点, (1)如果DE ∥ BC则△ADE与△ABC是位似图形吗?
冀教版九年级上册数学《相似多边形和图形的位似》PPT(第1课时)
O
D
A
B
C
A'
B'
C'
D'
O
D
A
B
C
一起探究
例3 如图,△ABC,画△A' B' C' ,使△A' B' C' ∽△ABC,且使相似比为1:5,要求:(1)位似中心在△ABC的一条边AB上; (2)以点C为位似中心.
(1)位似中心在△ABC的一条边AB上
(2)以点C为位似中心
对应边成比例,但对应角不一定相等
任意的两个菱形不一定相似
对应角相等,但对应边不一定成比例
任意的两个矩形不一定相似
观察图中的两个多边形,先直观判断它们是不是相似多边形,再验证你的结论.
相似
如:网格中易求线段长,则可用三边对应成比例,证明△ABC∽△A'B'C'及△ADC∽△A'B'C',相似比为1:2.且两对全等三角形的对应角相等.
O
D
A
B
C
A'
B'
C'
D'
利用位似,可以将一个图形放大或缩小.
1) 在四边形外任选一点O(如图),
对于上面的问题,还有其他方法吗?如果在四边形外任选一个点O,分别在OA、OB、OC、OD的反向延长线上取A',B' 、C'、D',使得 呢?如果点O取在四边形ABCD内部呢?分别画出这时得到的图形.
假设位似中心点O在AB上,相似比1:5,点O位置如图所示
o
●
●
A'
B'
C'
●
●
