图形的位似
第15讲 位似图形

第15讲位似图形目标导航课程标准1.了解位似图形、位似中心的概念,掌握位似图形的性质,理解位似变换是特殊的相似变换。
2.会画位似图形,能够利用位似把一个图形放大或缩小。
3.掌握位似图形坐标的变化规律,会利用这个规律求某些特殊点的坐标。
知识精讲知识点01 位似多边形的有关概念一般地,如果两个相似多边形任意一组对应顶点A,A 所在的直线都,且有,那么这样的两个多边形叫做位似多边形,点O叫做。
实际上,k就是这两个相似多边形的相似比。
注意:位似图形与相似图形的区别位似图形是一种特殊的相似图形,而相似图形未必能构成位似图形。
知识点02 位似图形的性质(1)位似图形上任意一对对应点到的距离之比等于相似比;(2) 位似图形上的每组和在同一条直线上;(3)位似图形的对应线段。
(4)位似图形是特殊的相似图形,因此位似图形具有。
知识点03 位似图形的画法1.位似变换利用位似图形的性质将一个图形进行或叫做位似变换。
2.画位似图形的一般步骤(1)确定位似中心。
(2)确定原图形的,通常是多边形的顶点。
(3)分别原图形中的和,并延长(或截取)。
(4)根据已知的相似比,确定所画位似图形 的位置。
(5) 各点,得到放大或缩小后的图形。
3.实例知识点04 平面直角坐标系中的位似变换1.位似多边形对应点的坐标的变化规律在平面直角坐标系中,将一个多边形每个顶点的横坐标、纵坐标都乘同一个数)0( k k ,则所对应的图形与原图形位似,位似中心是 ,它们的相似比为 。
2.平移、轴对称、旋转与位似变换的坐标变化规律 名称 变换规律变换方式平移对应点的横坐标(或纵坐标)加上(或减去)平移的单位长度全等变换轴对称 若以x 轴为对称轴,则对应点的横坐标相等,纵坐标互为相反数;若以y 轴为对称轴,则对应点的纵坐标相等,横坐标互为相反数。
旋转若一个图形绕原点旋转180,则旋转前后两个图形对应点的横坐标与纵坐标均互为相反数。
位似当以原点为位似中心时,变换前后两个图形对应点的横坐标、纵坐标之比的绝对值均等于相似比。
1.4图形的位似

B’
课本P30习题:第1,2题 学案跟踪训练:1
A
A`
O
B` C
A
C` C
∴△ A’B’C’就是所求作图形。
B C
A`
D
B
O
E
O
C`
B`
F
C
A
∴△ A’B’C’就是所求作图形。
∴△ DEF就是所求作图形。
A
A
A`
o
D
E B B C
∴△ ADE就是所求作图形。
B`
C`
C
∴△ A’B’C’就是所求作图形。
如何画位似图形? 1、关键是确定位似中心 2、先连结顶点与位似中心 3、然后按比例确定对应点的位置 4、再连结对应点
A2
●
B2
●
C C1 A2
(0,4) B1
B (6,4)
O B2 C2
A1
A (6,0)
以坐标原点为位似中心的位似变换的坐标规律:
原来图形上点的坐标为(x,y), 所求图形上点的坐标为(a, b), 所求图形与原来图形的位似比为 k, 那么: a k或 k x b k或 k y
C 1 ●
B1
●
A1
A ′ ●
B′
●
●
C′
(x,y) (1,2)
(3,0) 4,0)
x 4 1 3 y 4 2 3
C ●2 B2●●源自A2B2●
C2
●
A2●
●
A1 (4,0)
● ●
C1 (2,-2)
B1 (6,-2)
●
A1
●
B1
如果两个多边形是位似图 形,那么图形上任意一对 对应点到位似中心的距离 之比等于对应边的比。 注意: 1、位似图形是相似图形 的特殊情形,其相似比又 叫做它们的位似比. 2、位似图形的对应点和 位似中心在同一条直线上.
5.1.2图形的位似

§5.1.2图形的位似学习目标:1•知道平行投影的含义,能够确左物体在太阳光下的影子.2.知道物体形成影子的大小和方向.学习重点:了解平行投影的含义,能够确泄物体在太阳光下的影子。
了解不同时刻物体在太阳光下形成的影子的大小和方向是不同的。
理解在同一时刻,物体的影子与它们的髙度成比例.学习难点:经历操作、观察,由直观到推理,归纳总结到理论的过程。
1、______________________________________________________________ 预习课本P115-117o我的疑惑: __________________________________________ ,2、回答下列问题:(1)如何判断两个图形是否位似?(2)怎样求两个位似图形的相似比?(3)如何将画在纸上的一个图片放大,使放大前后对应线段的比为1: 2?你有哪些方法?二、课堂研学:3、动手操作,合作交流活动1:在平面直角坐标系中,AOAB三个顶点的坐标分别为0 (0,0), A (3,0),B (2,3).按要求完成下列问题:(1)将点0, A, B的横、纵坐标都乘以2,得到三个点0’,A' , B',请你在坐标系中找到这三个点。
(2)以这三个点为顶点的三角形与AOAB规律:将△OAB的横、纵坐标分别乘2和-2,得到的两个不同的三角形都是AOAB的位似图形,位似中心都是原点6相似比都是2,它们关于原点成中心对称。
活动2:在平面直角坐标系中,四边形OABC 的顶点坐标分别为0(0,0), A (5,0),B (5,3),C (2,4) •将点0, A, B, C 的横、纵坐标都乘丄,得到四个点, 2规律:在直角坐标系中,将一个多边形每个顶点的横.纵坐标都乘以同一个数k (kHO),所对应的图形与原图形位似,位似中心是 ______ ,它们的相似比为 Ik| .活动3:在平面直角坐标系中,四边形OABC 的顶点坐标分别为0(0,0), A (6,0),B (3,6),C (-3,3) •已知四边形0’ I B z C'与四边形OABC 是以原点0为位似 中心的位似四边形,且相似比是2: 3,(1)请写出四边形O' A' B‘ C'各个顶点的坐 标.(2) 与四边形OABC 相比,四边形0’ A z B‘ C z 对应顶点的坐标发生了什么变化?(3) 请画出四边形O' A' B‘ C'4、学习小结与反思: (1)以这四个点为顶点的四边形与四边形0ABC 位似吗?如果位似,指出位似中 心和相似比.图 4-42总结今天这节课有什么收获:三. 课堂小测:5、如图,如图,在直角坐标系中,四边形OABC 的顶点坐标分别是0(0,0),A(3,0), B (4,4),C (-2,3) •画出四边形0ABC 以0为位似中心的位似图形,使它与四边6、在平面直角坐标系中,A0BC 各顶点的坐标分别是0 (0, 0), B (6, 0),C (8, 4),将点0, B, C 的横坐标、纵坐标都乘丄,得到三个点,以这三个点 2为顶点的三角形与AOBC 位似吗?四、作业布置:1、 预习导学案,完成课前导学部分。
《图形的位似》

《图形的位似》日期:目录•位似图形概述•位似图形的判定•位似图形的性质推论•位似图形的作图方法•位似图形的应用实例•位似图形的拓展与展望位似图形概述如果两个图形以原点为旋转中心旋转某个角度后能够重合,则称这两个图形关于这个旋转中心位似。
位似图形位似图形旋转的中心点称为位似中心。
位似中心位似图形旋转后的长度与原长度之比称为位似比。
位似比位似图形是相似图形的一种特殊形式,因此具有相似图形的所有性质。
相似图形的性质旋转对称性变换可逆性位似图形关于位似中心的旋转对称性是其重要性质之一。
位似图形的变换是可逆的,即可以通过逆变换恢复原来的图形。
030201位似图形在艺术和设计中有着广泛的应用,如旋转对称的图案、分形艺术等。
艺术和设计计算机图形学中经常使用位似图形来创建复杂的图像和动画效果。
计算机图形学物理学中,位似图形可以用来描述波的传播、振动等现象。
物理学位似图形的判定位似图形的定义如果两个图形以某一点为基准,使得每个图形上任意一点到该基准点的距离之比都等于两个图形的相似比,那么这两个图形被称为位似图形。
如何判定根据位似图形的定义,我们可以从以下三个方面进行判定:相似比、位似中心和对应线段。
通过定义判定位似图形相似比的定义相似比是指两个相似图形的对应线段之比,这个比例通常用一个分数来表示。
如何判定如果两个图形具有相同的相似比,那么它们就是位似图形。
例如,如果两个三角形的对应边之比为2:1,那么它们就是位似图形。
通过相似比判定位似图形位似中心是指两个位似图形围绕的共同中心点,这个中心点也是两个图形上任意一点到该点的距离之比相等的点。
位似中心的定义如果两个图形具有相同的位似中心,那么它们就是位似图形。
例如,如果两个圆心重合,那么它们就是位似图形。
如何判定通过位似中心判定位似图形位似图形的性质推论位似中心与相似中心的关系位似中心是位似图形的特殊点,相似中心是相似图形的特殊点。
它们都是图形中的特殊位置。
位似中心和相似中心都与图形的形状和大小无关,只与图形的位置和形状有关。
图形的位似
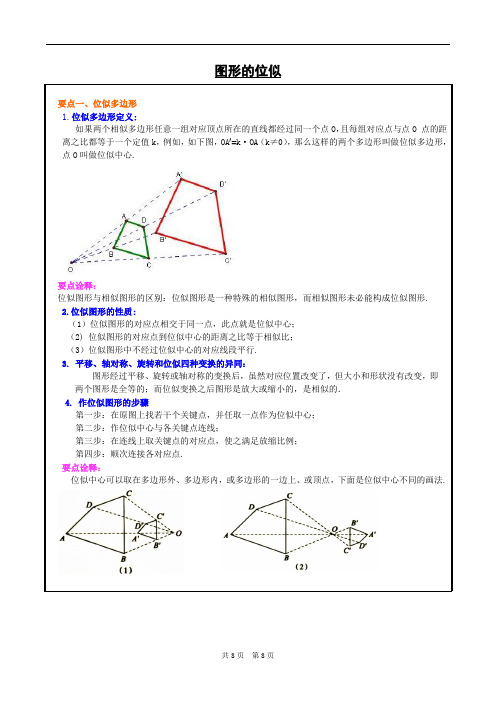
图形的位似要点一、位似多边形1.位似多边形定义:如果两个相似多边形任意一组对应顶点所在的直线都经过同一个点O,且每组对应点与点O 点的距离之比都等于一个定值k,例如,如下图,OA′=k·OA(k≠0),那么这样的两个多边形叫做位似多边形,点O叫做位似中心.要点诠释:位似图形与相似图形的区别:位似图形是一种特殊的相似图形,而相似图形未必能构成位似图形.2.位似图形的性质:(1)位似图形的对应点相交于同一点,此点就是位似中心;(2) 位似图形的对应点到位似中心的距离之比等于相似比;(3)位似图形中不经过位似中心的对应线段平行.3.平移、轴对称、旋转和位似四种变换的异同:图形经过平移、旋转或轴对称的变换后,虽然对应位置改变了,但大小和形状没有改变,即两个图形是全等的;而位似变换之后图形是放大或缩小的,是相似的.4.作位似图形的步骤第一步:在原图上找若干个关键点,并任取一点作为位似中心;第二步:作位似中心与各关键点连线;第三步:在连线上取关键点的对应点,使之满足放缩比例;第四步:顺次连接各对应点.要点诠释:位似中心可以取在多边形外、多边形内,或多边形的一边上、或顶点,下面是位似中心不同的画法.要点二、坐标系中的位似图形在平面直角坐标系中,将一个多边形每个顶点的横坐标、纵坐标都乘同一个数k (k ≠0),所对应的图形与原图形位似,位似中心是坐标原点,它们的相似比为|k |.要点诠释:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k ,那么位似图形对应点的坐标等于原来点的坐标乘以(或除以)k 或-k.一、典型例题类型一、位似多边形1. 下列每组的两个图形不是位似图形的是( ).A. B. C. D.举一反三【变式】在小孔成像问题中, 根据如图4所示,若O 到AB 的距离是18cm ,O 到CD 的距离是6cm ,则像CD 的长是物AB 长的 ( ).A. 3倍B.21 C.31 D.不知AB 的长度,无法判断2. 利用位似图形的方法把五边形ABCDE 放大1.5倍.举一反三【变式】在已知三角形内求作内接正方形.类型二、坐标系中的位似图形3.如图,在10×10的正方形网格中,点A,B,C,D均在格点上,以点A为位似中心画四边形AB′C′D′,使它与四边形ABCD位似,且相似比为2.(1)在图中画出四边形AB′C′D′;(2)填空:△AC′D′是三角形.4.如图△ABC的顶点坐标分别为A(1,1),B(2,3),C(3,0).(1)以点O为位似中心画△DEF,使它与△ABC位似,且相似比为2.(2)在(1)的条件下,若M(a,b)为△ABC边上的任意一点,则△DEF的边上与点M对应的点M′的坐标为.举一反三:【变式】如图,将△AOB中各顶点的纵坐标,横坐标分别乘-1,•得到的图形与原图形相比有什么变化?作出所得的图形,这个过程可以看作是一个什么图形变换?二、巩固练习一. 选择题1.下面给出了相似的一些命题:(1)菱形都相似;(2)等腰直角三角形都相似;(3)正方形都相似;(4)矩形都相似;(5)正六边形都相似;其中正确的有().A.2个 B.3个 C.4个 D.5个2.下列说法错误的是().A.位似图形一定是相似图形.B.相似图形不一定是位似图形.C.位似图形上任意一对对应点到位似中心的距离之比等于相似比.D.位似图形中每组对应点所在的直线必相互平行.3.下列说法正确的是() .A.分别在ABC的边AB、AC的反向延长线上取点D、E,使DE∥BC,则ADE是ABC放大后的图形.B.两位似图形的面积之比等于相似比.C.位似多边形中对应对角线之比等于相似比.D.位似图形的周长之比等于相似比的平方.4.如图,在平面直角坐标系中,已知点A(﹣3,6),B(﹣9,﹣3),以原点O为位似中心,相似比为,把△ABO缩小,则点A的对应点A′的坐标是()A.(﹣1,2)B.(﹣9,18)C.(﹣9,18)或(9,﹣18)D.(﹣1,2)或(1,﹣2)5. 下列命题:①两个正方形是位似图形;②两个等边三角形是位似图形;③两个同心圆是位似图形;④平行于三角形一边的直线截这个三角形的两边,所得的三角形与原三角形是位似图形.其中正确的有( ).A.1个B.2个C.3个D.4个6.如果点C为线段AB的黄金分割点,且AC>BC,则下列各式不正确的是().A. AB:AC=AC:BCB. AC=512AB-C.AB=512AC+D.BC≈0.618AB7.已知矩形ABCD中,AB=1,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点,若四边形EFDC与矩形ABCD相似,则AD=().A. 512-B.512+C.3D.2二.填空题8. 如果两个位似图形的对应线段长分别为3cm和5cm,且较小图形周长为30cm,则较大图形周长为__________.9.如图,在平面直角坐标系中,已知A(1,0),D(3,0),△ABC与△DEF位似,原点O是位似中心.若AB=1.5,则DE=.10.如图,以点O为位似中心,将五边形ABCDE放大后得到五边形A B C D E''''',已知OA=10cm,OA′=20cm,则五边形ABCDE的周长与五边形A B C D E'''''的周长的比值是__________.11. △ABC中,D、E分别在AB、AC上,DE∥BC,△ADE是△ABC缩小后的图形.若DE把△ABC的面积分成相等的两部分,则AD:AB=________.12. 把一矩形纸片对折,如果对折后的矩形与原矩形相似,则原矩形纸片的长与宽之比为____________________.13.如图,以O为位似中心,将边长为256的正方形OABC依次作位似变换,经第一次变化后得正方形OA1B1C1,其边长OA1缩小为OA的,经第二次变化后得正方形OA2B2C2,其边长OA2缩小为OA1的,经第,三次变化后得正方形OA3B3C3,其边长OA3缩小为OA2的,…,依次规律,经第n次变化后,所得正方形OA n B n C n的边长为正方形OABC边长的倒数,则n=.14. 如图,△ABC中,AB=AC=4,∠BAC=36°,∠ABC的平分线与AC边的交点D为边AC的黄金分割点(AD>DC),则BC=______________.三.综合题15.如图,D、E分别AB、AC上的点.(1)如果DE∥BC,那么△ADE和△ABC是位似图形吗?为什么?(2)如果△ADE和△ABC是位似图形,那么DE∥BC吗?为什么?16.如图,F在BD上,BC、AD相交于点E,且AB∥CD∥EF,(1)图中有哪几对位似三角形,选其中一对加以证明;(2)若AB=2,CD=3,求EF的长.17. 如图1,矩形ODEF的一边落在矩形ABCO的一边上,并且矩形ODEF∽矩形ABCO,其相似比为1:4,矩形ABCO的边AB=4,BC=43.(1)求矩形ODEF的面积;(2)将图1中的矩形ODEF绕点O逆时针旋转一周,连接EC、EA,△ACE的面积是否存在最大值或最小值?若存在,求出最大值或最小值;若不存在,请说明理由.。
8图形的位似

8图形的位似1.位似图形定义:如果两个图形不仅是相似图形,而且每组对应点所在的直线都经过同一点,那么这样的两个图形叫做位似图形,这个点叫做位似中心,这时的相似比又叫位似比。
2.位似是一种具有特殊位置关系的相似,故位似图形一定是相似图形,但相似图形不一定是位似图形.3.两个位似图形的位似中心只有一个.4.两个位似图形可能位于位似中心的两侧,也可能位于位似中心的同侧.5.【总结】位似图形的画法利用位似可以把一个图形放大或缩小,画位似图形的一般步骤:①确定位似中心;②分别连接位似中心和能代表原图的关键点并延长;③根据相似比,确定能代表所作的位似图形的关键点;④顺次连接上述各点,得到放大或缩小的图形.借助方格纸、格点图等简易工具可将图形放大或缩小,借助计算机也可以很好地将一个图形放大或缩小,此步骤的记忆要诀为:定中心——作射线——定对应点——连线画图.画多边形的位似图形时,位似中心可以任意取,把位似中心取在多边形内,或取在一条边上,或取在某一顶点上,都可以把一个多边形放大或缩小.(1)画位似图形的关键是能否准确地按比例画出各线段,只有线段的长度准确,画出的图形才能准确.(2)画位似图形的理论依据是位似图形的对应点和位似中心在同一条直线上,它们到位似中心的距离之比等于相似比(位似比).6.平面直角坐标系中的位似图形:在平面直角坐标系中,将一个多边形每个顶点的横、纵坐标都乘同一个数k(k≠0),所对应的图形与原图形位似,位似中心为坐标原点,它们的相似比是|k|.7.在平面直角坐标系中,以坐标原点为位似中心作出一个多边形的位似图形.(1)如果原图形与所得图形的相似比是1∶|k|(k为整数),那么就等于把这个多边形放大到原来的|k|倍,其位似图形的每个顶点的横、纵坐标就等于原多边形顶点的横、纵坐标乘k;(2)如果原图形与所得图形的相似比是|k|∶1(k为整数),那么就等于这个多边形缩小到原来的|k|倍,其位似图形的每个顶点的横、纵坐标就等于原多边形顶点的横、纵坐标乘1/k.8.变化规律为:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k.练习一下:1.下列关于位似图形的表述:①相似图形一定是位似图形,位似图形一定是相似图形;②位似图形一定有位似中心;③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么这两个图形是位似图形;④位似图形上任意两点与位似中心的距离之比等于位似比.其中正确命题的序号是 ()A.②③B.①②C.③④D.②③④2.如图所示,正五边形FGHMN是由正五边形ABCDE经过位似变换得到的,若AB∶FG=2∶3,则下列结论正确的是()A.2DE=3MNB.3DE=2MNC.3∠A=2∠FD.2∠A=3∠F3.如果两个位似图形的对应线段长分别是3,5,且较小图形的周长为30,则较大图形的周长为.4.两个位似图形中的对应角,对应顶点的连线必经过.5.如图所示,画一个三角形,使它与已知ΔABC位似,且原三角形与所画三角形的相似比为2∶1.6..在平面直角坐标系中,已知点E(-4,2),F(-2,-2),以原点O为位似中心,相似比为2,把ΔEFO缩小,则点E的对应点E’的坐标是()A.(-2,1)B.(-8,4)C.(-8,4)或(8,-4)D.(-2,1)或(2,-1)7.下图中的两个四边形是位似图形,它们的位似中心是()A.点MB.点NC.点OD.点P8.如图所示,在平面直角坐标系中,已知ΔABC三个顶点的坐标分别为A(-1,2), B(-3,4),C(-2,6).(1)画出ΔABC绕点A顺时针旋转90°后得到的ΔA1B1C1;(2)以原点为位似中心,画出将ΔA1B1C1三条边放大为原来的2倍后的ΔA2B2C2. 4.如图,幻灯片与屏幕平行,光源到幻灯片的距离是30 cm,幻灯片到屏幕的距离是1.5 m,幻灯片上小树的高度是10 cm,则屏幕上小树的高度是.。
图形的位似

图形的位似知识点一:位似的定义与位似作图图中的多边形相似吗?如果有,那么这种相似有什么特征?总结:位似图形:1.定义:如果两个相似图形的每组对应点所在的直线,那么这样的两个图形叫做位似图形,这个交点叫做中心,这两个图形的相似比又叫它们的2.性质:(1)位似变换是相似变换的特例,所有位似图形一定是但相似图形不一定是(2)位似图形的对应点和位似中心在,它们到位似中心的距离之比等于,(3)两个位似图形可能位于位似中心的两侧,也可能位于位似中心的一侧;(4)对应边平行或在一条直线上知识点二:位似与坐标变换如图,在平面直角坐标系中,有两点O(0,0),A(3,0),B(2,3)以原点O为位似中心,相似比为2:1,把△OAB扩大,观察对应点之间的坐标变化,你有什么发现总结:1. 在平面直角坐标系中,将一个多边形的每个顶点的横坐标、纵坐标都乘以同一个数K(),所对应图形与原图形,位似中心是它们的相似比是2.在平面直角坐标系中,如果位似变换以原点为位似中心,相似比为K,那么位似图形对应点的坐标的比是练习1:如图,△ABC在方格中(1)请在方格中建立平面直角坐标系,使点A、C的坐标分别为A(2,3),C(5,2)并求出B点的坐标(2)以原点O为位似中心,相似比为2,在第一象限内将△ABC放大,画出放大后的图形练习2:如图,在平面直角坐标系中,△ABC和△A′B′C′是以坐标原点O为位似中心的位似图形,且点B(3,1),B′(6,2).(1)请你根据位似的特征并结合点B的坐标变化回答下列问题:①若点A(2.5,3),则A′的坐标为;②△ABC与△A′B′C′的相似比;(2)若△ABC的面积为m,求△A′B′C′的面积.(用含m的代数式表示)练习3:如图,平面直角坐标系xoy中,点A,B的坐标分别为(3,0),(2,-3),△AB′O′是△ABO关于点A的位似图形,且O′的坐标为(-1,0).(1)画出△AB′O′;(2)点B′的坐标为.练习4:如图,将△ABC在网格中(网格中每个小正方形的边长均为1)依次进行位似变换、轴对称变换和平移变换后得到△A3B3C3.(1)△ABC与△A1B1C1的位似比等于;(2)在网格中画出△A1B1C1关于y轴的轴对称图形△A2B2C2;(3)请写出△A3B3C3是由△A2B2C2怎样平移得到的?(4)设点P(x,y)为△ABC内一点,依次经过上述三次变换后,点P的对应点的坐标为.提高练习:1.如图,正方形ABCD和正方形OEFG中,点A和F的坐标分别是(3,2),(-1,-1),则两个正方形的位似中心的坐标是2.如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(-1,0).以点C为位似中心,在x 轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,记所得的像是△A′B′C.设点B的对应点B′的横坐标是a,则点B的横坐标是3.如图,△ABE和△CDE是以点E为位似中心的位似图形,已知点A(3,4),点C(2,2),点D(3,1),则点D的对应点B的坐标是4.如图,△ABC的两个顶点BC均在第一象限,以点A(0,1)为位似中心,在y轴左方作△ABC的位似图形△AB’C’,△ABC与△AB’C’的位似比为1:2,若设点C的纵坐标是m,则其对应点C’的纵坐标是。
图形的位似课件

(1)
学习交流PPT
1
学习交流PPT
2
概念与性质
1.位似图形的概念
如果两个图形不仅相似,而且每
组对应点所在的直线都经过同一
点,对应边互相平行(重合),那么
这样的两个图形叫做位似图形,这
个点叫做位似中心.
学习交流PPT
3
辨一辨
1. 判断下列各对图形是不是位似图形.
(1)正五边形ABCDE与正五 边形A′B′C′D′E′;
• 位似图形的性质: 1.位似图形上的任意一对对应点到位似中心的距离 之比等于位似比
学习交流PPT
14
如果∆OAB和 ∆OCD是位似图形,那么
AB∥CD吗?为什么?
C
A
解:AB∥CD.理由是:
∆OAB和 ∆OCD是位似图形, O
BD
∆OAB∽
∆OCD ∠OAB=∠C
AB∥CD.
学习交流PPT
15
8
2.如图,以点O为位似中心,将五边形ABCDE
放大后得到五边形A′B′C′D′E′,已知
OA=10cm,OA′=20cm,则
AB:A′B′=
,五边形ABCDE的周
长与五边形A′B′C′D′E′的周长的比值是
学习交流PPT
9
把图1中的四边形ABCD缩小到原来的 一半.
作法一:如图2 ,在四边形ABCD外 任取一点O;
学习交流PPT
10
作法二:如图3,在四边形ABCD外任 取一点O;
学习交流PPT
11
作法三:如图4,在四边形ABCD内任 取一点O;
学习交流PPT
12
还有其它作法吗?
学习交流PPT
13
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
下面请欣赏如下图形的变换
☞ 观察与思考
下列图形中,每个图中的四边形ABCD和四边形 A′B′C′D′都是相似图形.分别观察这五个图,你发现每个图中的两个四边 形各对应点的连线有什么特征?
概念与性质
作业:完成思考题以及课本65页第2题
下课了!
结束寄语
图形的变换: • 对称,平移,旋转,相似,位 似,…… 可以帮助我们真 正了解数学的内在关系.
•
性质:位似图形上任意一对对应点到位似中心 的距离之比等于相似比.
若△ABC与△A’B’C’的相似比为:1:2,则 OA:OA’=( 1:2 )。
A’ A B O C B’
C’
练习与拓展
OA:OA’ =OB:OB’ =OC:OC’= 1:2
A A' .
O. B B’ C C’
1.如图,已知△ABC和点O.以O为位似中心,求作 △ABC的位似图形,并把△ABC的边长扩大到原来的两倍.
思考:是否相似图形都是位似图形?
判断下面的正方形是不是位似图形?
A D
不是
E (1) B C F G
显然,位似图形是相似图形的特殊情形.相似图形不 一定是位似图形,可位似图形一定是相似图形
思考:位似图形有何性质?
概念与性质
2. 位似图形的性质
OA 从第 (1),(2)图中,我们可以看到,△OAB∽△O A′B′,则 = OA′ OB AB AF AP AE EP FP = .从第(3)图中同样可以看到 = = = = OB′ A′B′ AD AC AB BC DC
思考:还有没其他作法?
C’ B’ A
. O
B C
A'
如果位似中心跑到三角形内部呢?
如果∆OAB和 ∆OCD是位似图形,那么 AB∥CD吗?为什么? C
A
解:AB∥CD.理由是: ∆OAB和 ∆OCD是位似图形,
∆OAB∽ ∆OCD ∠OAB=∠C
O
B
D
AB∥CD.
课堂小结
回味无穷
位似图形的概念: 如果两个图形不仅形状相同,而且每组对应顶点所 在的直线都经过同一个点,那么这样的两个图形叫 做位似图形,这个点叫做位似中心,这时的相似比又 称为位似比. 位似图形的性质: 1.位似图形上的任意一对对应点到位似中心的距离 之比等于位似比
义务教育课程标准 实验教科书人教版
图形的位似
掌握位似图形的概念和性质; 会判定位似图形; 会利用位似将一个图形大或缩小
回顾与反思
1. 前面我们已经学习了图形的哪些变换?
对称(轴对称与轴对称图形,中心对称与中心对 称图形):对称轴,对称中心. 平移:平移的方向,平移的距离. 旋转:旋转中心,旋转方向,旋转角度. 相似:相似比.
1.位似图形的概念
如果两个图形不仅相似,而且每组对应点
所在的直线都经过同一点,对应边互相平行,
那么这样的两个图形叫做位似图形,这个点
叫做位似中心.
相似 对应点的连 线相交一点 对应边平行
辨一辨
1. 判断下列各对图形是不是位似图形. (1)正五边形ABCDE与正五边形A′B′C′D′E′; 是 (2)等边三角形ABC与等边三角形A′B′C′. 是
