解析几何第四版吕林根课后习题答案第二章
解析几何第四版吕林根 期末复习 课后习题(重点)详解
第一章 矢量与坐标§1.3 数量乘矢量4、 设→→→+=b a AB 5，→→→+-=b a BC 82，)(3→→→-=b a CD ，证明：A 、B 、D 三点共线． 证明 ∵→→→→→→→→→→=+=-++-=+=AB b a b a b a CD BC BD 5)(382∴→AB 与→BD 共线，又∵B 为公共点，从而A 、B 、D 三点共线．6、 设L 、M 、N 分别是ΔABC 的三边BC 、CA 、AB 的中点，证明：三中线矢量AL , BM ,可 以构成一个三角形.证明： )(21AC AB AL +=)(21+=)(21CB CA CN +=0)(21=+++++=++∴7.、设L 、M 、N 是△ABC 的三边的中点，O 是任意一点，证明 ++=OL +OM +ON .[证明] += MB OM OB += NC ON OC +=)(OM +++++=++∴ =)(CN BM AL ON OM OL ++-++ 由上题结论知：0=++CN BM AL ON OM OL OC OB OA ++=++∴ 从而三中线矢量BM ,,构成一个三角形。
8.、如图1-5，设M 是平行四边形ABCD 的中心，O 是任意一点，证明OA +OB ++OD ＝4OM .[证明]：因为OM ＝21(OA +), OM ＝21(OB +), 所以 2OM ＝21(OA +OB +OC +) 所以OA +OB ++OD ＝4OM .10、 用矢量法证明梯形两腰中点连续平行于上、下两底边且等于它们长度和的一半．图1-5证明 已知梯形ABCD ，两腰中点分别为M 、N ，连接AN 、BN ． →→→→→→++=+=DN AD MA AN MA MN ，→→→→→→++=+=CN BC MB BN MB MN ，∴ →→→+=BC AD MN ，即§1.4 矢量的线性关系与矢量的分解3.、设一直线上三点A , B , P 满足AP ＝λ(λ≠－1),O 是空间任意一点，求证：OP ＝λλ++1[证明]：如图1-7，因为＝－OA ,PB ＝OB －,所以 －OA ＝λ (OB －),(1+λ)OP ＝+λ,从而 OP ＝λλ++1OB.4.、在ABC ∆中,设,1e =2e =.(1) 设E D 、是边BC 三等分点,将矢量,分解为21,e e 的线性组合; （2）设AT 是角A 的平分线(它与BC 交于T 点),将分解为21,e e 的线性组合解：（1）()12123131,e e e e -==-=-= ， 2111231323131e e e e e BD AB AD +=-+=+=，同理123132e e AE +=（2）因为||||TC ＝||11e e ,且 BT 与方向相同， 所以 BT ||21e e .由上题结论有AT ||||1||212211e e e e e +||||212112e e e e e e +.5．在四面体OABC 中，设点G 是ABC ∆的重心（三中线之交点），求矢量对于矢量,,,的分解式。
《解释几何 第四版》讲解与习题 第二章 轨迹与方程
x (tx b) 1 2 2 a b
2 2
在第二式中取t=0,得x=0，所以舍去第一式，取 从而
b(b 2 a 2t 2 ) y 2 b a 2t 2
在法二中，若令u=-t，则得椭圆的另一种表示式为
2a2bu x 2 b a 2u 2 ( u ) 2 2 2 y b(b a u ) 2 2 2 b a u
(x x0)2 + (y y0)2 + (z z0)2 = R2 (1) 称方程(1)为球面的标准方程. 特别: 当球心在原点O(0, 0, 0)时,
M0
M
R
球面方程: x2 + y2 + z2 = R2
例 4 求与原点O 及 M 0 ( 2,3,4)的距离之比为1 : 2的点的全 体所组成的曲面方程.
解
根据题意有 z 1
用平面z c 去截图形得圆：
z
( x 1)2 ( y 2)2 1 c (c 1)
当平面z c 上下移动时， 得到一系列圆
c
o
x
y
圆心在(1,2, c )，半径为 1 c
半径随c 的增大而增大. 图形上不封顶，下封底．
二、曲面的参数方程 1、双参数向量函数 在两个变数u,v的变动区域内定义的函数 r=r(u,v) 或 r(u,v)=x(u,v)e1+y(u,v)e2+z(u,v)e3 (2) 称为双参数向量函数，其中x(u,v),y(u,v),z(u,v)是变 向量r(u,v)的分量，它们都是变数u，v的函数。 当u,v取遍变动区域的一切 值时，径矢
a b r (a b) cos b cos i b a b (a b) sin b cos j b 特殊地，当 a 4b 应用公式
解析几何_吕林根_许子道_第四版_课后习题解答
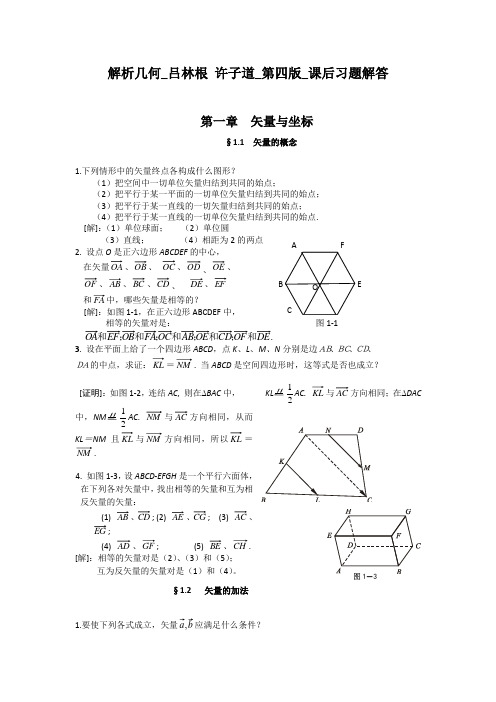
解析几何_吕林根 许子道_第四版_课后习题解答第一章 矢量与坐标§1.1 矢量的概念1.下列情形中的矢量终点各构成什么图形？（1）把空间中一切单位矢量归结到共同的始点；（2）把平行于某一平面的一切单位矢量归结到共同的始点； （3）把平行于某一直线的一切矢量归结到共同的始点；（4）把平行于某一直线的一切单位矢量归结到共同的始点. [解]：（1）单位球面； （2）单位圆（3）直线； （4）相距为2的两点2. 设点O 是正六边形ABCDEF 的中心，在矢量OA 、OB 、 OC 、OD 、OE 、 OF 、AB 、BC 、CD 、 DE 、EF 和FA 中，哪些矢量是相等的？[解]：如图1-1，在正六边形ABCDEF 中，相等的矢量对是： 图1-1 .DE OF CD OE AB OC FA OB EF OA 和；和；和；和；和3. 设在平面上给了一个四边形ABCD ，点K 、L 、M 、N 分别是边ＡＢ、ＢＣ、ＣＤ、ＤＡ的中点，求证：KL ＝NM . 当ABCD 是空间四边形时，这等式是否也成立？[证明]：如图1-2，连结AC , 则在∆BAC 中，21AC. KL 与AC 方向相同；在∆DAC 中，21AC . NM 与AC 方向相同，从而KL ＝NM 且KL 与NM 方向相同，所以KL ＝NM .4. 如图1-3，设ABCD -EFGH 是一个平行六面体，在下列各对矢量中，找出相等的矢量和互为相反矢量的矢量：(1) AB 、CD ; (2) AE 、CG ; (3) AC 、EG ;(4) AD 、GF ; (5) BE、CH . [解]：相等的矢量对是（2）、（3）和（5）； 互为反矢量的矢量对是（1）和（4）。
§1.2 矢量的加法1.要使下列各式成立，矢量b a ,应满足什么条件？E（1=+ （2+=+ （3-=+ （4+=- （5=[解]：（1）b a ,-=+（2）b a ,+=+（3≥且b a ,-=+ （4）b a ,+=（5）b a ,≥-=-§1.3 数量乘矢量1 试解下列各题．⑴ 化简)()()()(→→→→-⋅+--⋅-b a y x b a y x ．⑵ 已知→→→→-+=3212e e e a ，→→→→+-=321223e e e b ，求→→+b a ，→→-b a 和→→+b a 23．⑶ 从矢量方程组⎪⎩⎪⎨⎧=-=+→→→→→→by x ay x 3243，解出矢量→x ，→y ．解 ⑴→→→→→→→→→→→→→→-=+-+---+=-⋅+--⋅-ay b x b y a y b x a x b y a y b x a x b a y x b a y x 22)()()()(⑵ →→→→→→→→→→+=+-+-+=+3132132142232e e e e e e e e b a ，→→→→→→→→→→→-+-=+---+=-321321321342)223(2e e e e e e e e e b a ， →→→→→→→→→→→-+-=+---+=-3213213217103)223(2)2(323e e e e e e e e e b a ． 2 已知四边形ABCD 中，→→→-=c a AB 2，→→→→-+=c b a CD 865，对角线→AC 、→BD 的中点分别为E 、F ，求→EF ．解 →→→→→→→→→→→-+=-+-+=+=c b a c a c b a AB CD EF 533)2(21)865(212121．3 设→→→+=b a AB 5，→→→+-=b a BC 82，)(3→→→-=b a CD ，证明：A 、B 、D 三点共线． 证明 ∵→→→→→→→→→→=+=-++-=+=AB b a b a b a CD BC BD 5)(382∴→AB 与→BD 共线，又∵B 为公共点，从而A 、B 、D 三点共线．4 在四边形ABCD 中，→→→+=b a AB 2，→→→--=b a BC 4，→→→--=b a CD 35，证明ABCD 为梯形．证明∵→→→→→→→→→→→→→=--=-+--++=++=BC b a b a b a b a CD BC AB AD 2)4(2)35()4()2( ∴→AD ∥→BC ，∴ABCD 为梯形．6. 设L 、M 、N 分别是ΔABC 的三边BC 、CA 、AB 的中点，证明：三中线矢量AL , BM ,CN 可 以构成一个三角形.[证明]： )(21AC AB AL +=)(21BC BA BM +=)(21CB CA CN +=0)(21=+++++=++∴CB CA BC BA AC AB CN BM AL从而三中线矢量CN BM AL ,,构成一个三角形。
解析几何全册课件(吕林根版)精选全文完整版
（1）交换律：
（2）结合律：
（3）
上一页
下一页
返回
O
A1
A2
A3
A4
An-1
An
这种求和的方法叫做多边形法则
上一页
下一页
返回
向量减法
上一页
下一页
返回
A
B
C
上一页
返回
例2 试用向量方法证明：对角线互相平分的四边形必是平行四边形.
证
上一页
下一页
返回
解
设
为直线上的点，
6、线段的定比分点坐标
上一页
下一页
返回
由题意知：
上一页
下一页
返回
定理1.5.4 已知两个非零向量
7、其它相关定理
则
共线的充要条件是
定理1.5.6 已知三个非零向量
，则
共面的充要条件是
上一页
返回
空间一点在轴上的投影(Projection)
§1.6 向量在轴上的射影
解
根据题意有
所求方程为
上一页
下一页
返回
根据题意有
化简得所求方程
解
上一页
下一页
返回
例4 方程 的图形是怎样的？
根据题意有
图形上不封顶，下封底．
解
以上方法称为截痕法.
上一页
下一页
返回
以上几例表明研究空间曲面有两个基本问题：
线为
的连
的中点
对边
一组
设四面体
证
e
e
e
AP
e
AD
e
AC
e
《解析几何》(第四版)吕林根 许子道 编第2章轨迹与方程2.1平面曲线的方程
[串点成面·握全局]
一、近代交通业发展的原因、特点及影响 1．原因 (1)先进的中国人为救国救民，积极兴办近代交通业，促 进中国社会发展。 (2)列强侵华的需要。为扩大在华利益，加强控制、镇压 中国人民的反抗，控制和操纵中国交通建设。 (3)工业革命的成果传入中国，为近代交通业的发展提供 了物质条件。
轮船正招式成商立局，标志着中国新式航运业的诞生。
(2)1900年前后，民间兴办的各种轮船航运公司近百家，几乎都是
在列强排挤中艰难求生。
2．航空
(1)起步：1918年，附设在福建马尾造船厂的海军飞机工程处开始
研制 。
(2)发展水：上1飞918机年，北洋政府在交通部下设“
”；此后十年间，航空事业获得较快发展。
曲线的参数方程与普通方程的互化
曲线的参数方程 ,是解析几何联系实际的 一个重 要工具.
(1)化参数方程为普通方程 时,关键在于消去参 数t.
此时,还应注意 ①同一条曲线可以有多种不 同形式的参数方程,如
x 1t,
y
2
t.
与
x 1 3t, y 2 3t.
在消去t后都表示同一直线 x y 3.
ct, c, t
(t 0)
则其上任意三点P, Q,
R的坐标可以分别取
y
Q
H R
P
o
x
为
c
c
c
P(ct1, t1 ), Q(ct2 , t2 ) R(ct3, t3 ),
历史ⅱ岳麓版第13课交通与通讯 的变化资料
精品课件欢迎使用
[自读教材·填要点]
一、铁路，更多的铁路 1．地位 铁路是 交通建运设输的重点，便于国计民生，成为国民经济 发展的动脉。 2．出现 1881年，中国自建的第一条铁路——唐山 至开胥平各庄铁 路建成通车。 1888年，宫廷专用铁路落成。
《解析几何》(第四版)吕林根 许子道 编第2章轨迹与方程2.2曲面的方程
故动点轨迹为
y 0,
z
0,
x
c.
这是x轴上的线段.
② 当a c时,令b2 a2 c2,则动点轨迹为
x2 a2
y2 b2
z2 b2
1,
(旋转椭球面 ).
例 3 建立球心在点 M0 ( x0 , y0 , z0 )、半径为R
的球面方程.
解 设M( x, y, z)是球面上任一点，
根据题意有 | MM0 | R
OM r(u,v), 的终点M (x(u, v), y(u, v), z(u, v))所画出的轨迹一般
为一张曲面.(图1) 定义2.2.2 对u, v (a u b, c v d ),若由(2.2 5)
表示的向径r(u, v)的终点M总在曲面上,同时,曲面
上的任意点M总对应着以它为终点的向径, 而这向径
面,如
x2 y2 z2 1 0,
又 三元方程F(x, y, z) 0有时代表一条曲线(包
括直线),如
x2 y2 0,
代表直线 x y 0,即z 轴.
有时代表一个点，如
x2 y2 z2 0, 即坐标原点 (0,0,0). 曲面与方程研究中的两个基本问题： 1) 给定作为点的几何轨迹 的曲面,建立其方程.
（讨论旋转曲面）
2) 给定坐标x, y, z间的方程, 研究这方程的曲面的
形状. （讨论柱面、二次曲面）
以下讨论问题 1)的实例.
例1 求两坐标面 xoz, yoz所成二面角的平分面方 程.
解 因所求平分面是与xoz, yoz面有等距离的点的
轨迹, 所以
点M(x, y, z)在平分面上 y x.
§2.2曲面的方程
1.曲面的方程
曲面的实例： 水桶的表面、台灯的罩子面等．
《解析几何》(第四版)吕林根许子道编第2章轨迹与方程21平面曲线的方程
线直一同示表都后t 去消在
与 .t � 2 � y � � ,t � 1 � x �
如,程方数参的式形同 不种多有以可线曲条一同① 意注应还,时此
参去消于在键关 , 时 程方通普为程方数参化)1(
.t 数
程方数参的圆椭则 , � � � � � � 且数参为� 取以所
�� nis b� � y �� soc a � x �� nis b � � y
迹轨的点一的上周圆
圆求�动滚地动滑
程方通普得可即) 能可若( t 去消中)5 � 1. 2 ( 从
.0 � ) y , x ( F
无上是线直一在圆个一 1例
)6-1.2( , j ) � soc � 1( a � i ) � nis � �( a � r � � � , j a � CA , i � a � AO 以所 � �
齿为用采被常上业工在 , 线曲种这 , 线展切或
)31 -1. 2(
为程方数
参
式标坐的迹轨该得可则 ,) y , x ( 为标坐的点 P 设
当适择选要仅不 ,时 .3 � y � x
.程方通普成化能都程方数参有所是不并②
. t3 � 2 � y , t3 � 1 � x
程方数参为程方通普化 ) 2 (
三意任上线曲双轴等是 R , Q , P 设 7 例
上线曲双轴等一同在必 H 心垂的 RQP �
参的线曲双轴等知已设 , 图如 证
,
2 1
tc � 0 x
tc � 0 x
�
c � 2 t0y c � 1t 0 y
得, ② ÷ ①
②
,) 2 tc � 0x ( 3 t 2 t1t � c � 2 t 0 y
则
解析几何第四版吕林根课后习题答案一至三章
PA1 PO PA2 PO PAn PO 0
即
PA1 PA2 PAn n PO
§1.4 向量的线性关系与向量的分解
1．在平行四边形 ABCD 中， （1）设对角线 AZ a, BD b, 求 AB, BC , CD, DA. 解： AB
解?a?b?b?a?b?a?b?a?b?a?b?a?b?a?????????????????yxyyxxyyxxyxyx22?e?e?e?e?e?e?e?e?b?a?????????3132132142232?e?e?e?e?e?e?e?e?e?b?a???????????3213213213422232?e?e?e?e?e?e?e?e?e?b?a???????????321321321710322322323
OA OB + OC = OL + OM + ON .
7. 设 L、M、N 是△ABC 的三边的中点，O 是任意一点，证明 [证明] OA OL LA
OB OM MB OC ON NC OA OB OC OL OM ON ( LA MB NC )
1 1 1 1 b a , BC b a , CD b a , DA b a ．设边 BC 和 CD 的 2 2 2 2
（2）中点 M 和 N，且 AM P, AN q 求 BC , CD 。 解： AC
1 1 q P , BC 2MC 2 q P P q 3P 2 2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第二章 轨迹与方程 §2.1平面曲线的方程1.一动点M 到A )0,3(的距离恒等于它到点)0,6(-B 的距离一半，求此动点M 的轨迹方程，并指出此轨迹是什么图形？解：动点M 在轨迹上的充要条件是MB MA 21=。
设M 的坐标),(y x 有2222)6(21)3(y x y x ++=+- 化简得36)6(22=+-y x 故此动点M 的轨迹方程为36)6(22=+-y x此轨迹为椭圆2.有一长度为a 2a (＞0）的线段，它的两端点分别在x 轴正半轴与y 轴的正半轴上移动，是求此线段中点的轨迹。
A ，B 为两端点，M 为此线段的中点。
解：如图所示 设(,),A x o (,)B o y .则(,)22x y M .在Rt AOB 中有 222()(2)x y a +=.把M 点的坐标代入此式得:222()x y a +=(0,0)x y ≥≥.∴此线段中点的轨迹为222()x y a +=.3. 一动点到两定点的距离的乘积等于定值2m ,求此动点的轨迹.解:设两定点的距离为2a ,并取两定点的连线为x 轴, 两定点所连线段的中垂线为y 轴.现有:2AM BM m ⋅=.设(,)M x y 在Rt BNM 中222()a x y AM ++=. (1) 在Rt BNM 中 222()a x y BM -+=. (2) 由(1)(2)两式得:22222244()2()x y a x y m a +--=-.4.设,,P Q R 是等轴双曲线上任意三点,求证PQR 的重心H 必在同一等轴双曲线上.证明:设等轴双曲线的参数方程为x ct c y t =⎧⎪⎨=⎪⎩11(,)P x y ,22(,)Q x y ,33(,)R x y .重心H123123(,)33x x x y y y ++++5.任何一圆交等轴双曲线2xy c =于四点11(,)c P ct t ,22(,)c Q ct t ,33(,)c R ct t 及44(,)cS ct t .那么一定有12341t t t t =.证明:设圆的方程22220x y Dx Ey F ++++=.圆与等轴双曲线交点(,)cct t,则代入得2222220.c Ec c t Dct F t t++++=整理得: 24322220.c t Dct Ft Ect c ++++=可知(1,2,3,4)i =是它的四个根,则有韦达定理1234t t t t ⋅⋅⋅=242(1)1c c-=.8. 把下面的平面曲线的普通方程化为参数方程.⑴32x y =; ⑵ ()0,212121>=+a a yx ; ⑶()0,0333>=-+a axy y x .解:⑴⎪⎩⎪⎨⎧==ty t x 32令θ4cos a x =,代入方程212121a yx =+得θθθ42212212121sin ,sin cos a y a a a y==-=∴参数方程为⎪⎩⎪⎨⎧==θθ44sin cos a y a x .⑶令,tx y =代入方程0333=-+axy y x得()031233=-+atx x t()[]03132=-+⇒at x t x当0=x 时,;0=y 当313t atx +=时,3213t at y +=3130t at x x +==⇒或故参数方程为⎪⎪⎩⎪⎪⎨⎧+=+=3231313t at y t at x .§2.2 曲面的方程1、 一动点移动时，与)0,0,4(A 及xoy 平面等距离，求该动点的轨迹方程。
解：设在给定的坐标系下，动点),,(z y x M ，所求的轨迹为C ，则z Cz y x M =⇔∈),,(亦即z z y x =++-222)4(0)4(22=+-∴y x由于上述变形为同解变形，从而所求的轨迹方程为0)4(22=+-y x2、在空间，选取适当的坐标系，求下列点的轨迹方程：（1）到两定点距离之比为常数的点的轨迹； （2）到两定点的距离之和为常数的点的轨迹； （3）到两定点的距离之差为常数的点的轨迹；（4）到一定点和一定平面距离之比等于常数的点的轨迹。
解：（1）取二定点的连线为x 轴，二定点连接线段的中点作为坐标原点，且令两距离之比的常数为m ，二定点的距离为a 2，则二定点的坐标为)0,0,(),0,0,(a a -，设动点),,(z y x M ，所求的轨迹为C ，则222222)()(),,(z y a x m z y a x C z y x M +++=++-⇔∈亦即])[()(2222222z y a x m z y a x +++=++-经同解变形得：0)1()1(2))(1(2222222=-++-++-a m x m a z y x m 上式即为所要求的动点的轨迹方程。
（2）建立坐标系如（1），但设两定点的距离为c 2，距离之和常数为a 2。
设动点),,(z y x M ，要求的轨迹为C ， 则a z y c x z y c x Cz y x M 2)()(),,(222222=++++++-⇔∈亦即222222)(2)(z y c x a z y c x +++-=++-两边平方且整理后，得：)()(2222222222c a a z a y a x c a -=++- （1）222c a b c a -=∴>令从而（1）为22222222b a z a y a x b =++ 即：22222222b a z a y a x b =++由于上述过程为同解变形，所以（3）即为所求的轨迹方程。
（3）建立如（2）的坐标系，设动点),,(z y x M ，所求的轨迹为C ， 则a z y c x z y c x Cz y x M 2)()(),,(222222±=++++++-⇔∈类似于（2），上式经同解变形为：1222222=--cz b y a x其中 )(222a c ac b >-= （*）（*）即为所求的轨迹的方程。
（4）取定平面为xoy 面，并让定点在z 轴上，从而定点的坐标为),0,0(c ，再令距离之比为m 。
设动点),,(z y x M ，所求的轨迹为C ，则z m z y x C z y x M =++⇔∈222),,(将上述方程经同解化简为：02)1(22222=+--++c cz z m y x （*） （*）即为所要求的轨迹方程。
3. 求下列各球面的方程：（1）中心)3,1,2(-，半径为；6=R （2）中心在原点，且经过点)3,2,6(-； （3）一条直径的两端点是)3,1,4()5,32(--与 （4）通过原点与)4,0,0(),0,3,1(),0,0,4(- 解：（1）由本节例5 知，所求的球面方程为：36)3()1()2(222=-+++-z y x（2）由已知，球面半径73)2(6222=+-+=R所以类似上题，得球面方程为49222=++z y x（3）由已知，球面的球心坐标1235,1213,3242=-=-=+-==+=c b a ，球的半径21)35()31()24(21222=++++-=R ，所以球面方程为： 21)1()1()3(222=-+++-z y x（4）设所求的球面方程为：0222222=++++++l kz hy gx z y x 因该球面经过点)4,0,0(),0,3,1(),0,0,4(),0,0,0(-，所以⎪⎪⎩⎪⎪⎨⎧=-=++=+=08160621008160k h g g l （1） 解（1）有⎪⎪⎩⎪⎪⎨⎧=-=-==2210k g h l ∴所求的球面方程为0424222=+--++z y x z y x§2.3 母线平行于坐标轴的柱面方程1、画出下列方程所表示的曲面的图形。
（1）369422=+y x 解：各题的图形如下： （1）369422=+y x§2.4 空间曲线的方程1、平面c x =与0222=-+x y x 的公共点组成怎样的轨迹。
解：上述二图形的公共点的坐标满足⎩⎨⎧=-=⇒⎩⎨⎧==-+cx c c y c x x y x )2(02222 从而：（Ⅰ）当20<<c 时，公共点的轨迹为：⎪⎩⎪⎨⎧=-=cx c c y )2( 及 ⎪⎩⎪⎨⎧=--=cx c c y )2( 即为两条平行轴的直线；（Ⅱ）当0=c 时，公共点的轨迹为：⎩⎨⎧==0x y 即为z 轴； （Ⅲ）当2=c 时，公共点的轨迹为：⎩⎨⎧==2x y 即过)0,0,2(且平行于z 轴的直线； （Ⅳ）当2>c 或0<c 时，两图形无公共点。
2、指出下列曲面与三个坐标面的交线分别是什么曲线？（1）6416222=++z y x ； （2）64164222=-+z y x ； （3）64164222=--z y x ； （4）z y x 10922=+ 解：（1）曲面与xoy 面的交线为：⎩⎨⎧==+⇒⎩⎨⎧==++0640641622222z y x z z y x 此曲线是圆心在原点，半径8=R 且处在xoy 面上的圆。
同理可求出曲面6416222=++z y x 与yoz 面)0(=x 及zox 面)0(=y 的交线分别为：⎩⎨⎧==+0641622x z y ， ⎩⎨⎧==+0641622y z x它们分别是中心在原点，长轴在y 轴上，且处在yoz 面上的椭圆，以及中心在原点，长轴在x 轴上，且处在zox 面上的椭圆；（2）由面64164222=-+z y x 与xoy 面)0(=z ，yoz 面)0(=x ，zox 面)0(=y 的交线分别为：⎩⎨⎧==-+064164222z z y x ,⎩⎨⎧==-+064164222x z y x ,⎩⎨⎧==-+064164222y z y x 亦即：⎩⎨⎧==+064422z y x ,⎩⎨⎧==-016422x z y ,⎩⎨⎧==-0641622y z x即为中心在原点，长轴在x 轴上，且处在xoy 面上的椭圆；中心在原点，实轴在y 轴，且处在yoz 面上的双曲线，以及中心在原点，实轴在x 轴，且处在zox 面上的双曲线。
（3）曲面64164222=--z y x 与xoy 面)0(=z ，yoz 面)0(=x ，zox 面)0(=y 的交线分别为：⎩⎨⎧==--064164222z z y x ,⎩⎨⎧==--064164222x z y x ,⎩⎨⎧==--064164222y z y x 亦即⎩⎨⎧==-064422z y x ,⎩⎨⎧==--06416422x z y ,⎩⎨⎧==-0641622y z x即为中心在原点，实轴在x 轴，且处在xoy 面上的双曲线；无轨迹以及中心在原点，实轴在x 轴上，且处在zox 面上的双曲线。