工程中的计算方法课件6 数值积分
数值积分-计算方法

(k=0,1,…,n) 作代换x=a+th带入上式,变为: 其中:
(k=0,1,…,n) (1-1) 这个积分是有理多项式积分,它与被积函数f(x)和区间[a,b]无关。
只要确定n就能计算出系数
。 于是得到称为Newton—Cotes公式的求积公式: (1-2) 其中
称为Newton—Cotes系数。如表1所示。 表1 Newton—Cotes系数
§3.1计算n阶求积公式
若有m次代数精度,对(k=0,1,…)应有
而。
§3.2 Gauss求积公式的基本原理
更一般形式: (2-1) 为权函数,设>0,且在[a,b]上可积,构造n阶求积公式:
(2-2) 积分点使得(2-2)式达到2n+1次代数精度,则积分点称为Gauss 点,(2-2)式称为Gauss求积公式。
§2Newton—Cotes公式 §2.1Newton—Cotes公式的推导
当§1.1插值求积公式的插值节点为等距节点时,就得到Newton— Cotes公式。
将区间[a,b]n等分,,n+1个节点为 xk=a+kh (k=0,1,…,n)
在节点上对f(x)的Lagrange插值多项式是:
用Pn(x)代替f(x)构造求积公式: 记
y=(1-1/2*(sin(x)).^2).^(1/2); 在Matlab工作窗口中调用函数:
y2=gauss2('gaussf',0,pi/2) 运行结果为:
y2= 1.3508
第5章 结论
通过以上变成和计算,得到所求的两组积分:
应用Newton—Cotes积分公式所求的结果分别是 y1=1.5078,y2 = 1.3506,而应用Gauss-Legendre方法所求得的结果分别是y1=1.5705 和 y2= 1.3508。单从结果上看,我们也能看出,Newton—Cotes积分公式 和Gauss-Legendre积分公式在精度上的确存在着差异(两者n的取值不 同)。而结果上的差异来源很明显是插值积分在近似替代时产生的,结 合第1章理论依据的内容,Newton-Cotes积分公式的精度最高可达n+1 次,Gauss-Legendre积分公式的精度为2n+1次,由此可知,当n相同 时, Gauss -Legendre积分公式比Newton—Cotes积分公式具有更高的 代数精度。而就本题而言Gauss -Legendre积分公式具有5次代数精度, Newton—Cotes积分公式也具有5次代数精度。因此二者所求积分只存在 微小的差异,结果都比较准确。
《数值积分方法》课件

数值积分的分类
按方法分类
可分为直接法和间接法。直接法如蒙特卡洛方法,间 接法如梯形法则、辛普森法则等。
按精确度分类
可分为低阶和高阶方法。低阶方法如梯形法则,高阶 方法如复合梯形法则、复合辛普森法则等。
按使用范围分类
可分为有限区间上的数值积分和无限区间上的数值积 分。
02
直接法
矩形法
总结词:简单直观
在金融建模中的应用
期权定价模型
数值积分方法可以用于求解期权定价模型,从而为金融衍生品定价提供依据。例如,二叉 树模型和蒙特卡洛模拟等。
利率衍生品定价
在利率衍生品定价中,数值积分方法可以用于求解利率期限结构模型,例如LIBOR市场模 型等。
风险管理
通过数值积分方法,可以对金融风险进行量化评估和管理。例如,计算VaR(风险价值) 和CVaR(条件风险价值)等指标,以评估投资组合的风险暴露程度。
自适应插值控制法
总结词
自适应插值控制法是一种通过插值技术来提 高数值积分精度的控制方法。
详细描述
在数值积分过程中,自适应插值控制法利用 插值技术对积分函数进行逼近,以提高数值 积分的精度。这种方法能够根据积分区间和 积分函数的特性,自动选择合适的插值方法 ,以获得更高的积分精度。同时,自适应插 值控制法还能够有效地处理复杂积分函数和
80%
算法设计与实现
数值积分方法的设计与实现是计 算数学的重要研究内容,推动了 科学计算的发展。
数值积分的概念
定义
数值积分是对函数在某个区间 上的定积分进行数值逼近的方 法。
思想
通过选取适当的积分点和权函 数,将定积分的计算转化为数 值逼近问题。
近似公式
常用的数值积分公式有梯形公 式、辛普森公式、复合梯形公 式、复合辛普森公式等。
力学中的计算方法(数值积分)
n
2
收敛速度与误差估计:
定义 若一个积分公式的误差满足 称该公式是 p 阶收敛的。 Tn O(h2 ) , Sn
lim
h 0
R[ f ] C p h
且C 0,则
~
~
O(h4 ) , Cn
~
O(h6 )
运算量基 本相同
例:计算
4 2 0 1 x
1
dx
其中 xk
k 8
a
b
b2 a 2 2
3
=
代入 f(x) =
x2 :
b
a
x 2dx b
a 3 3
b a 2
代数精度 = 1
例:对于两点公式
b a
f ( x )dx A0 f (a ) A1 f (b)
求A0、A1,使其具有尽可能高的代数精度。
解:分别令f(x) = 1、x时,公式准确成立 则 f(x) = 1: A0+A1=b-a f(x) = x : A0a+A1b=(b2-a2)/2 解得:A0=A1=(b-a)/2 代入 f(x) = x2 :
2
2 2 h h 6 6 上例中若要求 | I Tn | 10 ,则 | Rn [ f ] | | f (1) f (0) | 10 12 6
h 0.00244949 即:取 n = 409
通常采取将区间不断对分的方法,即取 n = 2k 可用来判断迭代 上例中2k 409 k = 9 时,T512 = 3.14159202 是否停止。 2 1 h 1 注意到区间再次对分时 R2n [ f ] [ f (b) f (a )] Rn [ f ]
哈尔滨工程大学工程算法课件06常微分方程的数值求解

欧拉法得: yn 1 yn hf xn , yn 因此,局部截断误差是 o h 2 。
19
2 改进Euler法
2.1方法构造
dy f x, y ,对其从 xk 到 xk 1 进 在微分方程初值问题 dx 行定积分得:
y xk 1 y xk
yk 1 是未知,待求的,未知量在 f x, y 中这是
一个方程,如f是非线性或超越函数,此方程是无法直接解出来(要 依靠迭代法才能解出)。这类格式称为隐式格式。
21
2.3 算例
y y x 例:用改进欧拉公式求解 , h 0.2 y 0 2 解: f x, y y x h yk 1 yk f xk , yk f xk 1 , yk 1 2 h h 1 2 y 2 x x y k 1 k 1 h k h k 1 1 2 2 可以从隐式格式中解出 yk 1 问题的精确解是 y x e x x 1
16
精确解为: y x 2 x
2
可以看出误差随着计算在积累。
17
1.4 Euler法的特点和误差
迭代格式 特点
1 单步方法:
yn 1 yn hf xn , yn n 0,1, 2,, N 1
2 显示格式: 3 局部截断误差为O h2
18
第六章 常微分方程数值解
§6.0 引言
§6.1 欧拉方法 §6.2 龙格-库塔方法
§6.3 单步法的收敛性和稳定性
§6.4 线性多步法
1
§6.0 引言
1 主要考虑如下的一阶常微分方程初值问题 的求解:
dy f x, y dx y x0 y0
第五章 数值积分.ppt

1
dx 1
0
1 xdx 1
0
2
A0
A1
1 2
.
1
所以公式为: 0
f
( x)dx
1
2
f
0
f
1 .
12
三 、牛顿—柯特斯(Newton-Cotes)公式
定义3 等距节点下的插值型求积公式称为牛顿—柯特斯公式。
把区间 a,b分成 n 等分,每份的长度为 h (b a) / n ,
解: e0 1, e 2.71828 , e0.5 1.64872
所以利用梯形公式:
I
T1
1 2
1
2.71828
1.85914
;
利用 Simpson 公式:
I
S1
1 6
1
41.64872
2.71828
1.71851 .
对比真值 I 1.71828,可见 S1 更精确一些.
C
(n i
)
C
(n) ni
;
这可以从柯特斯系数的积分表达式中直接得到.
17
应用中必须考虑数值稳定性,设函数值计算产生误差为:
f xi fi i ,并记 max i ,则在牛顿—柯特斯公式计算中:
n
n
C(n) i
f
xi
C(n) i
fi
,误差是:
i0
f
( x)dx
ba 90
7
f
(a) 32
f
(x1) 12
f
(x2 )
数值积分实用PPT课件PPT课件

微积分学中,积分计算是利用 Newton – Leibniz
公式:
来计算的。
例,某气体由温度 T1 加热到 T2 时所需热量 Q 可由下式表示:
Q
T1 T2
Cp
.mdT
Cp .m 该气体的摩尔定压热容
不知道该气体的 与CTp的.m函数关系式,而实验测得该气体的
系数据如下表所示。
C p .m
与 T 的关
T/℃
25 100 150 200 250 300 350 400 450 500 600 700 800
32 k0
f
( x ) 12
k1
k0
4
f
( xk1 ) 2
n1
n1
32 f ( x ) 14 f ( x )
k0
k3 4
k 1
k
第27页/共39页
龙贝格算法
第28页/共39页
数值方法中常利用一序列{ F1、F2、…、Fk、…} 去逼近精确值,然后在理论上给出序列F的误差估计。
新思路:
能否在某种理论(截断误差估计)基础上,通过简单方法,在序列
值,而这些值又是成倍增加的,所以计算工作量较大。
第37页/共39页
程序例子:P207
作 业:
将P207的程序改为求解积分
eps=0.000001 结果(0.1115718)
1x
0 4 x2 dx
第38页/共39页
感谢您的观看。
数值分析课件第八章-数值积分.ppt
g(u)
n (u n j)
n/2
(u j)
j0
2
jn / 2
是奇函数,故R[f]=0。证毕。
8.3 复合求积公式
1、复合梯形公式
将[a,b]n等分,h=(b-a)/n,在每个子区间[xk, xk+1] (k=0,1,…,n-1)上采用梯形公式,得
I
b
n1
f (x)dx
n
Ln (x) lk (x) f (xk )
k 0
(lk (x)
n j0
(x xj) ) (xk x j )
jk
则
b
b
n
b
a f (x)dx a Ln (x)dx f (xk ) a lk (x)dx
k 0
若记
Ak
b
a lk (x)dx
b n (x x j ) dx a j0 (xk x j )
0
32 90
C2( 4 )
1 4 2!2!
4
t(t 1)(t 3)(t 4)dt
0
12 90
C3( 4 )
1 4 3!
4
t(t 1)(t 2)(t 4)dt
0
32 90
C4( 4 )
1 4 4!
4
t(t 1)(t 2)(t 3)dt
0
7 90
求积公式为
4
I4 ( f ) (b a)
定义1. 若求积公式
b
f (x)dx
a
n
i f (xi )
i0
对所有次数不超过 m次的代数多项式 Pk (x)(k m)都准确成立 ,即
b
n
a Pk (x)dx i Pk (xi )
计算方法数值积分插值型积分PPT课件
bn1 an1 n1
1
其系数
x
0
矩阵
x02
x
n 0
1 …
x1 …
x
2 1
…
…
x
n 1
…
1
x
n
x
2 n
当
xk (k 0,1,…, n)
互异时,有唯一
x
n n
解 {Ak }
定理4.1 n+1个节点的求积公式
插值型求积
b f(x)dx a
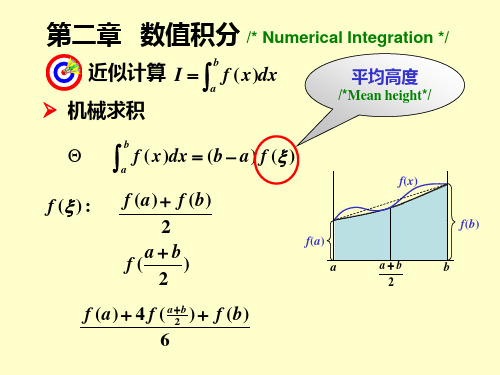
本段讲授机械求积方法.
由积分中值定理可知,对于连续函数f(x),在积分 区间[a, b]内存在一点ξ,使得 谜
b f(x)dx (b a)f(ξ), ξ [a, b] a
即所求的曲边梯形的面积恰好等于底为(b-a),高为 f ( ξ) 的矩形面积。但点ξ的具体位置是未知的, 因而f ( ξ )
计算方法 (Numerical Analysis)
第6次 数值积分-插值型积分-误差求积公式的收敛性与稳定性
第四章 数值积分
1. 数值积分引论 2. 机械求积方法 3. 以简单函数近似逼近被积函数方法-插值型
求积公式 4. 插值型求积公式的例子 5. 求积公式的收敛性和稳定性
数值积分引论
第四章 数值积分
代替原被积函数f(x),即
b f(x)dx b (x)dx
a
a
以此构造数值算法。
要求:
• 函数(x)
应该对f(x)有充分的逼近程度,并
且容易计算其积分。
• 通常,将(x) 选取为f(x)的插值多项式,
这样f(x)的积分就可以用其插值多项式的积分
计算方法课件第七章数值积分与数值微分.ppt
b f (4) ( )(x a)(x b)(x c)2 dx a
f (4) () b (x a)(x c)2 (x b)dx a
R[ f ] 1 f (4) ()(b a)(b a )4
180
2
1 f (4) ()(b a)5 (a b)
总存在求积系数 A0, A1,An,使求积公式至少有n次 代数精度。
事实上,只要令求积公式对于 f (x) 1, x, x2,, xn
都能准确成立即可得到下式:
b
n
dx
a
Ak
k 0
b
n
xdx
a
Ak xk
k 0
b xndx a
n
Ak xkn
k 0
则可通过给定的n+1个节点得到上述含n+1 个未知数、n+1个方程的方程组。
分近似值
b
n
I f (x)dx a
Ak f (xk ) In
b
n
k 0
I f (x)dx a
Ak f (xk ) R[ f ] In R[ f ]
k 0
其中R[f]称为求积公式的余项。xk (k 0,1,2,n)称为求
积节点 。Ak (k 0,1,2,n)称为求积系数。Ak 仅与求 积节点 xk 的选取有关,而不依赖与被积函数f(x)
第七章 数值积分与数值微分
§7.0 §7.1
§7.2 §7.3 §7.4 §7.5
数值积分概述 Newton Cotes 公式
复化求积公式 Romberg求积法 Gauss型求积公式 数值微分
§7.0 数值积分概述
由积分学基本定理知
b
第五章数值积分方法优秀课件
将其用于积分的近似计算,取ξ=b, 得
---积分右矩形公式
复合右矩形公式 如在区间[a,b]内插入节点xj=a+jh(j=0,1,···,n), h=(b-a)/n 得到复合右矩形求积公式:
利用拉格朗日中值定理 f(x)f(a)f'(x)x (a)(x[a,b])
T(f)baf(a)f(b)
2
Tn
n1
Ik
k 0
n1 k 0
h 2
f
(xk
)
f (xk1)
Tn(f)h 2f(a)2k n 1差减小→控制
复合梯形公式(节点加密)
x 1/2
x 3/2
x k 1/2
x n1/2
…
…
x0
x1
x2 xk
2
5.1 插值型求积公式
梯形公式误差
广义积分中值定理 若f在[a, b]上连续,g在[a, b]上可积,且g(x)在[a, b]
上不变号,存在x, x∈[a, b],使
bf(x)g(x)dxf(x)
b
g(x)dx
利用这一定理
a
a
梯形与曲边梯形面积的对比:
正负决定
5.1 插值型求积公式 三点二次拉格朗日插值积分--辛卜生公式 y=f(x) L2(x)
xk+1 xn-1
xn
Tnkn10Ikkn10h2f(xk)f(xk1) Tn
n1 k 0
Ik
n1 k 0
h 2
f
(xk )
f
(xk1)
Tn(f)h 2f(a)2kn 1 1f(xk)f(b)
I k k f(x) L1(x)axbbf(xa)L b1x(x)aafx(b)bbf(a)h 4 bxaaf(b) h 4 f x fk x k fx k 1 2 /2 f x h 4 k 1 f/2 x k 1 /2 f f x k x 1 k 1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6 数值积分如果函数)(x f 在区间],[b a 上连续,且原函数为)(x F ,则可用牛顿―莱布尼兹公式:)()()(a F b F dx x f ba-=⎰计算定积分。
然而很多函数无法用牛顿―莱布尼兹公式求定积分。
一个简单被积函数,例如错误!未找到引用源。
dx cx bx a ⎰++2,其不定积分可能很复杂,见下面的MA TLAB 实例: >> syms a b c x>> int(sqrt(a+b*x+c*x*x),x)ans=1/4*(2*c*x+b)/c*(a+b*x+c*x^2)^(1/2)+1/2/c^(1/2)*log((1/2*b+c*x )/c^(1/2)+(a+b*x+c*x^2)^(1/2))*a-1/8/c^(3/2)*log((1/2*b+c*x)/c^(1/2)+(a+b*x+c*x^2)^(1/2))*b^2所以有必要研究简单、高效的计算定积分的方法(即数值积分方法)。
数值积分的基本思想是构造一个简单函数)(x P n 来近似代替被积分函数)(x f ,然后通过求⎰ba n dx x P )(得⎰ba dx x f )(的近似值。
6.1 插值型求积公式设⎰=ba dx x f I )(*,插值型求积公式就是构造插值多项式)(x P n ,使⎰=≈ban dx x P I I )(*。
构造以a ,b 为结点的线性插值多项式)()()(1b f ab ax a f b a b x x P --+--=,[])()()(21)()()(1b f a f a b dx b f a b a x a f b a b x dx x P T b a b a +-=⎥⎦⎤⎢⎣⎡--+--==⎰⎰称为梯形公式。
以a,2ba c +=,b为三个插值节点,构造二次插值多项式)())(())(()())(())(()())(())(()(2bfcbabcxaxcfbcacbxaxafbacabxcxxP----+----+----=,则可以推出)()()()(212bfcfafdxxPS baλλλ++===⎰,)(61))(())((abdxbacabxcxba-=----=⎰λ,)(64))(())((1abdxbcacbxaxba-=----=⎰λ,)(61))(())((2abdxcbabcxaxba-=----=⎰λ。
由此得公式:[])()(4)(6bfcfafabS++-=,称为辛卜生(Simpson)求积公式。
(a)梯形公式(b)辛卜生公式图6.1 梯形公式和辛卜生公式根据经典拉格朗日插值公式)()()(knkknxfxlxP∑==,代入求定积分则有)())(()()(knkba kknkba kxfdxxldxxfxlI∑⎰∑⎰====,引入记号dxxl ba kk)(⎰=λ,)(knkkxfI∑==λ,kλ为求积系数,kx为求积节点。
注意:(1)积分结果为函数值的一个代数和,(2)abdxxlnkba k-=∑⎰=0)(。
如果积分区间比较大,直接使用上述求积公式难以保证计算精度。
通常采取复化求积方法提高计算精度:(1)等分求积区间,比如取步长nabh-=,将],[ba分为n等份,分割点为kh a x k +=,n k ,,2,1,0 =;(2)在区间 ],[1+k k x x 上使用梯形公式或辛卜生公式求得k I ; (3)取和∑-==10n k k I I 作为整个区间上的积分值。
将梯型公式和辛卜生公式应用于各子区间[]1,+k k x x ()1,,0-=n k 上得到子区间的定积分,再将子区间的定积分加起来得到整个区间的定积分近似值,相关公式称为复化梯型公式和复化辛卜生公式。
相对于复化梯型公式,复化辛卜生公式是一种精度较高的求积公式。
对于复化梯型公式,令[])()(21++=k k k x f x f hI ,则∑-==10n k kn I T[])()(2110+-=+=∑k k n k x f x f h[])()()()()()()()(21122110n n n n x f x f x f x f x f x f x f x f h++++++++=--- ⎥⎦⎤⎢⎣⎡++=∑-=)()(2)(211b f x f a f h n k k将所有子区间],[1+k k x x 二等分,在每个子区间上使用梯形公式可得:∑-=+++⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡+++⎥⎦⎤⎢⎣⎡++=101112)()2(4)2()(4n k k k k k k k n x f x x f h x x f x f h T⎥⎦⎤⎢⎣⎡++++++++++++=---)()2()2()()()2()2()(4111110100n n n n n n x f x x f x x f x f x f x x f x x f x f h 2)2(2101nn k k k T x x f h ++=∑-=+图6.2 复合梯形公式例 取n = 8用复化梯形公式计算积分dx x I ⎰+=10311。
解:()0.83471872432852212832412812)0(21818≈⎥⎦⎤+⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎢⎣⎡⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⨯=f f f f f f f f f T 表6.1k x0 1/8 1/4 3/8 1/2 5/8 3/4 7/8 1 )(k x f 1 0.9981 0.9846 0.9499 0.8889 0.8038 0.7033 0.59880.56.2 变步长积分法使用复化求积公式须给出合适的步长,步长太大精度难保证,步长太小增加计算量,预先给出一个合适的步长是十分困难的。
利用递推公式避免已计算节点的重复计算,可使计算量大幅减少。
变步长积分法思想是将区间逐次对分,比较前后两次计算结果,若前后两次计算结果很接近,满足精度要求即停止,否则再次对分,直到达到精度要求为止。
设将],[b a 区间n 等分,每段子区间长度为h ,共有n+1个分割点(含两端点),按复化梯形公式计算n T ,需要计算n+1个f (x )的值。
n T 2的全部分割点中有n+1个是原有的分割点。
复化梯形公式得积分有递推关系:2)2(21012nn k k k n T x x f h T ++=∑-=+基于复化梯形公式的变步长积分的程序代码如下:例 计算错误!未找到引用源。
⎰1dx x。
解:根据梯形公式和复化梯形公式2/)]1()0([1f f T +=,∑-=++=15.02)(221n k k n n x f h T T ,于是有表6.26.3 求积公式的误差为分析求积公式的误差,先给出两个定理:定理1:(积分中值定理)设)(x f 在区间],[b a 上连续,)(x g 在],[b a 区间上可积且不变号,则在],[b a 区间上至少有一个ξ满足⎰⎰=babadx x g f dx x g x f )()()()(ξ。
定理2:(介值定理)对于连续函数)(x f 、自然数n 及该函数定义域内的i x ,n i 21,=,存在ξ使)()(1ξf nx f ni i=∑=。
连续函数有一个基本性质:假设],[b a 区间上的连续函数)(x f 的最小值为m ,最大值为M ,则对于任意θ,只要θ满足M m ≤≤θ的,就存在ξ使θξ=)(f 。
应用这个性质容易证明定理1和定理2。
应用4.2节插值多项式余项定理,用n 次拉格朗日多项式插值函数)(x f 的误差为)()!1()()(1)1(x n f x R n n +++=ωξ。
对于插值多项式次数n 为1的情况,插值误差等于))((2)()(b x a x f x R --''=ξ。
令积分真实值记为⎰=ba dx x f I )(*,dx b f a b a x a f b a b x T ba ⎰⎥⎦⎤⎢⎣⎡--+--=)()(,结合积分中值定理,可以推导出梯形公式的截断误差为:3*)(12)())((2)())((2))((a b f dx b x a x f dxb x a x x f T I b a ba -''-=--''=--''=-⎰⎰ξξξ 将],[b a 区间n 等分,取nab h -=,考虑复化梯形积分公式的总误差。
该总误差是n 个等分区间段上用梯形公式计算定积分的误差之和,即:12)()(12)()(1212)(23103103*ξξξξf a b h f n h f h h f T I n i i n i i n ''--=''-=''-=''-=-∑∑-=-=6.4 收敛加速梯形法简单,但精度低,收敛的速度慢。
如何进一步提高收敛速度?设*I 是精确积分值,根据复化梯形公式,借用前一节中的符号及公式推导,基于定积分的基本定义可以得到:⎰∑∑''-≈''-=''-=--=-=ban i i n i i n dxx f h hf h h f T I )(12)(1212)(2102103*ξξ同样对于n T 2有⎰''-≈-b a n dx x f h T I )(4822*,所以41*2*≈--n n T I T I 。
整理得:)(3122*n n n T T T I -≈-根据上面的公式,可得到两个结论:(1)只要相邻两次迭代结果n T 与n T 2相当接近,就可以保证n T 2的误差很小;(2)n T 2的误差大致等于)(312n n T T -,用此误差值作为n T 2的补偿,可期望)(3122n n n T T T -+的精度更高。
也可以这样考虑,将所有n T 看做构成一个函数T ,变量为其步长的平方,即2h 。
当h 趋近0时,)(2h T 接近*I ,即*)0(I T =,连接点),2n n T h (和),121++n n T h (得一直线,其方程为:1221221221++++--+--=n nn n n n n n T h h h x T h h h x y 延伸该直线与Y 轴相交(见下图),计算交点的y 坐标值T ~的表达式,并假设n T 对应的步长等于1+n T 对应的步长的两倍,则有:34~11221221221n n n n n n n n n n T T T h h h T h h h T -=--+--=+++++这实质上就是一种迭代的加速:基于最后两次迭代的结果进行外推,从而提高精度。
